A High-Precision Inverse Finite Element Method for Shape Sensing and Structural Health Monitoring
Abstract
:1. Introduction
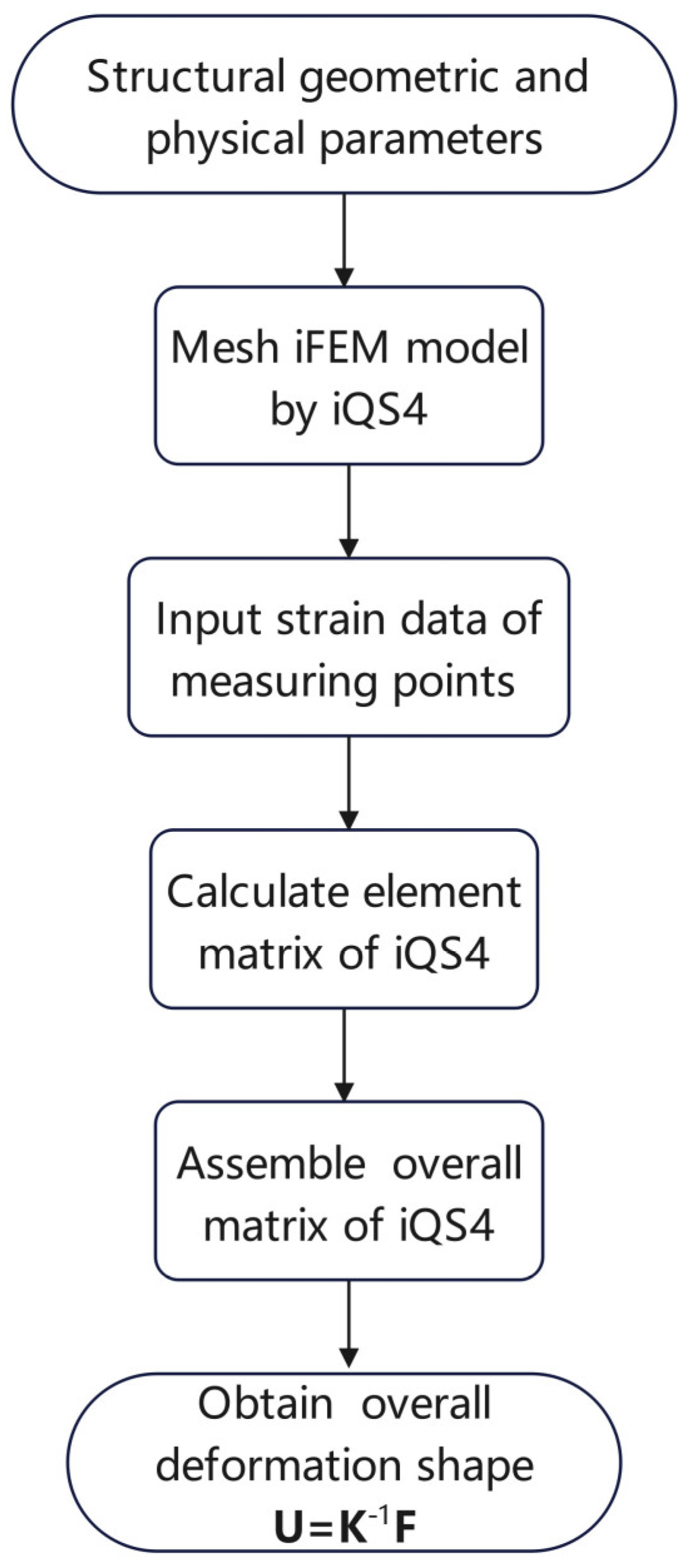
2. Methods of Calculation
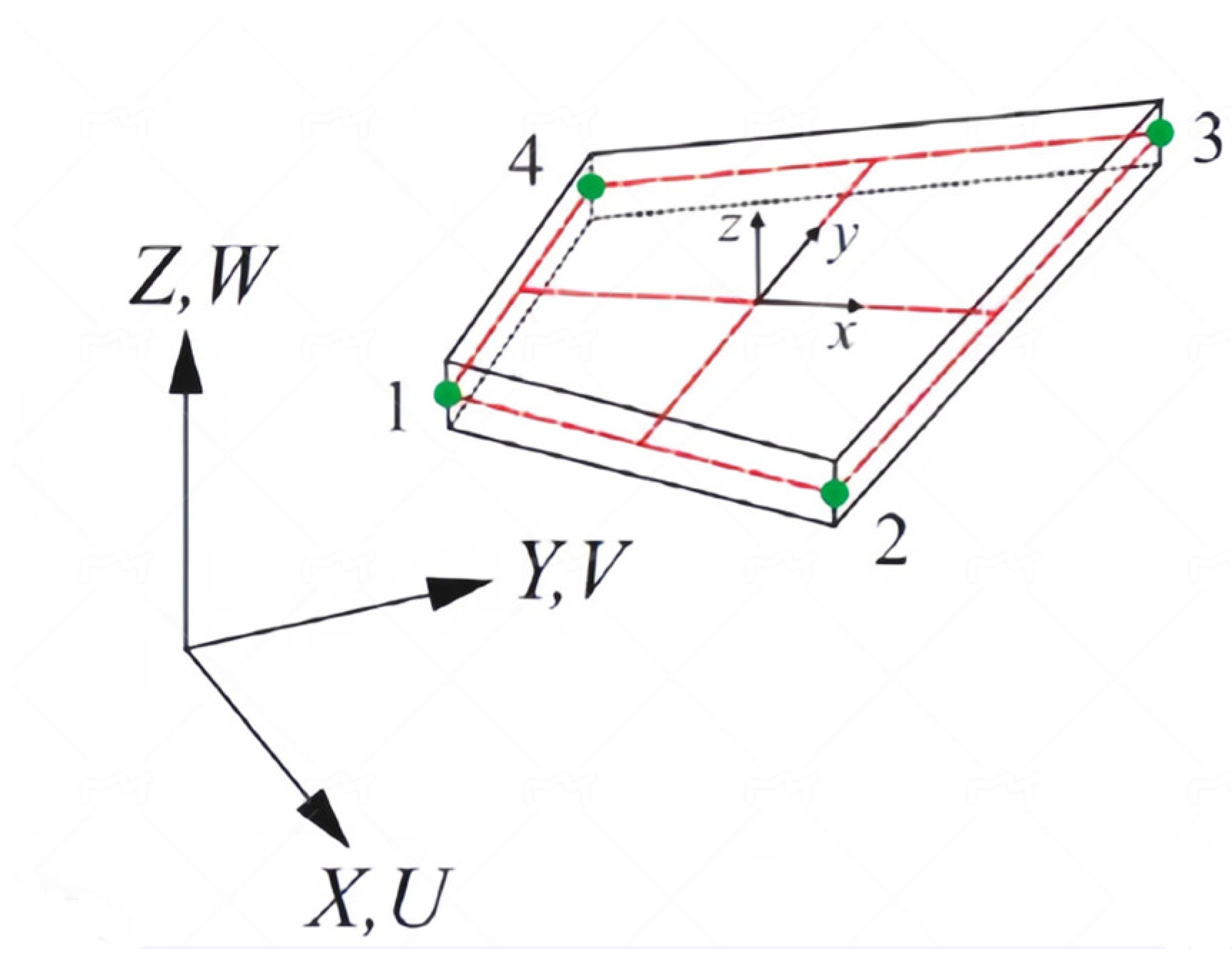
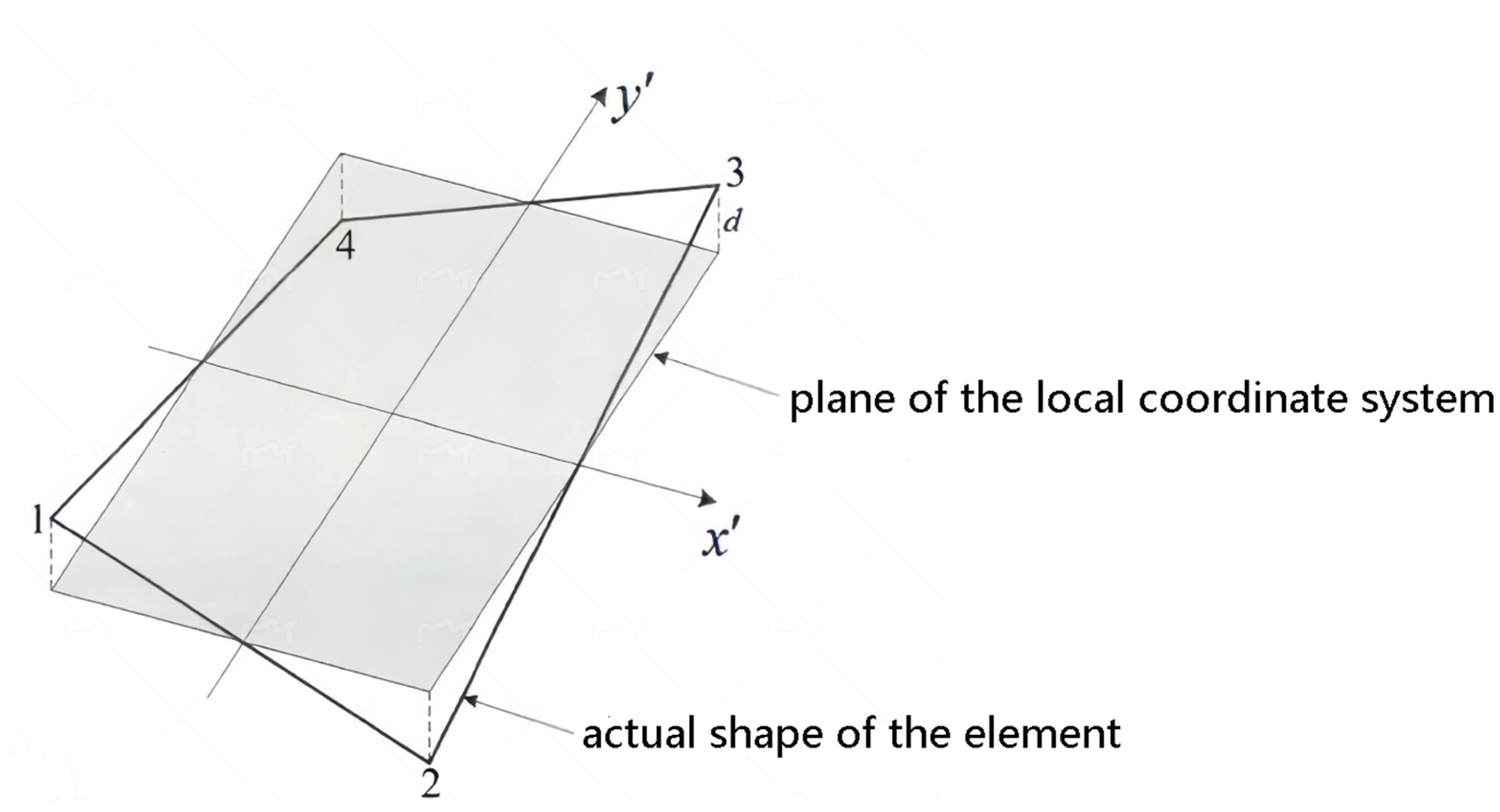
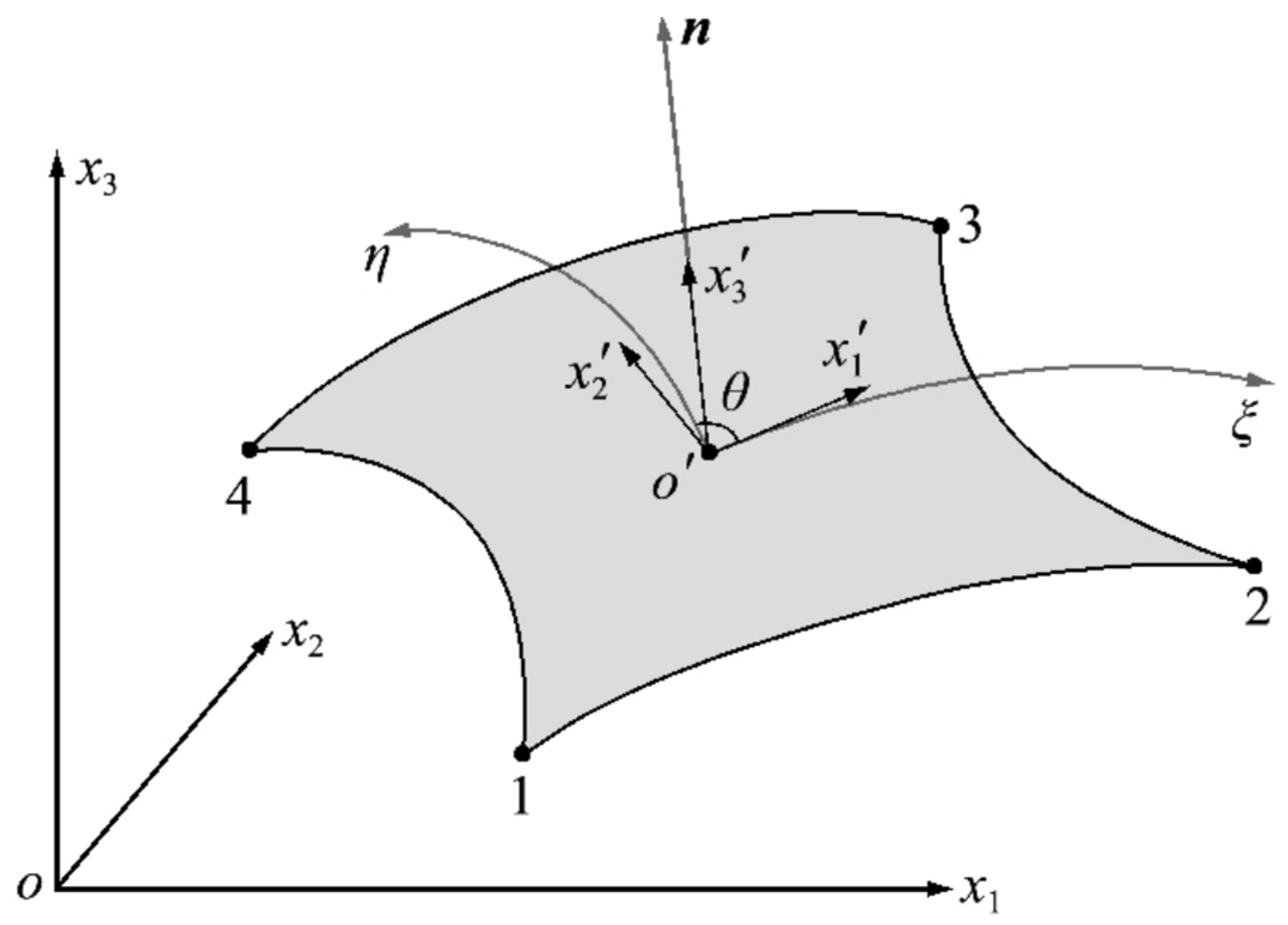
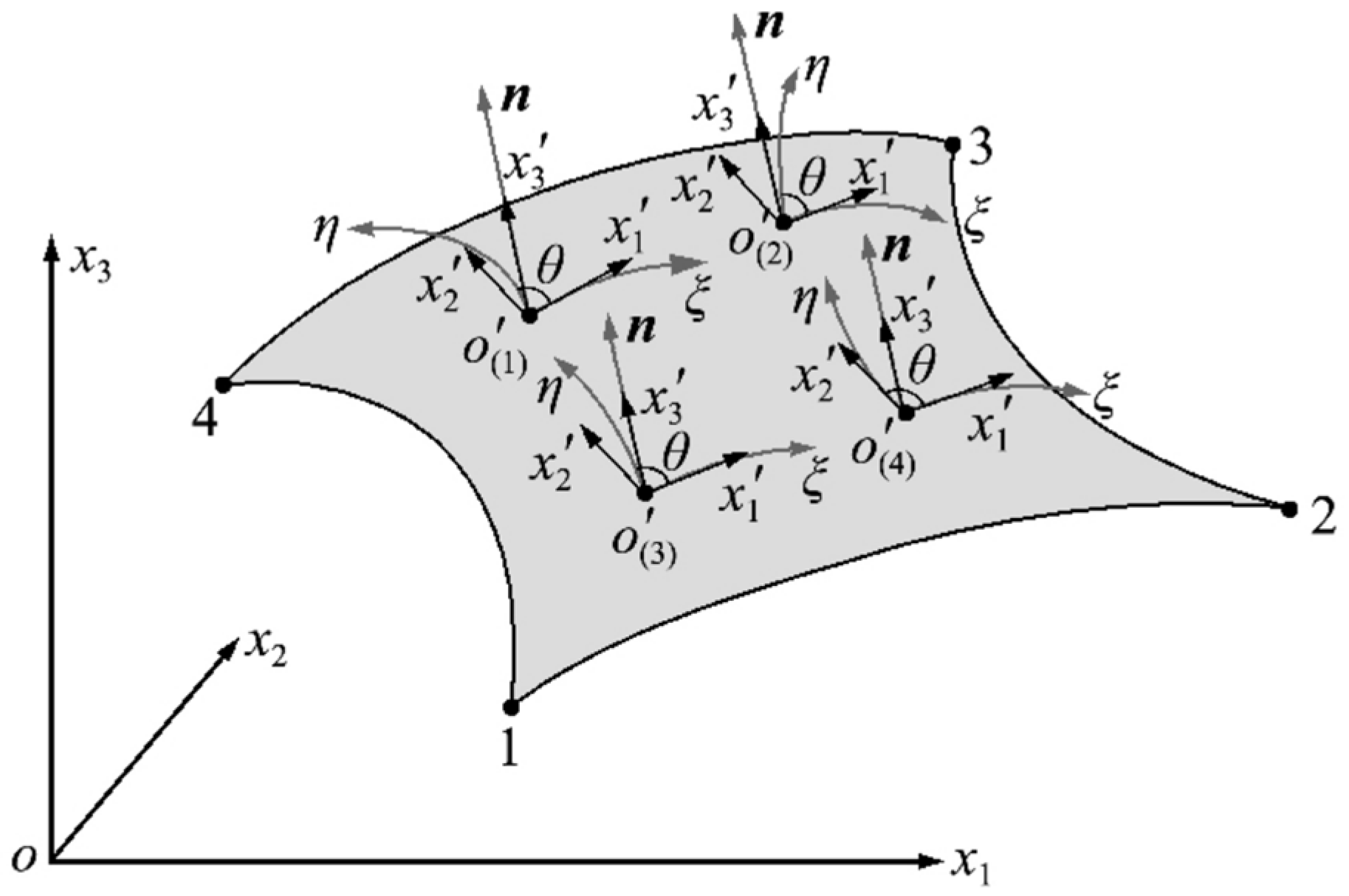
2.1. Methods for Establishing Local Coordinate System
2.2. Methods for Calculating Element Stiffness Integration
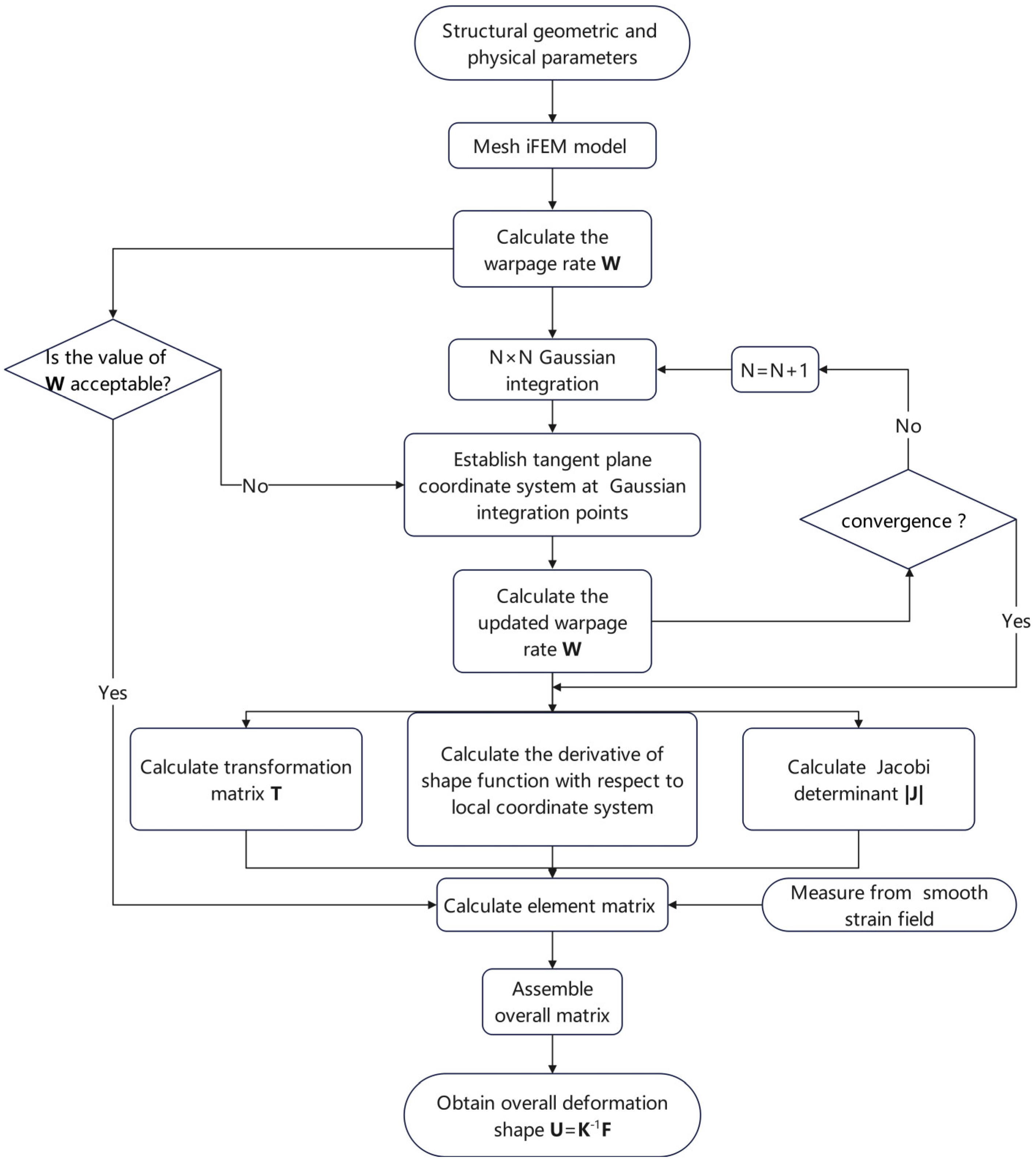
2.3. Algorithm Implementation
3. Numerical Examples
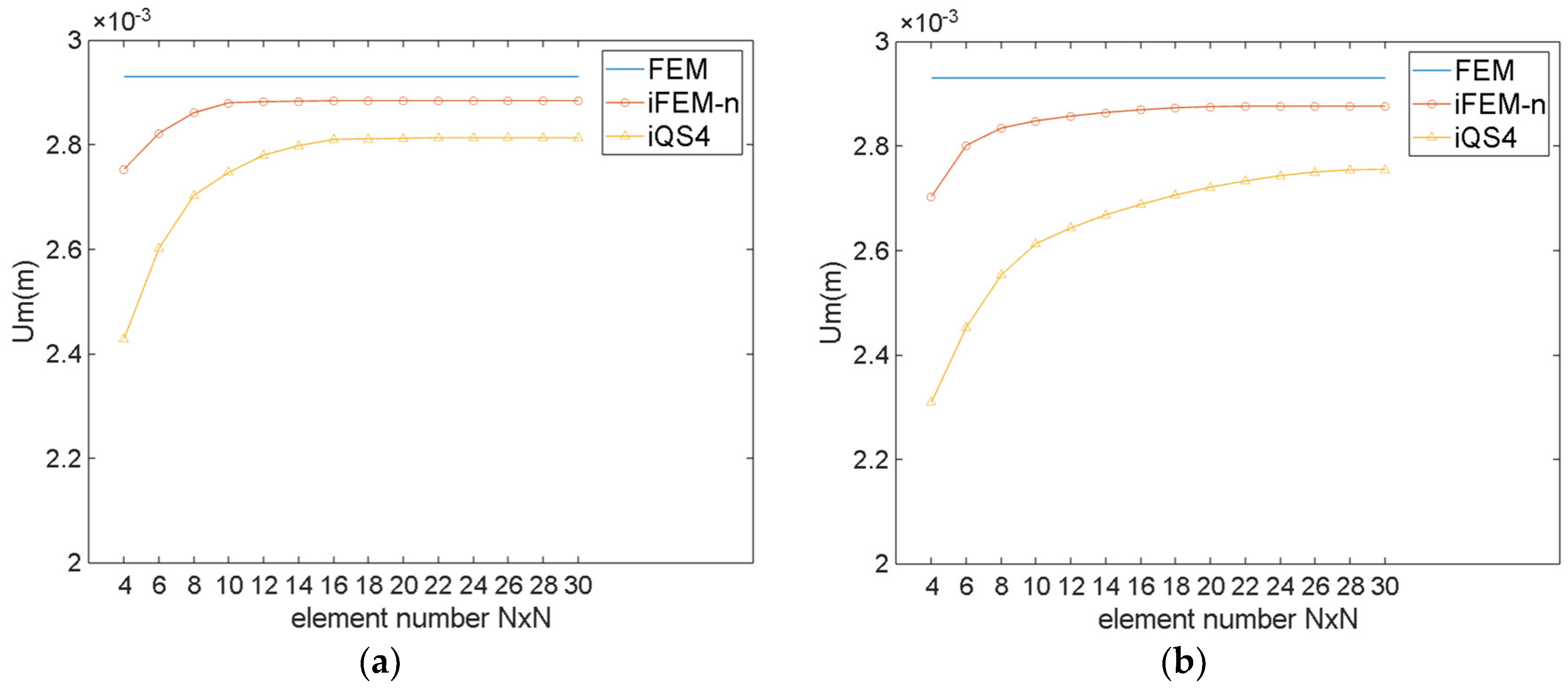
3.1. Twisted Plate
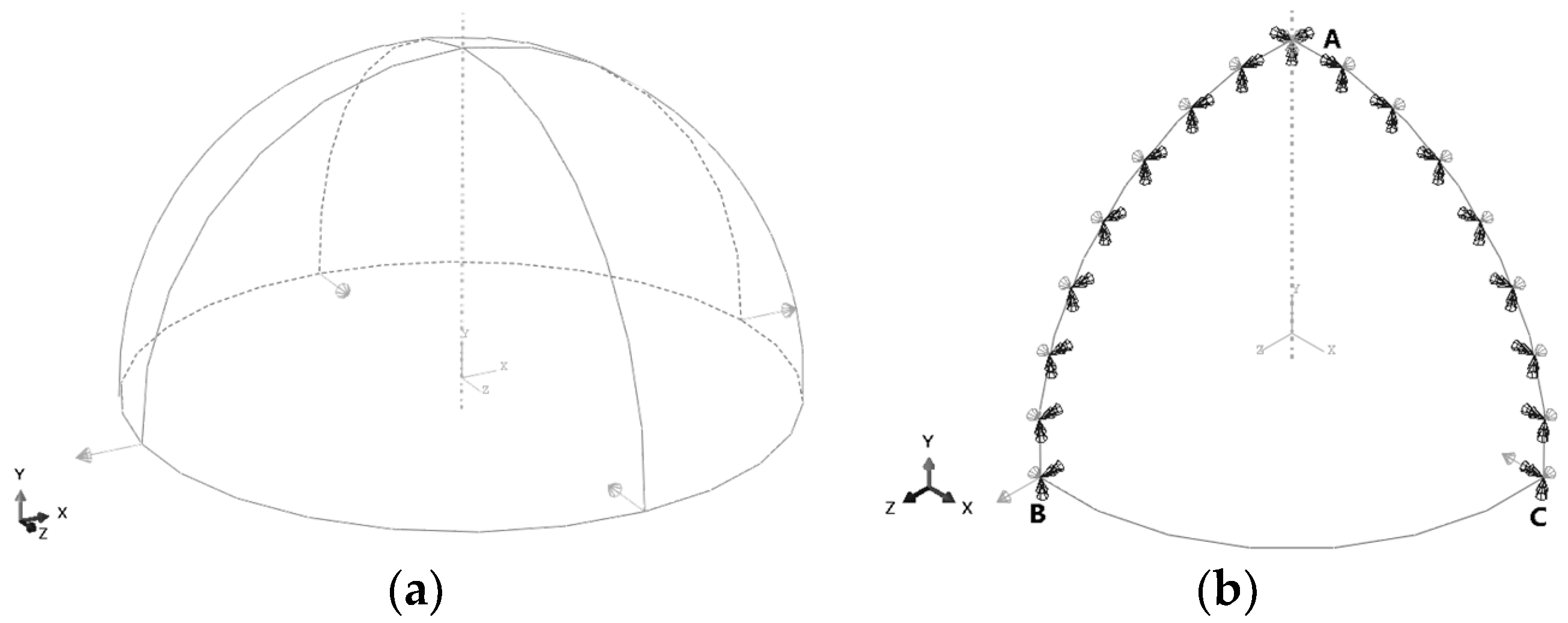
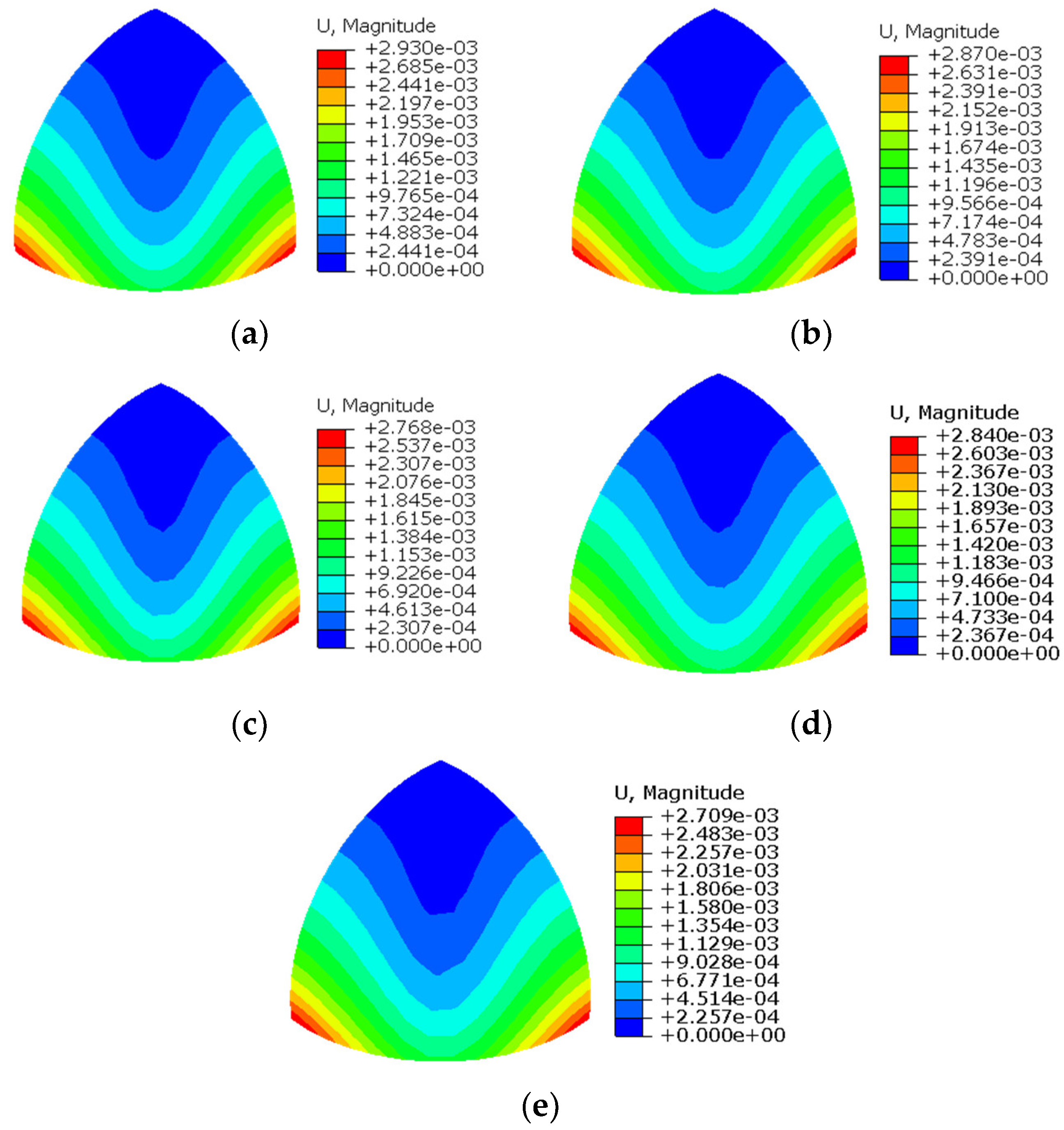
3.2. Hemispherical Shell
3.3. Summary of This Section
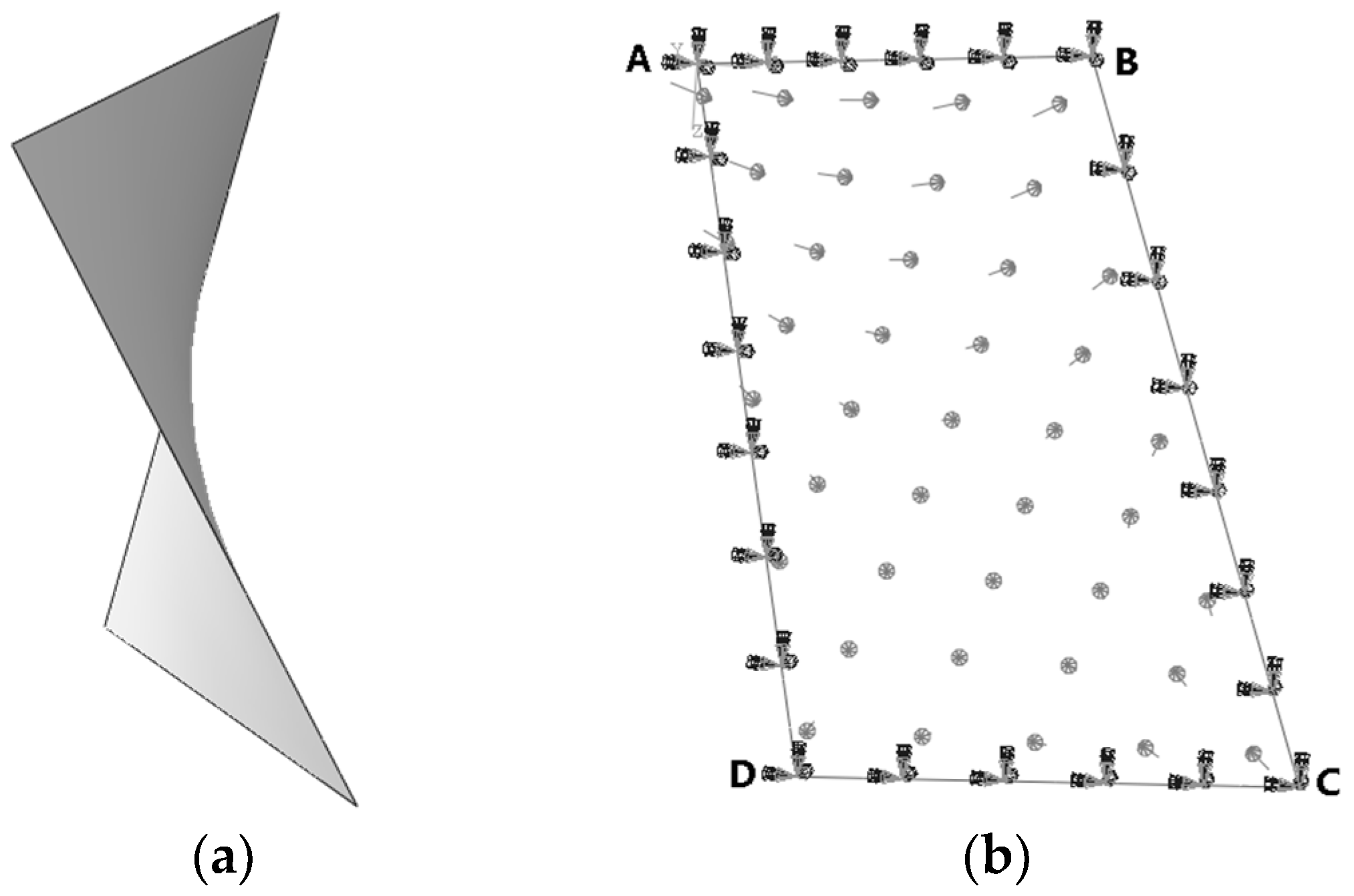
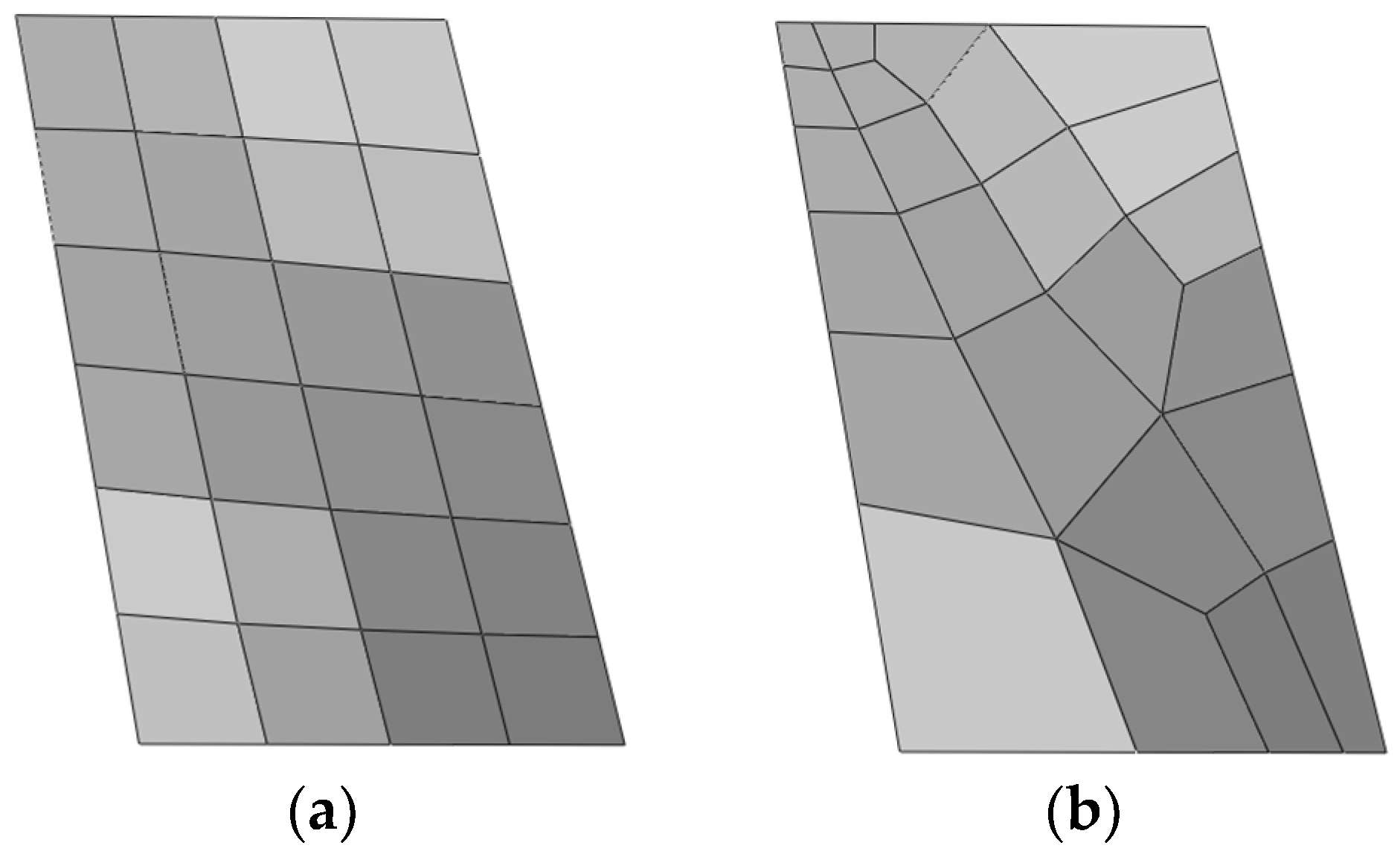
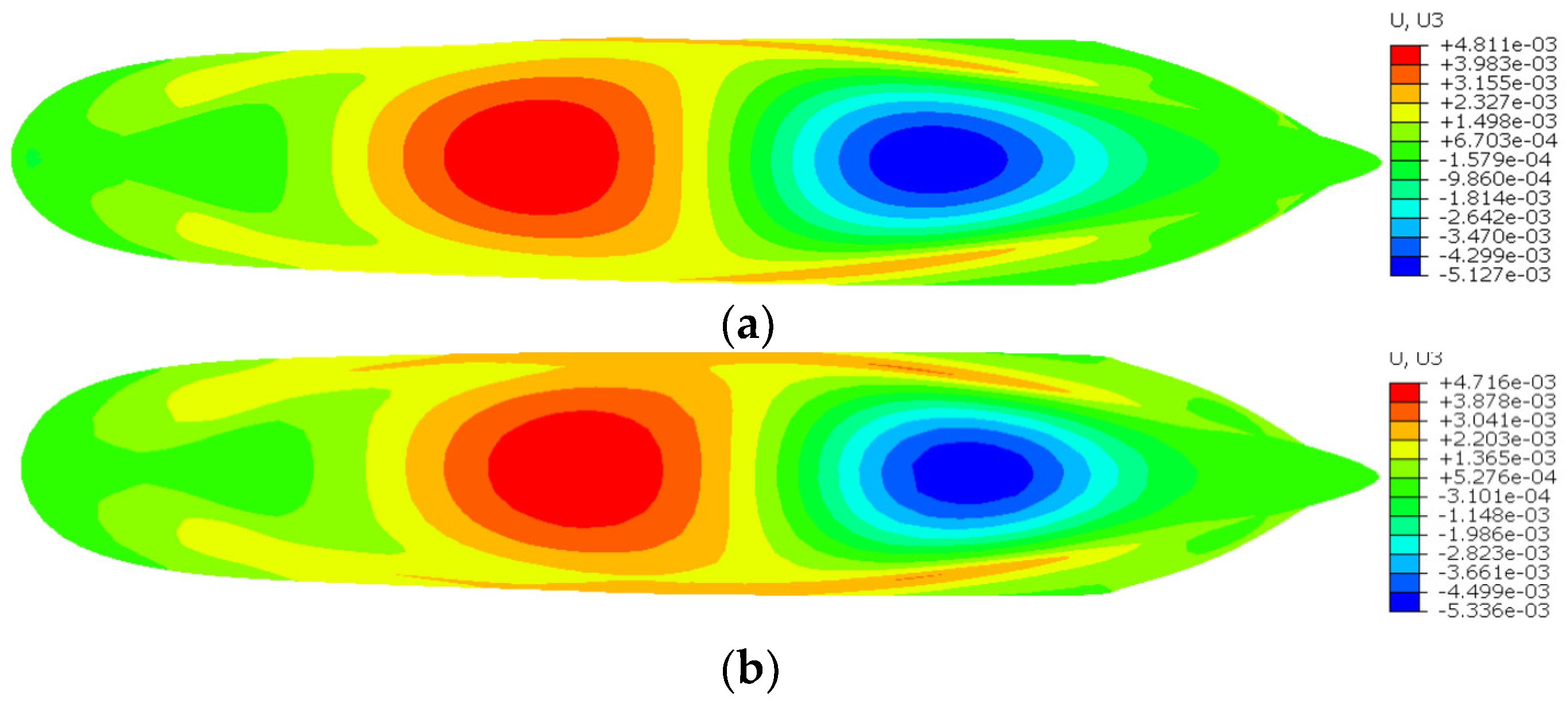
4. Practical Engineering Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Silva, J.P.; Chen, B.-Q.; Videiro, P.M. FPSO Hull Structures with Sandwich Plate System in Cargo Tanks. Appl. Sci. 2022, 12, 9628. [Google Scholar] [CrossRef]
- Li, G.; Xiong, Y.; Zhong, X.; Song, D.; Kang, Z.; Li, D.; Yang, F.; Wu, X. Characterizing Fishing Behaviors and Intensity of Vessels Based on BeiDou VMS Data: A Case Study of TACs Project for Acetes chinensis in the Yellow Sea. Sustainability 2022, 14, 7588. [Google Scholar] [CrossRef]
- Ortigosa, I.; Bardaji, R.; Carbonell, A.; Carrasco, O.; Castells-Sanabra, M.; Figuerola, R.; Hoareau, N.; Mateu, J.; Piera, J.; Puigdefabregas, J.; et al. Barcelona Coastal Monitoring with the “Patí a Vela”, a Traditional Sailboat Turned into an Oceanographic Platform. J. Mar. Sci. Eng. 2022, 10, 591. [Google Scholar] [CrossRef]
- Pilatis, A.N.; Pagonis, D.-N.; Serris, M.; Peppa, S.; Kaltsas, G. A Statistical Analysis of Ship Accidents (1990–2020) Focusing on Collision, Grounding, Hull Failure, and Resulting Hull Damage. J. Mar. Sci. Eng. 2024, 12, 122. [Google Scholar] [CrossRef]
- Katsoudas, A.S.; Silionis, N.E.; Anyfantis, K.N. Structural health monitoring for corrosion induced thickness loss in marine plates subjected to random loads. Ocean Eng. 2023, 273, 114037. [Google Scholar] [CrossRef]
- Paris, D.E.; Trevino, L. Integrated Intelligent Vehicle Management framework. In Proceedings of the 2008 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008; pp. 1–7. [Google Scholar]
- Kageyama, K.; Kimpara, I.; Suzuki, T. Smart marine structures: An approach tothe monitoring of ship structures with fiber-optic sensors. Smart Mater. Struct. 1998, 7, 472. [Google Scholar] [CrossRef]
- Torkildsen, H.E.; Grovlen, A.; Skaugen, A. Development and Applications of Full-Scale Ship Hull Health Monitoring Systems for the Royal Norwegian Navy; Norwegian Defence Research Establishment: Kjeller, Norwegian, 2005. [Google Scholar]
- Andersson, S.; Haller, K.; Hellbratt, S.E. Damage monitoring of ship FRP during exposure to explosion impacts. In Proceedings of the 18th International Conference on Composite Materials, Jeju Island, Republic of Korea, 21–26 August 2011. [Google Scholar]
- Sielski, R.A. Ship structural health monitoring research at the Office of Naval Research. JOM 2012, 64, 823–827. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, Y.; Zhang, L.; Wang, G.; Ju, Z.; Geng, X.; Jiang, M. Strain field reconstruction of high-speed train crossbeam based on FBG sensing network and load-strain linear superposition algorithm. IEEE Sens. J. 2021, 22, 3228–3235. [Google Scholar] [CrossRef]
- Kirkwood, H.J.; Zhang, S.Y.; Tremsin, A.S.; Korsunsky, A.M.; Baimpas, N.; Abbey, B. Neutron strain tomography using the radon transform. Mater. Today Proc. 2015, 2, S414–S423. [Google Scholar] [CrossRef]
- Li, J.; Yan, J.; Zhu, J.; Qing, X. K-BP neural network-based strain field inversion and load identification for CFRP. Measurement 2022, 187, 110227. [Google Scholar] [CrossRef]
- Bang, H.J.; Kim, H.I.; Lee, K.S. Measurement of strain and bending deflection of a wind turbine tower using arrayed FBG sensors. Int. J. Precis. Eng. Manuf. 2012, 13, 2121–2126. [Google Scholar] [CrossRef]
- Ko, W.L.; Richards, W.L.; Tran, V.T. Displacement Theories for In-Flight Deformed Shape Predictions of Aerospace Structures; (No. H-2652); NASA: Washington, DC, USA, 2007. [Google Scholar]
- Gherlone, M.; Cerracchio, P.; Mattone, M. Shape sensing methods: Review and experimental comparison on a wing-shaped plate. Prog. Aerosp. Sci. 2018, 99, 14–26. [Google Scholar] [CrossRef]
- Tessler, A.; Spangler, J.L. A Least-Squares Variational Method for Full-Field Reconstruction of Elastic Deformations in Shear-Deformable Plates and Shells. Comput. Methods Appl. Mech. Eng. 2005, 194, 327–339. [Google Scholar] [CrossRef]
- Tessler, A.; Spangler, J.L. A Variational Principle for Reconstruction of Elastic Deformations in Shear Deformable Plates and Shells; NASA/TM-2003-212445; NASA: Washington, DC, USA, 2003. [Google Scholar]
- Tessler, A.; Spangler, J.L. Inverse FEM for full-field reconstruction of elastic deformations in shear deformable plates and shells. In Proceedings of the 2nd European Workshop on Structural Health Monitoring, Munich, Germany, 7–9 July 2004. [Google Scholar]
- Quach, C.C.; Vazquez, S.L.; Tessler, A.; Moore, J.P.; Cooper, E.G.; Spangler, J.L. Structural anomaly detection using fiber optic sensors and inverse finite element method. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005. [Google Scholar]
- Kefal, A.; Oterkus, E.; Tessler, A.; Spangler, J.L. A quadrilateral inverse-shell element with drilling degrees of freedom for shape sensing and structural health monitoring. Eng. Sci. Technol. Int. J. 2016, 19, 1299–1313. [Google Scholar] [CrossRef]
- Kefal, A. An efficient curved inverse-shell element for shape sensing and structural health monitoring of cylindrical marine structures. Ocean. Eng. 2019, 188, 106262. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Structural health monitoring of marine structures by using inverse finite element method. In Analysis and Design of Marine Structures V; CRC Press: Boca Raton, FL, USA, 2015; pp. 341–349. [Google Scholar]
- Kefal, A.; Oterkus, E. Isogeometric iFEM analysis of thin shell structures. Sensors 2020, 20, 2685. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Displacement and stress monitoring of a chemical tanker based on inverse finite element method. Ocean. Eng. 2016, 112, 33–46. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Displacement and stress monitoring of a Panamax containership using inverse finite element method. Ocean. Eng. 2016, 119, 16–29. [Google Scholar] [CrossRef]
- Li, M.Y.; Kefal, A.; Cerik, B.; Oterkus, E. Structural Health Monitoring of Submarine Pressure Hull Using Inverse Finite Element Method. In Proceedings of the 7th International Conference on Marine Structures Marstruct, Dubrovnik, Croatia, 6–8 May 2019. [Google Scholar]
- Li, M.; Oterkus, E.; Oterkus, S. A Two-Dimensional Eight-Node Quadrilateral Inverse Element for Shape Sensing and Structural Health Monitoring. Sensors 2023, 23, 9809. [Google Scholar] [CrossRef]
- Li, M.; Dirik, Y.; Oterkus, E.; Oterkus, S. Shape sensing of NREL 5 MW offshore wind turbine blade using iFEMology. Ocean. Eng. 2023, 273, 114036. [Google Scholar] [CrossRef]
- Zhu, Q.; Wu, G.; Zeng, J.; Jiang, Z.; Yue, Y.; Xiang, C.; Zhan, J.; Zhao, B. Enhanced Strain Field Reconstruction in Ship Stiffened Panels Using Optical Fiber Sensors and the Strain Function-Inverse Finite Element Method. Appl. Sci. 2024, 14, 370. [Google Scholar] [CrossRef]
- Ganjdoust, F.; Kefal, A.; Tessler, A. A Novel Delamination Damage Detection Strategy Based on Inverse Finite Element Method for Structural Health Monitoring of Composite Structures. Mech. Syst. Signal Process. 2023, 192, 110202. [Google Scholar] [CrossRef]
- Esposito, M.; Roy, R.; Surace, C.; Gherlone, M. Hybrid Shell-Beam Inverse Finite Element Method for the Shape Sensing of Stiffened Thin-Walled Structures: Formulation and Experimental Validation on a Composite Wing-Shaped Panel. Sensors 2023, 23, 5962. [Google Scholar] [CrossRef] [PubMed]
- Roy, R.; Tessler, A.; Surace, C.; Gherlone, M. Efficient shape sensing of plate structures using the inverse Finite Element Method aided by strain pre-extrapolation. Thin-Walled Struct. 2022, 180, 109798. [Google Scholar] [CrossRef]
- Kefal, A.; Diyaroglu, C.; Yildiz, M.; Oterkus, E. Coupling of peridynamics and inverse finite element method for shape sensing and crack propagation monitoring of plate structures. Comput. Methods Appl. Mech. Eng. 2022, 391, 114520. [Google Scholar] [CrossRef]
- Zhu, H.; Du, Z.; Tang, Y. Numerical study on the displacement reconstruction of subsea pipelines using the improved inverse finite element method. Ocean. Eng. 2022, 248, 110763. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.A.; Ali, H.Q.; Yildiz, M.; Kefal, A. Experimental and numerical investigation on large deformation reconstruction of thin laminated composite structures using inverse finite element method. Thin-Walled Struct. 2022, 178, 109485. [Google Scholar] [CrossRef]
- Zhao, F.; Kefal, A.; Bao, H. Nonlinear deformation monitoring of elastic beams based on isogeometric iFEM approach. Int. J. Non-Linear Mech. 2022, 147, 104229. [Google Scholar] [CrossRef]
- Joe, F.T. Handbook of Grid Generation; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Prentice Hall: Upper Sudbury, NJ, USA, 1996. [Google Scholar]
- Burke, W.L. Applied Differential Geometry; The American Mathematical Monthly; Cambridge University Press: Cambridge, UK, 1985; Volume 95, p. 010. [Google Scholar]
- Gao, X.W.; Davies, T.G. Boundary Element Programming in Mechanics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Gao, X.W.; Liu, Y.F.; Lv, J. A New Method Applied to the Quadrilateral Membrane Element Witll Vertex Rigid Rotational Freedom. Math. Probl. Eng. 2016, 2016, 1045438. [Google Scholar] [CrossRef]
- Lachat, J.C.A. Further Development of the Boundary Integral Technique for Elastostatics. Ph.D. Thesis, University of Southampton, Southampton, UK, 1975. [Google Scholar]
- Becker, A.A. The Boundary Element Method in Engineering: A Complete Course; McGraw-Hill Companies: London, UK, 1992. [Google Scholar]


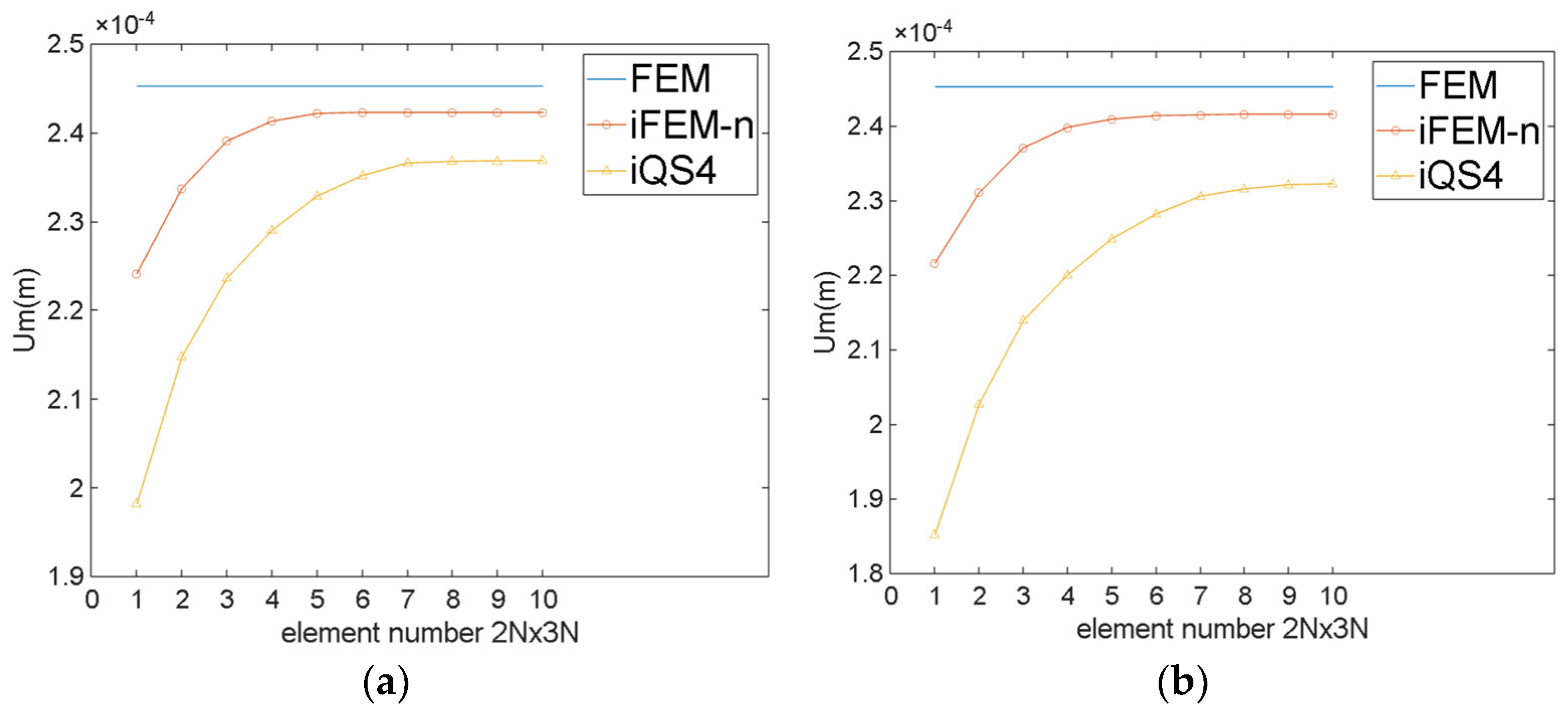

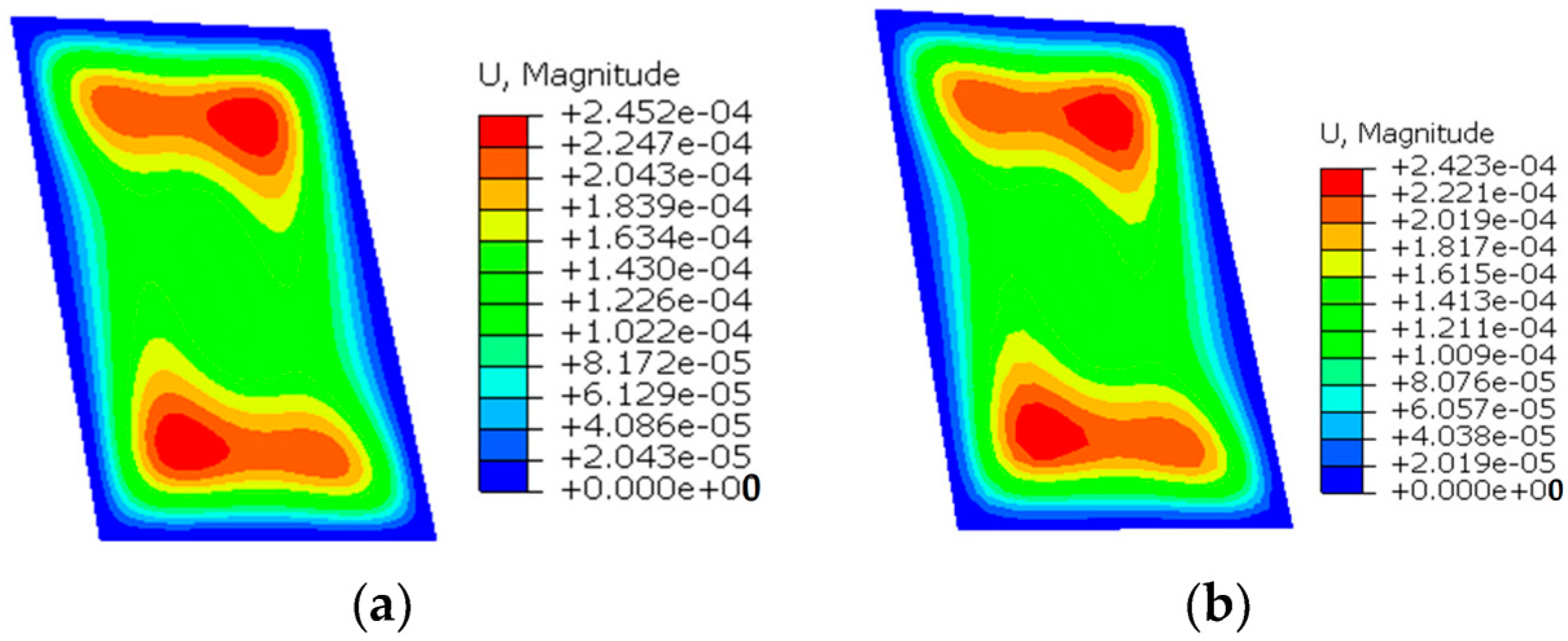






| Element Number 2N × 3N | Maximum Um(m) | ||||
|---|---|---|---|---|---|
| FEM | Regular Meshing | Irregular Meshing | |||
| iFEM-n | iQS4 | iFEM-n | iQS4 | ||
| 1 | 2.452 × 10−4 | 2.241 × 10−4 | 1.981 × 10−4 | 2.216 × 10−4 | 1.851 × 10−4 |
| 2 | 2.338 × 10−4 | 2.147 × 10−4 | 2.311 × 10−4 | 2.027 × 10−4 | |
| 3 | 2.391 × 10−4 | 2.236 × 10−4 | 2.370 × 10−4 | 2.139 × 10−4 | |
| 4 | 2.413 × 10−4 | 2.290 × 10−4 | 2.398 × 10−4 | 2.200 × 10−4 | |
| 5 | 2.420 × 10−4 | 2.342 × 10−4 | 2.409 × 10−4 | 2.248 × 10−4 | |
| 6 | 2.421 × 10−4 | 2.351 × 10−4 | 2.414 × 10−4 | 2.282 × 10−4 | |
| 7 | 2.422 × 10−4 | 2.355 × 10−4 | 2.414 × 10−4 | 2.305 × 10−4 | |
| 8 | 2.422 × 10−4 | 2.357 × 10−4 | 2.415 × 10−4 | 2.316 × 10−4 | |
| 9 | 2.422 × 10−4 | 2.358 × 10−4 | 2.415 × 10−4 | 2.321 × 10−4 | |
| 10 | 2.422 × 10−4 | 2.358 × 10−4 | 2.415 × 10−4 | 2.322 × 10−4 | |
| Element Number 2N × 3N | Maximum Dp (%) | |||
|---|---|---|---|---|
| Regular Meshing | Irregular Meshing | |||
| iFEM-n | iQS4 | iFEM-n | iQS4 | |
| 1 | 8.62 | 19.19 | 9.64 | 24.50 |
| 2 | 4.67 | 12.43 | 5.77 | 17.32 |
| 3 | 2.50 | 8.82 | 3.32 | 12.78 |
| 4 | 1.60 | 6.61 | 2.20 | 10.28 |
| 5 | 1.21 | 5.04 | 1.76 | 8.30 |
| 6 | 1.20 | 4.09 | 1.54 | 6.94 |
| 7 | 1.20 | 3.52 | 1.53 | 5.96 |
| 8 | 1.20 | 3.44 | 1.52 | 5.56 |
| 9 | 1.20 | 3.42 | 1.52 | 5.33 |
| 10 | 1.20 | 3.42 | 1.52 | 5.29 |
| General Particular | Value | Unit |
|---|---|---|
| Length between perpendiculars | 217.2 | m |
| Breadth | 39.6 | m |
| Depth | 24.9 | m |
| Design draught | 14.9 | m |
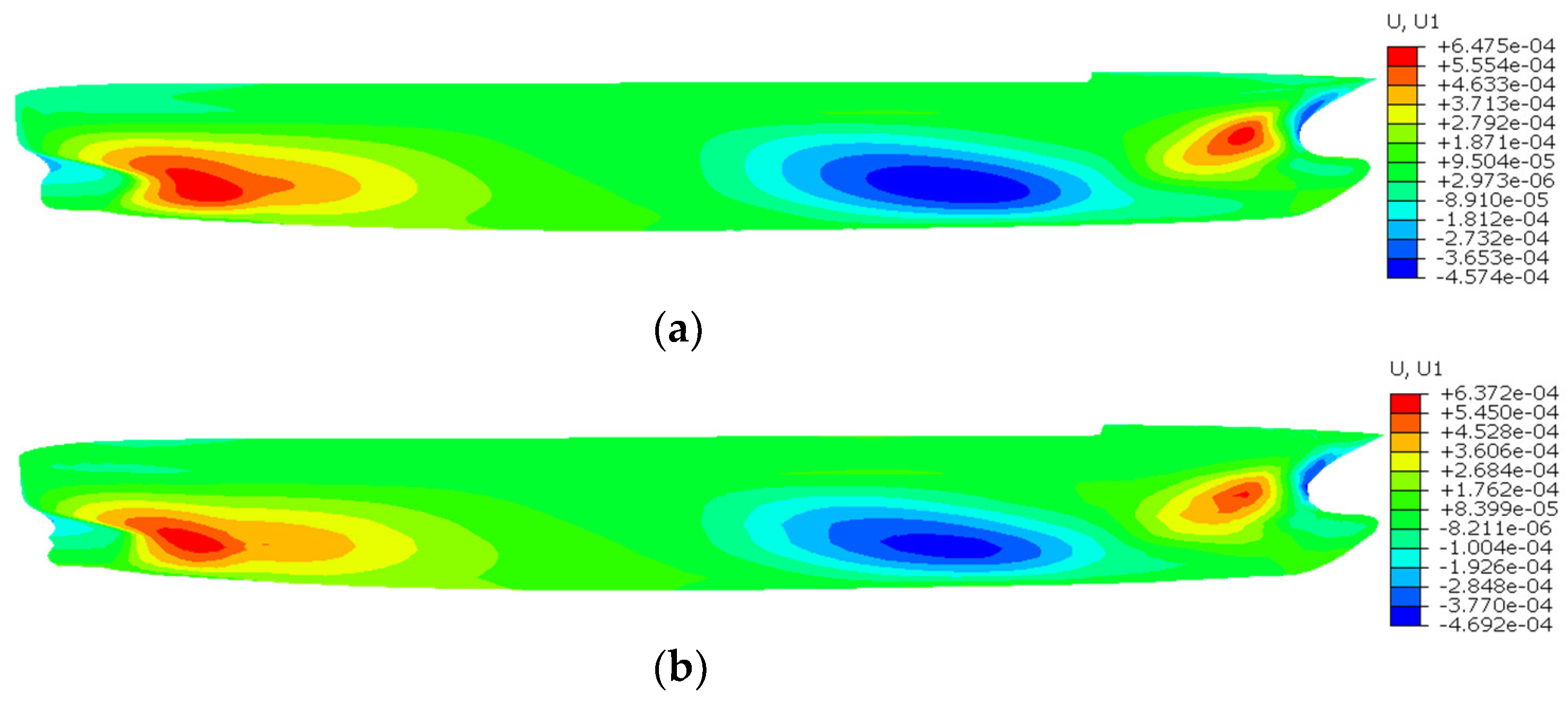
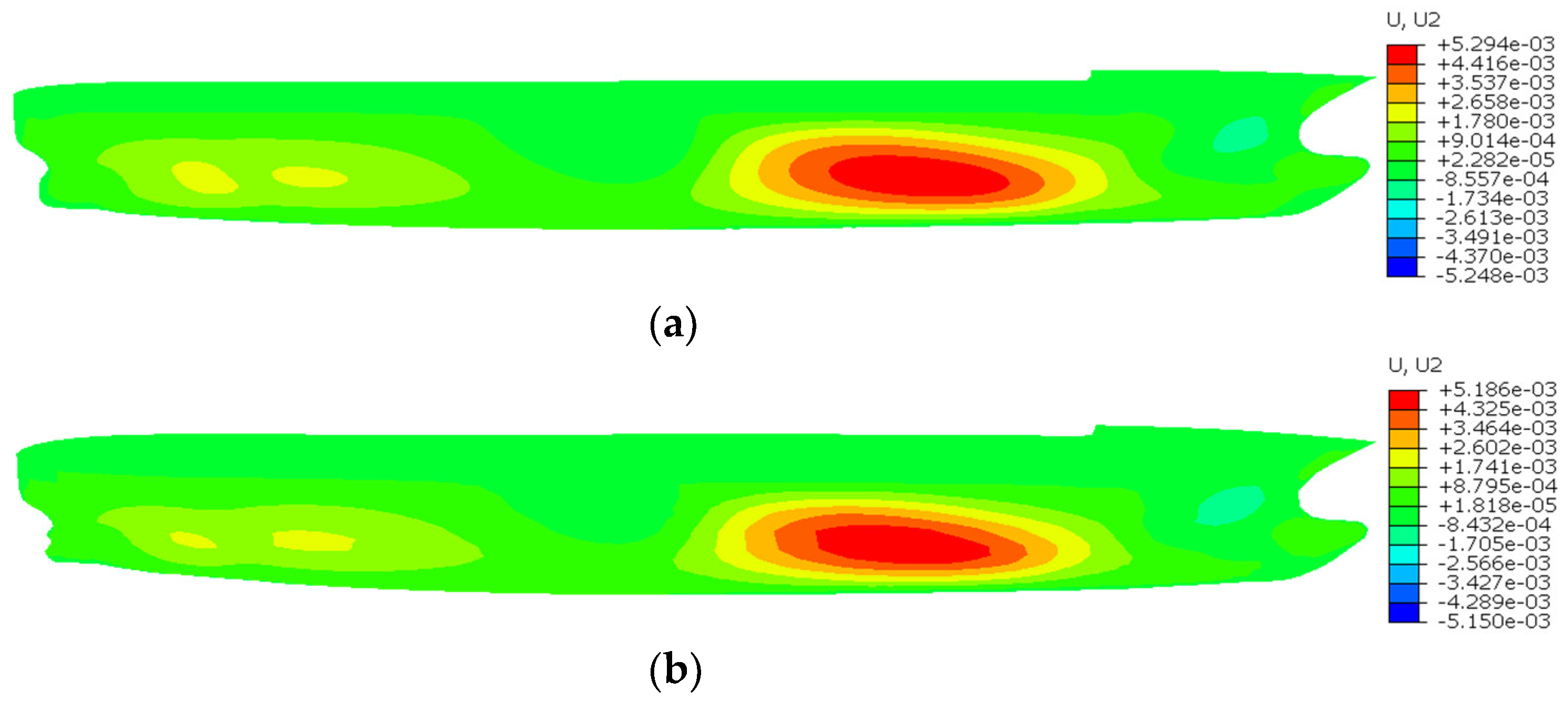
| Displacement Component | Displacement (m) | Difference (%) | |
|---|---|---|---|
| FEM | iFEM-H | ||
| U1 | 6.475 × 10−4 | 6.372 × 10−4 | 1.59 |
| U2 | 5.294 × 10−3 | 5.186 × 10−3 | 2.38 |
| U3 | 4.811 × 10−3 | 4.716 × 10−3 | 1.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, H.; Tang, J. A High-Precision Inverse Finite Element Method for Shape Sensing and Structural Health Monitoring. Sensors 2024, 24, 6338. https://doi.org/10.3390/s24196338
Yan H, Tang J. A High-Precision Inverse Finite Element Method for Shape Sensing and Structural Health Monitoring. Sensors. 2024; 24(19):6338. https://doi.org/10.3390/s24196338
Chicago/Turabian StyleYan, Hongsheng, and Jiangpin Tang. 2024. "A High-Precision Inverse Finite Element Method for Shape Sensing and Structural Health Monitoring" Sensors 24, no. 19: 6338. https://doi.org/10.3390/s24196338






