Modeling Development of a Diamagnetically Stabilized Magnetically Levitated Gravimeter
Abstract
1. Introduction
2. Methodology
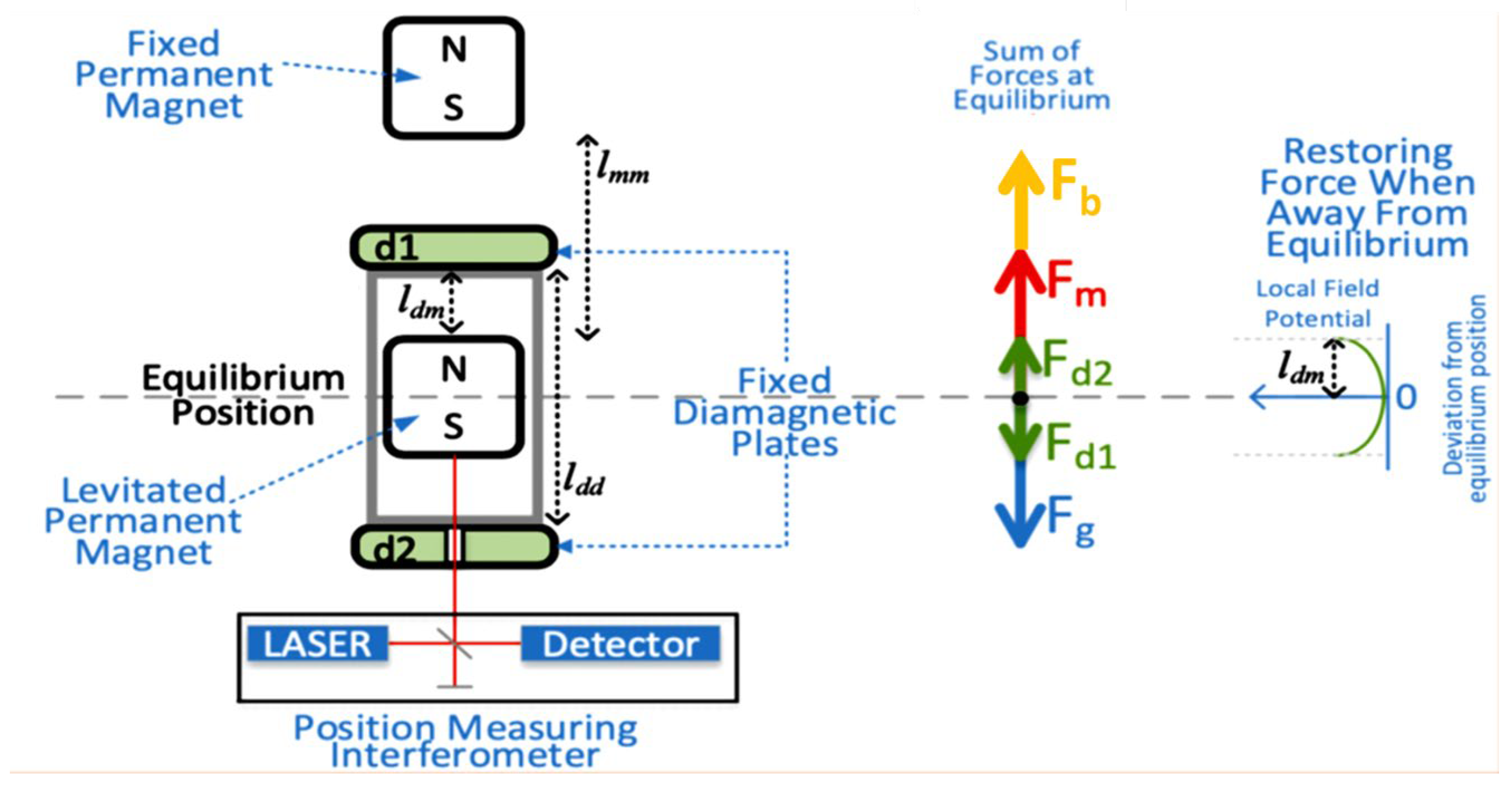
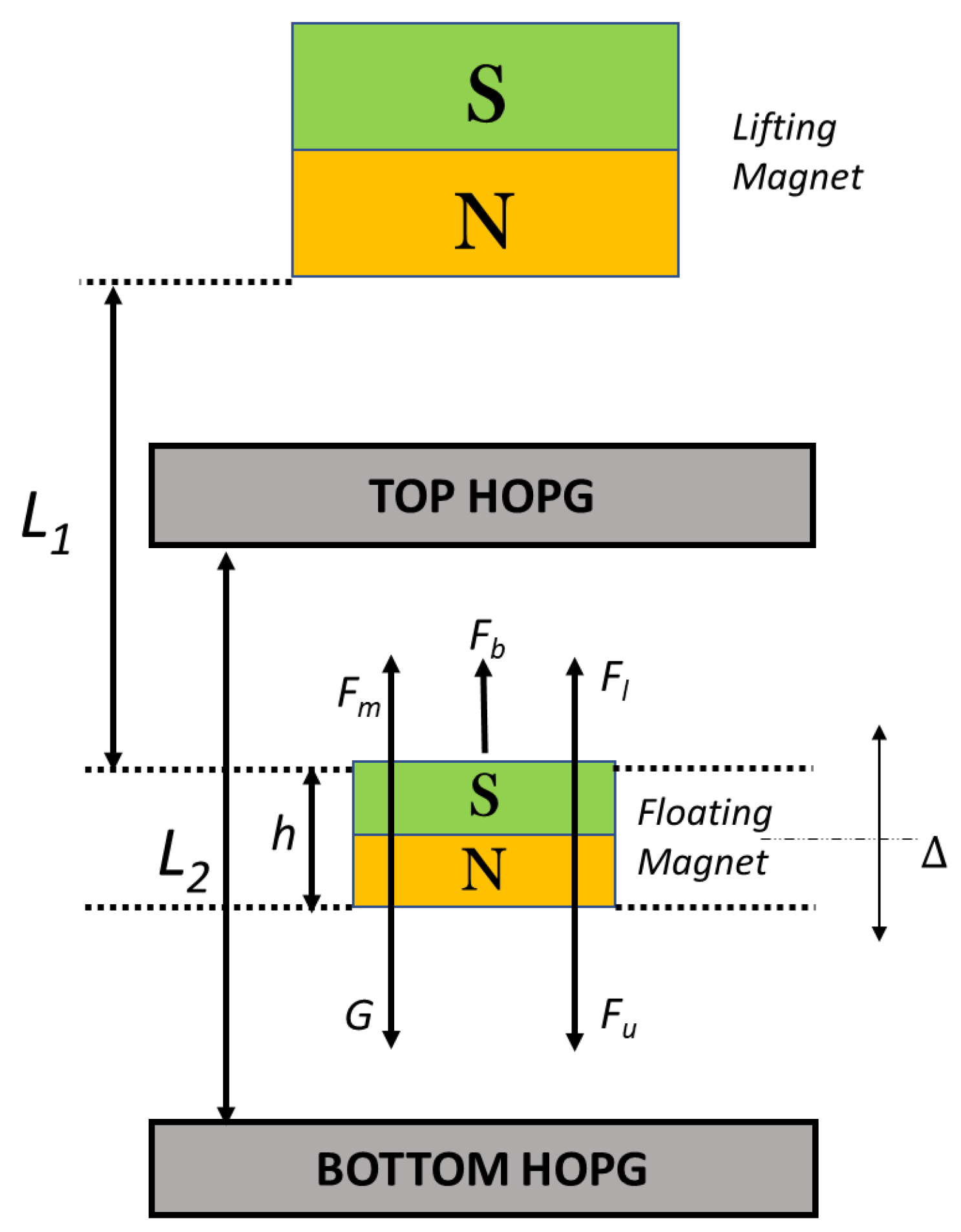
2.1. Proposed Gravimeter Device
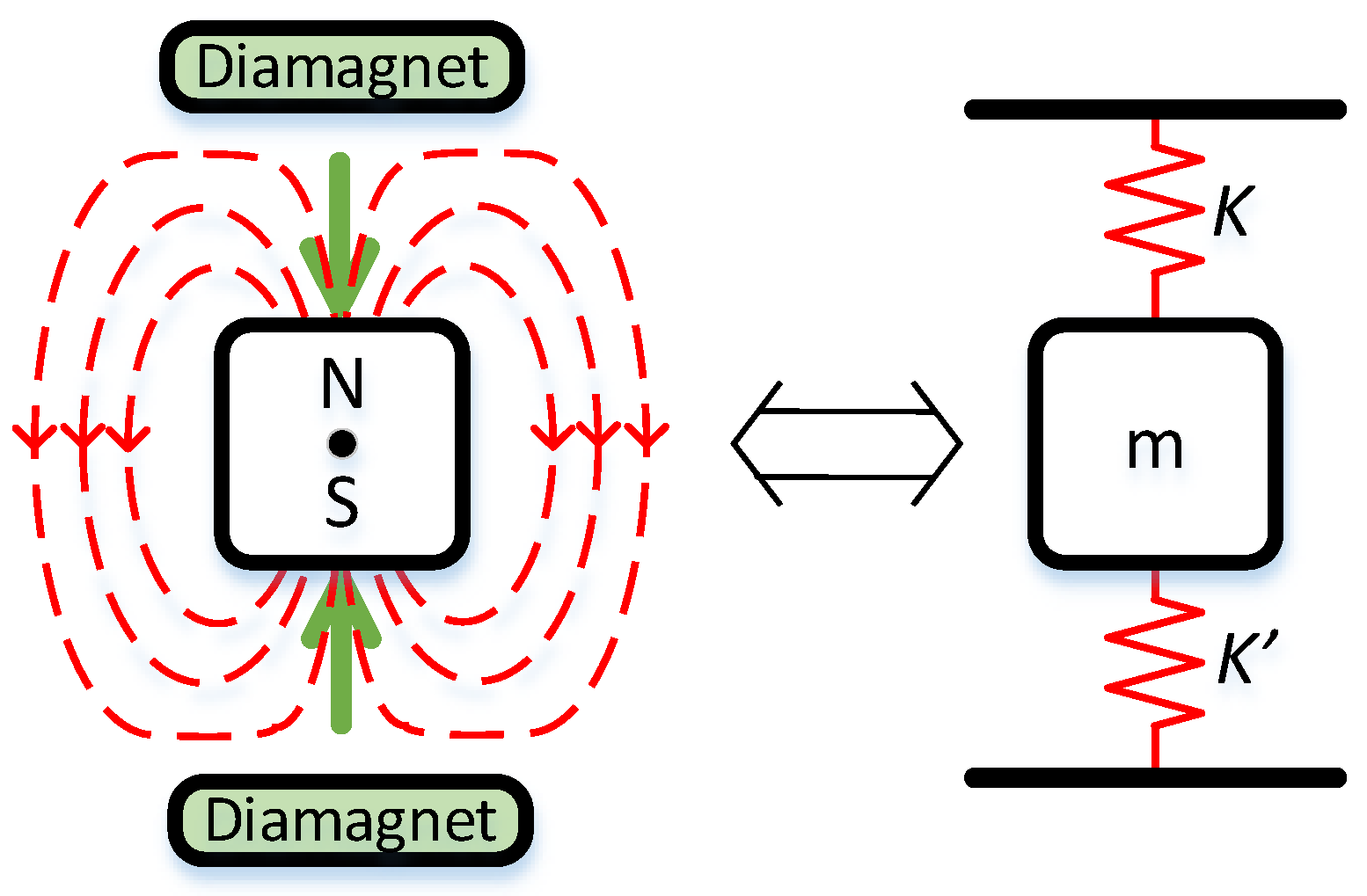
2.2. Basic Principles of Diamagnetically Stabilized Magnetic Levitation
2.3. Mathematical Foundations
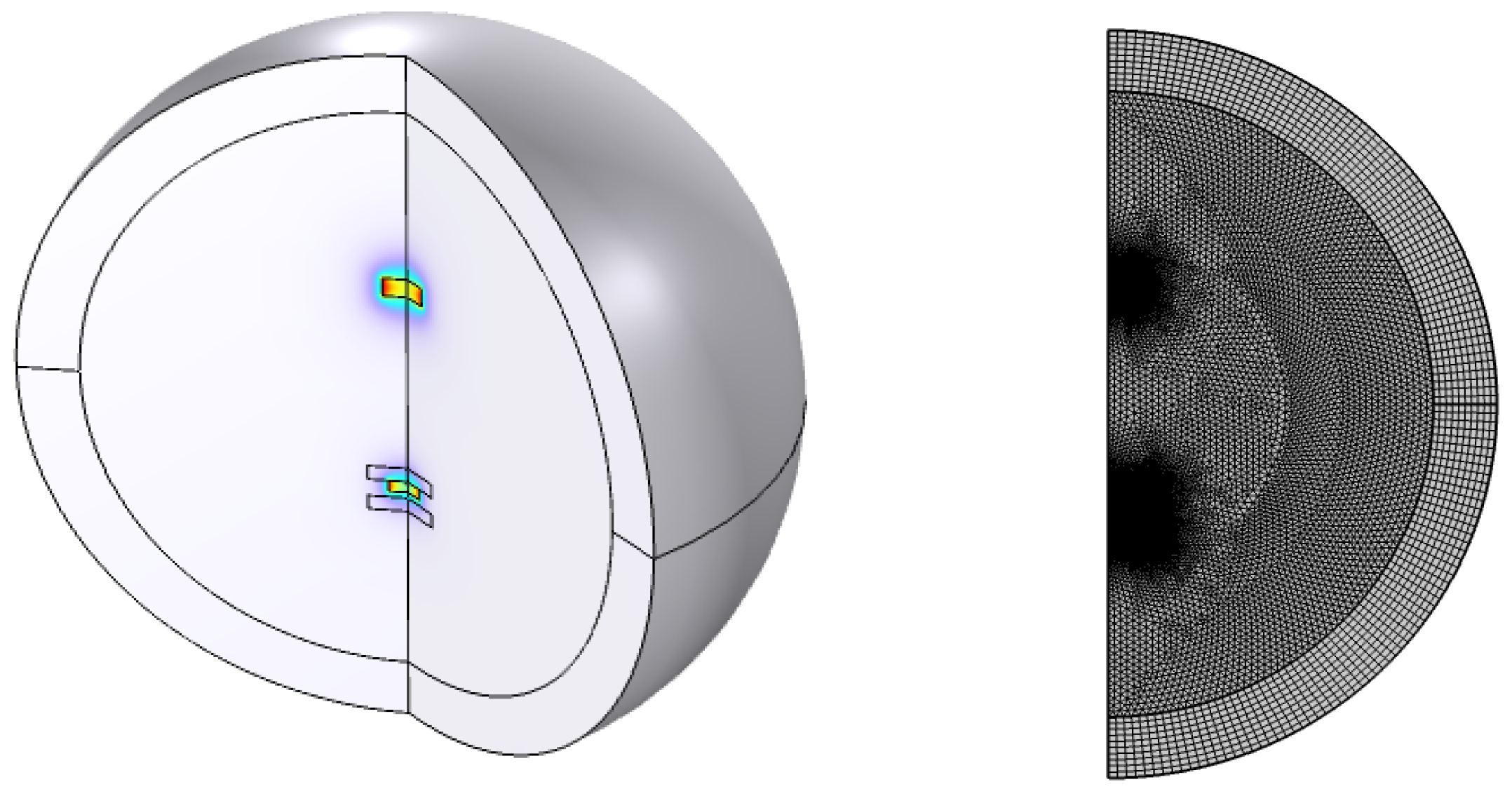
2.4. Model Implementation
3. Results and Discussion
3.1. Initial Sensitivity Analysis
3.2. Multidimensional Force–Displacement Parametric Study
3.3. Effect of Diamagnetic Bore on the Characteristic () Curve
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zuber, M.T.; Smith, D.E.; Lehman, D.H.; Hoffman, T.L.; Asmar, S.W.; Watkins, M.M. Gravity Recovery and Interior Laboratory (GRAIL): Mapping the Lunar Interior from Crust to Core. Space Sci. Rev. 2013, 178, 3–24. [Google Scholar] [CrossRef]
- Park, R.S.; Konopliv, A.S.; Yuan, D.N.; Asmar, S.; Watkins, M.M.; Williams, J.; Smith, D.E.; Zuber, M.T. A high-resolution spherical harmonic degree 1500 lunar gravity field from the GRAIL mission. Am. Geophys. Union Fall Meet. San Fr. 14–18 Dec. 2015 2015, 2015, G41B-01. [Google Scholar]
- Papanikolaou, T.D.; Tsoulis, D. Assessment of earth gravity field models in the medium to high frequency spectrum based on GRACE and GOCE dynamic orbit analysis. Geosciences 2018, 8, 441. [Google Scholar] [CrossRef]
- Love, A.E.H. Some Problems of Geodynamics: Being an Essay to Which the Adams Prize in the University of Cambridge was Adjudged in 1911; University Press: Cambridge, UK, 1926. [Google Scholar]
- Prasad, A.; Middlemiss, R.P.; Noack, A.; Anastasiou, K.; Bramsiepe, S.G.; Toland, K.; Utting, P.R.; Paul, D.J.; Hammond, G.D. A 19 day earth tide measurement with a MEMS gravimeter. Sci. Rep. 2022, 12, 13091. [Google Scholar] [CrossRef] [PubMed]
- Matsuyama, I.; Nimmo, F.; Keane, J.T.; Chan, N.H.; Taylor, G.J.; Wieczorek, M.A.; Kiefer, W.S.; Williams, J.G. GRAIL, LLR, and LOLA constraints on the interior structure of the Moon. Geophys. Res. Lett. 2016, 43, 8365–8375. [Google Scholar] [CrossRef]
- Laneuville, M.; Wieczorek, M.A.; Breuer, D.; Tosi, N. Asymmetric thermal evolution of the Moon. J. Geophys. Res. Planets 2013, 118, 1435–1452. [Google Scholar] [CrossRef]
- Hirt, C.; Claessens, S.J.; Kuhn, M.; Featherstone, W.E. Kilometer-resolution gravity field of Mars: MGM2011. Planet. Space Sci. 2012, 67, 147–154. [Google Scholar] [CrossRef]
- Hirt, C.; Kuhn, M. Convergence and divergence in spherical harmonic series of the gravitational field generated by high-resolution planetary topography—A case study for the Moon. J. Geophys. Res. Planets 2017, 122, 1727–1746. [Google Scholar] [CrossRef]
- Love, A.E.H. The yielding of the earth to disturbing forces. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1909, 82, 73–88. [Google Scholar] [CrossRef]
- Šprlák, M.; Han, S.-C. On the use of spherical harmonic series inside the minimum Brillouin sphere: Theoretical review and evaluation by GRAIL and LOLA satellite data. Earth-Sci. Rev. 2021, 222, 103739. [Google Scholar] [CrossRef]
- Kauahikaua, J.; Cashman, K.V.; Mattox, T.N.; Heliker, C.C.; Hon, K.A.; Mangan, M.T.; Thornber, C.R. Observations on basaltic lava streams in tubes from Kilauea Volcano, island of Hawai’i. J. Geophys. Res. Solid Earth 1998, 103, 27303–27323. [Google Scholar] [CrossRef]
- Blair, D.M.; Chappaz, L.; Sood, R.; Milbury, C.; Bobet, A.; Melosh, H.J.; Howell, K.C.; Freed, A.M. The structural stability of lunar lava tubes. Icarus 2017, 282, 47–55. [Google Scholar] [CrossRef]
- De Angelis, G.; Wilson, J.W.; Clowdsley, M.S.; Nealy, J.E.; Humes, D.H.; Clem, J.M. Lunar lava tube radiation safety analysis. J. Radiat. Res. 2002, 43, S41–S45. [Google Scholar] [CrossRef] [PubMed]
- Sood, R.; Chappaz, L.; Melosh, H.J.; Howell, K.C.; Milbury, C. Detection of Buried Empty Lunar Lava Tubes Using GRAIL Gravity Data. In Proceedings of the 2nd International Planetary Caves Conference, Flagstaff, AZ, USA, 20–23 October 2015; Volume 1883, p. 9016. [Google Scholar]
- Chappaz, L.; Sood, R.; Melosh, H.J.; Howell, K.C.; Blair, D.M.; Milbury, C.; Zuber, M.T. Evidence of large empty lava tubes on the Moon using GRAIL gravity. Geophys. Res. Lett. 2017, 44, 105–112. [Google Scholar] [CrossRef]
- James, P.; Ermakov, A.; Sori, M. Requirements for gravity measurements on the anticipated Artemis III mission. arXiv 2020, arXiv:2009.03514. [Google Scholar]
- Gal (Unit)—Wikipedia. Available online: https://en.wikipedia.org/wiki/Gal_(unit) (accessed on 7 June 2023).
- Nettleton, L.L. Determination of density for reduction of gravimeter observations. Geophysics 1939, 4, 176–183. [Google Scholar] [CrossRef]
- Parasnis, D.S.; Cook, A.H. A Study of Rock Densities in the English Midlands. Geophys. J. Int. 1952, 6, 252–271. [Google Scholar] [CrossRef]
- Malengreau, B.; Skinner, D.; Bromley, C.; Black, P. Geophysical characterisation of large silicic volcanic structures in the Coromandel Peninsula. N. Zealand J. Geol. Geophys. 2000, 43, 171–186. [Google Scholar] [CrossRef]
- Mankhemthong, N.; Doser, D.I.; Baker, M.R. Practical Estimation of Near-surface Bulk Density Variations Across the Border Ranges Fault System, Central Kenai Peninsula, Alaska. J. Environ. Eng. Geophys. 2012, 17, 151–158. [Google Scholar] [CrossRef]
- Besserer, J.; Nimmo, F.; Wieczorek, M.A.; Weber, R.C.; Kiefer, W.S.; McGovern, P.J.; Andrews-Hanna, J.C.; Smith, D.E.; Zuber, M.T. GRAIL gravity constraints on the vertical and lateral density structure of the lunar crust. Geophys. Res. Lett. 2014, 41, 5771–5777. [Google Scholar] [CrossRef]
- Jansen, J.; Andrews-Hanna, J.; Li, Y.; Lucey, P.; Taylor, G.; Goossens, S.; Lemoine, F.; Mazarico, E.; Head, J.; Milbury, C.; et al. Small-scale density variations in the lunar crust revealed by GRAIL. Icarus 2016, 291, 107. [Google Scholar] [CrossRef] [PubMed]
- Andrews-Hanna, J.C.; Asmar, S.W.; Head, J.W.; Kiefer, W.S.; Konopliv, A.S.; Lemoine, F.G.; Matsuyama, I.; Mazarico, E.; McGovern, P.J.; Melosh, H.J.; et al. Ancient igneous intrusions and early expansion of the Moon revealed by GRAIL gravity gradiometry. Science 2013, 339, 675–678. [Google Scholar] [CrossRef]
- Ojha, L.; Nerozzi, S.; Lewis, K. Compositional Constraints on the North Polar Cap of Mars from Gravity and Topography. Geophys. Res. Lett. 2019, 46, 8671–8679. [Google Scholar] [CrossRef]
- Wieczorek, M.A.; Neumann, G.A.; Nimmo, F.; Kiefer, W.S.; Taylor, G.J.; Melosh, H.J.; Phillips, R.J.; Solomon, S.C.; Andrews-Hanna, J.C.; Asmar, S.W.; et al. The Crust of the Moon as Seen by GRAIL. Science 2013, 339, 671. [Google Scholar] [CrossRef] [PubMed]
- Nimmo, F. A Sharper Picture of the Moon’s Bombardment History From Gravity Data. J. Geophys. Res. Planets 2018, 123, 2244–2247. [Google Scholar] [CrossRef]
- Hirabayashi, M.; Minton, D.; Melosh, H., IV.; Soderblom, J.M.; Milbury, C.; Huang, Y.H. Regolith thickness formation on the lunar surface. In AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, 2016; p. P53C-2235. [Google Scholar]
- Ojha, L.; Lewis, K. The Density of the Medusae Fossae Formation: Implications for its Composition, Origin, and Importance in Martian History. J. Geophys. Res. Planets 2018, 123, 1368–1379. [Google Scholar] [CrossRef]
- Lewis, K.W.; Peters, S.; Gonter, K.; Morrison, S.; Schmerr, N.; Vasavada, A.R.; Gabriel, T. A surface gravity traverse on Mars indicates low bedrock density at Gale crater. Science 2019, 363, 535–537. [Google Scholar] [CrossRef]
- Moore, W.B.; Schubert, G. The Tidal Response of Europa. Icarus 2000, 147, 317–319. [Google Scholar] [CrossRef]
- Moore, W.B.; Schubert, G. The tidal response of Ganymede and Callisto with and without liquid water oceans. Icarus 2003, 166, 223–226. [Google Scholar] [CrossRef]
- Iess, L.; Jacobson, R.A.; Ducci, M.; Stevenson, D.J.; Lunine, J.I.; Armstrong, J.W.; Asmar, S.W.; Racioppa, P.; Rappaport, N.J.; Tortora, P. The tides of Titan. Science 2012, 337, 457–459. [Google Scholar] [CrossRef]
- Bills, B.G.; Neumann, G.A.; Smith, D.E.; Zuber, M.T. Improved estimate of tidal dissipation within Mars from MOLA observations of the shadow of Phobos. J. Geophys. Res. Planets 2005, 110, 1–15. [Google Scholar] [CrossRef]
- Lainey, V.; Arlot, J.E.; Karatekin, Ö.; Van Hoolst, T. Strong tidal dissipation in Io and Jupiter from astrometric observations. Nature 2009, 459, 957–959. [Google Scholar] [CrossRef]
- Nimmo, F.; Porco, C.; Mitchell, C. Tidally Modulated Eruptions on Enceladus: Cassini is Observations and Models. Astron J. 2014, 148, 46. [Google Scholar] [CrossRef]
- Matsuyama, I. Tidal dissipation in the oceans of icy satellites. Icarus 2014, 242, 11–18. [Google Scholar] [CrossRef]
- Chyba, C.F. Energy for microbial life on Europa. Nature 2000, 403, 381–382. [Google Scholar] [CrossRef] [PubMed]
- Zhong, S.; Qin, C.; Geruo, G.; Wahr, J. Can tidal tomography be used to unravel the long-wavelength structure of the lunar interior? Geophys. Res. Lett. 2012, 39, L15201. [Google Scholar] [CrossRef]
- Elkins-Tanton, L.T.; Burgess, S.; Yin, Q.Z. The lunar magma ocean: Reconciling the solidification process with lunar petrology and geochronology. Earth Planet Sci. Lett. 2011, 304, 326–336. [Google Scholar] [CrossRef]
- Roberts, J.H.; Zhong, S. Degree-1 convection in the Martian mantle and the origin of the hemispheric dichotomy. J. Geophys. Res. Planets 2006, 111, 6013. [Google Scholar] [CrossRef]
- Grott, M.; Sohl, F.; Hussmann, H.; Grott, M.; Sohl, F.; Hussmann, H. Degree-one convection and the origin of Enceladus’ dichotomy. Icarus 2007, 191, 203–210. [Google Scholar] [CrossRef]
- Górski, K.M.; Bills, B.G.; Konopliv, A.S. A high resolution Mars surface gravity grid. Planet. Space Sci. 2018, 160, 84–106. [Google Scholar] [CrossRef]
- Latychev, K.; Mitrovica, J.X.; Ishii, M.; Chan, N.H.; Davis, J.L. Body tides on a 3-D elastic earth: Toward a tidal tomography. Earth Planet. Sci. Lett. 2009, 277, 86–90. [Google Scholar] [CrossRef]
- Montagner, J.-P.; Juhel, K.; Barsuglia, M.; Ampuero, J.P.; Chassande-Mottin, E.; Harms, J.; Whiting, B.; Bernard, P.; Clévédé, E.; Lognonné, P. Prompt gravity signal induced by the 2011 Tohoku-Oki earthquake. Nat. Commun. 2016, 7, 13349. [Google Scholar] [CrossRef] [PubMed]
- Rothleitner, C.; Svitlov, S.; Mérimèche, H.; Hu, H.; Wang, L.J. Development of new free-fall absolute gravimeters. Metrologia 2009, 46, 283–297. [Google Scholar] [CrossRef]
- Goodkind, J.M. The superconducting gravimeter. Rev. Sci. Instrum. 1999, 70, 4131–4152. [Google Scholar] [CrossRef]
- LaCoste, L.J.B. A New Type Long Period Vertical Seismograph. J. Appl. Phys. 1934, 5, 178–180. [Google Scholar] [CrossRef]
- Liu, S.; Feng, J.; Wang, Q.; Su, D.; Li, C.; Wu, S. Investigation on the dynamic characteristics of CG-6 relative gravimeter for the micro-gravity network. In Proceedings of the Tenth International Symposium on Precision Engineering Measurements and Instrumentation, Kunming, China, 8–10 August 2018; SPIE: Bellingham, WA, USA, 2019; Volume 11053, p. 110531V. [Google Scholar]
- Nabighian, M.N.; Ander, M.E.; Grauch, V.J.S.; Hansen, R.O.; LaFehr, T.R.; Li, Y.; Pearson, W.C.; Peirce, J.W.; Phillips, J.D.; Ruder, M.E. Historical development of the gravity method in exploration. Geophysics 2005, 70, 63ND–89ND. [Google Scholar] [CrossRef]
- Torge, W. Geodesy; De Gruyter: Berlin, Germany, 1991. [Google Scholar]
- Gabriel, G. Microgravimetry. In Groundwater Geophysics; Springer-Verlag: Berlin/Heidelberg, Germany, 2006; pp. 295–320. [Google Scholar]
- Faller, J.E. The measurement of little g: A fertile ground for precision measurement science. J. Res. Natl. Inst. Stand. Technol. 2005, 110, 559. [Google Scholar] [CrossRef]
- Schmidt, R.; Flechtner, F.; Meyer, U.; Reigber, C.; Barthelmes, F.; Förste, C.; Stubenvoll, R.; König, R.; Neumayer, K.H.; Zhu, S. Static and Time-Variable Gravity from GRACE Mission Data. In Observation of the Earth System from Space; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Valliant, H.D. The Lacoste & Romberg Air/Sea Gravity Meter: An Overview. In Handbook of Geophysical Exploration at Sea; CRC: Boca Raton, FL, USA, 2019; pp. 141–177. [Google Scholar]
- Wing, C.G. MIT vibrating string surface-ship gravimeter. J. Geophys. Res. 1969, 74, 5882–5894. [Google Scholar] [CrossRef]
- Middlemiss, R.P.; Bramsiepe, S.G.; Douglas, R.; Hough, J.; Paul, D.J.; Rowan, S.; Hammond, G.D. Field tests of a portable MEMS gravimeter. Sensors 2017, 17, 2571. [Google Scholar] [CrossRef]
- Kashinski, D.O.; Quinn, P.V., Sr. The Electrostatic Gravimeter: An Alternate Way of Measuring Gravitational Acceleration. arxiv 2006, arXiv:physics/0601067. [Google Scholar]
- Cansiz, A. Static and dynamic analysis of a diamagnetic bearing system. J. Appl. Phys. 2008, 103, 034510. [Google Scholar] [CrossRef]
- Reznik, B.; Kontny, A.; Fritz, J.; Gerhards, U. Shock-induced deformation phenomena in magnetite and their consequences on magnetic properties. Geochem. Geophys. Geosystems 2016, 17, 2374–2393. [Google Scholar] [CrossRef]
- Ding, J.; Gao, J.; Su, Y.; Zhang, K.; Duan, Z. A diamagnetically levitated vibration energy harvester for scavaging the horizontal vibration. Mater. Res. Express. 2019, 6, 025506. [Google Scholar] [CrossRef]
- Cheng, S.; Li, X.; Wang, Y.; Su, Y. Levitation characteristics analysis of a diamagnetically stabilized levitation structure. Micromachines 2021, 12, 982. [Google Scholar] [CrossRef]
- Thompson, G. Thales to Sextus: An Introduction to Ancient Philosophy; Waveland Press: Long Grove, IL, USA, 2016. [Google Scholar]
- Jackson, R. John Tyndall and the Early History of Diamagnetism. Ann. Sci. 2015, 72, 435. [Google Scholar] [CrossRef]






| Parameter | Lifting Magnet | Floating Magnet | Diamagnetic Sheet |
|---|---|---|---|
| Materials | NdFeB-52 | NdFeB-52 | HOPG |
| Size | | | |
| Residual Flux Density (Br) | | | - |
| Recoil permeability | - | ||
| Electrical conductivity | | | |
| Desity | | - | |
| Relative permeability | - | - | 0.95 |
| Relative permittivity | - | - | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafiq, K.R.B.; Joseph, A.; Yokochi, N.; James, P.; von Jouanne, A.; Yokochi, A. Modeling Development of a Diamagnetically Stabilized Magnetically Levitated Gravimeter. Sensors 2024, 24, 350. https://doi.org/10.3390/s24020350
Rafiq KRB, Joseph A, Yokochi N, James P, von Jouanne A, Yokochi A. Modeling Development of a Diamagnetically Stabilized Magnetically Levitated Gravimeter. Sensors. 2024; 24(2):350. https://doi.org/10.3390/s24020350
Chicago/Turabian StyleRafiq, Kazi Rifat Bin, Abigail Joseph, Naiya Yokochi, Peter James, Annette von Jouanne, and Alex Yokochi. 2024. "Modeling Development of a Diamagnetically Stabilized Magnetically Levitated Gravimeter" Sensors 24, no. 2: 350. https://doi.org/10.3390/s24020350
APA StyleRafiq, K. R. B., Joseph, A., Yokochi, N., James, P., von Jouanne, A., & Yokochi, A. (2024). Modeling Development of a Diamagnetically Stabilized Magnetically Levitated Gravimeter. Sensors, 24(2), 350. https://doi.org/10.3390/s24020350








