Transmit Beamforming Design Based on Multi-Receiver Power Suppression for STAR Digital Array
Abstract
:1. Introduction
2. System Model
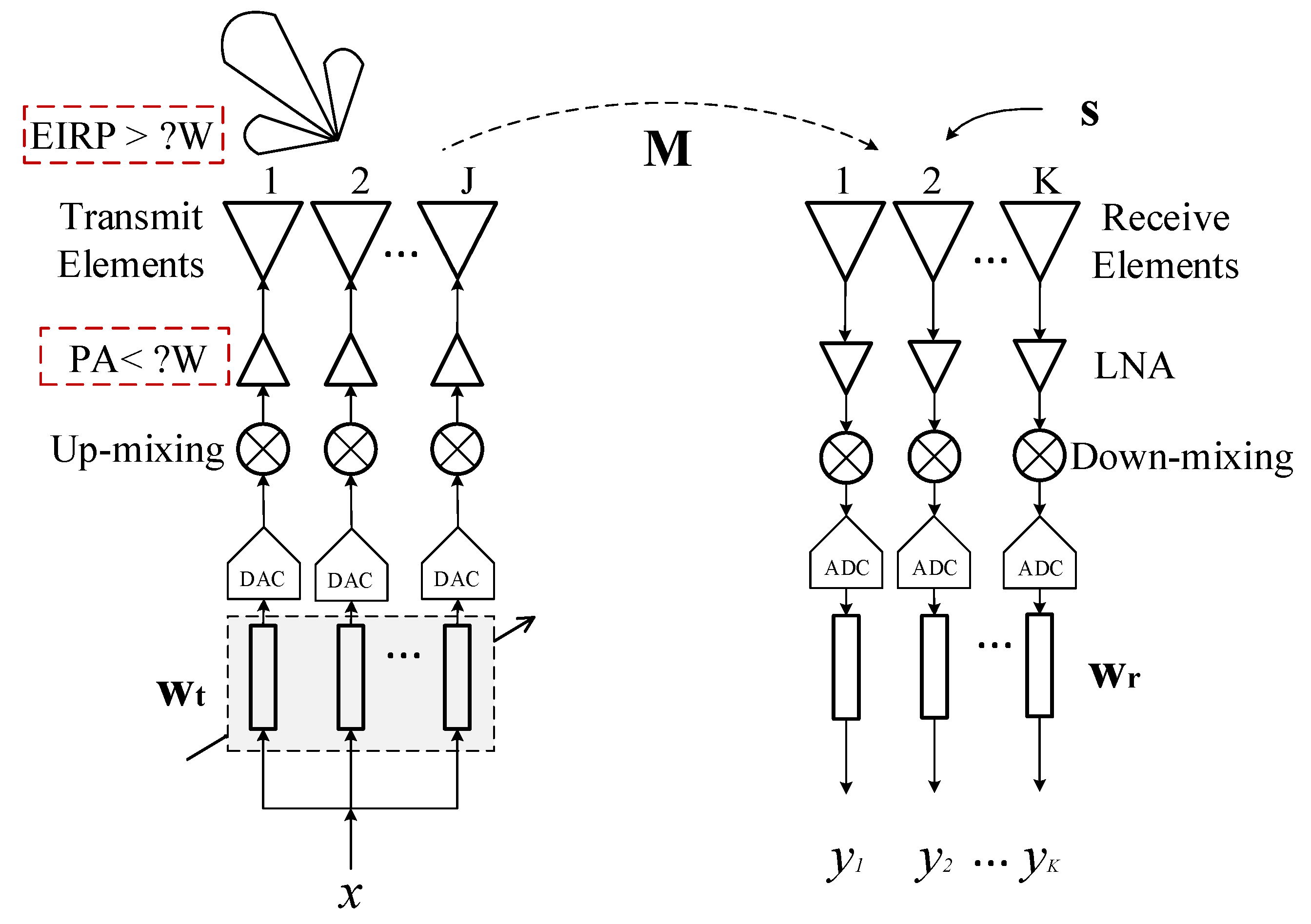
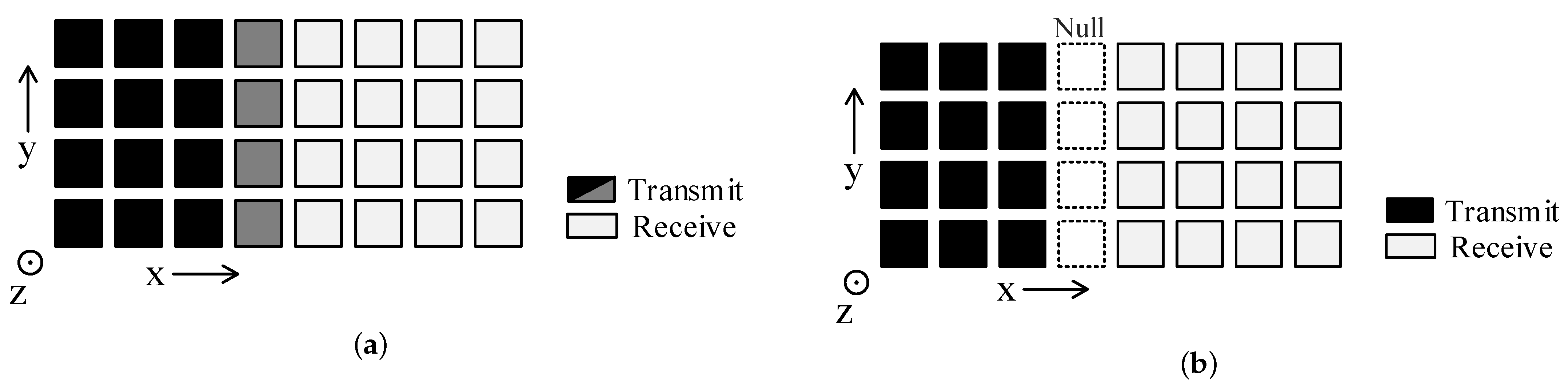
2.1. STAR Array Architecture
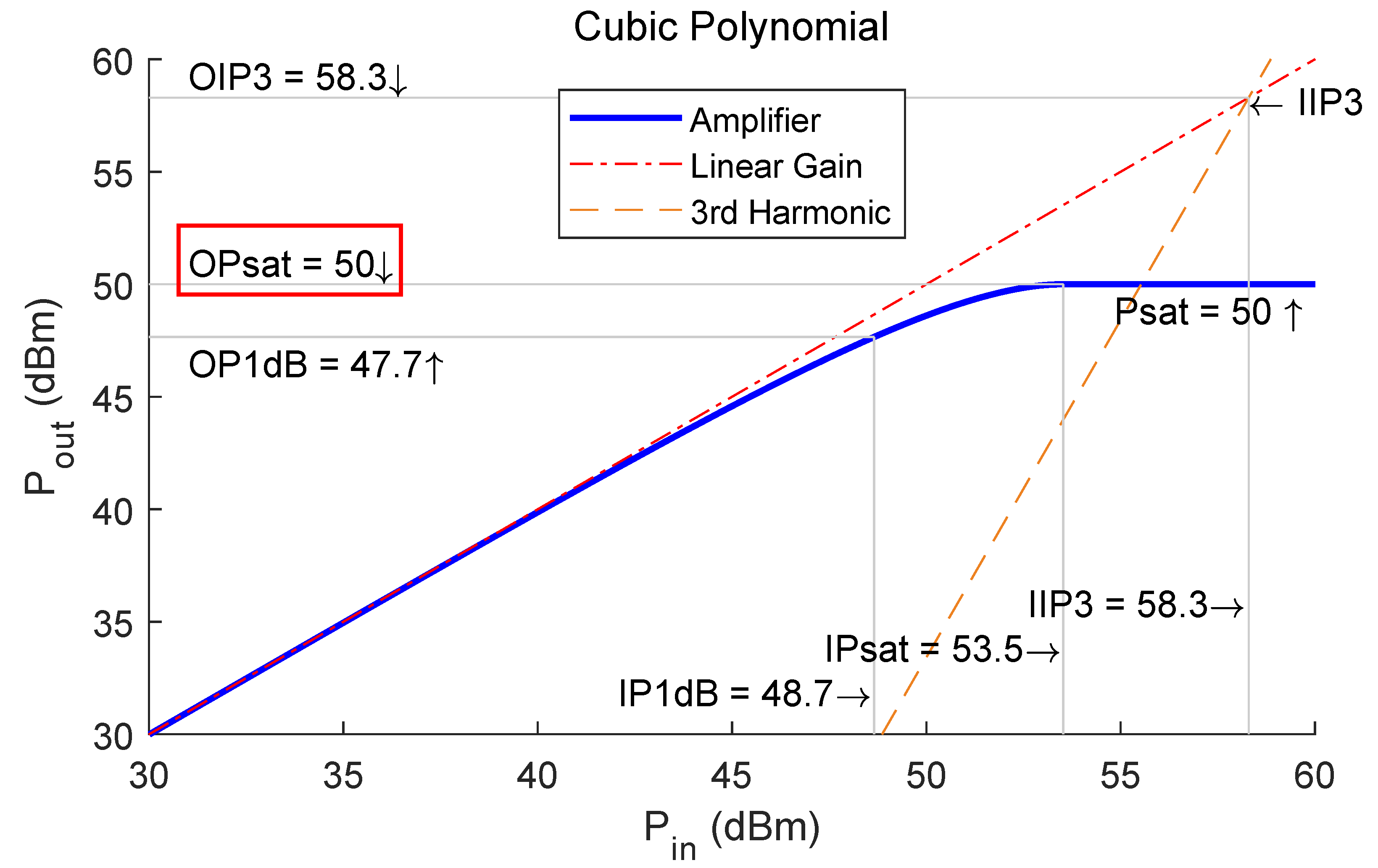
2.2. Power Amplifier Model
2.3. Transmit Beamforming Optimization
2.4. System Isolation Analysis
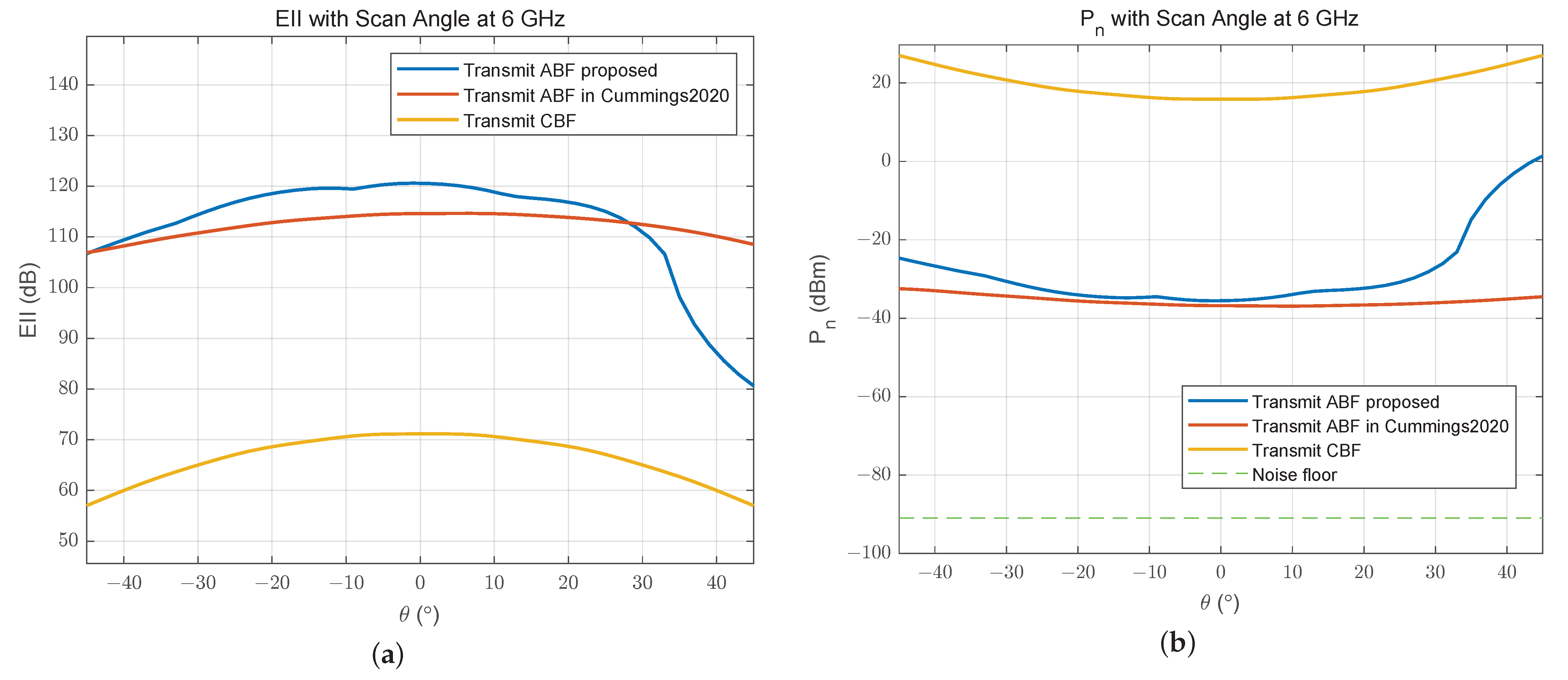
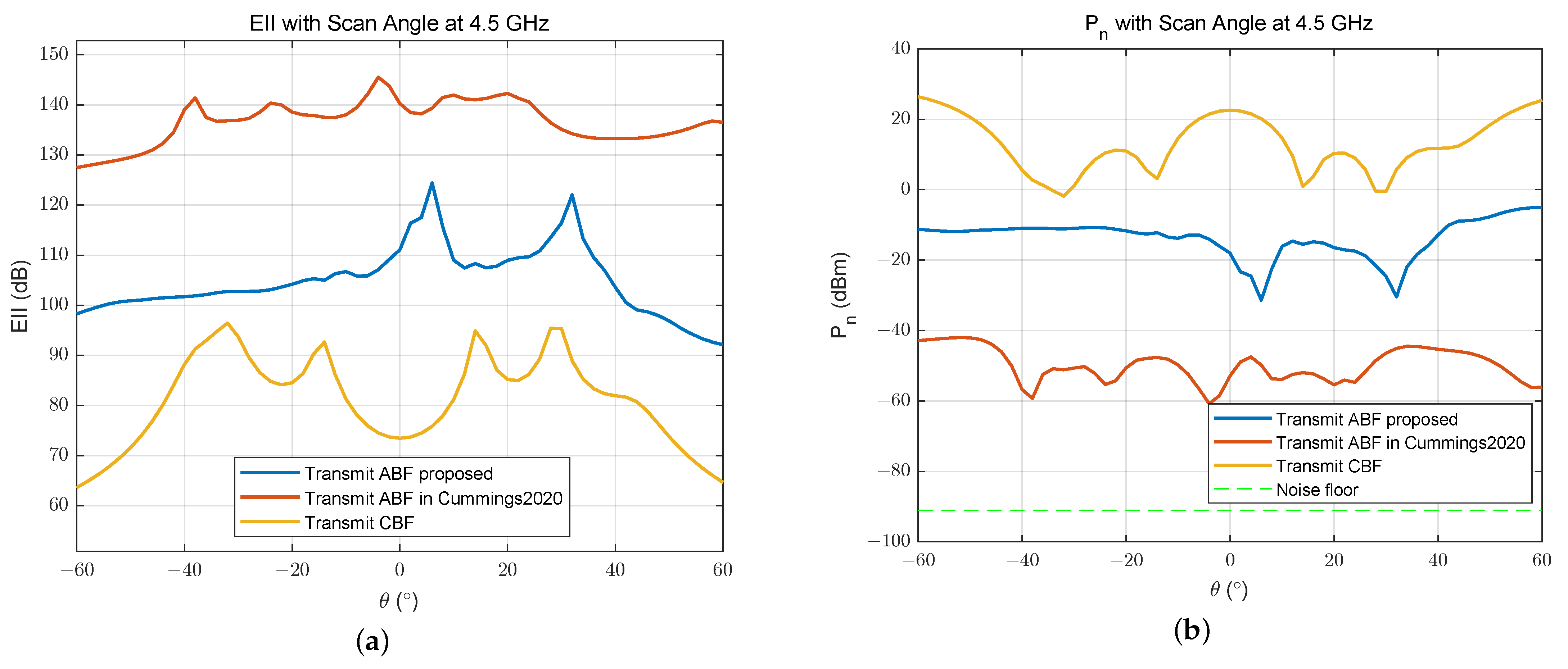
3. Simulation Results
3.1. STAR Phased Arrays Design
3.2. System Performance Analysis
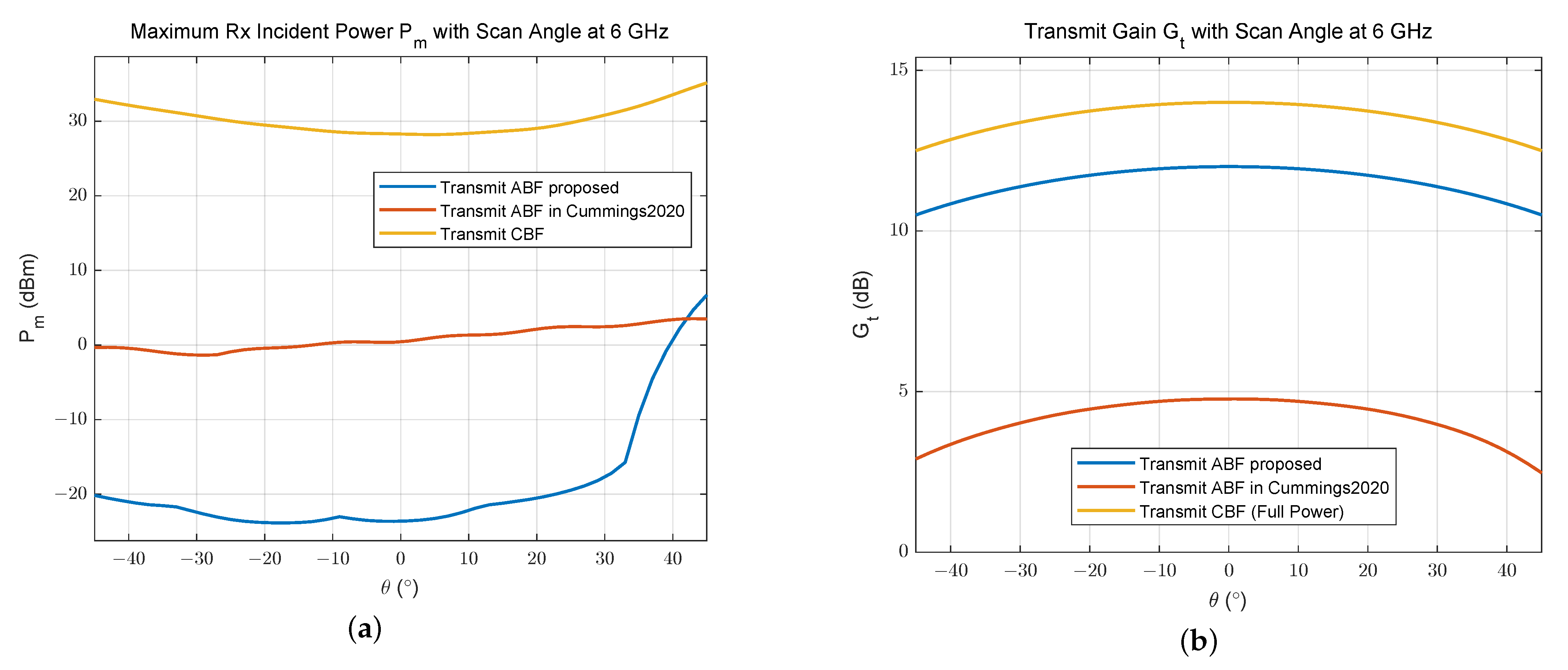
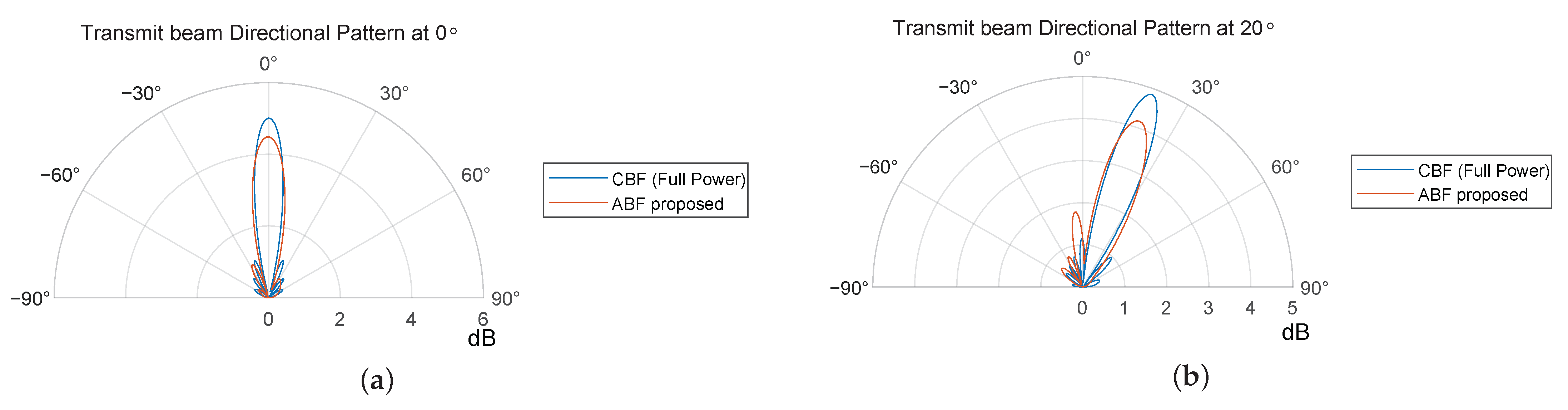
3.2.1. Linear Array Simulation Experiment
3.2.2. Plane Array Simulation Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bliss, D.W.; Parker, P.A.; Margetts, A.R. Simultaneous Transmission and Reception for Improved Wireless Network Performance. In Proceedings of the 2007 IEEE/SP 14th Workshop on Statistical Signal Processing, Madison, WI, USA, 26–29 August 2007; pp. 478–482. [Google Scholar]
- Nwankwo, C.D.; Zhang, L.; Quddus, A.; Imran, M.A.; Tafazolli, R. A survey of self-interference management techniques for single frequency full duplex systems. IEEE Access 2017, 6, 30242–30268. [Google Scholar] [CrossRef]
- Kolodziej, K.E.; Perry, B.T.; Herd, J.S. In-Band Full-Duplex Technology: Techniques and Systems Survey. IEEE Trans. Microw. Theory Tech. 2019, 67, 3025–3041. [Google Scholar] [CrossRef]
- Riihonen, T.; Korpi, D.; Rantula, O.; Rantanen, H.; Saarelainen, T.; Valkama, M. In-band full-duplex radio transceivers: A paradigm shifts in tactical communications and electronic warfare? IEEE Commun. Mag. 2017, 55, 30–36. [Google Scholar] [CrossRef]
- Herd, J.S.; Conway, M.D. The Evolution to Modern Phased Array Architectures. Proc. IEEE 2016, 104, 519–529. [Google Scholar] [CrossRef]
- Everett, E.; Shepard, C.; Zhong, L.; Sabharwal, A. SoftNull: Many-Antenna Full-Duplex Wireless via Digital Beamforming. IEEE Trans. Wirel. Commun. 2016, 15, 8077–8092. [Google Scholar] [CrossRef]
- Chen, T.; Dastjerdi, M.B.; Krishnaswamy, H.; Zussman, G. Wideband Full-Duplex Phased Array with Joint Transmit and Receive Beamforming: Optimization and Rate Gains. IEEE/ACM Trans. Netw. 2021, 29, 1591–1604. [Google Scholar] [CrossRef]
- Xie, M.; Wei, X.; Tang, Y.; Hu, D. A Robust Design for Aperture-Level Simultaneous Transmit and Receive with Digital Phased Array. Sensors 2021, 22, 109. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.; Wei, X.; Xie, M.; Tang, Y. A Method to Improve the Performance of Arrays for Aperture-Level Simultaneous Transmit and Receive. Int. J. Antennas Propag. 2022, 2022, 1687–5869. [Google Scholar] [CrossRef]
- Hu, D.; Wei, X.; Xie, M.; Tang, Y. A Sparse Design for Aperture-Level Simultaneous Transmit and Receive Arrays. Electronics 2022, 11, 3381. [Google Scholar] [CrossRef]
- Qiu, J.; Yao, Y.; Wu, G. Research on aperture-level simultaneous transmit and receive. J. Eng. 2019, 2019, 8006–8008. [Google Scholar] [CrossRef]
- Qiu, J.; Yao, Y.; Wu, G. Simultaneous transmit and receive based on phase-only digital beamforming. In Proceedings of the 2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 18–20 June 2021; pp. 890–893. [Google Scholar]
- Shi, C.; Pan, W.; Shen, Y.; Shao, S. Robust Transmit Beamforming for Self-Interference Cancellation in STAR Phased Array Systems. IEEE Signal Process. Lett. 2022, 29, 2622–2626. [Google Scholar] [CrossRef]
- Kolodziej, K.E.; Doane, J.P.; Perry, B.T.; Herd, J.S. Adaptive beamforming for multi-function in-band full-duplex applications. IEEE Wirel. Commun. 2021, 28, 28–35. [Google Scholar] [CrossRef]
- Doane, J.P.; Kolodziej, K.E.; Perry, B.T. Simultaneous Transmit and Receive with Digital Phased Arrays. In Proceedings of the 2016 IEEE International Symposium on Phased Array Systems and Technology (PAST), Waltham, MA, USA, 18–21 October 2016; pp. 1–6. [Google Scholar]
- Doane, J.P.; Kolodziej, K.E.; Perry, B.T. Simultaneous transmit and receive performance of an 8-channel digital phased array. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 1043–1044. [Google Scholar]
- Cummings, I.T.; Doane, J.P.; Schulz, T.J.; Havens, T.C. Aperture-Level Simultaneous Transmit and Receive with Digital Phased Arrays. IEEE Trans. Signal Process. 2020, 68, 1243–1258. [Google Scholar] [CrossRef]
- Cummings, I.T.; Schulz, T.J.; Havens, T.C.; Doane, J.P. Neural Networks for Real-Time Adaptive Beamforming in Simultaneous Transmit and Receive Digital Phased Arrays: Student Submission. In Proceedings of the 2019 IEEE International Symposium on Phased Array System & Technology (PAST), Waltham, MA, USA, 15–18 October 2019; pp. 1–8. [Google Scholar]
- López-Valcarce, R.; Martínez-Cotelo, M. Full-Duplex mmWave MIMO With Finite-Resolution Phase Shifters. IEEE Wirel. Commun. 2022, 21, 8979–8993. [Google Scholar] [CrossRef]
- Hong, Z.H.; Zhang, L.; Li, W.; Wu, Y.; Zhu, Z.; Park, S.I.; Ahn, S.; Kwon, S.; Hur, N.; Iradier, E.; et al. Frequency-Domain RF Self-Interference Cancellation for In-Band Full-Duplex Communications. IEEE Trans. Wirel. Commun. 2023, 22, 2352–2363. [Google Scholar] [CrossRef]
- Rahman, M.R.; Bojja Venkatakrishnan, S.; Nakatani, T.; Volakis, J.L. Wideband Self Interference Cancellation (SIC) RF Front End for Simultaneous Transmit and Receive (STAR) Radios. In Proceedings of the 2022 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (AP-S/URSI), Denver, CO, USA, 10–15 July 2022; pp. 948–949. [Google Scholar]
- Wu, D.; Sun, Y.-X.; Wang, B.; Lian, R. A Compact, Monostatic, Co-Circularly Polarized Simultaneous Transmit and Receive (STAR) Antenna with High Isolation. IEEE Antennas Wireless Propagat. Lett. 2020, 19, 1127–1131. [Google Scholar] [CrossRef]
- Morgan, D.R.; Ma, Z.; Kim, J.; Zierdt, M.G.; Pastalan, J. A Generalized Memory Polynomial Model for Digital Predistortion of RF Power Amplifiers. IEEE Trans. Signal Process. 2006, 54, 3852–3860. [Google Scholar] [CrossRef]
- Doane, J.P. Isolation Metrics for Single-Channel and Multi-Channel Simultaneous Transmit and Receive Systems. In Proceedings of the 2020 IEEE International Symposium on Antennas and Propagation and North American Radio Science Meeting, Montreal, QC, Canada, 5–10 July 2020; pp. 1761–1762. [Google Scholar]












| Acronym | Definition |
|---|---|
| STAR | Simultaneous Transmit and Receive |
| IBFD | In-band Full-duplex |
| FPGA | Field Programmable Gate Array |
| DSP | Digital Signal Processor |
| STAR | Simultaneous Transmit and Receive |
| ALSTAR | Aperture-Level Simultaneous Transmit and Receive |
| ELSTAR | Element-Level Simultaneous Transmit and Receive |
| MIMO | Multiple Input and Multiple Output |
| SoI | Signal of Interest |
| FDD | Frequency Division Duplex |
| TDD | Time Division Duplex |
| SI | Self-Interference |
| SIC | Self-Interference Cancellation |
| ADC/DAC | Analog-to-Digital Converter/Digital-to-Analog Converter |
| PA | Power Amplifier |
| SNR | Signal and Noise power Rate |
| SINR | Signal-to-Interference-plus-Noise power Rate |
| AWGN | Additive White Gaussian Noise |
| OPsat | Output Power of Saturation |
| EII | Effective Isotropic Isolation |
| EIRP | Effective Isotropic Radiated Power |
| EIS | Effective Isotropic Sensitivity |
| ABF | Adaptive Beamforming |
| CBF | Conventional Beamforming (Only Phase-Shift) |
| Array Type | Beamforming Method | EII (dB) | Receive Incident Power (dBm) | Transmit Gain Attenuation (dB) |
|---|---|---|---|---|
| 16-element Linear Array | CBF | 71.2/57.0/66.3 | 35.0/28.2/30.2 | No attenuation |
| ABF in [17] | 114.6/106.8/112.3 | 3.8/−1.3/0.9 | 10.8/9.2/9.5 | |
| ABF proposed | 120.6/80.6/112.4 | 3.0/3.0/3.0 | ||
| 32-element Plane Array | CBF | 96.3/63.6/81.8 | 31.8/24.3/27.4 | No attenuation |
| ABF in [17] | 145.1/127.5/136.6 | 19.8/6.6/13.0 | 12.2/5.1/7.7 | |
| ABF proposed | 124.9/92.2/105.0 | 3.0/3.0/3.0 |
| Beamforming Method | Maximum Incident Receive Power (dBm) | Number of ADC Quantizer Bits | Minimum Power of Quantized SoI (dBm) |
|---|---|---|---|
| CBF | 31.84 | 8 | |
| 12 | |||
| 16 | |||
| ABF in [17] | 19.83 | 8 | |
| 12 | |||
| 16 | |||
| ABF proposed | 8 | ||
| 12 | |||
| 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, T.; Wei, X.; Lai, J.; Xie, M. Transmit Beamforming Design Based on Multi-Receiver Power Suppression for STAR Digital Array. Sensors 2024, 24, 622. https://doi.org/10.3390/s24020622
Lin T, Wei X, Lai J, Xie M. Transmit Beamforming Design Based on Multi-Receiver Power Suppression for STAR Digital Array. Sensors. 2024; 24(2):622. https://doi.org/10.3390/s24020622
Chicago/Turabian StyleLin, Tairan, Xizhang Wei, Jingtong Lai, and Mingcong Xie. 2024. "Transmit Beamforming Design Based on Multi-Receiver Power Suppression for STAR Digital Array" Sensors 24, no. 2: 622. https://doi.org/10.3390/s24020622
APA StyleLin, T., Wei, X., Lai, J., & Xie, M. (2024). Transmit Beamforming Design Based on Multi-Receiver Power Suppression for STAR Digital Array. Sensors, 24(2), 622. https://doi.org/10.3390/s24020622







