Study of the Brain Functional Connectivity Processes During Multi-Movement States of the Lower Limbs
Abstract
:1. Introduction
2. Materials and Methods
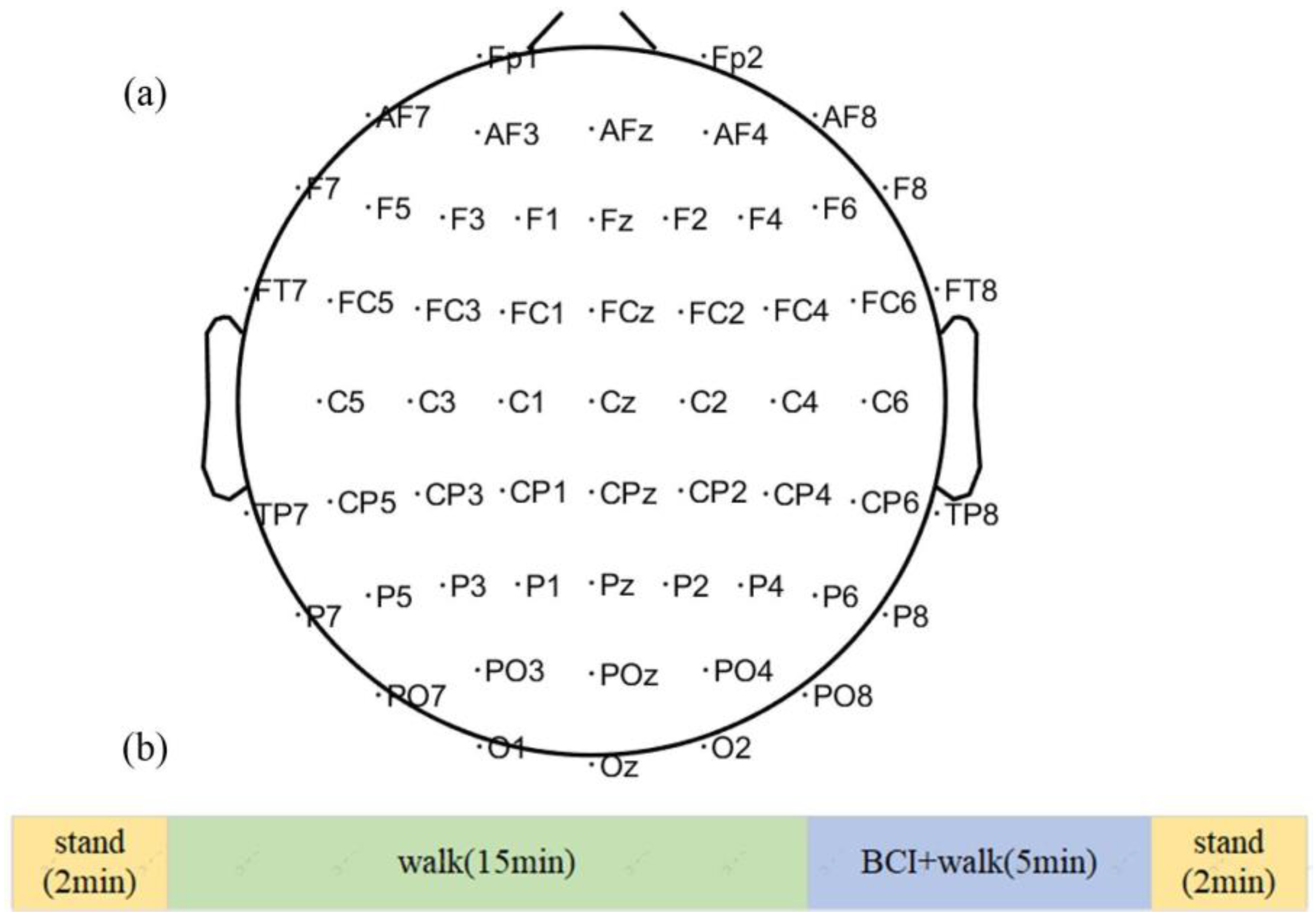
2.1. Datasets and Experiments Protocol
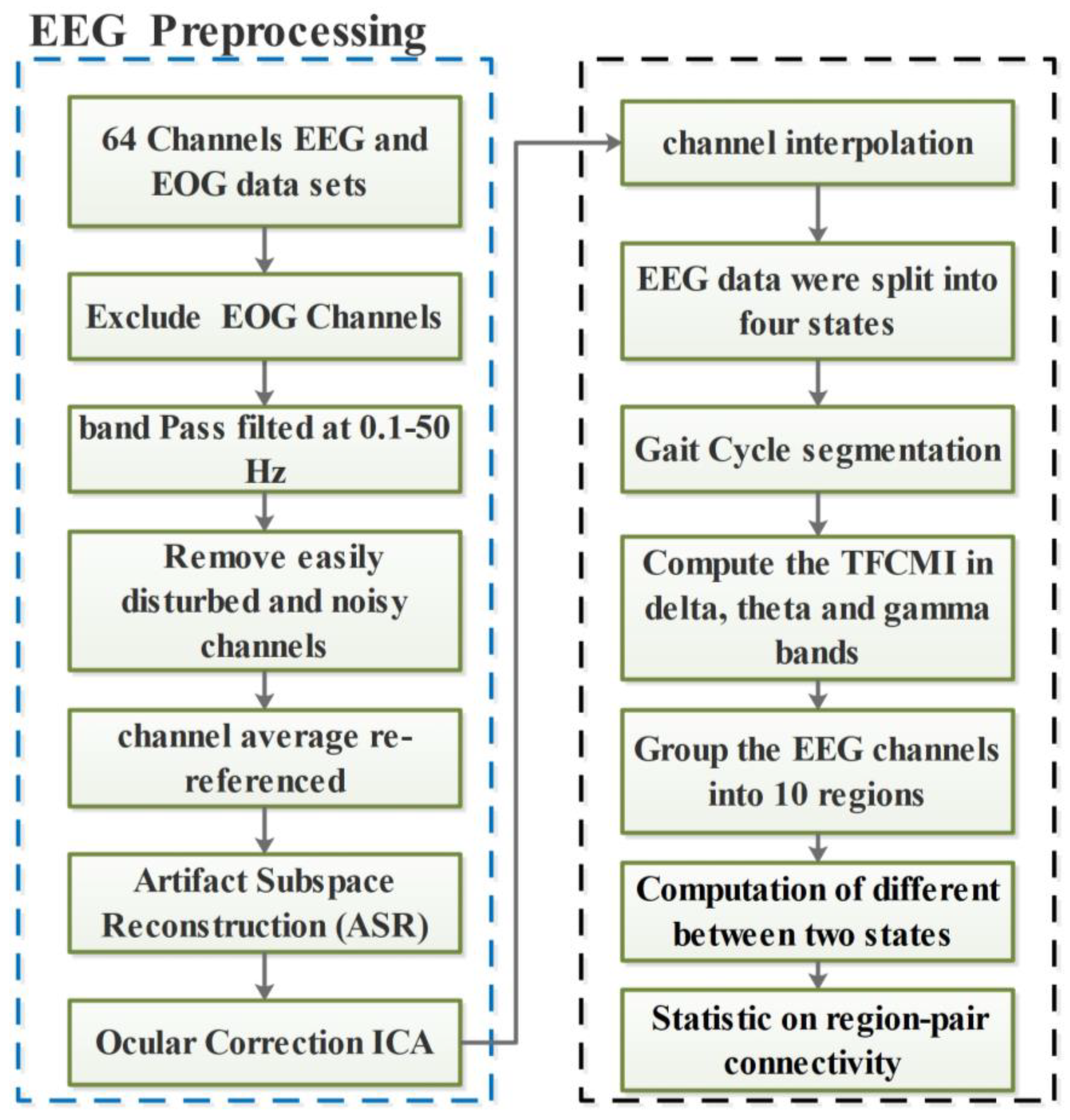
2.2. EEG Signal Processing and Preparation
2.3. Brain Connectivity Analysis Using TFCMI
2.4. Computation of Differences Between Two States
3. Results
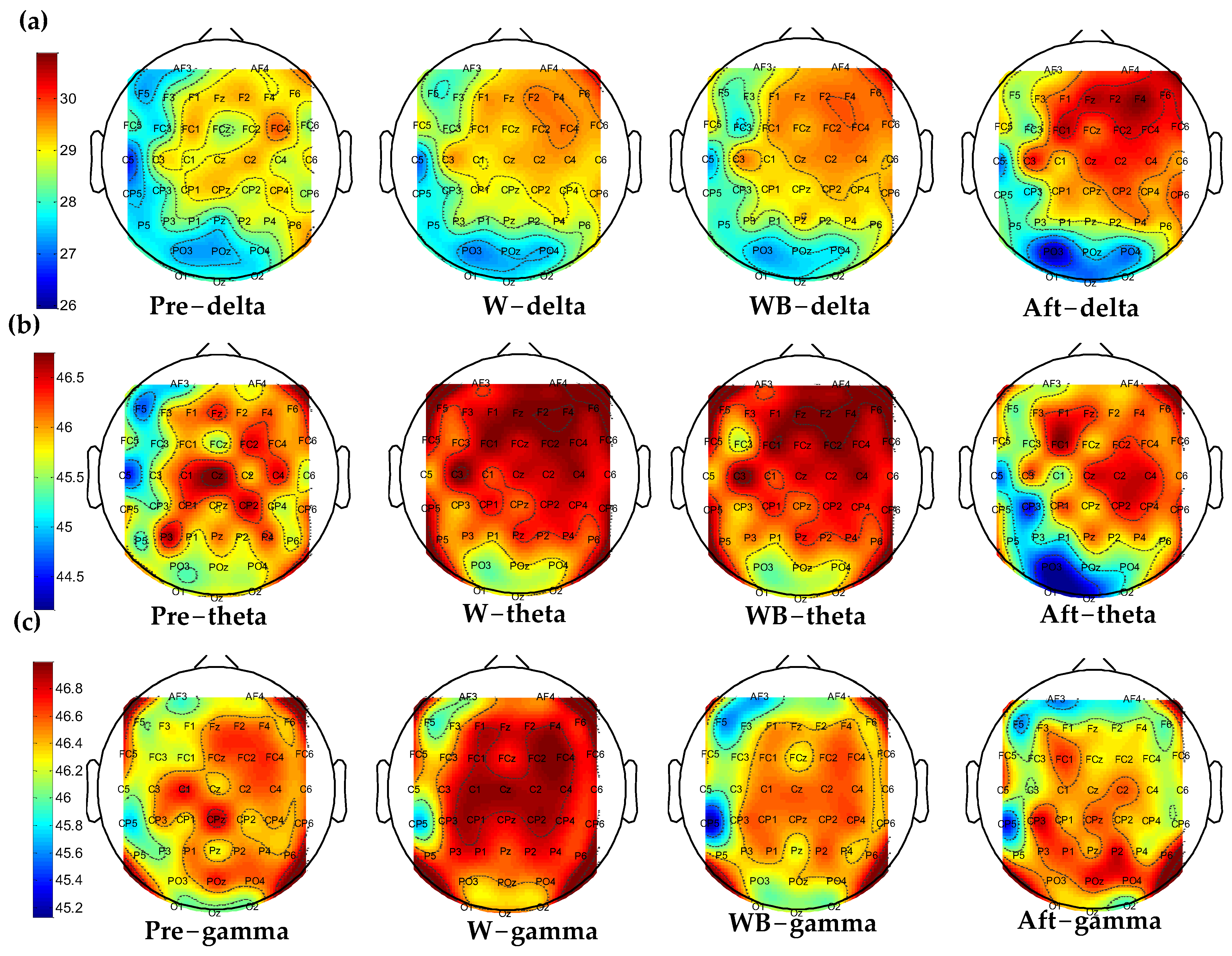
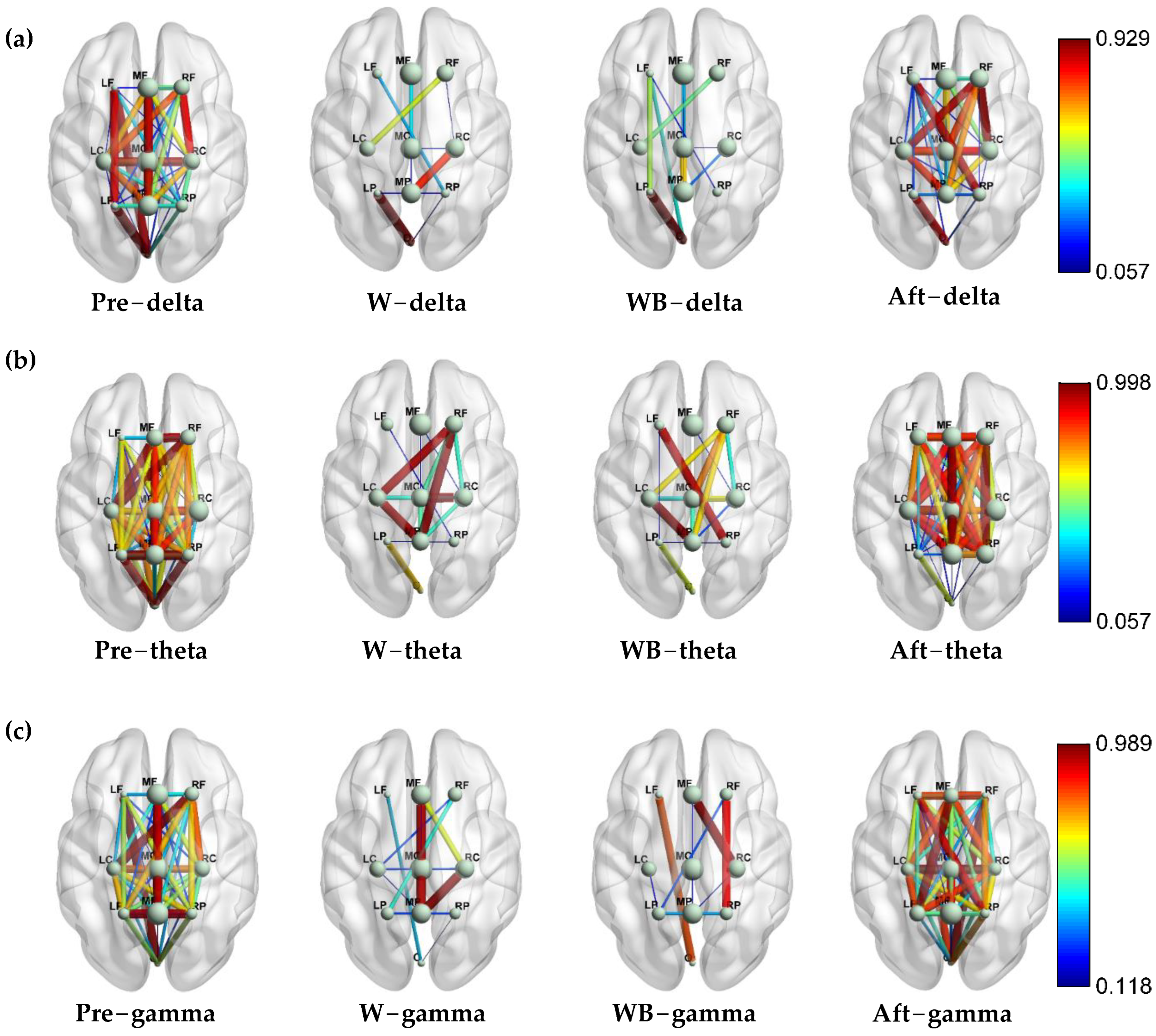
3.1. Accumulated Coupling Strength of Brain Connection in the Time–Frequency Domain
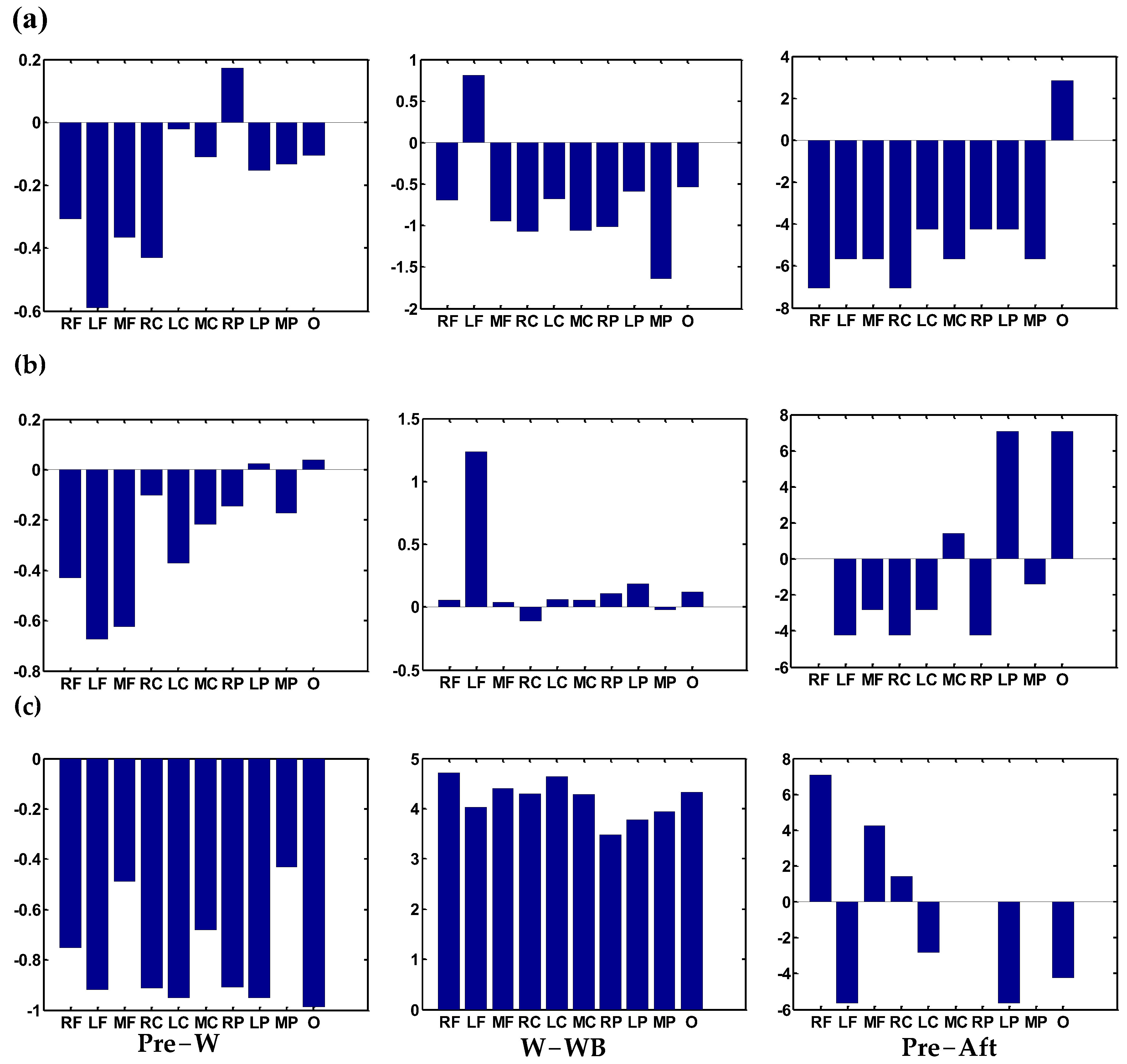
3.2. Accumulated Coupling Connectivity Difference Between Two States in the Time–Frequency Domain
3.3. Statistic on Region–Pair Connectivity
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barthélemy, D.; Grey, M.J.; Nielsen, J.B.; Bouyer, L. Involvement of the Corticospinal Tract in the Control of Human Gait. Prog. Brain Res. 2011, 192, 181–197. [Google Scholar] [CrossRef] [PubMed]
- Tobar, A.M.; Hyoudou, R.; Kita, K.; Nakamura, T.; Kambara, H.; Ogata, Y.; Hanakawa, T.; Koike, Y.; Yoshimura, N. Decoding of Ankle Flexion and Extension from Cortical Current Sources Estimated from Non-Invasive Brain Activity Recording Methods. Front. Neurosci. 2018, 11, 733. [Google Scholar] [CrossRef]
- Wei, P.; Zhang, J.; Tian, F.; Hong, J. A Comparison of Neural Networks Algorithms for EEG and SEMG Features Based Gait Phases Recognition. Biomed. Signal Process. Control 2021, 68, 102587. [Google Scholar] [CrossRef]
- Lau, T.M.; Gwin, J.T.; Ferris, D.P. Walking Reduces Sensorimotor Network Connectivity Compared to Standing. J. Neuroeng. Rehabil. 2014, 11, 14. [Google Scholar] [CrossRef] [PubMed]
- Wagner, J.; Solis-Escalante, T.; Grieshofer, P.; Neuper, C.; Müller-Putz, G.; Scherer, R. Level of Participation in Robotic-Assisted Treadmill Walking Modulates Midline Sensorimotor EEG Rhythms in Able-Bodied Subjects. Neuroimage 2012, 63, 1203–1211. [Google Scholar] [CrossRef] [PubMed]
- Bulea, T.C.; Kim, J.; Damiano, D.; Stanley, C.; Park, H.-S. User-Driven Control Increases Cortical Activity During Treadmill Walking: An EEG Study. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; ISBN 9781424479290. [Google Scholar]
- Gwin, J.T.; Gramann, K.; Makeig, S.; Ferris, D.P. Electrocortical Activity Is Coupled to Gait Cycle Phase during Treadmill Walking. Neuroimage 2011, 54, 1289–1296. [Google Scholar] [CrossRef]
- Gurve, D.; Delisle-Rodriguez, D.; Romero-Laiseca, M.; Cardoso, V.; Loterio, F.; Bastos, T.; Krishnan, S. Subject-Specific EEG Channel Selection Using Non-Negative Matrix Factorization for Lower-Limb Motor Imagery Recognition. J. Neural Eng. 2020, 17, 026029. [Google Scholar] [CrossRef]
- Kim, H.; Yoshimura, N.; Koike, Y. Characteristics of Kinematic Parameters in Decoding Intended Reaching Movements Using Electroencephalography (EEG). Front. Neurosci. 2019, 13, 1148. [Google Scholar] [CrossRef]
- Hekmatmanesh, A.; Nardelli, P.H.J.; Handroos, H. Review of the State-of-the-Art of Brain-Controlled Vehicles. IEEE Access 2021, 9, 110173–110193. [Google Scholar] [CrossRef]
- Tariq, M.; Trivailo, P.M.; Simic, M. EEG-Based BCI Control Schemes for Lower-Limb Assistive-Robots. Front. Hum. Neurosci. 2018, 12, 312. [Google Scholar] [CrossRef]
- Moioli, R.C.; Nardelli, P.H.J.; Barros, M.T.; Saad, W.; Hekmatmanesh, A.; Silva, P.E.G.; De Sena, A.S.; Dzaferagic, M.; Siljak, H.; Van Leekwijck, W.; et al. Neurosciences and Wireless Networks: The Potential of Brain-Type Communications and Their Applications. IEEE Commun. Surv. Tutorials 2021, 23, 1599–1621. [Google Scholar] [CrossRef]
- He, Y.; Luu, T.P.; Nathan, K.; Nakagome, S.; Contreras-Vidal, J.L. Data Descriptor: A Mobile Brainbody Imaging Dataset Recorded during Treadmill Walking with a Brain-Computer Interface. Sci. Data 2018, 5, 180074. [Google Scholar] [CrossRef] [PubMed]
- Luu, T.P.; Nakagome, S.; He, Y.; Contreras-Vidal, J.L. Real-Time EEG-Based Brain-Computer Interface to a Virtual Avatar Enhances Cortical Involvement in Human Treadmill Walking. Sci. Rep. 2017, 7, 8895. [Google Scholar] [CrossRef] [PubMed]
- Foong, R.; Ang, K.K.; Quek, C.; Guan, C.; Phua, K.S.; Kuah, C.W.K.; Deshmukh, V.A.; Yam, L.H.L.; Rajeswaran, D.K.; Tang, N.; et al. Assessment of the Efficacy of EEG-Based MI-BCI with Visual Feedback and EEG Correlates of Mental Fatigue for Upper-Limb Stroke Rehabilitation. IEEE Trans. Biomed. Eng. 2019, 67, 786–795. [Google Scholar] [CrossRef] [PubMed]
- Miller, G. NEUROSCIENCE: Neural Communication Breaks Down as Consciousness Fades and Sleep Sets in. Science 2005, 309, 2148a–2149a. [Google Scholar] [CrossRef]
- Micheloyannis, S.; Pachou, E.; Stam, C.J.; Vourkas, M.; Erimaki, S.; Tsirka, V. Using Graph Theoretical Analysis of Multi Channel EEG to Evaluate the Neural Efficiency Hypothesis. Neurosci. Lett. 2006, 402, 273–277. [Google Scholar] [CrossRef]
- Friston, K.J. Models of Brain Function in Neuroimaging. Annu. Rev. Psychol. 2005, 56, 57–87. [Google Scholar] [CrossRef]
- Lennie, P. The Cost of Cortical Computation Rat Neocortex. Neurons in Human Neocortex Are Larger. Curr. Biol. 2003, 13, 493–497. [Google Scholar] [CrossRef]
- Raichle, M.E.; Mintun, M.A. Brain Work and Brain Imaging. Annu. Rev. Neurosci. 2006, 29, 449–476. [Google Scholar] [CrossRef]
- Lu, C.F.; Teng, S.; Hung, C.I.; Tseng, P.J.; Lin, L.T.; Lee, P.L.; Wu, Y. Te Reorganization of Functional Connectivity during the Motor Task Using EEG Time-Frequency Cross Mutual Information Analysis. Clin. Neurophysiol. 2011, 122, 1569–1579. [Google Scholar] [CrossRef]
- Jiang, T.; He, Y.; Zang, Y.; Weng, X. Modulation of Functional Connectivity during the Resting State and the Motor Task. Hum. Brain Mapp. 2004, 22, 63–71. [Google Scholar] [CrossRef] [PubMed]
- Leocani, L.; Toro, C.; Manganotti, P.; Zhuang, P.; Hallett, M. Event-Related Coherence and Event-Related Desynchronization/Synchronization in the 10 Hz and 20 Hz EEG during Self- Paced Movements. Electroencephalogr. Clin. Neurophysiol.-Evoked Potentials 1997, 104, 199–206. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.C.; Hsieh, J.C.; Wu, Y.Z.; Lee, P.L.; Chen, S.S.; Niddam, D.M.; Yeh, T.C.; Wu, Y. Te Mutual-Information-Based Approach for Neural Connectivity during Self-Paced Finger Lifting Task. Hum. Brain Mapp. 2008, 29, 265–280. [Google Scholar] [CrossRef]
- Nathan, K.; Contreras-Vidal, J.L. Negligible Motion Artifacts in Scalp Electroencephalography (EEG) during Treadmill Walking. Front. Hum. Neurosci. 2016, 9, 708. [Google Scholar] [CrossRef]
- Delorme, A.; Makeig, S. EEGLAB: An Open Source Toolbox for Analysis of Single-Trial EEG Dynamics Including Independent Component Analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef]
- Choi, J.; Kim, H. Real-Time Decoding of EEG Gait Intention for Controlling a Lower-Limb Exoskeleton System. In Proceedings of the 2019 7th International Winter Conference on Brain-Computer Interface (BCI), Gangwon, Republic of Korea, 18–20 February 2019. [Google Scholar]
- Wei, P.; Zhang, J.; Wang, B.; Hong, J. Surface Electromyography and Electroencephalogram-Based Gait Phase Recognition and Correlations Between Cortical and Locomotor Muscle in the Seven Gait Phases. Front. Neurosci. 2021, 15, 607905. [Google Scholar] [CrossRef] [PubMed]
- Popivanov, D.; Dushanova, J. Cognitive Neuroscience NeuroReport Non-Linear EEG Dynamic Changes and Their Probable Relation to Voluntary Movement Organization. Neuroreport 1999, 10, 1397–1401. [Google Scholar] [CrossRef]
- Presacco, A.; Goodman, R.; Forrester, L.; Contreras-Vidal, J.L. Neural Decoding of Treadmill Walking from Noninvasive Electroencephalographic Signals. J. Neurophysiol. 2011, 106, 1875–1887. [Google Scholar] [CrossRef]
- Womelsdorf, T.; Johnston, K.; Vinck, M.; Everling, S. Theta-Activity in Anterior Cingulate Cortex Predicts Task Rules and Their Adjustments Following Errors. Proc. Natl. Acad. Sci. USA 2010, 107, 5248–5253. [Google Scholar] [CrossRef]
- Costa, Á.; Iáñez, E.; Úbeda, A.; Hortal, E.; Del-Ama, A.J.; Gil-Agudo, Á.; Azorín, J.M. Decoding the Attentional Demands of Gait through EEG Gamma Band Features. PLoS ONE 2016, 11, e0154136. [Google Scholar] [CrossRef]
- Xia, M.; Wang, J.; He, Y. BrainNet Viewer: A Network Visualization Tool for Human Brain Connectomics. PLoS ONE 2013, 8, e68910. [Google Scholar] [CrossRef] [PubMed]
- Attwell, D.; Laughlin, S.B. An Energy Budget for Signaling in the Grey Matter of the Brain. J. Cereb. Blood Flow Metab. 2001, 21, 1133–1145. [Google Scholar] [CrossRef] [PubMed]
- Gevins, A.; Smith, M.E.; McEvoy, L.; Yu, D. High-Resolution EEG Mapping of Cortical Activation Related to Working Memory: Effects of Task Difficulty, Type of Processing, and Practice. Cereb. Cortex 1997, 7, 374–385. [Google Scholar] [CrossRef] [PubMed]
- Luu, P.; Tucker, D.M.; Makeig, S. Frontal Midline Theta and the Error-Related Negativity: Neurophysiological Mechanisms of Action Regulation. Clin. Neurophysiol. 2004, 115, 1821–1835. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, J.; Hwang, G.; Curran, T.; Kahana, M.J. EEG Oscillations and Recognition Memory: Theta Correlates of Memory Retrieval and Decision Making. Neuroimage 2006, 32, 978–987. [Google Scholar] [CrossRef]
- Seeber, M.; Scherer, R.; Wagner, J.; Solis-Escalante, T.; Müller-Putz, G.R. EEG Beta Suppression and Low Gamma Modulation Are Different Elements of Human Upright Walking. Front. Hum. Neurosci. 2014, 8, 485. [Google Scholar] [CrossRef]

| Label | Cortical | Channels |
|---|---|---|
| RF | Right Frontal area | F2, F4, FC2, FC4 |
| LF | Left-Frontal area | F1, F3, FC1, FC3 |
| MF | Middle Frontal area | Fz, FCz |
| RC | Right Central area | C2, C4, FC2, CP2 |
| LC | Left Central area | C1, C3, CP1, FC1 |
| MC | Middle Central area | Cz, CPz, FCz |
| RP | Right Parietal area | CP2, CP4, P2, P4 |
| LP | Left-Parietal area | CP1, CP3, P1, P3 |
| MP | Middle Parietal area | CPz, Pz |
| O | Occipital | PO3, PO4, POz, O1, O2, Oz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, P.; Chen, T.; Zhang, J.; Li, J.; Hong, J.; Zhang, L. Study of the Brain Functional Connectivity Processes During Multi-Movement States of the Lower Limbs. Sensors 2024, 24, 7016. https://doi.org/10.3390/s24217016
Wei P, Chen T, Zhang J, Li J, Hong J, Zhang L. Study of the Brain Functional Connectivity Processes During Multi-Movement States of the Lower Limbs. Sensors. 2024; 24(21):7016. https://doi.org/10.3390/s24217016
Chicago/Turabian StyleWei, Pengna, Tong Chen, Jinhua Zhang, Jiandong Li, Jun Hong, and Lin Zhang. 2024. "Study of the Brain Functional Connectivity Processes During Multi-Movement States of the Lower Limbs" Sensors 24, no. 21: 7016. https://doi.org/10.3390/s24217016
APA StyleWei, P., Chen, T., Zhang, J., Li, J., Hong, J., & Zhang, L. (2024). Study of the Brain Functional Connectivity Processes During Multi-Movement States of the Lower Limbs. Sensors, 24(21), 7016. https://doi.org/10.3390/s24217016






