Intelligent Fault Diagnosis of Planetary Gearbox Across Conditions Based on Subdomain Distribution Adversarial Adaptation
Abstract
1. Introduction
- (1)
- A novel framework incorporating the time–frequency representation construction and subdomain distribution adversarial adaptation diagnosis method is proposed for the fault diagnosis of planetary gearboxes. It allows the model to generalize better across a wide range of operating conditions by aligning the subclass and overall class of data simultaneously, which enhances the fault diagnosis performance.
- (2)
- Time–frequency representation is adopted as the input of deep learning to provide intrinsic information of health state. The STFT is applied to extract time–frequency representation from vibration signals. It can reflect the variation of frequency components and amplitudes over time, which can characterize the non-stationary condition of planetary gearbox more confidently.
- (3)
- Local difference adversarial evaluation is used to discover the correlation of faults information by assessing conditional distribution differences between source and target subclass fault data. It can handle variations and discrepancies in fault data, thus revealing more in-depth information for transfer learning.
- (4)
- An experiment is designed to validate the proposed method. Data of planetary gear and bearing were collected on the test rig across different operational conditions for validation. The result demonstrates that the method is effective and superior to other methods for the fault diagnosis of planetary gearboxes.
2. Theoretical Background
2.1. Representation of Nonstationary Operating Condition
2.2. Feature Learning Based on Residual Algorithms
2.3. Domain Adversarial Training
2.4. Domain Confusion Training
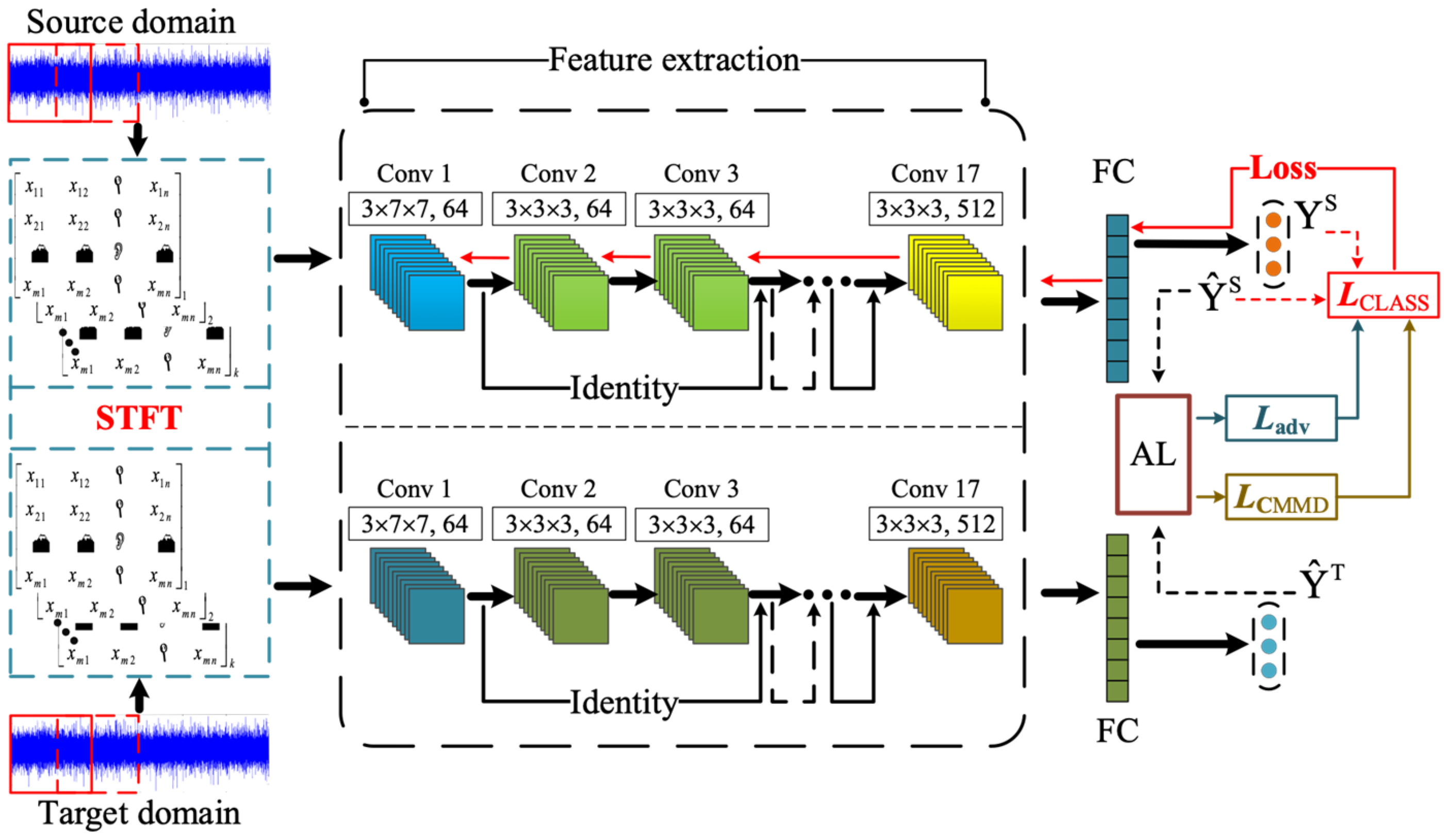
3. Subdomain Distribution Adversarial Adaptation Framework
3.1. Transfer Framework Design
3.2. Design of Loss Function
4. Experimental Validation and Result Analysis
4.1. Experimental Setup
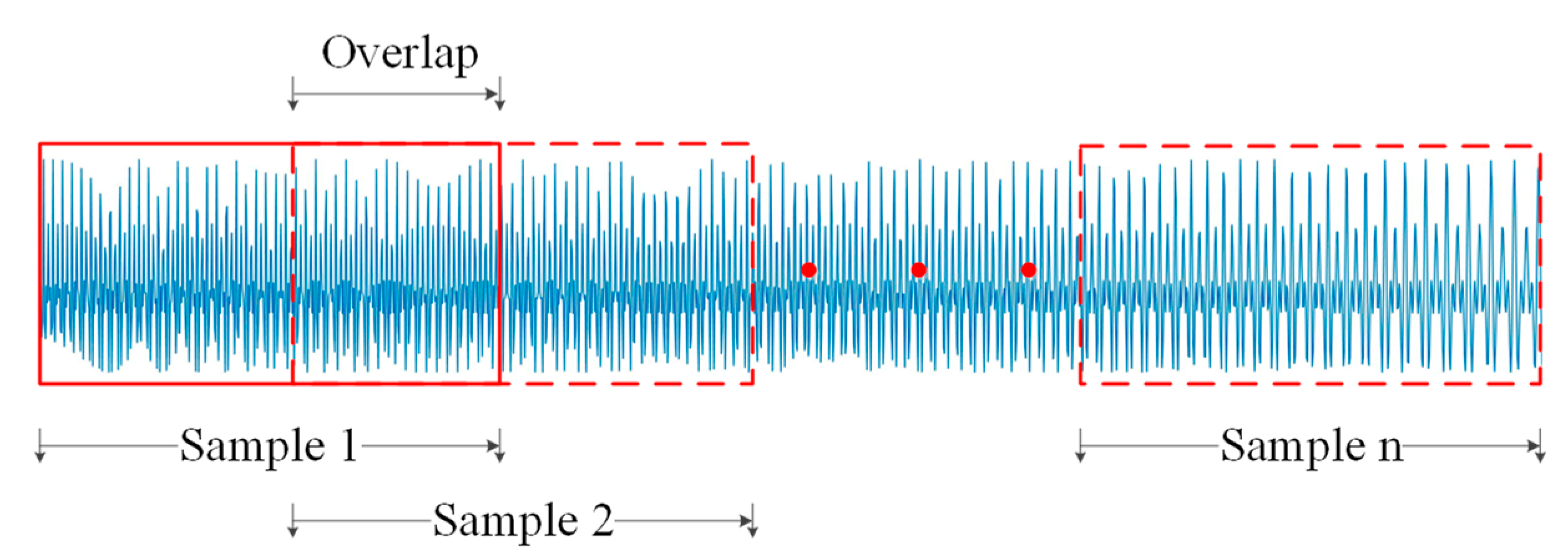
4.2. Experimental Dataset
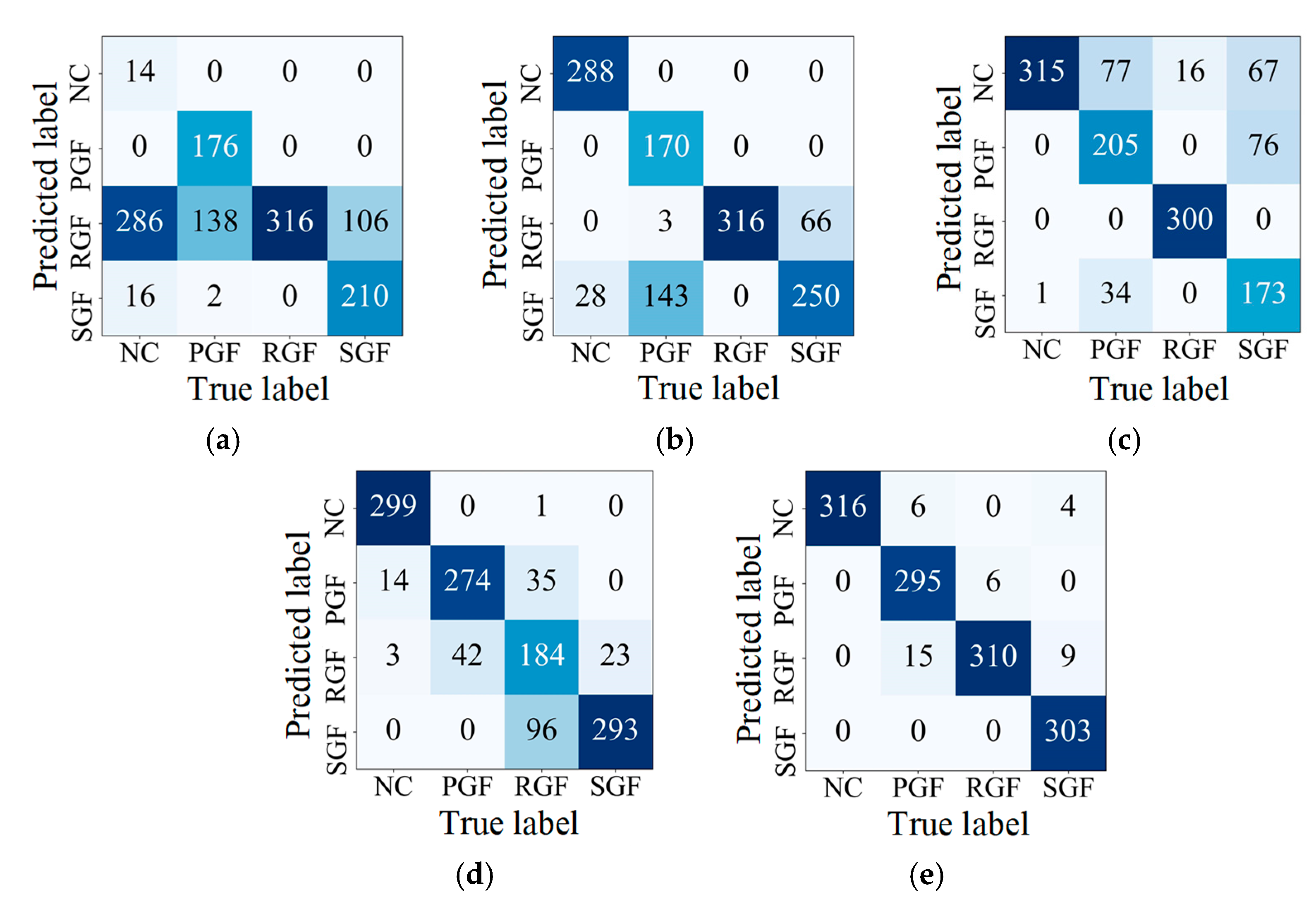
4.3. Method Validation and Diagnostic Results
- (1)
- Fault Diagnosis of Planetary Gear
- (2)
- Fault Diagnosis Results of Planetary Bearing
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, C.; Feng, Z. Application of multi-domain sparse features for fault identification of planetary gearbox. Measurement 2017, 104, 169–179. [Google Scholar] [CrossRef]
- Liang, X.; Zuo, M.J.; Feng, Z. Dynamic modeling of gearbox faults: A review. Mech. Syst. Signal Process. 2018, 98, 852–876. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Li, X. Big Data-Driven Intelligent Fault Diagnosis and Prognosis for Mechanical Systems; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Zhao, Z.; Han, H.; Wang, P.; Ma, H.; Zhang, S.; Yang, Y. An improved model for meshing characteristics analysis of spur gears considering fractal surface contact and friction. Mech. Mach. Theory 2021, 158, 104219. [Google Scholar] [CrossRef]
- Xiang, L.; An, C.; Zhang, Y.; Hu, A. Failure dynamic modelling and analysis of planetary gearbox considering gear tooth spalling. Eng. Fail. Anal. 2021, 125, 105444. [Google Scholar] [CrossRef]
- Feng, Z.; Zuo, M.J. Vibration signal models for fault diagnosis of planetary gearboxes. J. Sound Vib. 2012, 331, 4919–4939. [Google Scholar] [CrossRef]
- Feng, Z.; Zhang, D.; Zuo, M.J. Planetary gearbox fault diagnosis via joint amplitude and frequency demodulation analysis based on variational mode decomposition. Appl. Sci. 2017, 7, 775. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; Shi, J.; Shen, C.; Huang, W.; Zhu, Z. A coarse-to-fine decomposing strategy of VMD for extraction of weak repetitive transients in fault diagnosis of rotating machines. Mech. Syst. Signal Process. 2019, 116, 668–692. [Google Scholar] [CrossRef]
- Zhao, X.; Jia, M. Fault diagnosis of rolling bearing based on feature reduction with global-local margin Fisher analysis. Neurocomputing 2018, 315, 447–464. [Google Scholar] [CrossRef]
- Yu, J.; He, Y. Planetary gearbox fault diagnosis based on data-driven valued characteristic multigranulation model with incomplete diagnostic information. J. Sound Vib. 2018, 429, 63–77. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, Y.; Cheng, C.; Peng, Z. A hybrid classification autoencoder for semi-supervised fault diagnosis in rotating machinery. Mech. Syst. Signal Process. 2021, 149, 107327. [Google Scholar] [CrossRef]
- Zhang, K.; Tang, B.; Deng, L.; Tan, Q.; Yu, H. A fault diagnosis method for wind turbines gearbox based on adaptive loss weighted meta-ResNet under noisy labels. Mech. Syst. Signal Process. 2021, 161, 107963. [Google Scholar] [CrossRef]
- Yin, A.; Yan, Y.; Zhang, Z.; Li, C.; Sánchez, R.-V. Fault diagnosis of wind turbine gearbox based on the optimized LSTM neural network with cosine loss. Sensors 2020, 20, 2339. [Google Scholar] [CrossRef]
- Ullah, F.; Turab, A.; Ullah, S.; Cacciagrano, D.; Zhao, Y. Enhanced Network Intrusion Detection System for Internet of Things Security Using Multimodal Big Data Representation with Transfer Learning and Game Theory. Sensors 2024, 24, 4152. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhang, W.; Ding, Q. A robust intelligent fault diagnosis method for rolling element bearings based on deep distance metric learning. Neurocomputing 2018, 310, 77–95. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, N.; Shen, C. A new deep transfer learning method for bearing fault diagnosis under different working conditions. IEEE Sens. J. 2019, 20, 8394–8402. [Google Scholar] [CrossRef]
- Deng, Y.; Huang, D.; Du, S.; Li, G.; Zhao, C.; Lv, J. A double-layer attention based adversarial network for partial transfer learning in machinery fault diagnosis. Comput. Ind. 2021, 127, 103399. [Google Scholar] [CrossRef]
- Zhao, K.; Jiang, H.; Wang, K.; Pei, Z. Joint distribution adaptation network with adversarial learning for rolling bearing fault diagnosis. Knowl.-Based Syst. 2021, 222, 106974. [Google Scholar] [CrossRef]
- Han, T.; Liu, C.; Yang, W.; Jiang, D. Deep transfer network with joint distribution adaptation: A new intelligent fault diagnosis framework for industry application. ISA Trans. 2020, 97, 269–281. [Google Scholar] [CrossRef]
- Tan, Y.; Guo, L.; Gao, H.; Zhang, L. Deep coupled joint distribution adaptation network: A method for intelligent fault diagnosis between artificial and real damages. IEEE Trans. Instrum. Meas. 2020, 70, 3507212. [Google Scholar] [CrossRef]
- Tzeng, E.; Hoffman, J.; Zhang, N.; Saenko, K.; Darrell, T. Deep domain confusion: Maximizing for domain invariance. arXiv 2014, arXiv:1412.3474. [Google Scholar]
- Ganin, Y.; Lempitsky, V. Unsupervised domain adaptation by backpropagation. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1180–1189. [Google Scholar]
- Yu, C.; Wang, J.; Chen, Y.; Huang, M. Transfer learning with dynamic adversarial adaptation network. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 778–786. [Google Scholar]
- Feng, Z.; Liang, M.; Chu, F. Recent advances in time–frequency analysis methods for machinery fault diagnosis: A review with application examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar] [CrossRef]
- Song, L.; Tan, J. Rotation Error Prediction of CNC Spindle Based on Short-Time Fourier Transform of Vibration Sensor Signals and Improved Weighted Residual Network. Sensors 2024, 24, 4244. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Hu, Y.; Li, M.; Zheng, J. Fault diagnostics between different type of components: A transfer learning approach. Appl. Soft Comput. 2020, 86, 105950. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Satpal, S.; Sarawagi, S. Domain adaptation of conditional probability models via feature subsetting. In Knowledge Discovery in Databases: PKDD 2007, Proceedings of the 11th European Conference on Principles and Practice of Knowledge Discovery in Databases, Warsaw, Poland, 17–21 September 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 224–235. [Google Scholar]









| Input: Given source domain data pairs and target domain data . |
| Output: The well-trained model. |
| Begin |
| 1: Configure the adaptation layer in the diagnostic framework. |
| 2: Randomly initialize the ResNet18 parameters. |
| Training |
| for epoch in epochs do |
| 3: Simultaneously extract the feature information from the source domain data and target domain data . |
| 4: Computing the classification loss in the source task , . |
| 5: Calculate the adversarial loss between and . |
| 6: Calculate the conditional adaptation loss between and . |
| 7: Fine-tuning the classification loss by adversarial loss and adaptation loss . |
| 8: Updating network weight parameters by back propagation with updated loss |
| end for |
| Until The loss in the target task converges or the training epochs reach. |
| Induction Motor | Generator | |
| Rated power | 4 kW | 200 W |
| Rated voltage | 380 V | 24 V |
| No. of slots | 36 | 39 |
| No. of pole pairs | 2 | 6 |
| Gear Type | Planet | Sun | Ring |
| No. of gear teeth | 35 (3) | 36 | 108 |
| Diameter of Pitch Circle (mm) | Diameter of Rollers (mm) | No. of Rollers | Contact (°) |
| 19.5 | 3.5 | 10 | 0 |
| Length (mm) | Width (mm) | Depth (mm) | |
| Sun gear | 16.3 | 0.2 | 0.8 |
| Planet gear | 17 | 0.2 | 0.8 |
| Ring gear | 17.5 | 0.2 | 0.8 |
| Inner race (planet pin) | 18 | 1 | 0.5 |
| Outer race (planet bore) | 17 | 1 | 0.5 |
| Rolling element | 11.5 | 1 | 0.5 |
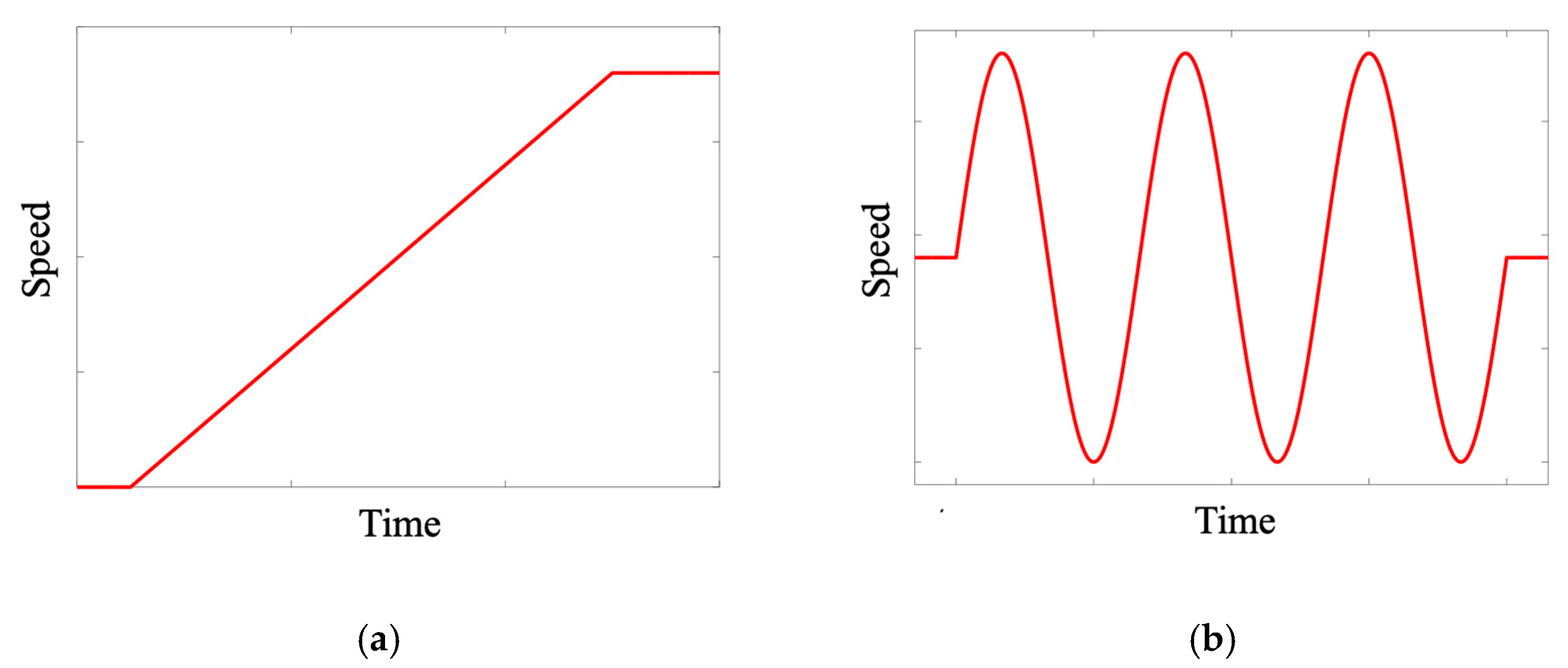
| Time-Varying Mode | Range of Motor Speed(rpm) | Symbol |
| Linearity | 0~720 | Vin/Bin |
| Sinusoidal | 150~330 | V1/B1 |
| 390~570 | V2/B2 | |
| 510~690 | V3/B3 |
| Motor Speed (rpm) | Transfer Tasks | Health Status | ||
| Source Domain | Target Domain | |||
| 1 | 0~720 | 150~330 | Vin–V1 | NC PGF RGF SGF |
| 2 | 390~570 | Vin–V2 | ||
| 3 | 510~690 | Vin–V3 | ||
| 4 | 150~330 | 390~570 | V1–V2 | |
| 5 | 390~570 | 150~330 | V2–V1 | |
| 6 | 150~330 | 510~690 | V1–V3 | |
| 7 | 510~690 | 150~330 | V3–V1 | |
| 8 | 390~570 | 510~690 | V2–V3 | |
| 9 | 510~690 | 390~570 | V3–V2 | |
| Motor Speed (rpm) | Transfer Tasks | Health Status | ||
| Source Domain | Target Domain | |||
| 1 | 0~720 | 150~330 | Bin-B1 | NC IRF ORF REF |
| 2 | 390~570 | Bin-B2 | ||
| 3 | 510~690 | Bin-B3 | ||
| 4 | 150~330 | 390~570 | B1-B2 | |
| 5 | 390~570 | 150~330 | B2-B1 | |
| 6 | 150~330 | 510~690 | B1-B3 | |
| 7 | 510~690 | 150~330 | B3-B1 | |
| 8 | 390~570 | 510~690 | B2-B3 | |
| 9 | 510~690 | 390~570 | B3-B2 | |
| ResNet18 | DAN | DDAN | DAAN | SDAA | |
| Vin-V1 | 59.5 ± 0.392 | 76.2 ± 0.232 | 70.4 ± 0.349 | 83.7 ± 0.295 | 95.3 ± 0.126 |
| Vin-V2 | 57.5 ± 0.329 | 77.3 ± 0.218 | 68.5 ± 0.327 | 86.7 ± 0.236 | 96.5 ± 0.096 |
| Vin-V3 | 56.4 ± 0.352 | 75.9 ± 0.187 | 77.2 ± 0.283 | 82.6 ± 0.228 | 95.9 ± 0.118 |
| V1-V2 | 43.3 ± 0.285 | 76.2 ± 0.262 | 74.7 ± 0.274 | 83.4 ± 0.324 | 97.2 ± 0.112 |
| V2-V1 | 44.9 ± 0.314 | 75.8 ± 0.278 | 73.5 ± 0.261 | 83.6 ± 0.332 | 96.8 ± 0.106 |
| V1-V3 | 39.8 ± 0.402 | 72.7 ± 0.365 | 71.3 ± 0.282 | 85.8 ± 0.343 | 97.5 ± 0.130 |
| V3-V1 | 40.3 ± 0.336 | 71.6 ± 0.322 | 70.5 ± 0.243 | 84.9 ± 0.349 | 97.1 ± 0.112 |
| V2-V3 | 46.7 ± 0.347 | 75.4 ± 0.349 | 83.6 ± 0.358 | 86.3 ± 0.273 | 96.9 ± 0.121 |
| V3-V2 | 48.3 ± 0.351 | 76.5 ± 0.318 | 82.3 ± 0.302 | 87.1 ± 0.285 | 97.3 ± 0.132 |
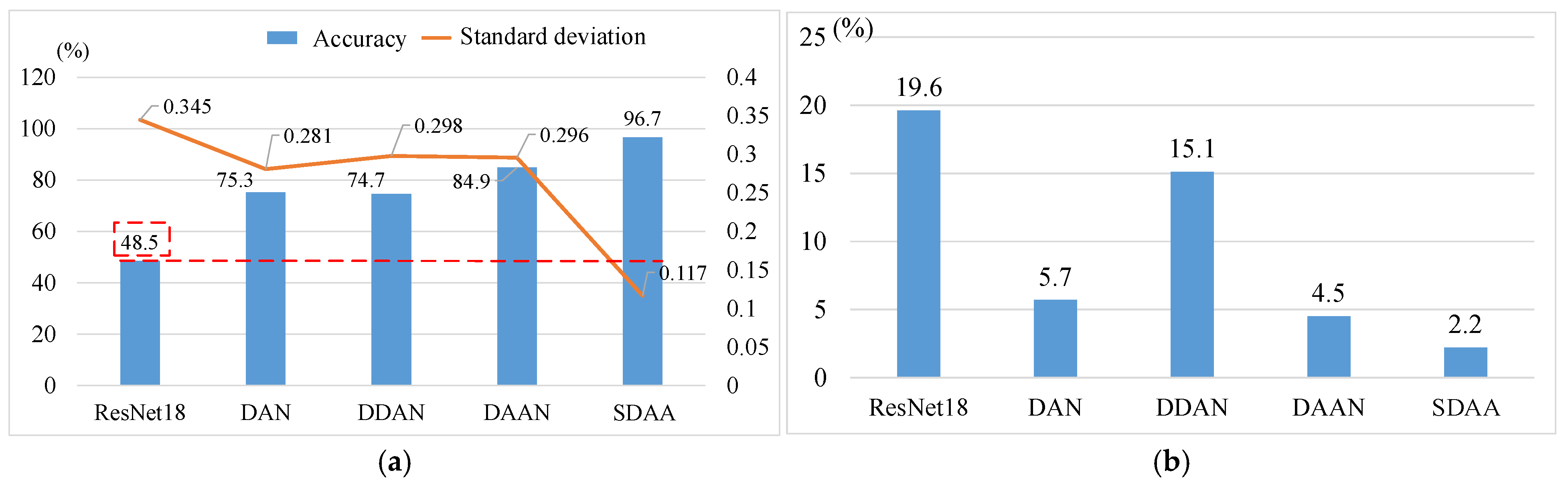
| Average | 48.5 ± 0.345 | 75.3 ± 0.281 | 74.7 ± 0.298 | 84.9 ± 0.296 | 96.7 ± 0.117 |
| ResNet18 | DAN | DDAN | DAAN | SDAA | |
| Bin-B1 | 53.3 ± 0.435 | 74.2 ± 0.341 | 65.4 ± 0.252 | 87.6 ± 0.284 | 93.6 ± 0.106 |
| Bin-B2 | 51.9 ± 0.542 | 75.3 ± 0.357 | 63.5 ± 0.231 | 83.5 ± 0.231 | 95.8 ± 0.083 |
| Bin-B3 | 49.8 ± 0.536 | 75.9 ± 0.226 | 68.2 ± 0.257 | 82.8 ± 0.198 | 94.7 ± 0.035 |
| B1-B2 | 42.4 ± 0.528 | 75.1 ± 0.216 | 73.7 ± 0.162 | 82.1 ± 0.302 | 95.9 ± 0.052 |
| B2-B1 | 43.5 ± 0.484 | 74.2 ± 0.252 | 74.3 ± 0.151 | 81.7 ± 0.294 | 94.6 ± 0.084 |
| B1-B3 | 39.6 ± 0.455 | 70.8 ± 0.256 | 67.4 ± 0.201 | 85.5 ± 0.132 | 94.8 ± 0.108 |
| B3-B1 | 40.2 ± 0.521 | 69.9 ± 0.218 | 68.8 ± 0.442 | 84.3 ± 0.118 | 95.7 ± 0.043 |
| B2-B3 | 45.3 ± 0.442 | 77.3 ± 0.351 | 84.2 ± 0.294 | 86.3 ± 0.154 | 96.7 ± 0.057 |
| B3-B2 | 46.5 ± 0.458 | 78.8 ± 0.386 | 84.7 ± 0.259 | 86.4 ± 0.134 | 95.2 ± 0.052 |
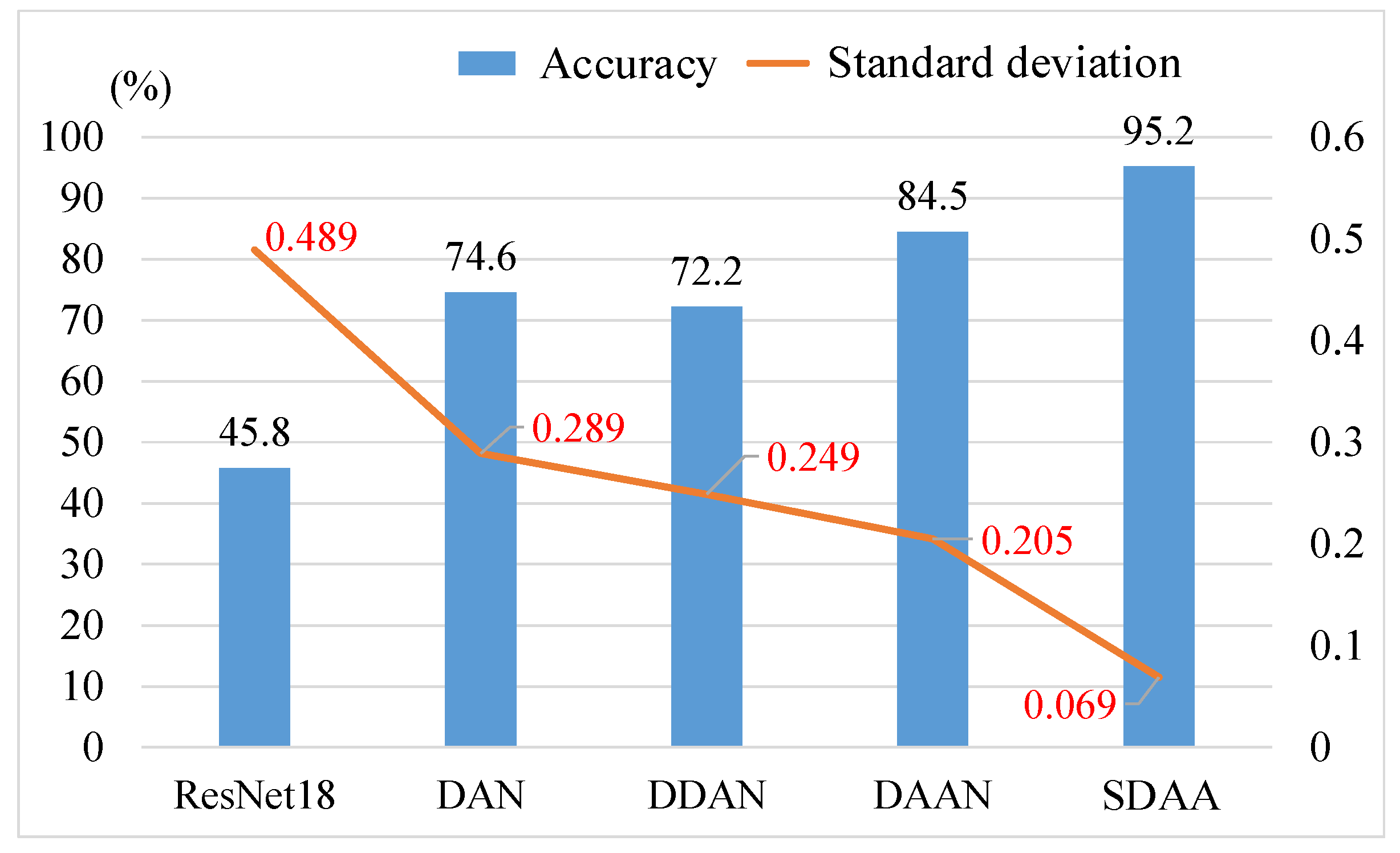
| Average | 45.8 ± 0.489 | 74.6 ± 0.289 | 72.2 ± 0.249 | 84.5 ± 0.205 | 95.2 ± 0.069 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, S.; Feng, Z.; Zhang, Y.; Du, M.; Yang, Y. Intelligent Fault Diagnosis of Planetary Gearbox Across Conditions Based on Subdomain Distribution Adversarial Adaptation. Sensors 2024, 24, 7017. https://doi.org/10.3390/s24217017
Han S, Feng Z, Zhang Y, Du M, Yang Y. Intelligent Fault Diagnosis of Planetary Gearbox Across Conditions Based on Subdomain Distribution Adversarial Adaptation. Sensors. 2024; 24(21):7017. https://doi.org/10.3390/s24217017
Chicago/Turabian StyleHan, Songjun, Zhipeng Feng, Ying Zhang, Minggang Du, and Yang Yang. 2024. "Intelligent Fault Diagnosis of Planetary Gearbox Across Conditions Based on Subdomain Distribution Adversarial Adaptation" Sensors 24, no. 21: 7017. https://doi.org/10.3390/s24217017
APA StyleHan, S., Feng, Z., Zhang, Y., Du, M., & Yang, Y. (2024). Intelligent Fault Diagnosis of Planetary Gearbox Across Conditions Based on Subdomain Distribution Adversarial Adaptation. Sensors, 24(21), 7017. https://doi.org/10.3390/s24217017








