Structural Damage Early Warning Method of Quayside Container Crane Based on Fuzzy Entropy Ratio Variation Deviation
Abstract
1. Introduction
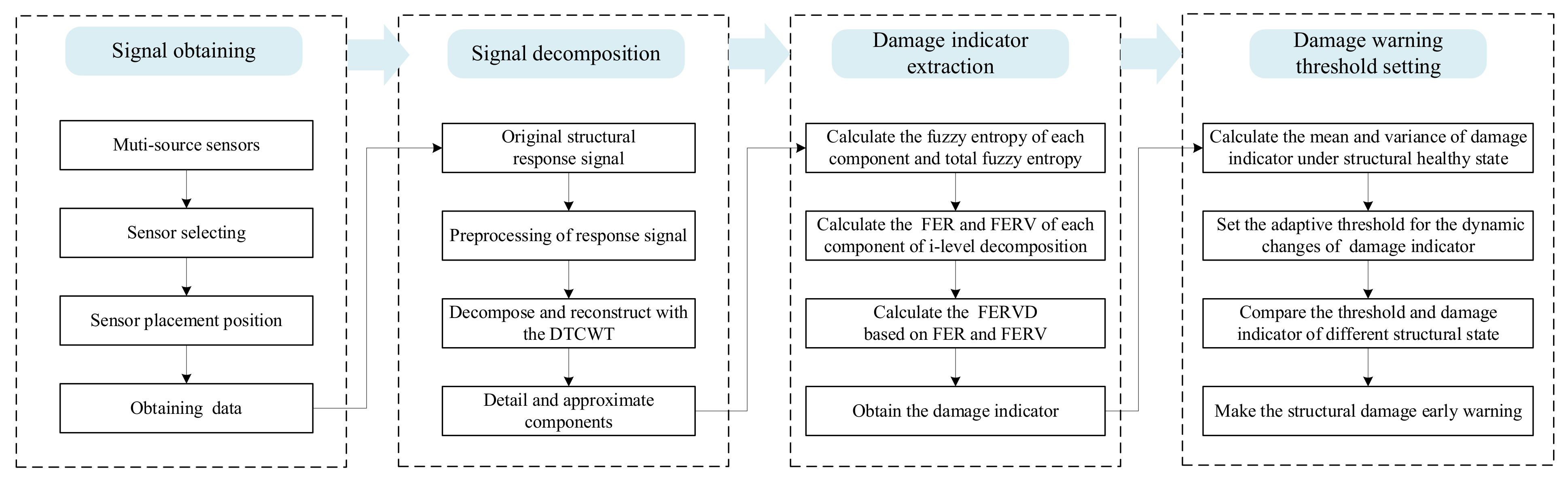
2. Methods
2.1. Fuzzy Entropy (FE)
2.2. Construction of FERVD Damage Warning Indicators
2.3. Setting of FERVD Warning Threshold
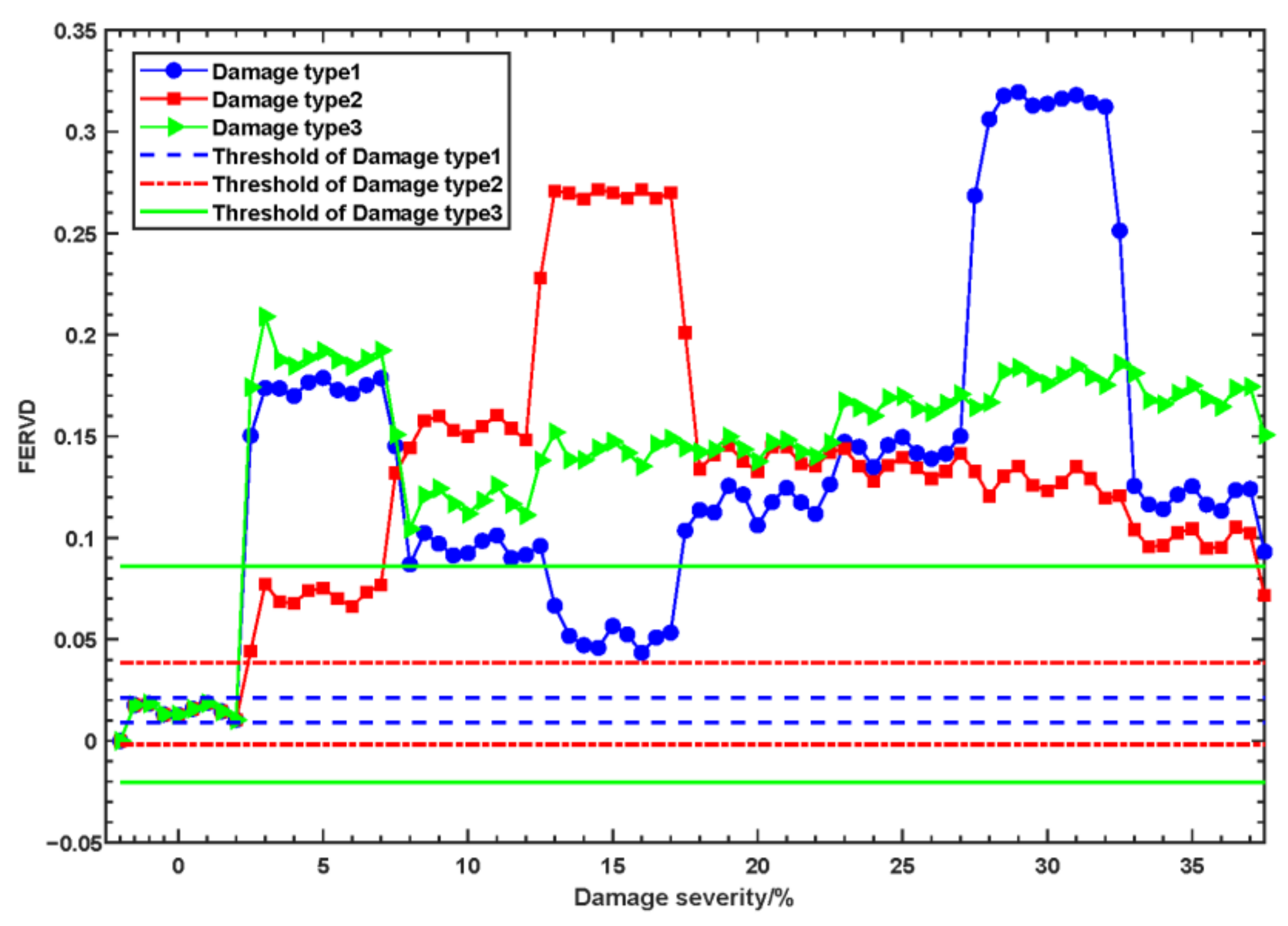
3. Numerical Example
3.1. Damage Simulation of Finite Element Model for Structure of QCCs
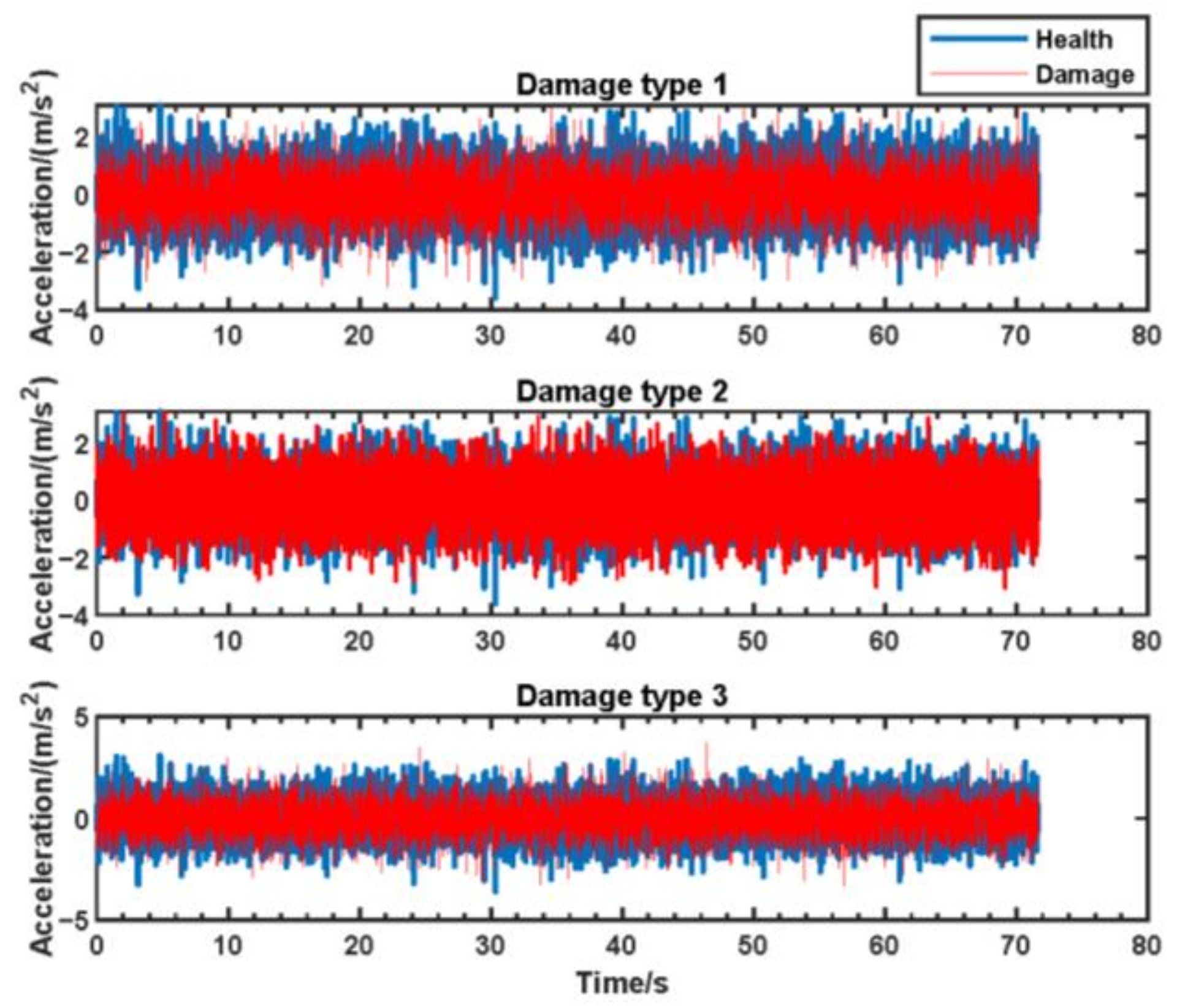
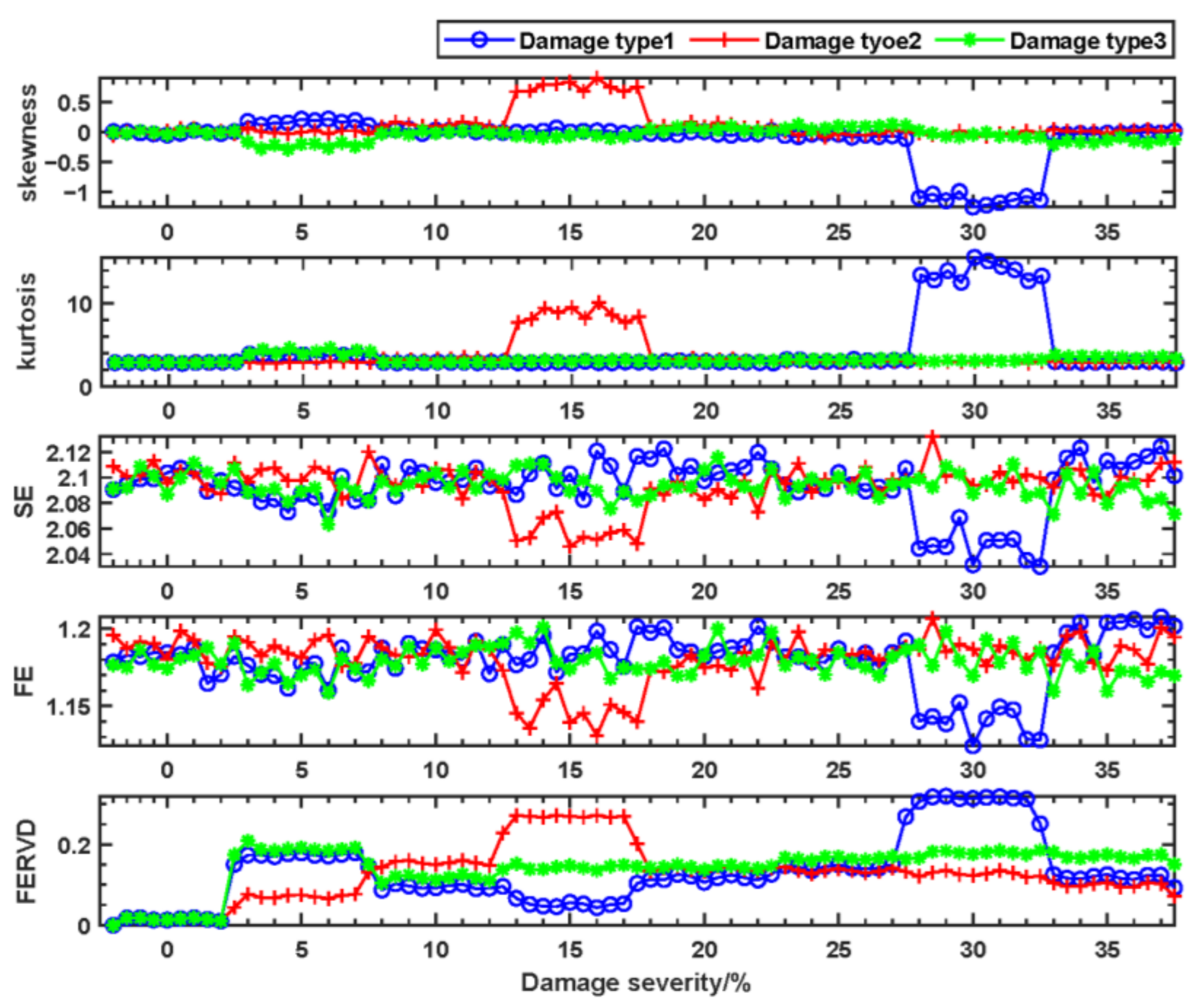
3.2. Results and Discussion
4. Case Study in Engineering
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to Machine Learning and Deep Learning applications. Mech. Syst. Signal Proc. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, C.; Yan, F. Condition monitoring of wind turbine based on incremental learning and multivariate state estimation technique. Renew. Energy 2022, 184, 343–360. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Inman, D.J. Wireless and real-time structural damage detection: A novel decentralized method for wireless sensor networks. J. Sound Vib. 2018, 424, 158–172. [Google Scholar] [CrossRef]
- Bull, L.; Worden, K.; Manson, G.; Dervilis, N. Active learning for semi-supervised structural health monitoring. J. Sound Vib. 2018, 437, 373–388. [Google Scholar] [CrossRef]
- Ihn, J.; Chang, F. Pitch-catch Active Sensing Methods in Structural Health Monitoring for Aircraft Structures. Struct. Health Monit. 2008, 7, 5–19. [Google Scholar] [CrossRef]
- Yi, T.; Huang, H.; Li, H. Development of sensor validation methodologies for structural health monitoring: A comprehensive review. Measurement 2017, 109, 200–214. [Google Scholar] [CrossRef]
- Kullaa, J. Distinguishing between sensor fault, structural damage, and environmental or operational effects in structural health monitoring. Mech. Syst. Signal Proc. 2011, 25, 2976–2989. [Google Scholar] [CrossRef]
- Achenbach, J.D. Structural health monitoring—What is the prescription? Mech. Res. Commun. 2009, 36, 137–142. [Google Scholar] [CrossRef]
- Babak, V.P.; Babak, S.V.; Eremenko, V.S.; Kuts, Y.V.; Myslovych, M.V.; Scherbak, L.M.; Zaporozhets, A.O. Models and Measures in Measurements and Monitoring; Springer International Publishing AG: Cham, Switzerland, 2021; Volume 360. [Google Scholar]
- Tronci, E.M.; De Angelis, M.; Betti, R.; Altomare, V. Vibration-based structural health monitoring of a RC-masonry tower equipped with non-conventional TMD. Eng. Struct. 2020, 224, 111212. [Google Scholar] [CrossRef]
- Hu, W.; Thöns, S.; Rohrmann, R.G.; Said, S.; Rücker, W. Vibration-based structural health monitoring of a wind turbine system. Part I: Resonance phenomenon. Eng. Struct. 2015, 89, 260–272. [Google Scholar] [CrossRef]
- Zhou, H.F.; Ni, Y.Q.; Ko, J.M. Structural damage alarming using auto-associative neural network technique: Exploration of environment-tolerant capacity and setup of alarming threshold. Mech. Syst. Signal Proc. 2011, 25, 1508–1526. [Google Scholar] [CrossRef]
- Babak, V.; Zaporozhets, A.; Khaidurov, V.; Scherbak, L.; Bohachev, I.; Tsiupii, T. Mathematical Models and Software for Studying the Elasticity of Building Structures and Their Systems; Springer International Publishing AG: Cham, Switzerland, 2023; Volume 454. [Google Scholar]
- Pan, Y.; Zhang, L.; Wu, X.; Zhang, K.; Skibniewski, M.J. Structural health monitoring and assessment using wavelet packet energy spectrum. Saf. Sci. 2019, 120, 652–665. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Wang, Y.W.; Zhang, C. A Bayesian approach for condition assessment and damage alarm of bridge expansion joints using long-term structural health monitoring data. Eng. Struct. 2020, 212, 110520. [Google Scholar] [CrossRef]
- Li, X.; Mao, H.; Li, B.; Xu, N. Dynamic early warning of rockburst using microseismic multi-parameters based on Bayesian network. Eng. Sci. Technol. Int. J. 2020, 24, 715–727. [Google Scholar] [CrossRef]
- Yang, R.; Qiao, T.; Pang, Y.; Yang, Y.; Zhang, H.; Yan, G. Infrared spectrum analysis method for detection and early warning of longitudinal tear of mine conveyor belt. Measurement 2020, 165, 107856. [Google Scholar] [CrossRef]
- Feng, X.; Liu, J.; Chen, B.; Xiao, Y.; Feng, G.; Zhang, F. Monitoring, Warning, and Control of Rockburst in Deep Metal Mines. Engineering 2017, 3, 538–545. [Google Scholar] [CrossRef]
- Qiu, J.; Liang, W.; Zhang, L.; Yu, X.; Zhang, M. The early-warning model of equipment chain in gas pipeline based on DNN-HMM. J. Nat. Gas Sci. Eng. 2015, 27, 1710–1722. [Google Scholar] [CrossRef]
- Vafaei, N.; Ribeiro, R.A.; Camarinha-Matos, L.M. Fuzzy early warning systems for condition based maintenance. Comput. Ind. Eng. 2019, 128, 736–746. [Google Scholar] [CrossRef]
- Chen, X.; Wang, P.; Hao, Y.; Zhao, M. Evidential KNN-based condition monitoring and early warning method with applications in power plant. Neurocomputing 2018, 315, 18–32. [Google Scholar] [CrossRef]
- Jia, X.Y.; Liu, J. Analysis of Early-Warning Threshold for Metro Construction Collapse Risk Based on D-S Evidence Theory and Rough Set. Wuhan Univ. J. Nat. Sci. 2017, 22, 510–516. [Google Scholar]
- Rafei, A.; Pasha, E.; Jamshidi, O.R. A warning threshold for monitoring tuberculosis surveillance data: An alternative to hidden Markov model. Trop. Med. Int. Health 2015, 20, 919–929. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Chen, H.; Du, X. Study on the early warning mechanism for real-time monitored structural responses of a historical timber building. Measurement 2020, 165, 108136. [Google Scholar] [CrossRef]
- Duan, D.; Han, S.; Wang, Z.; Pang, C.; Yao, L.; Liu, W.; Yang, J.; Zheng, C.; Gao, X. Multivariate state estimation-based condition monitoring of slurry circulating pumps for wet flue gas desulfurization of power plants. Eng. Fail. Anal. 2024, 159, 108099. [Google Scholar] [CrossRef]
- Li, Y.; Dai, W.; Zhu, L.; Zhao, B. A novel fault early warning method for mechanical equipment based on improved MSET and CCPR. Measurement 2023, 218, 113224. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wang, R.; Huang, W. A fault diagnosis scheme for rolling bearing based on local mean decomposition and improved multiscale fuzzy entropy. J. Sound Vib. 2016, 360, 277–299. [Google Scholar] [CrossRef]
- Yentes, J.M.; Hunt, N.; Schmid, K.K.; Kaipust, J.P.; McGrath, D.; Stergiou, N. The Appropriate Use of Approximate Entropy and Sample Entropy with Short Data Sets. Ann. Biomed. Eng. 2013, 41, 349–365. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate Entropy as a Measure of System Complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Zheng, J.; Cheng, J.; Yang, Y. A rolling bearing fault diagnosis approach based on LCD and fuzzy entropy. Mech. Mach. Theory 2013, 70, 441–453. [Google Scholar] [CrossRef]
- Chen, W.; Zhuang, J.; Yu, W.; Wang, Z. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef]
- Raka, S.; Combastel, C. Fault detection based on robust adaptive thresholds: A dynamic interval approach. Annu. Rev. Control 2013, 37, 119–128. [Google Scholar] [CrossRef]
- Shi, Z.; Gu, F.; Lennox, B.; Ball, A.D. The development of an adaptive threshold for model-based fault detection of a nonlinear electro-hydraulic system. Control Eng. Pract. 2005, 13, 1357–1367. [Google Scholar] [CrossRef]

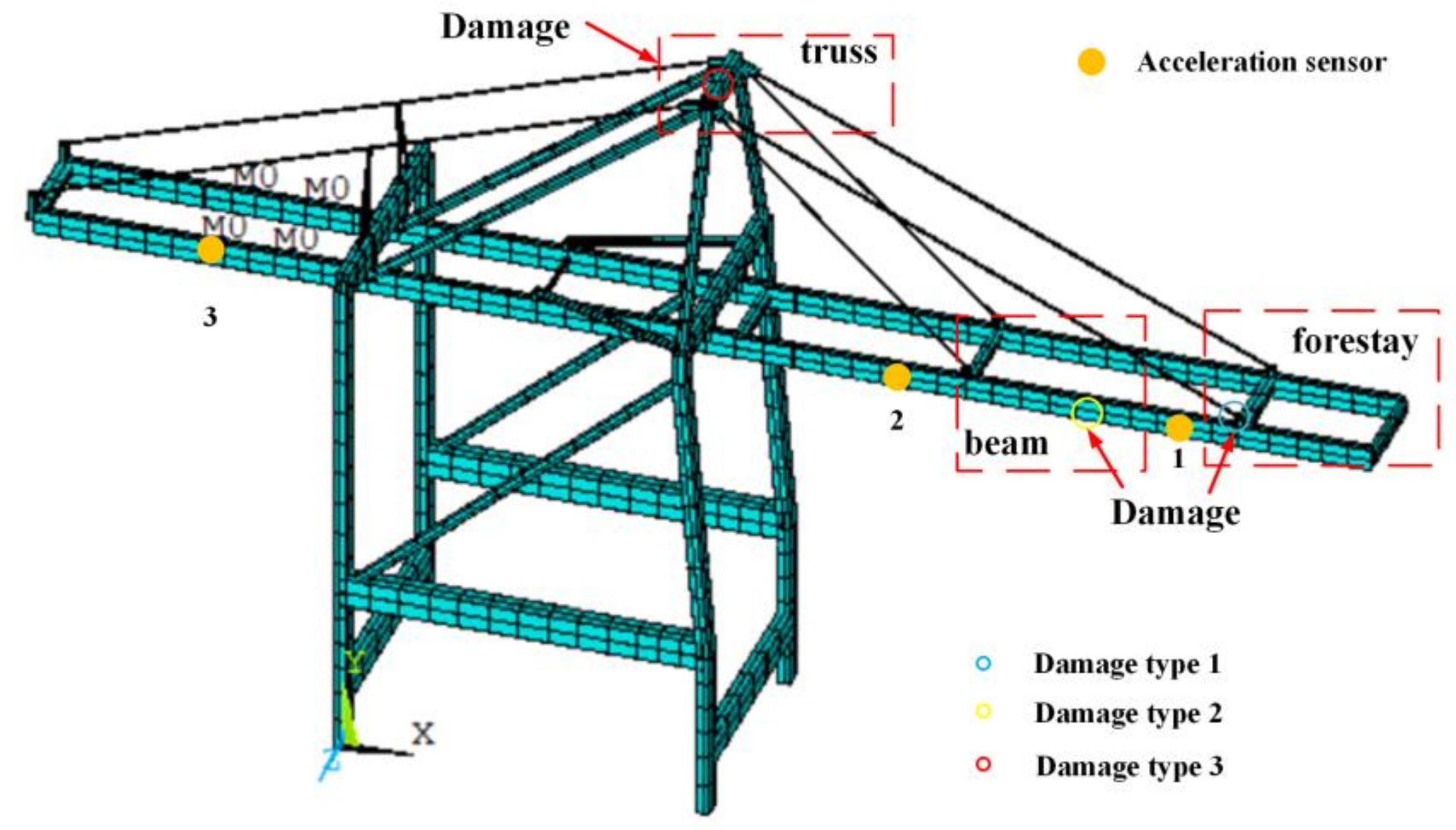





| Sensors | Monitoring Sites | Monitoring Directions |
|---|---|---|
| V1, V2 | the maximum forward extension of the front beam | X, Y |
| V3, V4 | the connection between the front beam and the middle forestry | X, Z |
| V5, V6 | the front beam near the sea-side door frame | X, Y |
| V7, V8 | the mid-span of the rear beam | X, Y |
| V9, V10 | the maximum backward extension of the rear beam | X, Y |
| Damaged Type | Description | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | stiffness reduction from 0% to 35% for the end of the forestay | |||||||
| 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | |
| 2 | stiffness reduction from 0% to 35% for the mid-span of the front beam | |||||||
| 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | |
| 3 | stiffness reduction from 0% to 35% for the top of the truss | |||||||
| 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | |
| Monitoring Points | Threshold | Mean Value of FERVD for Monitoring Data in Different Time Periods | ||||||
|---|---|---|---|---|---|---|---|---|
| 0 s~10 s | 11 s~20 s | 21 s~30 s | 31 s~40 s | 41 s~50 s | 51 s~60 s | 61 s~70 s | ||
| 1 | [0.0070~0.0389] | 0.0159 | 0.0307 | 0.0312 | 0.0348 | 0.0342 | 0.0285 | 0.0279 |
| 2 | [0.0115~0.0565] | 0.0225 | 0.0183 | 0.0280 | 0.0327 | 0.0291 | 0.0245 | 0.0314 |
| 3 | [0.0020~0.0681] | 0.0350 | 0.0426 | 0.0280 | 0.0318 | 0.0381 | 0.0391 | 0.0317 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhao, J.; Zhao, D.; Qin, X. Structural Damage Early Warning Method of Quayside Container Crane Based on Fuzzy Entropy Ratio Variation Deviation. Sensors 2024, 24, 7575. https://doi.org/10.3390/s24237575
Liu J, Zhao J, Zhao D, Qin X. Structural Damage Early Warning Method of Quayside Container Crane Based on Fuzzy Entropy Ratio Variation Deviation. Sensors. 2024; 24(23):7575. https://doi.org/10.3390/s24237575
Chicago/Turabian StyleLiu, Jiahui, Jian Zhao, Dong Zhao, and Xianrong Qin. 2024. "Structural Damage Early Warning Method of Quayside Container Crane Based on Fuzzy Entropy Ratio Variation Deviation" Sensors 24, no. 23: 7575. https://doi.org/10.3390/s24237575
APA StyleLiu, J., Zhao, J., Zhao, D., & Qin, X. (2024). Structural Damage Early Warning Method of Quayside Container Crane Based on Fuzzy Entropy Ratio Variation Deviation. Sensors, 24(23), 7575. https://doi.org/10.3390/s24237575






