A Novel Diagnostic Feature for a Wind Turbine Imbalance Under Variable Speed Conditions
Abstract
1. Introduction
- -
- To investigate the nonstationary dynamics of a wind turbine rotor via an equivalent mass–spring–damper system under centrifugal excitation.
- -
- To find a closed-form expression describing the dependency between the rotational speed and the fundamental rotation harmonic intensity.
- -
- To propose a speed-invariant diagnostic feature for imbalance fault diagnosis in wind turbines via simplifying the closed-form dependency for low-speed systems.
- -
- To adopt the short-time chirp Fourier transform and process the experimental vibration data collected from a 2.3 MW wind turbine with a permissible imbalance.
- -
- To obtain the local interference level and obtain the residuals describing the net feature values.
- -
- To normalize the residuals by the local interference levels.
- -
- To extract the conventional and the proposed diagnostic features and to investigate their dependencies on the rotational speed.
2. Theoretical Background, Diagnostic Feature Proposition and Experimental Setup
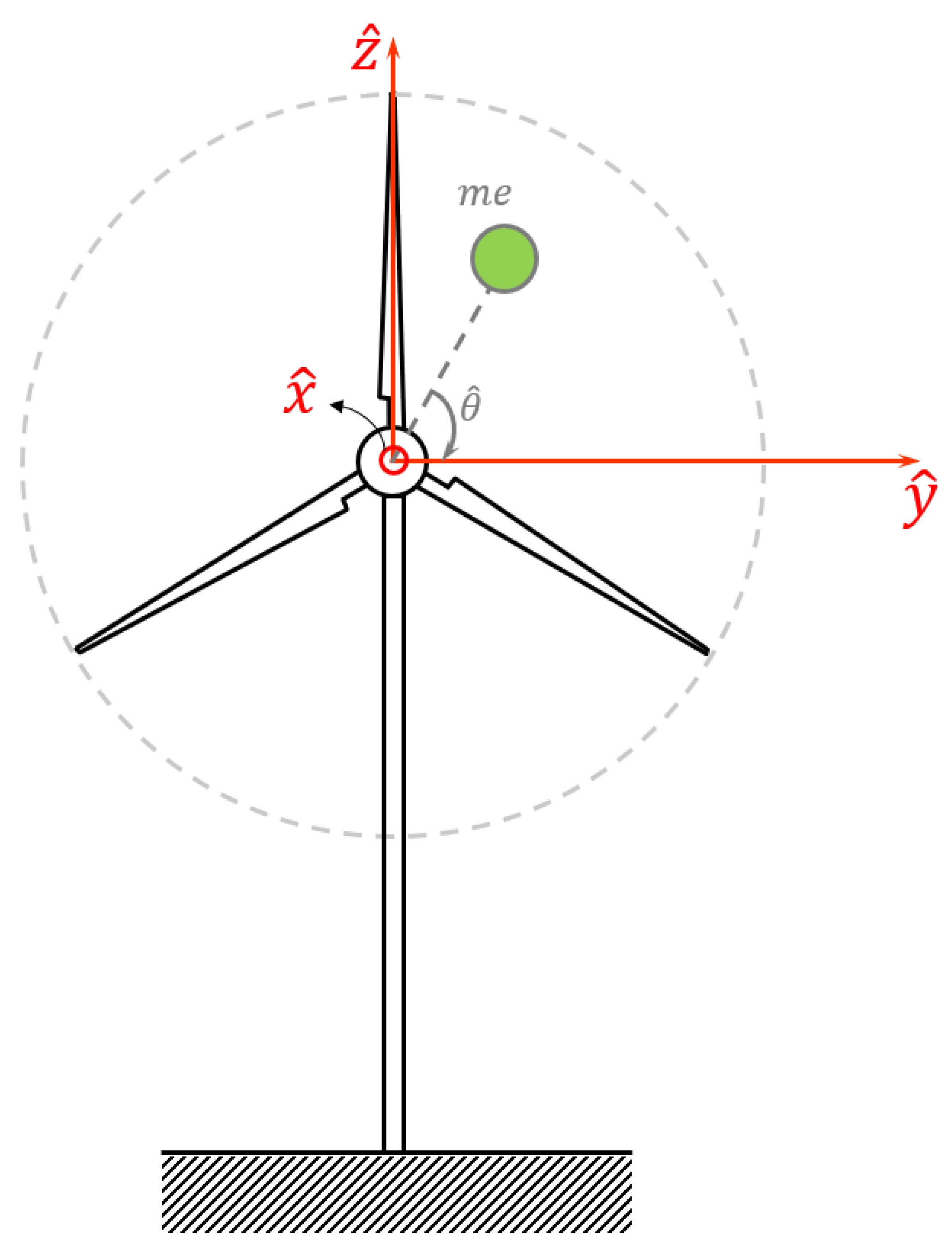
2.1. Theoretical Background
2.2. Feature Extraction
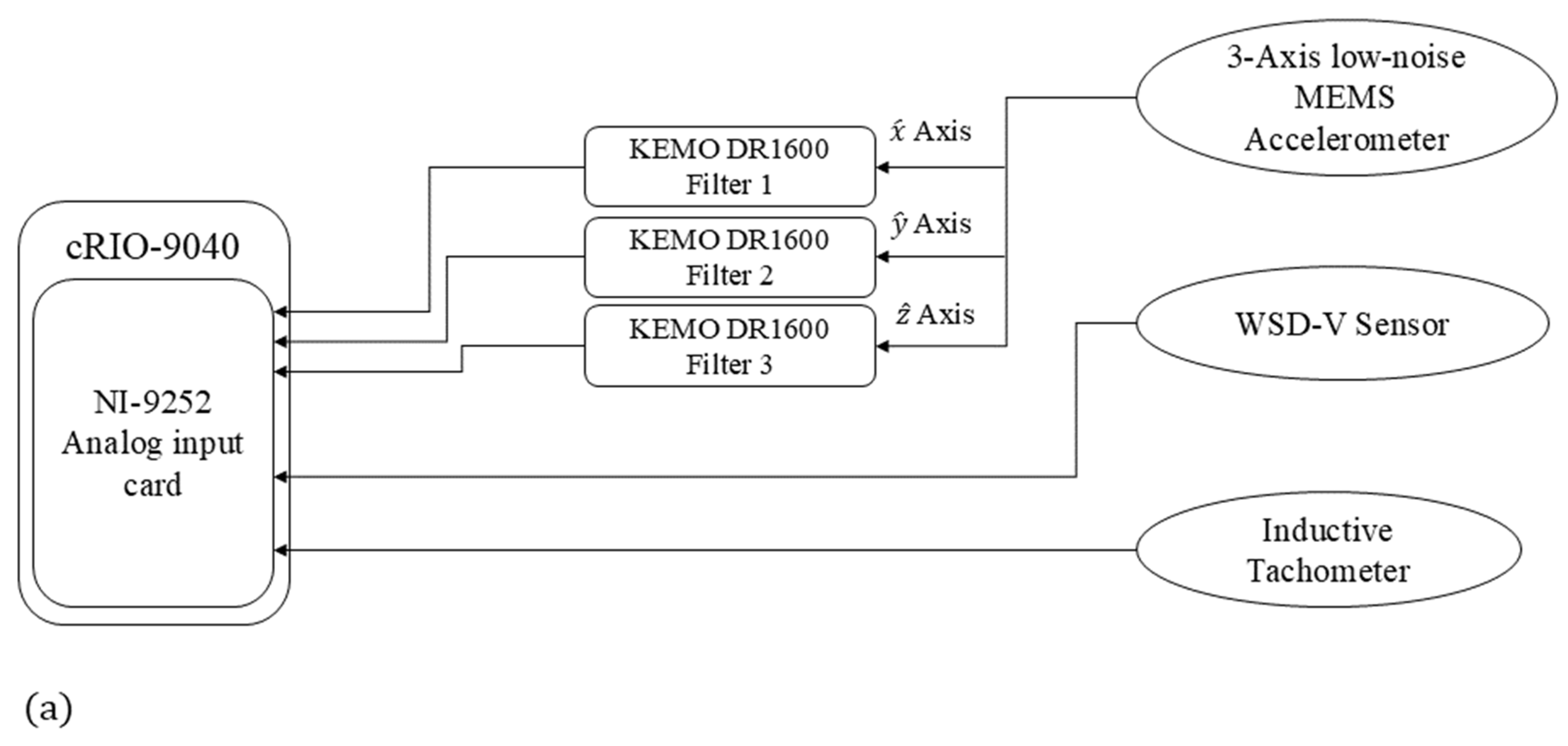
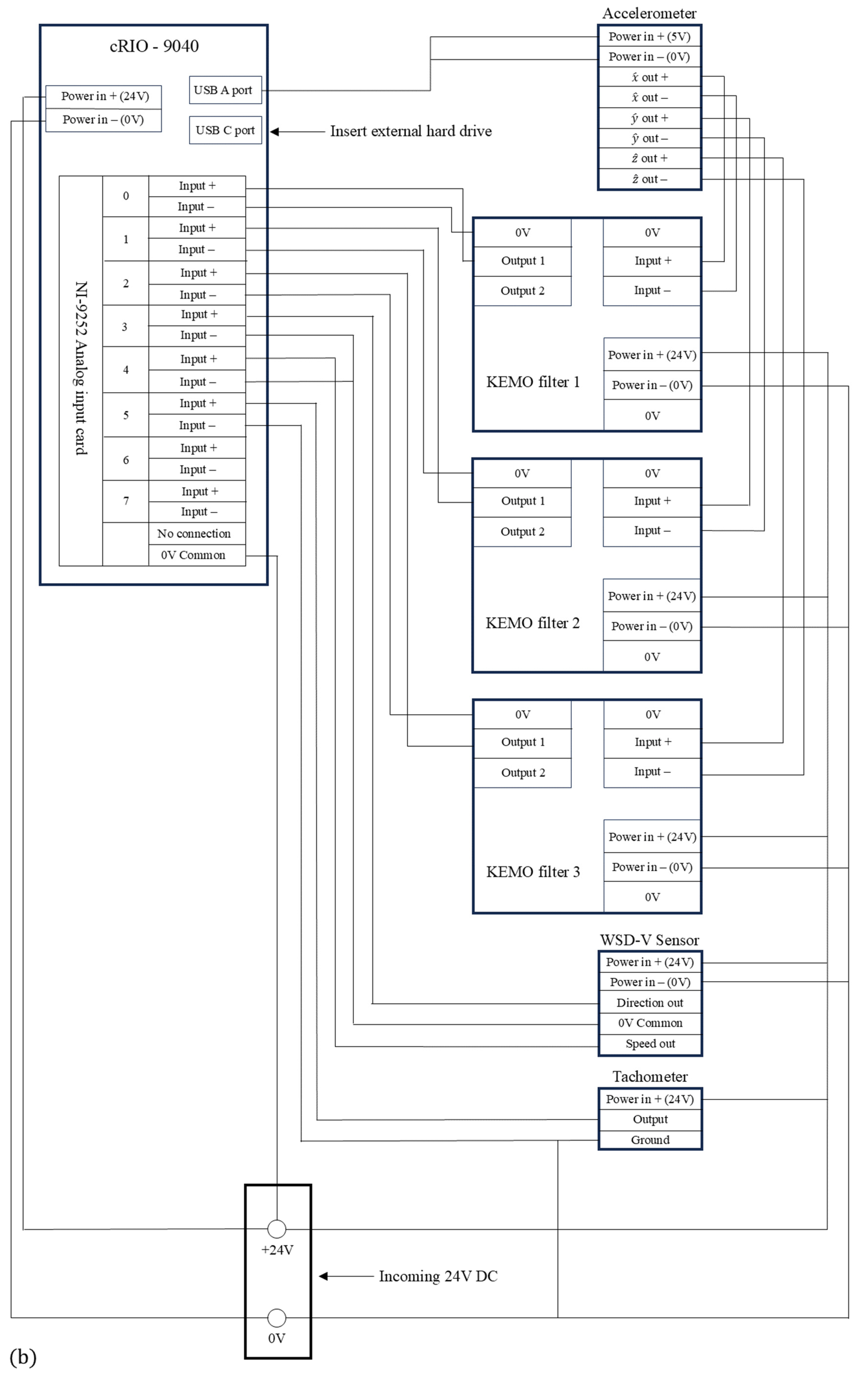
2.3. Experimental Setup
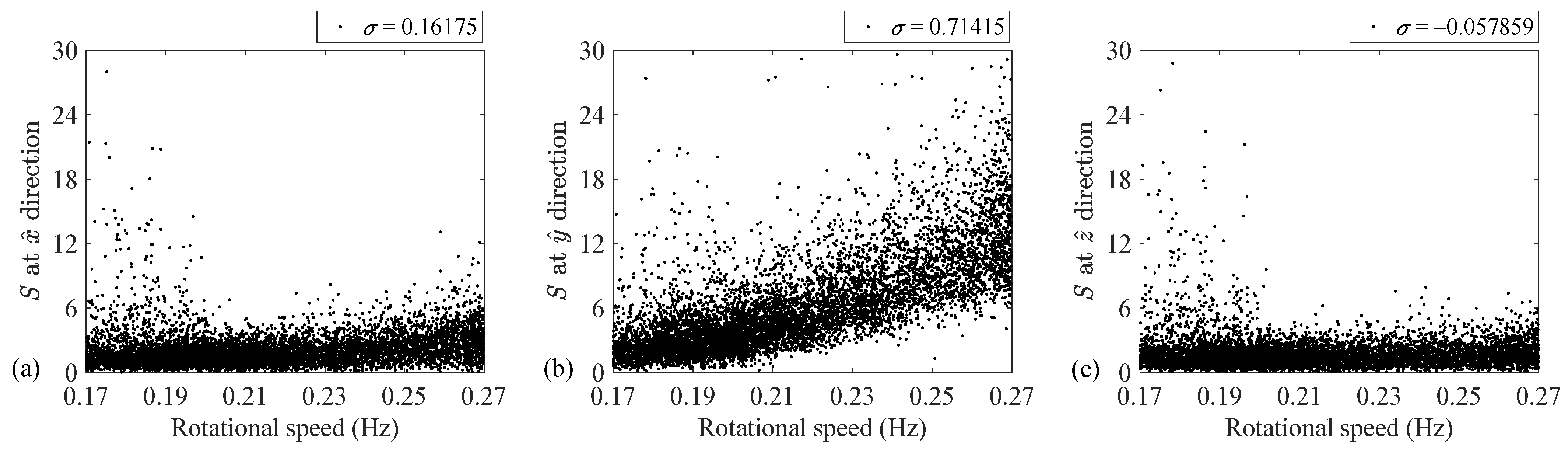
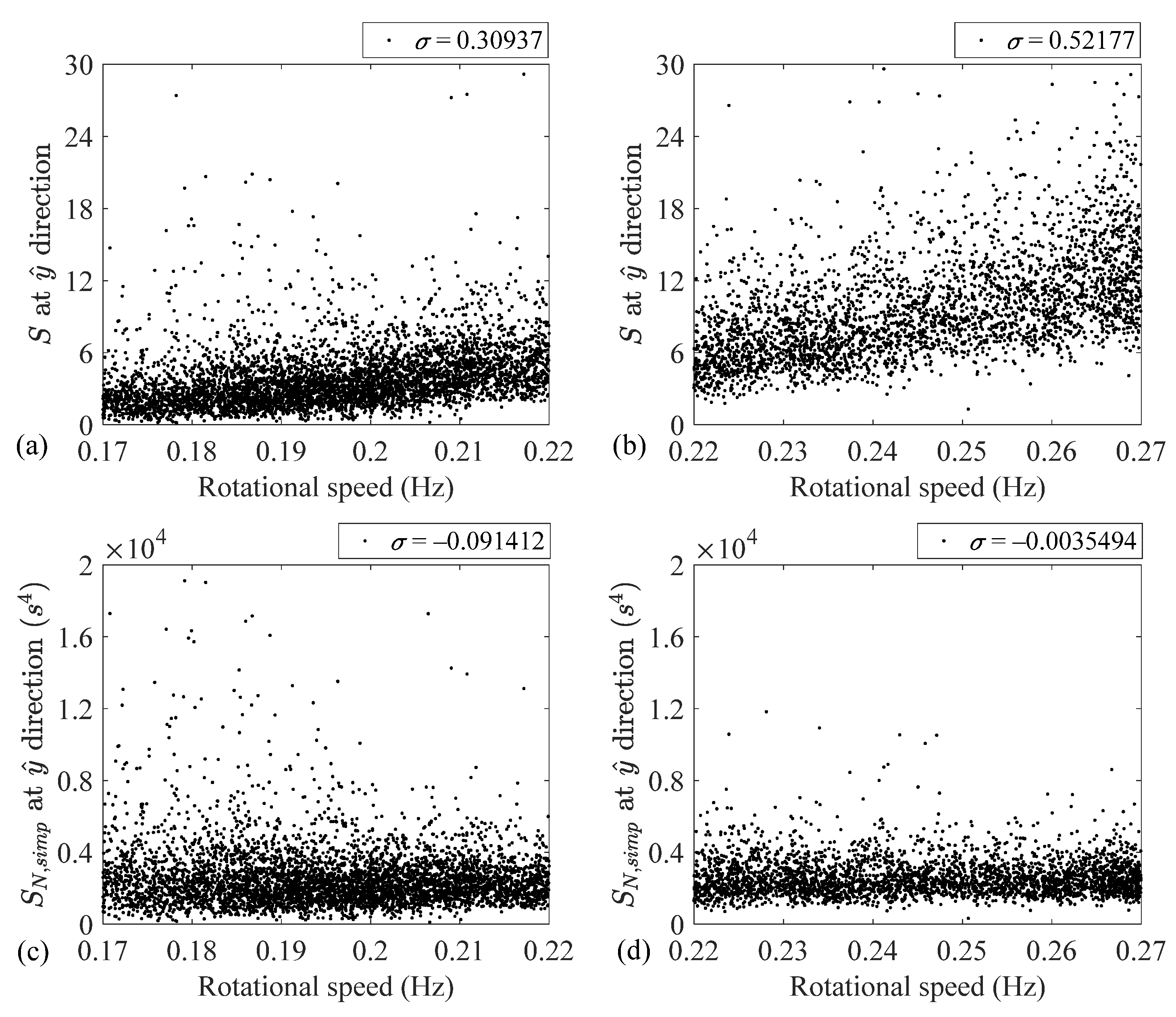
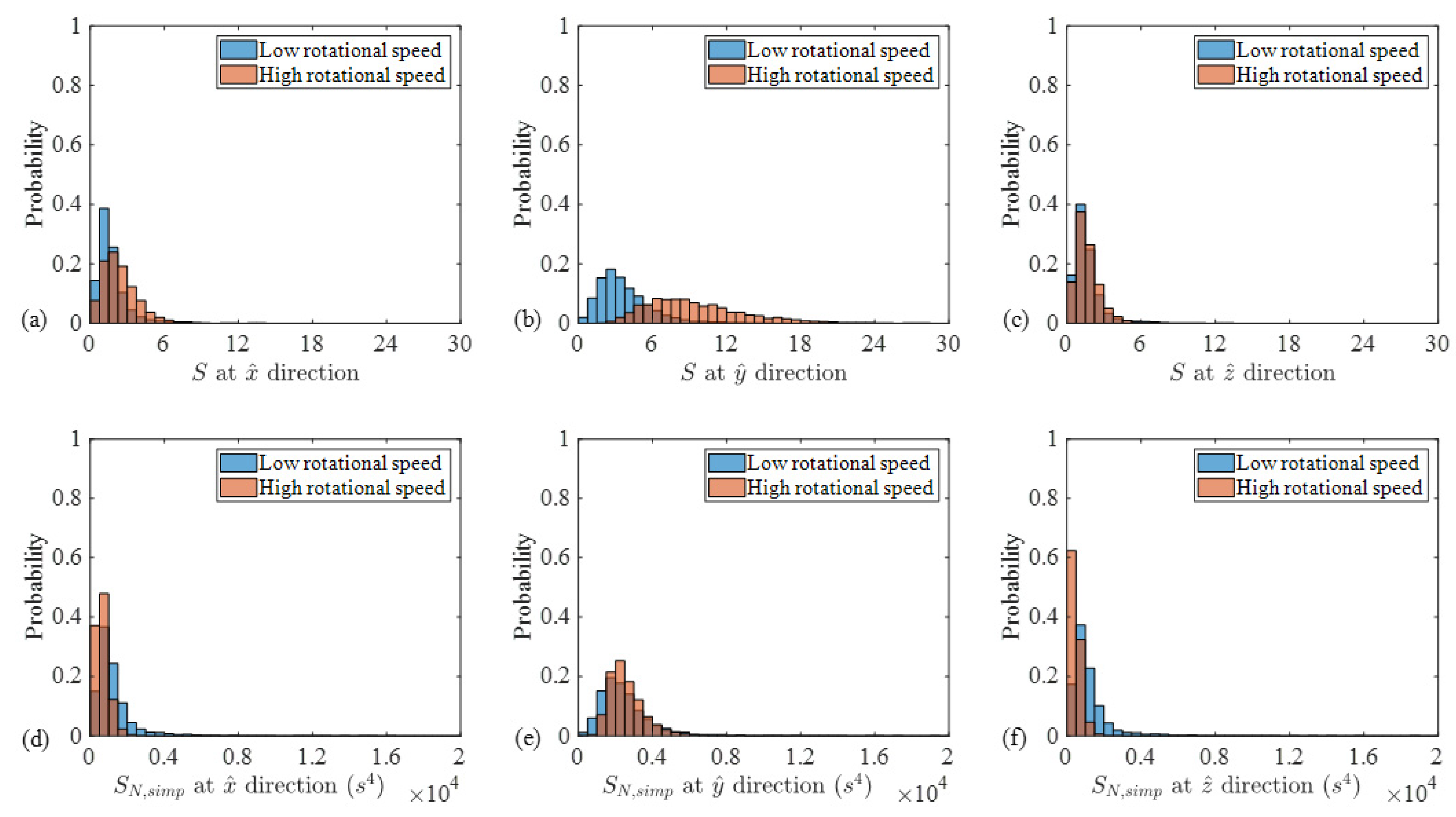
3. Results and Discussion
4. Conclusions
- -
- Investigate variable speed imbalance diagnosis in rotating machinery while simultaneously contracting a shaft misalignment.
- -
- Investigate variable speed imbalance diagnosis in rotating machinery while simultaneously contracting blade fatigue cracks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kusnick, J.; Adams, D.E.; Griffith, D.T. Wind turbine rotor imbalance detection using nacelle and blade measurements. Wind Energy 2015, 18, 267–276. [Google Scholar] [CrossRef]
- Barszcz, T. Vibration-Based Condition Monitoring of Wind Turbines; Springer Cham: Switzerland, 2019. [Google Scholar] [CrossRef]
- Niebsch, J.; Ramlau, R. Simultaneous estimation of mass and aerodynamic rotor imbalances for wind turbines. J. Math. Ind. 2014, 4, 12. [Google Scholar] [CrossRef][Green Version]
- Mehlan, F.C.; Nejad, A.R. Rotor imbalance detection and diagnosis in floating wind turbines by means of drivetrain condition monitoring. Renew. Energy 2023, 212, 70–81. [Google Scholar] [CrossRef]
- Badihi, H.; Zhang, Y.; Jiang, B.; Pillay, P.; Rakheja, S. A comprehensive review on signal-based and model-based condition monitoring of wind turbines: Fault diagnosis and lifetime prognosis. Proc. IEEE 2022, 110, 754–806. [Google Scholar] [CrossRef]
- Ghane, M.; Rasekhi Nejad, A.; Blanke, M.; Gao, Z.; Moan, T. Condition monitoring of spar-type floating wind turbine drivetrain using statistical fault diagnosis. Wind Energy 2018, 21, 575–589. [Google Scholar] [CrossRef]
- Choi, D.; Shin, W.; Ko, K.; Rhee, W. Static and dynamic yaw misalignments of wind turbines and machine learning based correction methods using LiDAR data. IEEE Trans. Sustain. Energy 2019, 10, 971–982. [Google Scholar] [CrossRef]
- Hübner, G.R.; Pinheiro, H.; de Souza, C.E.; Franchi, C.M.; da Rosa, L.D.; Dias, J.P. Detection of mass imbalance in the rotor of wind turbines using Support Vector Machine. Renew. Energy 2021, 170, 49–59. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, J.; Tao, Q.; Li, A.; Chen, Y. An unknown wafer surface defect detection approach based on Incremental Learning for reliability analysis. Reliab. Eng. Syst. Saf. 2024, 244, 109966. [Google Scholar] [CrossRef]
- Jain, J.R.; Kundra, T.K. Model based online diagnosis of unbalance and transverse fatigue crack in rotor systems. Mech. Res. Commun. 2004, 31, 557–568. [Google Scholar] [CrossRef]
- Jalan, A.K.; Mohanty, A.R. Model based fault diagnosis of a rotor–bearing system for misalignment and unbalance under steady-state condition. J. Sound Vib. 2009, 327, 604–622. [Google Scholar] [CrossRef]
- Sudhakar, G.N.D.S.; Sekhar, A.S. Identification of unbalance in a rotor bearing system. J. Sound Vib. 2011, 330, 2299–2313. [Google Scholar] [CrossRef]
- Lin, C.-L.; Liang, J.-W.; Huang, Y.-M.; Huang, S.-C. A novel model-based unbalance monitoring and prognostics for rotor-bearing systems. Adv. Mech. Eng. 2023, 15, 16878132221148019. [Google Scholar] [CrossRef]
- Bera, B.; Huang, S.-C.; Najibullah, M.; Lin, C.-L. An adaptive model-based approach to the diagnosis and prognosis of rotor-bearing unbalance. Machines 2023, 11, 976. [Google Scholar] [CrossRef]
- Rahman, M.M.; Uddin, M.N. Online unbalanced rotor fault detection of an IM drive based on both time and frequency domain analyses. IEEE Trans. Ind. Appl. 2017, 53, 4087–4096. [Google Scholar] [CrossRef]
- Gu, F.; Li, H.; Zou, Z.; Sun, X.; Ball, A.D. A numerical study of rotor eccentricity and dynamic load in induction machines for motor current analysis based diagnostics. Maint. Reliab. Cond. Monit. 2021, 1, 71–86. [Google Scholar]
- Khalique, U.; Xu, G.; Xining, Z.; Fei, L.; Ahmad, S.; Xun, Z.; Jin, Z. A novel detection method for diagnosis of rotor eccentricity in three-phase induction motor. Meas. Sci. Technol. 2021, 32, 114002. [Google Scholar] [CrossRef]
- Ewert, P. The application of the bispectrum analysis to detect the rotor unbalance of the induction motor supplied by the mains and frequency converter. Energies 2020, 13, 3009. [Google Scholar] [CrossRef]
- Rafaq, M.S.; Lee, H.; Park, Y.; Lee, S.B.; Fernandez, D.; Diaz-Reigosa, D.; Briz, F. A simple method for identifying mass unbalance using vibration measurement in permanent magnet synchronous motors. IEEE Trans. Ind. Electron. 2022, 69, 6441–6444. [Google Scholar] [CrossRef]
- Puerto-Santana, C.; Ocampo-Martinez, C.; Diaz-Rozo, J. Mechanical rotor unbalance monitoring based on system identification and signal processing approaches. J. Sound Vib. 2022, 541, 117313. [Google Scholar] [CrossRef]
- Ramlau, R.; Niebsch, J. Imbalance estimation without test masses for wind turbines. J. Sol. Energy Eng. 2009, 131, 011010. [Google Scholar] [CrossRef]
- Ewert, P.; Wicher, B.; Pajchrowski, T. Application of the STFT for detection of the rotor unbalance of a servo-drive system with an elastic interconnection. Electronics 2024, 13, 441. [Google Scholar] [CrossRef]
- Li, P.; Hu, W.; Hu, R.; Chen, Z. Imbalance fault detection based on the integrated analysis strategy for variable-speed wind turbines. Int. J. Electr. Power Energy Syst. 2020, 116, 105570. [Google Scholar] [CrossRef]
- Fyfe, K.R.; Munck, E.D.S. Analysis of computed order tracking. Mech. Syst. Signal Process. 1997, 11, 187–205. [Google Scholar] [CrossRef]
- Bossley, K.M.; McKendrick, R.J.; Harris, C.J.; Mercer, C. Hybrid computed order tracking. Mech. Syst. Signal Process. 1999, 13, 627–641. [Google Scholar] [CrossRef]
- Bonnardot, F.; El Badaoui, M.; Randall, R.B.; Danière, J.; Guillet, F. Use of the acceleration signal of a gearbox in order to perform angular resampling (with limited speed fluctuation). Mech. Syst. Signal Process. 2005, 19, 766–785. [Google Scholar] [CrossRef]
- Zhao, M.; Lin, J.; Wang, X.; Lei, Y.; Cao, J. A tacho-less order tracking technique for large speed variations. Mech. Syst. Signal Process. 2013, 40, 76–90. [Google Scholar] [CrossRef]
- Coats, M.D.; Randall, R.B. Single and multi-stage phase demodulation based order-tracking. Mech. Syst. Signal Process. 2014, 44, 86–117. [Google Scholar] [CrossRef]
- Lu, S.; Yan, R.; Liu, Y.; Wang, Q. Tacholess speed estimation in order tracking: A review with application to rotating machine fault diagnosis. IEEE Trans. Instrum. Meas. 2019, 68, 2315–2332. [Google Scholar] [CrossRef]
- Wu, J.; Zi, Y.; Chen, J.; Zhou, Z. Fault diagnosis in speed variation conditions via improved tacholess order tracking technique. Measurement 2019, 137, 604–616. [Google Scholar] [CrossRef]
- Wu, B.; Hou, L.; Wang, S.; Lian, X. A tacholess order tracking method based on the STFTSC algorithm for rotor unbalance fault diagnosis under variable-speed conditions. J. Comput. Inf. Sci. Eng. 2023, 24, 021009. [Google Scholar] [CrossRef]
- Xu, J.; Ding, X.; Gong, Y.; Wu, N.; Yan, H. Rotor imbalance detection and quantification in wind turbines via vibration analysis. Wind Eng. 2021, 46, 3–11. [Google Scholar] [CrossRef]
- Gelman, L.; Ottley, M. New processing techniques for transient signals with non-linear variation of the instantaneous frequency in time. Mech. Syst. Signal Process. 2006, 20, 1254–1262. [Google Scholar] [CrossRef]
- ISO 21940-11:2016; Mechanical Vibration—Rotor Balancing—Part 11: Procedures and Tolerances for Rotors with Rigid Behaviour. International Organization for Standardization: Geneva, Switzerland, 2016.
- Meirovitch, L. Fundamentals of Vibrations; Waveland Press: Long Grove, IL, USA, 2010. [Google Scholar]
- Gelman, L. Piecewise model and estimates of damping and natural frequency for a spur gear. Mech. Syst. Signal Process. 2007, 21, 1192–1196. [Google Scholar] [CrossRef]
- Faires, J.D.; Burden, R.L. Numerical Methods, 3rd ed.; Brooks/Cole: Salt Lake City, UT, USA, 2002. [Google Scholar]
- Markert, R.; Seidler, M. Analytically based estimation of the maximum amplitude during passage through resonance. Int. J. Solids Struct. 2001, 38, 1975–1992. [Google Scholar] [CrossRef]
- Askari, A.R.; Tahani, M. Investigating nonlinear vibration of a fully clamped nanobeam in presence of the van der Waals attraction. Appl. Mech. Mater. 2012, 226–228, 181–185. [Google Scholar] [CrossRef]
- Lenci, S.; Consolini, L.; Clementi, F. The use of the fitting time histories method to detect the nonlinear behaviour of laminated glass. J. Vib. Test. Syst. Dyn. 2017, 1, 1–14. [Google Scholar]
- Gelman, L.; Petrunin, I. The new multidimensional time/multi-frequency transform for higher order spectral analysis. Multidimens. Syst. Signal Process. 2007, 18, 317–325. [Google Scholar] [CrossRef]
- Gelman, L.; Kırlangıç, A.S. Novel vibration structural health monitoring technology for deep foundation piles by non-stationary higher order frequency response function. Struct. Control Health Monit. 2020, 27, e2526. [Google Scholar] [CrossRef]
- Farhat, M.H.; Gelman, L.; Conaghan, G.; Kluis, W.; Ball, A. Novel diagnosis technologies for a lack of oil lubrication in gearmotor systems, based on motor current signature analysis. Sensors 2022, 22, 9507. [Google Scholar] [CrossRef]
- Gelman, L.; Abdullahi, A.O.; Moshrefzadeh, A.; Ball, A.; Conaghan, G.; Kluis, W. Innovative conveyor belt monitoring via current signals. Electronics 2023, 12, 1804. [Google Scholar] [CrossRef]
- Xia, X.g. Discrete chirp-Fourier transform and its application to chirp rate estimation. IEEE Trans. Signal Process. 2000, 48, 3122–3133. [Google Scholar] [CrossRef] [PubMed]
- Gelman, L.; Patel, T.H.; Murray, B.; Thomson, A. Rolling bearing diagnosis based on the higher order spectra. Int. J. Progn. Health Manag. 2013, 4, 022. [Google Scholar] [CrossRef]
- Gelman, L.; Petrunin, I.; Parrish, C.; Walters, M. Novel health monitoring technology for in-service diagnostics of intake separation in aircraft engines. Struct. Control Health Monit. 2020, 27, e2479. [Google Scholar] [CrossRef]
- Gelman, L.; Kripak, D.; Fedorov, V.; Udovenko, L. Condition monitoring diagnosis methods of helicopter units. Mech. Syst. Signal Process. 2000, 14, 613–624. [Google Scholar] [CrossRef]
- Kendall, M.G. The Advanced Theory of Statistics, 4th ed.; Macmillan: New York, NY, USA, 1979. [Google Scholar]
- Gelman, L.; Petrunin, I.; Komoda, J. The new chirp-Wigner higher order spectra for transient signals with any known nonlinear frequency variation. Mech. Syst. Signal Process. 2010, 24, 567–571. [Google Scholar] [CrossRef]
- Gelman, L.; Soliński, K.; Ball, A. Novel higher-order spectral cross-correlation technologies for vibration sensor-based diagnosis of gearboxes. Sensors 2020, 20, 5131. [Google Scholar] [CrossRef]
- Gelman, L.; Soliński, K.; Ball, A. Novel instantaneous wavelet bicoherence for vibration fault detection in gear systems. Energies 2021, 14, 6811. [Google Scholar] [CrossRef]



| 0.02 | 0.09 | 0.27 | 0.38 | 0.12 | 0.06 | |
| 0.04 | 0.2 | 0.57 | 0.79 | 0.26 | 0.13 | |
| 0.08 | 0.35 | 0.94 | 1.26 | 0.45 | 0.23 |
| ADXL354B | PCB 3743F112G | |
|---|---|---|
| Type | 3-axis MEMS sensor | 3-axis MEMS sensor |
| Sensitivity | 200 mV/g | 1350 mV/g |
| Measurement range | ± | ± |
| Operational frequency range | 0–250 Hz | 0–1.5 kHz |
| Resonance frequency | 2.4 kHz | 1.2 kHz |
| Typical nonlinearity | 0.3% | 0.1% |
| Typical transverse sensitivity | 1% | 1% |
| Operating temperature range | −40 °C to +125 °C | −54 °C to +121 °C |
| Temperature sensitivity change within the operational range | ± | ± |
| S | ||
|---|---|---|
| direction | 0.05 | 0.13 |
| direction | 1.28 | 0.000 |
| direction | 0.002 | 0.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Askari, A.R.; Gelman, L.; King, R.; Hickey, D.; Ball, A.D. A Novel Diagnostic Feature for a Wind Turbine Imbalance Under Variable Speed Conditions. Sensors 2024, 24, 7073. https://doi.org/10.3390/s24217073
Askari AR, Gelman L, King R, Hickey D, Ball AD. A Novel Diagnostic Feature for a Wind Turbine Imbalance Under Variable Speed Conditions. Sensors. 2024; 24(21):7073. https://doi.org/10.3390/s24217073
Chicago/Turabian StyleAskari, Amir R., Len Gelman, Russell King, Daryl Hickey, and Andrew D. Ball. 2024. "A Novel Diagnostic Feature for a Wind Turbine Imbalance Under Variable Speed Conditions" Sensors 24, no. 21: 7073. https://doi.org/10.3390/s24217073
APA StyleAskari, A. R., Gelman, L., King, R., Hickey, D., & Ball, A. D. (2024). A Novel Diagnostic Feature for a Wind Turbine Imbalance Under Variable Speed Conditions. Sensors, 24(21), 7073. https://doi.org/10.3390/s24217073








