Estimation of Crack Tip Position in Adhesively Bonded Joints Subjected to Mode II Fatigue Loading
Abstract
1. Introduction
2. Experimental Procedures
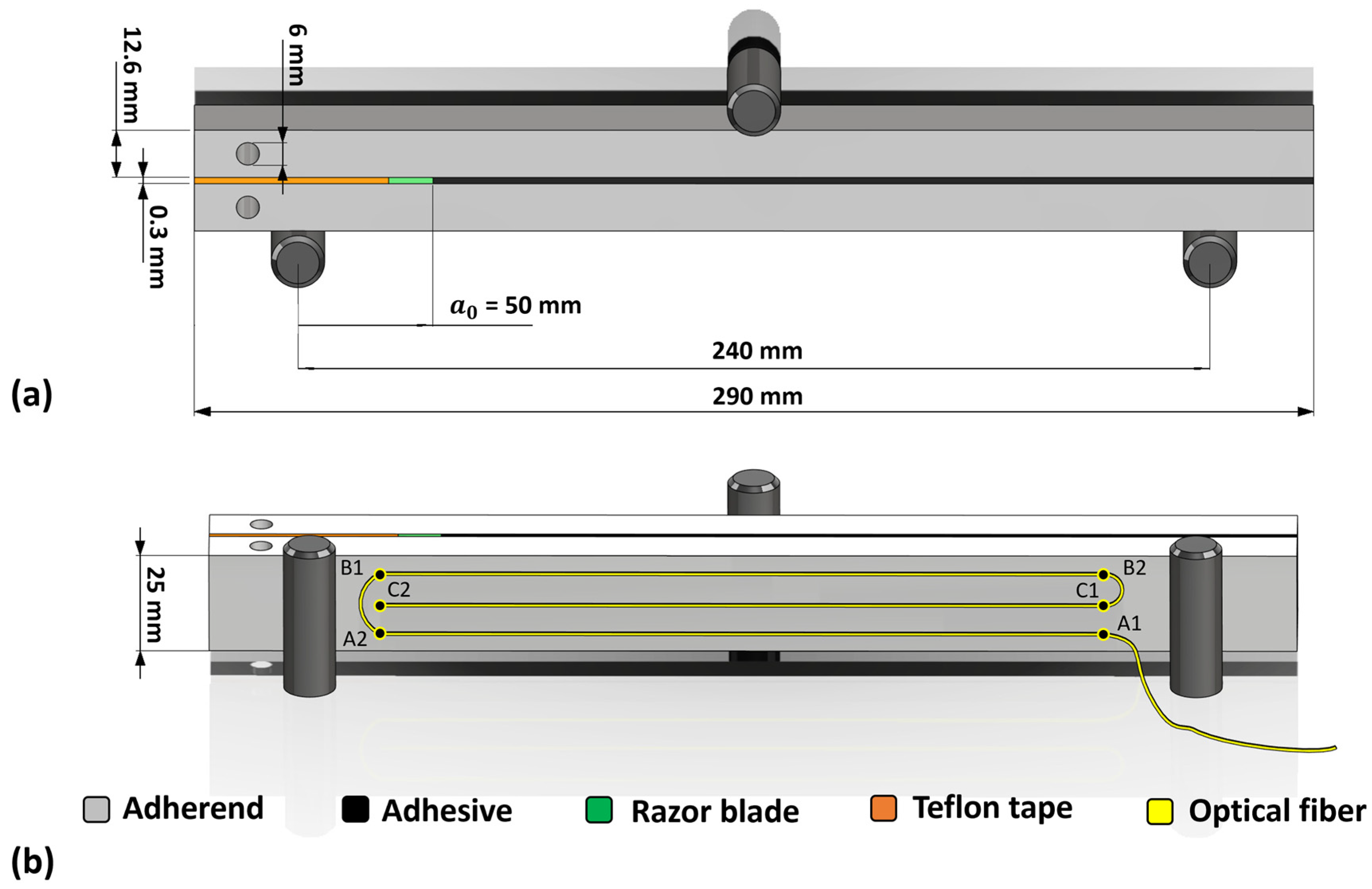
2.1. Materials and ENF Sample Fabrication
2.2. Fatigue Test Configuration
2.3. Crack Monitoring Setup
3. Results of Interrupted Fatigue Test (Static Acquisition)
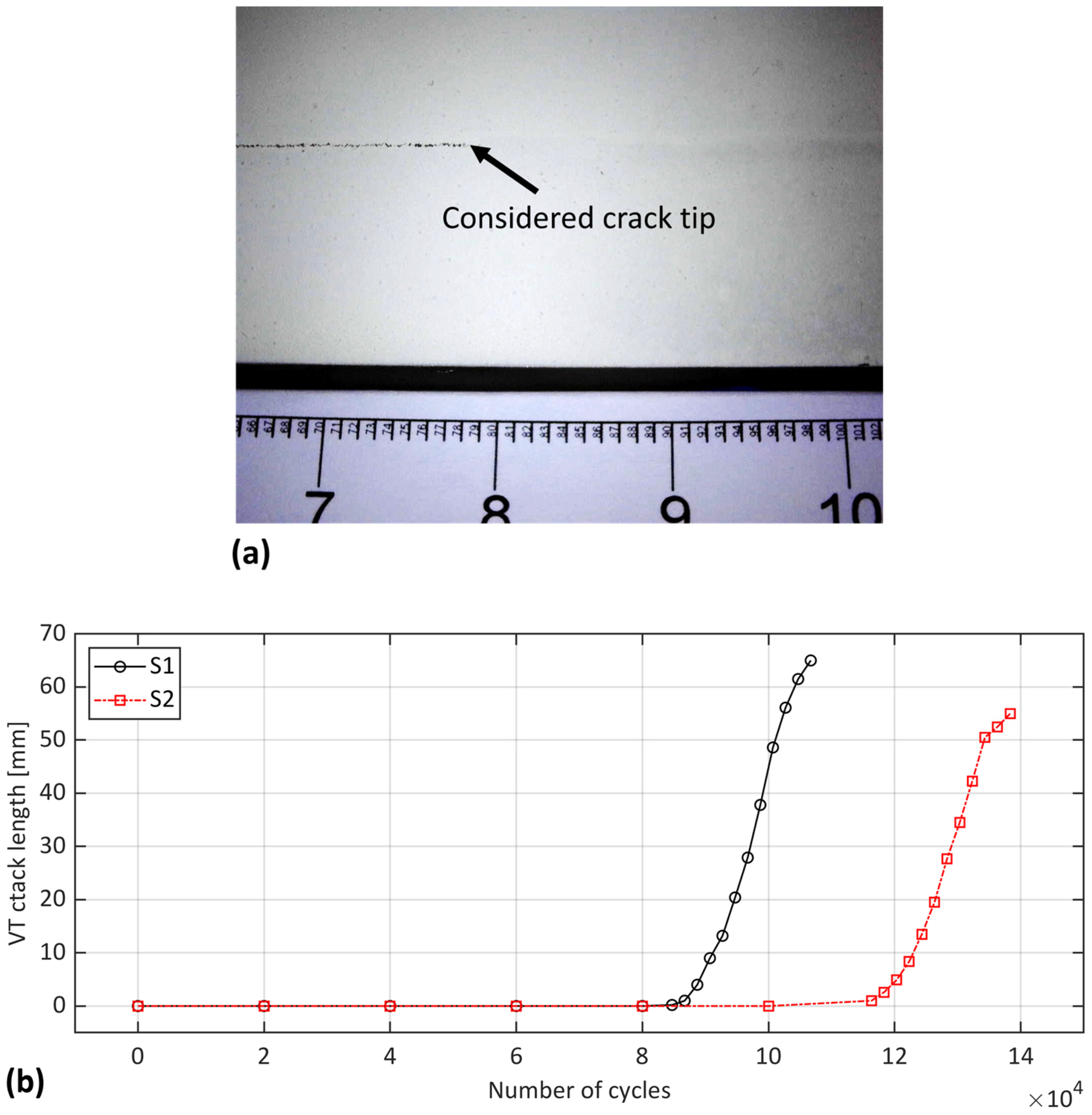
3.1. Visual Testing
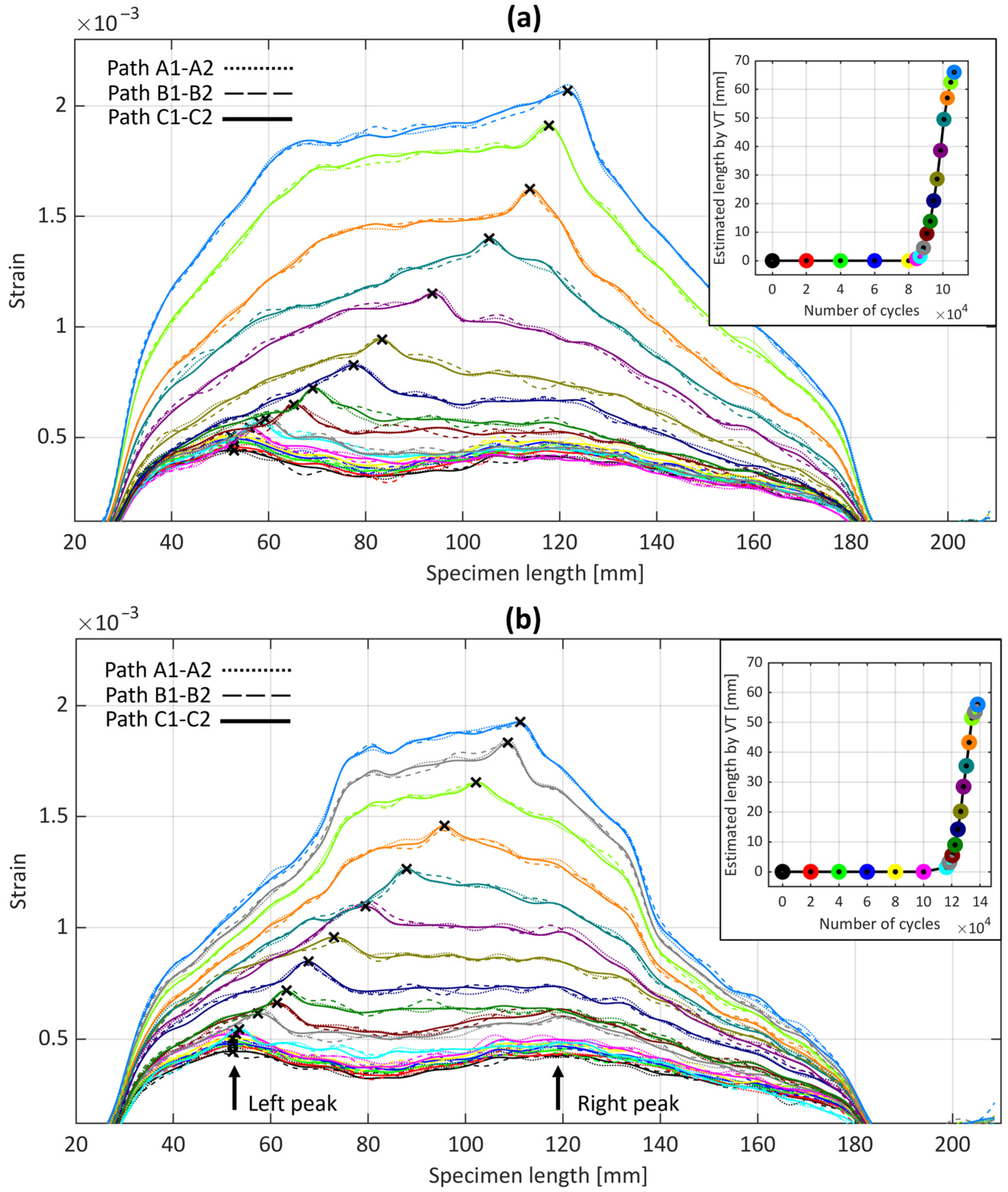
3.2. Digital Image Correlation
3.3. Optical Backscatter Reflectometry
3.4. Compliance-Based Beam Method
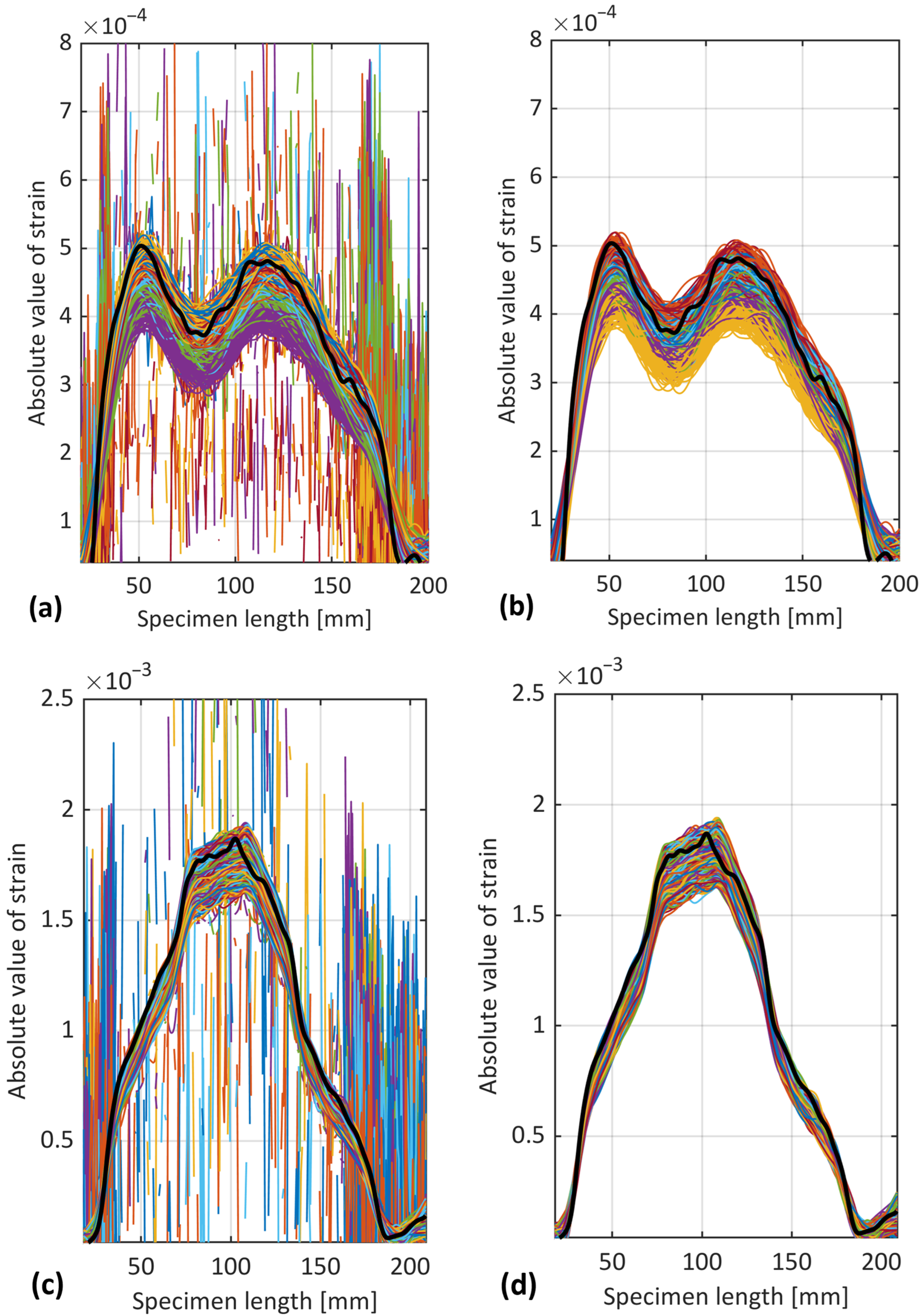
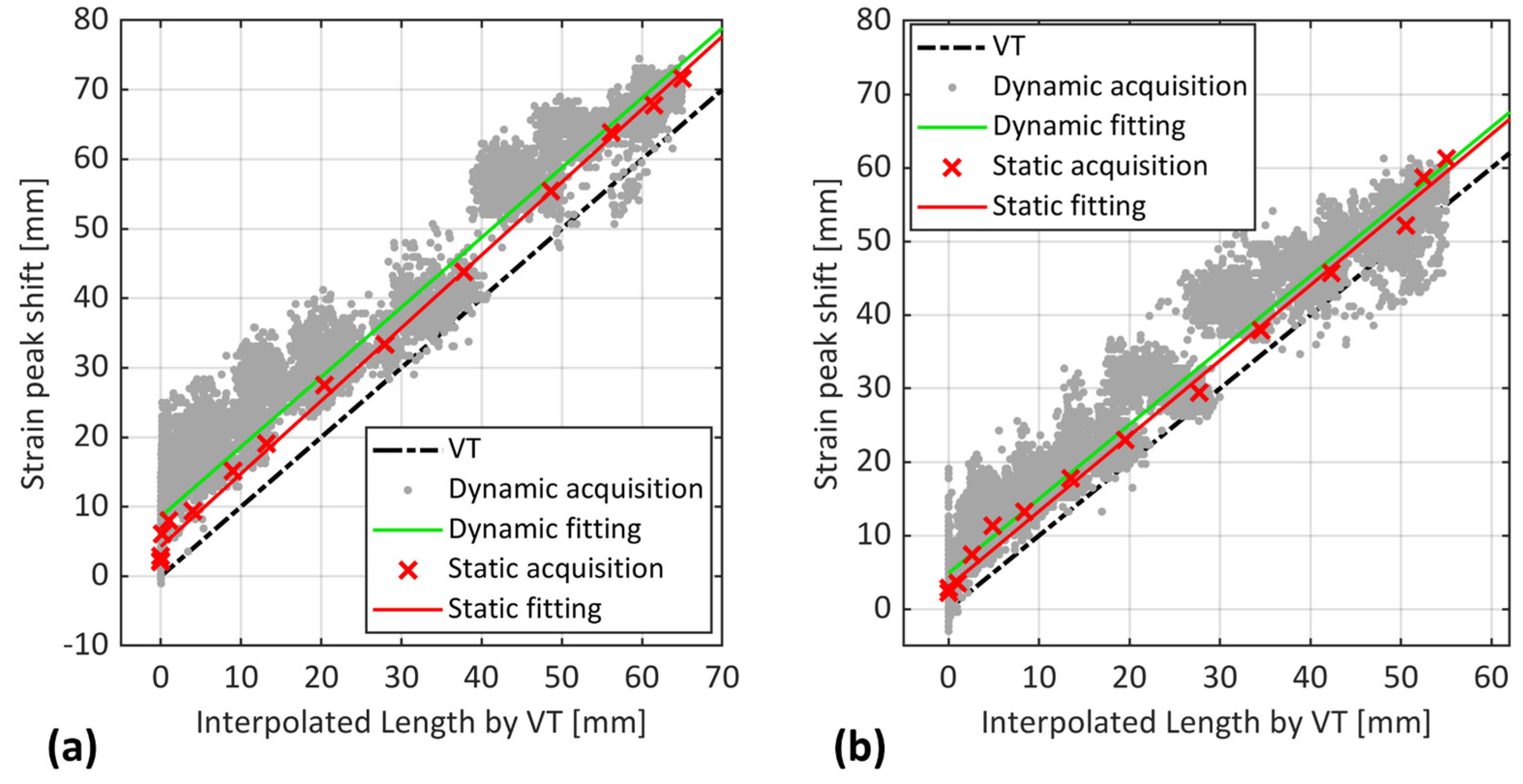
4. Results of Uninterrupted Fatigue Tests (Dynamic Acquisition)
5. Discussion
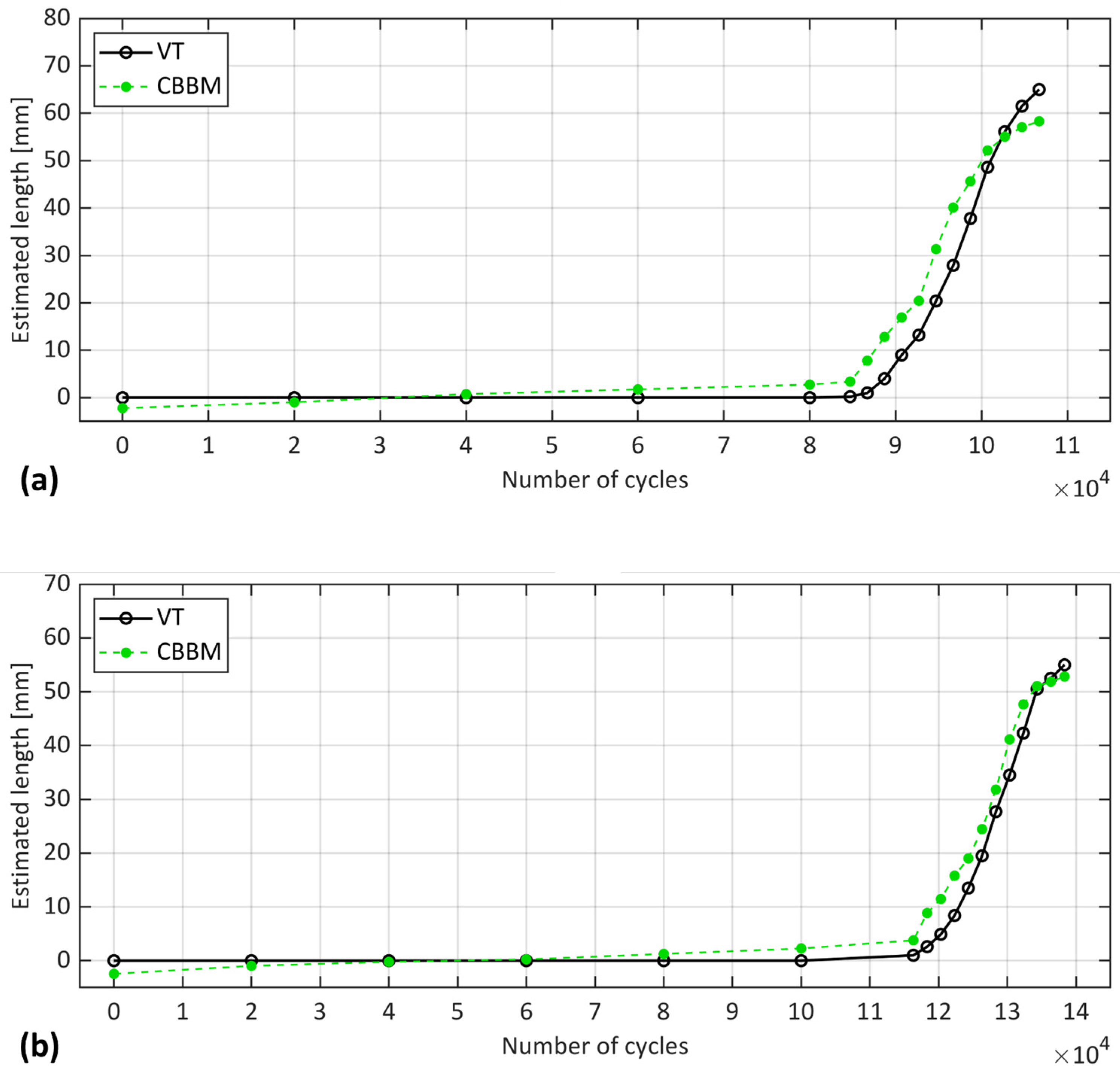
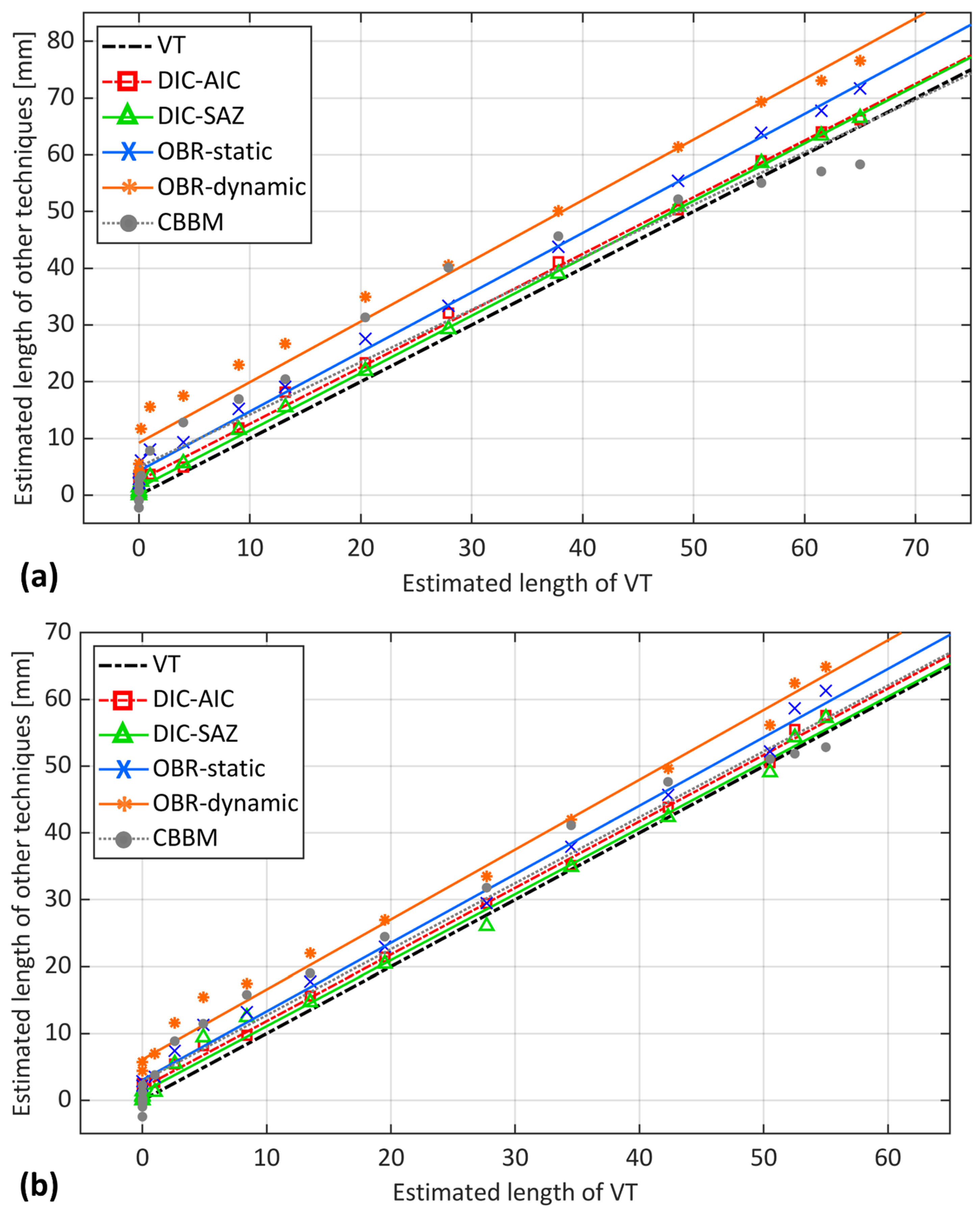
5.1. Comparison of the Considered Methods for Crack Length Estimation
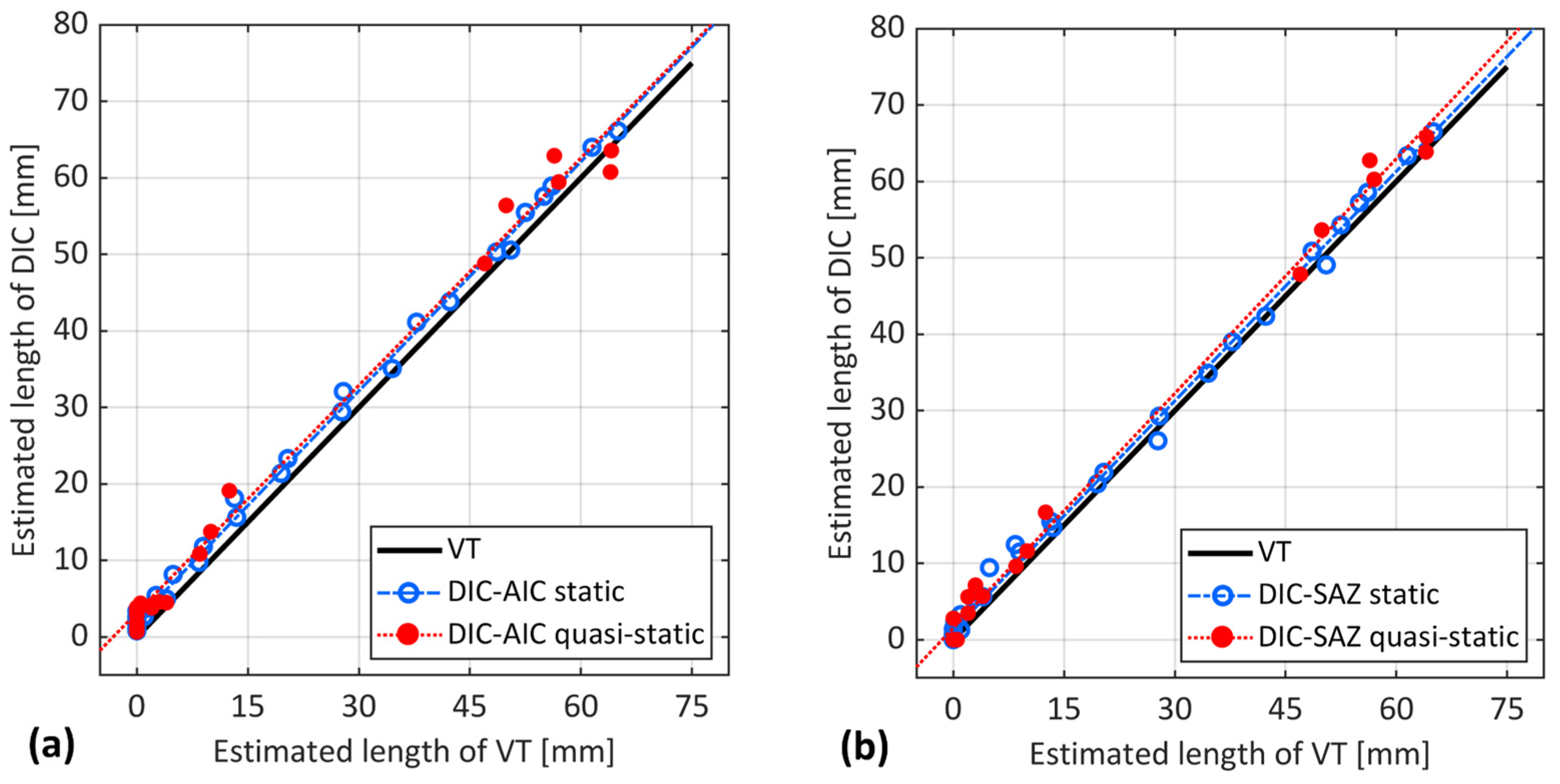
5.2. Comparison of Quasi-Static and Fatigue Loading Conditions
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kinloch, A.J. Adhesion and Adhesives: Science and Technology; Kinloch, A.J., Ed.; Springer: Dordrecht, The Netherlands, 1987; pp. 188–263. [Google Scholar]
- Akhavan-Safar, A.; Marques, E.A.S.; Carbas, R.J.C.; da Silva, L.F.M. Cohesive Zone Modelling for Fatigue Life Analysis of Adhesive Joints; Springer International Publishing: Cham, Switzerland, 2022; pp. 19–42. [Google Scholar]
- Fernández, M.V.; de Moura, M.F.; da Silva, L.F.; Marques, A.T. Characterization of composite bonded joints under pure mode II fatigue loading. Compos. Struct. 2013, 95, 222–226. [Google Scholar] [CrossRef]
- Floros, I.; Tserpes, K.; Löbel, T. Mode-I, mode-II and mixed-mode I+II fracture behavior of composite bonded joints: Experimental characterization and numerical simulation. Compos. Part B Eng. 2015, 78, 459–468. [Google Scholar] [CrossRef]
- Hazwan, M.N.; Asasaari, S.F.M.; Jye, W.K.; Tamin, M.N.; Ismail, M.S.; Kosnan, M.S.E.; Januddi, M.A.F.M.S.; Ismail, M.A.; Johar, M. Materials Innovations and Solutions in Science and Technology: With a Focus on Tropical Plant Biomaterials; Springer Nature: Cham, Switzerland, 2023; pp. 95–107. [Google Scholar]
- Da Silva, L.F.; Dillard, D.A.; Blackman, B.; Adams, R.D. Testing Adhesive Joints: Best Practices; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Matsuda, S.; Hojo, M.; Ochiai, S. Mesoscopic Fracture Mechanism of Mode II Delamination Fatigue Crack Propagation in Interlayer-Toughened CFRP. JSME Int. J. Ser. A 1997, 40, 423–429. [Google Scholar] [CrossRef][Green Version]
- Hojo, M.; Ando, T.; Tanaka, M.; Adachi, T.; Ochiai, S.; Endo, Y. Modes I and II interlaminar fracture toughness and fatigue delamination of CF/epoxy laminates with self-same epoxy interleaf. Int. J. Fatigue 2006, 28, 1154–1165. [Google Scholar] [CrossRef]
- Orell, O.; Jokinen, J.; Kanerva, M. Use of DIC in the characterisation of mode II crack propagation in adhesive fatigue testing. Int. J. Adhes. Adhes. 2023, 122, 103332. [Google Scholar] [CrossRef]
- Vinciquerra, A.J.; Davidson, B.D.; Schaff, J.R.; Smith, S.L. Determination of the Mode II Fatigue Delamination Toughness of Laminated Composites. J. Reinf. Plast. Compos. 2002, 21, 663–677. [Google Scholar] [CrossRef]
- Mohammadi, R.; Najafabadi, M.A.; Saghafi, H.; Zarouchas, D. Mode-II fatigue response of AS4/8552 carbon /epoxy composite laminates interleaved by electrospun nanofibers. Thin-Walled Struct. 2020, 154, 106811. [Google Scholar] [CrossRef]
- Kotrotsos, A.; Kostopoulos, V. Mode II Fatigue Delamination Growth and Healing of Bis-Maleimide Modified CFRPs by Using the Melt Electro-Writing Process Technique. J. Compos. Sci. 2023, 7, 350. [Google Scholar] [CrossRef]
- de Castro, D.S.V.; Matvieieva, N.; Grosso, M.; Camerini, C.G.; Kotik, H.G.; Heuer, H. Evaluation of Mode II Delamination Area by Non-destructive Techniques: Accuracy and Influence on Fracture Toughness Calculation. J. Nondestruct. Eval. 2021, 40, 58. [Google Scholar] [CrossRef]
- Meadows, L.; Sullivan, R.W.; Brown, K.; Ranatunga, V.; Vehorn, K.; Olson, S. Distributed optical sensing in composite laminates. J. Strain Anal. Eng. Des. 2017, 52, 410–421. [Google Scholar] [CrossRef]
- de Moura, M.; de Morais, A. Equivalent crack based analyses of ENF and ELS tests. Eng. Fract. Mech. 2008, 75, 2584–2596. [Google Scholar] [CrossRef]
- Rahman, S.A.; Subhani, M.; Ashraf, M. Mode-II progressive fracture of sawn timber and timber-adhesive bond: Experimental evaluation of end notched flexure (ENF) testing using DIC. Eur. J. Wood Wood Prod. 2023, 81, 1437–1453. [Google Scholar] [CrossRef]
- Murray, B.R.; Fonteyn, S.; Carrella-Payan, D.; Kalteremidou, K.-A.; Cernescu, A.; Van Hemelrijck, D.; Pyl, L. Crack Tip Monitoring of Mode I and Mode II Delamination in CF/Epoxies under Static and Dynamic Loading Conditions Using Digital Image Correlation. Proceedings 2018, 3, 389. [Google Scholar]
- Canal, L.P.; Sarfaraz, R.; Violakis, G.; Botsis, J.; Michaud, V.; Limberger, H.G. Monitoring strain gradients in adhesive composite joints by embedded fiber Bragg grating sensors. Compos. Struct. 2014, 112, 241–247. [Google Scholar] [CrossRef]
- Güemes, A.; Fernández-López, A.; Soller, B. Optical Fiber Distributed Sensing—Physical Principles and Applications. Struct. Health Monit. 2010, 9, 233–245. [Google Scholar] [CrossRef]
- Lima, R.; Migliavacca, F.; Martulli, L.; Carboni, M.; Bernasconi, A. Distributed fibre optic monitoring of mode I fatigue crack propagation in adhesive bonded joints and comparison with digital image correlation. Theor. Appl. Fract. Mech. 2022, 121, 103501. [Google Scholar] [CrossRef]
- Bernasconi, A.; Martulli, L.; Carboni, M. Fatigue crack growth analysis in composite bonded joints by back face distributed strain sensing and comparison with X-ray microtomography. Int. J. Fatigue 2022, 154, 106526. [Google Scholar] [CrossRef]
- Mehrabi, M.; Martulli, L.M.; Bernasconi, A.; Carboni, M. Estimating crack tip position in adhesively bonded joints subjected to mode II quasi-static loading. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 1262–1280. [Google Scholar] [CrossRef]
- Wahab, M.M.A. Fatigue in Adhesively Bonded Joints: A Review. ISRN Mater. Sci. 2012, 2012, 746308. [Google Scholar] [CrossRef]
- Bernasconi, A.; Lima, R.A.A.; Cardamone, S.; Campbell, R.B.; Slocum, A.H.; Giglio, M. Effect of temperature on cohesive modelling of 3M Scotch-Weld™ 7260 B/A epoxy adhesive. J. Adhes. 2020, 96, 437–460. [Google Scholar] [CrossRef]
- Cardamone, S.; Bernasconi, A.; Giglio, M. Characterization of the 3M Scotch-Weld™ 7260 B/A epoxy adhesive by cohesive damage models and application to a full-scale bonded sub-structure. J. Adhes. 2020, 96, 1270–1301. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L. Recent Progress in Distributed Fiber Optic Sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef] [PubMed]
- Eskandarian, M.; Jennings, R.; Cote, M.; Arsenault, B. Fracture Behavior of Typical Structural Adhesive Joints Under Quasi-Static and Cyclic Loadings. SAE Int. J. Mater. Manuf. 2010, 3, 622–627. [Google Scholar] [CrossRef][Green Version]
- Qiao, Y.; Guo, K.; Salviato, M. Size effect and scaling in quasi-static and fatigue fracture of graphene polymer nanocomposites. Polym. Compos. 2023. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehrabi, M.; Martulli, L.M.; Bernasconi, A.; Carboni, M. Estimation of Crack Tip Position in Adhesively Bonded Joints Subjected to Mode II Fatigue Loading. Sensors 2024, 24, 7676. https://doi.org/10.3390/s24237676
Mehrabi M, Martulli LM, Bernasconi A, Carboni M. Estimation of Crack Tip Position in Adhesively Bonded Joints Subjected to Mode II Fatigue Loading. Sensors. 2024; 24(23):7676. https://doi.org/10.3390/s24237676
Chicago/Turabian StyleMehrabi, M., L. M. Martulli, A. Bernasconi, and M. Carboni. 2024. "Estimation of Crack Tip Position in Adhesively Bonded Joints Subjected to Mode II Fatigue Loading" Sensors 24, no. 23: 7676. https://doi.org/10.3390/s24237676
APA StyleMehrabi, M., Martulli, L. M., Bernasconi, A., & Carboni, M. (2024). Estimation of Crack Tip Position in Adhesively Bonded Joints Subjected to Mode II Fatigue Loading. Sensors, 24(23), 7676. https://doi.org/10.3390/s24237676









