Frequency Instability Impact of Low-Cost SDRs on Doppler-Based Localization Accuracy
Abstract
:1. Introduction
2. Related Works
- The United States—Northrop Grumman, West Falls Church, VA (RQ-4 Global Hawk, MQ-4C Triton), General Atomics, San Diego, CA (MQ-9 Reaper, Predator ER, Avenger), Boeing, Arlington, VA (EA-18G Growler), and Kratos Defense & Security Solutions, San Diego, CA (XQ-58 Valkyrie);
- Israel—Elbit Systems, Haifa (Hermes 450, Hermes 900) and Israel Aerospace Industries (IAI), Lod (Eitan, Heron);
- Italy—Leonardo-Finmeccanica, Rome (Selex ES Falco);
- Germany—EMT, Penzberg (Luna X-2000);
- Türkiye—Turkish Aerospace Industries (TAI), Ankara (Gözcü) and Baykar, Istanbul (Bayraktar TB2 with SIGINT system BSI-101);
- Russia—Kronstadt Group, Moscow (Orion).
- We present the concept of a location sensor dedicated to a UAV application.
- We introduce a review of SDR platforms in terms of the possibility of using them to build a location sensor, which is characterized by appropriate frequency stability, weight, and size, limited by the capabilities of the UAV payload.
- Based on empirical studies, we classify SDR platforms regarding frequency stability.
- We conduct simulation studies to assess how SDR platforms’ frequency stability affects the SDF location errors.
- We present an overview of small-size frequency oscillators in terms of the possibility of using them to build a size-limited location sensor.
- We propose a hardware structure of a location sensor with an appropriate frequency stability, small weight and dimensions, and low power consumption.
3. Signal Doppler Frequency Location Method
3.1. Emitter Positioning
3.2. SDF Sensor Concept
4. Frequency Stability of Low-Cost SDR Platforms
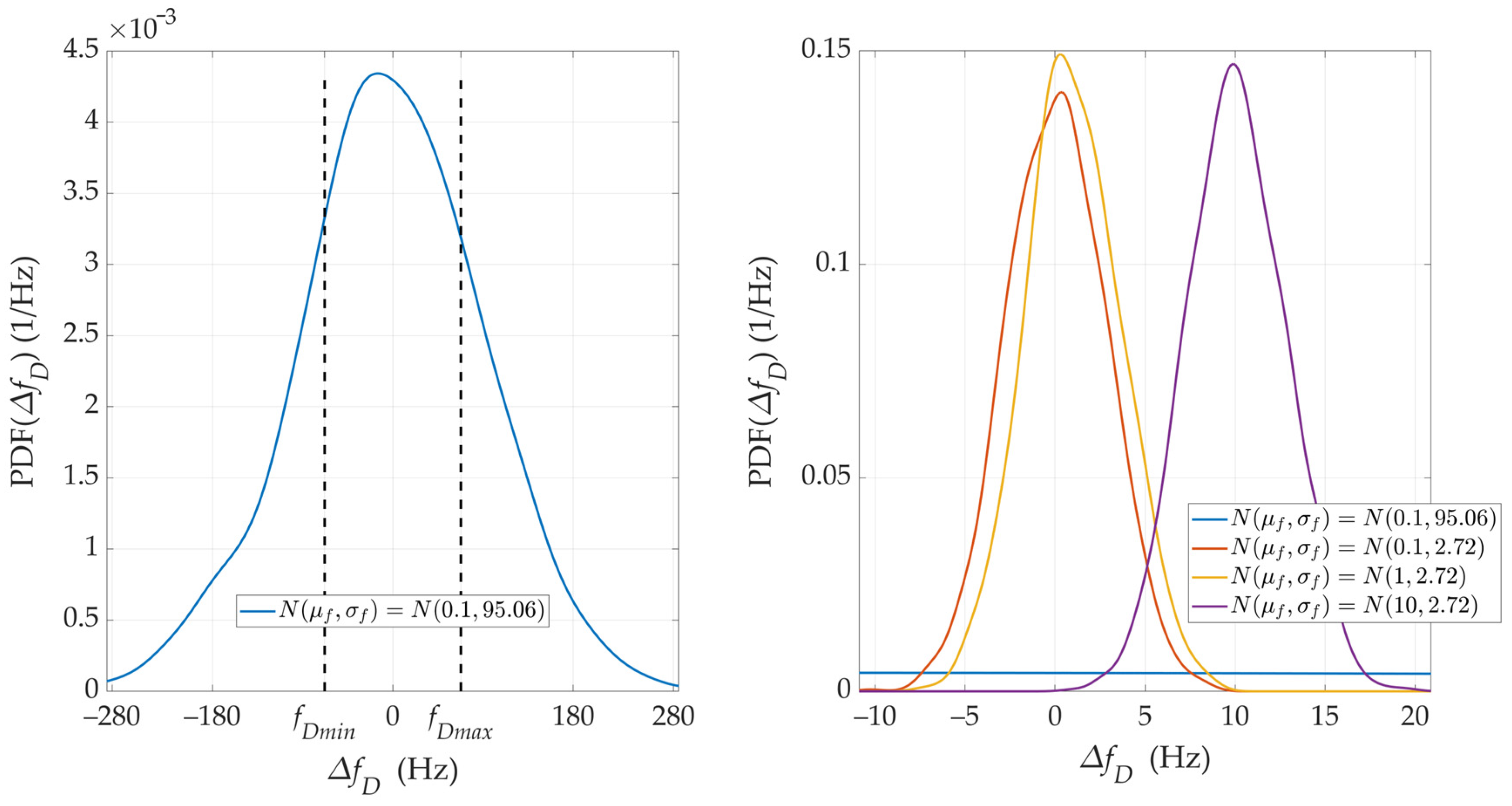
5. Simulation Studies
5.1. Scenarios and Assumptions
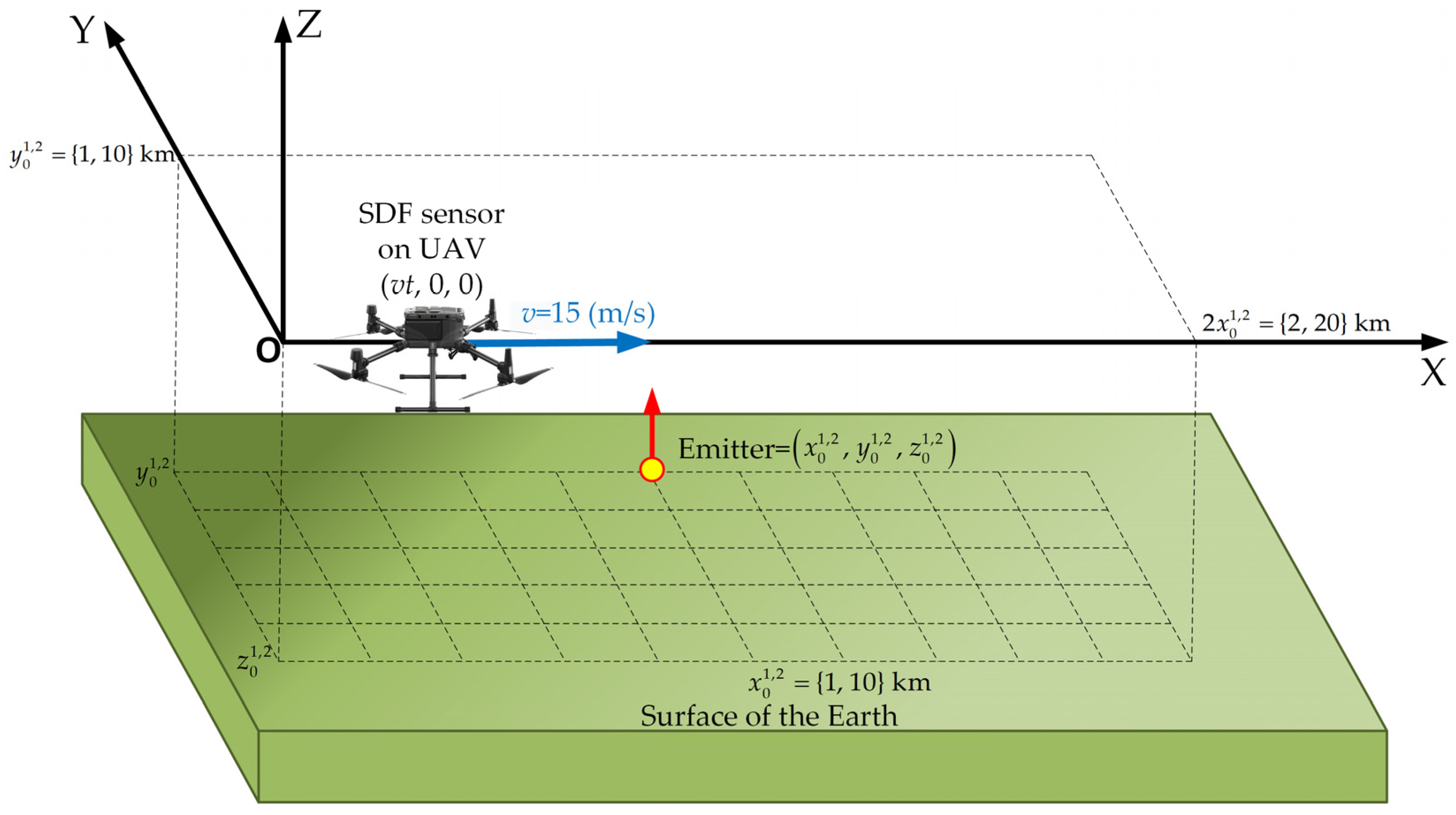
- An illustrative spatial scenario, as shown in Figure 4.
- To define emitter and sensor positions, we used the local Cartesian coordinate system.
- The emitter was localized at a point and in the short- and long-range scenarios, respectively.
- The movement trajectory length of the sensor (i.e., UAV) was equal to and in the short- and long-range scenarios, respectively.
- The simplified SDF (i.e., 2D) version was used.
- The location sensor estimated the instantaneous DFS every 0.1 s.
- The coordinates of the emitter were estimated every 1 s based on 300 DFSs (i.e., the acquisition time of the received signal was equal to ).
- A Monte Carlo simulation methodology was applied with K = 100 repetitions of statistical model realizations.
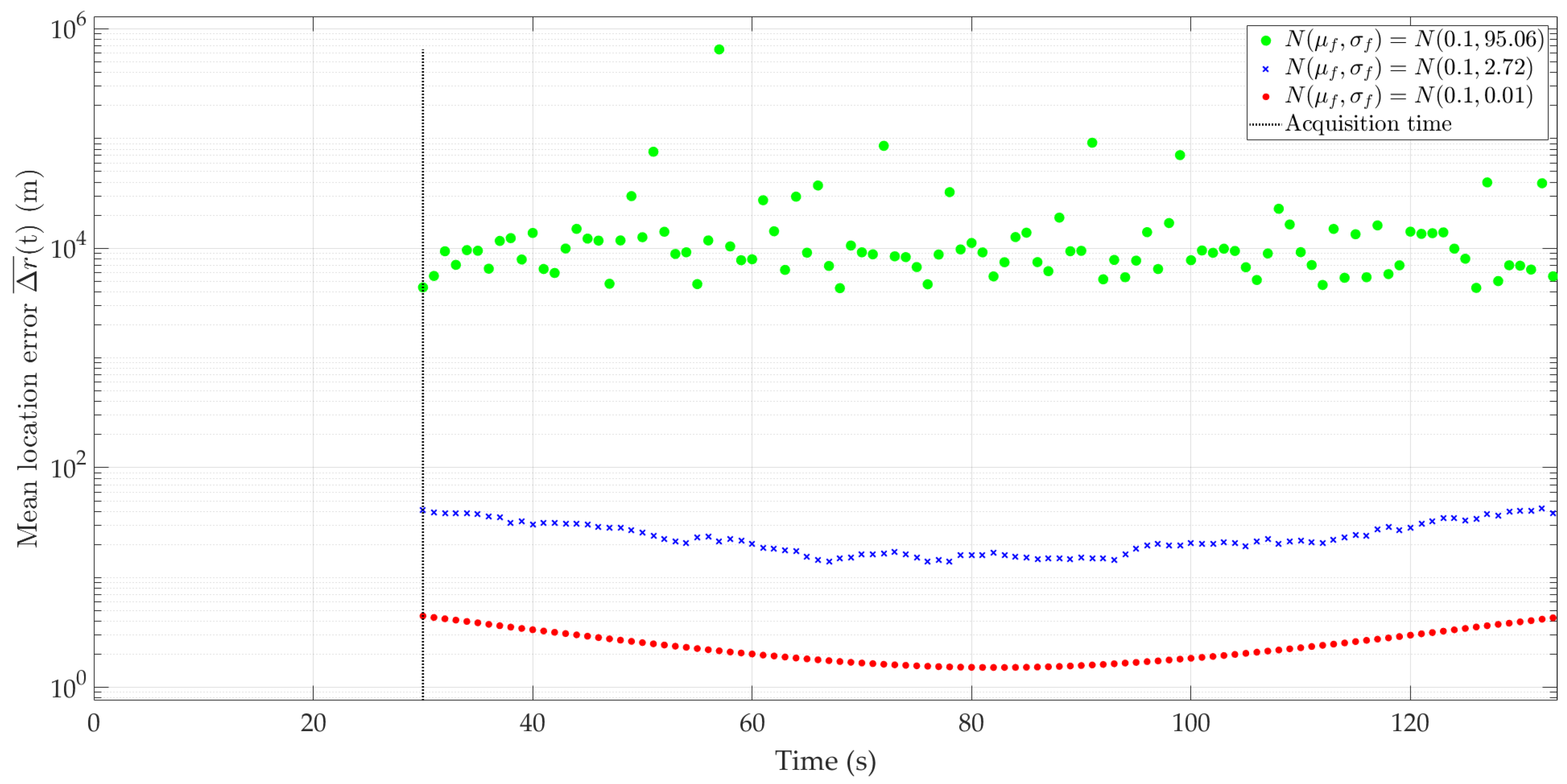
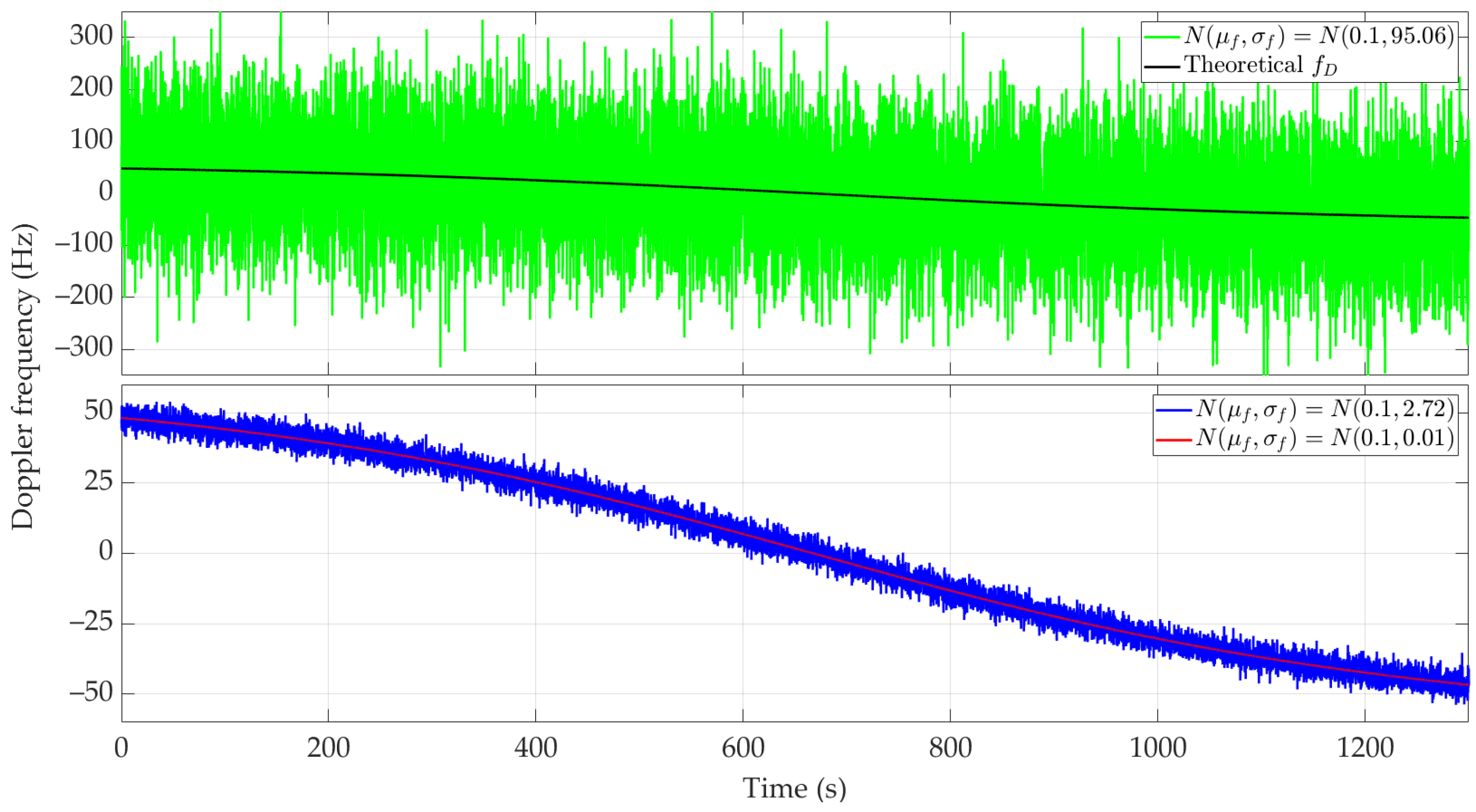
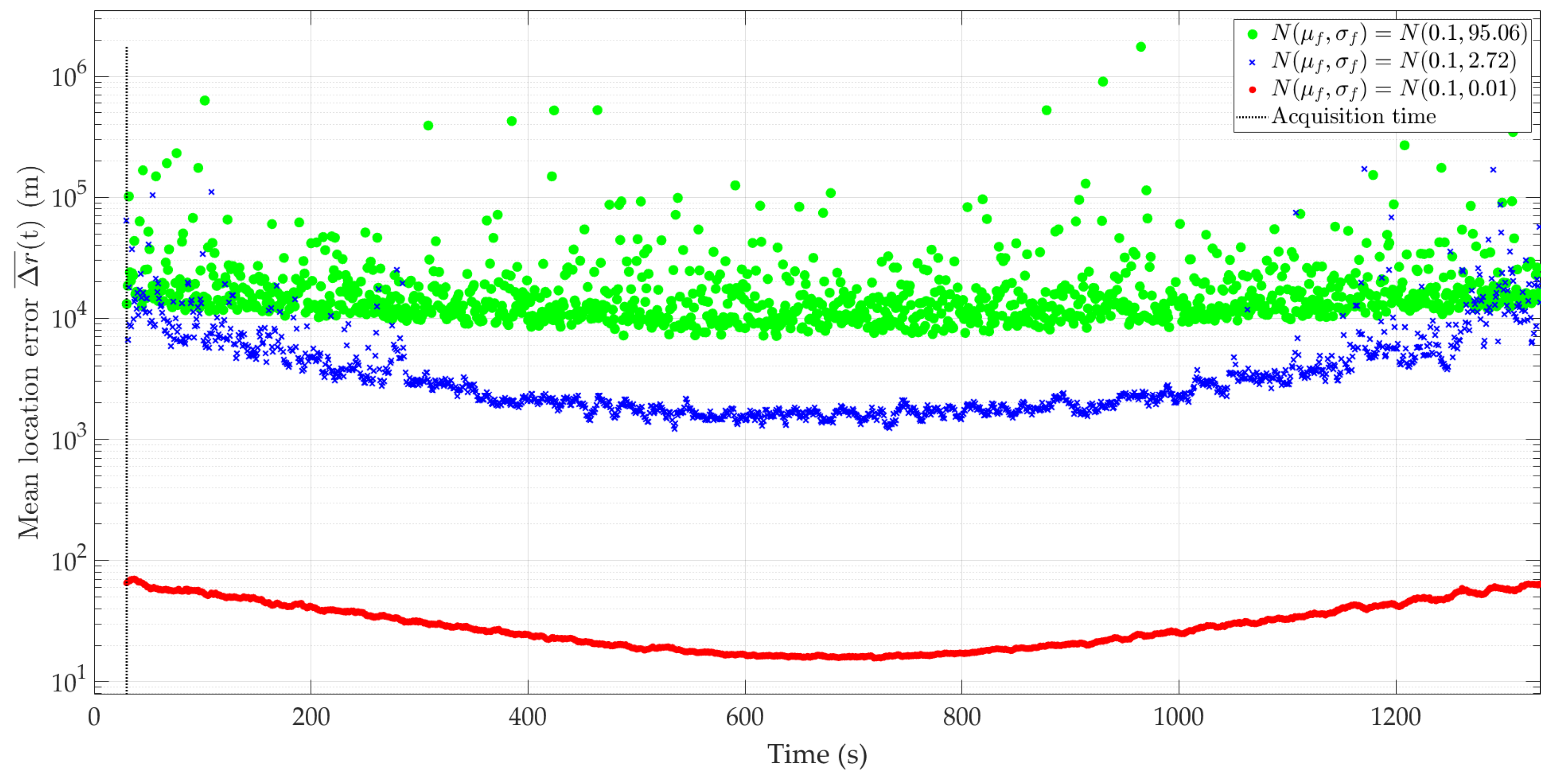
5.2. Results for Short-Range Scenario
5.3. Results for Long-Range Scenario
6. Synthesis of Results
6.1. Scenario Comparision
6.2. Comparison of Simulation and Empirical Results
6.3. SDR Comparison
6.4. Small-Size Frequency Oscillator Overview
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Addra, M.; Castel, D.; Dulongpont, J.; Genest, P. Microelectronics in Mobile Communications: A Key Enabler. IEEE Micro 1999, 19, 62–70. [Google Scholar] [CrossRef]
- Petricca, L. Micro and Nano Technologies for Unmanned Nano Air Vehicles (NAVs). Ph.D. Thesis, Buskerud and Vestfold University College, Kongsberg, Norway, 2014. [Google Scholar]
- Finn, A.; Scheding, S. Developments and Challenges for Autonomous Unmanned Vehicles; Intelligent Systems Reference Library; Springer: Berlin/Heidelberg, Germany, 2010; Volume 3, ISBN 978-3-642-10703-0. [Google Scholar]
- Ulversoy, T. Software Defined Radio: Challenges and Opportunities. IEEE Commun. Surv. Tutor. 2010, 12, 531–550. [Google Scholar] [CrossRef]
- Research and Markets Ltd. Software Defined Radio Market: Global Industry Trends, Share, Size, Growth, Opportunity and Forecast 2023–2028. Available online: https://www.researchandmarkets.com/reports/5642378/software-defined-radio-market-global-industry (accessed on 13 November 2023).
- Research and Markets Ltd. Global Commercial Unmanned Aerial Vehicle Drones Market by Drone Type (Fixed Wing Drones, Hybrid Drones, Multi Rotor Drones), Application (Agriculture, Audit, Surveillance, Inspection & Monitoring, Consumer Goods & Retail)—Forecast 2023–2030. Available online: https://www.researchandmarkets.com/reports/5336496/global-commercial-unmanned-aerial-vehicle-drones (accessed on 13 November 2023).
- Johnson, P. New Research Lab Leads to Unique Radio Receiver. E-Syst. Team 1985, 5, 6–7. [Google Scholar]
- Collins, T.F.; Getz, R.; Pu, D. Software-Defined Radio for Engineers; Illustrated Edition; Artech House Publishers: Boston, FL, USA; London, UK, 2018; ISBN 978-1-63081-457-1. [Google Scholar]
- Mitola, J. Software Radios: Survey, Critical Evaluation and Future Directions. IEEE Aerosp. Electron. Syst. Mag. 1993, 8, 25–36. [Google Scholar] [CrossRef]
- Chen, T.; Matinmikko, M.; Chen, X.; Zhou, X.; Ahokangas, P. Software Defined Mobile Networks: Concept, Survey, and Research Directions. IEEE Commun. Mag. 2015, 53, 126–133. [Google Scholar] [CrossRef]
- Software Defined Radio: Past, Present, and Future. Available online: https://www.ni.com/en/perspectives/software-defined-radio-past-present-future.html (accessed on 14 November 2023).
- Shakhatreh, H.; Sawalmeh, A.H.; Al-Fuqaha, A.; Dou, Z.; Almaita, E.; Khalil, I.; Othman, N.S.; Khreishah, A.; Guizani, M. Unmanned Aerial Vehicles (UAVs): A Survey on Civil Applications and Key Research Challenges. IEEE Access 2019, 7, 48572–48634. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Khan, M.A.; Noor, F.; Ullah, I.; Alsharif, M.H. Towards the Unmanned Aerial Vehicles (UAVs): A Comprehensive Review. Drones 2022, 6, 147. [Google Scholar] [CrossRef]
- Specht, M.; Widźgowski, S.; Stateczny, A.; Specht, C.; Lewicka, O. Comparative Analysis of Unmanned Aerial Vehicles Used in Photogrammetric Surveys. TransNav Int. J. Mar. Navig. Saf. Od Sea Transp. 2023, 17, 433–443. [Google Scholar] [CrossRef]
- Laghari, A.A.; Jumani, A.K.; Laghari, R.A.; Nawaz, H. Unmanned Aerial Vehicles: A Review. Cogn. Robot. 2023, 3, 8–22. [Google Scholar] [CrossRef]
- Chaturvedi, S.K.; Sekhar, R.; Banerjee, S.; Kamal, H. Comparative Review Study of Military and Civilian Unmanned Aerial Vehicles (UAVs). Incas Bull. 2019, 11, 183–198. [Google Scholar] [CrossRef]
- Ramesh, P.S.; Jeyan, J.V.M.L. Comparative Analysis of the Impact of Operating Parameters on Military and Civil Applications of Mini Unmanned Aerial Vehicle (UAV). In Proceedings of the 2020 3rd International Conference on Frontiers in Automobile and Mechanical Engineering (FAME), Chennai, India, 7–9 August 2020; p. 030034. [Google Scholar]
- Lyon, D.H. A Military Perspective on Small Unmanned Aerial Vehicles. IEEE Instrum. Meas. Mag. 2004, 7, 27–31. [Google Scholar] [CrossRef]
- Zhu, X. Analysis of Military Application of UAV Swarm Technology. In Proceedings of the 2020 3rd International Conference on Unmanned Systems (ICUS), Harbin, China, 27–28 November 2020; pp. 1200–1204. [Google Scholar]
- MarketsandMarkets Research Private Ltd. Military Drone Market—Global Size, Share & Industry Analysis. Available online: https://www.marketsandmarkets.com/Market-Reports/military-drone-market-221577711.html (accessed on 13 November 2023).
- Research and Markets Ltd. Military Drones Global Market Report 2023—Research and Markets. Available online: https://www.researchandmarkets.com/reports/5735293/military-drones-global-market-report (accessed on 13 November 2023).
- Giordani, M.; Zorzi, M. Non-Terrestrial Networks in the 6G Era: Challenges and Opportunities. IEEE Netw. 2021, 35, 244–251. [Google Scholar] [CrossRef]
- Rinaldi, F.; Maattanen, H.-L.; Torsner, J.; Pizzi, S.; Andreev, S.; Iera, A.; Koucheryavy, Y.; Araniti, G. Non-Terrestrial Networks in 5G & Beyond: A Survey. IEEE Access 2020, 8, 165178–165200. [Google Scholar] [CrossRef]
- Bastos, L.; Capela, G.; Koprulu, A.; Elzinga, G. Potential of 5G Technologies for Military Application. In Proceedings of the 2021 21st International Conference on Military Communication and Information Systems (ICMCIS), The Hague, The Netherlands, 4–5 May 2021; pp. 1–8. [Google Scholar]
- Zmysłowski, D.; Skokowski, P.; Malon, K.; Maślanka, K.; Kelner, J.M. Naval Use Cases of 5G Technology. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2023, 17, 595–603. [Google Scholar] [CrossRef]
- Knight, B. A Guide to Military Drones. Available online: https://www.dw.com/en/a-guide-to-military-drones/a-39441185 (accessed on 13 November 2023).
- Kelner, J.M.; Ziółkowski, C. Effectiveness of Mobile Emitter Location by Cooperative Swarm of Unmanned Aerial Vehicles in Various Environmental Conditions. Sensors 2020, 20, 2575. [Google Scholar] [CrossRef]
- Szczepanik, R.; Kelner, J.M. Two-Stage Overlapping Algorithm for Signal Doppler Frequency Location Method. In Proceedings of the 2023 Signal Processing Symposium (SPSympo), Karpacz, Poland, 26–28 September 2023; pp. 184–188. [Google Scholar]
- Rafa, J.; Ziółkowski, C. Influence of Transmitter Motion on Received Signal Parameters—Analysis of the Doppler Effect. Wave Motion 2008, 45, 178–190. [Google Scholar] [CrossRef]
- Kelner, J.M.; Ziółkowski, C. The use of SDF technology to BPSK and QPSK emission sources’ location (in Polish: Zastosowanie technologii SDF do lokalizowania źródeł emisji BPSK i QPSK). Przegląd Elektrotechniczny 2015, 91, 61–65. [Google Scholar] [CrossRef]
- Kelner, J.M.; Ziółkowski, C.; Marszałek, P. Influence of the Frequency Stability on the Emitter Position in SDF Method. In Proceedings of the 2016 17th International Conference on Military Communications and Information Systems (ICMCIS), Brussels, Belgium, 23–24 May 2016; pp. 1–6. [Google Scholar]
- Kelner, J.M.; Ziółkowski, C.; Nowosielski, L.; Wnuk, M.T. Localization of Emission Source in Urban Environment Based on the Doppler Effect. In Proceedings of the 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 15–18 May 2016; pp. 1–5. [Google Scholar]
- Ziółkowski, C.; Kelner, J.M. Doppler-Based Navigation for Mobile Protection System of Strategic Maritime Facilities in GNSS Jamming and Spoofing Conditions. IET Radar Sonar Navig. 2020, 14, 643–651. [Google Scholar] [CrossRef]
- Bednarz, K.; Wojtuń, J. Frequency Stability of Low Budget SDR Platforms in Location Procedures Based on Doppler Method (Stabilność Częstotliwości Niskobudżetowych Platform SDR w Procedurach Lokalizacji Opartych o Metody Dopplerowskie). Telecommun. Rev. Telecommun. News 2023, 96, 256–259. [Google Scholar] [CrossRef]
- ETSI EN 300 422-1 V2.2.1; Institute Wireless Microphones; Audio PMSE Equipment up to 3 GHz; Part 1: Audio PMSE Equipment up to 3 GHz; Harmonised Standard for Access to Radio Spectrum. European Telecommunications Standards: Sophia, France, 2021.
- Howe, D.A. Frequency Domain Stability Measurements: A Tutorial Introduction; U.S. Department of Commerce, National Bureau of Standards: Boulder, CO, USA, 1976. [Google Scholar]
- Howe, D.A. Frequency Stability. Available online: https://tf.nist.gov/general/pdf/1928.pdf (accessed on 15 November 2023).
- Allan, D.W. Statistics of Atomic Frequency Standards. Proc. IEEE 1966, 54, 221–230. [Google Scholar] [CrossRef]
- Bednarz, K.; Wojtuń, J.; Kelner, J.M.; Ziółkowski, C. Frequency Stability Measurements of Software-Defined Radios. Electronics, 2024; under preparation. [Google Scholar]
- Holland, O.; Bogucka, H.; Medeisis, A. The Universal Software Radio Peripheral (USRP) Family of Low-Cost SDRs. In Opportunistic Spectrum Sharing and White Space Access: The Practical Reality; Wiley: Hoboken, NJ, USA, 2015; pp. 3–23. [Google Scholar]
- ADALM-PLUTO Evaluation Board|Analog Devices. Available online: https://www.analog.com/en/design-center/evaluation-hardware-and-software/evaluation-boards-kits/adalm-pluto.html (accessed on 6 November 2023).
- Ettus Research, a National Instruments Brand USRP B200mini-i (1X1, 70 MHZ–6 GHZ). Available online: https://www.ettus.com/all-products/usrp-b200mini-i-2/ (accessed on 6 November 2023).
- Ettus Research, a National Instruments Brand USRP N210 Software Defined Radio (SDR). Available online: https://www.ettus.com/all-products/un210-kit/ (accessed on 6 November 2023).
- USRP Hardware Driver and USRP Manual: Daughterboards. Available online: https://files.ettus.com/manual_archive/n310_release-0.1/html/page_dboards.html (accessed on 8 November 2023).
- TX and RX Daughterboards For the USRP Software Radio System. Available online: https://www.olifantasia.com/gnuradio/usrp/files/datasheets/datasheet_daughterboards.pdf (accessed on 6 November 2023).
- bladeRF 2.0 Micro xA4. Available online: https://www.nuand.com/product/bladerf-xa4/ (accessed on 6 November 2023).
- NI USRP-2950R Specifications|Manualzz. Available online: https://manualzz.com/doc/26450509/ni-usrp-2950r-specifications (accessed on 13 November 2023).
- GROUP, E. NI USRP-2930 USRP Software Defined Radio Device (50 MHz~2.2 GHz, 1-Channel, GPSDO). Available online: https://emin.com.mm/niusrp-2930781910-01-ni-usrp-2930-usrp-software-defined-radio-device-50-mhz-2-2-ghz-1-channel-gpsdo-100661/pr.html (accessed on 13 November 2023).
- Office of Electronic Communications. Available online: https://www.uke.gov.pl/en/ (accessed on 15 November 2023).
- Consumer Drones Comparison—Compare Mavic Series and Other Consumer Drones—DJI. Available online: https://www.dji.com/pl/products/comparison-consumer-drones (accessed on 8 November 2023).
- Civil Drones (Unmanned Aircraft). Available online: https://www.easa.europa.eu/en/domains/civil-drones (accessed on 8 November 2023).
- Gu, X.; Zheng, C.; Li, Z.; Zhou, G.; Zhou, H.; Zhao, L. Cooperative Localization for UAV Systems from the Perspective of Physical Clock Synchronization. IEEE J. Sel. Areas Commun. 2024, 42, 21–33. [Google Scholar] [CrossRef]
- Kelner, J.M.; Ziółkowski, C.; Kachel, L. The Empirical Verification of the Location Method Based on the Doppler Effect. In Proceedings of the 2008 17th International Conference on Microwaves, Radar and Wireless Communications (MIKON), Wroclaw, Poland, 19–21 May 2008; Volume 3, pp. 755–758. [Google Scholar]
- Gajewski, P.; Ziółkowski, C.; Kelner, J.M. Space Doppler location method of radio signal sources (in Polish: Przestrzenna dopplerowska metoda lokalizacji źródeł sygnałów radiowych). Bull. Mil. Univ. Technol. 2011, 60, 187–200. [Google Scholar]
- Szczepanik, R.; Kelner, J.M. Software-Based Implementation of SDF Method Using SDR USRP Platform (in Polish: Programowa Implementacja Metody SDF z Wykorzystaniem Platformy SDR). Telecommun. Rev. Telecommun. News 2019, 92, 217–222. [Google Scholar] [CrossRef]
- Szczepanik, R.; Kelner, J.M. Localization of Modulated Signal Emitters Using Doppler-Based Method Implemented on Single UAV. In Proceedings of the 2023 Communication and Information Technologies (KIT), Vysoke Tatry, Slovakia, 11–13 October 2023; pp. 61–65. [Google Scholar]
- Tesch, D.A.; Berz, E.L.; Hessel, F.P. RFID Indoor Localization Based on Doppler Effect. In Proceedings of the 2015 16th International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 2–4 March 2015; pp. 556–560. [Google Scholar]
- ADALM-PLUTO SDR Hack: Tune 70 MHz to 6 GHz and GQRX Install. Available online: https://www.rtl-sdr.com/adalm-pluto-sdr-hack-tune-70-mhz-to-6-ghz-and-gqrx-install/ (accessed on 23 November 2023).
- Rubidium Frequency Standard-FS725. Available online: https://www.thinksrs.com/products/fs725.html (accessed on 6 November 2023).
- PRS10-Rubidium Frequency Standard. Available online: https://www.thinksrs.com/products/prs10.htm (accessed on 6 November 2023).
- Rubidium Frequency Standard Model AR133A. Available online: https://www.es-france.com/index.php?controller=attachment&id_attachment=13718 (accessed on 6 November 2023).
- Miniature Atomic Clock (MAC-SA.3Xm)|Microsemi. Available online: https://www.microsemi.com/product-directory/embedded-clocks-frequency-references/3825-miniature-atomic-clock-mac (accessed on 6 November 2023).
- RFS-M102 Miniature Size Rb Frequency Standard. Available online: https://www.morion-us.com/catalog_pdf/RFS-M102.pdf (accessed on 6 November 2023).
- Spectratime LPFRS-Safran Electronics & Defense|Rubidium Oscillator. Available online: https://www.everythingrf.com/products/rubidium-oscillators/orolia/895-1447-lpfrs (accessed on 6 November 2023).
- Rubidium Oscillators-IQD|Mouser. Available online: https://www.mouser.pl/new/iqd/iqd-rubidium-oscillators/?_gl=1*1k6ksie*_ga*NTIyNDYyMDc0LjE2OTkyOTI5MTQ.*_ga_15W4STQT4T*MTY5OTI5MjkxNC4xLjAuMTY5OTI5MjkxNC42MC4wLjA. (accessed on 6 November 2023).
- Nano Atomic Clock-NAC1. Available online: https://www.accubeat.com/nano-atomic-clock (accessed on 6 November 2023).
- Miniature Atomic Clock (MAC) SA5X User’s Guide. Available online: http://ww1.microchip.com/downloads/en/DeviceDoc/Miniature-Atomic-Clock-MAC-SA5X-Users-Guide-DS50002938A.pdf (accessed on 14 November 2023).
- E10-CPT-Quartzlock|Rubidium Oscillator. Available online: https://www.everythingrf.com/products/rubidium-oscillators/quartzlock/895-1536-e10-cpt (accessed on 6 November 2023).
- mRO-50 Ruggedized Rubidium Oscillator. Available online: https://www.safran-group.com/products-services/mro-50-ruggedized-rubidium-oscillator (accessed on 6 November 2023).
- CSAC-SA45S. Available online: https://www.microchip.com/en-us/product/csac-sa45s (accessed on 6 November 2023).
- Marlow, B.L.S.; Scherer, D.R. A Review of Commercial and Emerging Atomic Frequency Standards. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 2007–2022. [Google Scholar] [CrossRef] [PubMed]










| SDR Platform | Without Rubidium Oscillator | With Rubidium Oscillator | ||||
|---|---|---|---|---|---|---|
| (Hz) | (Hz) | (–) | (Hz) | (Hz) | (–) | |
| ADALM-PLUTO | 16,757.1 | 285.9 | 2.11∙10−7 | −55.155 | 5.113 | 3.77∙10−9 |
| B200mini-i | 1436.7 | 5.5 | 4.61∙10−9 | −0.004 | 1.287 | 9.48∙10−10 |
| N210 + WBX | 1010.3 | 179.9 | 1.21∙10−7 | 0.011 | 0.014 | 1.01∙10−11 |
| NI–2950R | 928.3 | 13.9 | 9.62∙10−9 | −0.011 | 0.012 | 8.71∙10−12 |
| bladeRF 2.0 micro xA4 | −37.5 | 34.7 | 2.40∙10−8 | −0.201 | 0.010 | 7.12∙10−12 |
| N210 + RFX1200 | 1180.1 | 78.6 | 6.08∙10−8 | 0.012 | 0.008 | 5.68∙10−12 |
| NI–2930 | 93.0 | 96.3 | 7.68∙10−8 | 0.009 | 0.005 | 3.91∙10−12 |
| Device Class | SDR Platform | (–) | (Hz) for f0 = 1358 MHz | |
|---|---|---|---|---|
| 1 | All tested SDRs without the external oscillator FS725 | 95.06 | ||
| 2 | ADALM-PLUTO B200mini-i | with FS725 | 2.72 | |
| 3 | N210 + WBX NI–2950R bladeRF 2.0 micro xA4 N210 + RFX1200 NI–2930 | with FS725 | 0.01 | |
| Frequency Stability Parameters (Hz) | Location Error (m) | |||
|---|---|---|---|---|
| N (10.0, 95.06) | 3149 | 119,810 | 14,980 | 18,213 |
| N (10.0, 2.72) | 153 | 511 | 251 | 94 |
| N (10.0, 0.01) | 151 | 474 | 246 | 88 |
| N (1.0, 95.06) | 3384 | 258,415 | 16,523 | 28,917 |
| N (1.0, 2.72) | 21 | 75 | 34 | 12 |
| N (1.0, 0.01) | 15 | 44 | 25 | 9 |
| N (0.1, 95.06) | 3329 | 97,601 | 15,013 | 16,527 |
| N (0.1, 2.72) | 14 | 45 | 24 | 8 |
| N (0.1, 0.01) | 2 | 4 | 2 | 1 |
| Frequency Stability Parameters (Hz) | Location Error (m) | |||
|---|---|---|---|---|
| N (10.0, 95.06) | 6767 | 3,576,176 | 26,340 | 128,434 |
| N (10.0, 2.72) | 2026 | 167,774 | 6391 | 10,594 |
| N (10.0, 0.01) | 1470 | 6685 | 2988 | 1421 |
| N (1.0, 95.06) | 6693 | 2,173,297 | 23,394 | 89,370 |
| N (1.0, 2.72) | 1187 | 162,559 | 4920 | 8730 |
| N (1.0, 0.01) | 147 | 637 | 299 | 142 |
| N (0.1, 95.06) | 6575 | 603,692 | 19,695 | 29,817 |
| N (0.1, 2.72) | 1233 | 227,920 | 5311 | 11,285 |
| N (0.1, 0.01) | 16 | 68 | 31 | 14 |
| Frequency Stability Parameters (Hz) | Short-Range Scenario | Long-Range Scenario | ||
|---|---|---|---|---|
| (%) | (%) | (%) | (%) | |
| N (1.0, 2.72) | 3.4 | 1.2 | 49.2 | 87.3 |
| N (1.0, 0.01) | 2.5 | 0.9 | 3.0 | 1.4 |
| N (0.1, 2.72) | 2.4 | 0.8 | 53.1 | 112.8 |
| N (0.1, 0.01) | 0.2 | 0.1 | 0.3 | 0.1 |
| Works (Year) | Vehicle (Speed) | Emitter/Signal Generator (Emitted Signal Type; Carrier Frequency) | Localization Sensor/Receiver | Location Error | Emitter–Receiver Maximum Distance |
|---|---|---|---|---|---|
| [53] (2008) | Car () | Hammeg HM81384-3 stabilized by FS 725 rubidium standard (transmitted signal: harmonic; ) | Rohde & Schwarz ESMC-R1 stabilized by FS 725 rubidium standard | <1.1 m | 56 m |
| [54] (2011) | Car () | Hammeg HM81384-3 stabilized by FS 725 rubidium standard (transmitted signal: harmonic; ) | Rohde & Schwarz ESMC-R1 stabilized by FS 725 rubidium standard | <2.3 m | 65 m |
| [30] (2015) | Car () | Hammeg HM81384-3 stabilized by FS 725 rubidium standard (transmitted signal: BPSK and QPSK; ) | Rohde & Schwarz EM550 stabilized by FS 725 rubidium standard | 2–9 m | 80 m |
| [55] (2019) | Car () | Rohde & Schwarz SMIQ02 stabilized by FS 725 rubidium standard (transmitted signal: harmonic; ) | Ettus Research USRP B200mini-i | 2–37 m | 148 m |
| [56] (2023) | UAV () | Ettus Research USRP B200mini-i stabilized by FS 725 rubidium standard (transmitted signal: BPSK, QPSK, and 16 QAM; ) | Ettus Research USRP B200mini-i | 2–17 m | 395 m |
| [57] (2015) | Conveyor belt () | RFID tag (transmitted signal: standard UHF RFID; ) | Impinj Speedway Revolution R420 RFID reader | 0.052 m | 2.4 m |
| No. | SDR Platform | Frequency Range (MHz) | Bandwidth (MHz) | Dimensions * (mm) | Weight (g) | |
|---|---|---|---|---|---|---|
| Tx | Rx | |||||
| 1 | ADALM-PLUTO | 70–3800 ** | 70–3800 ** | 20 ** | 78 × 117 × 23 | 116 |
| 2 | B200mini-i | 70–6000 | 70–6000 | 56 | 55 × 79 × 16 | 108 |
| 3 | N210 + WBX | 50–2200 | 50–2200 | 40 | 160 × 204 × 48 | 1160 |
| 4 | NI–2950R | 50–2200 | 50–2200 | 120 | 218 × 267 × 39 | 1787 |
| 5 | bladeRF 2.0 micro xA4 | 47–6000 | 70–6000 | 56 | 72 × 110 × 24 | 112 |
| 6 | N210 + RFX1200 | 1150–1450 | 1150–1450 | 40 | 160 × 204 × 48 | 1160 |
| 7 | NI–2930 | 50–2200 | 50–2200 | 40 | 160 × 204 × 48 | 1218 |
| No. | SDR Platform | (Hz) | (Hz) | (m) | |
|---|---|---|---|---|---|
| Short-Range Scenario | Long-Range Scenario | ||||
| 1 | ADALM-PLUTO | −55.155 | 5.113 | 1897.8 | 51,347.2 |
| 2 | B200mini-i | −0.004 | 1.287 | 3.4 | 668.6 |
| 3 | N210 + WBX | 0.011 | 0.014 | 0.1 | 6.4 |
| 4 | NI–2950R | −0.011 | 0.012 | 0.1 | 5.2 |
| 5 | bladeRF 2.0 micro xA4 | −0.201 | 0.010 | 1.7 | 28.6 |
| 6 | N210 + RFX1200 | 0.012 | 0.008 | 0.1 | 3.7 |
| 7 | NI–2930 | 0.009 | 0.005 | 0.1 | 2.5 |
| No. | Model | Type | ADEV @ 100 s | Power Consumption (W) | Dimensions * (mm) | Weight (g) |
|---|---|---|---|---|---|---|
| 1 | Stanford Research Systems PRS-10 [60] | Rb | 53 | 76.2 × 50.8 × 101.6 | 600 | |
| 2 | AccuBeat AR133A [61] | Rb | 18 | 77.0 × 77.0 × 25.4 | 295 | |
| 3 | Microsemi SA.31m, SA.33m, SA.35m [62] | Rb | 14 | 50.8 × 50.8 × 18.3 | 85 | |
| 4 | Morion RFS-M102 [63] | Rb | 18 | 51.0 × 51.0 × 25.0 | - | |
| 5 | Safran LPFRS [64] | Rb | 20 | 76.0 × 77.0 × 36.5 | 290 | |
| 6 | IQD IQRB-1 [65] | Rb | 20 | 50.8 × 50.8 × 25.0 | - | |
| 7 | AccuBeat NAC1 [66] | Rb | 2.4 | 41.1 × 35.8 × 22.0 | 75 | |
| 8 | Microchip MAC-SA5X (SA53, SA55) [67] | Rb | 8 | 50.8 × 50.8 × 18.3 | 100 | |
| 9 | Quartzlock E10-CPT [68] | Rb | 5.2 | 45.0 × 36.0 × 15.0 | 45 | |
| 10 | Safran mRO-50 Ruggedized [69] | Rb | 1.5 | 50.8 × 50.8 × 20.0 | 80 | |
| 11 | Microchip SA.45s CSAC [70] | Cs | 0.14 | 35.3 × 40.6 × 11.4 | 35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bednarz, K.; Wojtuń, J.; Kelner, J.M.; Różyc, K. Frequency Instability Impact of Low-Cost SDRs on Doppler-Based Localization Accuracy. Sensors 2024, 24, 1053. https://doi.org/10.3390/s24041053
Bednarz K, Wojtuń J, Kelner JM, Różyc K. Frequency Instability Impact of Low-Cost SDRs on Doppler-Based Localization Accuracy. Sensors. 2024; 24(4):1053. https://doi.org/10.3390/s24041053
Chicago/Turabian StyleBednarz, Kacper, Jarosław Wojtuń, Jan M. Kelner, and Krzysztof Różyc. 2024. "Frequency Instability Impact of Low-Cost SDRs on Doppler-Based Localization Accuracy" Sensors 24, no. 4: 1053. https://doi.org/10.3390/s24041053
APA StyleBednarz, K., Wojtuń, J., Kelner, J. M., & Różyc, K. (2024). Frequency Instability Impact of Low-Cost SDRs on Doppler-Based Localization Accuracy. Sensors, 24(4), 1053. https://doi.org/10.3390/s24041053







