A 19-Bit Small Absolute Matrix Encoder
Abstract
1. Introduction
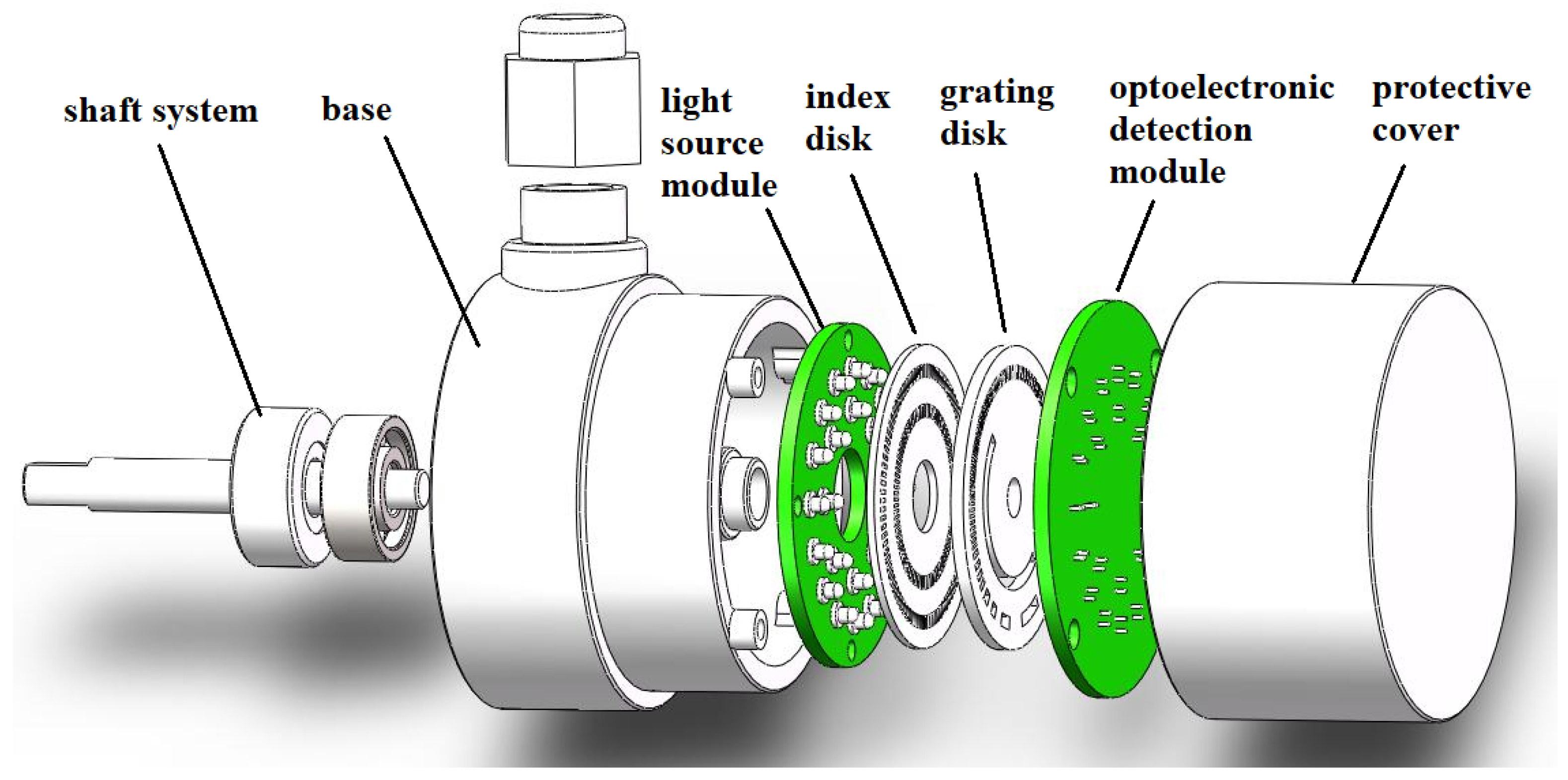
2. Working Principle
2.1. Design of Photoelectric Detection Circuit
- (1)
- Voltage amplification circuit
- (2)
- Shaping circuit
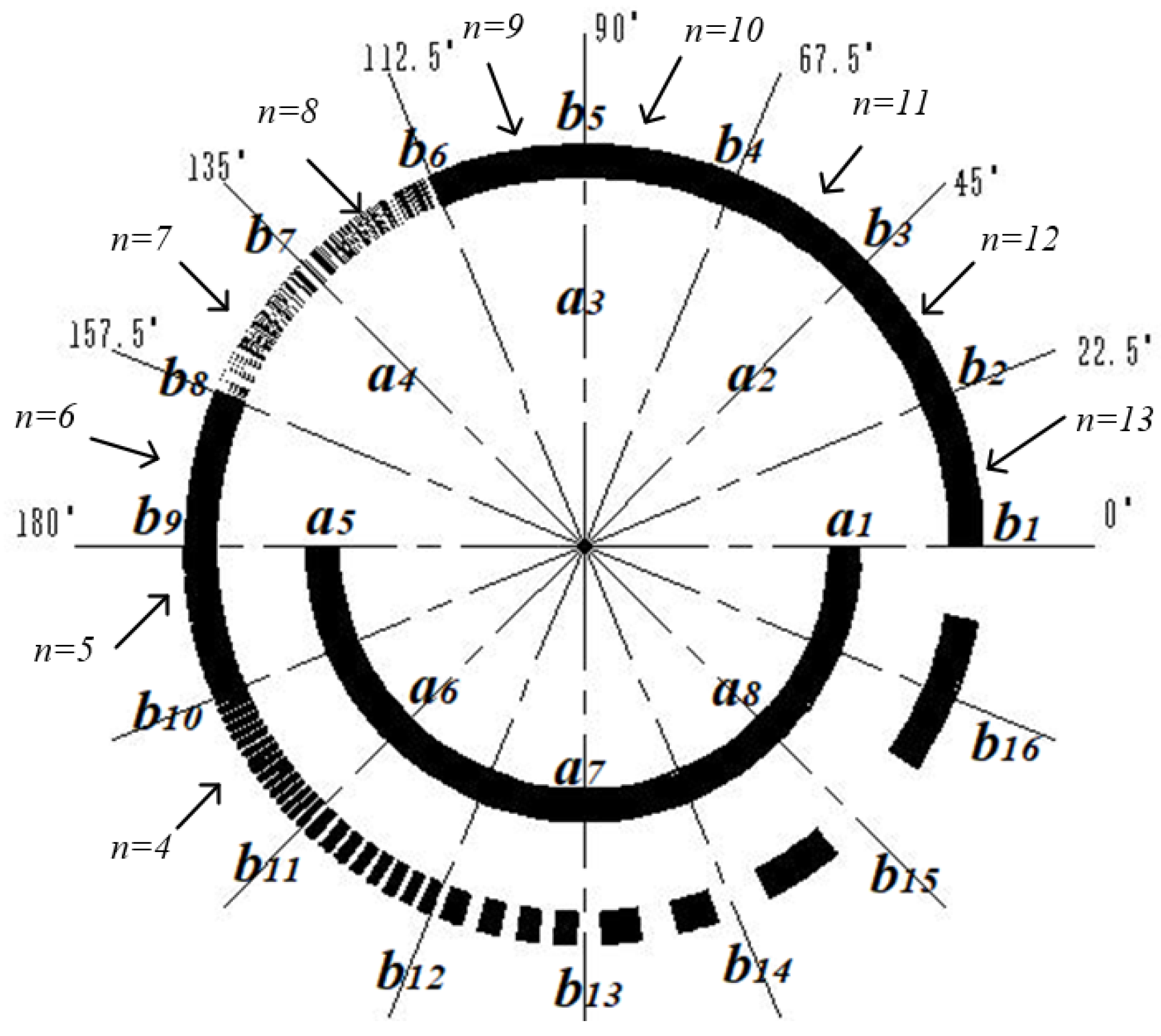
2.2. Design of Matrix Encoder
- (1)
- The circle a is exactly the same as the traditional Gray code track engraving method, which completes the encoding of 4-bit traditional code tracks through the placement of detectors.
- (2)
- The method of engraving each code track in each code area of circle b is consistent with traditional code tracks, and the center angle of the adjacent detectors in circle b is the same as the center angle occupied by each code area. Therefore, when the physical code disk is turned to any position, 16 detectors read each of the 16 code areas, ensuring that there is no dead angle recording of the code disk information within 360 °.
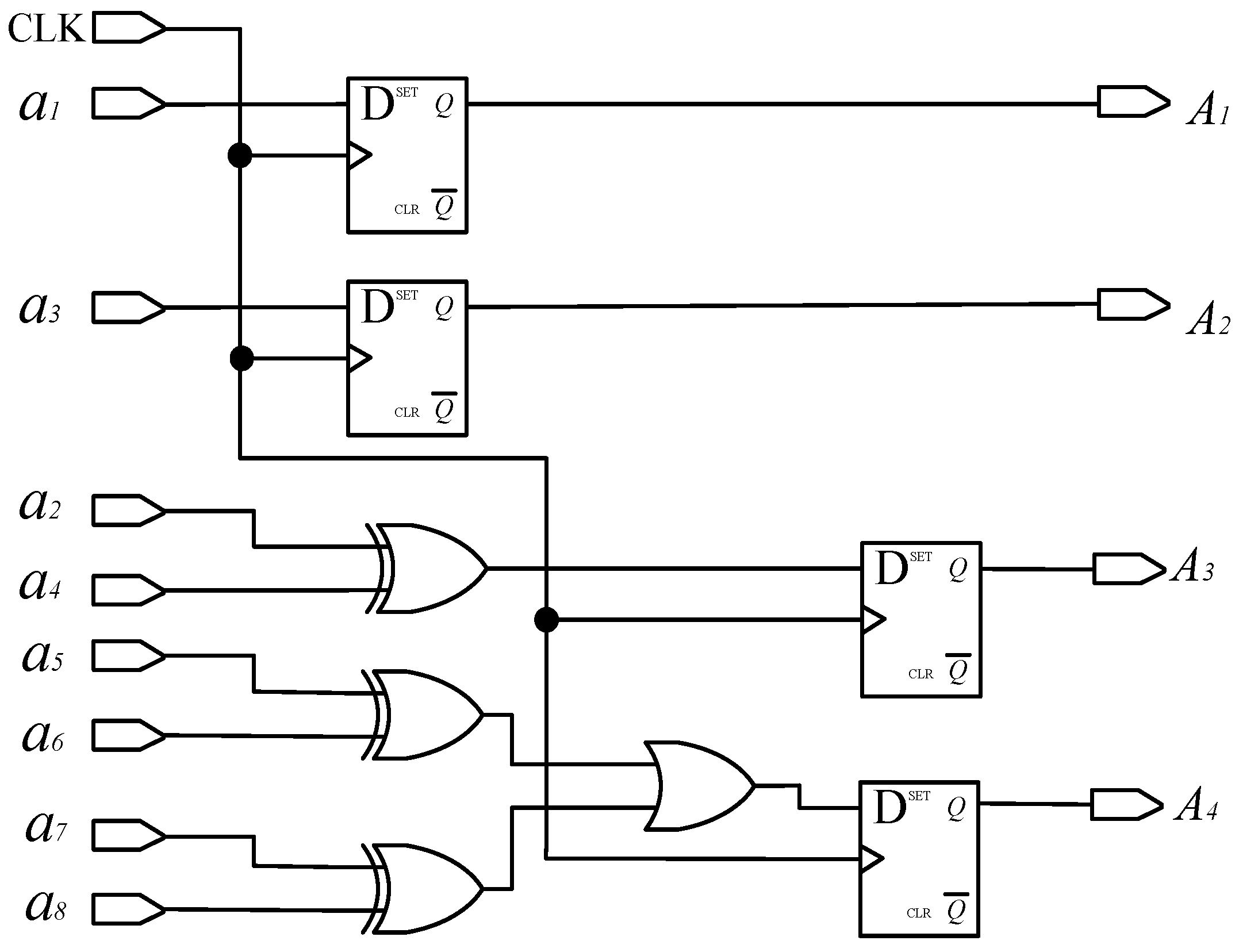
2.3. Decoding Principles
3. Simulation Analysis and Verification
- (1)
- Matrix decoding
- (2)
- Traditional Gray code → Natural binary code
4. Experimental Results and Error Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Das, S.; Chakraborty, B. Design and Realization of an Optical Rotary Sensor. IEEE Sens. J. 2018, 18, 2675–2681. [Google Scholar] [CrossRef]
- Johnson, M. Polarimetric 360° absolute rotary encoder. Adv. Opt. Technol. 2022, 11, 13–16. [Google Scholar] [CrossRef]
- Xi, R.; Hu, J.; Guo, H.; Du, S. Research on a single-ring absolute coder disc encoding and decoding technology combined with Huffman coding. In Proceedings of AOPC 2019: Optoelectronic Devices and Integration and Terahertz Technology and Applications; SPIE: London, UK, 2019; Volume 11334, p. 1133404. [Google Scholar]
- Jankowska, K.; Dybkowski, M. Classification of Optoelectronic Rotary Encoder Faults Based on Deep Learning Methods in Permanent Magnet Synchronous Motor Drive System. Electronics 2023, 12, 4184. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, R.; Yu, Y.; Yang, H. Small metal code disk based photoelectric encoder with high resolution. Laser Optoelectron Prog. 2019, 56, 180401. [Google Scholar] [CrossRef]
- Ying, S.; Qiuhua, W.; Ronghong, S. Subdivision error compensation method of small photoelectric encoder. J. Electron. Meas. Instrum. 2011, 25, 605–611. [Google Scholar]
- Iafolla, L.; Filipozzi, M.; Freund, S.; Zam, A.; Rauter, G.; Cattin, P.C. Proof of concept of a novel absolute rotary encoder. Sens. Actuators A Phys. 2020, 312, 112100. [Google Scholar] [CrossRef]
- Paul, S.; Chang, J. Design and Development of a Novel High-Resolution Absolute Rotary Encoder System Based on Affine n-digit N-ary Gray Code. J. Electr. Eng. Technol. 2018, 13, 943–952. [Google Scholar]
- Wan, Q.-H.; Wang, Y.-Y.; Sun, Y.; Yang, S.-W. A Novel Miniature Absolute Metal Rotary Encoder Based on Single-track Periodic Gray Code. In Proceedings of the IEEE International Conference on Instrumentation, Measurement, Computer, Communication & Control, Harbin, China, 8–10 December 2012. [Google Scholar]
- Iafolla, L.; Filipozzi, M.; Freund, S.; Zam, A.; Rauter, G.; Cattin, P.C. Machine learning-based method for linearization and error compensation of a novel absolute rotary encoder—ScienceDirect. Measurement 2020, 169, 108547. [Google Scholar] [CrossRef]
- Das, S.; Sarkar, T.S.; Chakraborty, B.; Dutta, H.S. Study on array of photo-detector based absolute rotary encoder. Sens. Actuators A Phys. 2016, 246, 114–122. [Google Scholar] [CrossRef]
- Baji’c, J.S.; Stupar, D.Z.; Daki’c, B.M.; Živanov, M.B.; Nagy, L.F. An absolute rotary position sensor based on cylindrical coordinate color space transformation. Sens. Actuators A Phys. 2015, 213, 27–34. [Google Scholar] [CrossRef]
- Pop, A.A. Incremental Encoder Speed Acquisition Using an STM32 Microcontroller and NI ELVIS. Sensors 2022, 22, 5127. [Google Scholar] [CrossRef] [PubMed]
- Matsuzoe, Y.; Tsuji, N.; Nakayama, T.; Fujita, K.; Yoshizawa, T. High-performance absolute rotary encoder using multitrack and M-code. Opt. Eng. 2003, 42, 124–131. [Google Scholar] [CrossRef]
- Hayashi, Y.; Shibata, S.; Kamabuchi, H.; Fukui, N.; Nashiki, M. Development of high resolution and compact absolute rotary encoder with batteryless multi-turn detecting function. J. Jpn. Soc. Precis. Eng. 2000, 66, 1177–1180. [Google Scholar] [CrossRef]
- Tresanchez, M.; Pallejà, T.; Teixidó, M.; Palacín, J. Using the image acquisition capabilities of the optical mouse sensor to build an absolute rotary encoder. Sens. Actuators A Phys. 2010, 157, 161–167. [Google Scholar] [CrossRef]
- Jiang, J.; Dai, J.; Yang, S.; Chang, Y. A 22-bit image encoder with optoelectronic integrated chip. Opt. Commun. 2022, 512, 128022. [Google Scholar] [CrossRef]
- Ren, W.; Jin, Z. Phase space visibility graph. Chaos Solitons Fractals 2023, 176, 114170. [Google Scholar] [CrossRef]
- Yang, X.; Liang, Y.; Zhang, W.; Wang, X.; Hao, D. Design of optoelectronic integrated chips for reflective encoders. Opt. Precis. Eng. 2023, 31, 1136–1149. [Google Scholar] [CrossRef]
- Yu, M.; Hou, N.; Wang, C.; Zhao, Y.; Chen, K.; Chi, Y. An Optoelectronic Detector with High Precision for Compact Grating Encoder Application. Electronics 2022, 11, 3486. [Google Scholar]








| Encoding Method | Number of Code Tracks | Resolution | Optical Characteristics | Monotropic | Algorithm Complexity | Response Speed | ||
|---|---|---|---|---|---|---|---|---|
| Parallel Light | Focusing and Imaging | Detector | ||||||
| Gray Code | n | 360/2n | No | No | Phototransistor | Yes | Low | Fast |
| Matrix code | 2 | 360/2n | No | No | Phototransistor | Yes | Medium | Medium |
| single-ring Gray code | 1 | Approaching 360/2n | Yes | Yes | CCD or CMOS | Yes | High | Slow |
| M-sequence code | 2 | 360/2n | Yes | Yes | CCD or CMOS | No | High | Slow |
| image encoding | 0 | Subpixel, ang-ular second level | Yes | Yes | CCD or CMOS | No | High | Slow |
| Model | Wavelength | Divergence Angle | Output Power | Voltage | Spectral Width | Spectral Temperature Drift | ||
|---|---|---|---|---|---|---|---|---|
| Value | Test Conditions | Maximum Value | Test Conditions | |||||
| SE2460-003 | 935 nm | 18° | 1.0 mW | IF = 50 mA | 1.6V | IF = 50 mA | 50 nm | 0.3 nm/°C |
| Model | Light Current | Receiving Angle | Rise and Fall Time | Dark Current | ||
|---|---|---|---|---|---|---|
| Value | Test Conditions | Value | Test Conditions | |||
| SD2440-003 | 1 mA | VCE = 5 V Radiancy H = 20 mW/cm2 | 24° | 15 μs | 100 nA | VCE = 5 V |
| Code Area | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Signal | |||||||||||||||||
| b1 | A19 | A18 | A17 | A16 | A15 | A14 | A13 | A12 | A11 | A10 | A9 | A8 | A7 | A6 | A5 | A5 | |
| b2 | A18 | A17 | A16 | A15 | A14 | A13 | A12 | A11 | A10 | A9 | A8 | A7 | A6 | A5 | A5 | A19 | |
| b3 | A17 | A16 | A15 | A14 | A13 | A12 | A11 | A10 | A9 | A8 | A7 | A6 | A5 | A5 | A19 | A18 | |
| b4 | A16 | A15 | A14 | A13 | A12 | A11 | A10 | A9 | A8 | A7 | A6 | A5 | A5 | A19 | A18 | A17 | |
| b5 | A15 | A14 | A13 | A12 | A11 | A10 | A9 | A8 | A7 | A6 | A5 | A5 | A19 | A18 | A17 | A16 | |
| b6 | A14 | A13 | A12 | A11 | A10 | A9 | A8 | A7 | A6 | A5 | A5 | A19 | A18 | A17 | A16 | A15 | |
| b7 | A13 | A12 | A11 | A10 | A9 | A8 | A7 | A6 | A5 | A5 | A19 | A18 | A17 | A16 | A15 | A14 | |
| b8 | A12 | A11 | A10 | A9 | A8 | A7 | A6 | A5 | A5 | A19 | A18 | A17 | A16 | A15 | A14 | A13 | |
| b9 | A11 | A10 | A9 | A8 | A7 | A6 | A5 | A5 | A19 | A18 | A17 | A16 | A15 | A14 | A13 | A12 | |
| b10 | A10 | A9 | A8 | A7 | A6 | A5 | A5 | A19 | A18 | A17 | A16 | A15 | A14 | A13 | A12 | A11 | |
| b11 | A9 | A8 | A7 | A6 | A5 | A5 | A19 | A18 | A17 | A16 | A15 | A14 | A13 | A12 | A11 | A10 | |
| b12 | A8 | A7 | A6 | A5 | A5 | A19 | A18 | A17 | A16 | A15 | A14 | A13 | A12 | A11 | A10 | A9 | |
| b13 | A7 | A6 | A5 | A5 | A19 | A18 | A17 | A16 | A15 | A14 | A13 | A12 | A11 | A10 | A9 | A8 | |
| b14 | A6 | A5 | A5 | A19 | A18 | A17 | A16 | A15 | A14 | A13 | A12 | A11 | A10 | A9 | A8 | A7 | |
| b15 | A5 | A5 | A19 | A18 | A17 | A16 | A15 | A14 | A13 | A12 | A11 | A10 | A9 | A8 | A7 | A6 | |
| b16 | A5 | A19 | A18 | A17 | A16 | A15 | A14 | A13 | A12 | A11 | A10 | A9 | A8 | A7 | A6 | A5 | |
| Code Area i | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Gray code | B0000 | B0001 | B0011 | B0010 | B0110 | B0111 |
| Logic code Mi | ||||||
| Code area i | 7 | 8 | 9 | 10 | 11 | 12 |
| Gray code | B0101 | B0100 | B1100 | B1101 | B1111 | B1110 |
| Logic code Mi | ||||||
| Code area i | 13 | 14 | 15 | 16 | ||
| Gray code | B1010 | B1011 | B1001 | B1000 | ||
| Logic code Mi |
| Angle | 0° | 15° | 30° | 45° | 60° | 75° | 90° | 105° |
|---|---|---|---|---|---|---|---|---|
| Measuring error (Prograde) | 0” | 2.5” | 3.1” | −2.4” | 2.3” | −1.2” | 2.3” | 3.4” |
| Measuring error (reversal) | 0” | 3.2” | 2.6” | −2.5” | −1.8 | 3.1” | −2.6” | 3.7” |
| Angle | 120° | 135° | 150° | 165° | 180° | 195° | 210° | 225° |
| Measuring error (Prograde) | 2.2” | −1.9” | 1.6” | 2.5” | −1.8” | 2.1” | 3.5” | −2.4” |
| Measuring error (reversal) | 2” | 2.4” | −3.5” | 1.9” | −2.2” | 1.8” | 2.3” | −1.6” |
| Angle | 240° | 255° | 270° | 285° | 300° | 315° | 330° | 345° |
| Measuring error (Prograde) | 2.6” | 3.1” | −2.6” | 2.7” | 3.9” | −2.6” | 3.1” | 2.2” |
| Measuring error (reversal) | −2.1” | 3.2” | −2.8” | 3.4” | 3.2” | 2.6” | −1.2” | 3.3” |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, L.; Cao, G.; Shang, C.; Ding, H. A 19-Bit Small Absolute Matrix Encoder. Sensors 2024, 24, 1400. https://doi.org/10.3390/s24051400
Geng L, Cao G, Shang C, Ding H. A 19-Bit Small Absolute Matrix Encoder. Sensors. 2024; 24(5):1400. https://doi.org/10.3390/s24051400
Chicago/Turabian StyleGeng, Liming, Guohua Cao, Chunmin Shang, and Hongchang Ding. 2024. "A 19-Bit Small Absolute Matrix Encoder" Sensors 24, no. 5: 1400. https://doi.org/10.3390/s24051400
APA StyleGeng, L., Cao, G., Shang, C., & Ding, H. (2024). A 19-Bit Small Absolute Matrix Encoder. Sensors, 24(5), 1400. https://doi.org/10.3390/s24051400






