Polar Decomposition of Jones Matrix and Mueller Matrix of Coherent Rayleigh Backscattering in Single-Mode Fibers
Abstract
1. Introduction
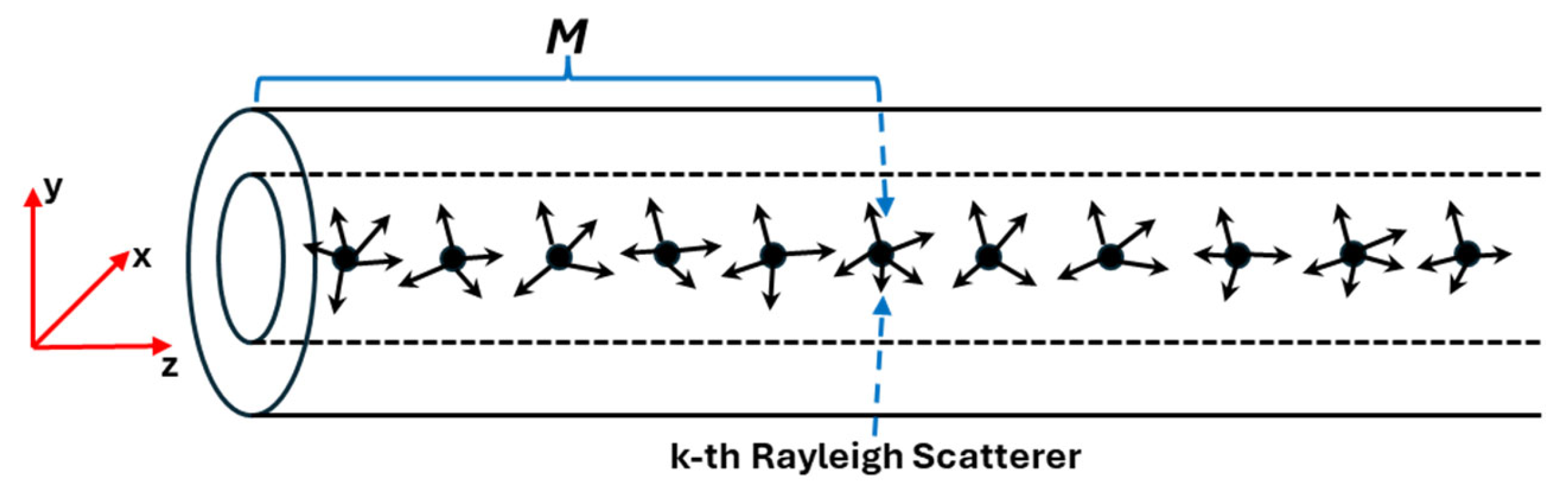
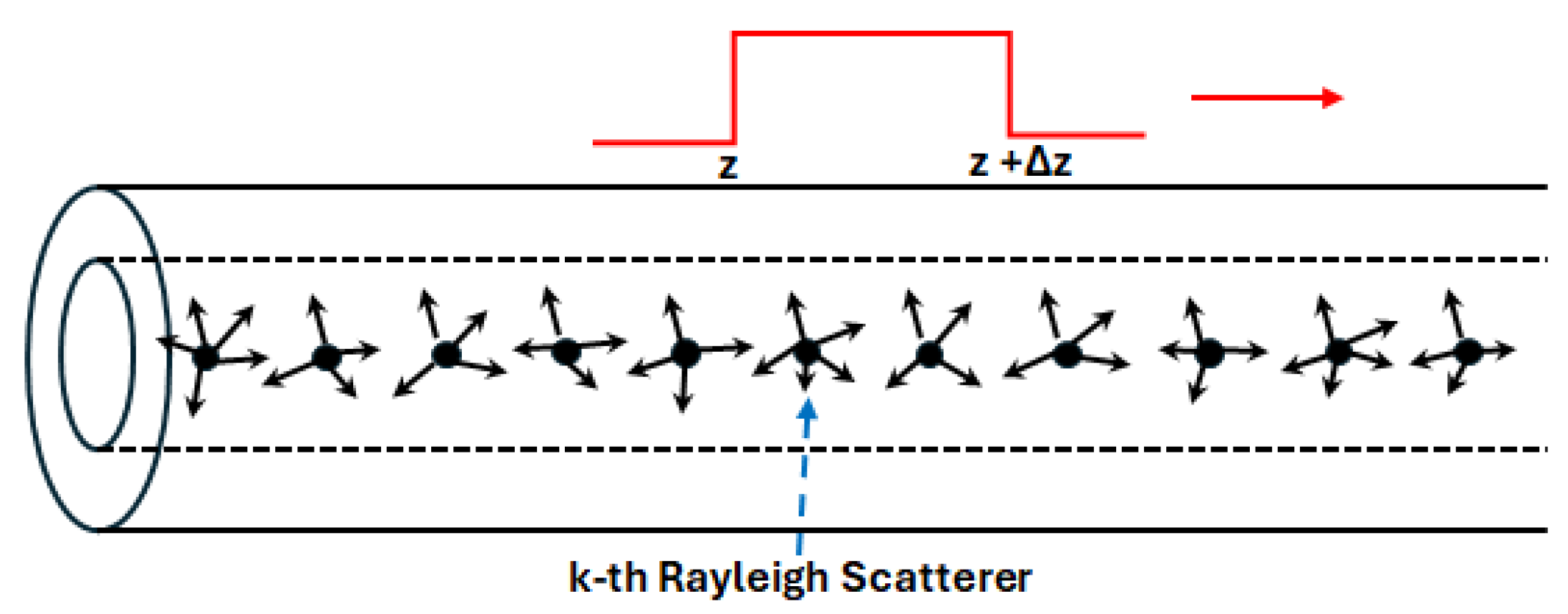
2. Polar Decomposition of the Jones Matrix of the Coherent RB
3. Polar Decomposition of the Mueller Matrix of the Coherent RB
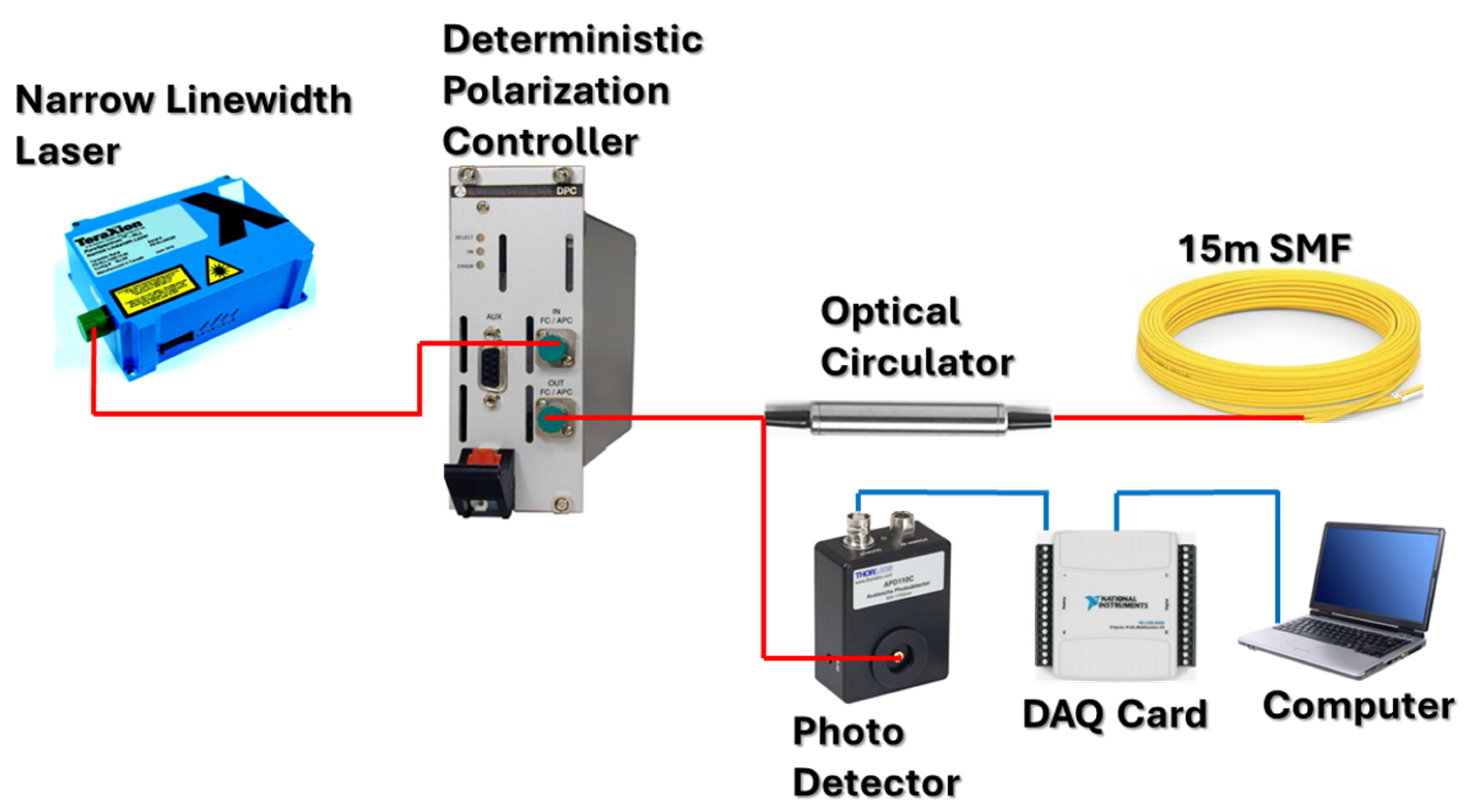
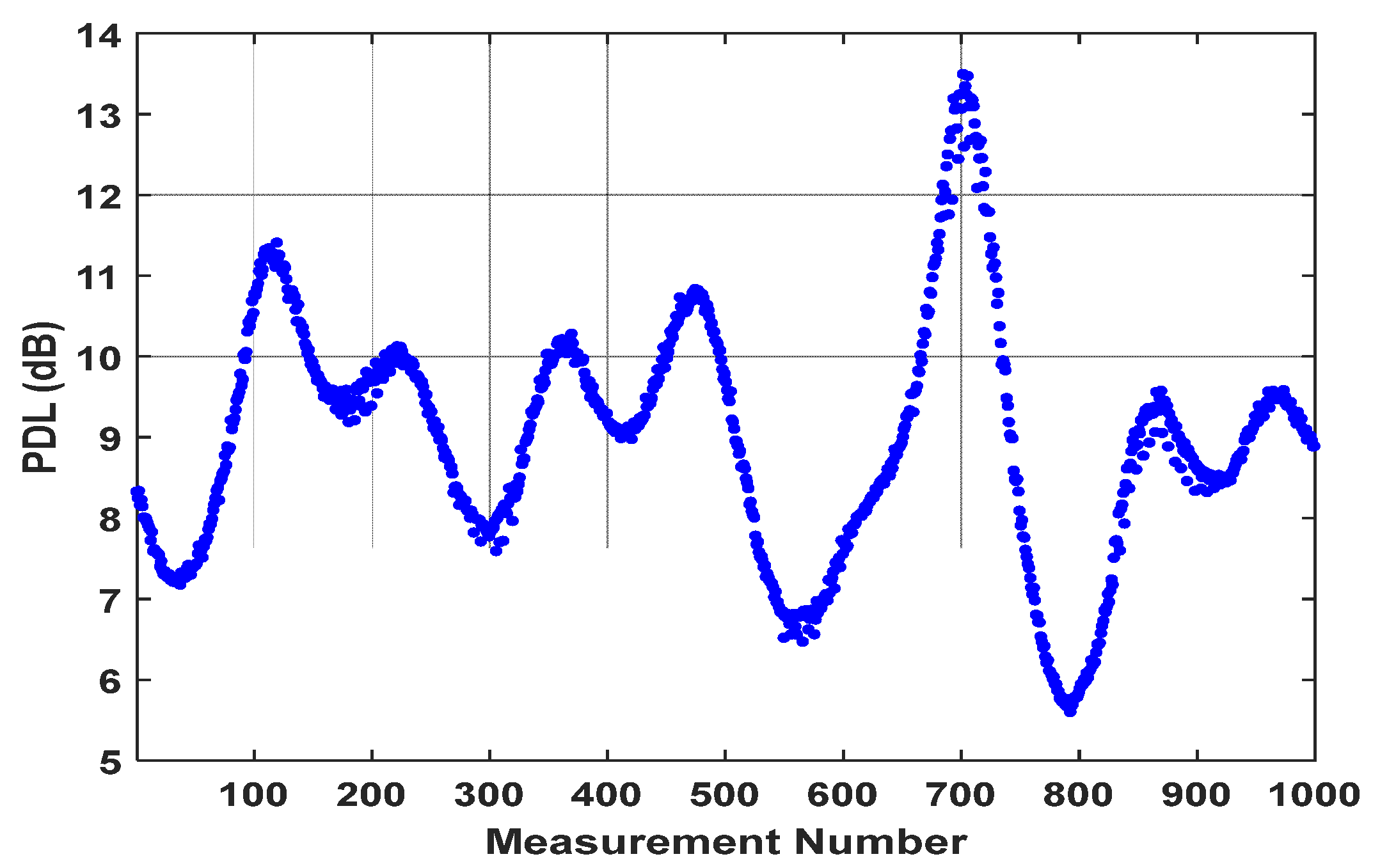
4. Phase and Intensity Measurement in φ-OTDR
4.1. Optical Power
4.2. Optical Phase
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
Appendix E
Appendix F
References
- Taylor, H.F.; Lee, C.E. Apparatus and Method for Fiber Optic Intrusion Sensing. U.S. Patent 5 194 847, 16 March 1993. [Google Scholar]
- Wellbrock, G.A.; Xia, T.J.; Huang, M.F.; Fang, J.; Chen, Y.H.; Narisetty, C.; Peterson, D., Jr.; Moore, J.M.; Scarpaci, A.; Westbrook, P.; et al. Perimeter intrusion detection with backscattering enhanced fiber using telecom cables as sensing backhaul. In Proceedings of the OFC 2022, San Diego, CA, USA, 6–10 March 2022. [Google Scholar]
- Zahoor, R.; Cerri, E.; Vallifuoco, R.; Zeni, L.; De Luca, A.; Caputo, F.; Minardo, A. Lamb wave detection for structural health monitoring using a ϕ-OTDR system. Sensors 2022, 22, 5962. [Google Scholar] [CrossRef]
- Zhou, Z.X.; Liu, H.; Zhang, D.W.; Han, Y.S.; Yang, X.Y.; Zheng, X.F.; Qu, J. Distributed partial discharge locating and detecting scheme based on optical fiber Rayleigh backscattering light interference. Sensors 2023, 23, 1828. [Google Scholar] [CrossRef] [PubMed]
- Muñoz, F.; Urricelqui, J.; Soto, M.A.; Rodriguez, M.J. Finding well-coupled optical fiber locations for railway monitoring using distributed acoustic sensing. Sensors 2023, 23, 6599. [Google Scholar] [CrossRef]
- Gurevich, B.; Tertyshnikov, K.; Bóna, A.; Sidenko, E.; Shashkin, P.; Yavuz, S.; Pevzner, R. The effect of the method of downhole deployment on distributed acoustic sensor measurements: Field experiments and numerical simulations. Sensors 2023, 23, 7501. [Google Scholar] [CrossRef]
- An, Y.; Ma, J.H.; Xu, T.W.; Cai, Y.P.; Liu, H.Y.; Sun, Y.T.; Yan, W.F. Traffic vibration signal analysis of DAS fiber optical cables with different coupling based on an improved wavelet thresholding method. Sensors 2023, 23, 5727. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.Q.; Fan, C.Z.; Xiao, X.P.; Zeng, Z.C.; Zhang, K.Q.; Li, H.; Yan, Z.J.; Sun, Q.Z. High-accuracy localization of pipeline microleakage by using distributed acoustic sensor. In Proceedings of the CLEO 2023, San Jose, CA, USA, 7–12 May 2023. [Google Scholar]
- Li, J.X.; Kim, T.; Lapusta, N.; Biondi, E.; Zhan, Z.W. The break of earthquake asperities imaged by distributed acoustic sensing. Nature 2023, 620, 800–806. [Google Scholar] [CrossRef] [PubMed]
- Titov, A.; Fan, Y.L.; Kutun, K.; Jin, G. Distributed acoustic sensing (DAS) response of rising Taylor bubbles in slug flow. Sensors 2022, 22, 1266. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, B.; Ye, Q.; Cai, H. Recent progress in distributed fiber acoustic sensing with φ-OTDR. Sensors 2020, 20, 6594. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, H.; Araki, E.; Kimura, T.; Guo, F.J.; Shiraishi, K.; Tonegawa, T.; Obana, K.; Arai, R.; Kaiho, Y.; Nakamura, Y.; et al. Detection of hydroacoustic signals on a fiber-optic submarine cable. Sci. Rep. 2021, 11, 2797. [Google Scholar] [CrossRef]
- Cheng, F.; Chi, B.X.; Lindsey, N.J.; Dawe, T.C.; Ajo-Franklin, J.B. Utilizing distributed acoustic sensing and ocean bottom fiber optic cables for submarine structural characterization. Sci. Rep. 2021, 11, 5613. [Google Scholar] [CrossRef]
- Zhan, Z.W. Submarine fiber seismic sensing as a critical tool for coastal safety. In Proceedings of the SubOptic 2023, Bangkok, Thailand, 13–16 March 2023. [Google Scholar]
- Buisman, M. Monitoring water column and sediments using DAS. In Proceedings of the 2023 IEEE International Workshop on Metrology for the Sea, Learning to Measure Sea Health Parameters (MetroSea), La Valletta, Malta, 4–6 October 2023. [Google Scholar]
- Cao, W.H.; Cheng, G.L.; Xing, G.X.; Liu, B. Near-field target localization based on the distributed acoustic sensing optical fiber in shallow water. Opt. Fiber Technol. 2023, 75, 103198. [Google Scholar] [CrossRef]
- Ip, E.; Huang, Y.K.; Wang, T.; Aono, Y.; Asahi, K. Distributed acoustic sensing for datacenter optical interconnects using self-homodyne coherent detection. In Proceedings of the OFC 2022, San Diego, CA, USA, 6–10 March 2022. [Google Scholar]
- Lv, A.Q.; Li, J. On-line monitoring system of 35 kV 3-core submarine power cable based on φ-OTDR. Sens. Actuator A Phys. 2018, 273, 134–139. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Shan, Y.; Sun, Z.; Zhu, F.; Zhang, X. Polarization dependence of phase-sensitive optical time-domain reflectometry and its suppression method based on orthogonal-state of polarization pulse pair. Opt. Eng. 2016, 55, 074109. [Google Scholar] [CrossRef]
- Guerrier, S.; Dorize, C.; Awwad, E.; Renaudier, J. A dual-polarization Rayleigh backscatter model for phase-sensitive OTDR applications. In Proceedings of the Optical Sensors and Sensing Congress, San Jose, CA, USA, 25–27 June 2019. [Google Scholar]
- Guerrier, S.; Dorize, C.; Awwad, E.; Renaudier, J. Introducing coherent MIMO sensing, a fading-resilient, polarization-independent approach to φ-OTDR. Opt. Express 2020, 28, 21081–21094. [Google Scholar] [CrossRef] [PubMed]
- Masoudi, A.; Newson, T.P. Analysis of distributed optical fiber acoustic sensors through numerical modelling. Opt. Express 2017, 25, 32021–32040. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Xiong, F.; Zhang, X.; Chen, X.; Ding, Z.; Zheng, Y.; Wang, F.; Chen, M. A space-division multiplexing method for fading noise suppression in the φ-OTDR system. Sensors 2021, 21, 1694. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Zhang, H.L.; Hu, D.J.J. Polarization properties of coherently superposed Rayleigh backscattered light in single-mode fibers. Sensors 2023, 23, 7769. [Google Scholar] [CrossRef]
- Lu, S.Y.; Chipman, R.A. Homogenous and inhomogeneous Jones matrices. J. Opt. Soc. Am. A 1994, 11, 766–773. [Google Scholar] [CrossRef]
- Whitney, C. Pauli-algebraic operators in polarization optics. J. Opt. Soc. Am. 1971, 61, 1207–1213. [Google Scholar] [CrossRef]
- Jones, R.C. A new calculus for the treatment of optical systems II. Proof of three general equivalence theorems. J. Opt. Soc. Am. 1941, 31, 493–499. [Google Scholar] [CrossRef]
- He, Z.Y.; Liu, Q.W. Optical fiber distributed acoustic sensors: A review. J. Lightw. Technol. 2021, 39, 3671–3686. [Google Scholar] [CrossRef]
- Lu, S.Y.; Chipman, R.A. Interpretation of Mueller matrices based on polar decomposition. J. Opt. Soc. Am. A 1996, 13, 1106–1113. [Google Scholar] [CrossRef]
- Craig, R.M. Accurate spectral characterization of polarization-dependent loss. J. Lightw. Technol. 2003, 21, 432–437. [Google Scholar] [CrossRef]
- Jopson, R.M.; Nelson, L.E.; Kogelnik, H. Measurement of second-order polarization-mode dispersion vectors in optical fibers. IEEE Photonics Technol. Lett. 1999, 11, 1153–1155. [Google Scholar] [CrossRef]
- Diebel, J. Representing Attitude: Euler Angles, Unit Quaternions, and Rotation Vectors. Available online: https://www.astro.rug.nl/software/kapteyn-beta/_downloads/attitude.pdf (accessed on 28 January 2024).
| PDL | ||||||
|---|---|---|---|---|---|---|
| Birefringence | Yes | No | Yes | No | No | No |
| Phase | No | No | No | No | No | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, H.; Zhang, H.; Hu, D.J.J. Polar Decomposition of Jones Matrix and Mueller Matrix of Coherent Rayleigh Backscattering in Single-Mode Fibers. Sensors 2024, 24, 1760. https://doi.org/10.3390/s24061760
Dong H, Zhang H, Hu DJJ. Polar Decomposition of Jones Matrix and Mueller Matrix of Coherent Rayleigh Backscattering in Single-Mode Fibers. Sensors. 2024; 24(6):1760. https://doi.org/10.3390/s24061760
Chicago/Turabian StyleDong, Hui, Hailiang Zhang, and Dora Juan Juan Hu. 2024. "Polar Decomposition of Jones Matrix and Mueller Matrix of Coherent Rayleigh Backscattering in Single-Mode Fibers" Sensors 24, no. 6: 1760. https://doi.org/10.3390/s24061760
APA StyleDong, H., Zhang, H., & Hu, D. J. J. (2024). Polar Decomposition of Jones Matrix and Mueller Matrix of Coherent Rayleigh Backscattering in Single-Mode Fibers. Sensors, 24(6), 1760. https://doi.org/10.3390/s24061760






