Damage Detection in Glass Fibre Composites Using Cointegrated Hyperspectral Images
Abstract
:1. Introduction
2. Materials and Methods
2.1. Damage Detection Using Hyperspectral Imaging
2.2. Cointegration Analysis
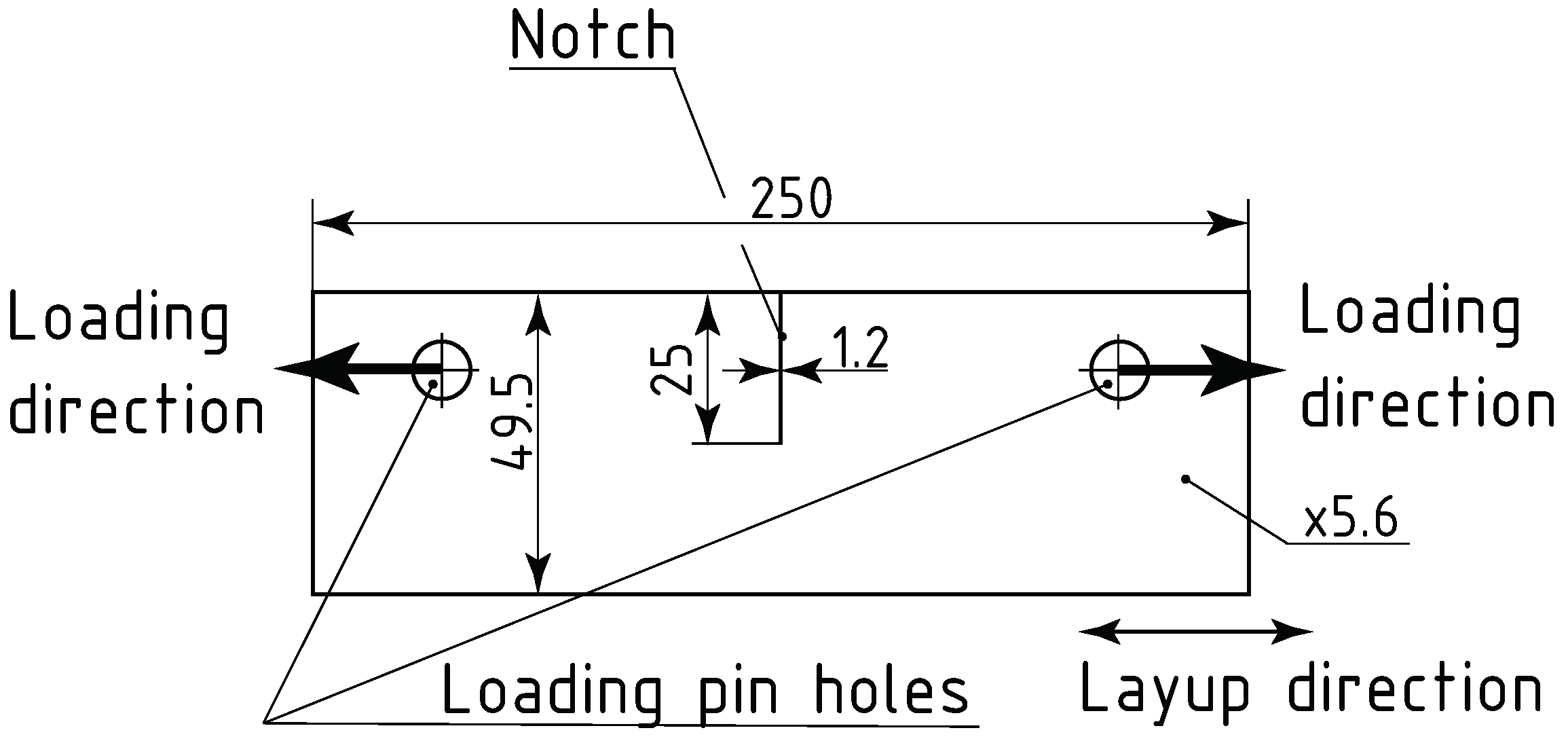
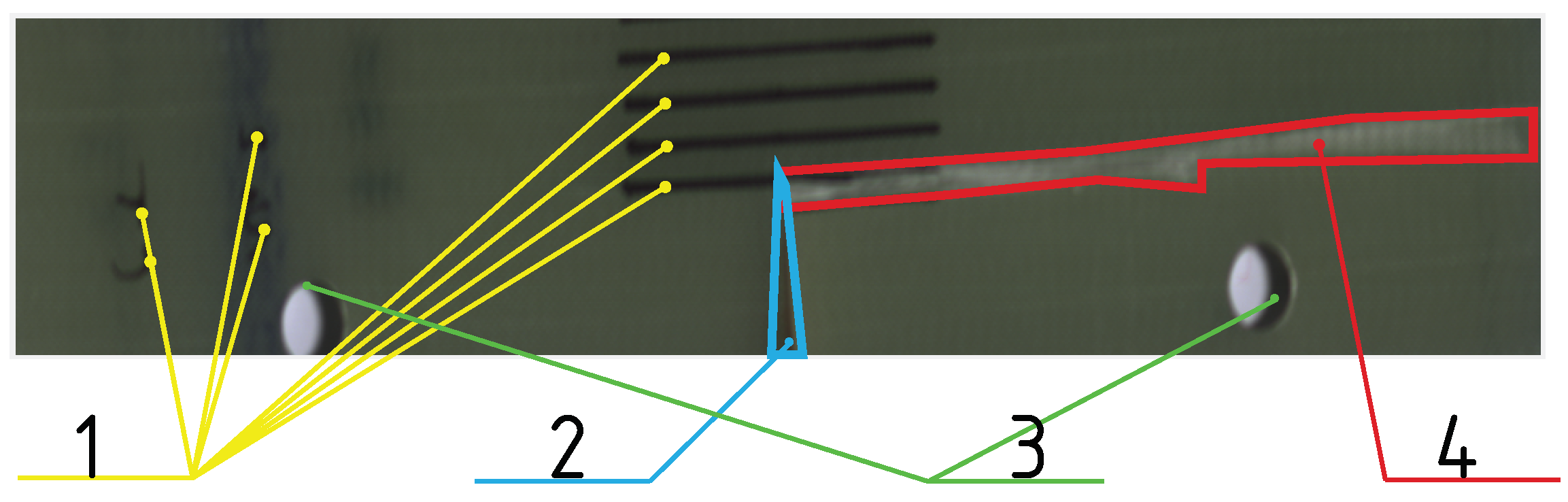
2.3. The Specimens
2.4. Hyperspectral Imaging Equipment
2.5. Hyperspectral Image Preprocessing
2.6. Data Conditioning Using Cointegration Analysis
2.7. Classification Algorithms
3. Results
3.1. Data Conditioning Results
3.2. Classification without the Data Conditioning
3.3. Classification with the Data Conditioning
4. Discussion
5. Conclusions
- The application of cointegration analysis improves the results of classification, especially in regard to decreasing the number and spatial distribution of false positives;
- In hyperspectral imaging, the benefits of data conditioning apply universally to classification algorithms, regardless of the specific algorithm used;
- In hyperspectral imaging, the concept of signal stationarity can be considered in the spectral domain, instead of the traditional temporal domain, while still keeping its properties.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACE | Adaptive Cosine Estimator |
| ADF | Augmented Dickey–Fuller test |
| ANN | Artificial neural network |
| AR | Autoregressive |
| DF | Dickey–Fuller test |
| DN | Digital Number |
| GFRP | Glass Fibre-Reinforced Plastic |
| HSI | Hyperspectral Imaging |
| NDT | Non-destructive Testing |
| NiR | Near Infrared |
| Probability Density Function | |
| SHM | Structural Health Monitoring |
| SVM | Support vector machine |
| SWiR | Short-Wave Infrared |
| VECM | Vector Error Correction Model |
| VNiR | Visible and Near Infrared |
References
- Qureshi, J. A Review of Fibre Reinforced Polymer Structures. Fibers 2022, 10, 27. [Google Scholar] [CrossRef]
- Feng, P.; Wang, J.; Wang, Y.; Loughery, D.; Niu, D. Effects of corrosive environments on properties of pultruded GFRP plates. Compos. Part B Eng. 2014, 67, 427–433. [Google Scholar] [CrossRef]
- Beura, S.; Chakraverty, A.P.; Thatoi, D.N.; Mohanty, U.K.; Mohapatra, M. Failure modes in GFRP composites assessed with the aid of SEM fractographs. Mater. Today Proc. 2021, 41, 172–179. [Google Scholar] [CrossRef]
- Lee, Y.J.; Jhan, Y.T.; Chung, C.H. Fluid–structure interaction of FRP wind turbine blades under aerodynamic effect. Compos. Part B Eng. 2012, 43, 2180–2191. [Google Scholar] [CrossRef]
- Dai, J.; Li, M.; Chen, H.; He, T.; Zhang, F. Progress and challenges on blade load research of large-scale wind turbines. Renew. Energy 2022, 196, 482–496. [Google Scholar] [CrossRef]
- Laudani, A.A.M.; Vryonis, O.; Lewin, P.L.; Golosnoy, I.O.; Kremer, J.; Klein, H.; Thomsen, O.T. Numerical simulation of lightning strike damage to wind turbine blades and validation against conducted current test data. Compos. Part A Appl. Sci. Manuf. 2022, 152, 106708. [Google Scholar] [CrossRef]
- Mellouli, H.; Kalleli, S.; Mallek, H.; Ben Said, L.; Ayadi, B.; Dammak, F. Electromechanical behavior of piezolaminated shell structures with imperfect functionally graded porous materials using an improved solid-shell element. Comput. Math. Appl. 2024, 155, 1–13. [Google Scholar] [CrossRef]
- Wang, W.; Xue, Y.; He, C.; Zhao, Y. Review of the Typical Damage and Damage-Detection Methods of Large Wind Turbine Blades. Energies 2022, 15, 5672. [Google Scholar] [CrossRef]
- Arsenault, T.J.; Achuthan, A.; Marzocca, P.; Grappasonni, C.; Coppotelli, G. Development of a FBG based distributed strain sensor system for wind turbine structural health monitoring. Smart Mater. Struct. 2013, 22, 075027. [Google Scholar] [CrossRef]
- Xu, D.; Liu, P.F.; Chen, Z.P.; Leng, J.X.; Jiao, L. Achieving robust damage mode identification of adhesive composite joints for wind turbine blade using acoustic emission and machine learning. Compos. Struct. 2020, 236, 111840. [Google Scholar] [CrossRef]
- Chakrapani, S.K.; Barnard, D.J.; Dayal, V. Review of ultrasonic testing for NDE of composite wind turbine blades. AIP Conf. Proc. 2019, 2102, 100003. [Google Scholar] [CrossRef]
- Kim, W.; Yi, J.H.; Kim, J.T.; Park, J.H. Vibration-based Structural Health Assessment of a Wind Turbine Tower Using a Wind Turbine Model. Procedia Eng. 2017, 188, 333–339. [Google Scholar] [CrossRef]
- Sanati, H.; Wood, D.; Sun, Q. Condition Monitoring of Wind Turbine Blades Using Active and Passive Thermography. Appl. Sci. 2018, 8, 2004. [Google Scholar] [CrossRef]
- Dong, C.Z.; Catbas, F.N. A review of computer vision–based structural health monitoring at local and global levels. Struct. Health Monit. 2021, 20, 692–743. [Google Scholar] [CrossRef]
- Rizk, P.; Al Saleh, N.; Younes, R.; Ilinca, A.; Khoder, J. Hyperspectral imaging applied for the detection of wind turbine blade damage and icing. Remote Sens. Appl. Soc. Environ. 2020, 18, 100291. [Google Scholar] [CrossRef]
- Długosz, J.; Dao, P.B.; Staszewski, W.J.; Uhl, T. Damage Detection in Composite Materials Using Hyperspectral Imaging. In European Workshop on Structural Health Monitoring; Springer: Cham, Switzerland, 2023; pp. 463–473. [Google Scholar] [CrossRef]
- Wawerski, A.; Siemiątkowska, B.; Józwik, M.; Fajdek, B.; Partyka, M. Machine Learning Method and Hyperspectral Imaging for Precise Determination of Glucose and Silicon Levels. Sensors 2024, 24, 1306. [Google Scholar] [CrossRef]
- Wang, Y.; Ou, X.; He, H.J.; Kamruzzaman, M. Advancements, limitations and challenges in hyperspectral imaging for comprehensive assessment of wheat quality: An up-to-date review. Food Chem. X 2024, 21, 101235. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Bao, W.; Xu, X.; Zhou, Y. Hyperspectral image classification based on local feature decoupling and hybrid attention SpectralFormer network. Int. J. Remote Sens. 2024, 45, 1727–1754. [Google Scholar] [CrossRef]
- Ghous, U.; Sarfraz, M.; Ahmad, M.; Li, C.; Hong, D. (2+1)D Extreme Xception Net for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 5159–5172. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent Advances on Spectral–Spatial Hyperspectral Image Classification: An Overview and New Guidelines. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1579–1597. [Google Scholar] [CrossRef]
- Carrasco, O.; Gomez, R.B.; Chainani, A.; Roper, W.E. Hyperspectral imaging applied to medical diagnoses and food safety. In Proceedings of the AeroSense 2003, Orlando, FL, USA, 21–25 April 2003; p. 215. [Google Scholar] [CrossRef]
- Clark, R.N.; Swayze, G.A. Mapping Minerals, Amorphous Materials, Environmental Materials, Vegetation, Water, Ice and Snow, and Other Materials: The USGS Tricorder Algorithm; Technical Report; Environmental Science, Materials Science; Lunar and Planetary Institute: Houston, TX, USA, 1995. [Google Scholar]
- DeJong, D.N.; Nankervis, J.C.; Savin, N.E.; Whiteman, C.H. Integration Versus Trend Stationary in Time Series. Econometrica 1992, 60, 423. [Google Scholar] [CrossRef]
- Dao, P.B. Cointegration method for temperature effect removal in damage detection based on lamb waves. Diagnostyka 2013, 14, 61–67. [Google Scholar]
- Dickey, D.A.; Fuller, W.A. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. J. Am. Stat. Assoc. 1979, 74, 427. [Google Scholar] [CrossRef]
- Granger, C.W. Some properties of time series data and their use in econometric model specification. J. Econom. 1981, 16, 121–130. [Google Scholar] [CrossRef]
- Chen, Q.; Kruger, U.; Leung, A.Y.T. Cointegration Testing Method for Monitoring Nonstationary Processes. Ind. Eng. Chem. Res. 2009, 48, 3533–3543. [Google Scholar] [CrossRef]
- Cross, E.J.; Worden, K.; Chen, Q. Cointegration: A novel approach for the removal of environmental trends in structural health monitoring data. Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 467, 2712–2732. [Google Scholar] [CrossRef]
- Johansen, S. Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models. Econometrica 1991, 59, 1551. [Google Scholar] [CrossRef]
- Sargan, J.D. Wages and prices in the United Kingdom: A study in econometric methodology. Econom. Anal. Natl. Econ. Plan. 1964, 16, 25–54. [Google Scholar]
- Holtz-Eakin, D.; Newey, W.; Rosen, H.S. Estimating Vector Autoregressions with Panel Data. Econometrica 1988, 56, 1371. [Google Scholar] [CrossRef]
- Shakir Abbood, I.; aldeen Odaa, S.; Hasan, K.F.; Jasim, M.A. Properties evaluation of fiber reinforced polymers and their constituent materials used in structures—A review. Mater. Today Proc. 2021, 43, 1003–1008. [Google Scholar] [CrossRef]
- Bent, F.; Sørensen, W.J.; Holmes, P.B.; Branner, K. Blade materials, testing methods and structural design. In Wind Power Generation and Wind Turbine Design; WIT Press: Billerica, MA, USA, 2010; Volume 44. [Google Scholar] [CrossRef]
- ASTM E1922; Standard Test Method for Translaminar Fracture Toughness of Laminated and Pultruded Polymer Matrix Composite Materials. ASTM International: Conshohocken, PA USA, 2015. [CrossRef]
- Geladi, P.L.M. Calibration. In Techniques and Applications of Hyperspectral Image Analysis; John Wiley & Sons, Ltd.: Chichester, UK, 2007; pp. 203–220. [Google Scholar] [CrossRef]
- Fox, T.; Elder, E.; Crocker, I. Image Registration and Fusion Techniques. In PET-CT in Radiotherapy Treatment Planning; Elsevier: Amsterdam, The Netherlands, 2008; pp. 35–51. [Google Scholar] [CrossRef]
- Sara, D.; Mandava, A.K.; Kumar, A.; Duela, S.; Jude, A. Hyperspectral and multispectral image fusion techniques for high resolution applications: A review. Earth Sci. Inform. 2021, 14, 1685–1705. [Google Scholar] [CrossRef]
- Ruffin, C.; King, R.L.; Younan, N.H. A Combined Derivative Spectroscopy and Savitzky-Golay Filtering Method for the Analysis of Hyperspectral Data. GIScience Remote Sens. 2008, 45, 1–15. [Google Scholar] [CrossRef]
- Dao, P.B.; Staszewski, W.J. Cointegration and how it works for structural health monitoring. Measurement 2023, 209, 112503. [Google Scholar] [CrossRef]





| Data Series | T-Statistic | Critical Value | Null Rejected |
|---|---|---|---|
| Damaged spectral signature | −0.5655 | −2.8681 | False |
| Healthy spectral signature | −2.2881 | −2.8681 | False |
| VECM Model | T-Statistic | Critical Value | Null Rejected |
|---|---|---|---|
| No deterministic terms | 17.9372 | 12.3206 | True |
| With deterministic constant | 18.2173 | 20.2619 | False |
| With deterministic trend | 14.1937 | 15.4948 | False |
| With deterministic trend and constant | 37.8892 | 25.8723 | True |
| Sensitivity | Specificity | Precision | Accuracy | F1 Score | |
|---|---|---|---|---|---|
| Neural network | 0.695 | 0.824 | 0.263 | 0.814 | 0.381 |
| Gaussian kernel SVM | 0.618 | 0.777 | 0.199 | 0.764 | 0.301 |
| Cubic kernel SVM | 0.713 | 0.847 | 0.296 | 0.836 | 0.418 |
| Sensitivity | Specificity | Precision | Accuracy | F1 Score | |
|---|---|---|---|---|---|
| Neural network | |||||
| Gaussian kernel SVM | |||||
| Cubic kernel SVM |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Długosz, J.; Dao, P.B.; Staszewski, W.J.; Uhl, T. Damage Detection in Glass Fibre Composites Using Cointegrated Hyperspectral Images. Sensors 2024, 24, 1980. https://doi.org/10.3390/s24061980
Długosz J, Dao PB, Staszewski WJ, Uhl T. Damage Detection in Glass Fibre Composites Using Cointegrated Hyperspectral Images. Sensors. 2024; 24(6):1980. https://doi.org/10.3390/s24061980
Chicago/Turabian StyleDługosz, Jan, Phong B. Dao, Wiesław J. Staszewski, and Tadeusz Uhl. 2024. "Damage Detection in Glass Fibre Composites Using Cointegrated Hyperspectral Images" Sensors 24, no. 6: 1980. https://doi.org/10.3390/s24061980
APA StyleDługosz, J., Dao, P. B., Staszewski, W. J., & Uhl, T. (2024). Damage Detection in Glass Fibre Composites Using Cointegrated Hyperspectral Images. Sensors, 24(6), 1980. https://doi.org/10.3390/s24061980








