An Analysis of Loss Functions for Heavily Imbalanced Lesion Segmentation
Abstract
1. Introduction
2. Materials and Methods
2.1. Public Datasets
2.1.1. White Matter Hyperintensities (WMH) Challenge 2017 [4]
- UMC Utrecht, 3 T Philips Achieva: 3D T1-weighted sequence (192 slices, slice size: 256 × 256, voxel size: 1.00 × 1.00 × 1.00 mm3, repetition time (TR)/echo time (TE): 7.9/4.5 ms), 2D FLAIR sequence (48 slices, slice size: 240 × 240, voxel size: 0.96 × 0.95 × 3.00 mm3, TR/TE/inversion time (TI): 11,000/125/2800 ms).
- NUHS Singapore, 3 T Siemens TrioTim: 3D T1-weighted sequence (192 slices, slice size: 256 × 256, voxel size: 1.00 × 1.00 × 1.00 mm3, TR/TE/TI: 2, 300/1.9/900 ms), 2D FLAIR sequence (48 slices, slice size: 256 × 256, voxel size: 1.00 × 1.00 × 3.00 mm3, TR/TE/TI: 9000/82/2500 ms).
- VU Amsterdam, 3 T GE Signa HDxt: 3D T1-weighted sequence (176 slices, slice size: 256 × 256, voxel size: , TR/TE: 7.8/3.0 ms), 3D FLAIR sequence (132 slices, slice size: 83 × 256, voxel size: , TR/TE/TI: 8000/126/2340 ms).
2.1.2. Ljubljana Longitudinal Multiple Sclerosis Lesion Dataset [1]
2.1.3. Data Preparation
2.2. Network Architecture
2.3. Loss Functions
2.3.1. Cross-Entropy
2.3.2. Focal Loss
2.3.3. Generalised Dice Loss
2.3.4. Weighted Gradient Loss
2.4. Experimental Design
2.5. Implementation Details
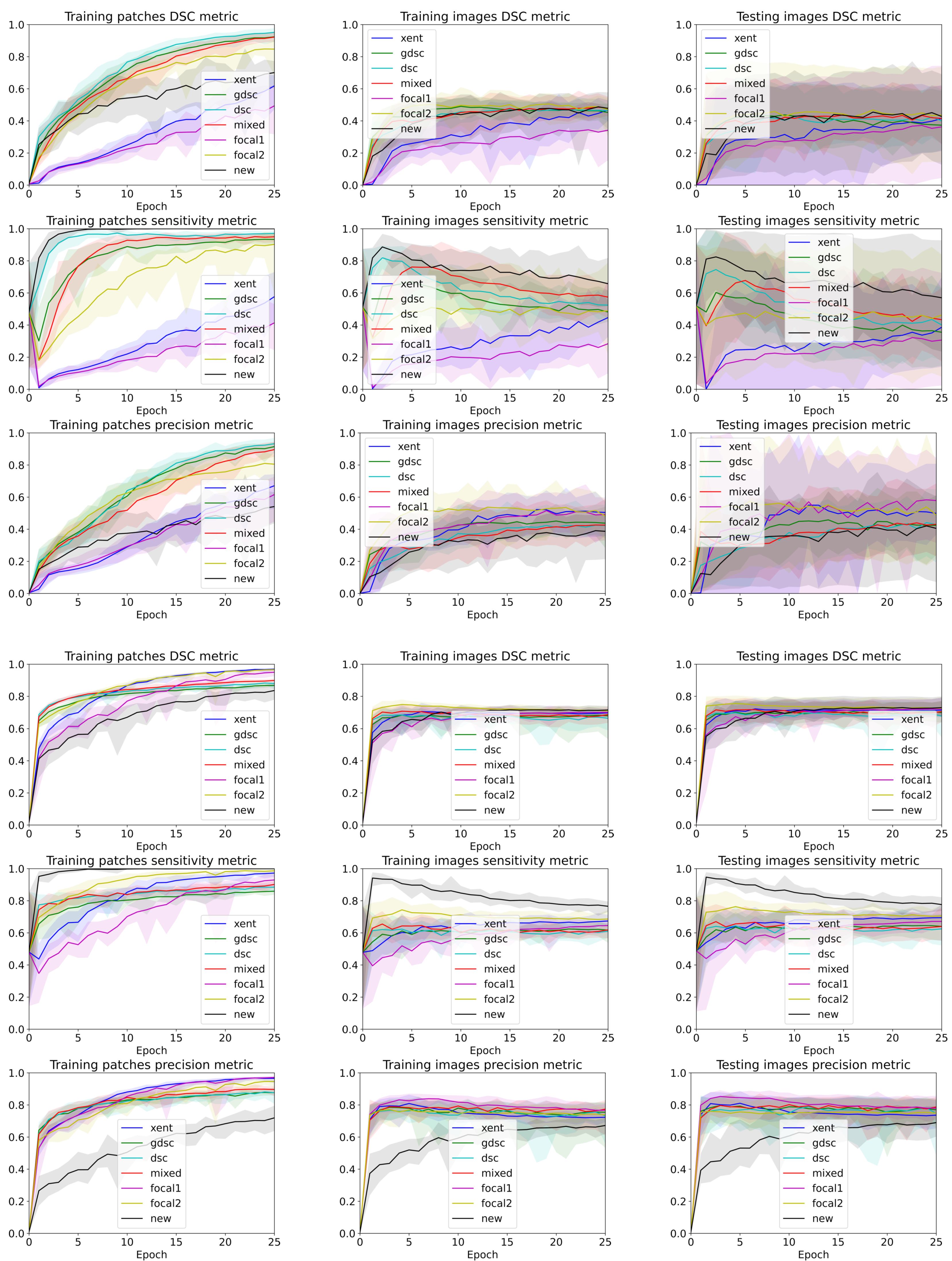
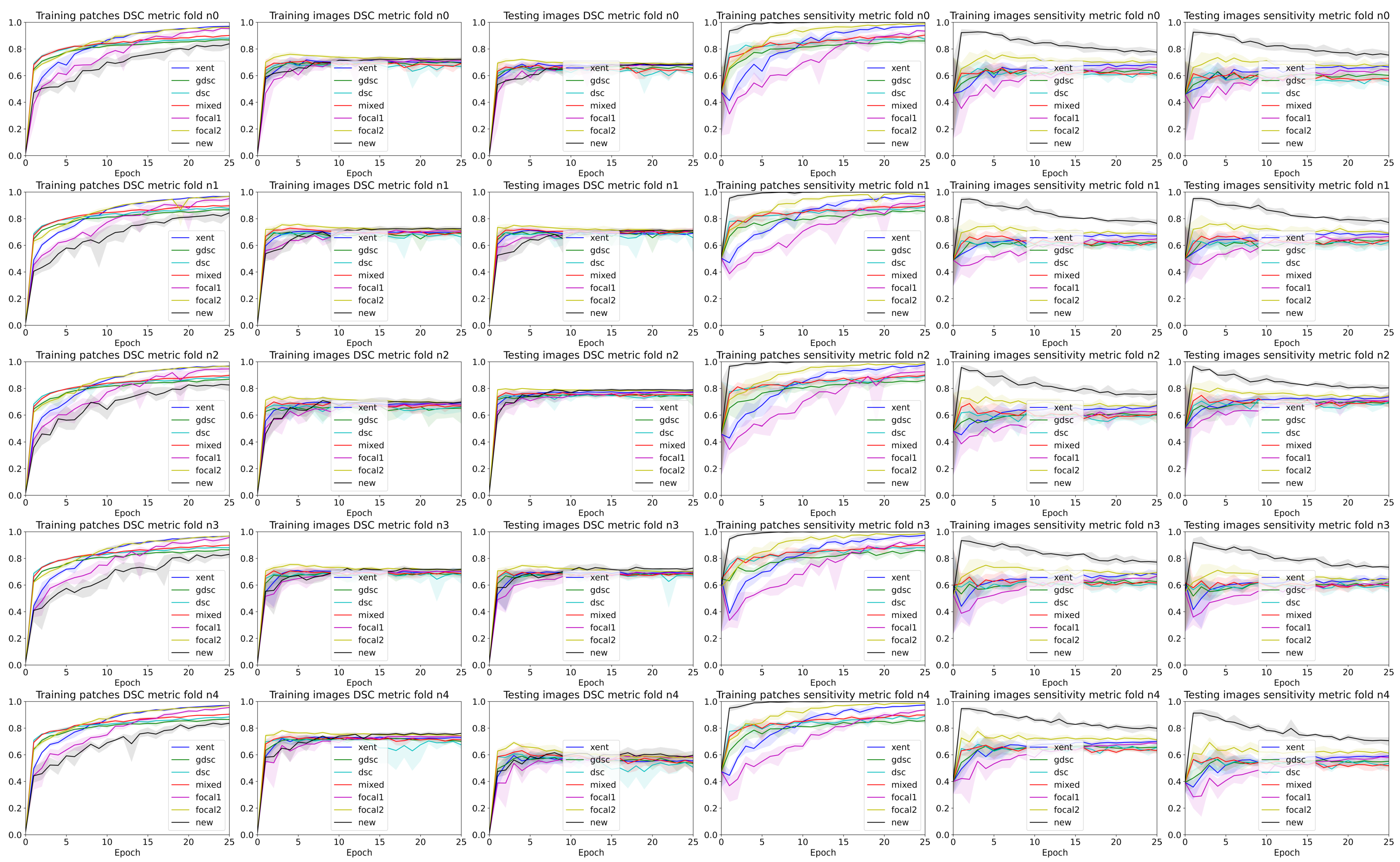
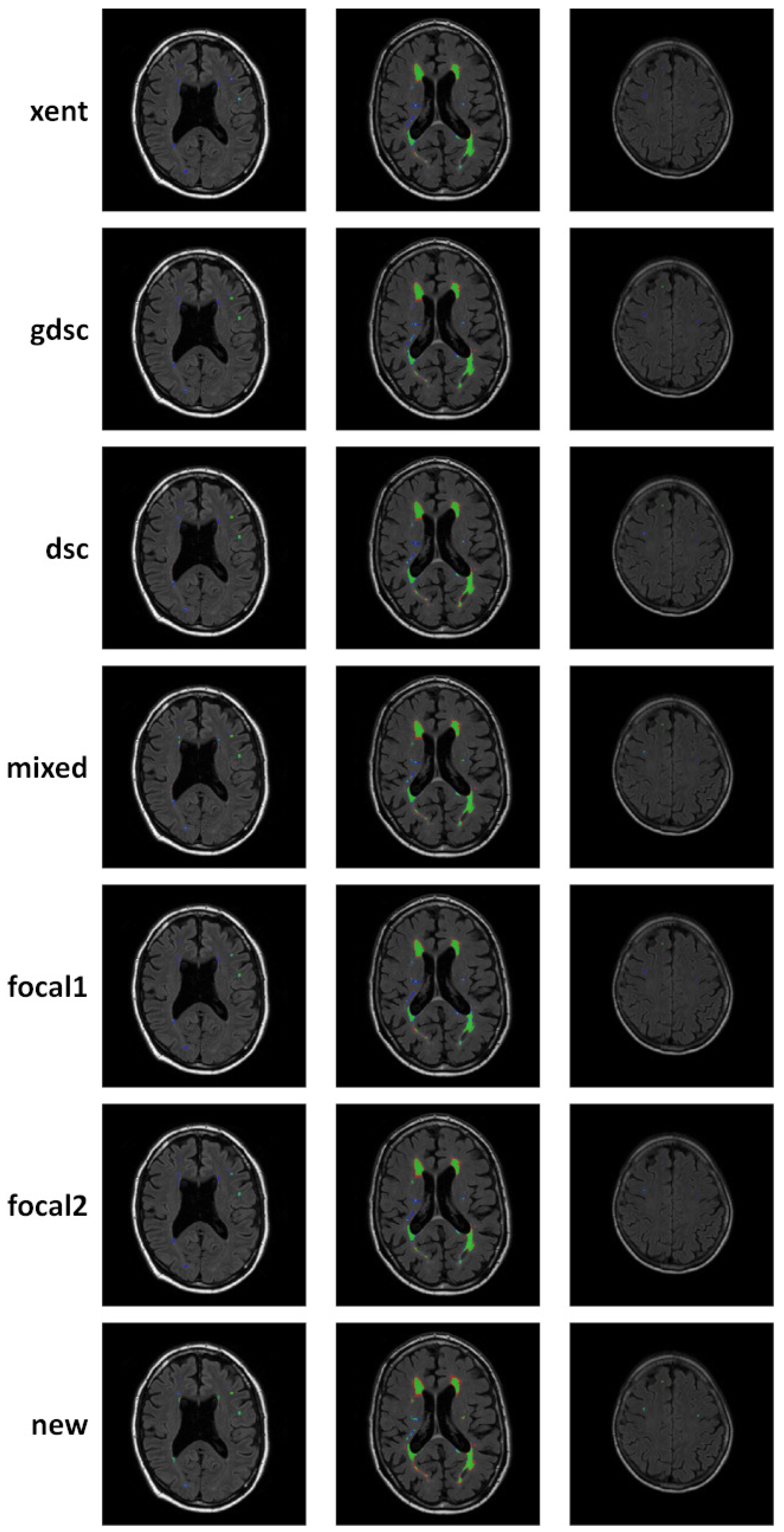
3. Results
4. Discussion
4.1. The Effect of Confident Errors on the Loss Function
4.2. The Effect of Randomness during Training
4.3. The Discrepancy between Patch-Based Results and Image-Based Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Mathematical Analysis of the Dice Loss
Appendix A.1. The Dice Similarity Coefficient for Binary Masks
Appendix A.2. The Probabilistic Dice Function
Appendix A.3. The Dice Loss
References
- Lesjak, Ž.; Pernuš, F.; Likar, B.; Špiclin, Ž. Validation of White-Matter Lesion Change Detection Methods on a Novel Publicly Available MRI Image Database. Neuroinformatics 2016, 1, 403–420. [Google Scholar] [CrossRef] [PubMed]
- Commowick, O.; Istace, A.; Kain, M.; Laurent, B.; Leray, F.; Simon, M.; Pop, S.C.; Girard, P.; Améli, R.; Ferré, J.C.; et al. Objective evaluation of multiple sclerosis lesion segmentation using a data management and processing infrastructure. Nat. Sci. Rep. 2018, 8, 1–17. [Google Scholar] [CrossRef]
- Vanderbecq, Q.; Xu, E.; Ströer, S.; Couvy-Duchesne, B.; Diaz Melo, M.; Dormont, D.; Colliot, O. Comparison and validation of seven white matter hyperintensities segmentation software in elderly patients. Neuroimage Clin. 2020, 27, 102357. [Google Scholar] [CrossRef] [PubMed]
- Kuijf, H.; Biesbroek, J.; Bresser, J.; Heinen, R.; Andermatt, S.; Bento, M.; Berseth, M.; Belyaev, M.; Cardoso, M.; Casamitjana, A.; et al. Standardized Assessment of Automatic Segmentation of White Matter Hyperintensities and Results of the WMH Segmentation Challenge. IEEE Trans. Med. Imag. 2019, 38, 2556–2568. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.K.; Greenspan, H.; Davatzikos, C.; Duncan, J.S.; Van Ginneken, B.; Madabhushi, A.; Prince, J.L.; Rueckert, D.; Summers, R.M. A Review of Deep Learning in Medical Imaging: Imaging Traits, Technology Trends, Case Studies with Progress Highlights, and Future Promises. Proc. IEEE 2021, 109, 820–838. [Google Scholar] [CrossRef] [PubMed]
- Bernal, J.; Kushibar, K.; Asfaw, D.S.; Valverde, S.; Oliver, A.; Martí, R.; Lladó, X. Deep convolutional neural networks for brain image analysis on magnetic resonance imaging: A review. Artif. Intell. Med. 2019, 95, 64–81. [Google Scholar] [CrossRef]
- Isensee, F.; Jaeger, P.F.; Kohl, S.A.A.; Maier-Hein, K.H. nnU-Net: A self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods 2021, 18, 203–211. [Google Scholar] [CrossRef] [PubMed]
- Valverde, S.; Cabezas, M.; Roura, E.; González-Villà, S.; Pareto, D.; Vilanova, J.C.; Ramió-Torrentà, L.; Rovira, A.; Oliver, A.; Lladó, X. Improving automated multiple sclerosis lesion segmentation with a cascaded 3D convolutional neural network approach. Neuroimage 2017, 155, 159–168. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Kamnitsas, K.; Glocker, B. Analyzing Overfitting under Class Imbalance in Neural Networks for Image Segmentation. IEEE Trans. Med. Imag. 2021, 40, 1065–1077. [Google Scholar] [CrossRef]
- Valverde, S.; Salem, M.; Cabezas, M.; Pareto, D.; Vilanova, J.C.; Ramió-Torrentà, L.; Rovira, À.; Salvi, J.; Oliver, A.; Lladó, X. One-shot domain adaptation in multiple sclerosis lesion segmentation using convolutional neural networks. Neuroimage Clin. 2019, 21, 101638. [Google Scholar] [CrossRef]
- Milletari, F.; Navab, N.; Ahmadi, S. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Sudre, C.H.; Li, W.; Vercauteren, T.; Ourselin, S.; Jorge Cardoso, M. Generalised Dice Overlap as a Deep Learning Loss Function for Highly Unbalanced Segmentations. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support Workshop—MICCAI, Québec City, QC, Canada, 14 September 2017; pp. 240–248. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Ma, J.; Chen, J.; Ng, M.; Huang, R.; Li, Y.; Li, C.; Yang, X.; Martel, A.L. Loss odyssey in medical image segmentation. Med. Image Anal. 2021, 71, 102035. [Google Scholar] [CrossRef] [PubMed]
- Kononenko, I. Bayesian neural networks. Biol. Cybern. 1989, 61, 361–370. [Google Scholar] [CrossRef]
- Hernández-Lobato, J.M.; Adams, R. Probabilistic backpropagation for scalable learning of bayesian neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015; pp. 1861–1869. [Google Scholar]
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and scalable predictive uncertainty estimation using deep ensembles. arXiv 2017, arXiv:1612.01474v3. [Google Scholar]
- Izmailov, P.; Vikram, S.; Hoffman, M.D.; Wilson, A.G.G. What Are Bayesian Neural Network Posteriors Really Like? In Proceedings of the 38th International Conference on Machine Learning, Online, 18–24 July 2021; pp. 4629–4640. [Google Scholar]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning dense volumetric segmentation from sparse annotation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Athens, Greece, 17–21 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 424–432. [Google Scholar]
- Cabezas, M.; Luo, Y.; Kyle, K.; Ly, L.; Wang, C.; Barnett, M. Estimating lesion activity through feature similarity: A dual path Unet approach for the MSSEG2 MICCAI challenge. In Proceedings of the MSSEG-2 Challenge Proceedings—MICCAI 2021, Strasbourg, France, 2 September 2021; pp. 107–110. [Google Scholar]
- Barnett, M.; Wang, D.; Beadnall, H.; Bischof, A.; Brunacci, D.; Butzkueven, H.; Brown, J.W.L.; Cabezas, M.; Das, T.; Dugal, T.; et al. A real-world clinical validation for AI-based MRI monitoring in multiple sclerosis. NPJ Digit. Med. 2023, 6, 196. [Google Scholar] [CrossRef] [PubMed]
- Dice, L.R. Measures of the amount of ecologic association between species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Ostmeier, S.; Axelrod, B.; Isensee, F.; Bertels, J.; Mlynash, M.; Christensen, S.; Lansberg, M.G.; Albers, G.W.; Sheth, R.; Verhaaren, B.F.; et al. USE-Evaluator: Performance metrics for medical image segmentation models supervised by uncertain, small or empty reference annotations in neuroimaging. Med. Image Anal. 2023, 90, 102927. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Zhang, C.; Cabezas, M.; Song, Y.; Tang, Z.; Liu, D.; Cai, W.; Barnett, M.; Wang, C. Multiple Sclerosis Lesion Analysis in Brain Magnetic Resonance Images: Techniques and Clinical Applications. IEEE J. Biomed. Health Inform. 2022, 26, 2680–2692. [Google Scholar] [CrossRef] [PubMed]
- Kayhan, O.S.; Gemert, J.C.v. On translation invariance in cnns: Convolutional layers can exploit absolute spatial location. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 14274–14285. [Google Scholar]
- Islam, M.A.; Kowal, M.; Jia, S.; Derpanis, K.G.; Bruce, N.D. Global pooling, more than meets the eye: Position information is encoded channel-wise in CNNs. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 793–801. [Google Scholar]
- Carass, A.; Roy, S.; Gherman, A.; Reinhold, J.C.; Jesson, A.; Arbel, T.; Maier, O.; Handels, H.; Ghafoorian, M.; Platel, B.; et al. Evaluating White Matter Lesion Segmentations with Refined Sørensen-Dice Analysis. Sci. Rep. 2020, 10, 8242. [Google Scholar] [CrossRef] [PubMed]
- Crum, W.; Camara, O.; Hill, D. Generalized Overlap Measures for Evaluation and Validation in Medical Image Analysis. IEEE Trans. Med. Imaging 2006, 25, 1451–1461. [Google Scholar] [CrossRef] [PubMed]




| Dataset | % (Brain) | % (Batch) | Mean Lesion Size | Lesion Number |
|---|---|---|---|---|
| WMH2017 | 1.54 ± 1.48 [1.57] | 1.53 ± 2.40 [1.73] | 111.1750 | 3679 |
| LIT longitudinal | 0.14 ± 0.18 [0.15] | 0.48 ± 0.84 [0.51] | 116.13 | 156 |
| Loss | Sensitivity () | Precision (P) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Patch | Train | Test | Patch | Train | Test | Patch | Train | Test | |
| LIT longitudinal dataset | |||||||||
| xent | 0.64 | 0.51 | 0.46 | 0.62 | 0.55 | 0.49 | 0.54 | 0.48 | 0.46 |
| gdsc | 0.93 | 0.54 | 0.53 | 0.96 | 0.81 | 0.77 | 0.82 | 0.20 | 0.29 |
| dsc | 0.96 | 0.55 | 0.52 | 0.99 | 0.89 | 0.84 | 0.54 | 0.29 | 0.24 |
| mixed | 0.93 | 0.55 | 0.54 | 0.98 | 0.86 | 0.82 | 0.74 | 0.18 | 0.24 |
| focal1 | 0.59 | 0.48 | 0.46 | 0.52 | 0.49 | 0.49 | 0.55 | 0.53 | 0.49 |
| focal2 | 0.89 | 0.60 | 0.56 | 0.97 | 0.70 | 0.63 | 0.78 | 0.48 | 0.38 |
| new | 0.79 | 0.58 | 0.56 | 1.00 | 0.94 | 0.90 | 0.36 | 0.14 | 0.23 |
| WMH challenge 2017 | |||||||||
| xent | 0.96 | 0.68 | 0.42 | 0.95 | 0.60 | 0.55 | 0.97 | 0.80 | 0.47 |
| gdsc | 0.86 | 0.71 | 0.69 | 0.85 | 0.64 | 0.63 | 0.88 | 0.79 | 0.76 |
| dsc | 0.88 | 0.56 | 0.54 | 0.87 | 0.55 | 0.65 | 0.89 | 0.60 | 0.60 |
| mixed | 0.89 | 0.56 | 0.44 | 0.89 | 0.58 | 0.63 | 0.90 | 0.62 | 0.47 |
| focal1 | 0.94 | 0.71 | 0.68 | 0.91 | 0.64 | 0.59 | 0.97 | 0.80 | 0.81 |
| focal2 | 0.96 | 0.72 | 0.72 | 0.98 | 0.72 | 0.69 | 0.94 | 0.73 | 0.75 |
| new | 0.79 | 0.70 | 0.71 | 1.00 | 0.85 | 0.81 | 0.65 | 0.61 | 0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabezas, M.; Diez, Y. An Analysis of Loss Functions for Heavily Imbalanced Lesion Segmentation. Sensors 2024, 24, 1981. https://doi.org/10.3390/s24061981
Cabezas M, Diez Y. An Analysis of Loss Functions for Heavily Imbalanced Lesion Segmentation. Sensors. 2024; 24(6):1981. https://doi.org/10.3390/s24061981
Chicago/Turabian StyleCabezas, Mariano, and Yago Diez. 2024. "An Analysis of Loss Functions for Heavily Imbalanced Lesion Segmentation" Sensors 24, no. 6: 1981. https://doi.org/10.3390/s24061981
APA StyleCabezas, M., & Diez, Y. (2024). An Analysis of Loss Functions for Heavily Imbalanced Lesion Segmentation. Sensors, 24(6), 1981. https://doi.org/10.3390/s24061981





