Correcting Hardening Artifacts of Aero-Engine Blades with an Iterative Linear Fitting Technique Framework
Abstract
1. Introduction
2. Theoretical Basis and Methods
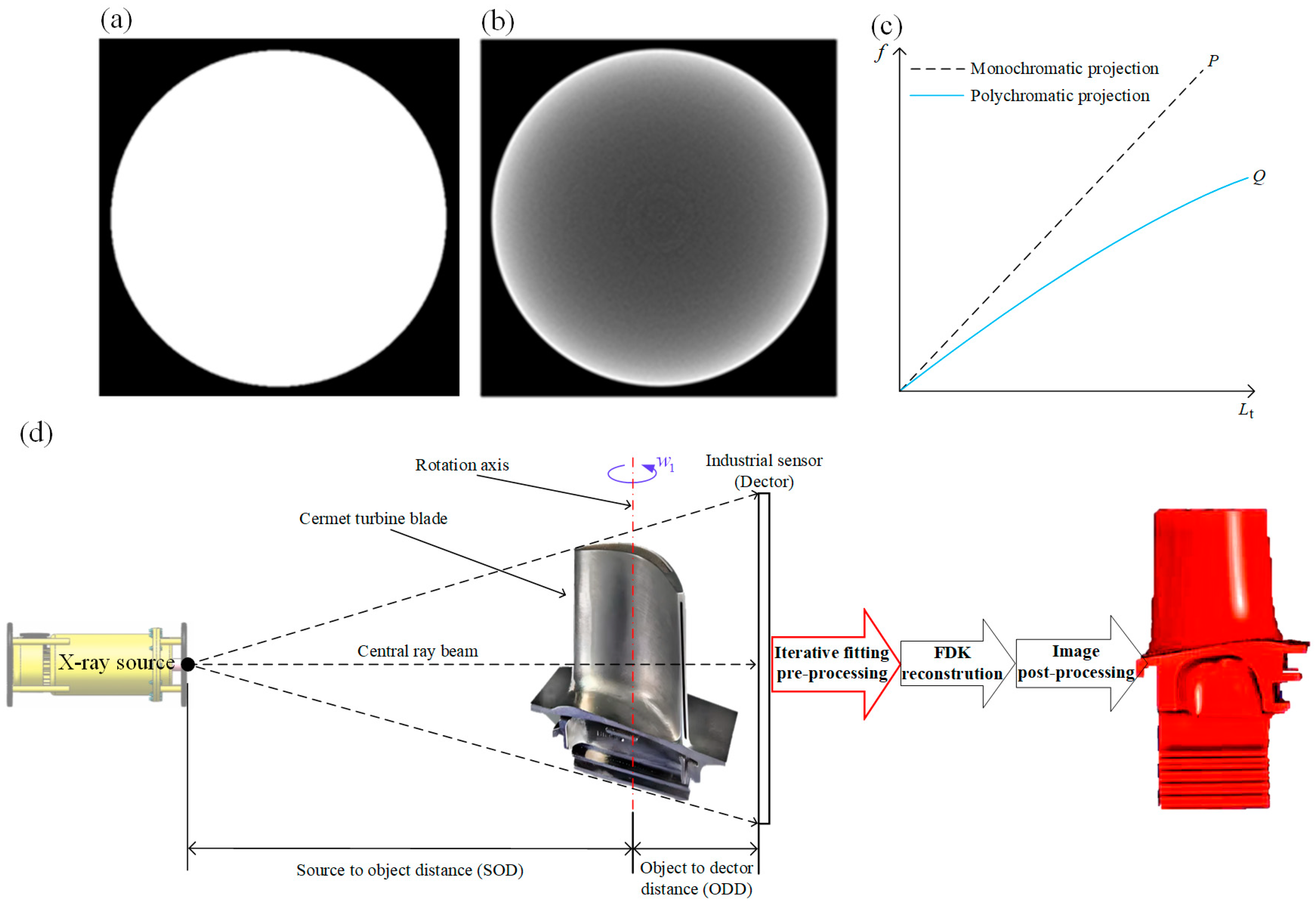
2.1. Feasibility Analysis of Linear Fitting Correction
2.2. Framework Overview
3. Results and Discussion
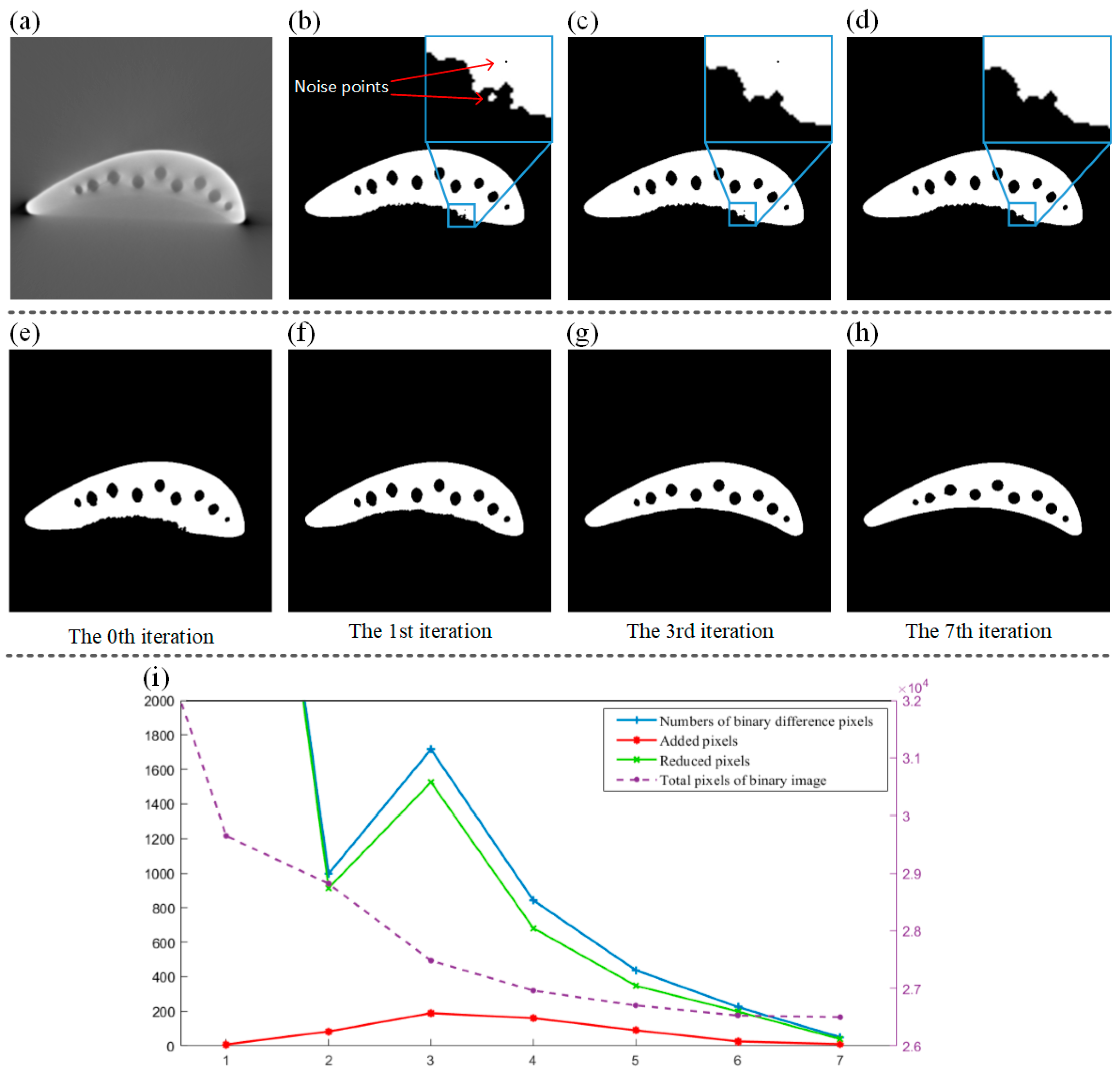
3.1. Iterative Binarization Processing
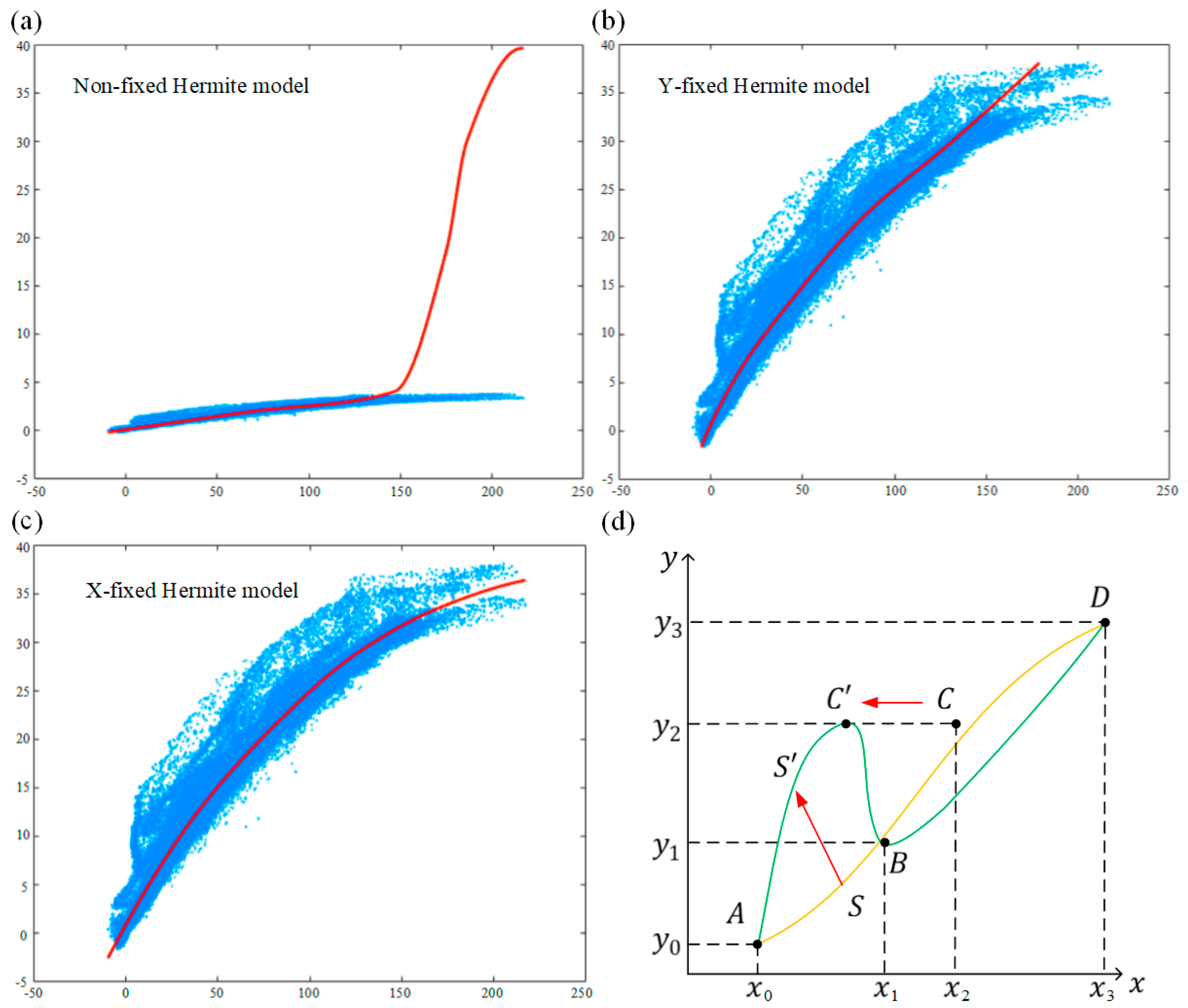
3.2. Fitting Function Selection
3.3. Fitting Effect Verification
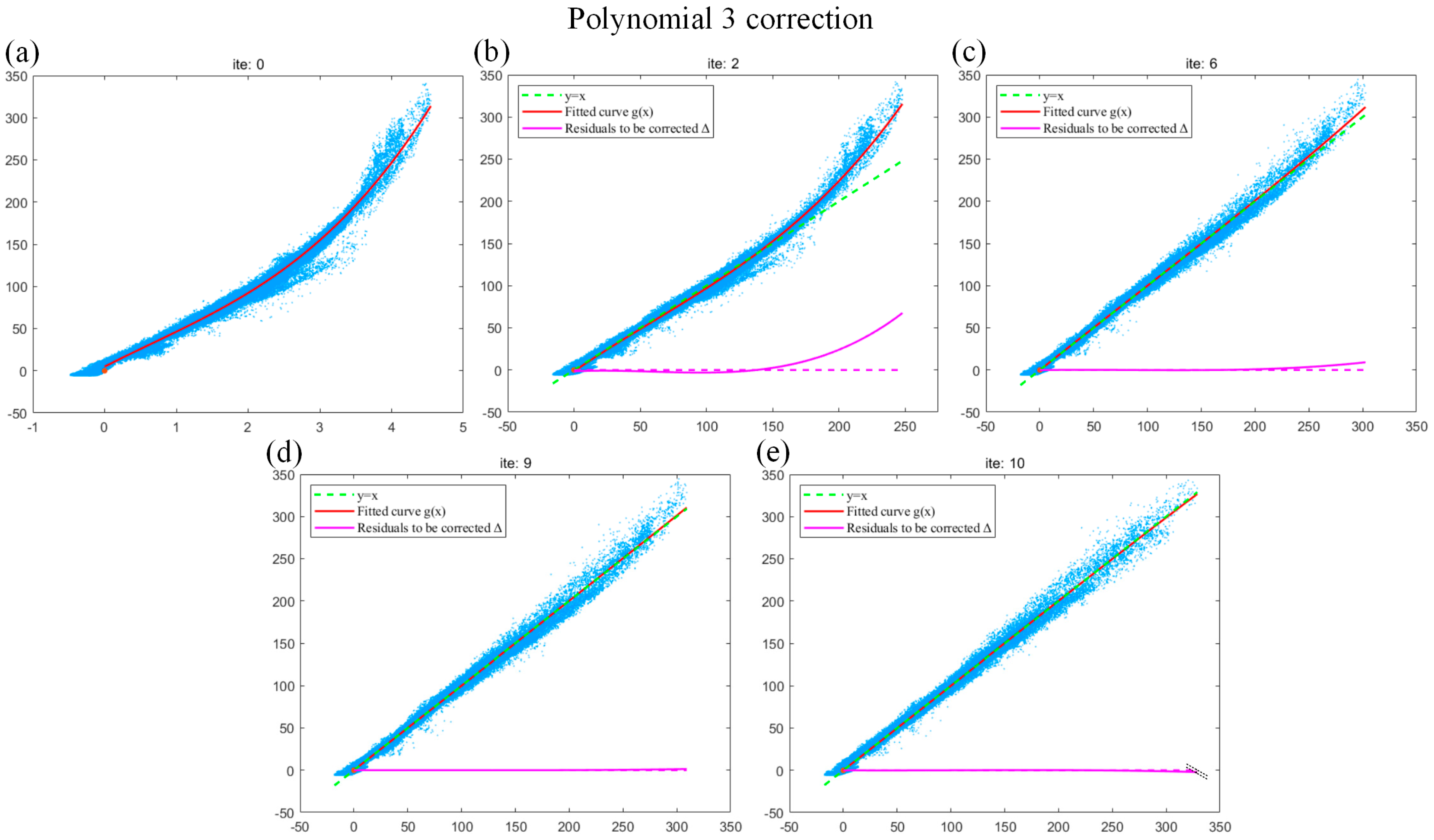
3.3.1. Analysis of Different Iterative Fitting Curves
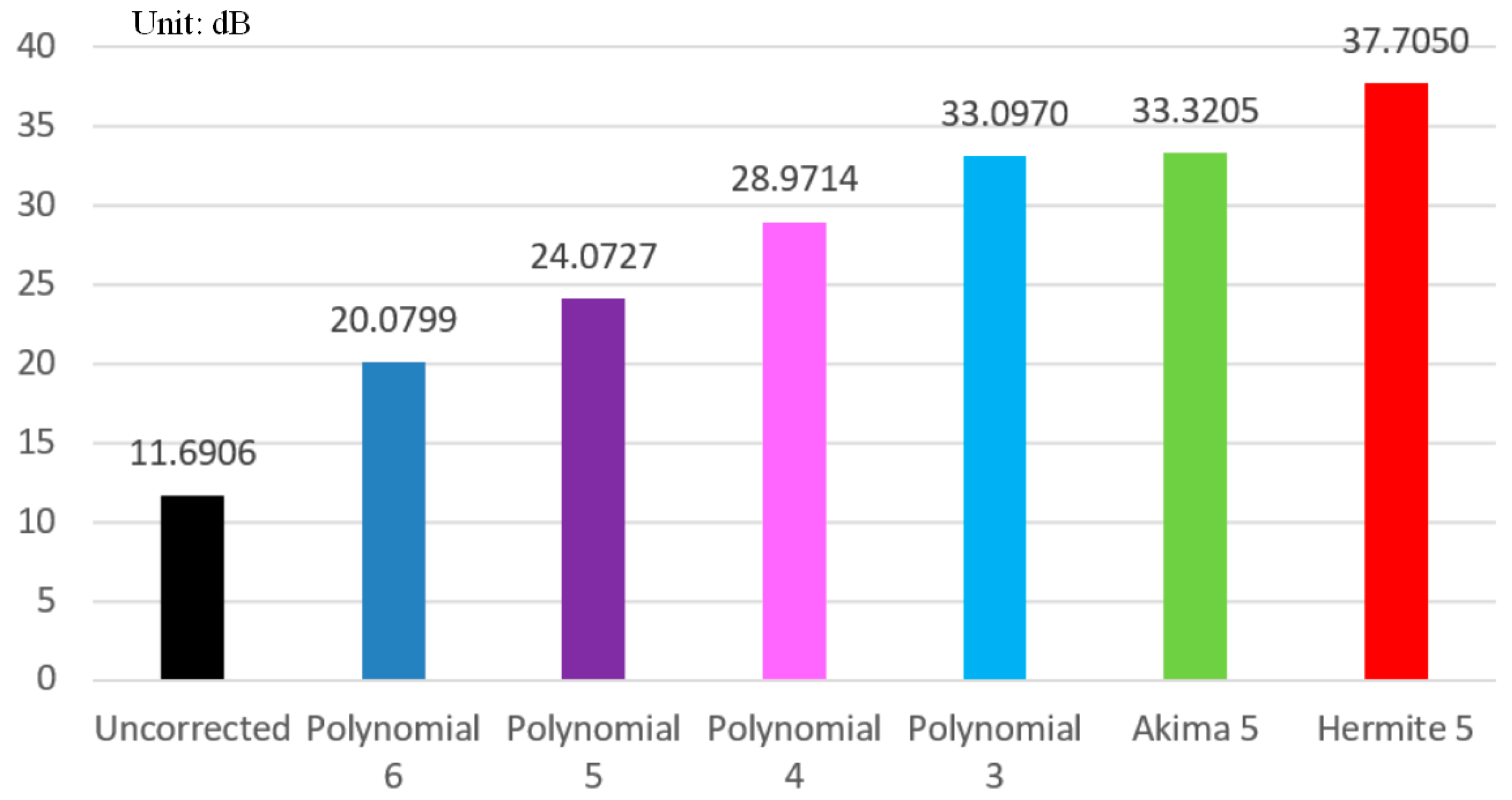
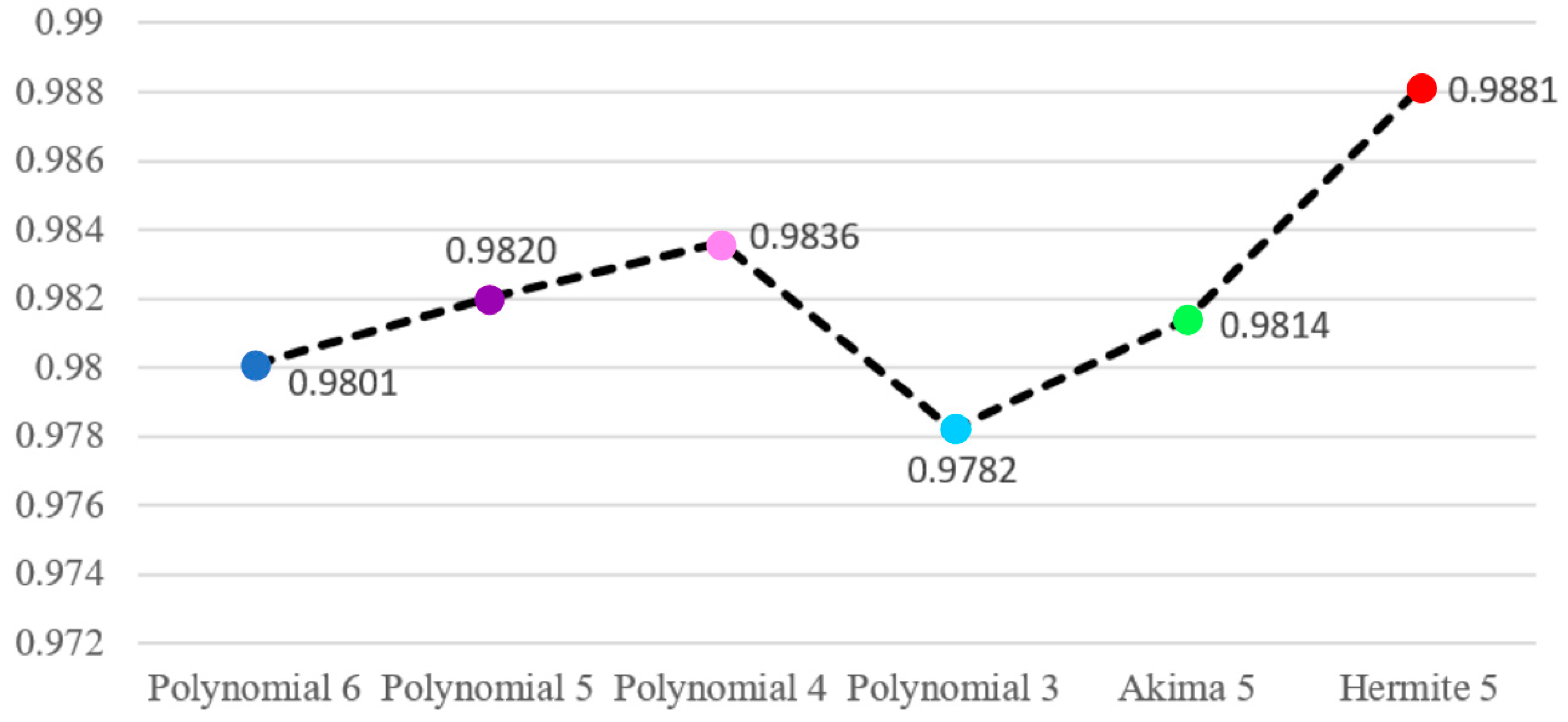
3.3.2. Tomographic Images of Different Iteratively Fitting Methods and Their Evaluations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Image Quantitative Evaluation Indicators
References
- Madonna, V.; Giangrande, P.; Galea, M. Electrical power generation in aircraft: Review, challenges, and opportunities. IEEE Trans. Transp. Electrif. 2018, 4, 646–659. [Google Scholar] [CrossRef]
- Aygun, H.; Erkara, S.; Turan, O. Comprehensive exergo-sustainability analysis for a next generation aero engine. Energy 2022, 239, 122364. [Google Scholar] [CrossRef]
- Kim, S.; Im, J.H.; Kim, M.; Kim, J.; Kim, Y.I. Diagnostics using a physics-based engine model in aero gas turbine engine verification tests. Aerosp. Sci. Technol. 2023, 133, 108102. [Google Scholar] [CrossRef]
- Gnadt, A.R.; Speth, R.L.; Sabnis, J.S.; Barrett, S.R. Technical and environmental assessment of all-electric 180-passenger commercial aircraft. Prog. Aerosp. Sci. 2019, 105, 1–30. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Quarta, M. Hybrid multigene genetic programming-artificial neural networks approach for dynamic performance prediction of an aeroengine. Aerosp. Sci. Technol. 2020, 103, 105902. [Google Scholar] [CrossRef]
- Gao, Y.; Fu, J. 3D nearest neighbor index model combined with Nano-CT to analyze SiC particles in ZrB2–SiC ceramics. Ceram. Int. 2023, 49, 2941–2955. [Google Scholar] [CrossRef]
- Wood, C.E.; O’Brien, N.; Denysov, A.; Blumensath, T. Computed laminography of CFRP using an X-ray cone-beam and robotic sample manipulator systems. IEEE Trans. Nucl. Sci. 2019, 66, 655–663. [Google Scholar] [CrossRef]
- Deyhle, H.; Towsyfyan, H.; Biguri, A.; Mavrogordato, M.; Boardman, R.; Blumensath, T. Spatial resolution of a laboratory based X-ray cone-beam laminography scanning system for various trajectories. NDT E Int. 2020, 111, 102222. [Google Scholar] [CrossRef]
- De Chiffre, L.; Carmignato, S.; Kruth, J.-P.; Schmitt, R.; Weckenmann, A. Industrial applications of computed tomography. CIRP Ann. 2014, 63, 655–677. [Google Scholar] [CrossRef]
- Hassler, U.; Garnero, L.; Rizo, P. X-ray dual-energy calibration based on estimated spectral properties of the experimental system. IEEE Trans. Nucl. Sci. 1998, 45, 1699–1712. [Google Scholar] [CrossRef]
- Herman, G.T. Correction for beam hardening in computed tomography. Phys. Med. Biol. 1979, 24, 81. [Google Scholar] [CrossRef]
- De Man, B.; Nuyts, J.; Dupont, P.; Marchal, G.; Suetens, P. An iterative maximum-likelihood polychromatic algorithm for CT. IEEE Trans. Med. Imaging 2001, 20, 999–1008. [Google Scholar] [CrossRef]
- Stonestrom, J.P.; Alvarez, R.E.; Macovski, A. A framework for spectral artifact corrections in X-ray CT. IEEE Trans. Biomed. Eng. 1981, 28, 128–141. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.H.; Whalen, R.T.; Beaupre, G.S.; Yen, S.Y.; Napel, S. Reconstruction algorithm for polychromatic CT imaging: Application to beam hardening correction. IEEE Trans. Med. Imaging 2000, 19, 1–11. [Google Scholar] [PubMed]
- Han, R.; Zeng, F.; Li, J.; Yao, Z.; Guo, W.; Zhao, J. A Dilated Residual Network for Turbine Blade ICT Image Artifact Removal. Sensors 2023, 23, 1028. [Google Scholar] [CrossRef] [PubMed]
- Ay, M.R.; Mehranian, A.; Maleki, A.; Ghadiri, H.; Ghafarian, P.; Zaidi, H. Experimental assessment of the influence of beam hardening filters on image quality and patient dose in volumetric 64-slice X-ray CT scanners. Phys. Medica 2013, 29, 249–260. [Google Scholar] [CrossRef] [PubMed]
- Van de Casteele, E.; Van Dyck, D.; Sijbers, J.; Raman, E. A model-based correction method for beam hardening artefacts in X-ray microtomography. J. X-Ray Sci. Technol. 2004, 12, 43–57. [Google Scholar]
- Hammersberg, P.; Mångård, M. Correction for beam hardening artefacts in computerised tomography. J. X-Ray Sci. Technol. 1998, 8, 75–93. [Google Scholar]
- Van Gompel, G.; Van Slambrouck, K.; Defrise, M.; Batenburg, K.J.; De Mey, J.; Sijbers, J.; Nuyts, J. Iterative correction of beam hardening artifacts in CT. Med. Phys. 2011, 38, S36–S49. [Google Scholar] [CrossRef] [PubMed]
- Coleman, A.; Sinclair, M. A beam-hardening correction using dual-energy computed tomography. Phys. Med. Biol. 1985, 30, 1251. [Google Scholar] [CrossRef]
- Kyriakou, Y.; Meyer, E.; Prell, D.; Kachelrieß, M. Empirical beam hardening correction (EBHC) for CT. Med. Phys. 2010, 37, 5179–5187. [Google Scholar] [CrossRef] [PubMed]
- Brabant, L.; Pauwels, E.; Dierick, M.; Van Loo, D.; Boone, M.; Van Hoorebeke, L. A novel beam hardening correction method requiring no prior knowledge, incorporated in an iterative reconstruction algorithm. Ndt E Int. 2012, 51, 68–73. [Google Scholar] [CrossRef]
- Marshall Jr, W.H.; Alvarez, R.E.; Macovski, A. Initial results with prereconstruction dual-energy computed tomography (PREDECT). Radiology 1981, 140, 421–430. [Google Scholar] [CrossRef] [PubMed]
- Feldkamp, L.A.; Davis, L.C.; Kress, J.W. Practical cone-beam algorithm. Josa A 1984, 1, 612–619. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- De Boor, C.; Höllig, K.; Sabin, M. High accuracy geometric Hermite interpolation. Comput. Aided Geom. Des. 1987, 4, 269–278. [Google Scholar] [CrossRef]
- Akima, H. A new method of interpolation and smooth curve fitting based on local procedures. J. ACM (JACM) 1970, 17, 589–602. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Hore, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Washington, DC, USA, 23–26 August 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2366–2369. [Google Scholar]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef]


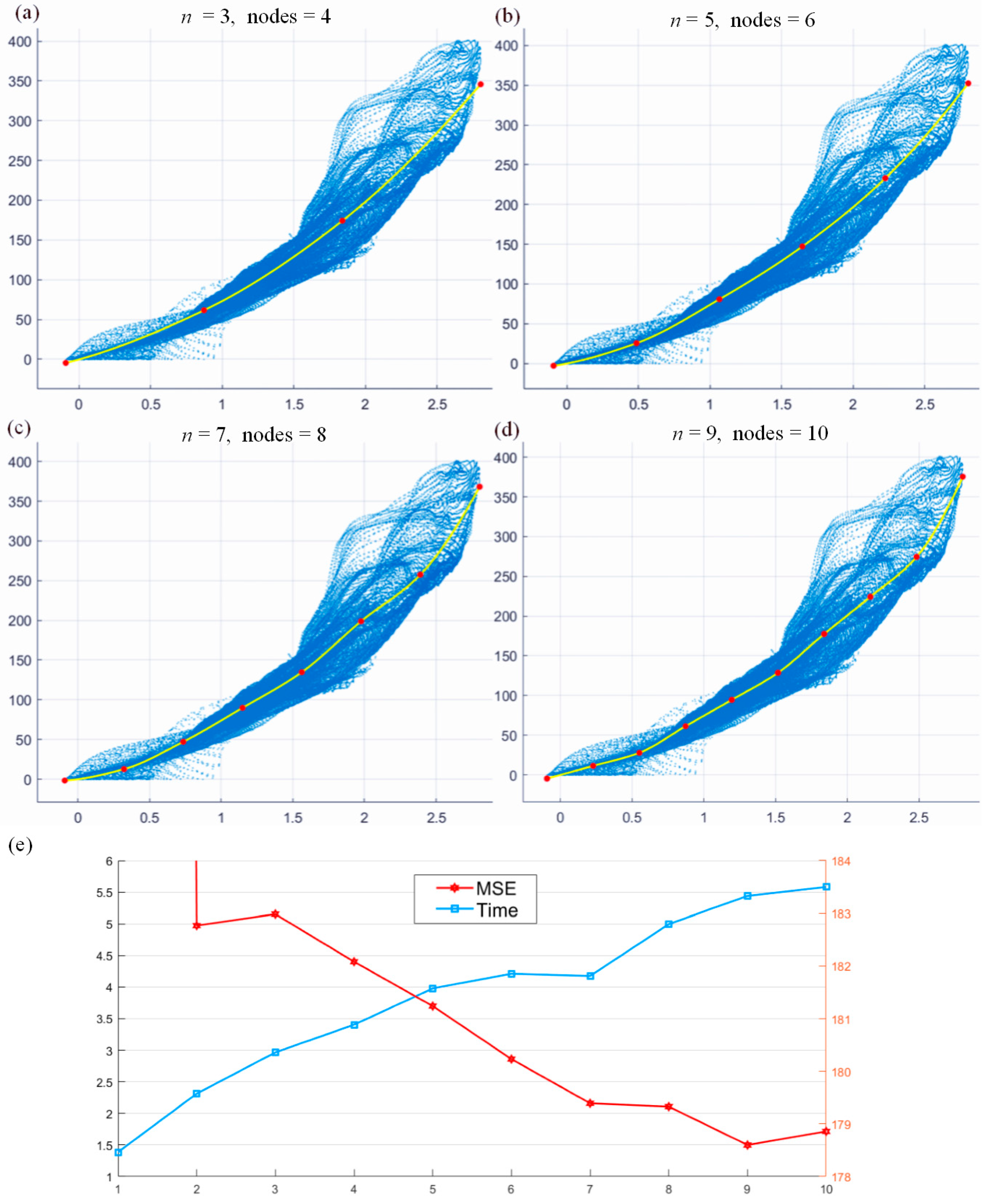




| n | 1 | 2 | 3 | 5 | 6 | 8 | 10 |
| MSE | 386.05 | 182.77 | 182.98 | 181.24 | 180.23 | 179.33 | 178.86 |
| Time | 1.39 s | 2.31 s | 2.97 s | 3.98 s | 4.22 s | 4.99 s | 5.52 s |
| Uncorrected | Polynomial 6 | Polynomial 5 | Polynomial 4 | Polynomial 3 | Akima 5 | Hermite 5 | |
|---|---|---|---|---|---|---|---|
| RMSE | 0.2665 | 0.1015 | 0.0641 | 0.0365 | 0.0227 | 0.0221 | 0.0133 |
| PSNR | 11.6906 dB | 20.0799 dB | 24.0727 dB | 28.9714 dB | 33.0970 dB | 33.3205 dB | 37.7050 dB |
| FSIM | 0.8838 | 0.9801 | 0.9820 | 0.9836 | 0.9782 | 0.9814 | 0.9881 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Fu, J.; Chen, X. Correcting Hardening Artifacts of Aero-Engine Blades with an Iterative Linear Fitting Technique Framework. Sensors 2024, 24, 2001. https://doi.org/10.3390/s24062001
Gao Y, Fu J, Chen X. Correcting Hardening Artifacts of Aero-Engine Blades with an Iterative Linear Fitting Technique Framework. Sensors. 2024; 24(6):2001. https://doi.org/10.3390/s24062001
Chicago/Turabian StyleGao, Yenan, Jian Fu, and Xiaolong Chen. 2024. "Correcting Hardening Artifacts of Aero-Engine Blades with an Iterative Linear Fitting Technique Framework" Sensors 24, no. 6: 2001. https://doi.org/10.3390/s24062001
APA StyleGao, Y., Fu, J., & Chen, X. (2024). Correcting Hardening Artifacts of Aero-Engine Blades with an Iterative Linear Fitting Technique Framework. Sensors, 24(6), 2001. https://doi.org/10.3390/s24062001






