Open-Ended Coaxial Probe for Effective Reconstruction of Biopsy-Excised Tissues’ Dielectric Properties
Abstract
:1. Introduction
2. Materials and Methods
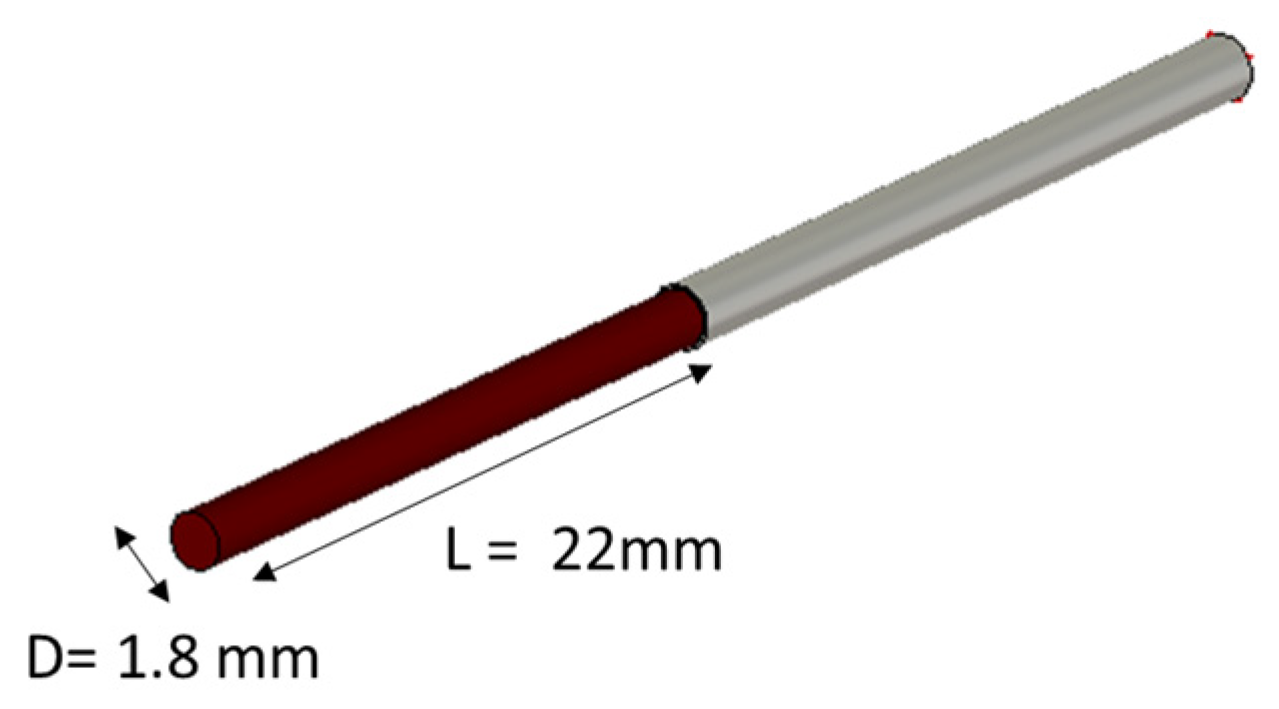
2.1. Open-Ended Coaxial Probe Design
2.2. Coated Open-Ended Coaxial Probe
3. Results and Discussion
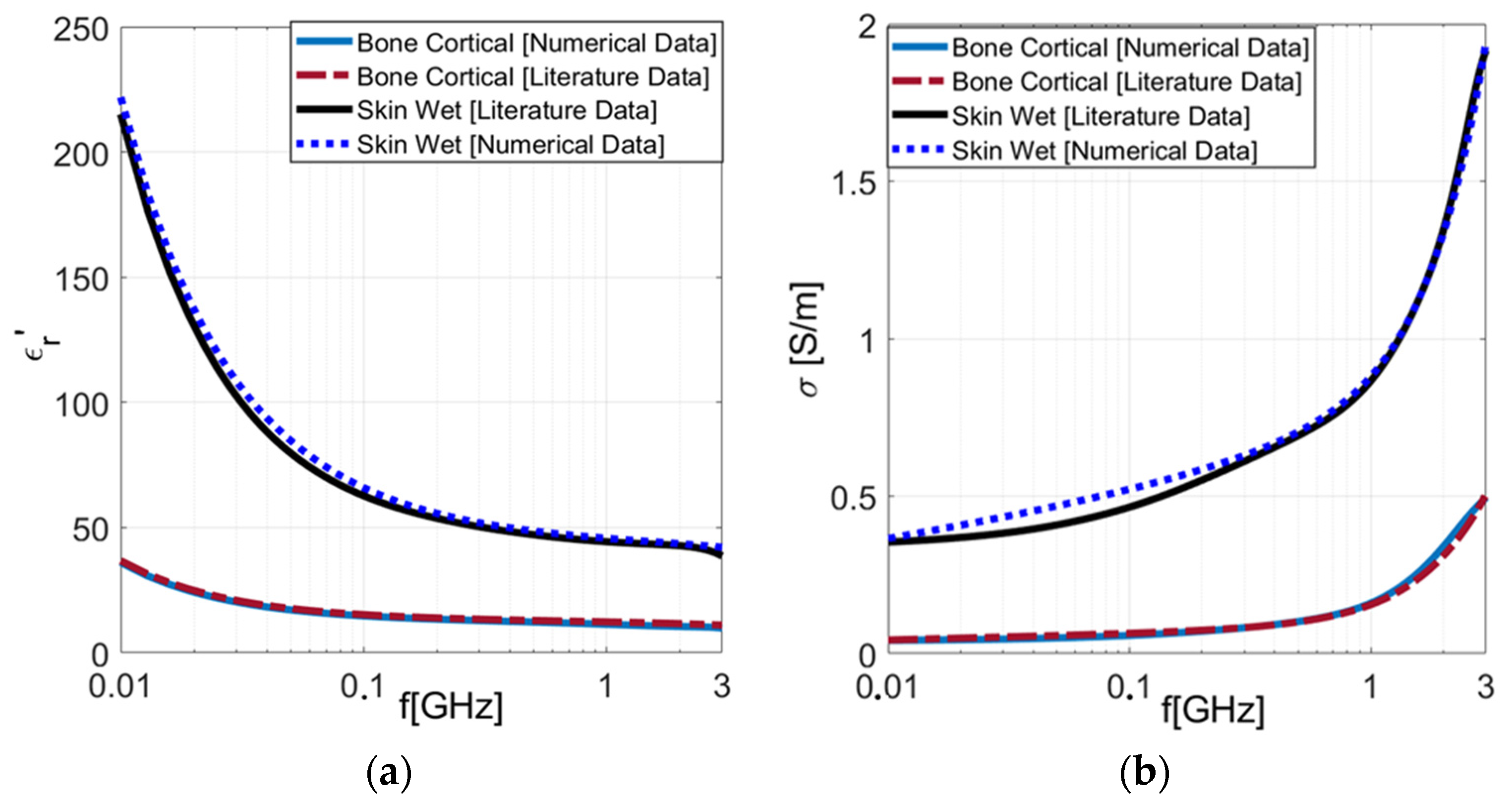
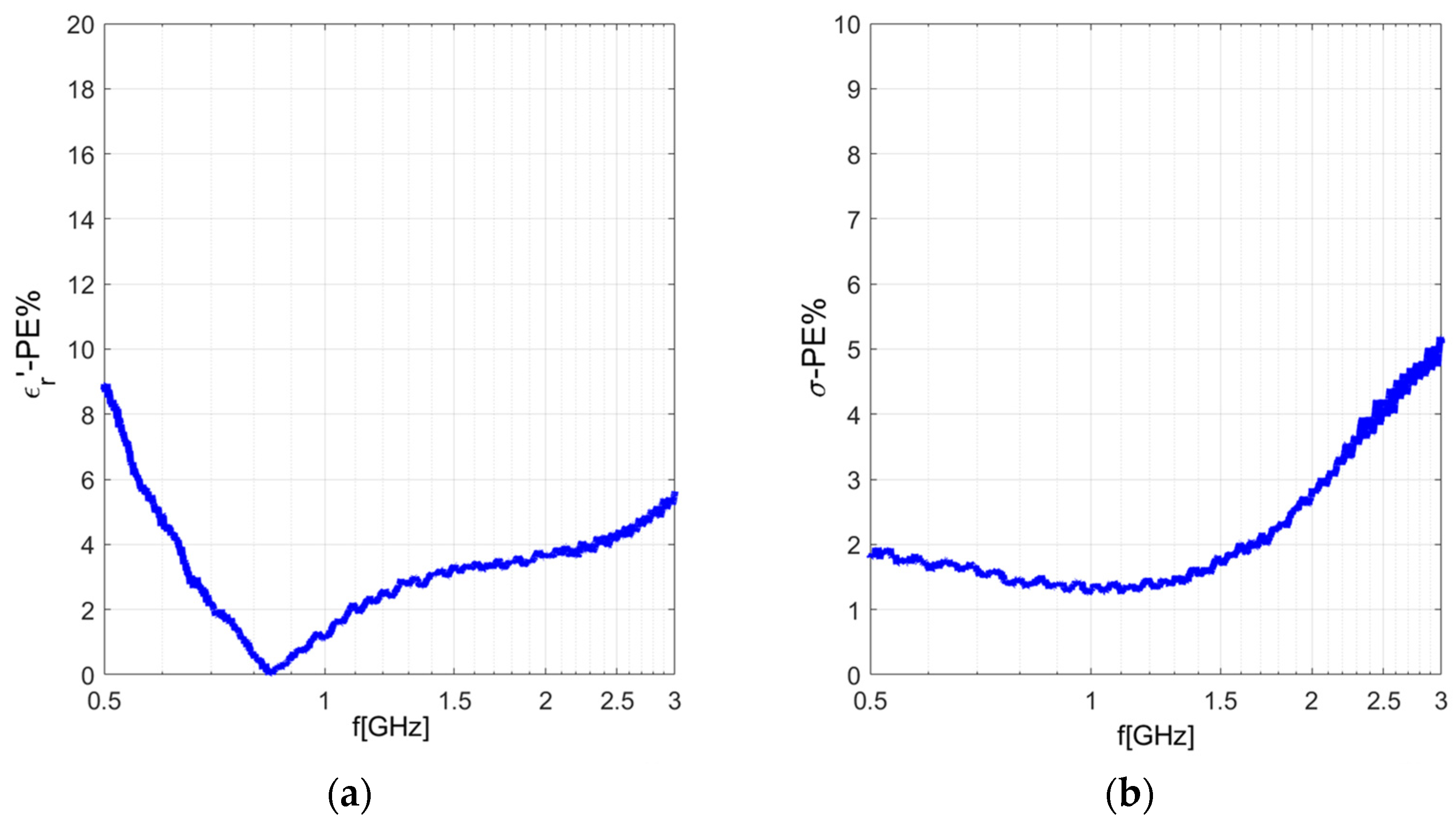
3.1. Numerical Results
3.1.1. Metallic-Coated Open-Ended Coaxial Probe
3.1.2. Comparison between Metallic-Coated and Teflon-Coated Open-Ended Coaxial Probes
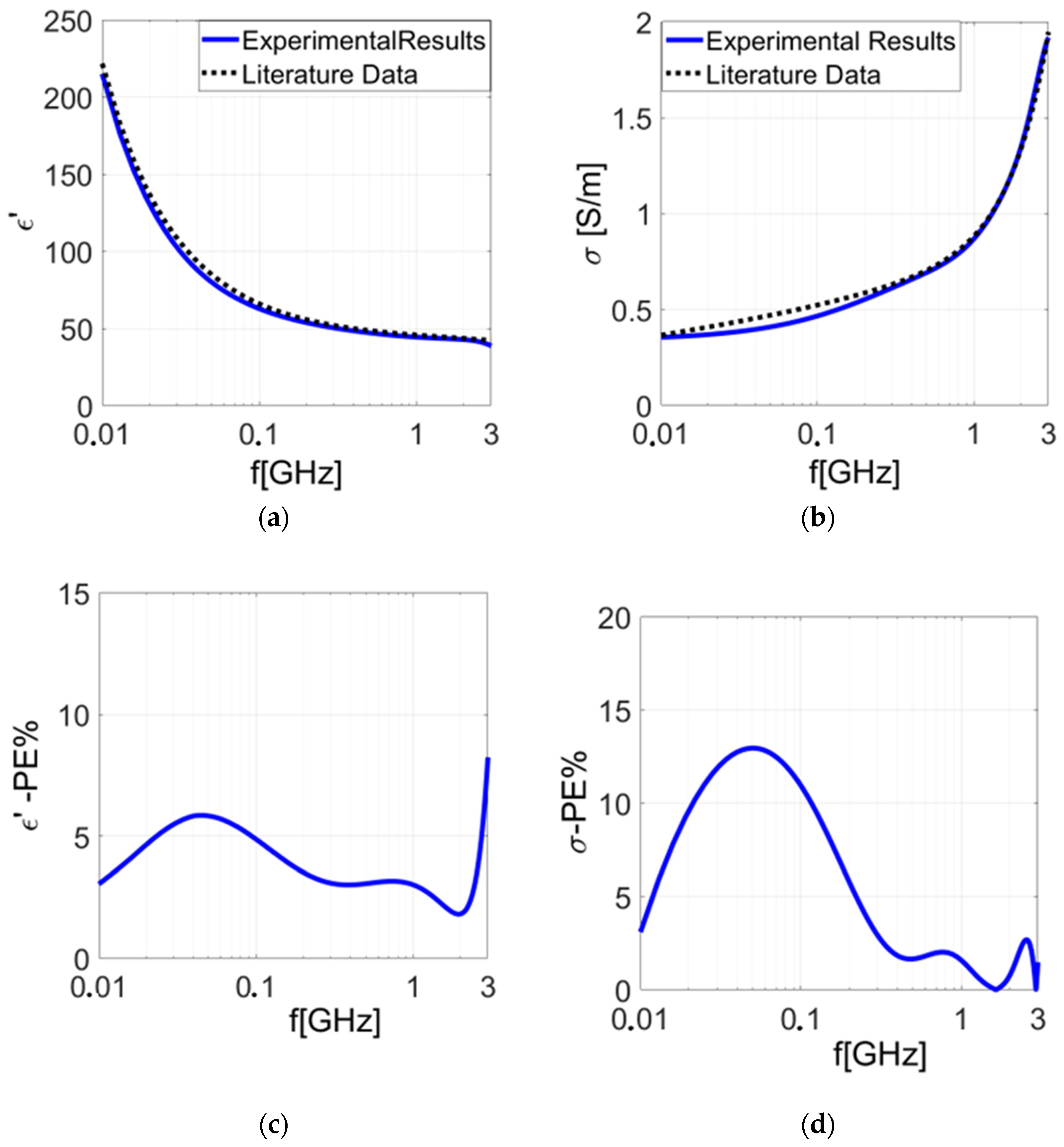
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- O’Flynn, E.A.M.; Wilson, A.R.M.; Michell, M.J. Image-guided breast biopsy: State-of-the-art. Clin. Radiol. 2010, 65, 259–270. [Google Scholar] [CrossRef]
- Available online: https://healthcare-quality.jrc.ec.europa.eu/ecibc/european-breast-cancer-guidelines (accessed on 25 March 2024).
- Liberman, L. Percutaneous image-guided core breast biopsy. Radiol. Clin. N. Am. 2002, 40, 483–500. [Google Scholar] [CrossRef]
- Helbich, T.H.; Matzek, W.; Fuchsjäger, M.H. Stereotactic and ultrasound-guided breast biopsy. Eur. Radiol. 2004, 14, 383–393. [Google Scholar] [CrossRef] [PubMed]
- Canicattì, E.; Sánchez-Bayuela, D.Á.; Romero Castellano, C.; Aguilar Angulo, P.M.; Giovanetti González, R.; Cruz Hernández, L.M.; Ruiz Martín, J.; Tiberi, G.; Monorchio, A. Dielectric Characterization of Breast Biopsied Tissues as Pre-Pathological Aid in Early Cancer Detection: A Blinded Feasibility Study. Diagnostics 2023, 13, 3015. [Google Scholar] [CrossRef] [PubMed]
- Popovic, D.; McCartney, L.; Beasley, C.; Lazebnik, M.; Okoniewski, M.; Hagness, S.C.; Booske, J.H. Precision open-ended coaxial probes for in vivo and ex vivo dielectric spectroscopy of biological tissues at microwave frequencies. IEEE Trans. Microw. Theory Tech. 2005, 53, 1713–1722. [Google Scholar] [CrossRef]
- La Gioia, A.; Porter, E.; Merunka, I.; Shahzad, A.; Salahuddin, S.; Jones, M.; O’Halloran, M. Open-Ended Coaxial Probe Technique for Dielectric Measurement of Biological Tissues: Challenges and Common Practices. Diagnostics 2018, 8, 40. [Google Scholar] [CrossRef] [PubMed]
- Joines, W.T.; Zhang, Y.; Li, C.; Jirtle, R.L. The measured electrical properties of normal and malignant human tissues from 50 to 900 MHz. Med. Phys. 1994, 21, 547–550. [Google Scholar] [CrossRef] [PubMed]
- O’Rourke, A.P.; Lazebnik, M.; Bertram, J.M.; Converse, M.C.; Hagness, S.C.; Webster, J.G.; Mahvi, D.M. Dielectric properties of human normal, malignant and cirrhotic liver tissue: In vivo and ex vivo measurements from 0.5 to 20 GHz using a precision open-ended coaxial probe. Phys. Med. Biol. 2007, 52, 4707–4719. [Google Scholar] [CrossRef]
- Schepps, J.L.; Foster, K.R. The UHF and microwave dielectric properties of normal and tumour tissues: Variation in dielectric properties with tissue water content. Phys. Med. Biol. 1980, 25, 1149–1159. [Google Scholar] [CrossRef]
- Guardiola, M.; Buitrago, S.; Fernández-Esparrach, G.; O’Callaghan, J.M.; Romeu, J.; Cuatrecasas, M.; Córdova, H.; González Ballester, M.Á.; Camara, O. Dielectric properties of colon polyps, cancer, and normal mucosa: Ex vivo measurements from 0.5 to 20 GHz. Med. Phys. 2018, 45, 3768–3782. [Google Scholar] [CrossRef]
- Campbell, A.M.; Land, D.V. Dielectric properties of female human breast tissue measured in vitro at 3.2 GHz. Phys. Med. Biol. 1992, 37, 193–210. [Google Scholar] [CrossRef]
- Lazebnik, M.; Okoniewski, M.; Booske, J.H.; Hagness, S.C. Highly Accurate Debye Models for Normal and Malignant Breast Tissue Dielectric Properties at Microwave Frequencies. IEEE Microw. Wirel. Compon. Lett. 2007, 17, 822–824. [Google Scholar] [CrossRef]
- Chaudhary, S.S.; Mishra, R.K.; Swarup, A.; Thomas, J.M. Dielectric properties of normal & malignant human breast tissues at radiowave & microwave frequencies. Indian J. Biochem. Biophys. 1984, 21, 76–79. [Google Scholar] [PubMed]
- Sha, L.; Ward, E.R.; Stroy, B. A review of dielectric properties of normal and malignant breast tissue. In Proceedings of the IEEE SoutheastCon 2002 (Cat. No.02CH37283), Columbia, SC, USA, 5–7 April 2002; pp. 457–462. [Google Scholar] [CrossRef]
- Choi, J.W.; Cho, J.; Lee, Y.; Yim, J.; Kang, B.; Keun Oh, K.; Hee Jung, W.; Jung Kim, H.; Cheon, C.; Lee, H.D.; et al. Microwave Detection of Metastasized Breast Cancer Cells in the Lymph Node; Potential Application for Sentinel Lymphadenectomy. Breast Cancer Res. Treat. 2004, 86, 107–115. [Google Scholar] [CrossRef]
- Hussein, M.; Awwad, F.; Jithin, D.; El Hasasna, H.; Athamneh, K.; Iratni, R. Breast cancer cells exhibits specific dielectric signature in vitro using the open-ended coaxial probe technique from 200 MHz to 13.6 GHz. Sci. Rep. 2019, 9, 4681. [Google Scholar] [CrossRef] [PubMed]
- Fornes-Leal, A.; Garcia-Pardo, C.; Frasson, M.; Pons Beltrán, V.; Cardona, N. Dielectric characterization of healthy and malignant colon tissues in the 0.5–18 GHz frequency band. Phys. Med. Biol. 2016, 61, 7334–7346. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, T. Multiclass Classification of Hepatic Anomalies with Dielectric Properties: From Phantom Materials to Rat Hepatic Tissues. Sensors 2020, 20, 530. [Google Scholar] [CrossRef]
- Yilmaz, T.; Kılıç, M.A.; Erdoğan, M.; Çayören, M.; Tunaoğlu, D.; Kurtoğlu, İ.; Yaslan, Y.; Çayören, H.; Arıkan, A.E.; Teksöz, S.; et al. Machine learning aided diagnosis of hepatic malignancies through in vivo dielectric measurements with microwaves. Phys. Med. Biol. 2016, 61, 5089–5102. [Google Scholar] [CrossRef] [PubMed]
- Naqvi, S.A.R.; Mobashsher, A.T.; Mohammed, B.; Foong, D.; Abbosh, A. Benign and Malignant Skin Lesions: Dielectric Characterization, Modelling and Analysis in Frequency Band 1 to 14 GHz. IEEE Trans. Biomed. Eng. 2023, 70, 628–639. [Google Scholar] [CrossRef]
- Fontana, N.; Canicatti, E.; Monorchio, A. An application of the virtual transmission line model of an open-ended coaxial probe for dielectric properties characterization of biological tissues. In Proceedings of the 2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, Atlanta, GA, USA, 7–12 July 2019; pp. 341–342. [Google Scholar] [CrossRef]
- Burdette, E.C.; Cain, F.L.; Seals, J. In Vivo Probe Measurement Technique for Determining Dielectric Properties at VHF through Microwave Frequencies. IEEE Trans. Microw. Theory Tech. 1980, 28, 414–427. [Google Scholar] [CrossRef]
- Smith, S.R.; Foster, K.R. Dielectric properties of low-water-content tissues. Phys. Med. Biol. 1985, 30, 965–973. [Google Scholar] [CrossRef] [PubMed]
- Hagl, D.M.; Popovic, D.; Hagness, S.C.; Booske, J.H.; Okoniewski, M. Sensing volume of open-ended coaxial probes for dielectric characterization of breast tissue at microwave frequencies. IEEE Trans. Microw. Theory Tech. 2003, 51, 1194–1206. [Google Scholar] [CrossRef]
- La Gioia, A.; Santorelli, A.; O’Halloran, M.; Porter, E. Predicting the Sensing Radius of a Coaxial Probe Based on the Probe Dimensions. IEEE Trans. Antennas Propag. 2020, 68, 6704–6716. [Google Scholar] [CrossRef]
- Aydinalp, C.; Joof, S.; Dilman, I.; Akduman, I.; Yilmaz, T. Characterization of Open-Ended Coaxial Probe Sensing Depth with Respect to Aperture Size for Dielectric Property Measurement of Heterogeneous Tissues. Sensors 2022, 22, 760. [Google Scholar] [CrossRef] [PubMed]
- Martellosio, A.; Pasian, M.; Bozzi, M.; Perregrini, L.; Mazzanti, A.; Svelto, F.; Summers, P.E.; Renne, G.; Preda, L.; Bellomi, M. Dielectric Properties Characterization From 0.5 to 50 GHz of Breast Cancer Tissues. IEEE Trans. Microw. Theory Tech. 2017, 65, 998–1011. [Google Scholar] [CrossRef]
- Canicattì, E.; Sánchez-Bayuela, D.Á.; Castellano, C.R.; González, R.G.; Hernández, L.M.C.; Angulo, P.M.A.; Martín, J.R.; Monorchio, A.; Tiberi, G. Dielectric Characterization of Small Breast Biopsy Via Miniaturized Open-Ended Coaxial Probe. In Proceedings of the 2022 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (AP-S/URSI), Denver, CO, USA, 10–15 July 2022; pp. 1332–1333. [Google Scholar] [CrossRef]
- Canicatti, E.; Brizi, D.; Monorchio, A.; Fontana, N.; Tiberi, G. Dielectric Characterization of Biological Samples by Using an Open-ended Coaxial Probe. In Proceedings of the 2020 IEEE International Symposium on Antennas and Propagation and North American Radio Science Meeting, Montreal, QC, Canada, 5–10 July 2020; pp. 639–640. [Google Scholar] [CrossRef]
- Canicatti, E.; Fontana, N.; Barmada, S.; Monorchio, A. Dielectric Characterization Improvement of Biopsy Samples Via a Coated Open-Ended Coaxial Probe. In Proceedings of the 2022 Microwave Mediterranean Symposium (MMS), Pizzo Calabro, Italy, 9–13 May 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Cst Studio Suite® 3D Electromagnetic Analysis Software Package. Available online: https://www.3ds.com/products/simulia/cst-studio-suite (accessed on 25 March 2024).
- Berube, D.; Ghannouchi, F.M.; Savard, P. A comparative study of four open-ended coaxial probe models for permittivity measurements of lossy dielectric/biological materials at microwave frequencies. IEEE Trans. Microw. Theory Tech. 1996, 44, 1928–1934. [Google Scholar] [CrossRef]
- Athey, T.W.; Stuchly, M.A.; Stuchly, S.S. Measurement of Radio Frequency Permittivity of Biological Tissues with an Open-Ended Coaxial Line: Part I. IEEE Trans. Microw. Theory Tech. 1982, 30, 82–86. [Google Scholar] [CrossRef]
- Peyman, A.; Gabriel, C.; Grant, E.H. Complex permittivity of sodium chloride solutions at microwave frequencies. Bioelectromagnetics 2007, 28, 264–274. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.sigmaaldrich.com/IT/it/product/sigald/s9888 (accessed on 21 November 2021).
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271–2293. [Google Scholar] [CrossRef]
- Espin-Lopez, P.F.; Pasian, M.; Barbolini, M.; Dell’Acqua, F. Snow Cover Monitoring Using Microwave Radars: Dielectric Characterization, Fabrication, and Testing of a Synthetic Snowpack. In Proceedings of the IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 5097–5100. [Google Scholar] [CrossRef]
- Bobowski, J.S.; Johnson, T. Permittivity measurements of biological samples by an open-ended coaxial line. Prog. Electromagn. Res. B 2012, 40, 159–183. [Google Scholar] [CrossRef]
- Wang, Y.; Chung, D.D.L. Effect of the fringing electric field on the apparent electric permittivity of cement-based materials. Compos. B Eng. 2017, 126, 192–201. [Google Scholar] [CrossRef]
- You, K.Y.; Sim, M.S. Precision Permittivity Measurement for Low-Loss Thin Planar Materials Using Large Coaxial Probe from 1 to 400 MHz. J. Manuf. Mater. Process. 2018, 2, 81. [Google Scholar] [CrossRef]
- You, K.Y.; Salleh, J.; Abbas, Z. Effects of Length and Diameter of Open-Ended Coaxial Sensor on its Reflection Coefficient. Radioengineering 2012, 21, 496–503. [Google Scholar]
- Available online: https://matweb.com/search/datasheet.aspx?matguid=bdaf87c3a6ea43a3bf57c6381192c07f&ckck=1 (accessed on 25 March 2024).



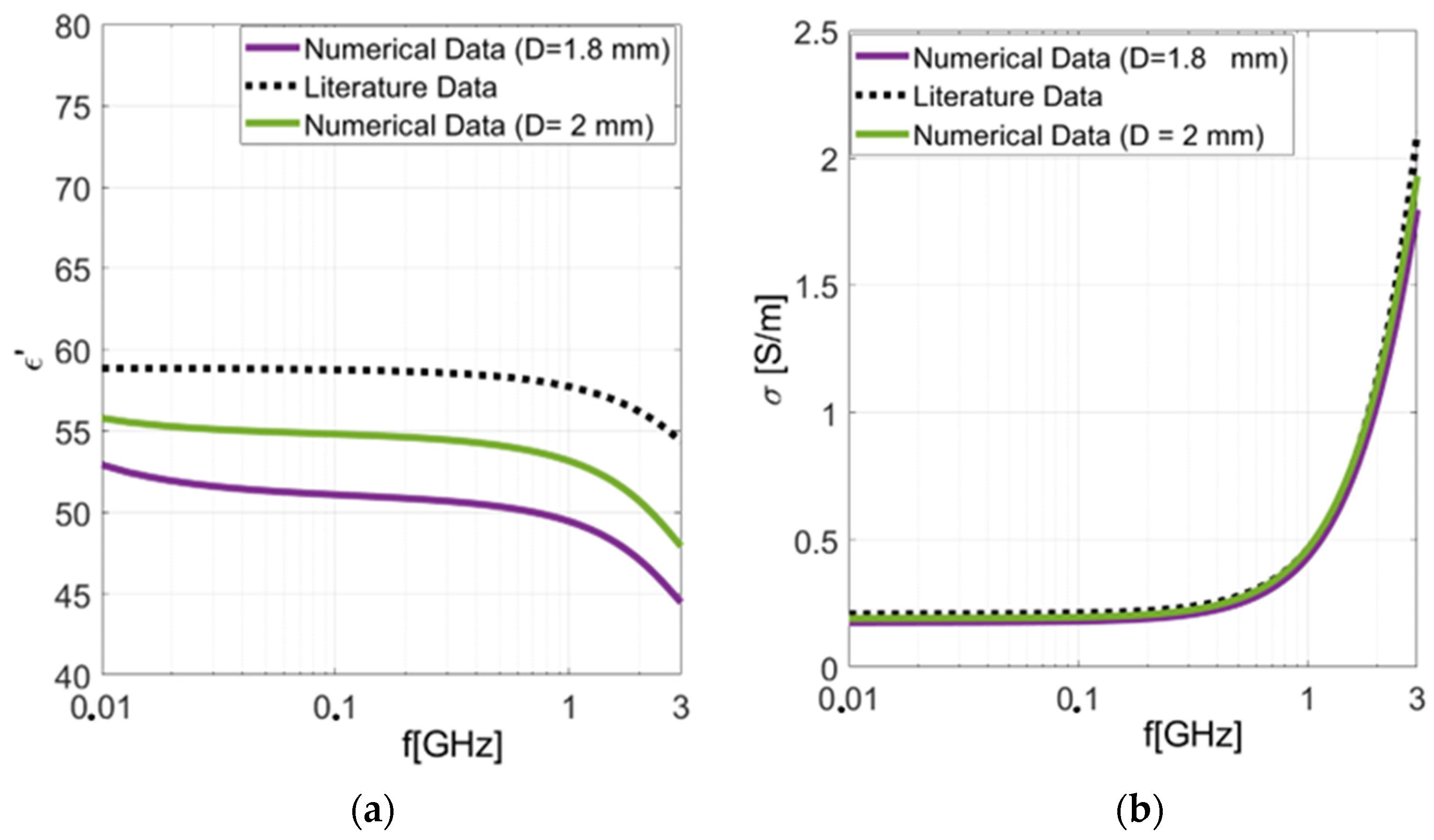
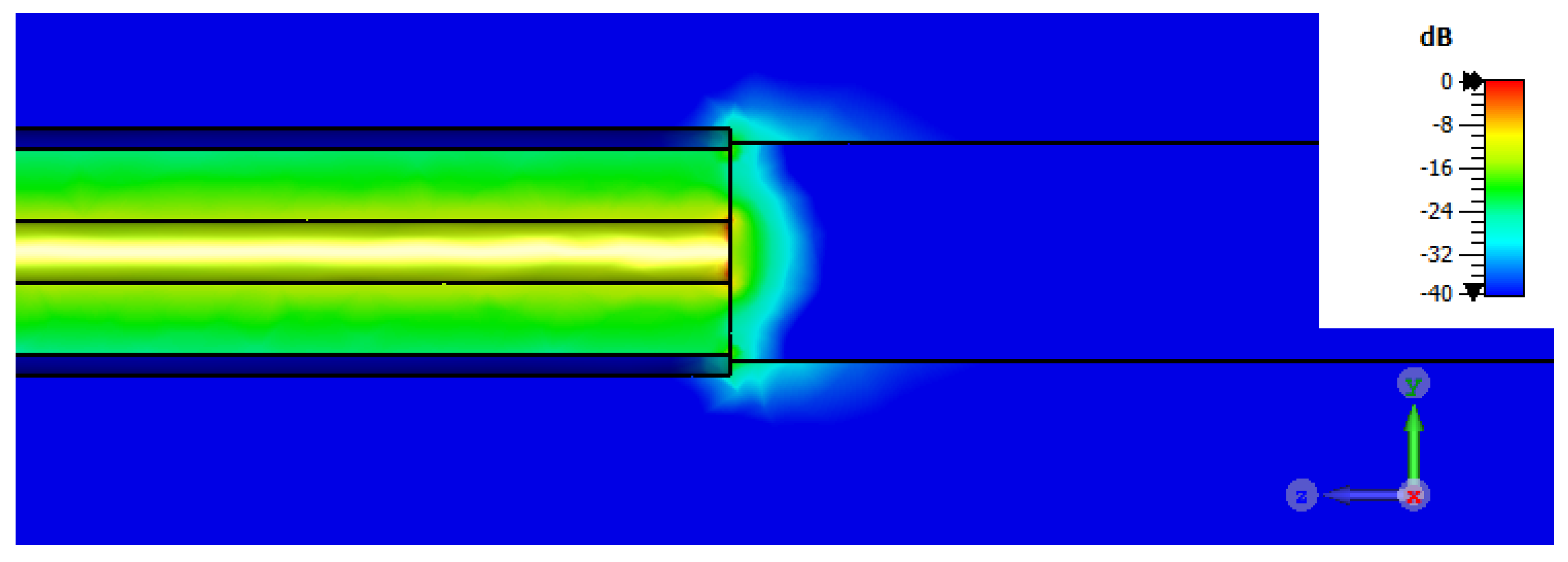
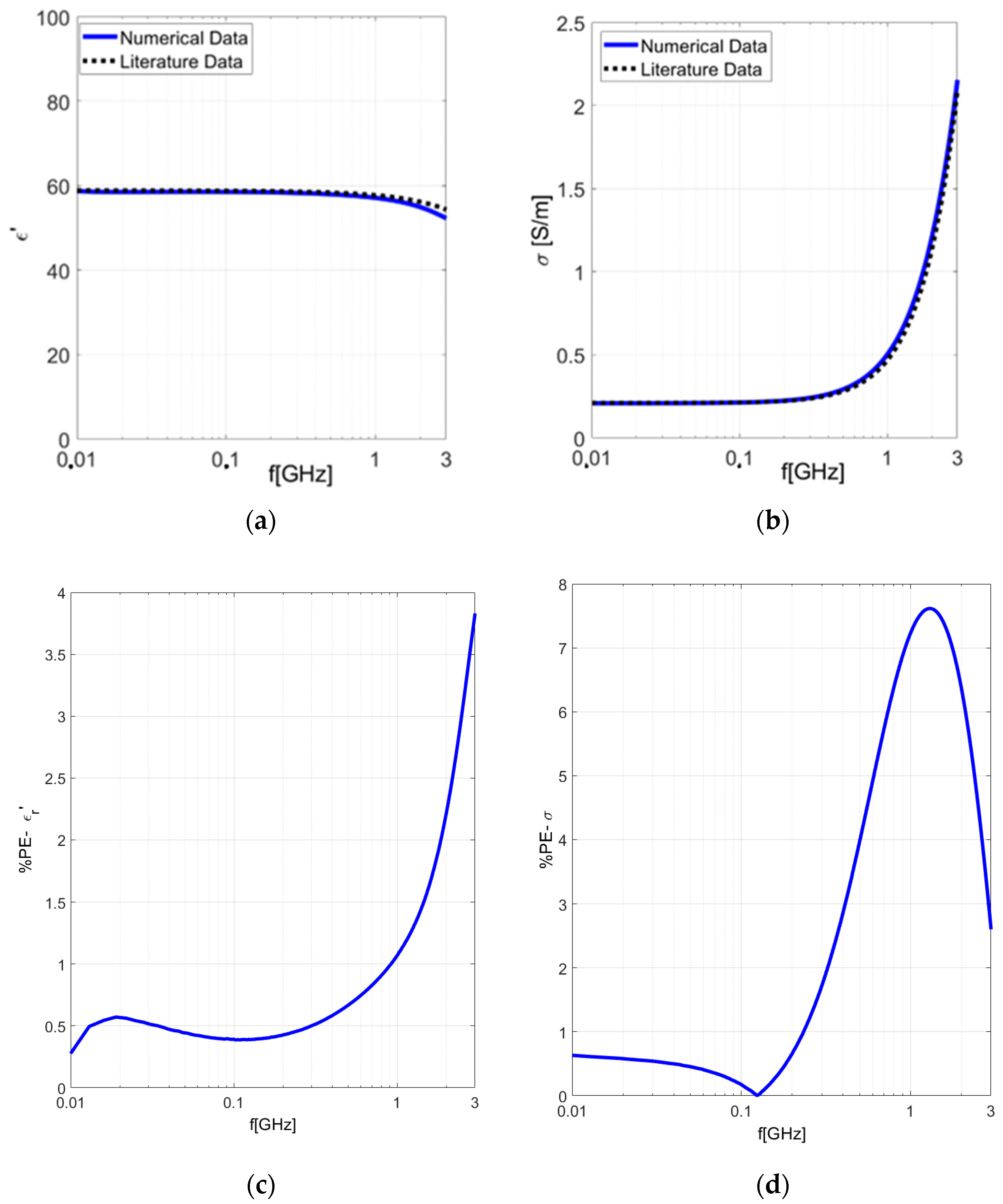

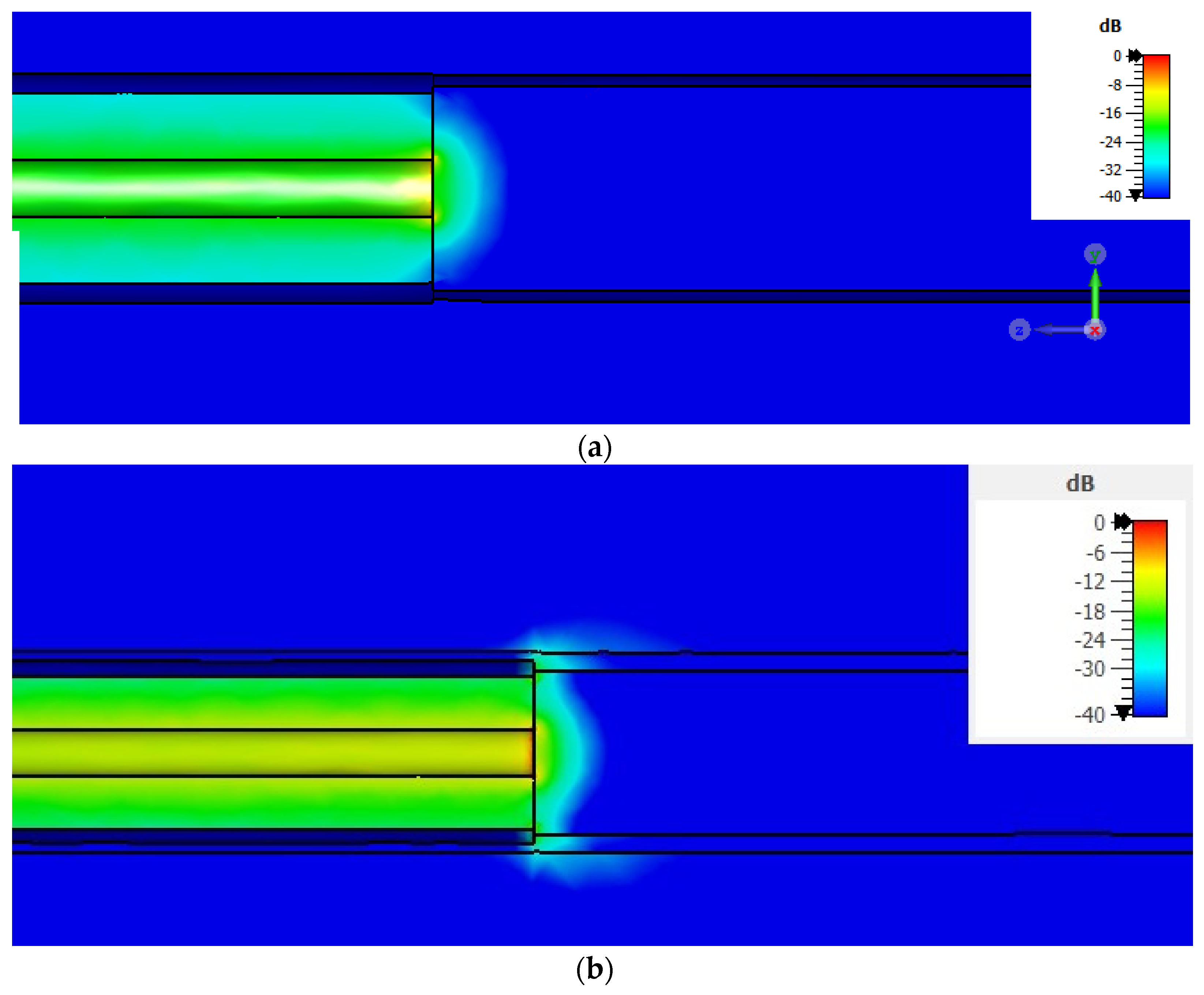




| Test Case | PE (ε′) | PE (σ) |
|---|---|---|
| Numerical Cylindrical Liver D = 1.8 mm | 14.43% | 7.28% |
| Numerical Cylindrical Liver D = 2 mm | 8.6% | 2.1% |
| Test Case | PE (ε′) | PE (σ) |
|---|---|---|
| 1.8 mm Numerical Liver: Metallic Coating | 1% | 7.2% |
| 1.8 mm Numerical Liver: Dielectric Coating | 7.8% | 0.66% |
| Test Case | PE (ε′) | PE (σ) |
|---|---|---|
| Experimental Liver: Metallic Coating | 0.89% | 12.15% |
| Experimental Liver: Dielectric Coating | 0.88% | 0.068% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Canicattì, E.; Fontana, N.; Barmada, S.; Monorchio, A. Open-Ended Coaxial Probe for Effective Reconstruction of Biopsy-Excised Tissues’ Dielectric Properties. Sensors 2024, 24, 2160. https://doi.org/10.3390/s24072160
Canicattì E, Fontana N, Barmada S, Monorchio A. Open-Ended Coaxial Probe for Effective Reconstruction of Biopsy-Excised Tissues’ Dielectric Properties. Sensors. 2024; 24(7):2160. https://doi.org/10.3390/s24072160
Chicago/Turabian StyleCanicattì, Eliana, Nunzia Fontana, Sami Barmada, and Agostino Monorchio. 2024. "Open-Ended Coaxial Probe for Effective Reconstruction of Biopsy-Excised Tissues’ Dielectric Properties" Sensors 24, no. 7: 2160. https://doi.org/10.3390/s24072160
APA StyleCanicattì, E., Fontana, N., Barmada, S., & Monorchio, A. (2024). Open-Ended Coaxial Probe for Effective Reconstruction of Biopsy-Excised Tissues’ Dielectric Properties. Sensors, 24(7), 2160. https://doi.org/10.3390/s24072160





