A UWB-Ego-Motion Particle Filter for Indoor Pose Estimation of a Ground Robot Using a Moving Horizon Hypothesis
Abstract
1. Introduction
- Estimating the heading and position of a ground robot fusing ego-motion with UWB for a single-tag multi-anchor setup.
- Reductions to separate the influence of the bias from the model equations to reduce the number of operations and reduce the computational load.
- The algorithm runs in real time and has been used to control a robot in the lab.
2. Materials and Methods
2.1. Nomenclature
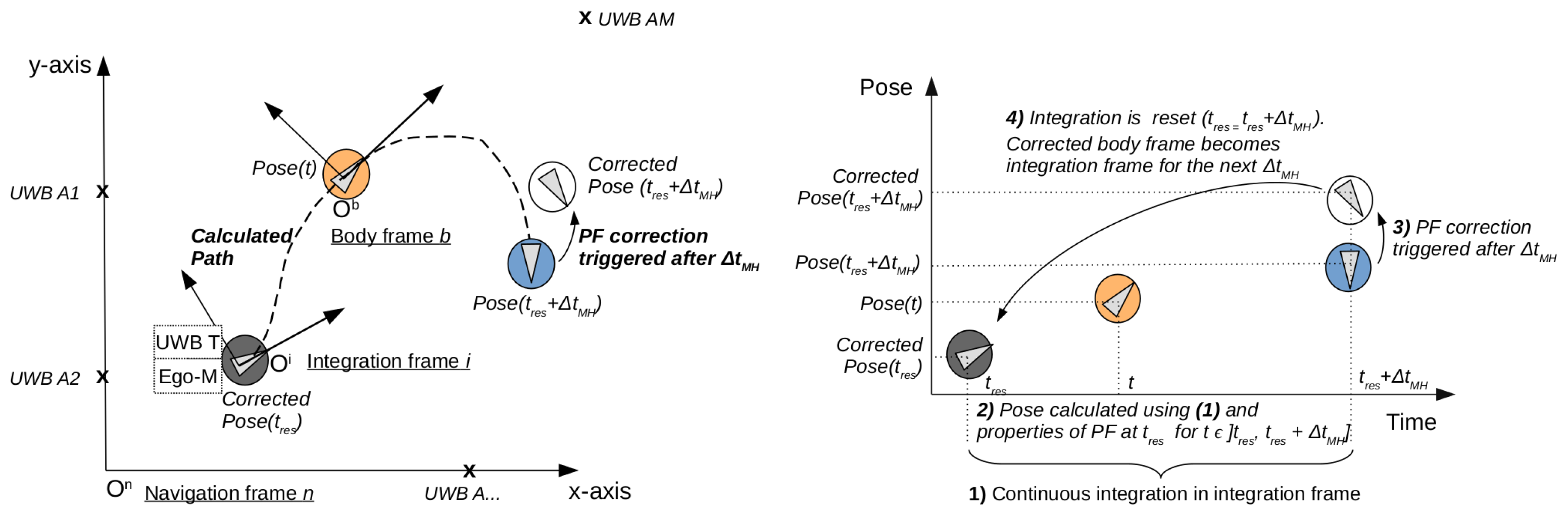
2.2. Algorithm Overview
2.3. The Particle Filter
2.3.1. (A) Prediction
2.3.2. (B) Initialization
2.3.3. (C) Diffusion
2.3.4. (D) Transformation
2.3.5. (E) Correction
2.3.6. (F) Sampling and Integration Reset
2.4. Additional Points
2.4.1. Particle Depletion
2.4.2. Operation Reduction
2.5. Limitations
2.5.1. Moving Horizon Duration Trade-Off
2.5.2. Gyroscope Calibration
2.5.3. Unobservability of Orientation
2.5.4. UWB Position vs. Ranges
3. Results
3.1. Experimental Setup
- Modalities: In the first experiment, the different modalities were tested, and Table 5 lists the modalities used. The experiment was conducted in the LOS with the first four anchors. The next two experiments were performed with the better performing modality.
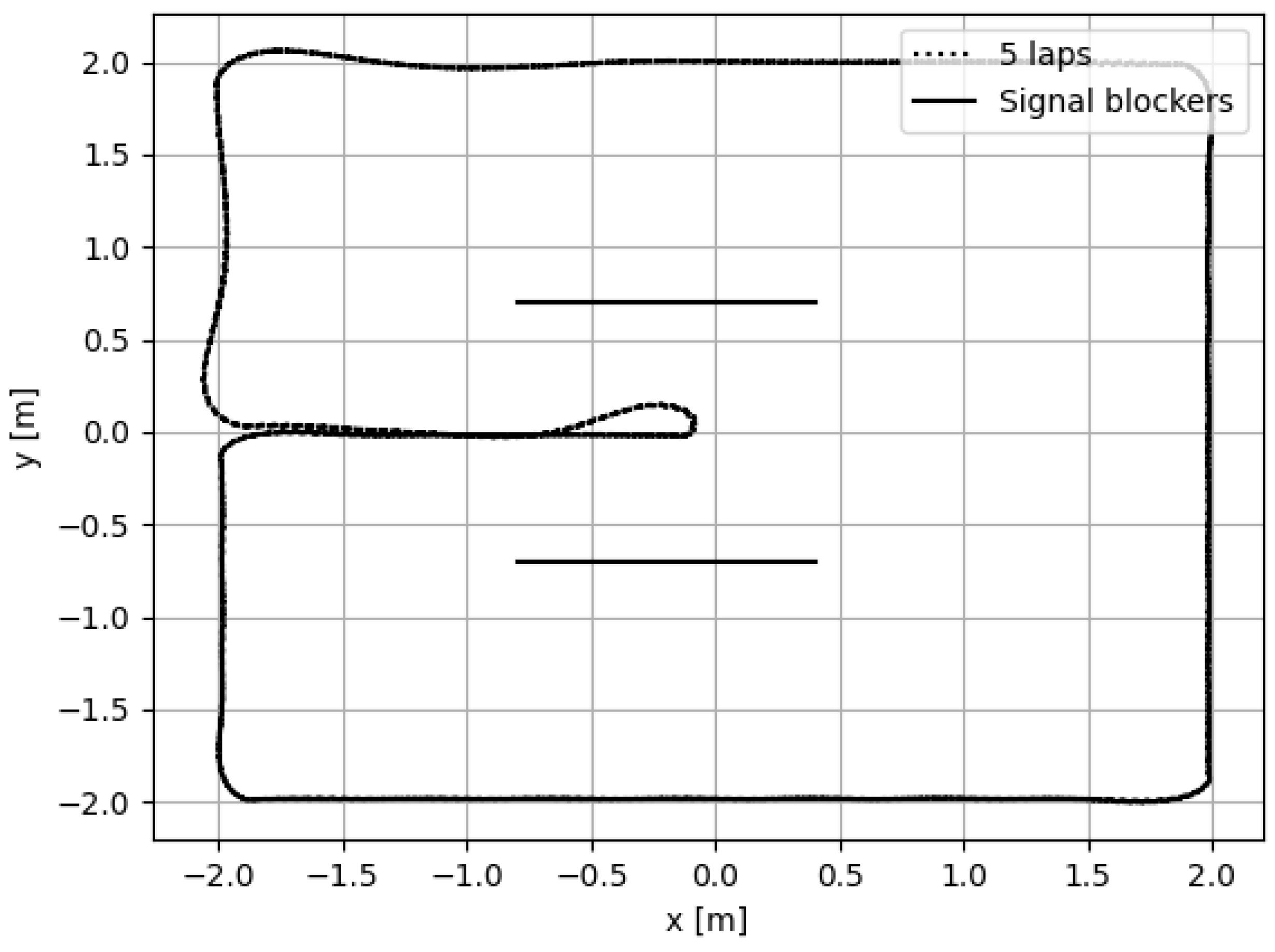
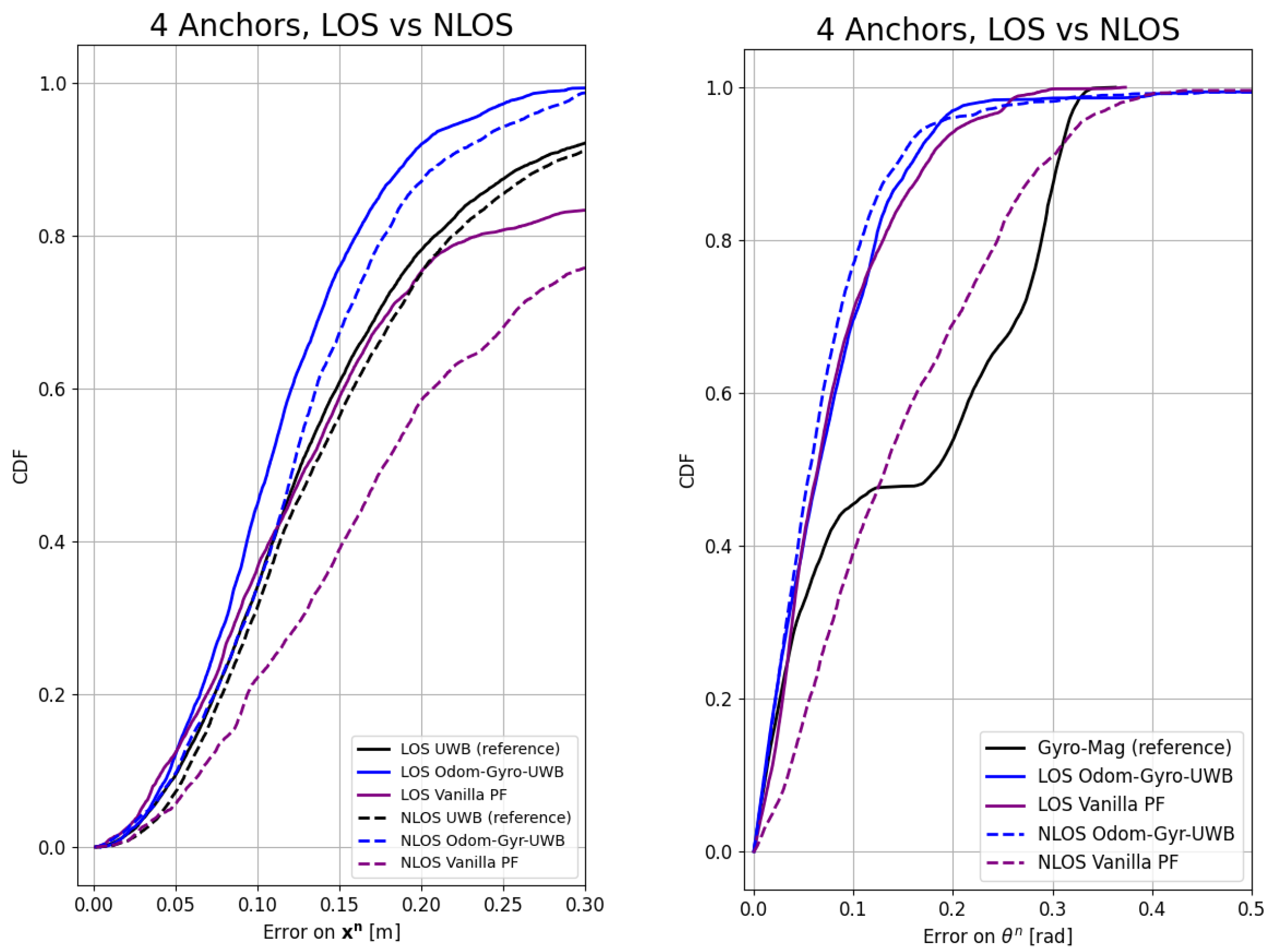
- Influence of NLOS: In the second experiment, the influence of NLOS was tested. For this, the first experiment was repeated, but two walls were placed, which occluded the LOS for different anchors on the trajectory.
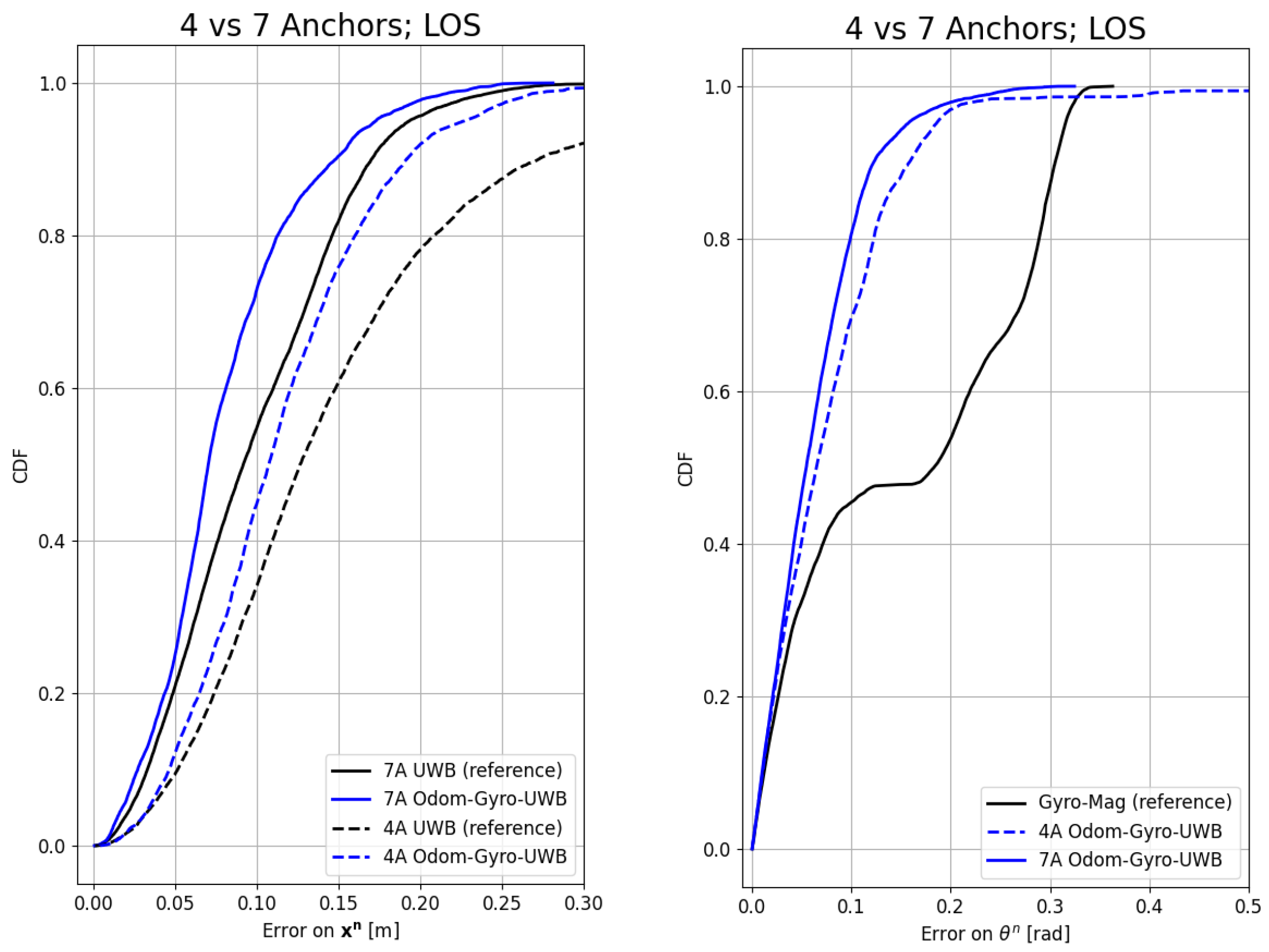
- Influence of the number of anchors: In the last experiment, the influence of the number of anchors was tested, by redoing the first experiment, but with seven anchors instead of four.
3.2. Offline Tracking
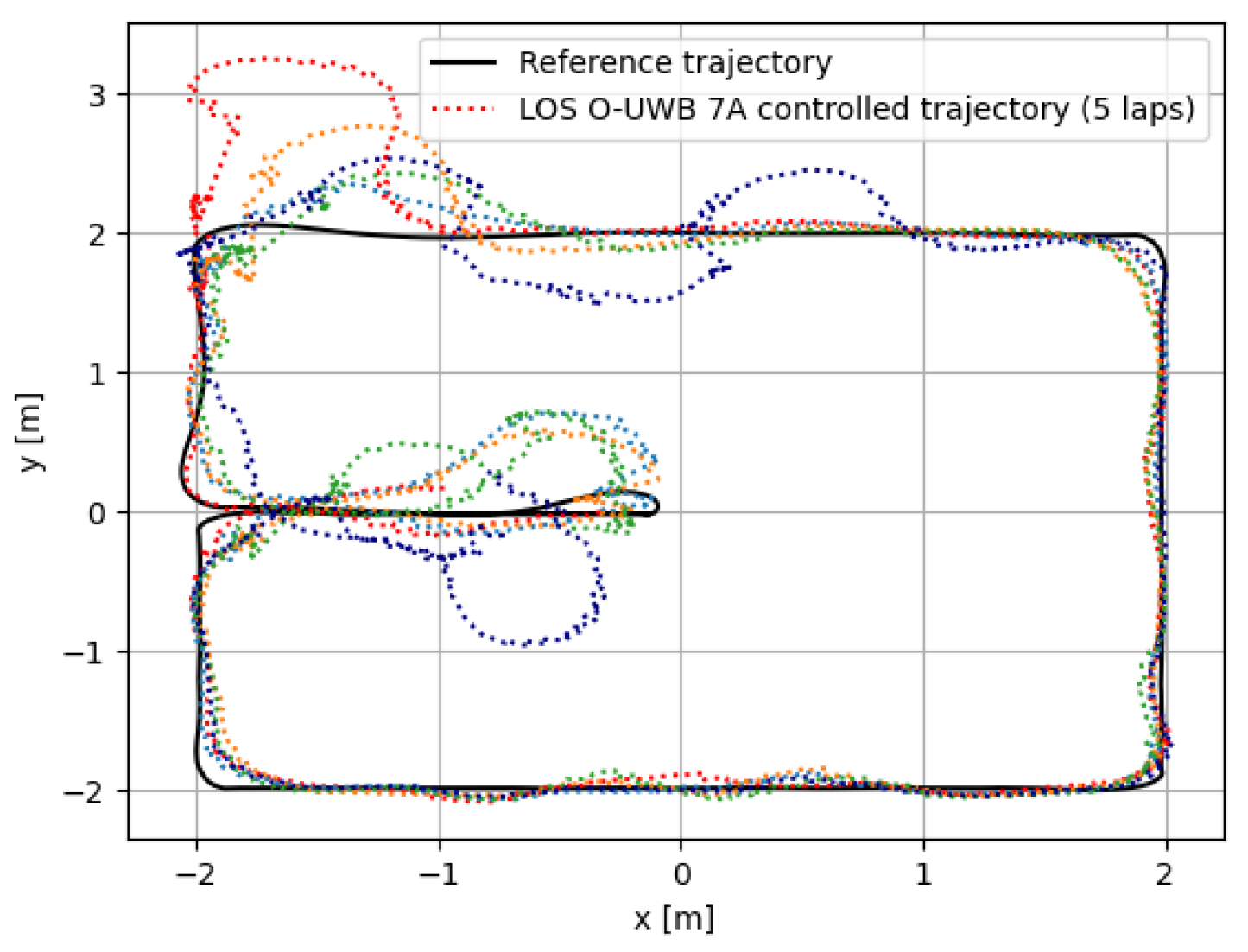
3.3. Real-Time Control Experiment
4. Discussion
4.1. Offline Tracking Performance
4.1.1. Modalities
4.1.2. LOS Condition
4.1.3. Number of Anchors
4.2. Online Pose Control
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Wang, S.; Xie, Y.; Xiong, T.; Wu, M. A Review of Sensing Technologies for Indoor Autonomous Mobile Robots. Sensors 2024, 24, 1222. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Cheng, C.; Zhang, Y.; Li, X.; Sun, L. A Neural Network-Based Navigation Approach for Autonomous Mobile Robot Systems. Appl. Sci. 2022, 12, 7796. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Z.; Zhao, R.; Lu, J.; Wang, Y.; Jia, P. Review on UWB-based and multi-sensor fusion positioning algorithms in indoor environment. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; Volume 5, pp. 1594–1598. [Google Scholar] [CrossRef]
- Elsanhoury, M.; Mäkelä, P.; Koljonen, J.; Välisuo, P.; Shamsuzzoha, A.; Mantere, T.; Elmusrati, M.; Kuusniemi, H. Precision Positioning for Smart Logistics Using Ultra-Wideband Technology-Based Indoor Navigation: A Review. IEEE Access 2022, 10, 44413–44445. [Google Scholar] [CrossRef]
- Van Herbruggen, B.; Gerwen, J.V.V.; Luchie, S.; Durodié, Y.; Vanderborght, B.; Aernouts, M.; Munteanu, A.; Fontaine, J.; Poorter, E.D. Selecting and Combining UWB Localization Algorithms: Insights and Recommendations from a Multi-Metric Benchmark. IEEE Access 2024, 12, 16881–16901. [Google Scholar] [CrossRef]
- Fontaine, J.; Ridolfi, M.; Van Herbruggen, B.; Shahid, A.; De Poorter, E. Edge inference for UWB ranging error correction using autoencoders. IEEE Access 2020, 8, 139143–139155. [Google Scholar] [CrossRef]
- Cao, Y.; Yang, C.; Li, R.; Knoll, A.; Beltrame, G. Accurate position tracking with a single UWB anchor. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 2344–2350. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, G.; Zhu, D.; Di, E. Adaptive Multi-Sensor Data Fusion Positioning Algorithm Based On Long Short Term Memory Neural Networks. In Proceedings of the 2020 IEEE 20th International Conference on Communication Technology (ICCT), Nanning, China, 28–31 October 2020; pp. 566–570. [Google Scholar] [CrossRef]
- Li, Y.; Ying, Y.; Dong, W. A Computationally Efficient Moving Horizon Estimation for Flying Robots’ Localization Regarding a Single Anchor. In Proceedings of the 2021 IEEE International Conference on Robotics and Biomimetics (ROBIO), Sanya, China, 27–31 December 2021; pp. 675–680. [Google Scholar] [CrossRef]
- Pfeiffer, S.; Wagter, C.D.; Croon, G.C.D. A Computationally Efficient Moving Horizon Estimator for Ultra-Wideband Localization on Small Quadrotors. IEEE Robot. Autom. Lett. 2021, 6, 6725–6732. [Google Scholar] [CrossRef]
- Petukhov, N.; Zamolodchikov, V.; Zakharova, E.; Shamina, A. Synthesis and Comparative Analysis of Characteristics of Complex Kalman Filter and Particle Filter in Two-dimensional Local Navigation System. In Proceedings of the 2019 Ural Symposium on Biomedical Engineering, Radioelectronics and Information Technology (USBEREIT), Yekaterinburg, Russia, 25–26 April 2019; pp. 225–228. [Google Scholar] [CrossRef]
- Nguyen, T.M.; Hanif Zaini, A.; Wang, C.; Guo, K.; Xie, L. Robust Target-Relative Localization with Ultra-Wideband Ranging and Communication. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 2312–2319. [Google Scholar] [CrossRef]
- Yu, W.; Li, J.; Yuan, J.; Ji, X. Indoor Mobile robot positioning based on UWB And Low Cost IMU. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; Volume 5, pp. 1239–1246. [Google Scholar] [CrossRef]
- Lisus, D.; Cossette, C.C.; Shalaby, M.; Forbes, J.R. Heading Estimation Using Ultra-Wideband Received Signal Strength and Gaussian Processes. IEEE Robot. Autom. Lett. 2021, 6, 8387–8393. [Google Scholar] [CrossRef]
- Mai, V.; Kamel, M.; Krebs, M.; Schaffner, A.; Meier, D.; Paull, L.; Siegwart, R. Local Positioning System Using UWB Range Measurements for an Unmanned Blimp. IEEE Robot. Autom. Lett. 2018, 3, 2971–2978. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.M.; Xie, L. Range-Focused Fusion of Camera-IMU-UWB for Accurate and Drift-Reduced Localization. IEEE Robot. Autom. Lett. 2021, 6, 1678–1685. [Google Scholar] [CrossRef]
- Hausman, K.; Weiss, S.; Brockers, R.; Matthies, L.; Sukhatme, G.S. Self-calibrating multi-sensor fusion with probabilistic measurement validation for seamless sensor switching on a UAV. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4289–4296. [Google Scholar] [CrossRef]
- Sadruddin, H.; Mahmoud, A.; Atia, M. An Indoor Navigation System using Stereo Vision, IMU and UWB Sensor Fusion. In Proceedings of the 2019 IEEE SENSORS, Montreal, QC, Canada, 27–30 October 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Nguyen, T.M.; Cao, M.; Yuan, S.; Lyu, Y.; Nguyen, T.H.; Xie, L. LIRO: Tightly Coupled Lidar-Inertia-Ranging Odometry. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 14484–14490. [Google Scholar] [CrossRef]
- Zhen, W.; Scherer, S. Estimating the Localizability in Tunnel-like Environments using LiDAR and UWB. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 4903–4908. [Google Scholar] [CrossRef]
- Kok, M.; Hol, J.D.; Schön, T.B. Using Inertial Sensors for Position and Orientation Estimation. Found. Trends Signal Process. 2017, 11, 1–153. [Google Scholar] [CrossRef]
- Magnago, V.; Corbalán, P.; Picco, G.P.; Palopoli, L.; Fontanelli, D. Robot Localization via Odometry-assisted Ultra-wideband Ranging with Stochastic Guarantees. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 1607–1613. [Google Scholar] [CrossRef]
- Gholami, M.; Ström, E.; Sottile, F.; Dardari, D.; Conti, A.; Gezici, S.; Rydström, M.; Spirito, M. Static positioning using UWB range measurements. In Proceedings of the 2010 Future Network & Mobile Summit, Florence, Italy, 16–18 June 2010; pp. 1–10. [Google Scholar]
- Van Herbruggen, B.; Jooris, B.; Rossey, J.; Ridolfi, M.; Macoir, N.; Van den Brande, Q.; Lemey, S.; De Poorter, E. Wi-PoS: A low-cost, open source ultra-wideband (UWB) hardware platform with long range sub-GHz backbone. Sensors 2019, 19, 16. [Google Scholar] [CrossRef] [PubMed]
- Avzayesh, M.; Abdel-Hafez, M.; AlShabi, M.; Gadsden, S. The smooth variable structure filter: A comprehensive review. Digit. Signal Process. 2021, 110, 102912. [Google Scholar] [CrossRef]



| Reference (Year) | Method | Single Tag | Orientation without Magnetometer | No Additional Calibration |
|---|---|---|---|---|
| [7] (2020) | Extended Kalman filter | ✓ | ✓ | |
| [8] (2020) | Long Short-Term Memory neural network | ✓ | ✓ | |
| [9] (2021) | Gradient Descent Optimizer | ✓ | ✓ | |
| [10] (2021) | Gradient Descent Optimizer | ✓ | ✓ | |
| [11] (2019) | Particle filter | ✓ | ✓ | |
| [12] (2018) | Multi-tag reference frame | ✓ | ✓ | |
| [13] (2021) | Extended Kalman filter | ✓ | ✓ | |
| [14] (2021) | Antenna shape with pre-trained Gaussian process model | ✓ | ✓ | |
| [15] (2018) | Multi-tag reference frame | ✓ | ✓ | |
| ours | Moving horizon particle filter | ✓ | ✓ | ✓ |
| Notation | Description |
|---|---|
| , , | Position, velocity, and acceleration of the robot expressed in reference frame r for modality m. |
| Angular velocity of the robot. | |
| Rotation matrix from reference frame to . | |
| Angle around z-axis from the reference frame to in the planar case. | |
| Bias vector in case the gyroscope and/or accelerometer are used. | |
| Noise vector expressed in reference frame r for modality m. Assumed to be zero mean Gaussian. | |
| Variance of a zero mean Gaussian of a measured or derived variable v of modality m. | |
| Transformation matrix for variable v. | |
| Origin of a reference frame. | |
| t, , | The current time, the reset time, and the moving horizon duration, respectively. |
| Moving average of the variable v over a period | |
| equal to the moving horizon duration starting from the reset time | |
| . |
| Anchor ID | [m] | [m] | [m] |
|---|---|---|---|
| A1 | 3.86 | −5.31 | 0.44 |
| A2 | 3.98 | 5.42 | 2.86 |
| A3 | −3.99 | −5.29 | 2.65 |
| A4 | 3.86 | −5.31 | 2.66 |
| A5* | −4.05 | 5.45 | 0.41 |
| A6* | −3.99 | −5.29 | 0.44 |
| A7* | −4.05 | 5.45 | 2.62 |
| Sensor Model | |
|---|---|
| Accelerometer | InvenSense MPU-9250 from TDK InvenSense, San Jose, CA, USA |
| Gyroscope | InvenSense MPU9250 from TDK InvenSense, San Jose, CA, USA |
| Magnetometer | InvenSense MPU9250 from TDK InvenSense, San Jose, CA, USA |
| Wheel encoders | DYNAMIXEL XL430-W250, from ROBOTIS Co., Ltd., Seoul, Republic of Korea |
| UWB | Wi-Pos [24] (DW1000 from Qorvo, Greensboro, NC, USA) |
| Ego-Motion Modality Used in the Particle Filter | |
| Odom–UWB (in red) | Only odometry is used for the ego-motion prediction. Correction is performed with UWB. |
| Odom–Gyro–UWB (in blue) | Odometry is used for the translation in the body frame, while the gyroscope provides the rotational motion during the prediction. Correction is performed with UWB. |
| IMU–UWB (in green) | Accelerometers are used for the translation in the body frame, while the gyroscope provides the rotational motion during the prediction. Correction is performed with UWB. (For the IMU, 1000 particles were used instead of 100.) |
| Reference Modality to Compare with | |
| UWB (in black) | The UWB pose is directly calculated from the ranges. It does not provide orientation. |
| Gyro–Mag (in black) | Gyroscope corrected with a magnetometer for orientation. Widely used in most applications today. |
| Vanilla PF (in purple) | A vanilla particle filter implementation using the odometry and gyroscope as sources similar to the Odom–Gyro–UWB modality. However, this particle filter does not use the moving horizon, as is proposed in this paper. |
| Time Parameters (SF = Sampling Frequencies) | |
| 1 s | |
| UWB SF | 5 Hz |
| IMU SF | 50 Hz |
| Odom SF | 25 Hz |
| UWB Uncertainty Parameters (#A = # Anchors) | |
| 7 Anchors LOS | 0.25 m |
| 4 Anchors LOS | 0.40 m |
| 4 Anchors NLOS | 0.45 m |
| Ego-Motion Uncertainty Parameters | |
| 0.2 | |
| 1. | |
| 0.5 | |
| 0.2 | |
| Error on the Orientation in Rad | ||||||
| Modalities Analysis | ||||||
| Modality | # of Anchors | NLOS | P50 | P90 | RMSE | Max Error |
| Odom–Gyro–UWB | 4 | 0.06 | 0.16 | 0.12 | 1.0 | |
| Odom–UWB | 4 | 0.11 | 0.38 | 0.42 | 2.9 | |
| IMU–UWB | 4 | 0.43 | 0.75 | 0.49 | 0.95 | |
| Vanilla PF | 4 | 0.06 | 0.17 | 0.09 | 0.37 | |
| Gyro–Mag | NA | NA | 0.18 | 0.31 | 0.20 | 0.36 |
| Only gyroscope | NA | NA | 1.5 | 2.7 | 1.7 | 3.14 |
| Only odometry | NA | NA | 1.3 | 2.5 | 1.5 | 3.14 |
| Error on the Orientation in Rad | ||||||
| LOS vs. NLOS | ||||||
| Modality | # of Anchors | NLOS | P50 | P90 | RMSE | Max Error |
| Odom–Gyro–UWB | 4 | 0.06 | 0.16 | 0.12 | 1.0 | |
| Odom–Gyro–UWB | 4 | ✓ | 0.06 | 0.14 | 0.11 | 0.88 |
| Vanilla PF | 4 | 0.17 | 0.09 | 0.37 | ||
| Vanilla PF | 4 | ✓ | 0.13 | 0.29 | 0.14 | 3.05 |
| Gyro–Mag | NA | NA | 0.18 | 0.31 | 0.20 | 0.36 |
| Error on the Orientation in Rad | ||||||
| Number of Anchors | ||||||
| Modality | # of Anchors | NLOS | P50 | P90 | RMSE | Max Error |
| Odom–Gyro–UWB | 4 | 0.06 | 0.16 | 0.12 | 1.0 | |
| Odom–Gyro–UWB | 7 | 0.05 | 0.12 | 0.08 | 0.32 | |
| Gyro–Mag | NA | NA | 0.18 | 0.31 | 0.20 | 0.36 |
| Error on the Position in m | ||||||
| Modalities’ Analysis | ||||||
| Modality | # of Anchors | NLOS | P50 | P90 | RMSE | Max Error |
| Odom–Gyro–UWB | 4 | 0.11 | 0.19 | 0.13 | 0.36 | |
| Odom–UWB | 4 | 0.14 | 0.31 | 0.21 | 1.1 | |
| IMU–UWB | 4 | 0.20 | 0.41 | 0.27 | 1.0 | |
| Vanilla PF | 4 | 0.13 | 0.41 | 0.18 | 0.72 | |
| UWB | 4 | 0.13 | 0.27 | 0.18 | 0.71 | |
| Gyro–Mag–IMU | NA | NA | 22 × 103 | 45 × 103 | 27 × 103 | NA |
| Gyro–Mag–Odometry | NA | NA | 5.3 | 8.2 | 5.6 | NA |
| Error on the Position in m | ||||||
| LOS vs. NLOS | ||||||
| Modality | # of Anchors | NLOS | P50 | P90 | RMSE | Max Error |
| Odom–Gyro–UWB | 4 | 0.11 | 0.19 | 0.13 | 0.36 | |
| Odom–Gyro–UWB | 4 | ✓ | 0.14 | 0.21 | 0.14 | 0.37 |
| Vanilla PF | 4 | 0.13 | 0.41 | 0.18 | 0.72 | |
| Vanilla PF | 4 | ✓ | 0.18 | 0.52 | 0.23 | 0.79 |
| UWB | 4 | 0.13 | 0.27 | 0.18 | 0.71 | |
| UWB | 4 | ✓ | 0.13 | 0.29 | 0.18 | 0.65 |
| Error on the Position in m | ||||||
| Number of Anchors | ||||||
| Modality | # of Anchors | NLOS | P50 | P90 | RMSE | Max Error |
| Odom–Gyro–UWB | 4 | 0.11 | 0.19 | 0.13 | 0.36 | |
| Odom–Gyro–UWB | 7 | 0.07 | 0.15 | 0.09 | 0.28 | |
| UWB | 4 | 0.13 | 0.27 | 0.18 | 0.71 | |
| UWB | 7 | 0.09 | 0.17 | 0.11 | 0.39 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Durodié, Y.; Decoster, T.; Van Herbruggen, B.; Vanhie-Van Gerwen, J.; De Poorter, E.; Munteanu, A.; Vanderborght, B. A UWB-Ego-Motion Particle Filter for Indoor Pose Estimation of a Ground Robot Using a Moving Horizon Hypothesis. Sensors 2024, 24, 2164. https://doi.org/10.3390/s24072164
Durodié Y, Decoster T, Van Herbruggen B, Vanhie-Van Gerwen J, De Poorter E, Munteanu A, Vanderborght B. A UWB-Ego-Motion Particle Filter for Indoor Pose Estimation of a Ground Robot Using a Moving Horizon Hypothesis. Sensors. 2024; 24(7):2164. https://doi.org/10.3390/s24072164
Chicago/Turabian StyleDurodié, Yuri, Thomas Decoster, Ben Van Herbruggen, Jono Vanhie-Van Gerwen, Eli De Poorter, Adrian Munteanu, and Bram Vanderborght. 2024. "A UWB-Ego-Motion Particle Filter for Indoor Pose Estimation of a Ground Robot Using a Moving Horizon Hypothesis" Sensors 24, no. 7: 2164. https://doi.org/10.3390/s24072164
APA StyleDurodié, Y., Decoster, T., Van Herbruggen, B., Vanhie-Van Gerwen, J., De Poorter, E., Munteanu, A., & Vanderborght, B. (2024). A UWB-Ego-Motion Particle Filter for Indoor Pose Estimation of a Ground Robot Using a Moving Horizon Hypothesis. Sensors, 24(7), 2164. https://doi.org/10.3390/s24072164









