An Improved OMP Algorithm for Enhancing the Anti-Interference Performance of Array Antennas
Abstract
1. Introduction
2. The Principle of CS
2.1. The Sampling Process of Compressed Sensing
2.2. Compressed Sensing Signal Reconstruction Algorithm
2.3. Orthogonal Matching Pursuit (OMP)
| Algorithm 1: Orthogonal matching pursuit (OMP) |
| Input: |
| Output: |
| 1 Initialization , |
| 2 Normalize all columns of to unit L2 norm; |
| 3 for k = 1,2, …, K do |
| 4 Step 1: |
| 5 Step 2: |
| 6 Step 3: |
| 7 Step 4: |
| 8 Step 5: |
| 9 end |
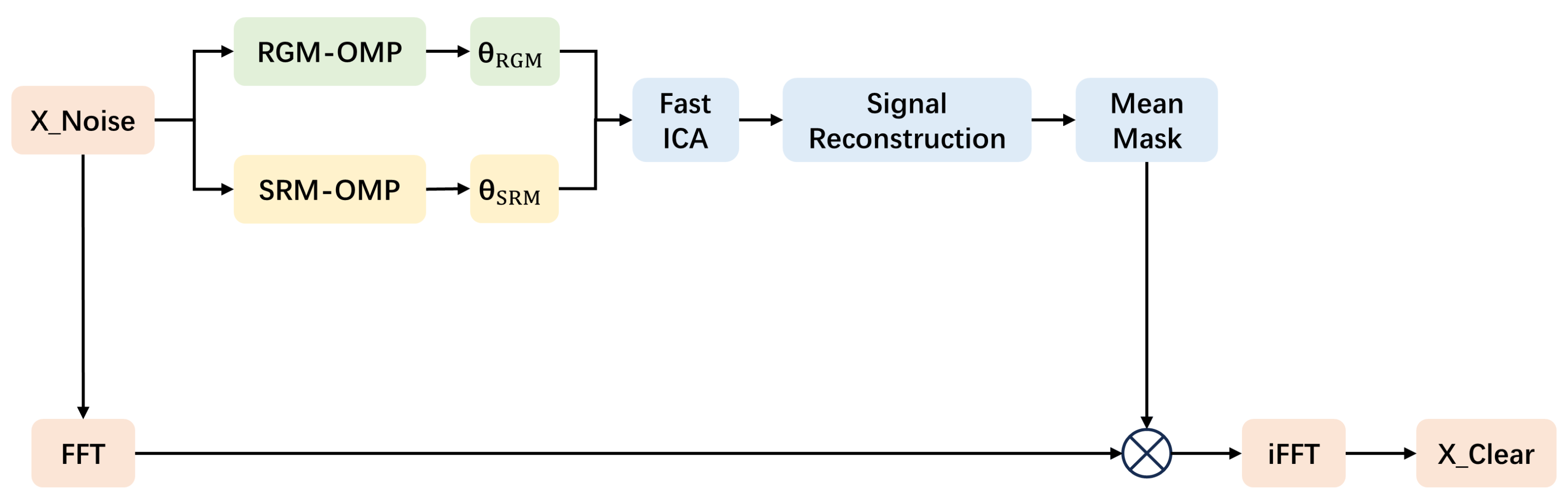
3. Dual-Threshold Mask OMP Based on ICA
3.1. Principle of ICA
3.2. DTM_OMP_ICA
| Algorithm 2: Dual-threshold mask OMP based on ICA (DTM_OMP_ICA) |
| Input: |
| Output: |
| 1 Initialization ; |
| 2 do |
| 3 Step 1: ; |
| 4 Step 2: ; |
| 5 Step 3: ; |
| 6 path1 do |
| 7 Step 1: ; |
| 8 Step 2: ; ; |
| 9 Step 3: ; |
| 10 end path1 |
| 11 path2 do |
| 12 Step 1: ; |
| 13 Step 2: ; ; |
| 14 Step 3: ; |
| 15 end path2 |
| 16 Step 4: ; |
| 17 Step 5: ; |
| 18 Step 6: ; |
| 19 Step 7: ; |
| 20 Step 8: ; |
| 21 end |
4. Experiments and Results
4.1. Multi-Frequency Signals with Noise Experiment
4.1.1. Data
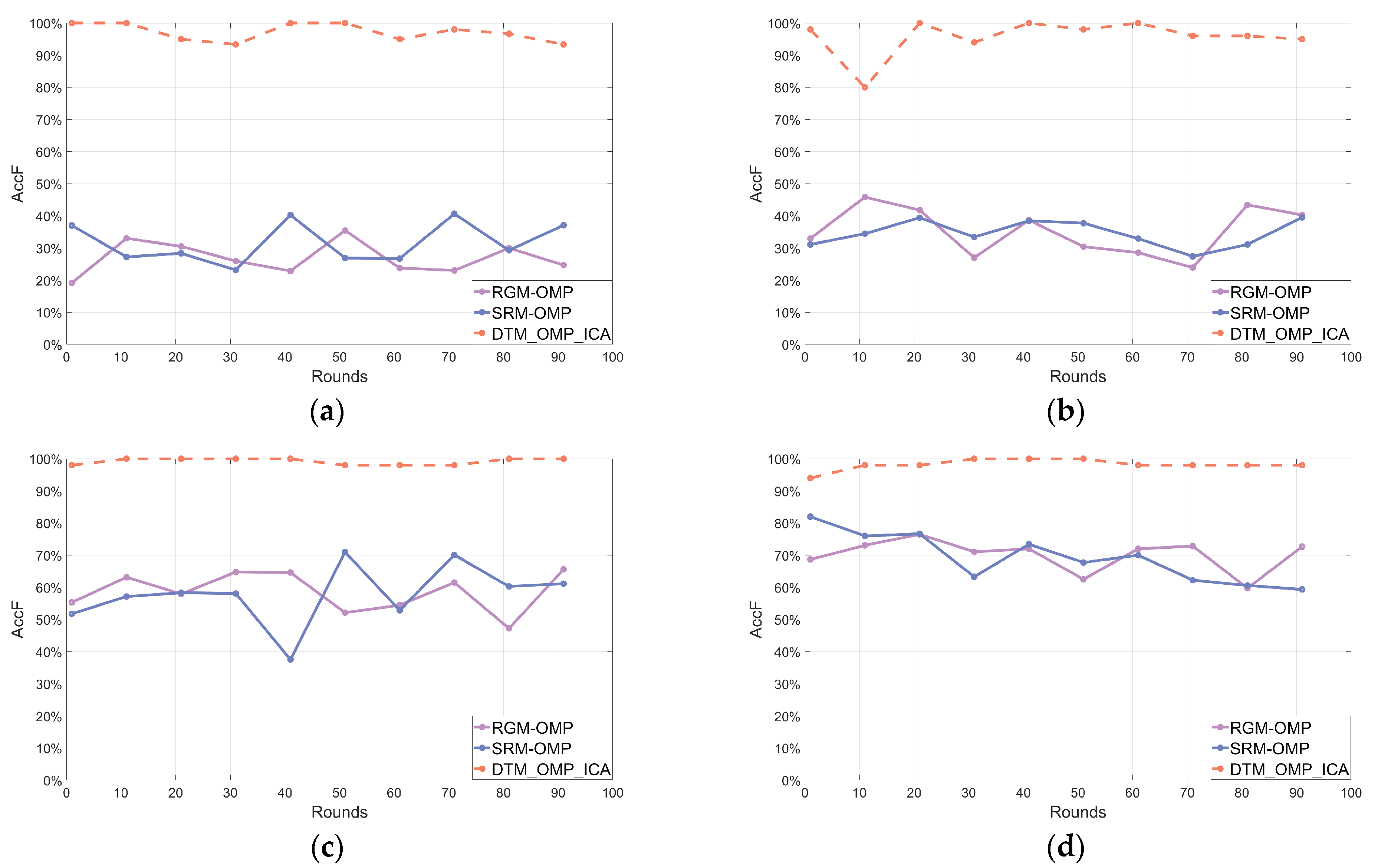
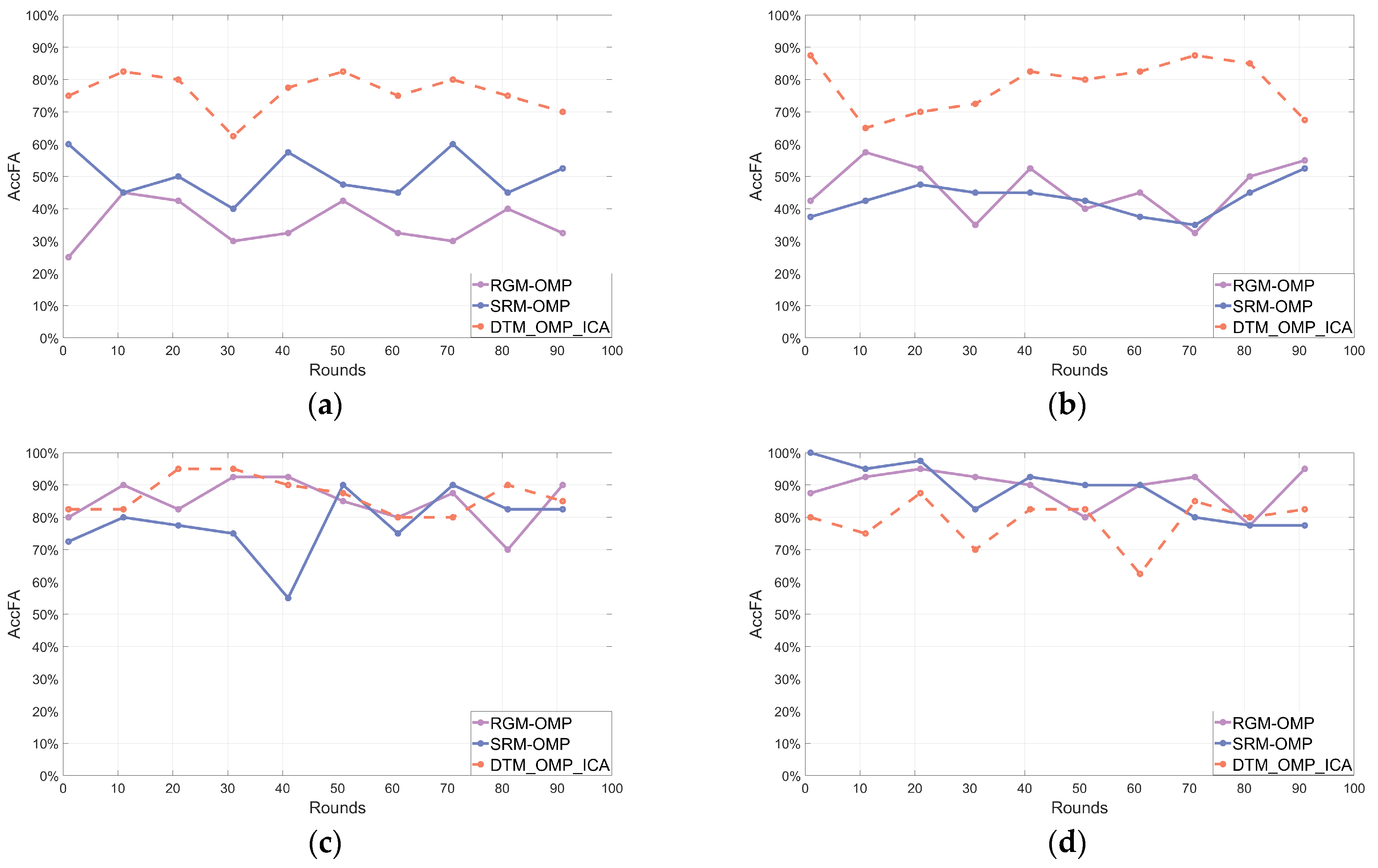
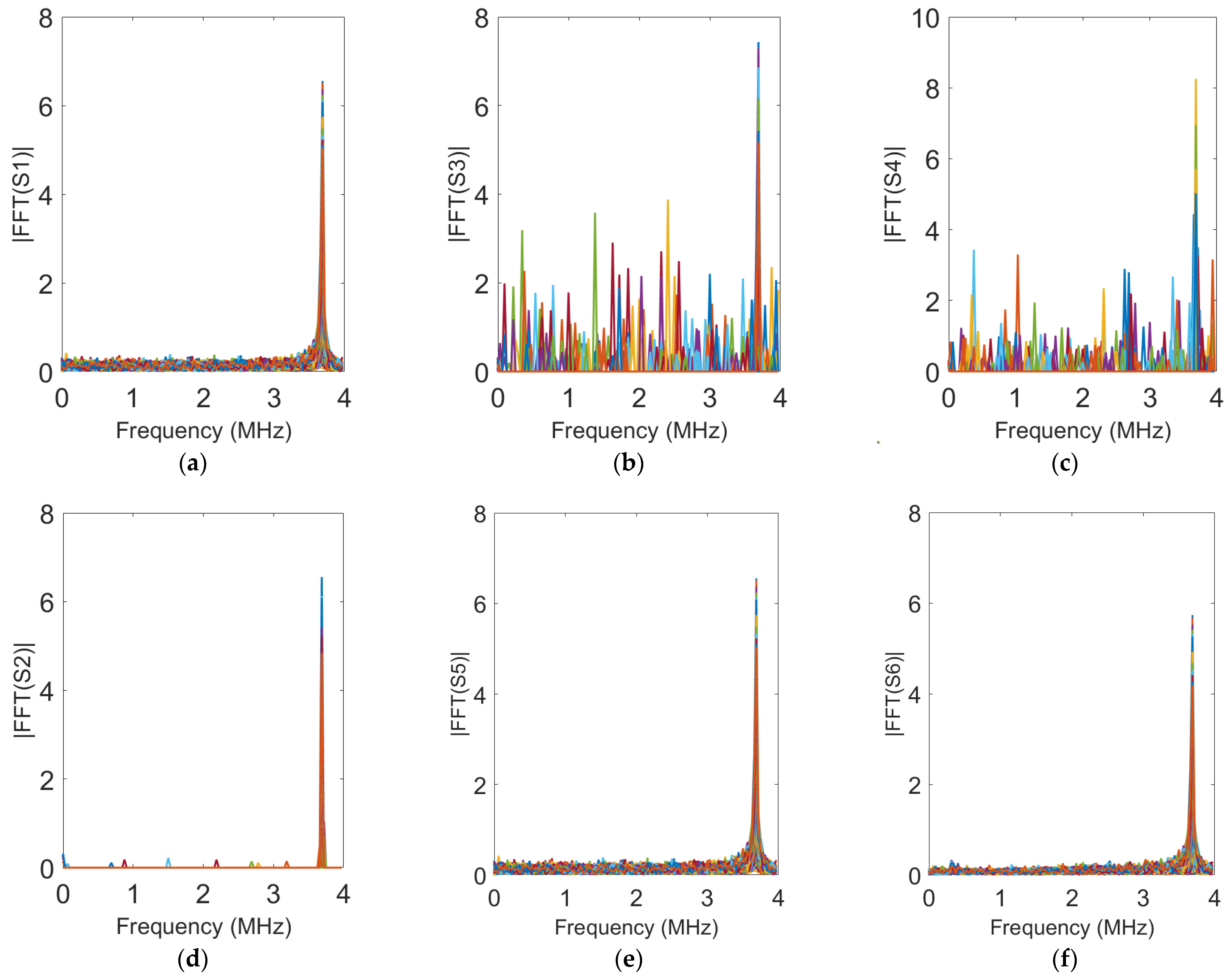
4.1.2. Results of Multi-Frequency Signal with Noise
Spectral Analysis of Reconstructed Signals
Evaluations of Reconstructed Signals
- (i)
- Evaluation of Signal Reconstruction AccuracyThis paper employs statistical parameters ((21)–(23)) to perform algorithm stability analysis.
- A.
- The accuracy of reconstructed signal frequencies, denoted as :
where represents the number of times the correct frequencies appear in the reconstructed signal and is the total number of frequency components in the reconstructed signal.- B.
- The error rate of reconstructed signal frequencies, denoted as :
where represents the number of times incorrect frequencies appear in the reconstructed signal.- C.
- The accuracy of both the frequency and amplitude of the reconstructed signal, denoted as :
- (ii)
- Evaluation of Signal Reconstruction Stability
- (iii)
- Time Consumption
4.2. Array Antenna Signal Denoising Experiment
4.2.1. Data
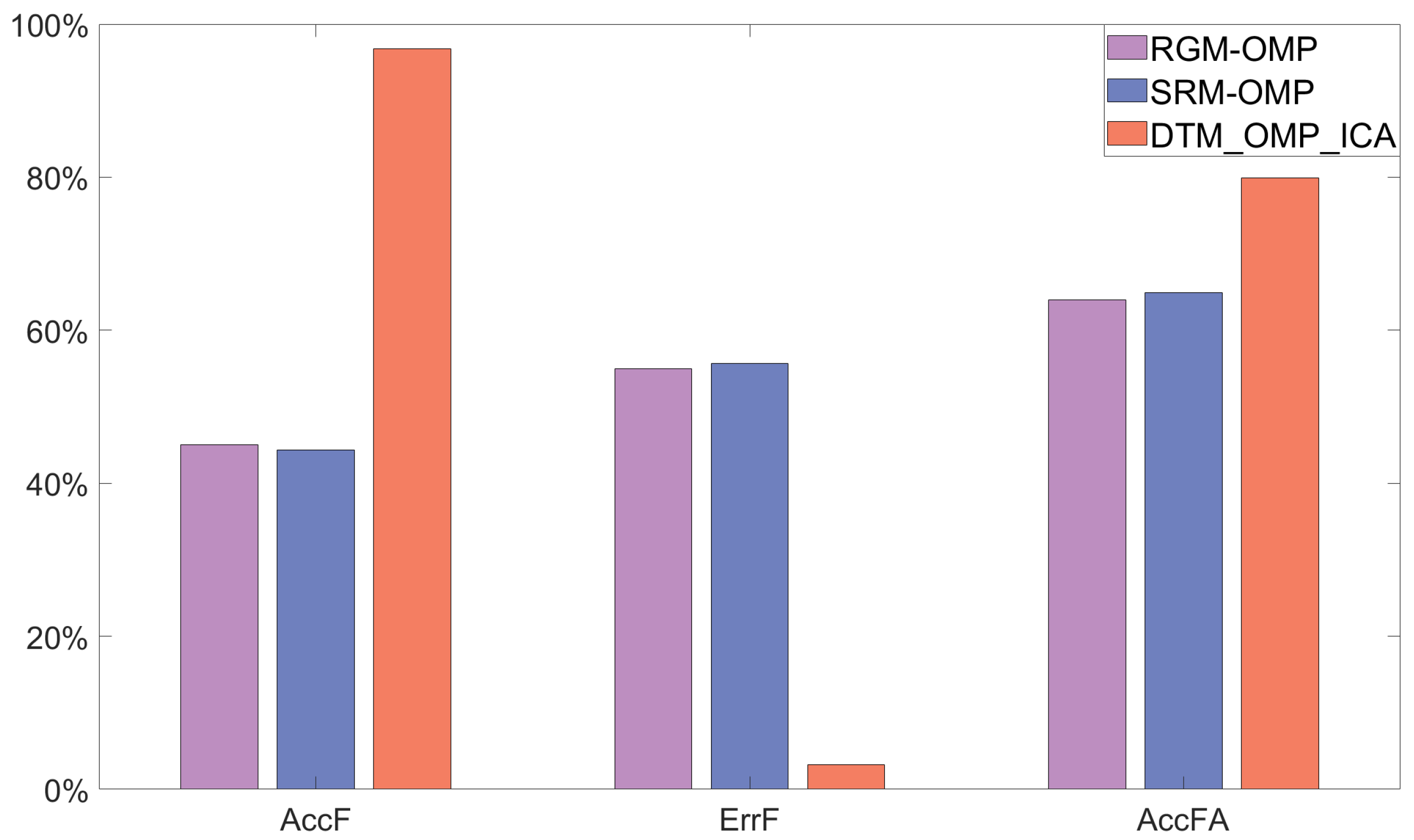
4.2.2. Results of Simulated Radar Signal Processing
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ausherman, D.A.; Kozma, A.; Walker, J.L.; Jones, H.M.; Poggio, E.C. Developments in radar imaging. IEEE Trans. Aerosp. Electron. Syst. 1984, AES-20, 363–400. [Google Scholar]
- Bahl, P.; Padmanabhan, V.N. RADAR: An in-building RF-based user location and tracking system. In Proceedings of the IEEE INFOCOM 2000. Conference on Computer Communications. Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies (Cat. No. 00CH37064), Tel Aviv, Israel, 26–30 March 2000; Volume 2, pp. 775–784. [Google Scholar]
- Griffiths, H.D.; Baker, C.J. Passive coherent location radar systems. Part 1: Performance prediction. IEE Proc.-Radar Sonar Navig. 2005, 152, 153–159. [Google Scholar] [CrossRef]
- Chen, D.; Chen, B.; Qin, G. Angle estimation using ESPRIT in MIMO radar. Electron. Lett. 2008, 44, 1. [Google Scholar]
- Chen, J.; Hong, G.; Su, W. Angle estimation using ESPRIT without pairing in MIMO radar. Electron. Lett. 2008, 44, 1422–1423. [Google Scholar]
- Stove, A.G. Linear FMCW radar techniques IEE Proceedings F (Radar and Signal Processing). IET Digit. Libr. 1992, 139, 343–350. [Google Scholar]
- Li, Y.A.; Hung, M.H.; Huang, S.J.; Lee, J. A fully integrated 77 GHz FMCW radar system in 65 nm CMOS. In Proceedings of the 2010 IEEE International Solid-State Circuits Conference-(ISSCC), San Francisco, CA, USA, 7–11 February 2010; pp. 216–217. [Google Scholar]
- Brooker, G.M. Understanding millimetre wave FMCW radars. In Proceedings of the 1st International Conference on Sensing Technology, Palmerston North, New Zealand, 21–23 November 2005. [Google Scholar]
- Reindl, L.; Ruppel, C.C.; Berek, S.; Knauer, U.; Vossiek, M.; Heide, P.; Oréans, L. Design, fabrication, and application of precise SAW delay lines used in an FMCW radar system. IEEE Trans. Microw. Theory Tech. 2001, 49, 787–794. [Google Scholar] [CrossRef]
- Piper, S.O. Receiver frequency resolution for range resolution in homodyne FMCW radar. In Proceedings of the Conference Proceedings National Telesystems Conference 1993, Atlanta, GA, USA, 16–17 June 1993; pp. 169–173. [Google Scholar]
- Oppenheim, A.V.; Schafer, R.W.; Buck, J.R. Discrete-Time Signal Processing, 2nd ed.; Prentice Hall: Upper On River City, NJ, USA, 1999. [Google Scholar]
- Parks, T.W.; Burrus, C.S. Digital Filter Design; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Hayes, M.H. Statistical Digital Signal Processing and Modeling; John Wiley & Sons: Hoboken, NJ, USA, 1982. [Google Scholar]
- Candès, E.J. Compressive sampling. In Proceedings of the International Congress of Mathematicians, Madrid, Spain, 22–30 August 2006; pp. 1433–1452. [Google Scholar]
- Candès, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Ex act signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J. Signal recovery from random projections. In Proceedings of the SPIE 5674, Computational Imaging III, San Jose, CA, USA, 11 March 2005; pp. 56–74. [Google Scholar]
- Donoho, D.L.; Tsaig, Y. Extensions of compressed sensing. Signal Process. 2006, 86, 533–548. [Google Scholar]
- Schwartz, J.; Steinberg, B. Ultrasparse, ultrawide band arrays. IEEE Trans. Ultrason. Ferro Electr. Freq. Control. 1998, 45, 376–393. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Zhou, M.; Ren, A.; Tian, Z. Remote monitoring of human vital signs based on 77-GHz mm-wave FMCW radar. Sensors 2020, 20, 2999. [Google Scholar] [CrossRef]
- Wang, G.; Gu, C.; Inoue, T.; Li, C. A hybrid FMCW-interferometry radar for indoor precise positioning and versatile life activity monitoring. IEEE Trans. Microw. Theory Tech. 2014, 62, 2812–2822. [Google Scholar] [CrossRef]
- Herman, M.A.; Strohmer, T. High-resolution radar via compressed sensing. IEEE Trans. Signal Process. 2009, 57, 2275–2284. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Duarte-Carvajalino, J.M.; Sapiro, G. Learning to sense sparse signals: Simultaneous sensing matrix and sparsifying dictionary optimization. IEEE Trans. Image Process. 2009, 18, 1395–1408. [Google Scholar] [CrossRef] [PubMed]
- Erbe, C.; Reichmuth, C.; Cunningham, K.; Lucke, K.; Dooling, R. Communication masking in marine mammals: A review and research strategy. Mar. Pollut. Bull. 2016, 103, 15–38. [Google Scholar] [CrossRef] [PubMed]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Zi, J.; Lv, D.; Liu, J.; Huang, X.; Yao, W.; Gao, M.; Xi, R.; Zhang, Y. Improved Swarm Intelligent Blind Source Separation Based on Signal Cross-Correlation. Sensors 2021, 22, 118. [Google Scholar] [CrossRef] [PubMed]
- Candes, E.J. The restricted isometry property and its implications for compressed sensing. Comptes Rendus. Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Baraniuk, R.; Davenport, M.; DeVore, R.; Wakin, M. A simple proof of the restricted isometry property for random matrices. Constr. Approx. 2008, 28, 253–263. [Google Scholar] [CrossRef]
- Rosen, J.B. The gradient projection method for nonlinear programming. Part I. Linear constraints. J. Soc. Ind. Appl. Math. 1960, 8, 181–217. [Google Scholar] [CrossRef]
- Rosen, J.B. The gradient projection method for nonlinear programming. Part II. Nonlinear constraints. J. Soc. Ind. Appl. Math. 1961, 9, 514–532. [Google Scholar] [CrossRef]
- Li, S.; Zhao, G.; Zhang, W.; Qiu, Q.; Sun, H. ISAR imaging by two-dimensional convex optimization-based compressive sensing. IEEE Sens. J. 2016, 16, 7088–7093. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, J.; Ren, S.; Li, Q. A reducing iteration orthogonal matching pursuit algorithm for compressive sensing. Tsinghua Sci. Technol. 2016, 21, 71–79. [Google Scholar] [CrossRef]
- Wu, D.; Zhu, W.P.; Swamy, M.N.S. The theory of compressive sensing matching pursuit considering time-domain noise with application to speech enhancement. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 682–696. [Google Scholar] [CrossRef]
- Do, T.T.; Gan, L.; Nguyen, N.; Tran, T.D. Sparsity adaptive matching pursuit algorithm for practical compressed sensing. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 581–587. [Google Scholar]
- Needell, D.; Vershynin, R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit. IEEE J. Sel. Top. Signal Process. 2010, 4, 310–316. [Google Scholar] [CrossRef]
- Needell, D.; Vershynin, R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit. Found. Comput. Math. 2009, 9, 317–334. [Google Scholar]
- Yang, G.; Zhang, Q.; Que, P.W. Matching-pursuit-based adaptive wavelet-packet atomic decomposition applied in ultrasonic inspection. Russ. J. Nondestruct. Test. 2007, 43, 62–68. [Google Scholar] [CrossRef]
- Li, S.; Fang, L. Signal denoising with random refined orthogonal matching pursuit. IEEE Trans. Instrum. Meas. 2011, 61, 26–34. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Near-optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Zhang, G.; Jiao, S.; Xu, X.; Wang, L. Compressed sensing and reconstruction with bernoulli matrices. In Proceedings of the 2010 IEEE International Conference on Information and Automation, Harbin, China, 20–23 June 2010; pp. 455–460. [Google Scholar]
- Stewart, G.W. The efficient generation of random orthogonal matrices with an application to condition estimators. SIAM J. Numer. Anal. 1980, 17, 403–409. [Google Scholar] [CrossRef]
- Haupt, J.; Bajwa, W.U.; Raz, G.; Nowak, R. Toeplitz compressed sensing matrices with applications to sparse channel estimation. IEEE Trans. Inf. Theory 2010, 56, 5862–5875. [Google Scholar] [CrossRef]
- Indyk, P. Sparse Recovery Using Sparse Random Matrices. In Proceedings of the LATIN 2010: Theoretical Informatics, 9th Latin American Symposium, Oaxaca, Mexico, 19–23 April 2010; p. 157. [Google Scholar]
- Meena, V.; Abhilash, G. Robust recovery algorithm for compressed sensing in the presence of noise. IET Signal Process. 2016, 10, 227–236. [Google Scholar] [CrossRef]
- Thomas, T.J.; Arun, A.; Sheeba, R.J. Compressed Sensing Recovery using Modified Newton Gradient Pursuit Algorithm and its Application to ECG with Denoising. In Proceedings of the 2018 International Conference on Signal Processing and Communications (SPCOM), Bangalore, India, 16–19 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 412–416. [Google Scholar]
- Li, L.; Fang, Y.; Liu, L.; Peng, H.; Kurths, J.; Yang, Y. Overview of compressed sensing: Sensing model, reconstruction algorithm, and its applications. Appl. Sci. 2020, 10, 5909. [Google Scholar] [CrossRef]
- Cheng, C.; Lin, D. Based on compressed sensing of orthogonal matching pursuit algorithm image recovery. J. Internet Things 2020, 2, 37–45. [Google Scholar] [CrossRef]
- Leys, C.; Ley, C.; Klein, O.; Bernard, P.; Licata, L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. J. Exp. Soc. Psychol. 2013, 49, 764–766. [Google Scholar] [CrossRef]
- Jha, S.K.; Yadava, R.D.S. Denoising by singular value decomposition and its application to electronic nose data processing. IEEE Sens. J. 2010, 11, 35–44. [Google Scholar] [CrossRef]
- Chang, S.G.; Yu, B.; Vetterli, M. Adaptive wavelet thresholding for image denoising and compression. IEEE Trans. Image Process. 2000, 9, 1532–1546. [Google Scholar] [CrossRef]




| Parameter | Value | Introduction |
|---|---|---|
| K | 8 | The sparsity of the signal in its orthogonal transformation basis (since the Fourier transform is two-sided, the sparsity is 4 × 2). |
| N | 1024 | The original number of sampled points in the signal. |
| t | 128 (unit: ms) | Duration of the Signal. |
| fs | 8000 (unit: Hz) | The signal’s sampling frequency based on the Nyquist sampling theorem will be used for subsequent frequency domain analysis of the reconstructed signal. |
| Round | Round 1 | Round 10 | Round 50 | Round 100 | |
|---|---|---|---|---|---|
| Algorithm | |||||
| RGM-OMP | 45.41 (ms) | 227.62 (ms) | 880.43 (ms) | 1839.89 (ms) | |
| SRM-OMP | 46.43 (ms) | 277.01 (ms) | 926.09 (ms) | 1915.21 (ms) | |
| DTM_OMP_ICA | 91.14 (ms) | 414.41 (ms) | 1446.20 (ms) | 2785.59 (ms) | |
| Variables | Significance |
|---|---|
| Represents the chirp period, pulse time | |
| Sampling interval | |
| represents the number of chirp cycles | |
| The aperture of the array antennas | |
| represents the frequency modulation slope | |
| The number of equivalent virtual antenna arrays | |
| Speed of light | |
| Represents the carrier frequency |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Zhang, Y.; Yu, Y.; Lv, D.; Xi, R.; Li, W.; Gu, L.; Wang, Z. An Improved OMP Algorithm for Enhancing the Anti-Interference Performance of Array Antennas. Sensors 2024, 24, 2291. https://doi.org/10.3390/s24072291
Gao M, Zhang Y, Yu Y, Lv D, Xi R, Li W, Gu L, Wang Z. An Improved OMP Algorithm for Enhancing the Anti-Interference Performance of Array Antennas. Sensors. 2024; 24(7):2291. https://doi.org/10.3390/s24072291
Chicago/Turabian StyleGao, Mingyuan, Yan Zhang, Yueyun Yu, Danju Lv, Rui Xi, Wei Li, Lianglian Gu, and Ziqian Wang. 2024. "An Improved OMP Algorithm for Enhancing the Anti-Interference Performance of Array Antennas" Sensors 24, no. 7: 2291. https://doi.org/10.3390/s24072291
APA StyleGao, M., Zhang, Y., Yu, Y., Lv, D., Xi, R., Li, W., Gu, L., & Wang, Z. (2024). An Improved OMP Algorithm for Enhancing the Anti-Interference Performance of Array Antennas. Sensors, 24(7), 2291. https://doi.org/10.3390/s24072291






