Exploration-Based Planning for Multiple-Target Search with Real-Drone Results
Abstract
:1. Introduction
- A method to search for an unknown number of static targets at unknown positions that uses an intensity-function multi-target filter to handle highly uncertain sensors and is the first to combine such a filter with an explicit exploration objective in the planner;
- Detailed simulation results in which we compare our method to three baselines, including a lawnmower and two active search methods;
- A real experiment involving a Parrot Mambo that searches indoors for targets located on the floor and via which we compare our method to lawnmower and active-search methods.
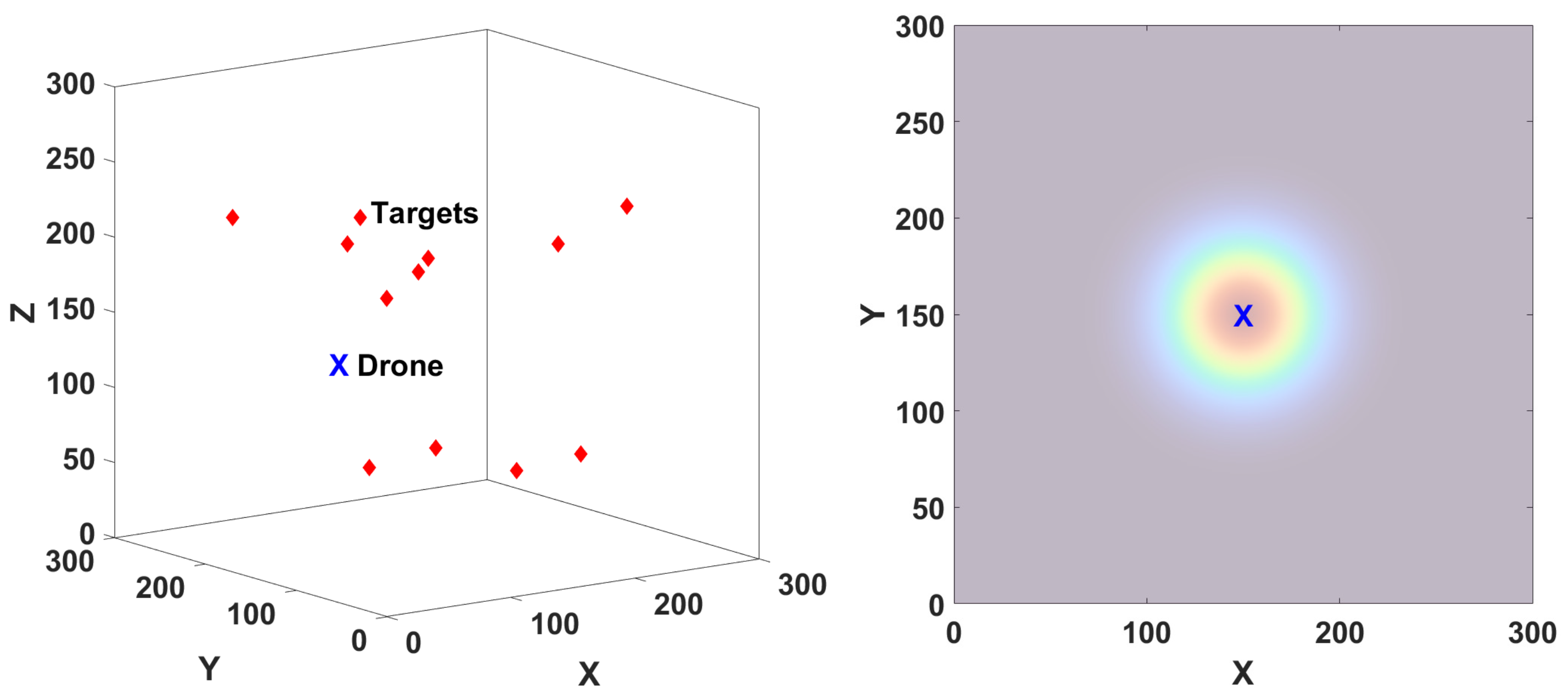
2. Problem Formulation
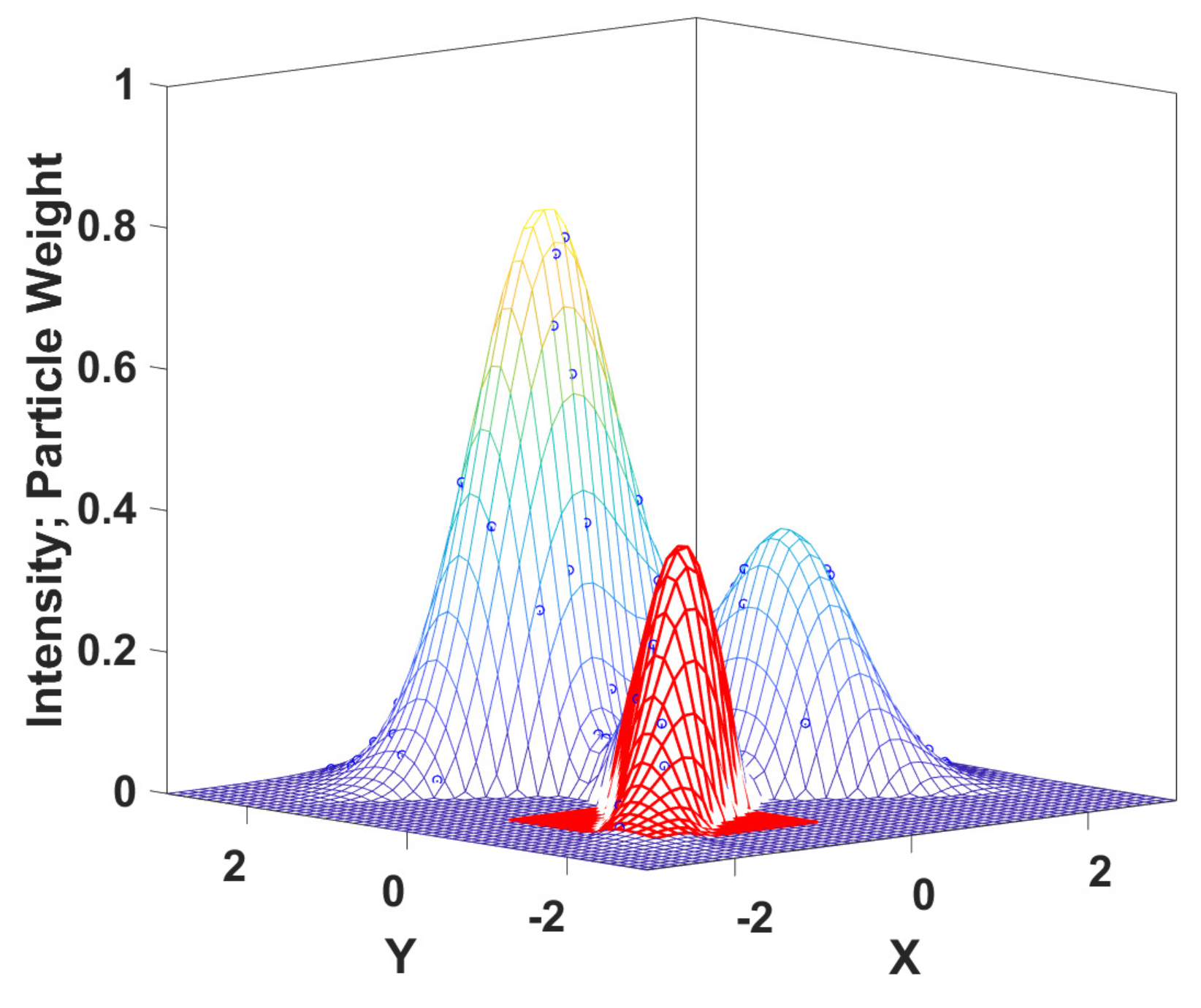
3. Background on PHD Filtering
4. Exploration-Based Search
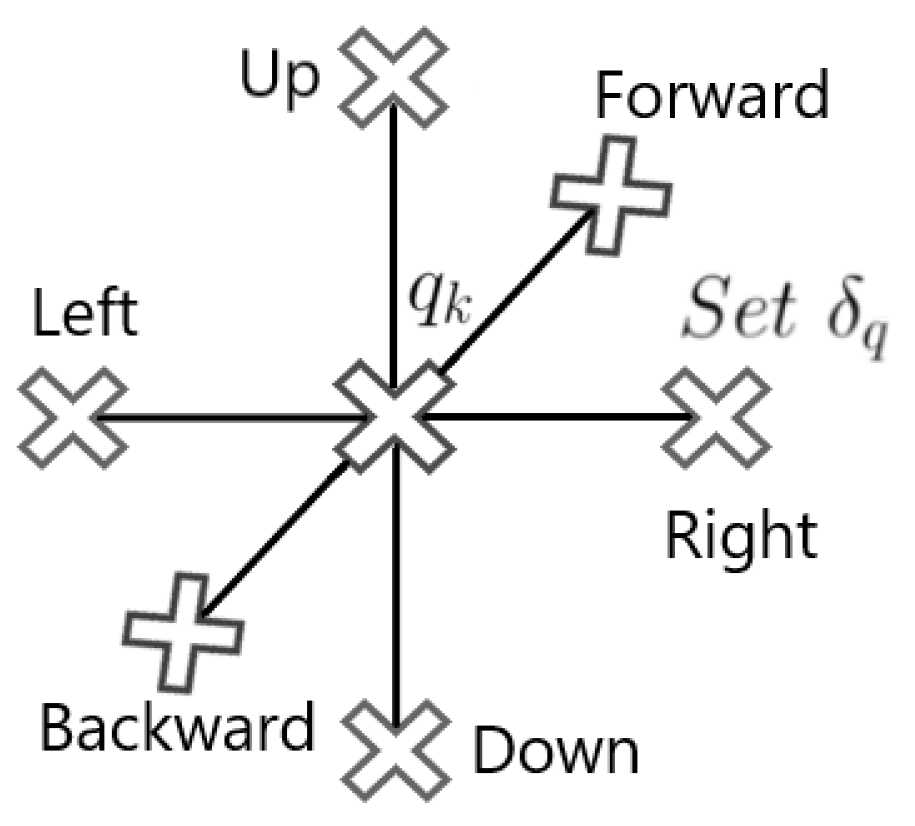
4.1. Planner
4.2. Marking and Removal of Found Targets
4.3. Obstacle Avoidance
| Algorithm 1 Target search at step k |
|
5. Simulation Results
- E1: Influence of the planner horizon: We consider 12 targets uniformly distributed at random locations. The trajectory length is chosen to be 330 steps. Figure 4 shows the number of target detections over time for a varying horizon . It can be seen that horizon 1 is statistically indistinguishable from 2 and 3. Therefore, we choose horizon for the remaining simulations as it is computationally more efficient.
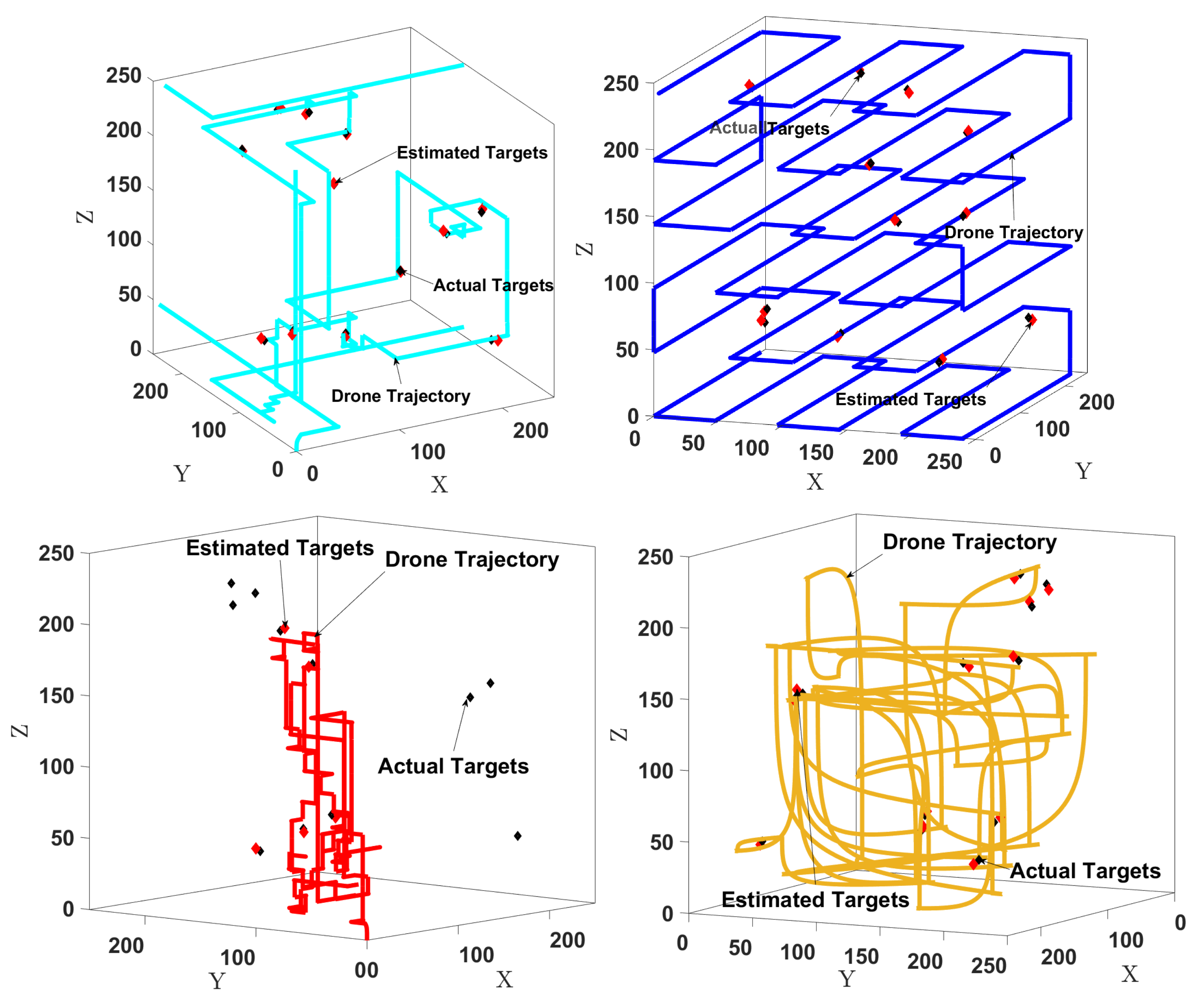
- E2: Planner performance for uniformly distributed targets: We consider 12 targets uniformly and randomly distributed throughout E. The trajectory length is chosen to be 812 steps since the lawnmower needs this length to complete the search of the whole space. The length is the same for all algorithms for fairness.

- E3: Planner performance for clustered targets: We consider 12 targets placed in 2 clusters of 6 targets, each at a random location. The trajectory length is the same as for . Figure 7 (top) shows the number of targets detected over time. We see that the performance of our algorithm is again better than those of the three baselines. Figure 7 (bottom) shows the positions of the actual targets as well as the target locations estimated by our method. The root mean squared error (RMSE) between the actual and estimated positions is 3.14 m, which is relatively small for a domain with a size of m3. This RMSE value depends on the covariance of the Gaussian noise in the sensor model (4) and the threshold values in Algorithm 1. For instance, we can reduce the error by making the cluster width threshold smaller, as we show in the next experiment.
- E4: Threshold value versus RMSE. For 12 targets uniformly distributed at random locations, we used 20 different values of the cluster radius threshold that varied in range from 0.5 to 2.4. The results in Figure 8 (left) show the RMSE values between the actual and estimated target locations as a function of the threshold value . Errors are directly related to threshold values and can be made smaller by reducing . Doing this, of course, increases the number of steps taken by the drone to find all the targets, as shown in Figure 8 (right).
- E5: Target refinement with center probabilities: In this experiment, we compare the performance when the target refinement component is MI versus when the center-probabilities version (13) is used. Exploration is included. We consider 12 uniformly and randomly distributed targets. The trajectory length is 330 steps. Figure 9 shows the number of targets detected over time. The algorithm found all targets in a nearly equal amount of steps using the two options for target refinement. The main difference is in computational time: the MI-based algorithm takes an average of 0.041 s per step to plan, while using center probabilities is faster, with an average of 0.018 s per step.Figure 7. Top: Average number of clustered targets detected in 10 random maps. Bottom: Estimation error using our method.Figure 7. Top: Average number of clustered targets detected in 10 random maps. Bottom: Estimation error using our method.Figure 8. Results for E4. Left: Target position error for different thresholds. Right: Number of steps taken by the drone to find all targets.Figure 8. Results for E4. Left: Target position error for different thresholds. Right: Number of steps taken by the drone to find all targets.Figure 9. Detected average number of targets with MI and the center-probabilities methods in 10 random maps.Figure 9. Detected average number of targets with MI and the center-probabilities methods in 10 random maps.
- E6: Trajectory with no targets: We show in Figure 10 (left) how the drone explores the environment in the absence of targets. The trajectory length is chosen as 600 steps. The drone flies similarly to a lawnmower pattern because in the absence of target measurements, the exploration component drives it to cover the whole environment.
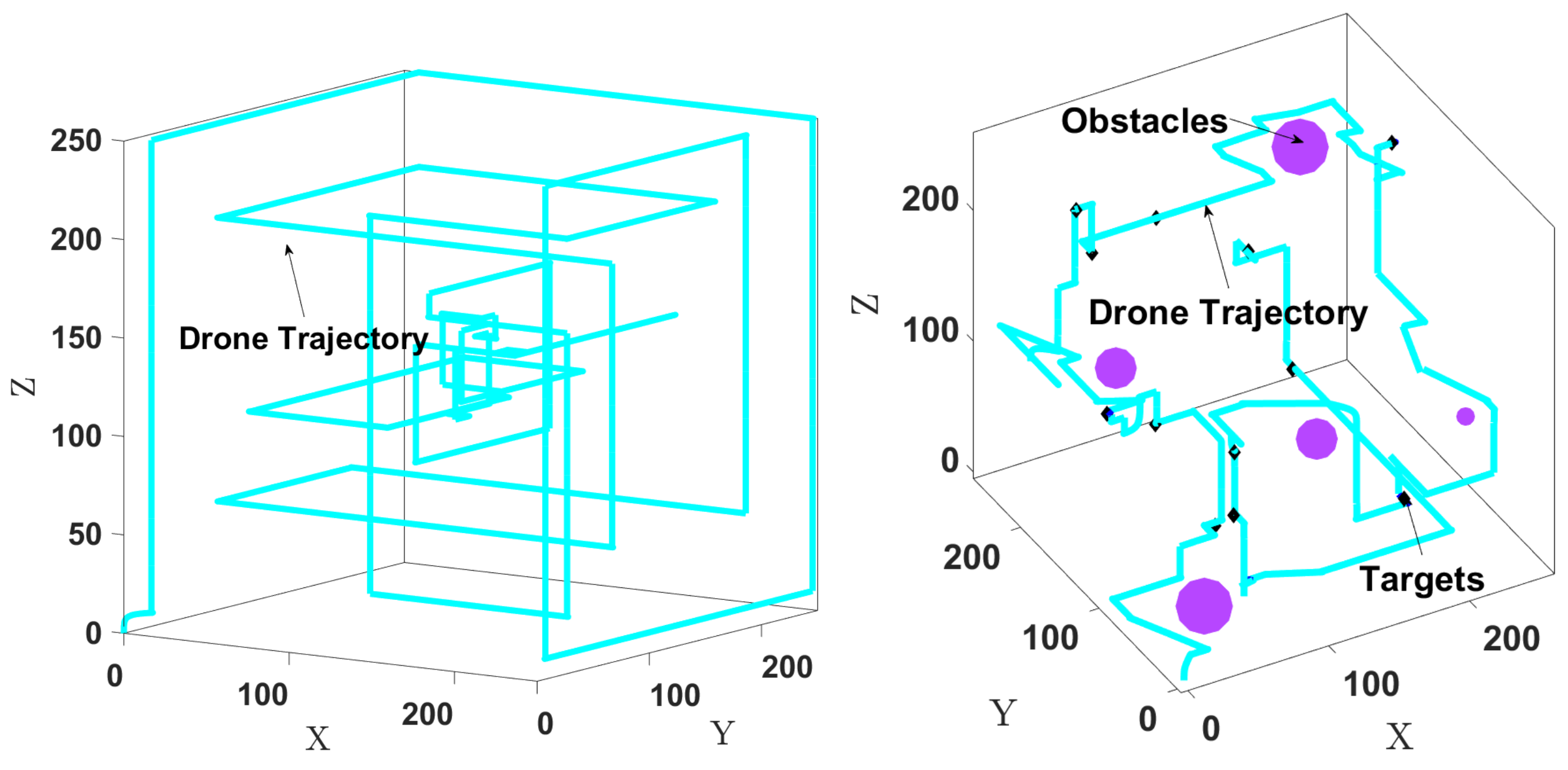
- E7: Obstacle avoidance: We consider 12 targets and 5 obstacles with various sizes placed manually at arbitrary locations, as shown in Figure 10 (right). The trajectory length is 380 steps. For obstacle avoidance, is set to 11 m, and is used in (15). Figure 10 (right) shows the drone searching for the targets while avoiding the obstacles. It takes about 380 steps to find all the targets, compared to 330 steps without obstacles.
6. Experimental Results
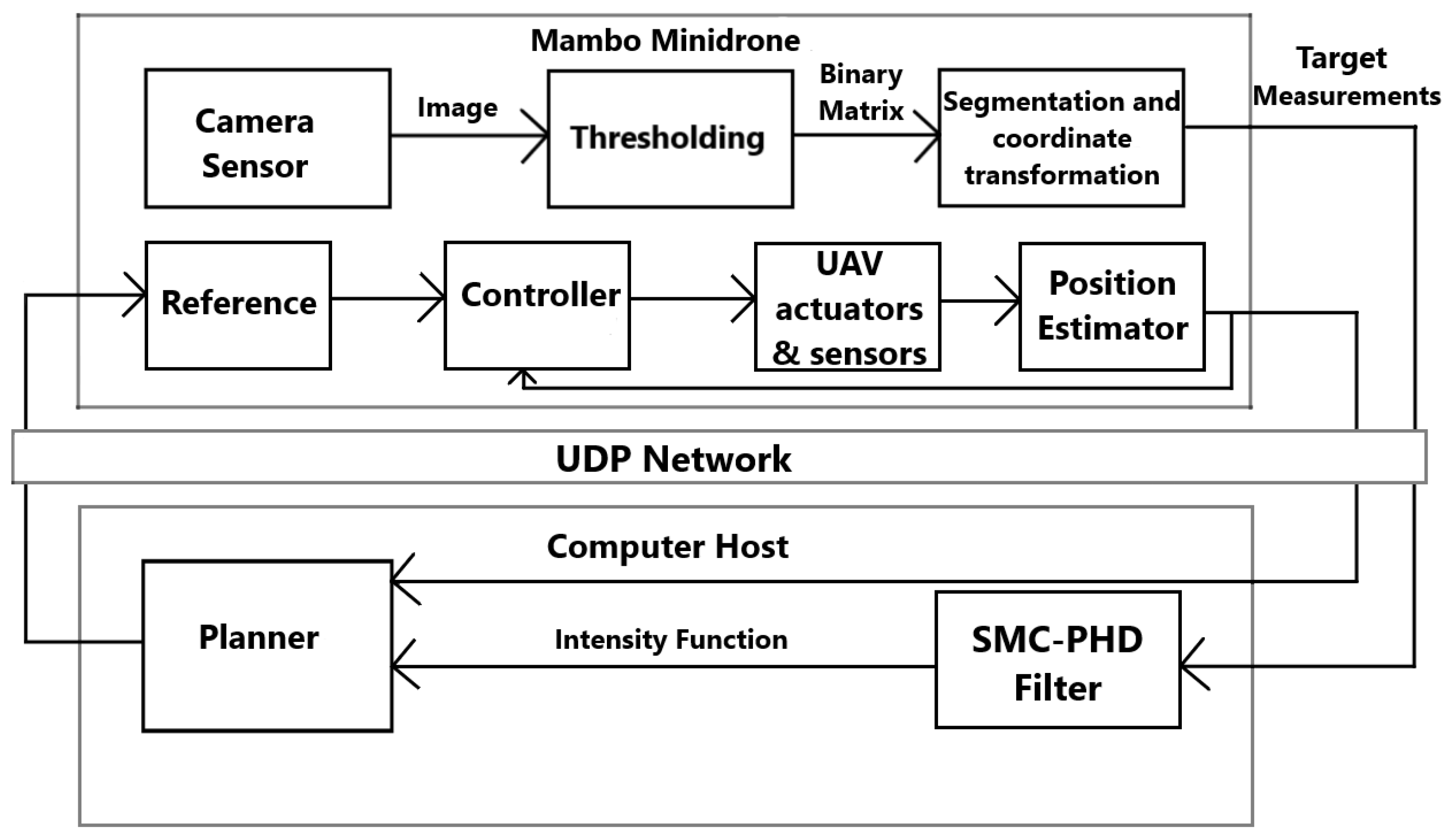
6.1. Hardware, Sensing, and Control
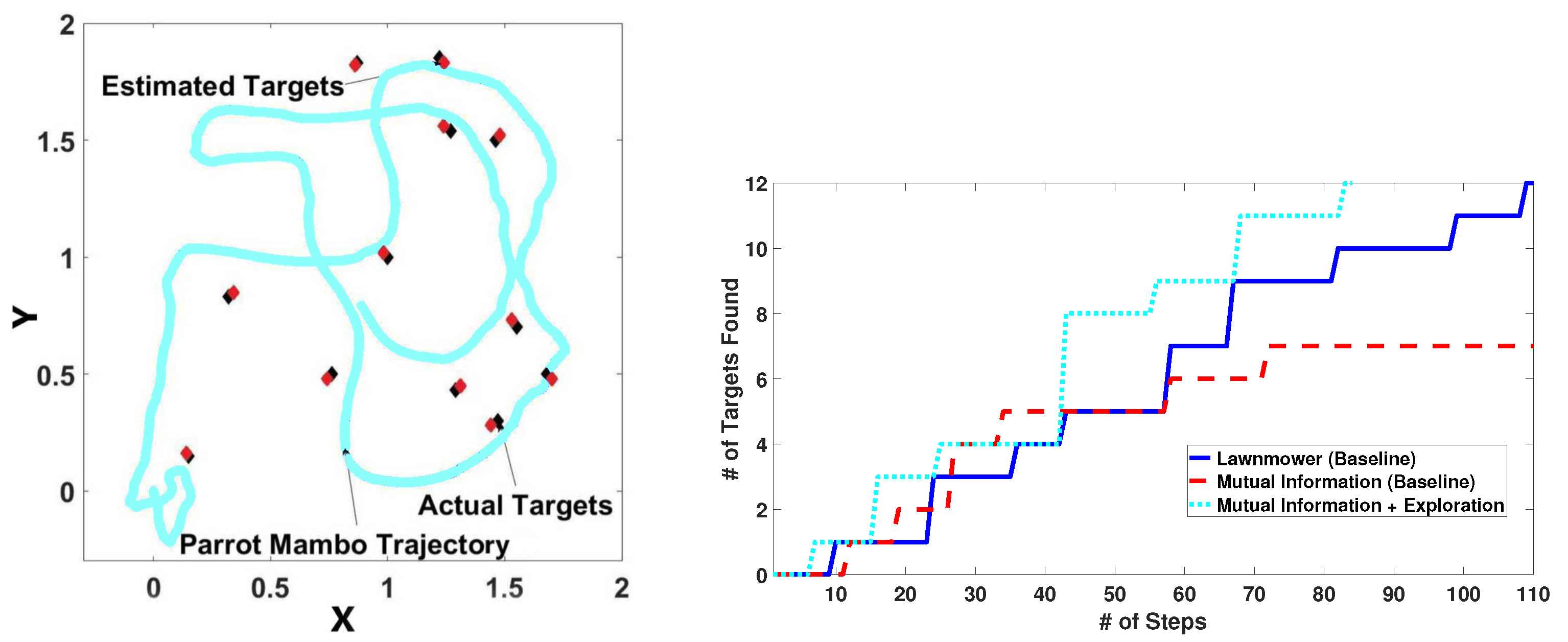
6.2. High-Level Setup and Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FOV | Field of View |
| PHD | Probability Hypothesis Density |
| SMC | Sequential Monte Carlo |
| MI | Mutual Information |
Appendix A. Smc-Phd Filter
References
- Pallin, M.; Rashid, J.; Ögren, P. Formulation and Solution of the Multi-agent Concurrent Search and Rescue Problem. In Proceedings of the IEEE International Symposium on Safety, Security, and Rescue Robotics, New York, NY, USA, 25–27 October 2021; pp. 27–33. [Google Scholar]
- Papaioannou, S.; Kolios, P.; Theocharides, T.; Panayiotou, C.G.; Polycarpou, M.M. A Cooperative Multiagent Probabilistic Framework for Search and Track Missions. IEEE Trans. Control Netw. Syst. 2021, 8, 847–857. [Google Scholar] [CrossRef]
- Olcay, E.; Bodeit, J.; Lohmann, B. Sensor-based Exploration of an Unknown Area with Multiple Mobile Agents. IFAC-PapersOnLine 2020, 53, 2405–8963. [Google Scholar] [CrossRef]
- Vo, B.N.; Singh, S.; Doucet, A. Sequential Monte Carlo Methods for Multitarget Filtering with Random Finite Sets. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1224–1245. [Google Scholar]
- Dames, P. Distributed Multi-Target Search and Tracking Using the PHD filter. Auton. Robot. 2020, 44, 673–689. [Google Scholar] [CrossRef]
- Charrow, B.; Michael, N.; Kumar, V.R. Active Control Strategies for Discovering and Localizing Devices with Range-Only Sensors. In Algorithmic Foundations of Robotics XI; Springer: Cham, Switzerland, 2014; Volume 107, pp. 51–71. [Google Scholar]
- Ivić, S. Motion Control for Autonomous Heterogeneous Multiagent Area Search in Uncertain Conditions. IEEE Trans. Cybern. 2022, 52, 3123–3135. [Google Scholar] [CrossRef] [PubMed]
- Trenev, I.; Tkachenko, A.; Kustov, A. Movement stabilization of the Parrot Mambo quadcopter along a given trajectory based on PID controllers. IFAC-Papers Online 2021, 54, 227–232. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, A.; He, X.; Bian, X. Multi-Target Coordinated Search Algorithm for Swarm Robotics Considering Practical Constraints. Front. Neurorobot. 2021, 15, 144–156. [Google Scholar] [CrossRef]
- Yan, F.; Di, K.; Jiang, J.; Jiang, Y.; Fan, H. Efficient decision-making for multiagent target searching and occupancy in an unknown environment. Robot. Auton. Syst. 2019, 114, 41–56. [Google Scholar] [CrossRef]
- Wang, L.; Su, F.; Zhu, H.; Shen, L. Active sensing based cooperative target tracking using UAVs in an urban area. In Proceedings of the 2010 2nd International Conference on Advanced Computer Control, Shenyang, China, 27–29 March 2010; Volume 2, pp. 486–491. [Google Scholar]
- Juliá, M.; Gil, A.; Reinoso, O. A comparison of path planning strategies for autonomous exploration and mapping of unknown environments. Auton. Robot. 2012, 33, 427–444. [Google Scholar] [CrossRef]
- Dang, T.; Khattak, S.; Mascarich, F.; Alexis, K. Explore Locally, Plan Globally: A Path Planning Framework for Autonomous Robotic Exploration in Subterranean Environments. In Proceedings of the 19th International Conference on Advanced Robotics, Belo Horizonte, Brazil, 2–6 December 2019; pp. 9–16. [Google Scholar]
- Murillo, M.; Sánchez, G.; Genzelis, L.; Giovanini, L. A Real-Time Path-Planning Algorithm based on Receding Horizon Techniques. J. Intellegent Robot. Syst. 2018, 91, 445–457. [Google Scholar] [CrossRef]
- Bircher, A.; Kamel, M.; Alexis, K.; Oleynikova, H.; Siegwart, R. Receding horizon path planning for 3D exploration and surface inspection. Auton. Robot. 2018, 42, 291–306. [Google Scholar] [CrossRef]
- Kim, J. Tracking Controllers to Chase a Target Using Multiple Autonomous Underwater Vehicles Measuring the Sound Emitted From the Target. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 4579–4587. [Google Scholar] [CrossRef]
- Tyagi, P.; Kumar, Y.; Sujit, P.B. NMPC-based UAV 3D Target Tracking In The Presence of Obstacles and Visibility Constraints. In Proceedings of the International Conference on Unmanned Aircraft Systems, Athens, Greece, 15–18 June 2021; pp. 858–867. [Google Scholar]
- Dames, P.; Tokekar, P.; Kumar, V. Detecting, localizing, and tracking an Unknown Number of Moving Targets Using a Team of Mobile Robots. Int. J. Robot. Res. 2017, 36, 1540–1553. [Google Scholar] [CrossRef]
- Lin, L.; Goodrich, M.A. Hierarchical Heuristic Search Using a Gaussian Mixture Model for UAV Coverage Planning. IEEE Trans. Cybern. 2014, 44, 2432–2544. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Ren, J.; Li, Y. Multi-mode filter target tracking method for mobile robot using multi-agent reinforcement learning. Eng. Appl. Artif. Intell. 2024, 127, 107398. [Google Scholar] [CrossRef]
- Shen, G.; Lei, L.; Zhang, X.; Li, Z.; Cai, S.; Zhang, L. Multi-UAV Cooperative Search Based on Reinforcement Learning with a Digital Twin Driven Training Framework. IEEE Trans. Veh. Technol. 2023, 72, 8354–8368. [Google Scholar] [CrossRef]
- Xia, J.; Luo, Y.; Liu, Z.; Zhang, Y.; Shi, H.; Liu, Z. Cooperative multi-target hunting by unmanned surface vehicles based on multi-agent reinforcement learning. Def. Technol. 2023, 29, 80–94. [Google Scholar] [CrossRef]
- Wang, X.; Fang, X. A multi-agent reinforcement learning algorithm with the action preference selection strategy for massive target cooperative search mission planning. Expert Syst. Appl. 2023, 231, 120643. [Google Scholar] [CrossRef]
- Xiao, J.; Tan, Y.X.M.; Zhou, X.; Feroskhan, M. Learning Collaborative Multi-Target Search for a Visual Drone Swarm. In Proceedings of the Preprints of IEEE Conference on Artificial Intelligence, Santa Clara, CA, USA, 5–6 June 2023; pp. 5–7. [Google Scholar]
- Zhou, Y.; Liu, Z.; Shi, H.; Li, S.; Ning, N.; Liu, F.; Gao, X. Cooperative multi-agent target searching: A deep reinforcement learning approach based on parallel hindsight experience replay. Complex Intell. Syst. 2023, 9, 4887–4898. [Google Scholar] [CrossRef]
- Barouch, M.; Irad, B.G.; Evgeny, K. Detection of Static and Mobile Targets by an Autonomous Agent with Deep Q-Learning Abilities. Entropy 2022, 24, 1168. [Google Scholar] [CrossRef]
- Guangcheng, W.; Fenglin, W.; Yu, J.; Minghao, Z.; Kai, W.; Hong, Q. A Multi-AUV Maritime Target Search Method for Moving and Invisible Objects Based on Multi-Agent Deep Reinforcement Learning. Sensors 2022, 22, 8562. [Google Scholar] [CrossRef] [PubMed]
- Kong, X.; Zhou, Y.; Li, Z.; Wang, S. Multi-UAV simultaneous target assignment and path planning based on deep reinforcement learning in dynamic multiple obstacles environments. Front. Neurorobotics 2024, 17, 1302898. [Google Scholar] [CrossRef]
- Wenshan, W.; Guoyin, Z.; Qingan, D.; Dan, L.; Yingnan, Z.; Sizhao, L.; Dapeng, L. Multiple Unmanned Aerial Vehicle Autonomous Path Planning Algorithm Based on Whale-Inspired Deep Q-Network. Drones 2023, 7, 572. [Google Scholar] [CrossRef]
- Chen, J.; Dames, P. Active Multi-Target Search Using Distributed Thompson Sampling. Tech. Rep. Res. Sq. 2022. [Google Scholar] [CrossRef]
- Shirsat, A.; Berman, S. Decentralized Multi-target Tracking with Multiple Quadrotors using a PHD Filter. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 and 19–21 January 2021. [Google Scholar]
- Chen, J.; Dames, P. Collision-Free Distributed Multi-Target Tracking Using Teams of Mobile Robots with Localization Uncertainty. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 6968–6974. [Google Scholar]
- Dames, P.; Kumar, V. Autonomous Localization of an Unknown Number of Targets without Data Association Using Teams of Mobile Sensors. IEEE Trans. Autom. Sci. Eng. 2015, 12, 850–864. [Google Scholar] [CrossRef]
- Xu, X.; Hou, Q.; Wu, C.; Fan, Z. Improved GSO Algorithms and Their Applications in Multi-Target Detection and Tracking Field. IEEE Access 2020, 8, 119609–119623. [Google Scholar] [CrossRef]
- Sung, Y.; Tokekar, P. GM-PHD Filter for Searching and Tracking an Unknown Number of Targets with a Mobile Sensor with Limited FOV. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2122–2134. [Google Scholar] [CrossRef]
- Ke, C.; Lei, C.; Wei, Y. Multi-Sensor Control for Jointly Searching and Tracking Multi-Target Using the Poisson Multi-Bernoulli Mixture. In Proceedings of the 11th International Conference on Control, Automation and Information Sciences, Hanoi, Vietnam, 21–24 November 2022; pp. 240–247. [Google Scholar]
- Per, B.R.; Daniel, A.; Gustaf, H. Sensor Management for Search and Track Using the Poisson Multi-Bernoulli Mixture Filter. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2771–2783. [Google Scholar]
- Shan, J.; Yang, Y.; Liu, H.; Liu, T. Infrared Small Target Tracking Based on OSTrack Model. IEEE Access 2023, 11, 123938–123946. [Google Scholar] [CrossRef]
- Tindall, L.; Mair, E.; Nguyen, T.Q. Radio Frequency Signal Strength Based multi-target Tracking with Robust Path Planning. IEEE Access 2023, 11, 43472–43484. [Google Scholar] [CrossRef]
- Arkin, R.C.; Diaz, J. Line-of-sight constrained exploration for reactive multiagent robotic teams. In Proceedings of the 7th International Workshop on Advanced Motion Control, Maribor, Slovenia, 3–5 July 2002; pp. 455–461. [Google Scholar]
- Bourgault, F.; Makarenko, A.A.; Williams, S.B.; Grocholsky, B.; Durrant-Whyte, H.F. Information-based adaptive robotic exploration. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; Volume 1, pp. 540–545. [Google Scholar]
- Lifeng, Z.; Tzoumas, V.; Pappas, G.J.; Tokekar, P. Resilient Active Target Tracking with Multiple Robots. IEEE Robot. Autom. Lett. 2019, 4, 129–136. [Google Scholar]
- Vo, B.N.; Vo, B.T.; Phung, D. Labeled Random Finite Sets and the Bayes Multi-Target Tracking Filter. IEEE Trans. Signal Process. 2014, 6, 6554–6567. [Google Scholar] [CrossRef]
- Vo, B.N.; Beard, W.; Mahler, R. The Gaussian Mixture Probability Hypothesis Density Filter. IEEE Trans. Signal Process. 2006, 54, 4091–4104. [Google Scholar] [CrossRef]
- Beard, M.; Vo, B.T.; Vo, B.N. Bayesian Multi-Target Tracking with Merged Measurements Using Labelled Random Finite Sets. IEEE Trans. Signal Process. 2015, 63, 1433–1447. [Google Scholar] [CrossRef]
- Otte, M.; Kuhlman, M.; Sofge, D. Competitive target search with multi-agent teams: Symmetric and asymmetric communication constraints. Auton. Robot. 2018, 42, 1207–1230. [Google Scholar] [CrossRef]
- Yousuf, B.; Lendek, Z.; Buşoniu, L. Exploration-Based Search for an Unknown Number of Targets Using a UAV. IFAC-PapersOnLine 2022, 55, 93–98. [Google Scholar] [CrossRef]
- Khelloufi, A.; Achour, N.; Passama, R.; Cherubini, A. Sensor-based navigation of omnidirectional wheeled robots dealing with both collisions and occlusions. Robotica 2020, 38, 617–638. [Google Scholar] [CrossRef]
- Lars, G.; Jürgen, P. Nonlinear Model Predictive Control; Springer: London, UK, 2011; pp. 43–66. [Google Scholar]
- Zheng, X.; Galland, S.; Tu, X.; Yang, Q.; Lombard, A.; Gaud, N. Obstacle Avoidance Model for UAVs with Joint Target based on Multi-Strategies and Follow-up Vector Field. Procedia Comput. Sci. 2020, 170, 257–264. [Google Scholar] [CrossRef]
- Süto, B.; Codrean, A.; Lendek, Z. Optimal Control of Multiple Drones for Obstacle Avoidance. IFAC-PapersOnLine 2023, 56, 5980–5986. [Google Scholar] [CrossRef]
- Maer, V.M. Design and Reference Solution of an Autonomous Quadcopter Racing Competition. Master’s Thesis, Technical University of Cluj-Napoca, Cluj-Napoca, Romania, 2020. [Google Scholar]
- Milan, S.; Vaclav, H.; Roger, B. Image Processing, Analysis and Machine Vision, 4th ed.; Global Engineering: Fairfax, VA, USA, 2008. [Google Scholar]
- Jing, Z.; Yang, C.; Shuai, F.; Yu, K.; Wen, C.C. Fast Haze Removal for Nighttime Image Using Maximum Reflectance Prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7016–7024. [Google Scholar]
- Yun, L.; Zhongsheng, Y.; Jinge, T.; Yuche, L. Multi-Purpose Oriented Single Nighttime Image Haze Removal Based on Unified Variational Retinex Model. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 1643–1657. [Google Scholar]
- Mahler, R. Statistical Multisource-Multitarget Information Fusion; Artech: Norwood, MA, USA, 2007. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousuf, B.; Lendek, Z.; Buşoniu, L. Exploration-Based Planning for Multiple-Target Search with Real-Drone Results. Sensors 2024, 24, 2868. https://doi.org/10.3390/s24092868
Yousuf B, Lendek Z, Buşoniu L. Exploration-Based Planning for Multiple-Target Search with Real-Drone Results. Sensors. 2024; 24(9):2868. https://doi.org/10.3390/s24092868
Chicago/Turabian StyleYousuf, Bilal, Zsófia Lendek, and Lucian Buşoniu. 2024. "Exploration-Based Planning for Multiple-Target Search with Real-Drone Results" Sensors 24, no. 9: 2868. https://doi.org/10.3390/s24092868
APA StyleYousuf, B., Lendek, Z., & Buşoniu, L. (2024). Exploration-Based Planning for Multiple-Target Search with Real-Drone Results. Sensors, 24(9), 2868. https://doi.org/10.3390/s24092868









