A New Approach for Infrared Temperature Measurement Sensor Systems and Temperature Control for Domestic Induction Hobs
Abstract
:1. Introduction
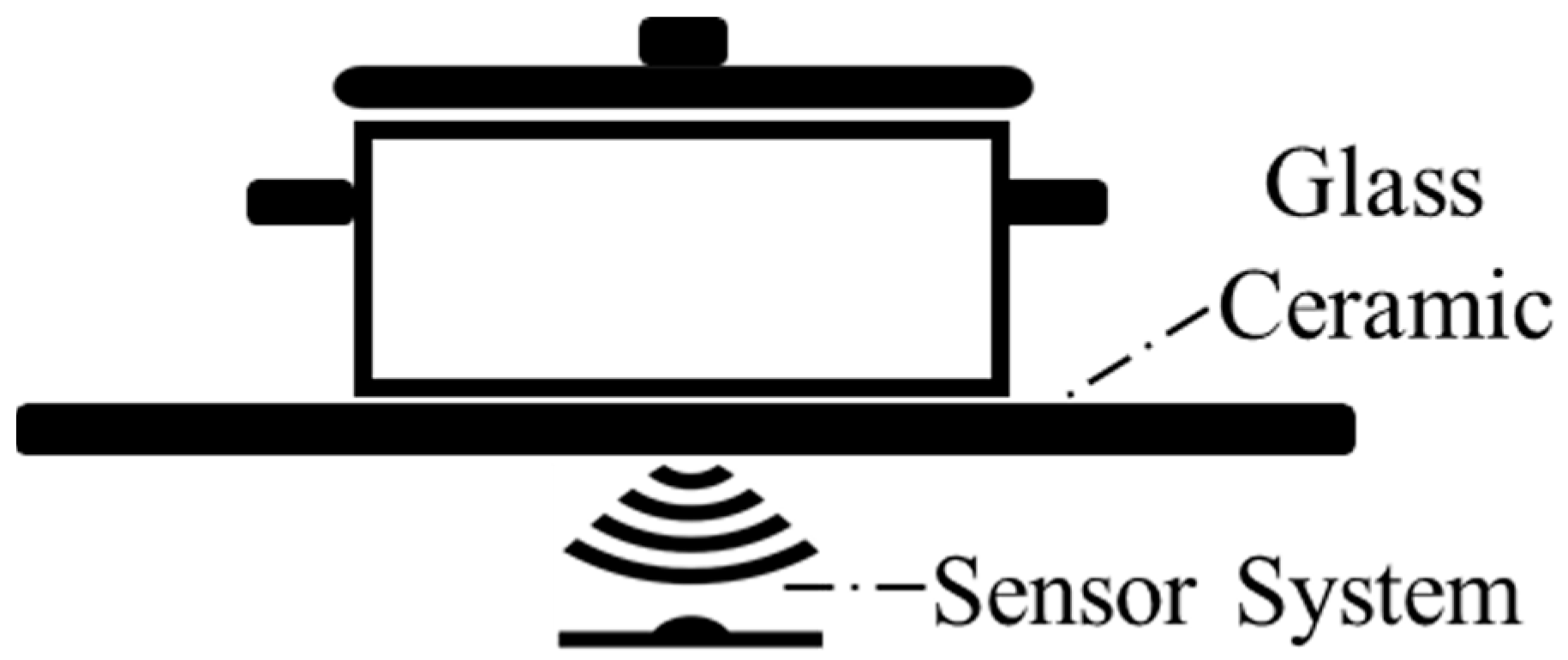
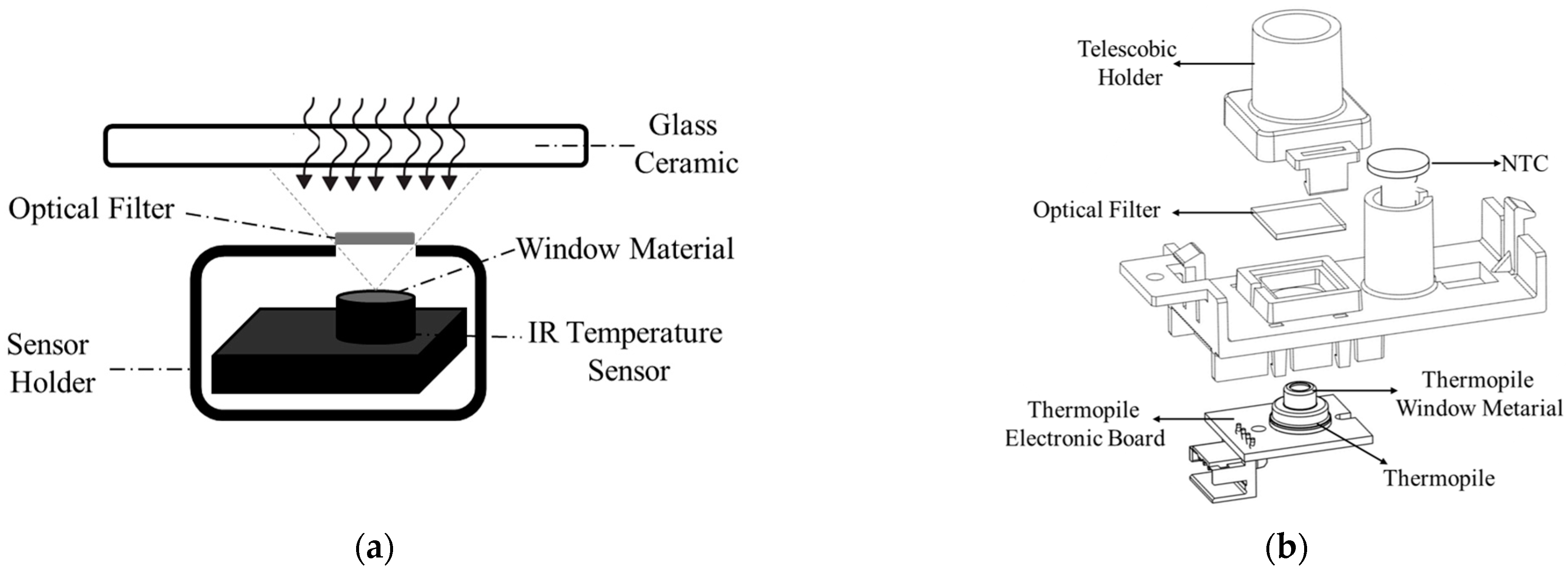
2. Proposed Sensor System and Sensor Selection
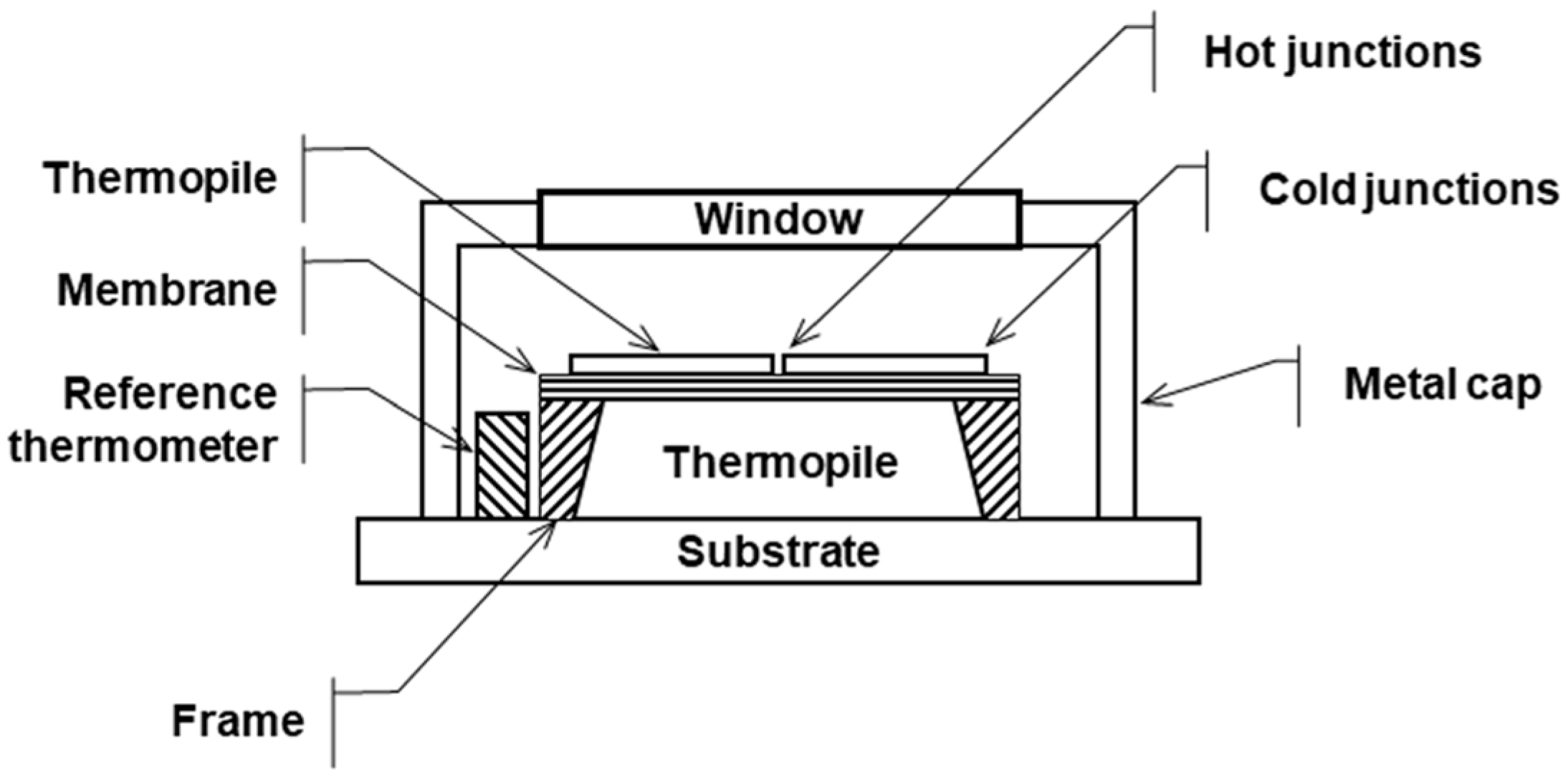
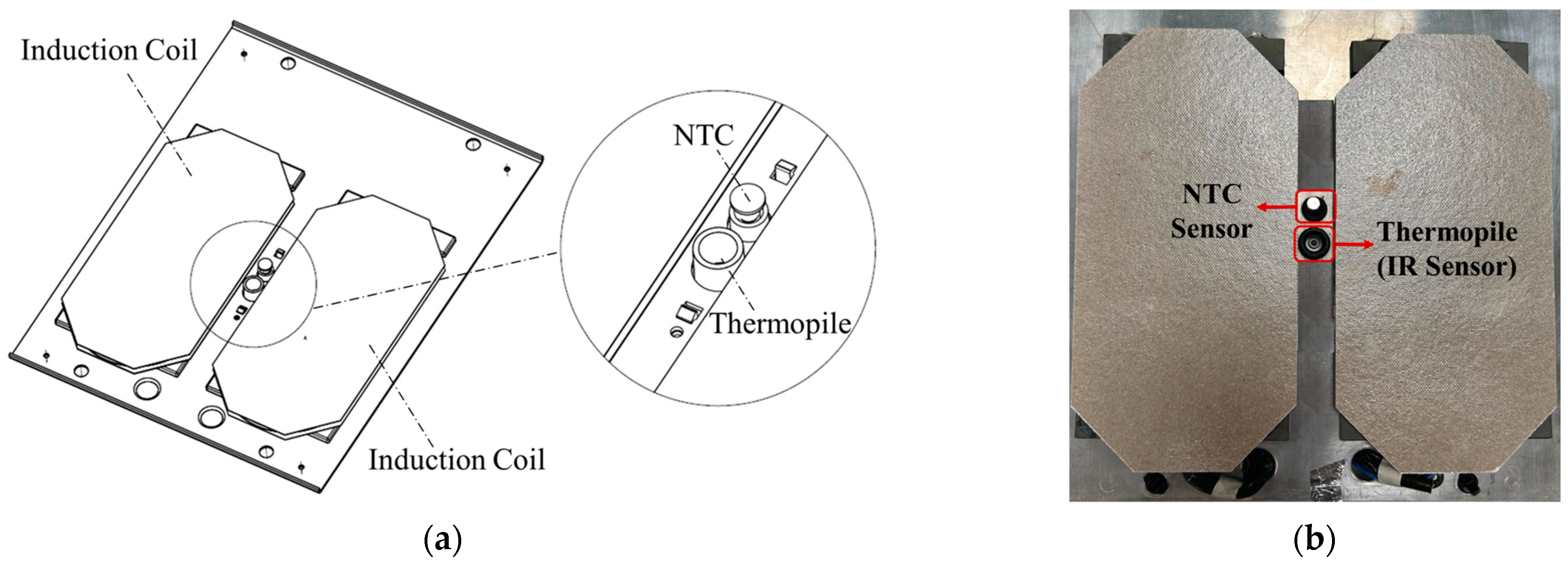
2.1. Infrared Temperature Sensor Selection
- Measurement accuracy;
- Electrical noise resistance;
- IR measurement wavelength range;
- Measurement range;
- Operating temperature range;
- Field of view (FoV).
2.1.1. Experimental Studies for IR Temperature Sensor Performance
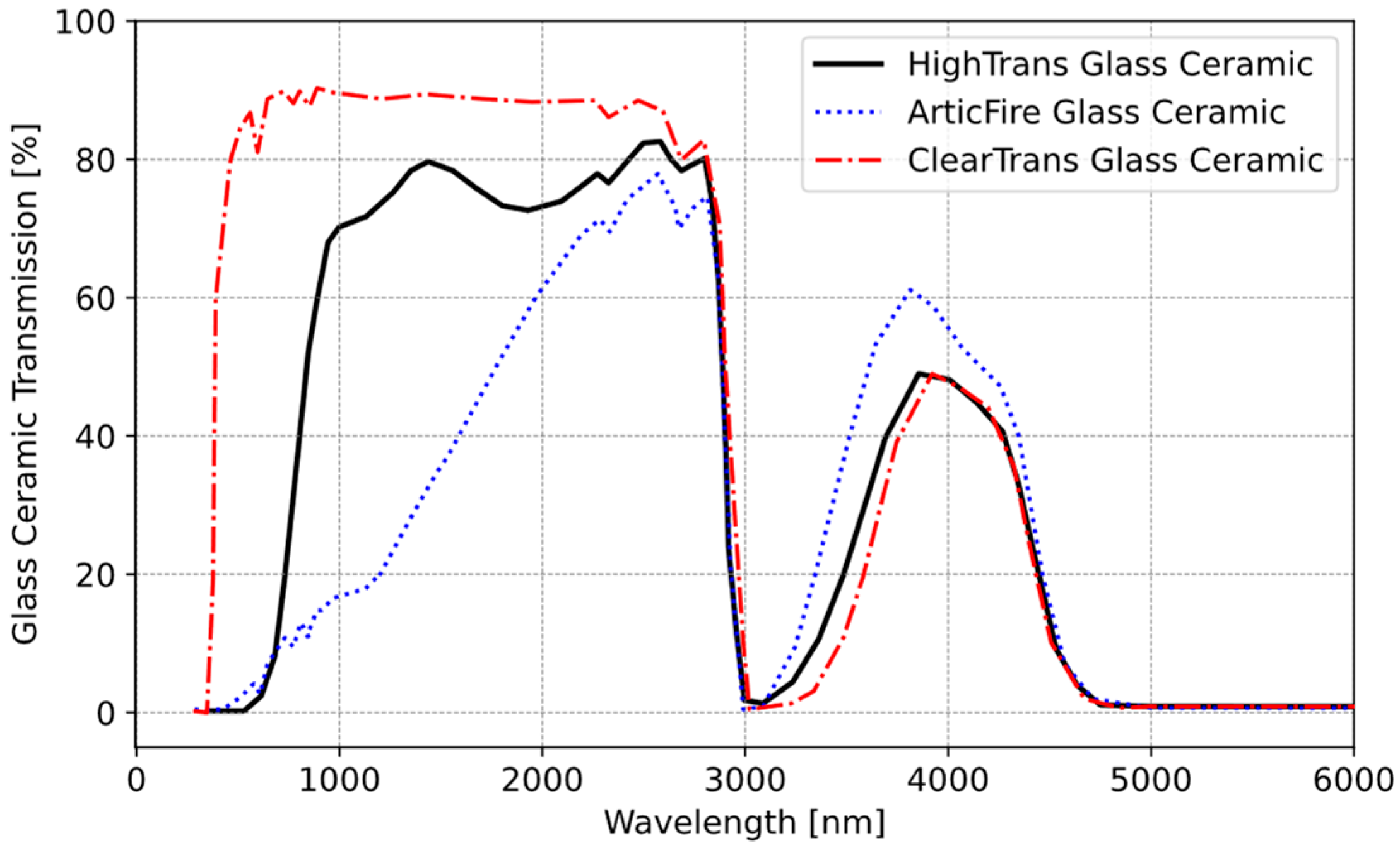
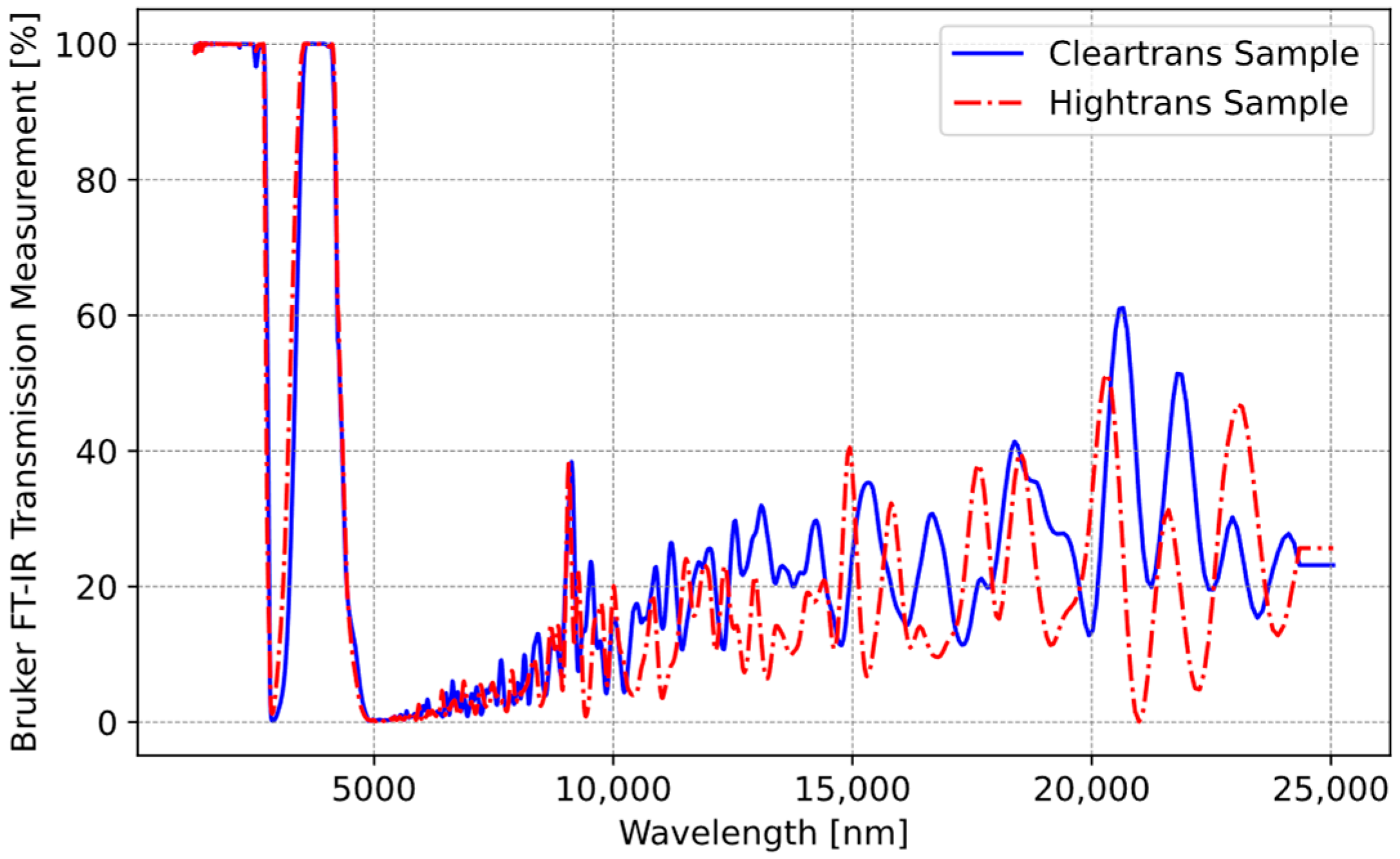
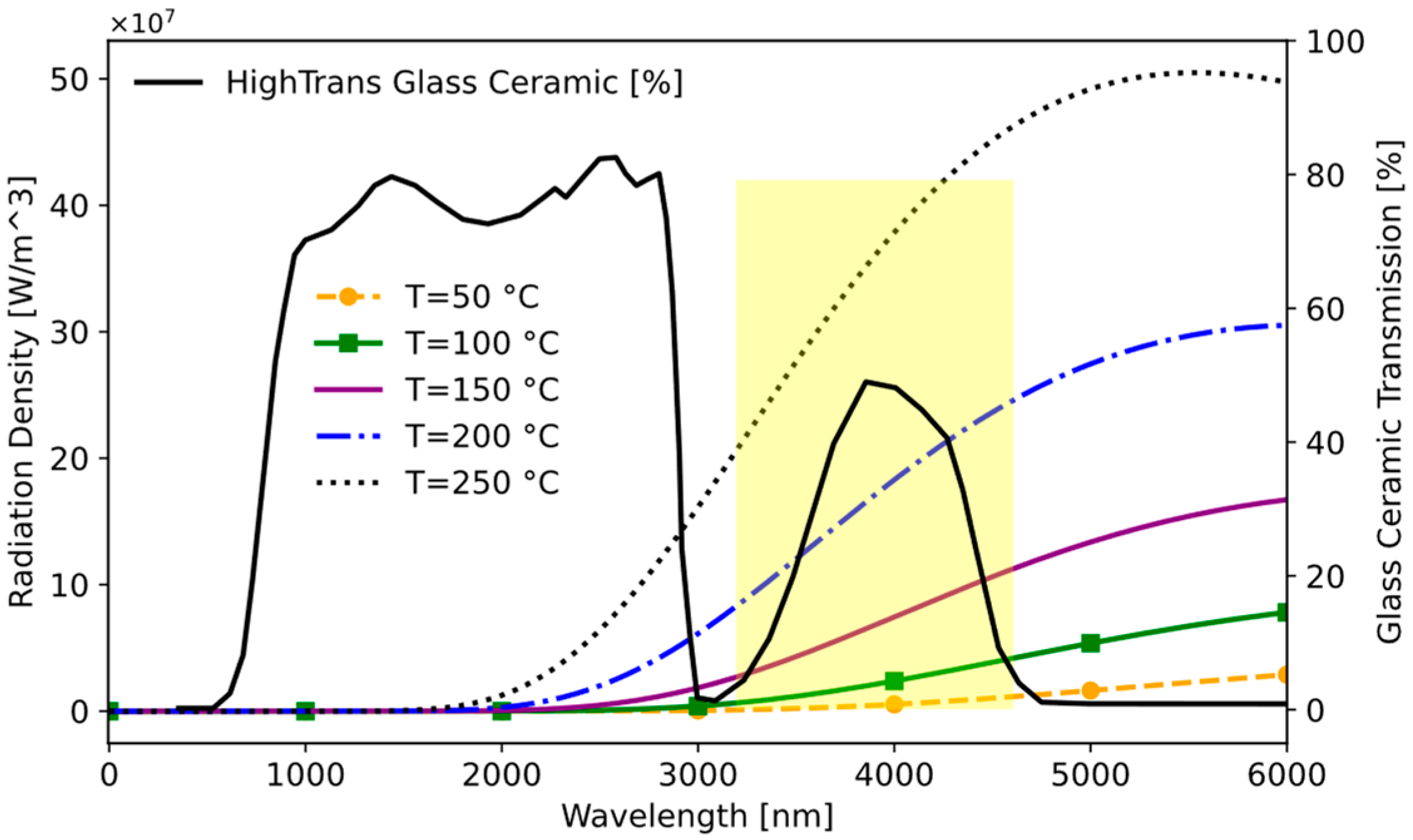
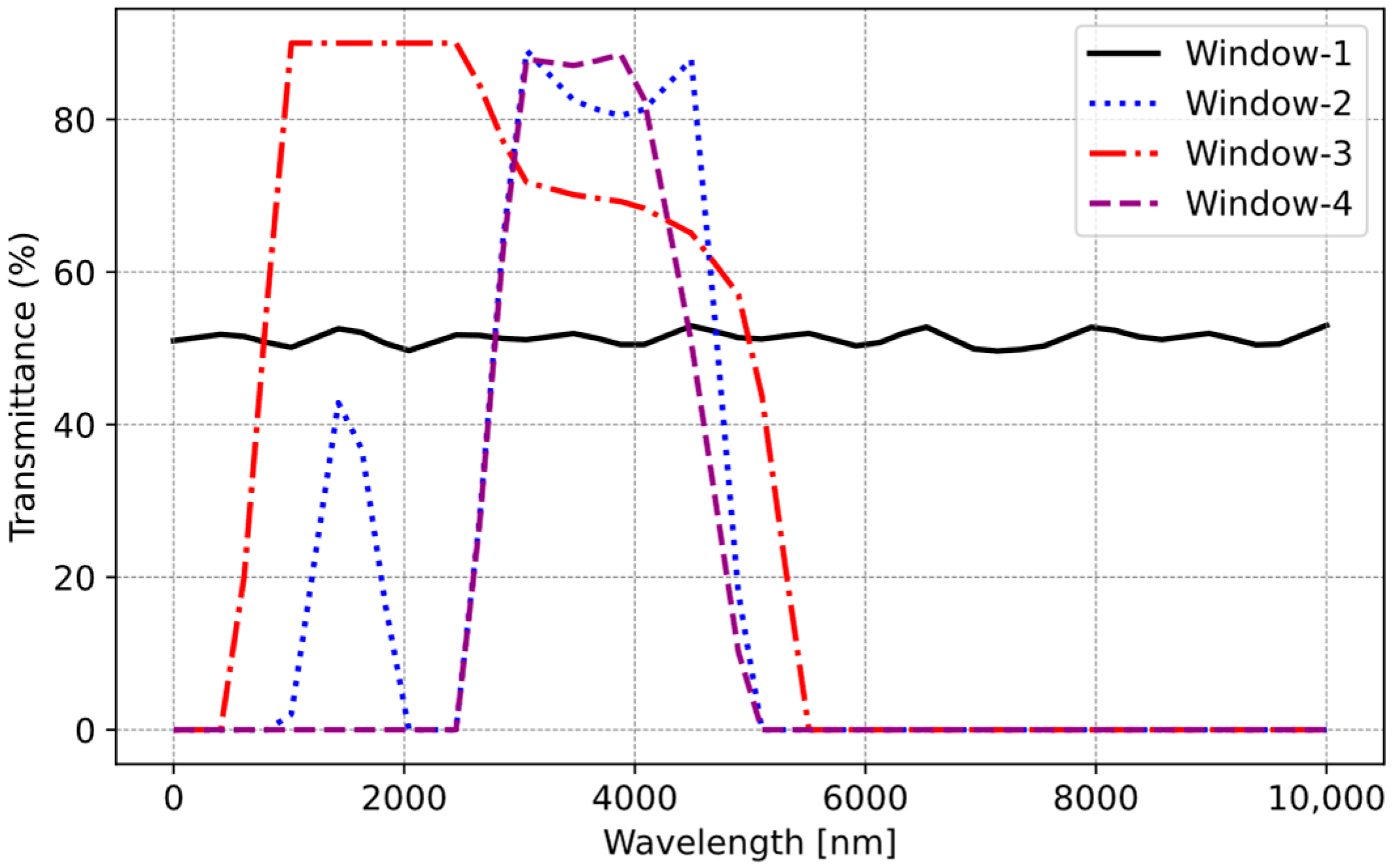
2.1.2. Selection of Window Material for IR Temperature Sensor
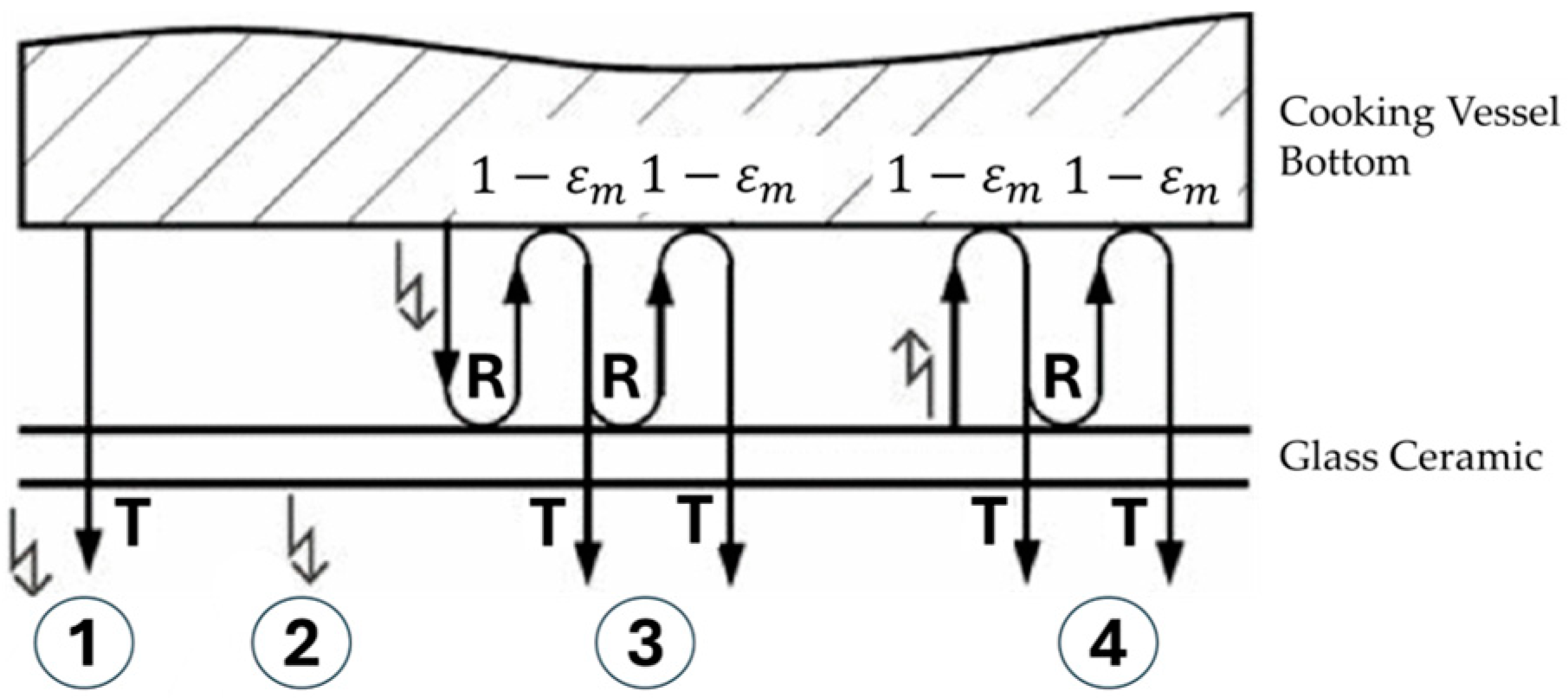
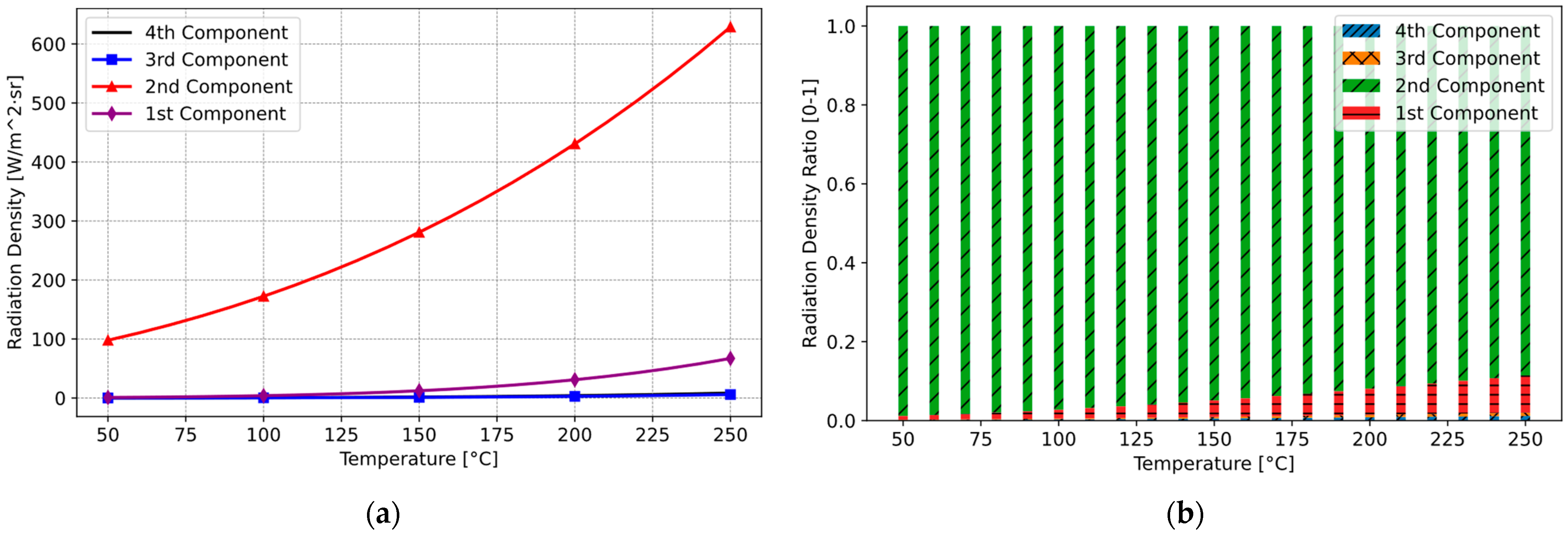
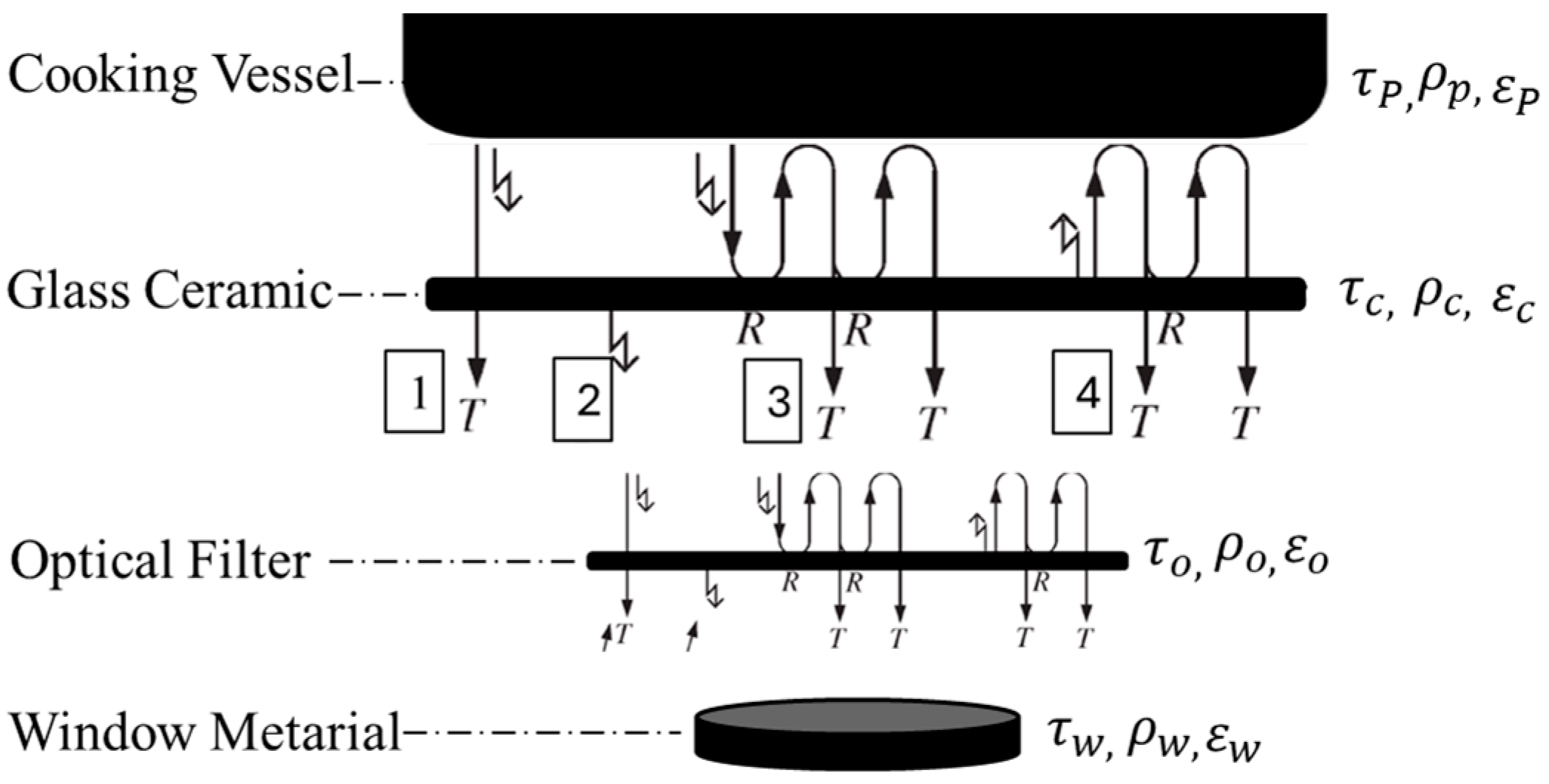
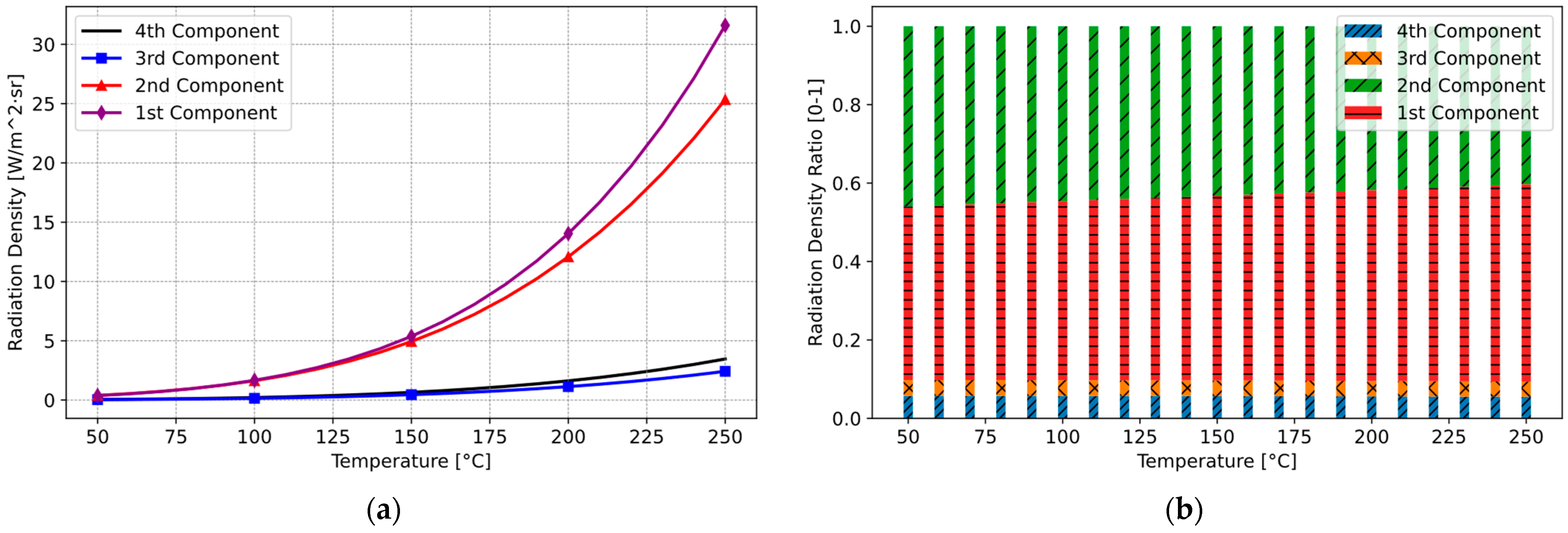
3. Thermal Radiation Modelling and Improvement of Sensor
3.1. Thermal Radiation Modelling of Infrared Emissions for Induction Hobs
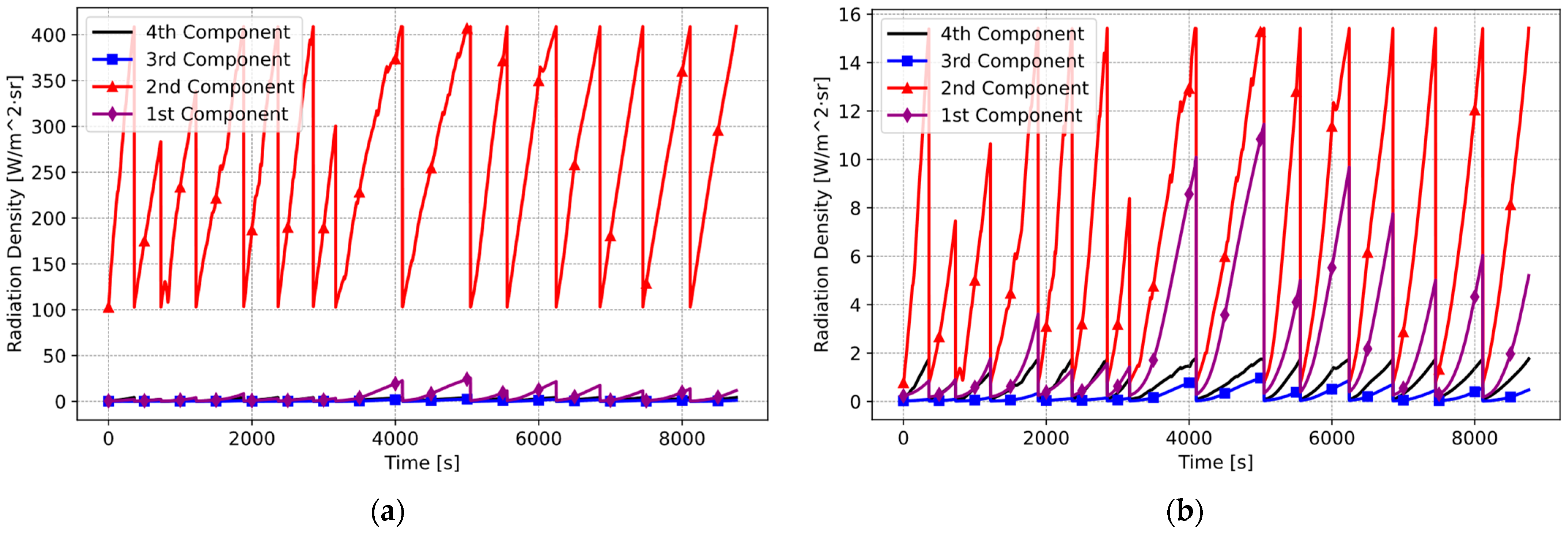
3.2. Computer-Based Simulation for the Proposed Sensor System
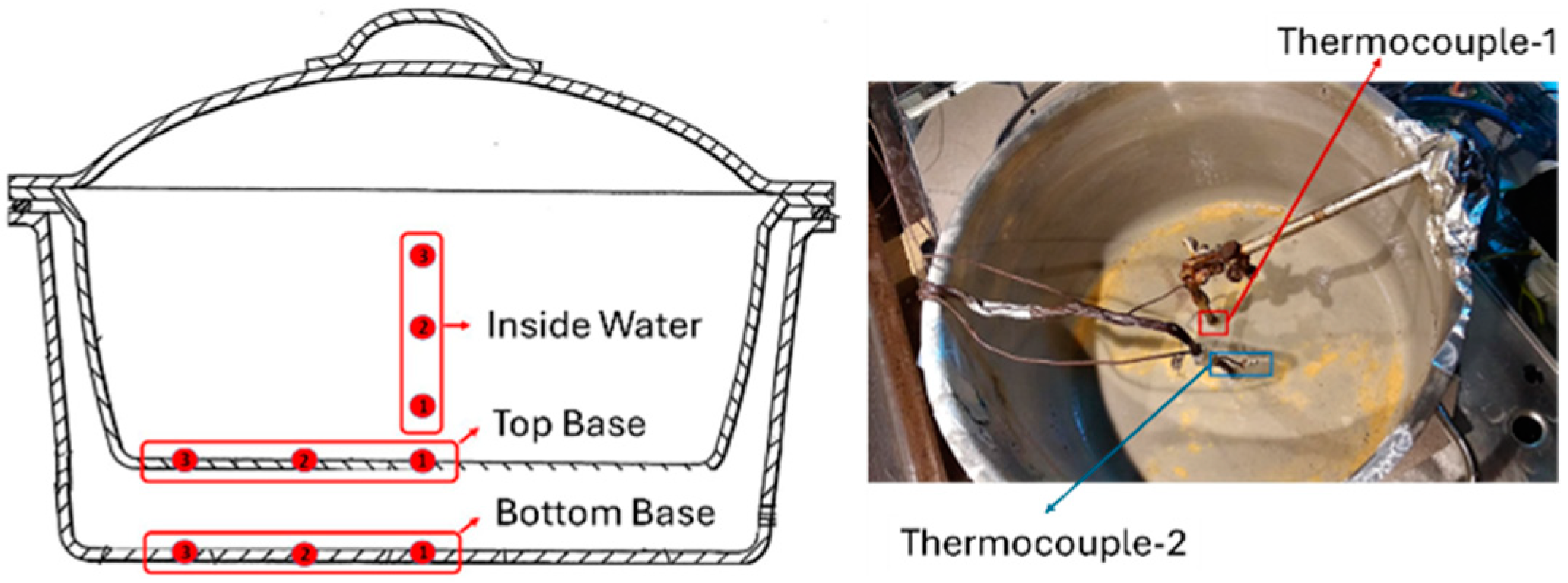
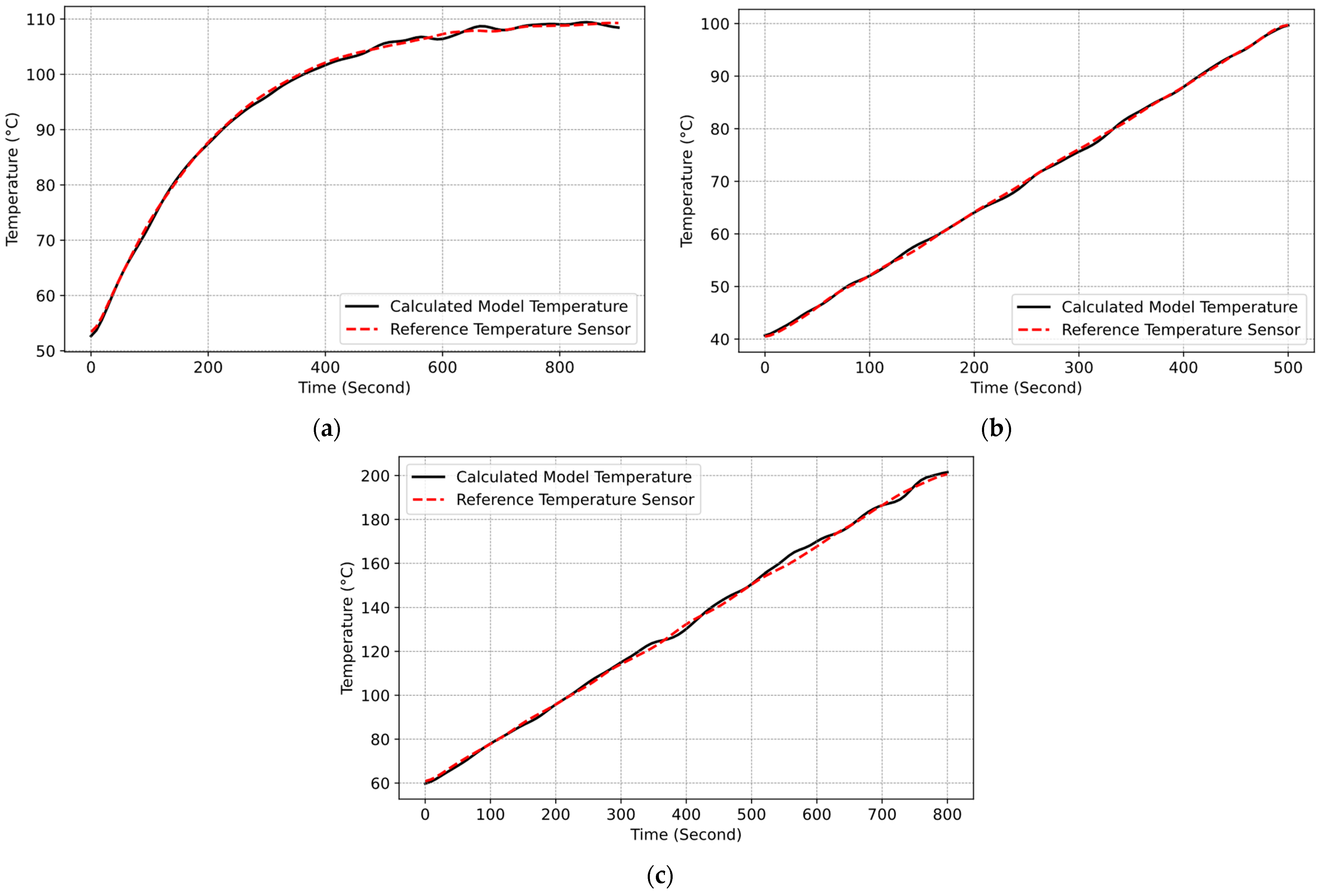
3.3. Model Validation of Simulation with Real Cooking Data
3.4. Experimental Validation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vishnuram, P.; Ramachandiran, G.; Babu, T.S.; Nastasi, B. Induction heating in domestic cooking and industrial melting applications: A systematic review on modelling, converter topologies and control schemes. Energies 2021, 14, 6634. [Google Scholar] [CrossRef]
- Acero, J.; Burdio, J.M.; Barragan, L.A.; Navarro, D.; Alonso, R.; Ramon, J.; Monterde, F.; Hernandez, P.; Llorente, S.; Garde, I. Domestic induction appliances. IEEE Ind. Appl. Mag. 2010, 16, 39–47. [Google Scholar] [CrossRef]
- Bansal, P.; Vineyard, E.; Abdelaziz, O. Advances in household appliances—A review. Appl. Therm. Eng. 2011, 31, 3748–3760. [Google Scholar] [CrossRef]
- Lucia, O.; Maussion, P.; Dede, E.J.; Burdio, J.M. Induction heating technology and its applications: Past developments, current technology, and future challenges. IEEE Trans. Ind. Electron. 2013, 61, 2509–2520. [Google Scholar] [CrossRef]
- Lucia, O.; Acero, J.; Carretero, C.; Burdio, J.M. Induction heating appliances: Toward more flexible cooking surfaces. IEEE Ind. Electron. Mag. 2013, 7, 35–47. [Google Scholar] [CrossRef]
- Prist, M.; Pallotta, E.; Cicconi, P.; Russo, A.; Monteriu, A.; Germani, M.; Longhi, S. An automatic temperature control for induction cooktops to reduce energy consumption. In Proceedings of the 2018 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 12–14 January 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Paesa, D.; Franco, C.; Llorente, S.; Lopez-Nicolas, G.; Sagues, C. Adaptive simmering control for domestic induction cookers. IEEE Trans. Ind. Appl. 2011, 47, 2257–2267. [Google Scholar] [CrossRef]
- Cabeza-Gil, I.; Calvo, B.; Grasa, J.; Franco, C.; Llorente, S.; Martínez, M. Thermal analysis of a cooking pan with a power control induction system. Appl. Therm. Eng. 2020, 180, 115789. [Google Scholar] [CrossRef]
- García, D.P. Reset Observers and Temperature Control for Induction Hobs/David Paesa García. Ph.D. Thesis, Universidad de Zaragoza, Zaragoza, Spain, 2011. [Google Scholar]
- Paesa, D.; Franco, C.; Llorente, S.; Lopez-Nicolas, G.; Sagues, C. QFT-Based Robust Simmering Control for Domestic Induction Cookers Using an Infrared Sensor. In Proceedings of the 2010 IEEE Industry Applications Society Annual Meeting, Houston, TX, USA, 3–7 October 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Chellaiyan, V.G.; Fasna, J.L.; Mallika, L.S.V. Food safety awareness and food handling practices among rural population of Tamil Nadu. Int. J. Community Med. Public Health 2018, 5, 1441. [Google Scholar] [CrossRef]
- Paesa, D.; Llorente, S.; Sagues, C.; Aldana, O. Adaptive observers applied to pan temperature control of induction hobs. IEEE Trans. Ind. Appl. 2009, 45, 1116–1125. [Google Scholar] [CrossRef]
- Bautista, M.G.A.; Suganob, N.J.; Concepcion, R.; Bandala, A.; Dadios, E. Automated Cooking Systems: Benefits, Challenges, and Future Directions. In Proceedings of the 2023 IEEE 15th International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment, and Management (HNICEM), Coron, Palawan, Philippines, 19–23 November 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Dong, Z.; Li, Y.; Zhang, S.; Shang, F. Fuzzy temperature control of induction cooker. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 3051–3056. [Google Scholar] [CrossRef]
- Imaz, E.; Alonso, R.; Heras, C.; Salinas, I.; Carretero, E.; Carretero, C. Infrared thermometry system for temperature measurement in induction heating appliances. IEEE Trans. Ind. Electron. 2014, 61, 2622–2630. [Google Scholar] [CrossRef]
- Lasobras, J.; Alonso, R.; Carretero, C.; Carretero, E.; Imaz, E. Infrared sensor-based temperature control for domestic induction cooktops. Sensors 2014, 14, 5278–5295. [Google Scholar] [CrossRef] [PubMed]
- Graf, A.; Arndt, M.; Sauer, M.; Gerlach, G. Review of micromachined thermopiles for infrared detection. Meas. Sci. Technol. 2007, 18, R59–R75. [Google Scholar] [CrossRef]
- Backherms, V.; Beier, D.; Michl, B.; Schöning, S. Cooking System and Method for Operating the Same. EP2775784A1, 10 September 2014. [Google Scholar]
- Tominaga, H.; Watanabe, K.; Hirota, I.; Tabuchi, S.; Isoda, K. Induction Cooking Device. EP2124506A1, 25 November 2009. [Google Scholar]
- Park, J.I. Cooking Device Including Optical Sensor. KR20190111407A, 2 October 2019. [Google Scholar]
- Dörk, B.; Bockmeyer, M.; Zenker, T.; Weiss, E.; Ohl, G.; Taplan, M.; Dedek, R.; Backes, S. Glass Ceramic Cooktop with an Infrared Sensor. EP3196175B1, 27 October 2021. Available online: https://worldwide.espacenet.com/publicationDetails/biblio?CC=EP&NR=3196175B1&KC=B1&FT=D&ND=5&date=20211027&DB=&locale=en_EP (accessed on 29 October 2024).
- Carretero, C.; Lasobras, J.; Alonso, R.; Carretero, E.; Imaz, E. Radiation heat measurement model for temperature estimation in induction heating appliances. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 3265–3269. [Google Scholar] [CrossRef]
- Pascual, A.; Acero, J.; Burdio, J.; Llorente, S.; Carretero, C. Self-protection systems for domestic induction heating based on ferromagnetic materials with low Curie temperature. In Proceedings of the 2022 IEEE 31st International Symposium on Industrial Electronics (ISIE), Anchorage, AK, USA, 1–3 June 2022; pp. 314–319. [Google Scholar] [CrossRef]
- Schieferdecker, J.; Quad, R.; Holzenkämpfer, E.; Schulze, M. Infrared thermopile sensors with high sensitivity and very low temperature coefficient. Sens. Actuators A Phys. 1995, 47, 422–427. [Google Scholar] [CrossRef]
- Ben Mbarek, S.; Alcheikh, N.; Younis, M.I. Recent advances on MEMS based Infrared Thermopile detectors. Microsyst. Technol. 2022, 28, 1751–1764. [Google Scholar] [CrossRef]
- Ganwani, M.; Shaikh, B.; Sinha, S. Design and Investigation of MEMS-Based Thermopile Detector Arrays for Infrared Sensing Applications. In Proceedings of the APSCON 2024–2024 IEEE Applied Sensing Conference, Goa, India, 22–24 January 2024. [Google Scholar] [CrossRef]
- Minitab, L.L.C. Minitab Statistical Software 21.1.0. 2024. Available online: https://www.minitab.com (accessed on 29 October 2024).
- Agilent Technologies 34970A Data Acquisition System. Available online: https://www.keysight.com (accessed on 29 October 2024).
- Chroma Systems Solutions Chroma 66202 Power Analyzer. Available online: https://www.chromausa.com (accessed on 29 October 2024).
- Jeong, J.; An, S.; Kim, T.; Joung, W. Transient Thermal Characteristics of a Heated Infrared Temperature Sensor for Noncontact Medical Thermometry. Int. J. Thermophys. 2022, 43, 62. [Google Scholar] [CrossRef] [PubMed]
- Bruker Corporation. Vertex 70 FT-IR Spectrometer. Available online: https://www.bruker.com (accessed on 29 October 2024).
- UL 858; UL Standard for Safety Household Electric Ranges. Underwriters Laboratories: Northbook, IL, USA, 2024.
- VDE 0700-1; VDE Household and Similar Electrical Appliances. Verband der Elektrotechnik (VDE): Berlin, Germany, 2024.
- Howell, J.R.; Menguc, M.P.; Siegel, R. Thermal Radiation Heat Transfer; CRC Press: Los Angeles, FL, USA, 2010. [Google Scholar] [CrossRef]
- Microsoft Corporation. Visual Studio Code Environment 1.96.0. 2024. Available online: https://code.visualstudio.com (accessed on 29 October 2024).
- Python Software Foundation. Python 3.13.1. 2024. Available online: https://www.python.org (accessed on 29 October 2024).
- The MathWorks Inc. MATLAB R2024a. 2024. Available online: https://www.mathworks.com (accessed on 29 October 2024).
- Lu, G.; Wu, F.; Zheng, M.; Chen, C.; Zhou, X.; Diao, C.; Liu, F.; Du, G.; Xue, C.; Jiang, H.; et al. Perfect optical absorbers in a wide range of incidence by photonic heterostructures containing layered hyperbolic metamaterials. Opt. Express 2019, 27, 5326–5336. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.M.; Wu, X.; Fu, C. Validity of Kirchhoff’s law for semitransparent films made of anisotropic materials. J. Quant. Spectrosc. Radiat. Transf. 2020, 245, 106904. [Google Scholar] [CrossRef]








| Power-Controlled Systems | Temperature-Controlled Systems |
|---|---|
| Only the power level can be selected by the user, and the actual cooking vessel temperature is unknown. | Target temperature values can be selected directly, and the hob alerts the user regarding actual temperatures. |
| Cooking outcomes heavily rely on the user’s skills and habits. | Repeatable and professional recipes are easy to follow for excellent cooking results. |
| There is a risk of smoke or fire if the power level is set too high or the cooking vessel is left unattended. This poses serious safety risks. | Hazardous situations are mitigated, as the cooking vessel temperature is continuously monitored and maintained. |
| No. of Experiment | No. of Sensor | Cooking Vessel | Power (W) | Temperature (°C) |
|---|---|---|---|---|
| 1 | 1 | A | 2300 | 25–100 |
| 4 | 1 | A | 3400 | 25–250 |
| 28 | 4 | A | 3400 | 25–250 |
| … | … | … | … | … |
| 64 | 4 | B | 3400 | 25–250 |
| Parameter | Specification |
|---|---|
| Sensor type | Single thermopile element |
| Communication | Digital (SMBUS) |
| Outputs | Object temp., self temp. |
| Window material | Optional (uncoated silicon, BPF) |
| Transmittance | ≥85%, 3000–5000 nm (for BPF) |
| Emissivity of window | 0.08 3000–5000 nm (for BPF) |
| Reflectance of window | 0.07 3000–5000 nm (for BPF) |
| Time constant | Max. 20 msec |
| Accuracy | ±1 °C |
| Responsivity | 30 V/W (without filter) |
| Specific detectivity | 0.6 108 cm√Hz/W |
| Operating temperature | (−20 °C) … (+100 °C) |
| Measurement range | (−20 °C) … (+400 °C) |
| Field of view | 20° |
| FoV tolerance | X-axis: ±2°, Y-axis: ±2° |
| Supply voltage | 5 V (±0.5 V) |
| Noise voltage for thermopile | 25 nV/√Hz/W |
| Current consumption | Max 7 mA |
| Output current | Max 80 mA |
| Transmittance () | Emissivity () | Reflectance () | |
|---|---|---|---|
| Cooking vessel | 0 | 0.59 | 0.41 |
| IR sensor window | ≥85%, 3–5 μm (BPF) | 0.08%, 3–5 μm (BPF) | 0.07%, 3–5 μm (BPF) |
| Glass ceramic | 0.05 |
| Transmittance () | Emissivity () | Reflectance () | |
|---|---|---|---|
| Cooking vessel | 0 | 0.59 | 0.41 |
| Optical filter | 0.05 | ||
| IR sensor window | ≥85%, 3–5 μm (BPF) | 0.08%, 3–5 μm (BPF) | 0.07%, 3–5 μm (BPF) |
| Glass ceramic | 0.05 |
| No. of Test | Target Temperature (°C) | Time (Minutes) | Traditional Energy (Wh) | Temperature-Controlled Energy (Wh) |
|---|---|---|---|---|
| 1 | 100 | 30 | 568 | 381 |
| 2 | 150 | 45 | 1314 | 920 |
| 3 | 200 | 45 | 1861 | 1340 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altuntaş, H.; Arslan, M.S. A New Approach for Infrared Temperature Measurement Sensor Systems and Temperature Control for Domestic Induction Hobs. Sensors 2025, 25, 235. https://doi.org/10.3390/s25010235
Altuntaş H, Arslan MS. A New Approach for Infrared Temperature Measurement Sensor Systems and Temperature Control for Domestic Induction Hobs. Sensors. 2025; 25(1):235. https://doi.org/10.3390/s25010235
Chicago/Turabian StyleAltuntaş, Hakan, and Mehmet Selçuk Arslan. 2025. "A New Approach for Infrared Temperature Measurement Sensor Systems and Temperature Control for Domestic Induction Hobs" Sensors 25, no. 1: 235. https://doi.org/10.3390/s25010235
APA StyleAltuntaş, H., & Arslan, M. S. (2025). A New Approach for Infrared Temperature Measurement Sensor Systems and Temperature Control for Domestic Induction Hobs. Sensors, 25(1), 235. https://doi.org/10.3390/s25010235






