Planetary Laser Interferometric Seismoacoustic Observatory
Abstract
1. Introduction
2. Types of Laser Strainmeters
2.1. Laser Strainmeter at Shultz Cape
2.2. Krasnokamensk Laser Strainmeter
2.3. Laser Strainmeter at Svobodny Cape
2.4. Baksan Laser Strainmeter
2.5. Laser Strainmeter on Popova Island and near Katsiveli Settlement
2.6. Quantitative Sensitivity Analysis
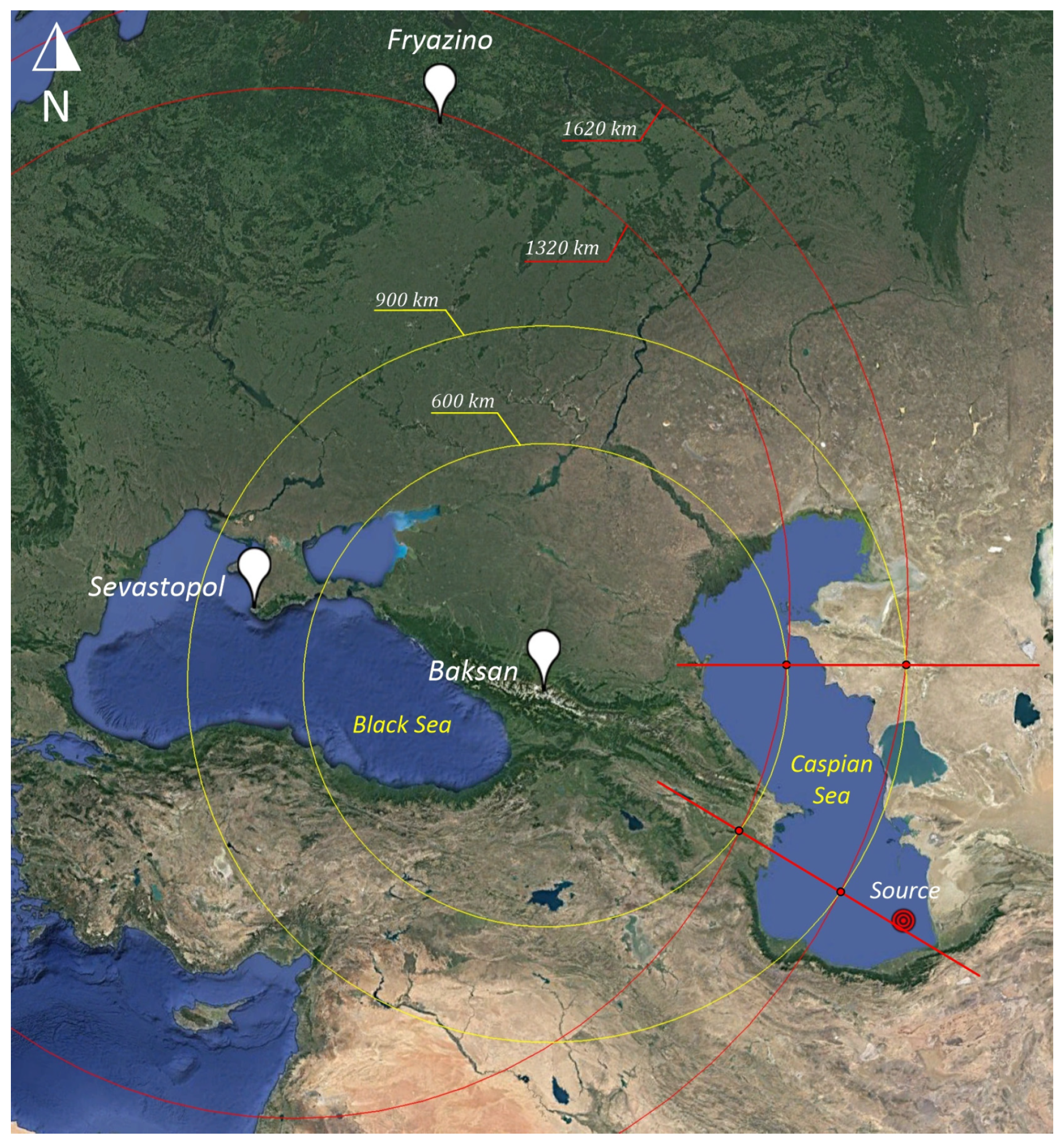
3. Operating Principle of Planetary Laser Interferometric Seismoacoustic Observatory: Triangulation
3.1. Triangulation Method of Finding Direction to Wave Source
- Distance from source to receiving points.
- We calculate the time of arrival at each point.
- We take into account that Baksan is point “0”, i.e., subtract the time of the wave arrival to Baksan from the remaining arrival times.
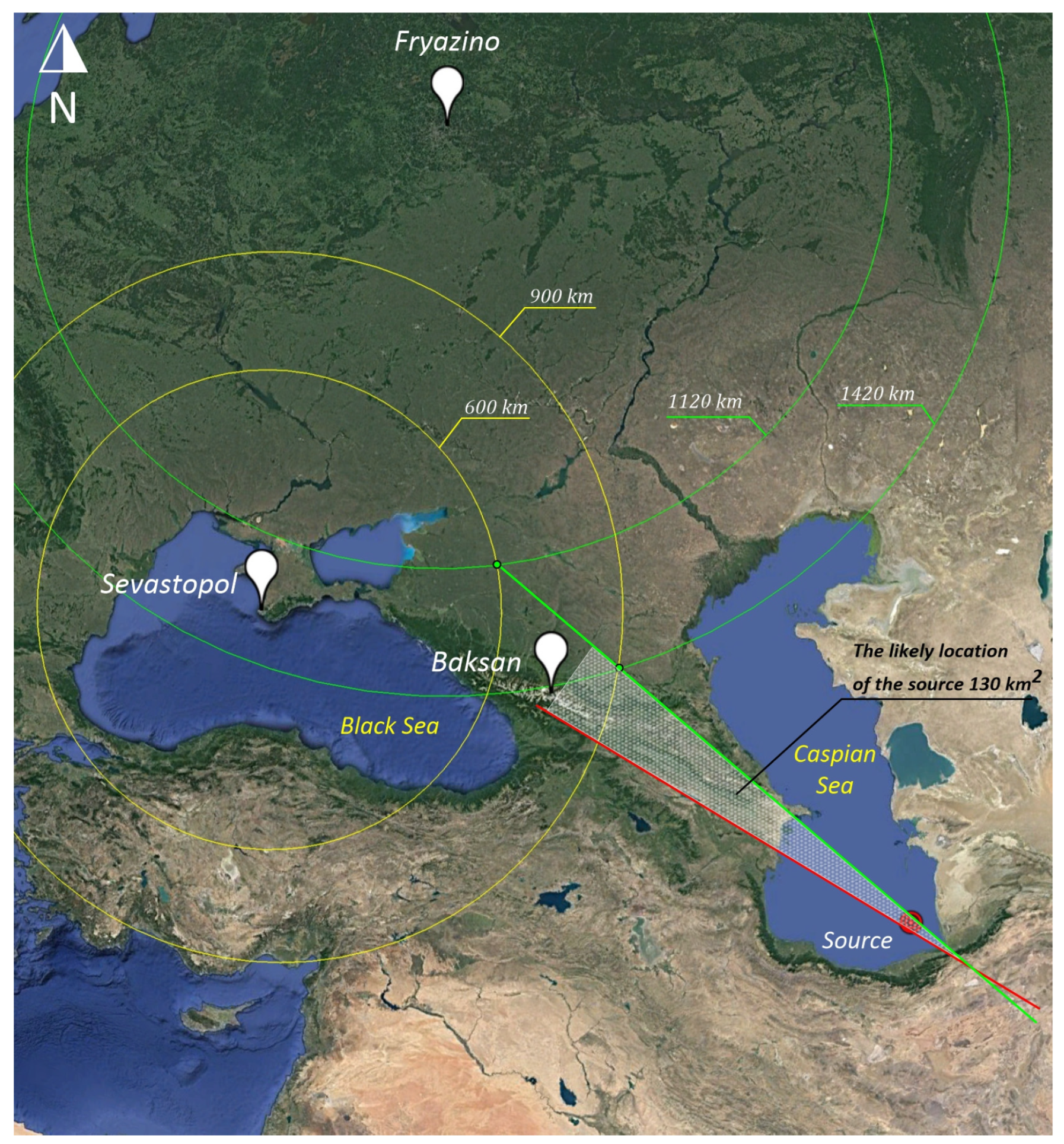
3.2. Baksan–Sevastopol
3.3. Sevastopol–Fryazino
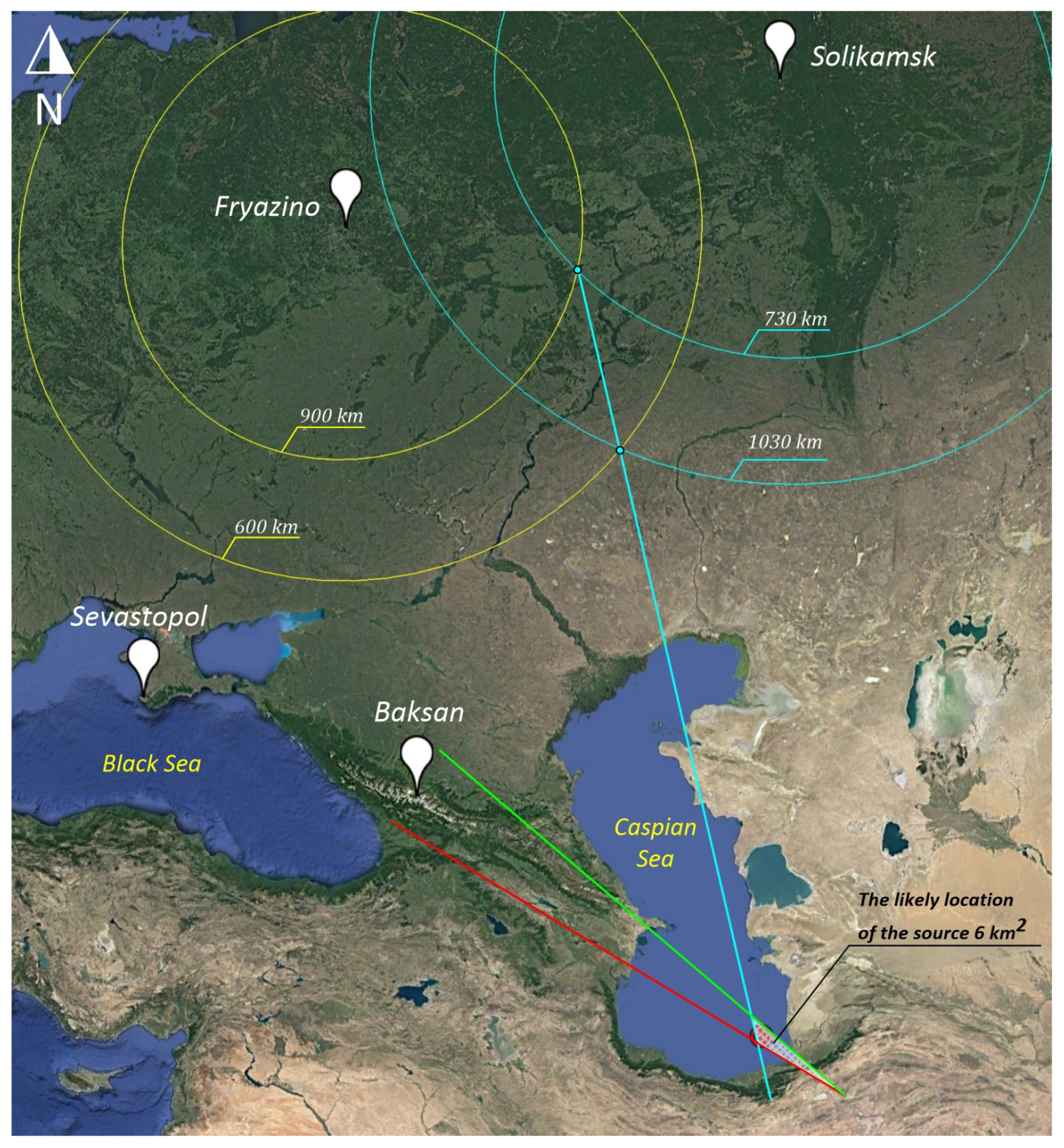
3.4. Fryazino–Solikamsk
4. Two-Dimensional Laser Strainmeter
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Benioff, H. A linear strain seismograph. Bull. Seismol. Soc. Amer. 1935, 25, 283–309. [Google Scholar] [CrossRef]
- Quartz strainmeter. Catalog of Geophysical Equipment. (Information Guide); Nauka: Moscow, Russia, 1981; Issue 4; pp. 146–148. [Google Scholar]
- Olson, L.E.; Sutton, J.H.; Ewing, M. Observation of the Earth’s own vibrations using strain and pendulum seismographs. In The Earth’s Own Vibrations; Mir: Moscow, Russia, 1964; pp. 80–105. [Google Scholar]
- Bilham, R.G. The location of Earth strain instrumentation. Phil. Trans. Roy. Soc. Lond. A 1973, 274, 429–433. [Google Scholar]
- Levine, J.; Hall, J.L. Design and operation of a methane absorption stabilized laser strainmeter. J. Geophys. Res. 1972, 77, 2595–2610. [Google Scholar] [CrossRef]
- Vali, V.; Krogstad, R.; Moss, R. Interferometer with OKG for measuring deformations of the Earth’s surface. TIIER 1965, 9, 186–194. [Google Scholar]
- Vali, V.; Bostrom, R.C. Laser interferometer with a base of 1000 m. Instrum. Sci. Res. 1968, 39, 52–61. [Google Scholar]
- Vali, V.; Bostrom, R.C. Some earth strain observations with a thousand meter laser interferometer. Earth Planet. Sci. Lett. 1968, 4, 436–438. [Google Scholar] [CrossRef]
- Vali, V. Lasers, measurements deformations of the Earth’s crust using a laser. In What Physicists Are Thinking About; Nauka: Moscow, Russia, 1965; pp. 125–138. [Google Scholar]
- King, G.C.; Gerard, V.B. Earth tides recorded by the 55-m Cambridge laser strainmeter. Geophys. J. Roy. Astr. Soc. 1974, 39, 269–282. [Google Scholar]
- Berger, R.J.; Hall, J.L. Pressure shift and broadening of methane line at 3.39 μ studied by laser-saturated molecular absorption. Phys. Rev. Lett. 1969, 22, 4. [Google Scholar] [CrossRef]
- Kamenev, O.T.; Kulchin, Y.N.; Petrov, Y.S.; Khiznyak, R.V.; Romashko, R.V. Fiber-optic seismometer on the basis of Mach-Zehnder interferometer. Sens. Actuators A Phys. 2016, 244, 133–137. [Google Scholar] [CrossRef]
- Kulchin, Y.N.; Voznesensky, S.S.; Gamayunov, E.L.; Golik, S.S.; Ilyin, A.A.; Kamenev, O.T.; Nikitin, A.I.; Pavlov, A.N.; Popik, A.Y.; Romashko, R.V.; et al. Photonic methods and technologies for monitoring the ocean and atmosphere. Quantum Electron. 2020, 50, 475–488. [Google Scholar] [CrossRef]
- Podlesnykh, A.A.; Kamenev, O.T.; Petrov, Y.S. 3 × 3 coupler Mach–Zehnder interferometric strainmeter. Bull. Russ. Acad. Sci. Phys. 2022, 86, S175–S178. [Google Scholar] [CrossRef]
- Kamenev, O.T.; Petrov, Y.S.; Podlesnykh, A.A.; Kolchinskiy, V.; Zavestovskaya, I.N. Optoelectronic Deformograph for Seismic Deformation Monitoring Systems. Bull. Lebedev Phys. Inst. 2023, 50, 469–472. [Google Scholar] [CrossRef]
- Dolgikh, G.I.; Butyrin, P.G.; Dolgikh, S.G.; Dyagilev, R.A.; Shvets, V.A.; Yakovenko, S.V. Recording of Infrasound Deformation Perturbations by Spatially Separated Laser Strainmeters. Dokl. Earth Sci. 2011, 441, 1583–1586. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Dolgikh, G.I.; Kovalev, S.N.; Koren’, I.A.; Ovcharenko, V.V. A Two-Coordinate Laser Strainmeter. Izv. Phys. Solid Earth 1998, 34, 946–950. [Google Scholar]
- Dolgikh, G.I.; Budrin, S.S.; Dolgikh, S.G.; Zakurko, A.G.; Kosarev, O.V.; Ovcharenko, V.V.; Plotnikov, A.A.; Chupin, V.A.; Shvets, V.A.; Yakovenko, S.V. A Complex Spatially Dispersed Polygon in the Far East for Earth Observations. Meas. Tech. 2016, 59, 252–255. [Google Scholar] [CrossRef]
- Dolgikh, G.I.; Dolgikh, S.G.; Rasskazov, I.Y.; Lugovoy, V.A.; Saksin, B.G. A 50 m Laser Strainmeter System Installed in Transbaikalia: Testing Results. Russ. Geol. Geophys. 2016, 57, 1771–1777. [Google Scholar] [CrossRef]
- Milyukov, V.K.; Klyachko, B.S.; Myasnikov, A.V.; Striganov, P.S.; Yanin, A.F.; Vlasov, A.N. A Laser Interferometer-Deformograph For Monitoring The Crust Movement. Instrum. Exp. Tech. 2005, 48, 780–795. [Google Scholar] [CrossRef]
- Dubrov, M.N.; Larionov, I.A.; Alexandrov, D.V.; Kravtsov, V.V. System of Laser Interferometers with a Large Spatial Difference to Study the Seismic-Deformation Oscillations of the Ea. Radioteh. I Èlektron. 2023, 68, 703–717. [Google Scholar] [CrossRef]





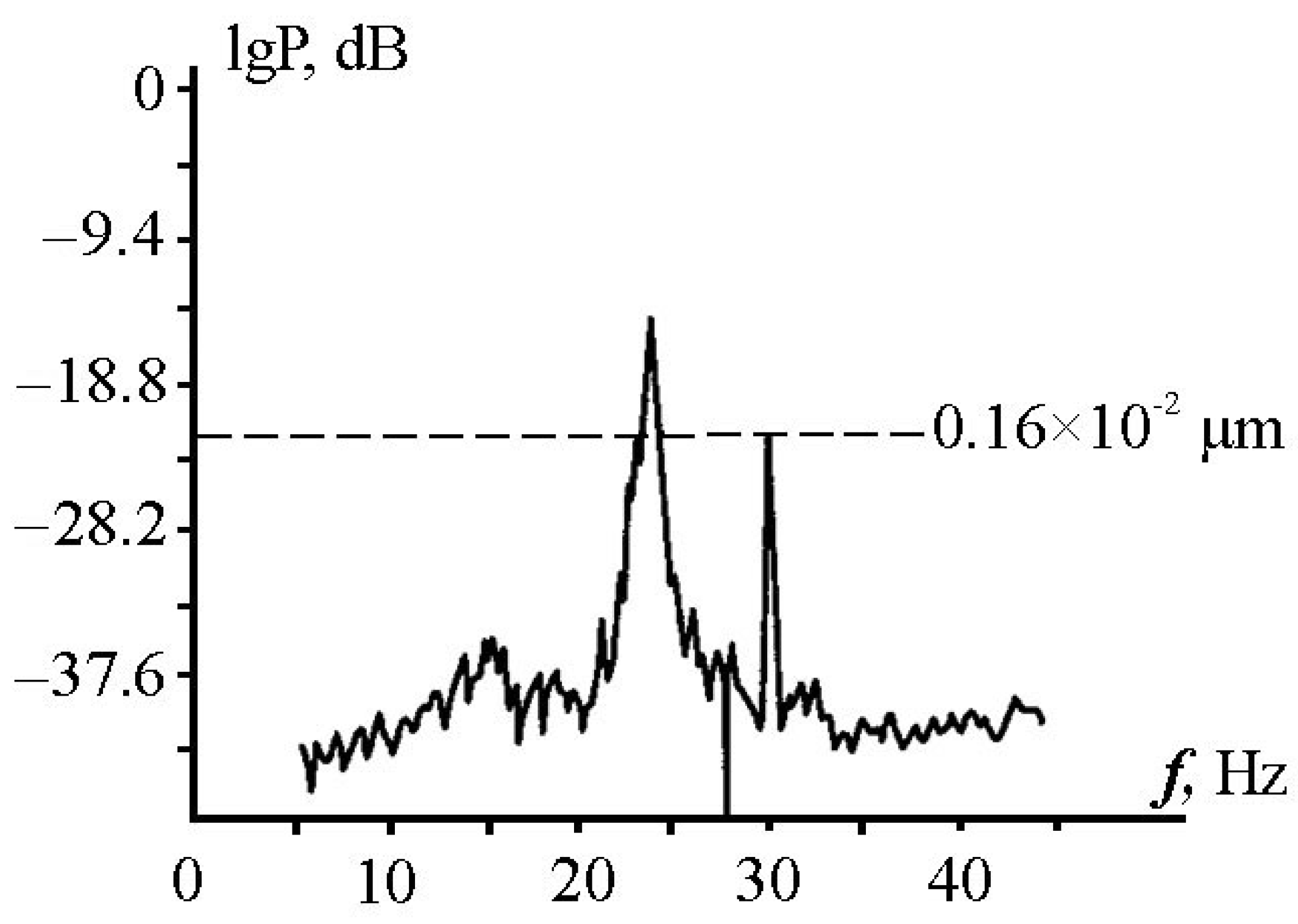
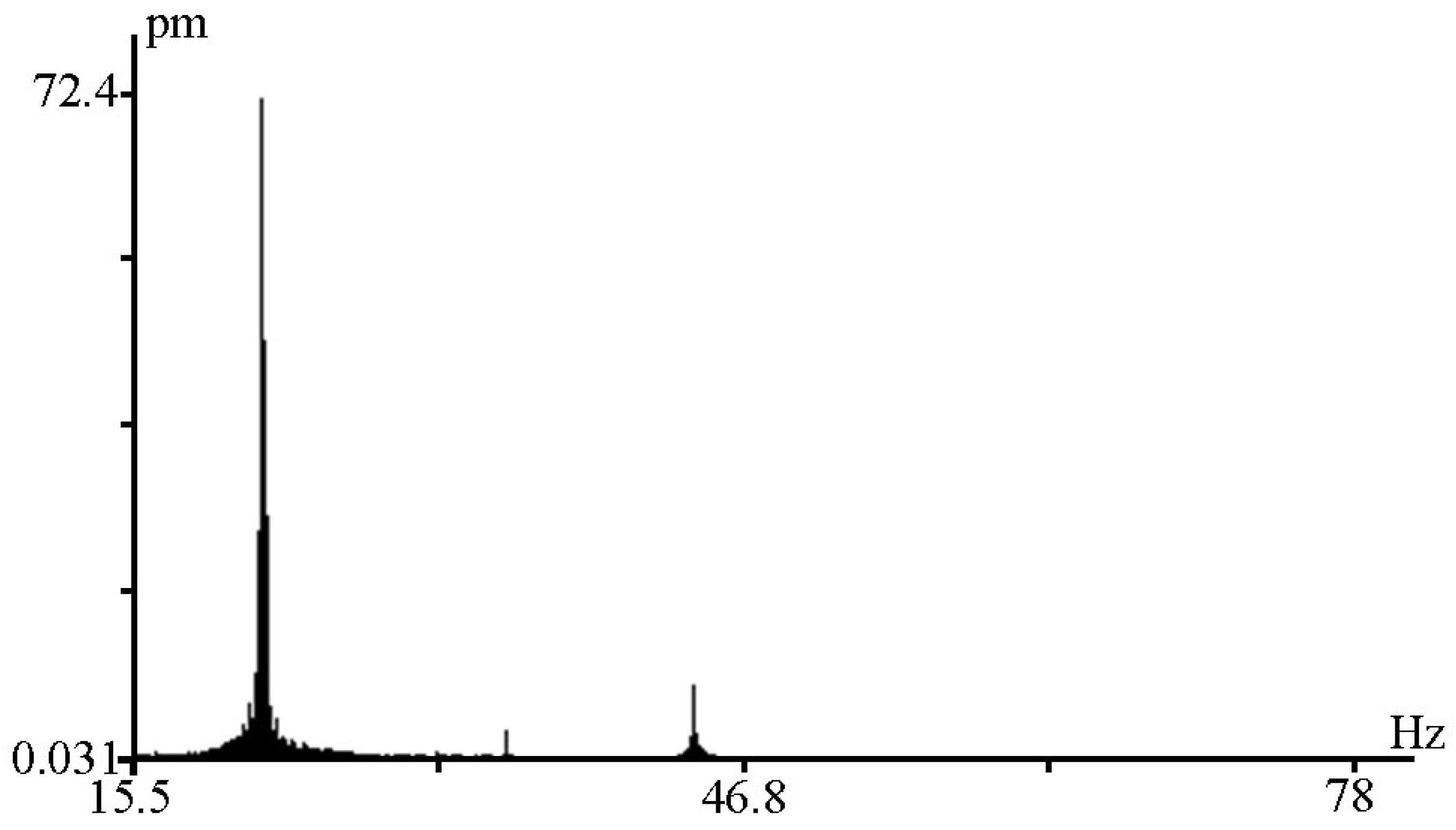

| № | Strainmeter Location | Coordinates | Length, m | Angle Relative to the “North-South” Line, ° | |
|---|---|---|---|---|---|
| 1 | Shultz Cape | 42°34′48.00″ N | 131°09′24.00″ E | 52.5 | 18 |
| 2 | Shultz Cape | 42°34′48.00″ N | 131°09′24.00″ E | 17.5 | 110 |
| 3 | Krasnokamensk | 50°03′14.00″ N | 118°10′31.00″ E | 50 | 30 |
| 4 | Svobodny Cape | 46°50′54.00″ N | 143°25′57.00″ E | 20 | 9 |
| 5 | Baksan | 43°16′37.00″ N | 42°41′35.00″ E | 75 | 150 |
| 6 | Popova Island | 42°28′45.00″ N | 131°43′30.00″ E | 20 | 46 |
| 7 | Katsiveli | 44°23′24.00″ N | 33°58′48.00″ E | 30 | 29 |
| № | Strainmeter Location | Distance from Source, km | Propagation Time (t), s | Disturbance Arrival Time (Δt), s | Distance (S), km |
|---|---|---|---|---|---|
| 1 | Svobodny Cape | 1570 | 494 | 0 | 0 |
| 2 | Shultz Cape | 2570 | 809 | 315 | 1000 |
| 3 | Krasnokamensk | 2870 | 904 | 409 | 1300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dolgikh, G.; Budrin, S.; Dolgikh, S.; Bolsunovskii, M.; Ivanov, M. Planetary Laser Interferometric Seismoacoustic Observatory. Sensors 2025, 25, 48. https://doi.org/10.3390/s25010048
Dolgikh G, Budrin S, Dolgikh S, Bolsunovskii M, Ivanov M. Planetary Laser Interferometric Seismoacoustic Observatory. Sensors. 2025; 25(1):48. https://doi.org/10.3390/s25010048
Chicago/Turabian StyleDolgikh, Grigory, Sergey Budrin, Stanislav Dolgikh, Mikhail Bolsunovskii, and Mikhail Ivanov. 2025. "Planetary Laser Interferometric Seismoacoustic Observatory" Sensors 25, no. 1: 48. https://doi.org/10.3390/s25010048
APA StyleDolgikh, G., Budrin, S., Dolgikh, S., Bolsunovskii, M., & Ivanov, M. (2025). Planetary Laser Interferometric Seismoacoustic Observatory. Sensors, 25(1), 48. https://doi.org/10.3390/s25010048






