Sub-MHz EMAR for Non-Contact Thickness Measurement: How Ultrasonic Wave Directivity Affects Accuracy
Abstract
1. Introduction
| Author | Operating Frequency in MHz | Sample Thickness | Accuracy | Highlights |
|---|---|---|---|---|
| Kawashima et al. [33] | Up to 150 | 20 μm to 1mm | N/A | High frequency |
| Hobbis et al. [34] | >5 | 0.28 mm to 2.8 mm | 0.08 μm (max. std) | Moving specimen |
| Dixon et al. [29] | >5 | 100 μm to 500 μm | 0.2% (relative) | Rapid ‘single shot’ measurement |
| Chen et al. [35] | >1 | 0.5 mm to 3 mm | <4% (relative) | Laser/EMAT configuration |
| Li et al. [36] | >2 | up to 8 mm | <2.5% (relative) | Sloped specimen |
| Yusa et al. [37] | 1 to 4 | up to 10 mm | ±0.2 mm (absolute) | Probabilistic evaluation |
| Cai et al. [38] | 2 to 6 | up to 10 mm | 0.9% (relative) | Specimen thickness step change |
| This work | 0.04 to 1 | 20mm | <0.2% (relative) | Wave directivity impact on accuracy |
- Reduced supply voltage: As the EMAT consists of a coil, the overall impedance, and therefore, the required excitation voltage, is lower when the operation frequency is decreased. Indeed, as will be demonstrated in this work, EMAR is successfully operated at voltages below 60 V.
- Improved human and electrical safety: The lower operating voltage minimizes electrical hazards to personnel, eases compliance with safety regulations, and facilitates adaptation to standards for use in explosion-risk environments.
- Lower attenuation in the material: Depending on the ultrasonic frequency, the wave is naturally attenuated due to the material properties. In general, the attenuation in metals is lower at low frequencies and increases at higher frequencies [40]. That fact also promotes operation in the sub-MHz range.
2. Materials and Methods
2.1. EMAT
- Magnetization
- Magnetostriction
- Lorentz forces
EMAT Design
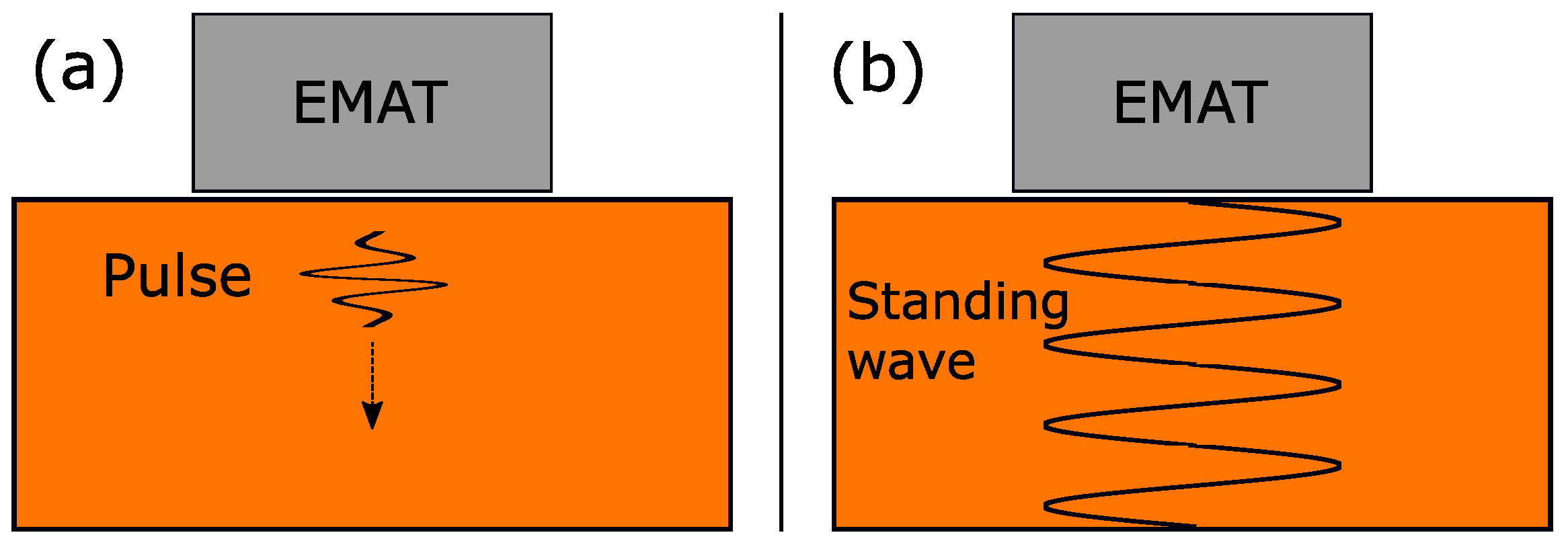
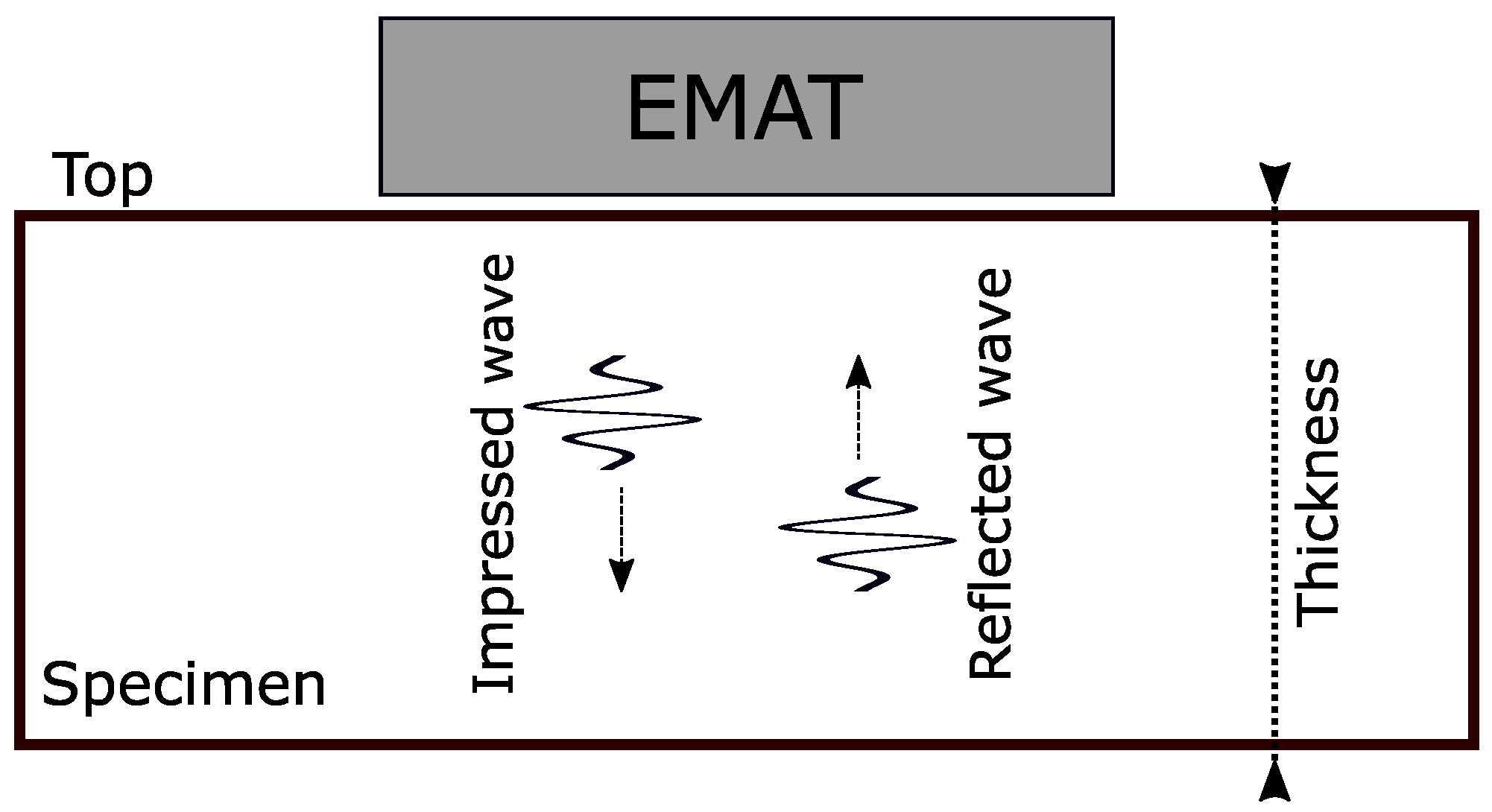
2.2. EMAR Working Principle
2.3. Test Samples
3. Simulation Setup
System Identification
4. Simulation Results
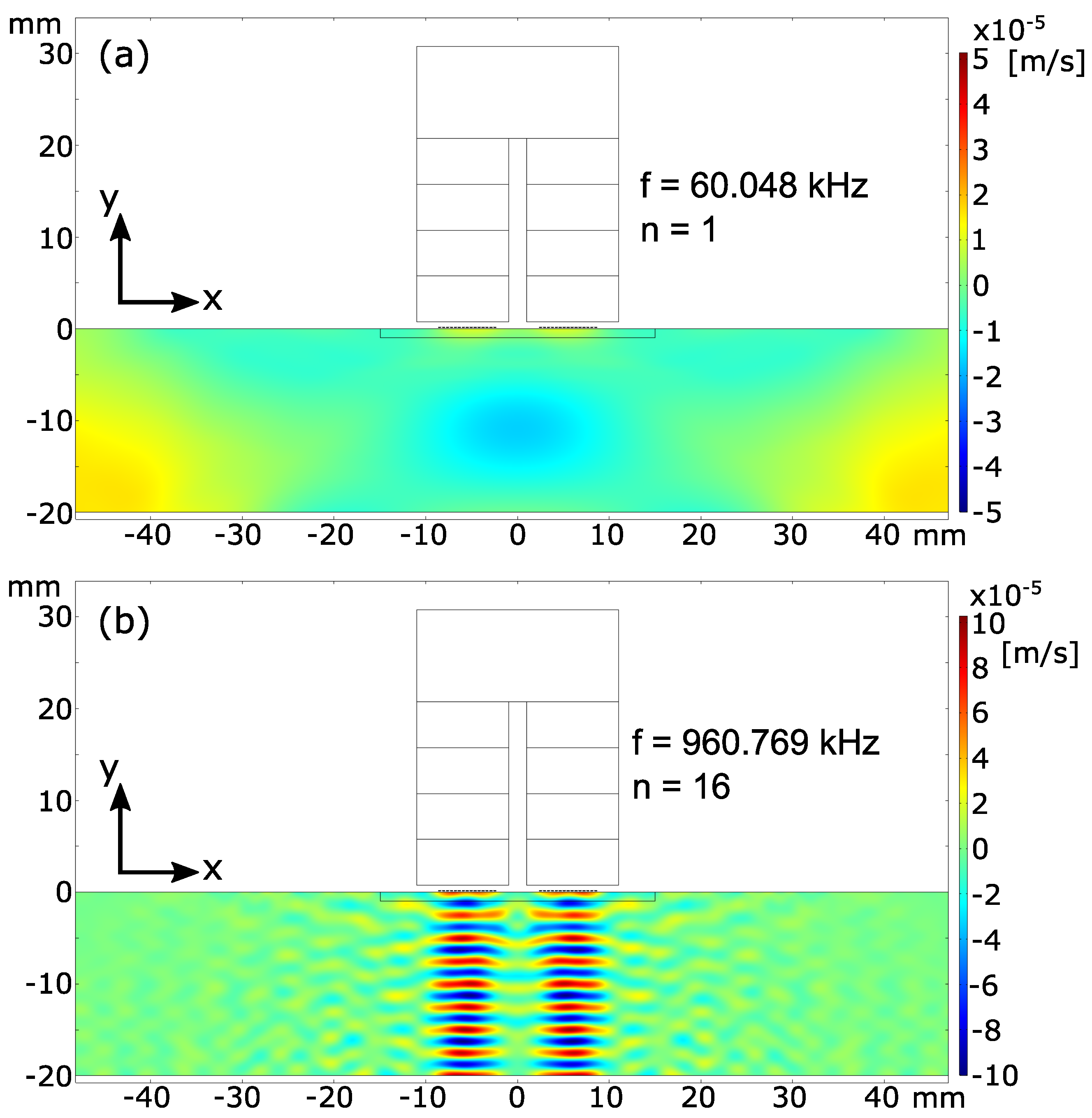
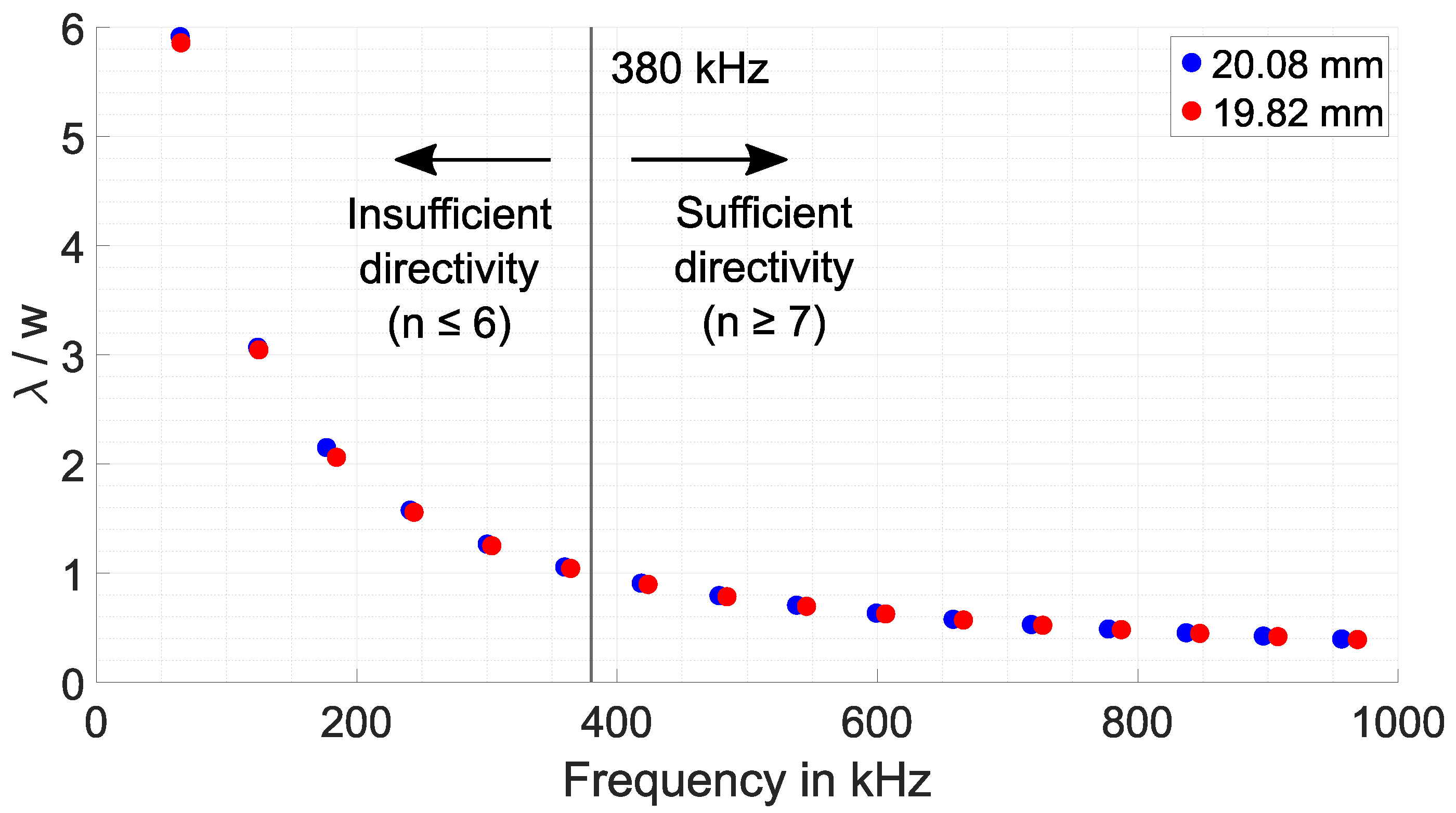
Directivity
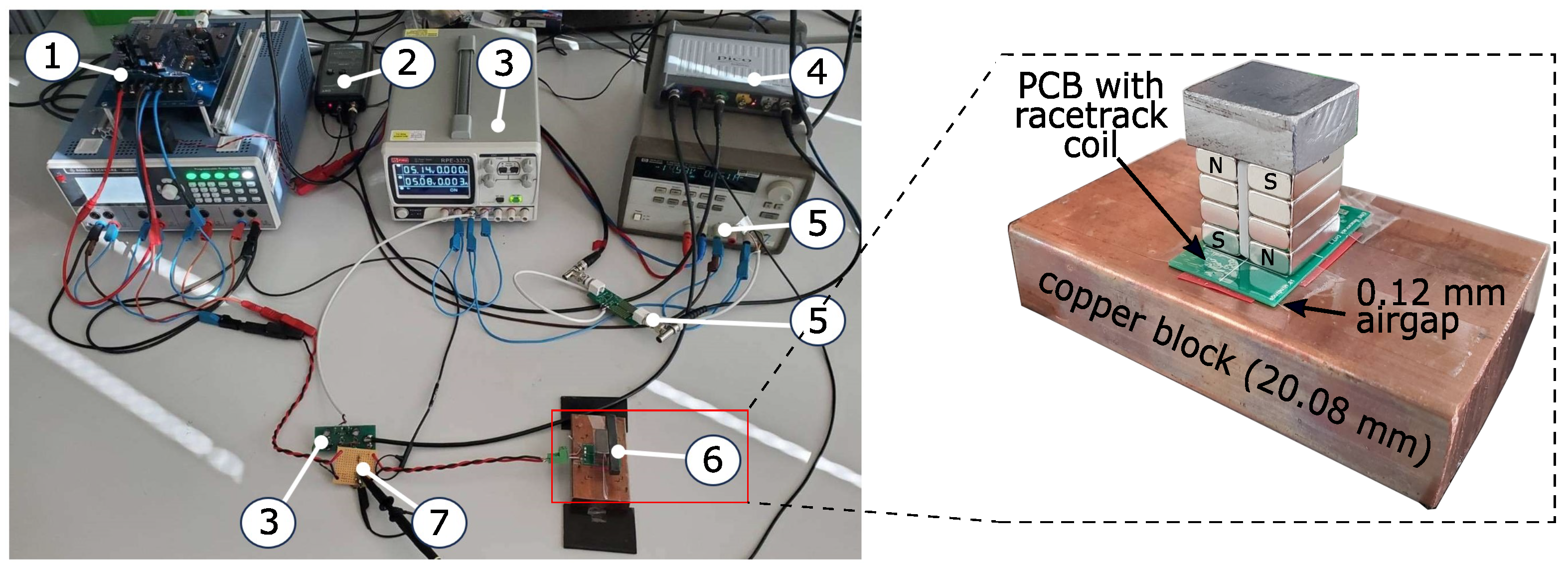
5. Measurement Setup and Signal Processing
Measurement Procedure
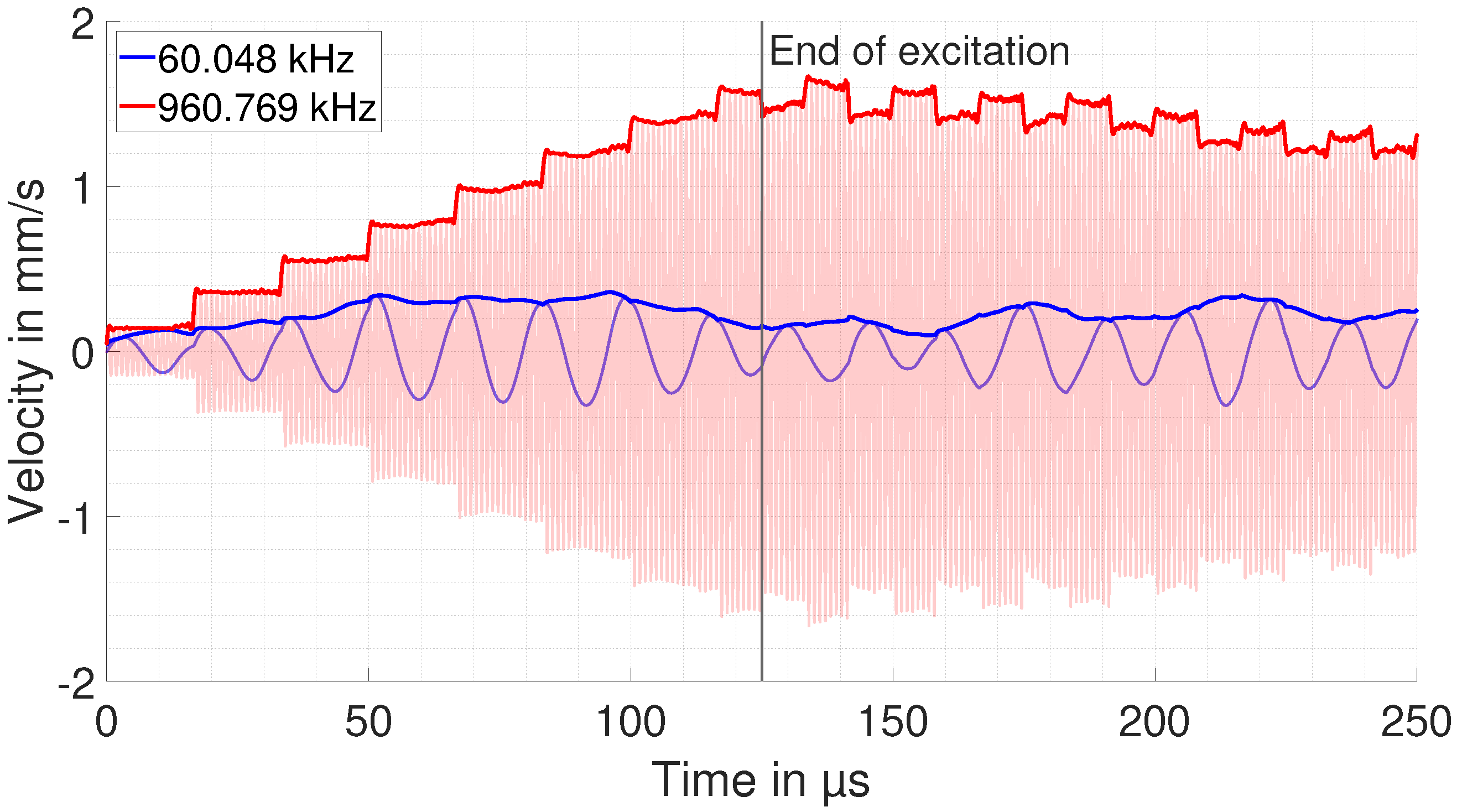
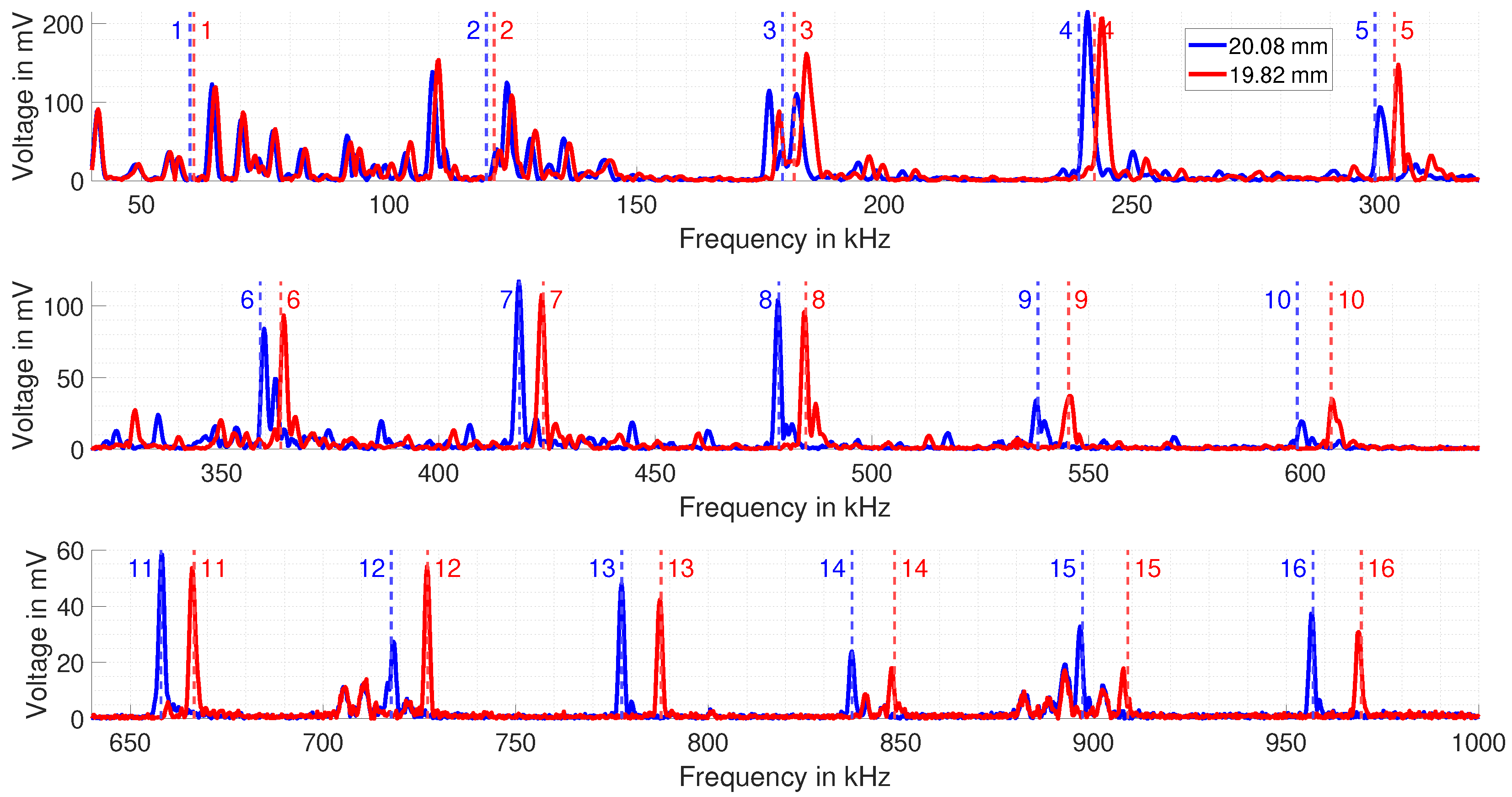
6. Measurement Results
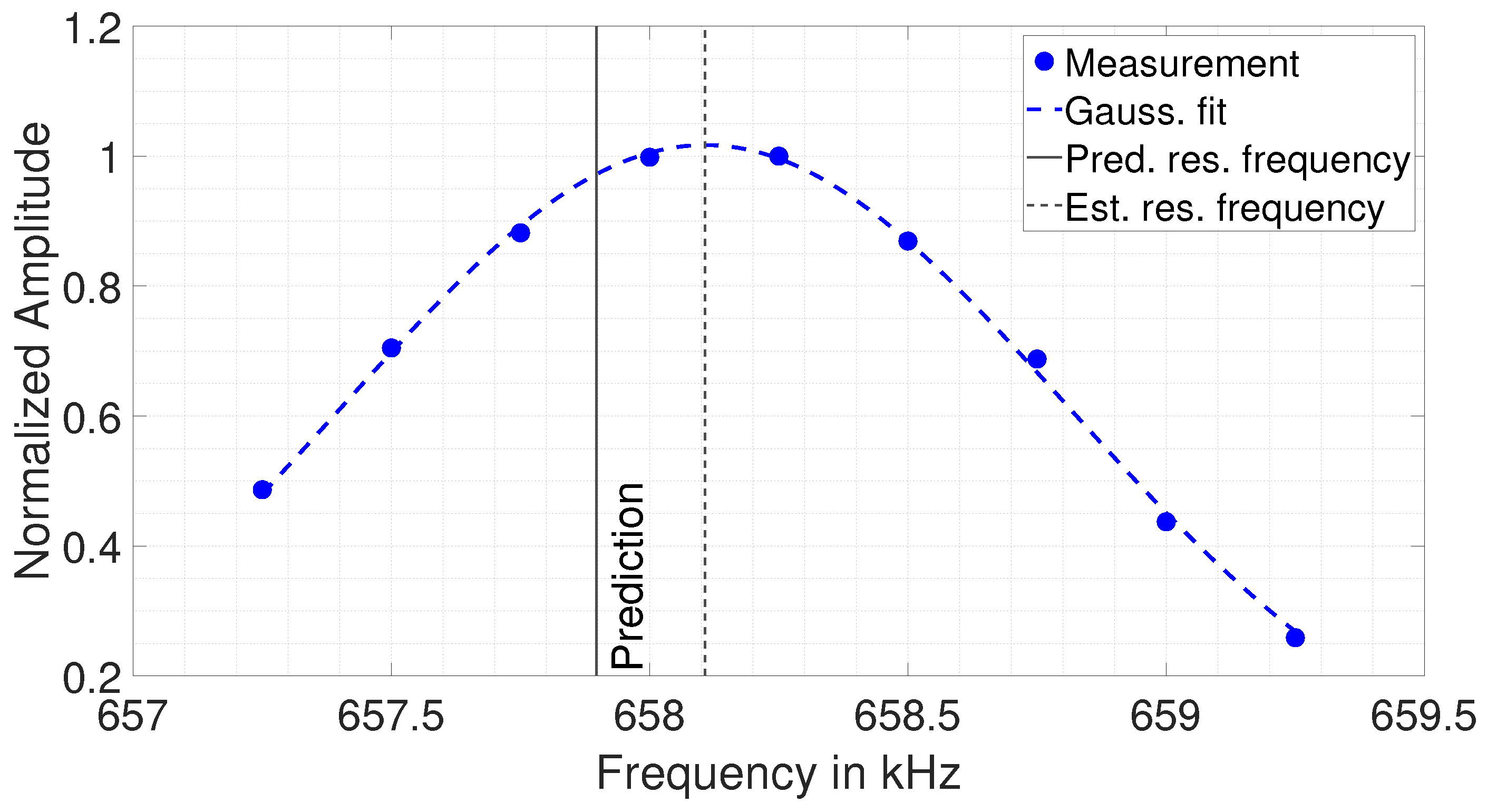
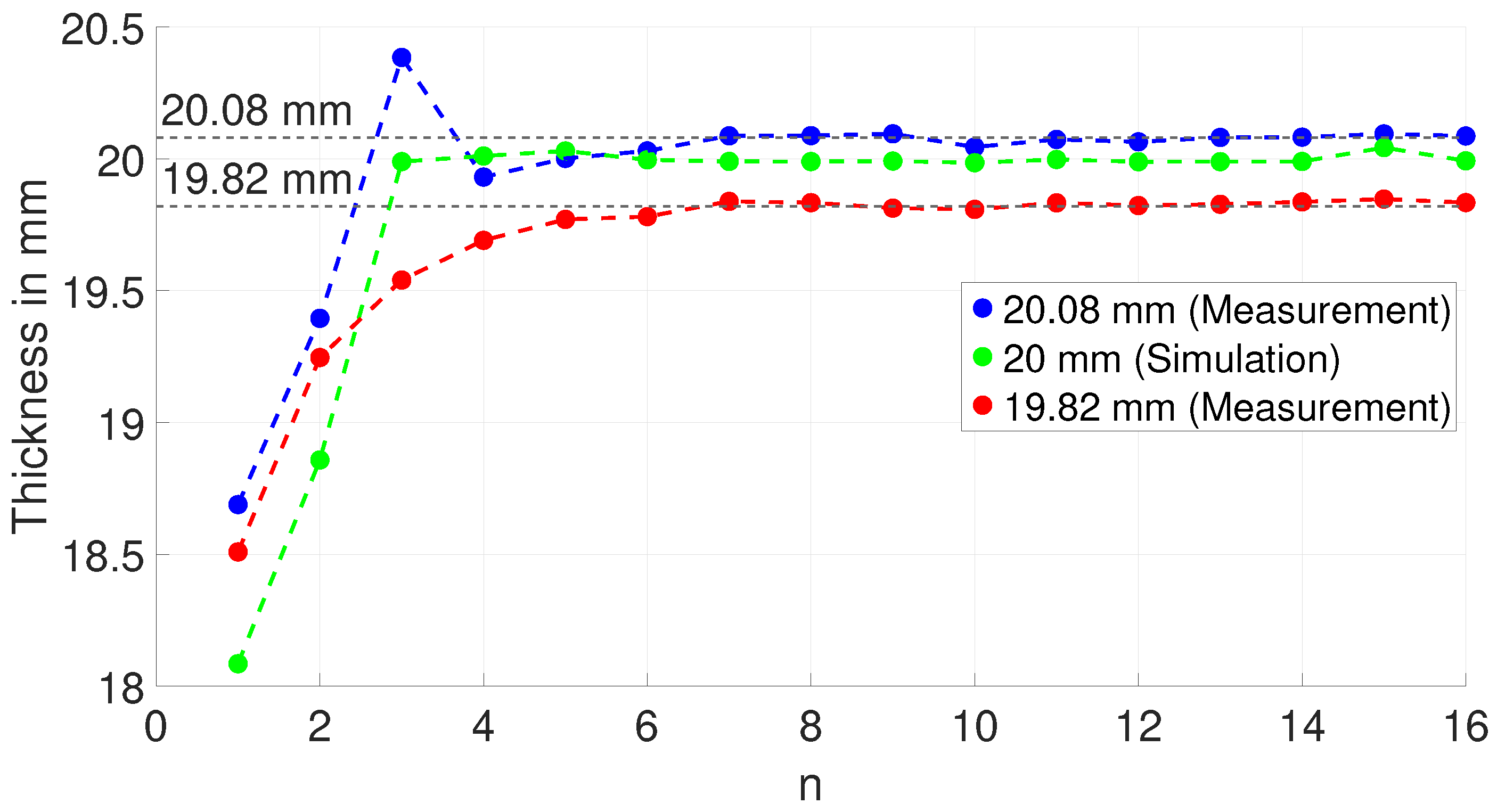
7. Thickness Estimation
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Billings, J.K. Noncontact ultrasonic gauging for industrial applications. J. Acoust. Soc. Am. 1986, 79, S60. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.; Wang, Z. Inversion Method in Pulsed Eddy Current Testing for Wall Thickness of Ferromagnetic Pipes. IEEE Trans. Instrum. Meas. 2020, 69, 9766–9773. [Google Scholar] [CrossRef]
- Heinlein, S.; Mariani, S.; Milewczyk, J.; Vogt, T.; Cawley, P. Improved thickness measurement on rough surfaces by using guided wave cut-off frequency. NDT E Int. 2022, 132, 102713. [Google Scholar] [CrossRef]
- Kumar, N.P.; Patankar, V.; Kulkarni, M. Ultrasonic Gauging and Imaging of Metallic Tubes and Pipes: A Review; International Atomic Energy Agency (IAEA): Vienna, Austria, 2020. [Google Scholar]
- Li, F.; Bell, A.; Damjanovic, D.; Jo, W.; Ye, Z.G.; Zhang, S. Recent Advances in Piezoelectric Materials for Electromechanical Transducer Applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 2999–3002. [Google Scholar] [CrossRef]
- Cegla, F.B.; Cawley, P.; Allin, J.; Davies, J. High-temperature (>500 °C) wall thickness monitoring using dry-coupled ultrasonic waveguide transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 156–167. [Google Scholar] [CrossRef] [PubMed]
- Sait, S.; Abbas, Y.; Boubenider, F. Estimation of thin metal sheets thickness using piezoelectric generated ultrasound. Appl. Acoust. 2015, 99, 85–91. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, S.; Luo, Y.; Xu, B.; Hao, W. Nondestructive analysis of debonding in composite/rubber/rubber structure using ultrasonic pulse-echo method. Nondestruct. Test. Eval. 2021, 36, 515–527. [Google Scholar] [CrossRef]
- Song, J.; Guo, D.; Jia, J.; Tu, S. A new on-line ultrasonic thickness monitoring system for high temperature pipes. Int. J. Press. Vessel. Pip. 2022, 199, 104691. [Google Scholar] [CrossRef]
- Zarei, A.; Pilla, S. Laser ultrasonics for nondestructive testing of composite materials and structures: A review. Ultrasonics 2024, 136, 107163. [Google Scholar] [CrossRef]
- Lefevre, F.; Jenot, F.; Ouaftouh, M.; Duquennoy, M.; Ourak, M. Laser generated guided waves and finite element modeling for the thickness gauging of thin layers. Rev. Sci. Instrum. 2010, 81, 034901. [Google Scholar] [CrossRef]
- Hirao, M.; Ogi, H. Electromagnetic Acoustic Transducers; Springer: Tokyo, Japan, 2017. [Google Scholar] [CrossRef]
- Zhai, G.; Li, Y.; Qin, Y.; Liu, Y. Design Method of Multiwavelength EMATs Based on Spatial Domain Harmonic Control. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 2259–2270. [Google Scholar] [CrossRef]
- Rueter, D.; Morgenstern, T. Ultrasound generation with high power and coil only EMAT concepts. Ultrasonics 2014, 54, 2141–2150. [Google Scholar] [CrossRef]
- Siegl, A.; Schweighofer, B.; Bergmann, A.; Wegleiter, H. An Electromagnetic Acoustic Transducer for Generating Acoustic Waves in Lithium-Ion Pouch Cells. In Proceedings of the 2022 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Ottawa, ON, Canada, 16–19 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Z.; Miao, Y.; Yuan, W.; Liu, Z. Study of a spiral-coil EMAT for rail subsurface inspection. Ultrasonics 2020, 108, 106169. [Google Scholar] [CrossRef]
- Pei, N.; Zhao, B.; Bond, L.J.; Xu, C. Analysis of the directivity of longitudinal waves based on double-fold coil phased EMAT. Ultrasonics 2022, 125, 106788. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Li, Z.; Wang, S.; Jiang, C. Analytical modelling and analysis of the meander-line coil EMATs. Ultrasonics 2025, 146, 107493. [Google Scholar] [CrossRef] [PubMed]
- Lunn, N.; Dixon, S.; Potter, M. High temperature EMAT design for scanning or fixed point operation on magnetite coated steel. NDT E Int. 2017, 89, 74–80. [Google Scholar]
- Zhai, G.; Liang, B.; Li, X.; Ge, Y.; Wang, S. High-temperature EMAT with double-coil configuration generates shear and longitudinal wave modes in paramagnetic steel. NDT E Int. 2022, 125, 102572. [Google Scholar] [CrossRef]
- Siegl, A.; Leithner, S.; Schweighofer, B.; Wegleiter, H. Excitation of Mechanical Resonances in the Stationary Ring of a Mechanical Seal by a Continuously Operated Electromagnetic Acoustic Transducer. Sensors 2023, 23, 1015. [Google Scholar] [CrossRef]
- Zuo, P. Underwater quantitative thickness mapping through marine growth for corrosion measurement using shear wave EMAT with high lift-off performance. Ultrasonics 2024, 143, 107426. [Google Scholar] [CrossRef]
- Han, S.W.; Cho, S.H.; Kang, T.; Moon, S.I. Design and test of electromagnetic acoustic transducer applicable to wall-thinning inspection of containment liner plates. Trans. Korean Soc. Press. Vessel. Pip. 2019, 15, 46–52. [Google Scholar]
- Rieger, K.; Erni, D.; Rueter, D. Examination of the Liquid Volume Inside Metal Tanks Using Noncontact EMATs From Outside. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 1314–1327. [Google Scholar] [CrossRef]
- Shi, Y.; Tian, S.; Jiang, J.; Lei, T.; Wang, S.; Lin, X.; Xu, K. Thickness Measurements with EMAT Based on Fuzzy Logic. Sensors 2024, 24, 4066. [Google Scholar] [CrossRef]
- Huang, S.; Zhao, W.; Zhang, Y.; Wang, S. Study on the lift-off effect of EMAT. Sens. Actuators A Phys. 2009, 153, 218–221. [Google Scholar] [CrossRef]
- Abderahmane, A.; Clausse, B.; Lhémery, A.; Daniel, L. Mechanisms of elastic wave generation by EMAT in ferromagnetic media. Ultrasonics 2024, 138, 107218. [Google Scholar] [CrossRef]
- Hirao, M.; Ogi, H. Electromagnetic acoustic resonance and materials characterization. Ultrasonics 1997, 35, 413–421. [Google Scholar] [CrossRef]
- Dixon, S.; Edwards, C.; Palmer, S. High accuracy non-contact ultrasonic thickness gauging of aluminium sheet using electromagnetic acoustic transducers. Ultrasonics 2001, 39, 445–453. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X.; Li, W.; Deng, M. Non-contact characterization of material anisotropy of additive manufacturing components by electromagnetic acoustic resonance technique. Meas. Sci. Technol. 2023, 35, 026001. [Google Scholar] [CrossRef]
- Yoshida, M.; Asano, T. A new method to measure the oxide layer thickness on steels using electromagnetic acoustic resonance. J. Nondestruct. Eval. 2003, 22, 11–21. [Google Scholar] [CrossRef]
- Liu, T.; Pei, C.; Cheng, X.; Zhou, H.; Xiao, P.; Chen, Z. Adhesive debonding inspection with a small EMAT in resonant mode. NDT E Int. 2018, 98, 110–116. [Google Scholar] [CrossRef]
- Kawashima, K.; Wright, O.B.; Hyoguchi, T. High frequency resonant electromagnetic generation and detection of ultrasonic waves. Jpn. J. Appl. Phys. 1994, 33, 2837. [Google Scholar] [CrossRef]
- Hobbis, A.; Aruleswaran, A. Non-contact thickness gauging of aluminium strip using EMAT technology. Nondestruct. Test. Eval. 2005, 20, 211–220. [Google Scholar] [CrossRef]
- Chen, W.; Lu, C.; Li, X.; Shi, W.; Zhou, Y.; Liu, Y.; Zhang, S. A novel laser-EMAT ultrasonic longitudinal wave resonance method for wall thickness measurement at high temperatures. Ultrasonics 2024, 141, 107340. [Google Scholar] [CrossRef]
- Li, Y.; Cai, Z.; Chen, L. Detection of Sloped Aluminum Plate Based on Electromagnetic Acoustic Resonance. IEEE Trans. Instrum. Meas. 2022, 71, 6000812. [Google Scholar] [CrossRef]
- Yusa, N.; Song, H.; Iwata, D.; Uchimoto, T.; Takagi, T.; Moroi, M. Probabilistic evaluation of EMAR signals to evaluate pipe wall thickness and its application to pipe wall thinning management. NDT E Int. 2021, 122, 102475. [Google Scholar] [CrossRef]
- Cai, Z.; Sun, Y.; Lu, Z.; Zhao, Q. Research on Identification and Detection of Aluminum Plate Thickness Step Change Based on Electromagnetic Acoustic Resonance. Magnetochemistry 2023, 9, 86. [Google Scholar] [CrossRef]
- Engineering ToolBox. Solids and Metals—Speed of Sound. Available online: https://www.engineeringtoolbox.com/sound-speed-solids-d_713.html (accessed on 4 October 2024).
- Ono, K. A Comprehensive Report on Ultrasonic Attenuation of Engineering Materials, Including Metals, Ceramics, Polymers, Fiber-Reinforced Composites, Wood, and Rocks. Appl. Sci. 2020, 10, 2230. [Google Scholar] [CrossRef]
- Khalili, P.; Cegla, F. Excitation of Single-Mode Shear-Horizontal Guided Waves and Evaluation of Their Sensitivity to Very Shallow Crack-Like Defects. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 818–828. [Google Scholar] [CrossRef]
- Sarris, G.; Haslinger, S.G.; Huthwaite, P.; Lowe, M.J.S. Fatigue State Characterization of Steel Pipes Using Ultrasonic Shear Waves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2023, 70, 72–80. [Google Scholar] [CrossRef] [PubMed]
- Siegl, A.; Schweighofer, B.; Wegleiter, H. A Sensor Model to Simulate the Excitation and Propagation of Lamb Waves in Lithium-Ion Pouch Cells. IEEE Sens. Lett. 2023, 7, 6004504. [Google Scholar] [CrossRef]
- AmesWeb. Modulus of Elasticity for Metals. Available online: https://amesweb.info/Materials/Modulus-of-Elasticity-Metals.aspx (accessed on 4 October 2024).
- Koti, V.; George, R.; Shakiba, A.; Murthy, K. Mechanical properties of copper nanocomposites reinforced with uncoated and nickel coated carbon nanotubes. FME Trans. 2018, 46, 623–630. [Google Scholar] [CrossRef]
- Oppenheim, A.; Schafer, R.; Buck, J. Discrete-Time Signal Processing; Prentice Hall international editions; Prentice Hall: Saddle River, NJ, USA, 1999. [Google Scholar]








| Thickness | Wave Speed | First Resonance (n = 1) |
|---|---|---|
| 1 mm | 2300 m s−1 [39] | 1.15 MHz |
| 20 mm | 58 kHz |
| Parameter | Range | Choice |
|---|---|---|
| Young’s Modulus in GPa | 110–138 | 133.5 |
| Density in kg/m3 | 8900–8960 | 8900 |
| Poisson’s ratio | 0.3–0.34 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siegl, A.; Auer, D.; Schweighofer, B.; Hochfellner, A.; Klösch, G.; Wegleiter, H. Sub-MHz EMAR for Non-Contact Thickness Measurement: How Ultrasonic Wave Directivity Affects Accuracy. Sensors 2025, 25, 4746. https://doi.org/10.3390/s25154746
Siegl A, Auer D, Schweighofer B, Hochfellner A, Klösch G, Wegleiter H. Sub-MHz EMAR for Non-Contact Thickness Measurement: How Ultrasonic Wave Directivity Affects Accuracy. Sensors. 2025; 25(15):4746. https://doi.org/10.3390/s25154746
Chicago/Turabian StyleSiegl, Alexander, David Auer, Bernhard Schweighofer, Andre Hochfellner, Gerald Klösch, and Hannes Wegleiter. 2025. "Sub-MHz EMAR for Non-Contact Thickness Measurement: How Ultrasonic Wave Directivity Affects Accuracy" Sensors 25, no. 15: 4746. https://doi.org/10.3390/s25154746
APA StyleSiegl, A., Auer, D., Schweighofer, B., Hochfellner, A., Klösch, G., & Wegleiter, H. (2025). Sub-MHz EMAR for Non-Contact Thickness Measurement: How Ultrasonic Wave Directivity Affects Accuracy. Sensors, 25(15), 4746. https://doi.org/10.3390/s25154746









