Combining a Standardized Growth Class Assessment, UAV Sensor Data, GIS Processing, and Machine Learning Classification to Derive a Correlation with the Vigour and Canopy Volume of Grapevines
Abstract
1. Introduction
- Is there a significant difference between spectral, structural, and texture input features and their combinations for model prediction metrics and the robustness of the results?
- Which classifiers after hyperparameter tuning provide the best overall prediction performance?
- Which growth classes have the highest positive prediction matches, and which have the lowest matches? Is there a pattern in class-specific metrics that can be addressed in the model prediction process and the selected input feature groups?
- Based on the findings from the previous points, what are the advantages and limitations of the growth class assessment after Porten [43], and how could the evaluation, database, methodology, and classification process be optimized to improve the prediction and separability of the growth classes in the future?
2. Materials and Methods
2.1. Test Site and Field Data Acquisition (Ground Truth Data)
2.2. Vine Growth and Growth Classification Assessment After Porten (2020)
2.3. Growth and Infection Classification Assessment After Porten (2020)
2.4. Manual Ground Truth Labeling of Vines
2.5. UAV Data Acquisition, Preparation, and Processing
2.5.1. Localization and Spatial Reference System of the Geodata
2.5.2. UAV Sensor Data Acquisition
2.5.3. Photogrammetry
2.5.4. Single Vine Geopositions
2.6. Geoprocessing Workflow
2.6.1. Vine Row Mask for Feature Extraction
2.6.2. Spectral Feature Type for Classification (Vegetation Indices)
2.6.3. Structural Feature Types for Classification
2.6.4. Texture Feature Types for Classification
2.6.5. Extraction Mask Generation
2.6.6. Pixel-Based Mask
2.6.7. OBIS (Object-Based Image Segmentation)-Based Mask
2.6.8. Merging Vine Row Masks
2.6.9. Spatial Data Aggregation (Zonal Statistics)
2.6.10. Calculation of the Canopy Height Model (CHM) Volume for Single Vines
2.7. Growth Class Estimation Modeling
3. Results
3.1. CHM Volume Results
3.2. Overall Growth Class Prediction
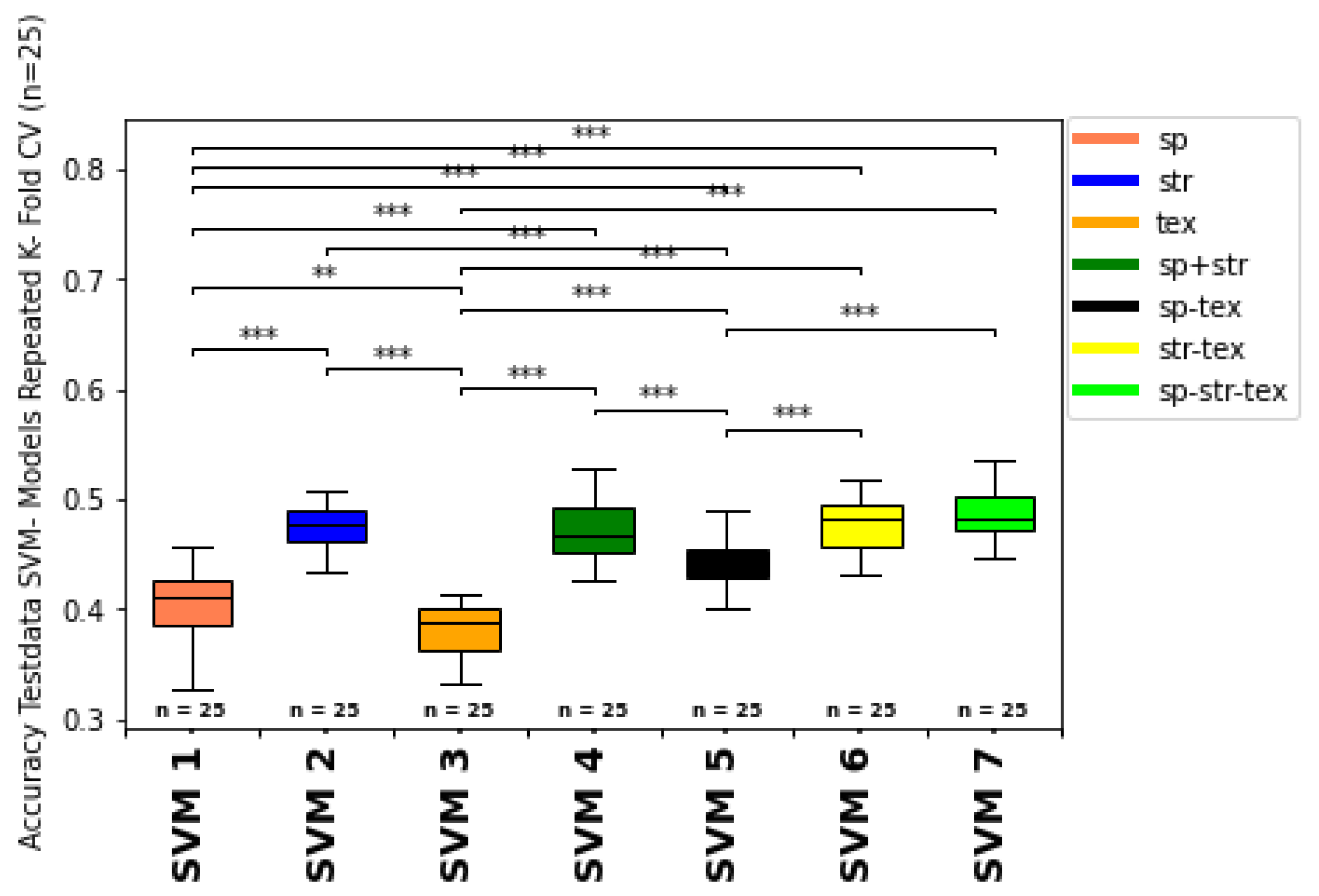
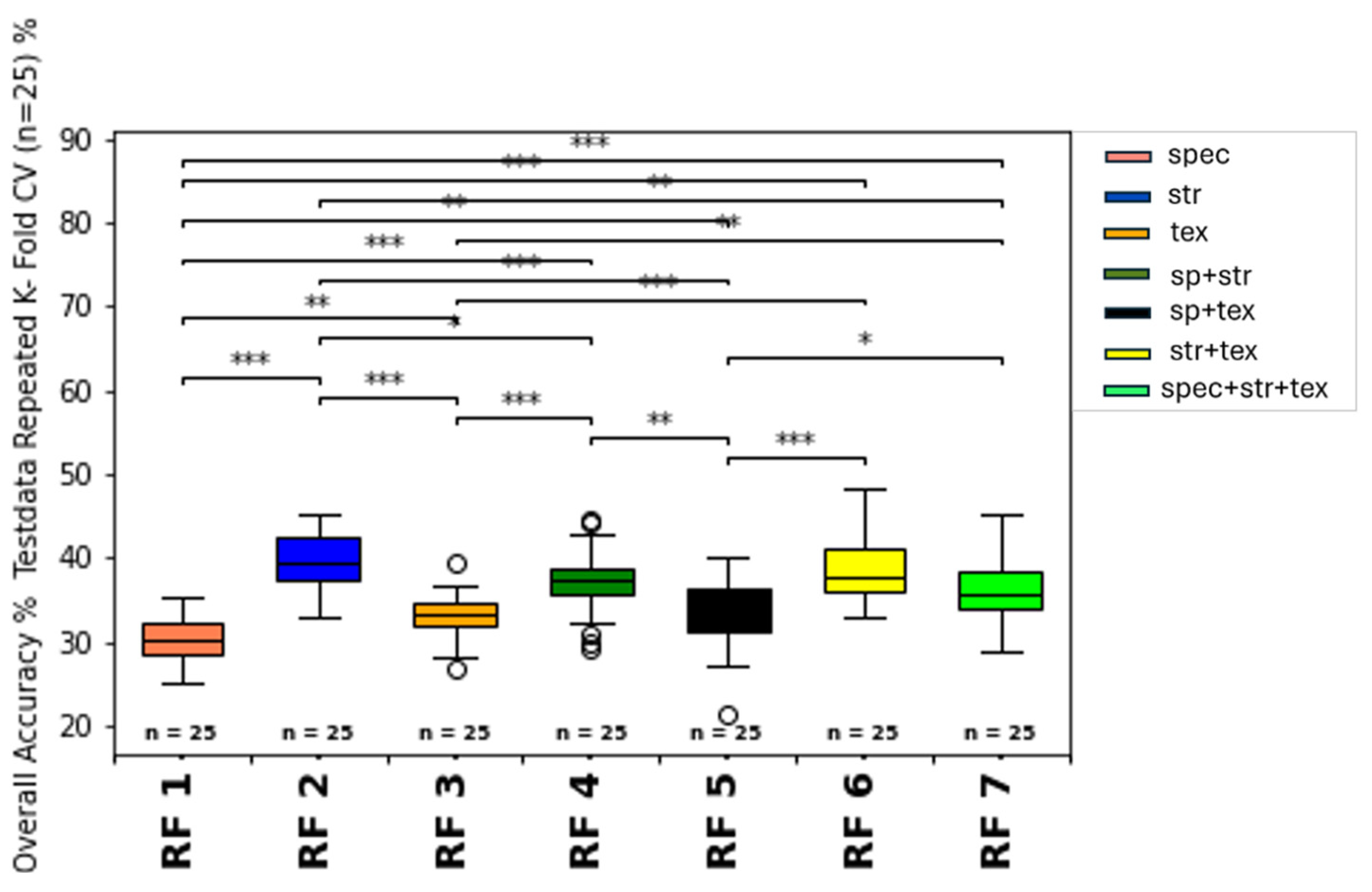
3.2.1. Spectral Feature Group Estimation
3.2.2. Structural-Feature-Based Growth Class Estimation
3.2.3. Texture-Feature-Based Growth Class Estimation
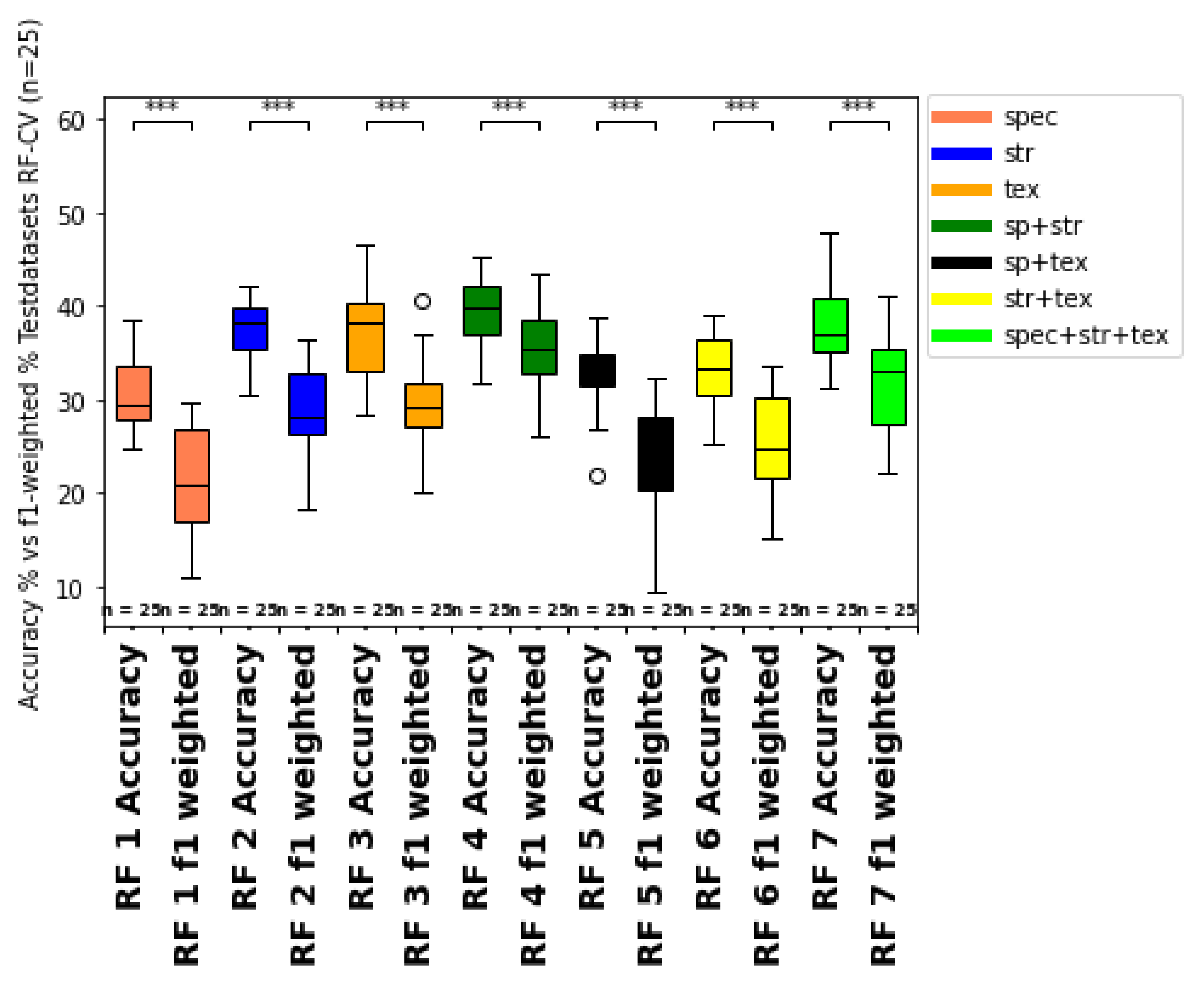
3.2.4. Summary of Impact of Feature Types and Feature Type Combination on Model Classification
3.2.5. Overall Growth Class Prediction
4. Discussion
4.1. Extraction Masks
4.2. Structural Parameters and CHM Volume
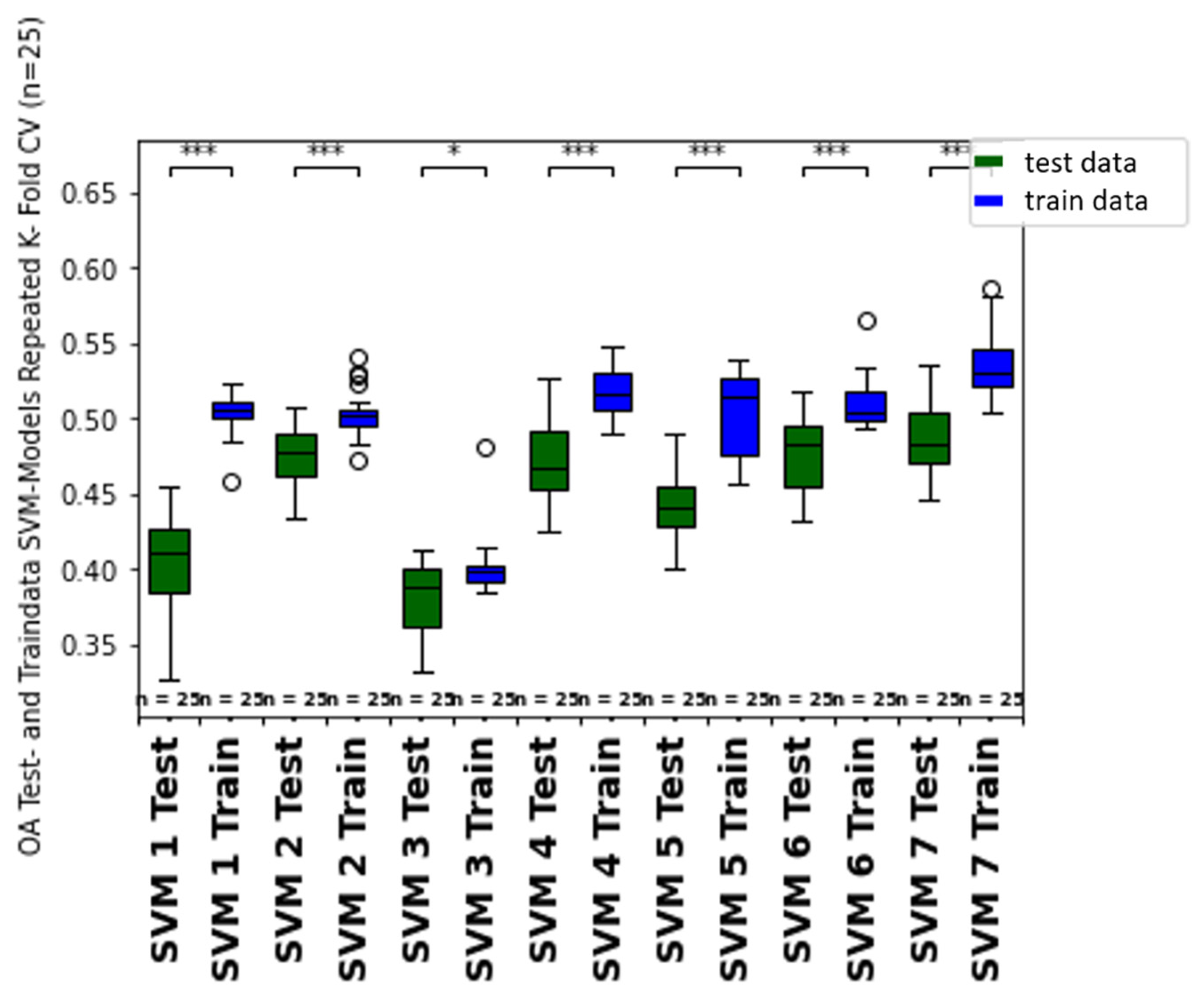
4.3. Model Validation
4.4. Model Performance Evaluation
4.4.1. Influence of Spectral Features
4.4.2. Influence of Structural Features
4.4.3. Influence of Texture Features
4.4.4. Combining Different Feature Types
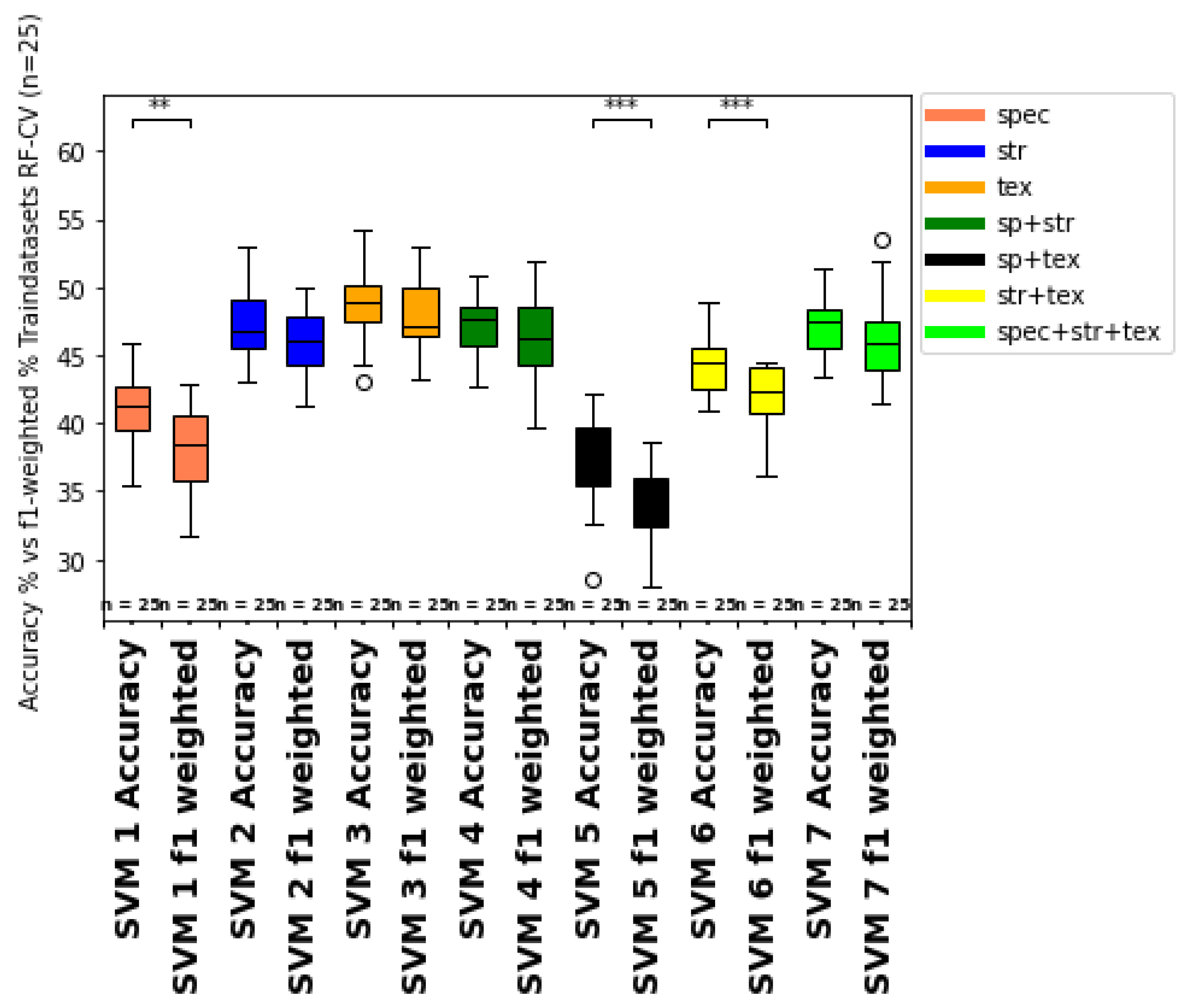
4.5. Comparison of Machine Learning Classifiers (RFC vs. SVM)
4.6. Class-Specific Accuracies of the Best Model
5. Conclusions and Future Work
- (1)
- Combining spectral, structural, and texture features indicates the best classification results for both machine learning classifiers (Random Forest Classifier and Support Vector Machine Classifier). Nevertheless, SVM performed better than RFC, due to classifier properties and ground truth data set characteristics.
- (2)
- The structural input features are the most positively influencing feature type. The canopy structural features achieved higher accuracy and f1-weighted scores, than models using spectral or textural features alone or combined. Canopy structural features most likely provide a more accurate representation of canopy architecture than spectral and texture features.
- (3)
- Although less influential than structural features, canopy spectral and texture features are also an essential indicator for growth class estimation. They may also offer a means to overcome saturation issues associated with spectral features from nadir camera positions.
- (4)
- The class-specific accuracies show that most growth classes were correctly predicted, or the mismatch between the predicted and labeled classes was only minor. Therefore, the class-specific accuracy would increase to over 80 or 90% when considering the neighborhood growth classes as matches. Nevertheless, some classes, like growth class 0, 1, or 9, are difficult to separate with sufficient probability due to different error sources and distortions. These include subjective ground truth labeling (inter- and intrapersonal sources of error), uncertainty in distinguishing the growth classes, different approaches of the individual classification methods, complex correlation and varying influence strength of input parameters to the particular ML growth class prediction, and other disruptive influences (e.g. radiometric interference) during data acquisition.
- (5)
- The comparison of training and test datasets overall accuracy and growth class specific user and producer accuracies of the class-specific prediction hint to overfitting of the different models for both classifiers (SVM, RFC). Moreover, the difference between unbalanced (accuracy) and balanced prediction metrics (f1-weighted score) indicate imbalance of the ground truth dataset, which should be further considered and improved in future studies, for example, by integrating ground truth data from other years, growth stages and other vine fields.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANOVA | Analysis Of Variance |
| API | Application Programming Interface |
| CHM | Canopy Height Model |
| CRS | Coordinate Reference System |
| CSM | Crop Surface Model |
| DSM | Digital Surface Model |
| DTM EPSG | Digital Terrain Model European Petroleum Survey Group Geodesy |
| ETRS | European Terrestrial Reference System |
| GCP | Ground Control Points |
| GDAL | Geospatial Data Abstraction Library |
| GIS | Geographic Information System |
| GLCM | Gray-Level Co-occurrence Matrix |
| GNDVI | Green Normalized Vegetation Index |
| GNSS | Global Navigation Satellite System |
| GPR | Gaussian Process Regressor |
| GPS | Global Positioning System |
| LAI | Leaf Area Index |
| LiDAR | Light Detection and Ranging |
| ML | Machine Learning |
| NDVI | Normalized Difference Vegetation Indices |
| NDREI | Normalized Difference Red Edge Index |
| NDWI | Normalized Difference Water Index |
| NIR | Near Infrared |
| OA OBIA | Overall Accuracy Object-Based Image Analysis |
| OBIS | Object-Based Image Segmentation |
| OSAVI | Optimized Soil Adjusted Vegetation Indices |
| QGIS | Quantum GIS |
| PLSR | Partial Least Square Regression |
| RE RGB | Red-Edge Red Green Blue |
| RFC | Random Forest Classifier |
| RMSE | Root Mean Squared Error |
| SAGA | System for Automatic Geoscientific Analysis |
| SAPOS | SAtelitten POSitionierungsdienst der deutschen Landvermessung |
| SfM | Structure from Motion |
| SVM | Support Vector Machines |
| TSAVI | Transformed Soil Adjusted Vegetation Indice |
| VI | Vegetation Indices |
| UAV | Unmanned Aerial Vehicle |
| UTM | Universal Transverse Mercator |
References
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Lllorens, J.; Llop, J.; Escola, A. Ultrasonic and LIDAR Sensors for Electronic Canopy Characterization in vineyards, Advances to improve Pesticide Application methods. Sensors 2011, 11, 2177–2194. [Google Scholar] [CrossRef]
- Campos, J.; García-Ruíz, F. Assessment of Vineyard Canopy Characteristics from Vigour Maps Obtained Using UAV and Satellite Imagery. Sensors 2021, 21, 2363. [Google Scholar] [CrossRef]
- Moreno, H.; Andújar, D. Proximal sensing for geometric characterization of vines: A review of the latest advances. Comput. Electron. Agric. 2023, 210, 107901. [Google Scholar] [CrossRef]
- Tardaguila, J.; Stoll, M.; Guitiérrez, S.; Profitt, T.; Diago, M.P. A review: Smart applications and digital technologies in viticulture. Smart Agric. Technol. 2021, 1, 100005. [Google Scholar] [CrossRef]
- Ferro, M.V.; Catania, P. Technologies and Innovative Methods for Precision Viticulture: A Comprehensive Review. Horticulture 2023, 9, 399. [Google Scholar] [CrossRef]
- Zualkernan, I.; Abuhani, D.A.; Hussain, M.H.; Khan, J.; El Mohandes, M. Machine Learning from Precision Agriculture Using Imagery from Unmanned Aerial Vehicle (UAVs): A Survey. Drones 2023, 7, 382–418. [Google Scholar] [CrossRef]
- Matese, A.; Di Gennaro, S.F. Technology in precision viticulture: A state of the art review. Int. J. Wine Res. 2015, 7, 69–81. [Google Scholar] [CrossRef]
- Khaliq, A.; Comba, L.; Biglia, A.; Aimonino, D.R.; Chiaberge, M.; Gay, P. Comparison of Satellite and UAV-Based Multispectral Imagery for Vineyard Variability Assessment. Remote Sens. 2019, 11, 436. [Google Scholar] [CrossRef]
- Sassu, A.; Gambella, F.; Ghiani, L.; Mercenaro, L.; Caria, M.; Pazzona, A.L. Advances in Unmanned Aerial System Remote Sensing for Precision Viticulture. Sensors 2021, 21, 956. [Google Scholar] [CrossRef]
- Galidaki, G.; Panagiotopoulou, L.; Vardoulaki, T. Use of UAV-borne multispectral data and vegetation indices for discriminating and mapping three Indigenous vine varieties of Greece. J. Cent. Eur. Agric. 2021, 22, 762–770. [Google Scholar] [CrossRef]
- Bellvert, J.; Girona, J. The Use of Multispectral and Thermal Images as a Tool for Irrigation Scheduling in Vineyards. Options Méditerranéenes. Ser. B Stud. Res. 2012, 67, 131–137. [Google Scholar]
- Comba, L.; Gay, P.; Primicerio, J.; Aimonino, D.R. Vineyard Detection from Unmanned Aerial Systems Images. Comput. Electron. Agric. 2015, 114, 78–87. [Google Scholar] [CrossRef]
- Pádua, L.; Marques, P.; Hruška, J.; Adão, T.; Bessa, J.; Sousa, A.; Peres, E.; Morais, R.; Sousa, J.J. Vineyard Properties Extraction Combining UAS-based RGB Imagery with Elevation Data. Int. Remote Sens 2018, 39, 5377–5401. [Google Scholar] [CrossRef]
- Nolan, A.P.; Park, S.; O’Connell, M.; Fuentes, S.; Ryu, D.; Chung, H. Detection and segmentation of vine rows using high resolution UAS imagery in a commercial vineyard. In Proceedings of the 21 International Congress on Modelling and Simulation, Gold Cost, Australia, 29 November–4 December 2015; Modelling and Simulation Society of Australia and New Zealand (MSSANZ): Canberra, Australia, 2015. [Google Scholar]
- Song, Z.; Zhang, Z.; Yang, S.; Ding, D.; Ning, J. Identifying sunflower lodging based on image fusion and deep semantic segmentation with UAV remote sensing imaging. Comput. Electron. Agric. 2020, 179, 105812. [Google Scholar] [CrossRef]
- Cinat, P.; Di Gennaro, S.F.; Berton, A.; Matese, A. Comparison of Unsupervised Algorithms for Vineyard Canopy Segmentation from UAV Multispectral Images. Remote Sens. 2019, 11, 1023–1046. [Google Scholar] [CrossRef]
- Delenne, C.; Durrieu, S.; Rabatel, G.; Deshayes, M.; Bailly, J.-S.; Lelong, C. Textural approaches for vineyard detection and characterization using very high spatial resolution remote-sensing data. J. Remote Sens. 2008, 29, 341–345. [Google Scholar] [CrossRef]
- Ivorra, E.; Sánchez, A.J.; Camarasa, J.G.; Diago, M.P.; Tardaguila, J. Assessment of grape cluster yield components based on 3D descriptors using stereo vision. Food Control 2015, 50, 273–282. [Google Scholar] [CrossRef]
- Palleja, T.; Landers, A.J. Real time canopy density validation using ultrasonic envelope signals and point quadrat analysis. Comput. Electron. Agric. 2017, 134, 43–50. [Google Scholar] [CrossRef]
- Mesas-Carrascosa, F.J.; Castro, A.I.; Torres-Sánchez, J.; Triviῇo-Tarradas, P.; Jiménez-Brenes, F.M.; Garcia-Ferrer, A.; López-Granados, F. Classification of 3D-Point Clouds Using Color Vegetation Indices for Precision Viticulture and Digitizing Applications. Sensors 2020, 21, 956. [Google Scholar] [CrossRef]
- Comba, L.; Biglia, A.; Aimonino, D.R.; Gay, P. Unsupervised detection of vineyards by 3D point-cloud UAV photogrammetry for precision agriculture. Comput. Electron. Agr. 2018, 155, 84–95. [Google Scholar] [CrossRef]
- Yang, Y.; Shen, X.; Cao, L. Estimation of the Living Vegetation Volume (LVV) for Individual Urban Street Trees Based on Vehicle-Mounted LiDAR Data. Remote Sens. 2024, 16, 16662–16687. [Google Scholar] [CrossRef]
- Barros, T.; Conde, P.; Gonçalves, G.; Premebida, C.; Monteiro, M.; Ferreira, C.; Nunes, U. Multispectral Vineyard Segmentation: A Deep Learning Comparison Study. Comput. Electron. Agric. 2022, 195, 106782. [Google Scholar] [CrossRef]
- Poblete, T.; Ortega-Farías, S.; Moreno, M.; Bardeen, M. Artificial Neuronal Network to Predict Vine Water Status Spatial Variability Using Multispectral Information Obtained from an Unmanned Aerial Vehicle (UAV). Sensors 2017, 17, 2488. [Google Scholar] [CrossRef]
- Jurado, J.M.; Pádua, L.; Feito, F.R.; Sousa, J.J. Automatic Grapevine Trunk Detection on UAV-Based Point Cloud. Remote Sens. 2020, 12, 3043. [Google Scholar] [CrossRef]
- del-Campo-Sanchez, A.; Moreno, M.; Ballesteros, R.; Hernandez-Lopez, D. Geometric Characterization of Vines from 3D Point Clouds Obtained with Laser Scanner Systems. Remote Sens. 2019, 11, 2365. [Google Scholar] [CrossRef]
- De Castro, A.; Jiménez-Brenes, F.M.; Torres-Sánchez, J.; Peña, J.M.; Borra-Serrano, I.; López-Granados, F. 3-D Characterization of Vineyards Using a Novel UAV Imagery-Based OBIA Procedure for Precision Viticulture Applications. Remote Sens 2018, 10, 584. [Google Scholar] [CrossRef]
- Jiménez-Brenes, F.M.; López-Granados, F.; Torres-Sánchez, J.; Peña, J.M.; Ramírez, P.; Castillejo-González, I.L.; de Castro, A.I. Automatic UAV-based detection of Cynodon dactylon for site specific vineyard management. PLoS ONE 2019, 14, e0218132. [Google Scholar] [CrossRef]
- Chedid, E.; Avia, K.; Dumas, V.; Ley, L.; Reibel, N.; Butterlin, G.; Soma, M.; Lopez-Lozano, R.; Baret, F.; Merdinoglu, D.; et al. LiDAR is Effective in Characterization Vine Growth and Detecting Associated Genetic Loci. Plant Phenomics 2023, 5, 16. [Google Scholar] [CrossRef] [PubMed]
- Cantürk, M.; Zabawa, L.; Pavlic, D.; Dreier, A.; Klingbeil, L.; Kuhlmann, H. UAV-based individual plant detection and geometric parameter extraction in vineyards. Front. Plant Sci. 2023, 14, 1244384. [Google Scholar] [CrossRef] [PubMed]
- Gavrilović, M.; Jovanović, D.; Božović, P.; Benka, P.; Govedarica, M. Vineyard Zoning and Vine Detection Using Machine Learning in Unmanned Aerial Vehicle Imagery. Remote Sens. 2024, 16, 584. [Google Scholar] [CrossRef]
- Dhakal, R.; Maimaitijiang, M.; Chang, J.; Caffe, M. Utilizing Spectral, Structural and Textural Features for Oat Above-Ground Biomass Using UAV-based Multispectral Data and Machine Learning. Sensors 2023, 23, 9708–9729. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhao, Q.; Han, F.; Zhang, J.; Jiang, P. Canopy and Height Estimation of Trees in a Shelter Forest Based on Fusion of an Airborne Multispectral Image and Photogrammetric Point Cloud. J. Sens. 2021, 14, 1251–1271. [Google Scholar] [CrossRef]
- Matese, A.; Di Gennaro, S.F. Beyond the traditional NDVI index as a key factor to mainstream the use of UAV in precision viticulture. Sci. Rep. 2021, 11, 2711–2723. [Google Scholar] [CrossRef] [PubMed]
- Comba, L.; Biglia, A.; Ricauda Aimonino, D.; Tortia, C.; Mania, E.; Guidoni, S.; Gay, P. Leaf Area Index evaluation in vineyards using 3D point clouds from UAV imagery. Sci. Rep. 2020, 11, 881–896. [Google Scholar] [CrossRef]
- Aboutalebi, M.; Torres-Rua, A.F.; Kustas, W.P.; Nieto, H.; Coopmans, C.; McKee, M. Assessment of different methods for shadow detection in high resolution optical imagery and evaluation of shadow impact on calculation of NDVI and evapotranspiration. Irrig. Sci. 2019, 37, 407–429. [Google Scholar] [CrossRef]
- Giovos, R.; Tassopoulos, D.; Kalivas, D.; Lougkos, N.; Priovolou, A. Remote Sensing Vegetation Indices in Viticulture: A Critical Review. Agriculture 2021, 11, 457–477. [Google Scholar] [CrossRef]
- Shahi, T.B.; Xu, C.-Y.; Neupane, A.; Guo, W. Machine Learning methods for precision agriculture with UAV imagery: A review. Electron. Res. Arch. 2022, 30, 4277–4317. [Google Scholar] [CrossRef]
- Bellvert, J.; Girona, J.; Zarco-Tejada, P.J. Seasonal evolution of crop water stress index in grapevine varieties determined with high-resolution remote sensing thermal imagery. Irrig. Sci. 2014, 33, 81–93. [Google Scholar] [CrossRef]
- Santesteban, L.G.; Di Gennaro, S.F.; Herrero-Langreo, A.; Miranda, C.; Royo, J.B.; Matese, A. High-Resolution UAV based Thermal Imaging to Estimate the Instantaneous and Seasonal Variability of Plant Water Status Within A Vineyard. Agric. Water Mang. 2017, 183, 49–59. [Google Scholar] [CrossRef]
- Espinoza, C.Z.; Khot, L.R.; Sankaran, S.; Jacoby, P.W. High Resolution Multispectral and Thermal Remote Sensing-Based Crop Water Stress assessment in Subsurface Irrigated Grapevines. Remote Sens. 2017, 9, 961. [Google Scholar] [CrossRef]
- Porten, M. Validierung des Vegetativen und Generativen Wuchszustandes von Reben in variierenden Bewirtschaftungs-und Stressbelastungssystemen. Ph.D. Dissertation, Trier University, Trier, Germany, 2020. Available online: https://ubt.opus.hbz-nrw.de/frontdoor/index/index/docId/1522 (accessed on 3 November 2024).
- Zhang, X.; Han, L.; Dong, Y.; Shi, Y.; Huang, W.; Han, L. A deep learning-based approach for automated yellow rust disease detection from high-resolution hyperspectral UAV images. Remote Sens. 2019, 11, 1554. [Google Scholar] [CrossRef]
- Nevavuori, P.; Narra, N.; Lipping, T. Crop yield prediction with deep convolutional neural networks. Comput. Electron. Agric. 2019, 163, 32–43. [Google Scholar] [CrossRef]
- Negro, C.; Sabella, E.; Nicolì, F.; Pierro, R.; Materazzi, A.; Panattoni, A.; Aprile, A.; Nutricati, E.; Vergine, M.; Miceli, A.; et al. Biochemical Changes in Leaves of Vitis vinifera cv. Sangiovese Infected by Bois Noir Phytoplasma. Pathogens 2020, 9, 262–289. [Google Scholar] [CrossRef] [PubMed]
- Fischer, M.; Ashnaei, S.P. Grapevine, esca complex, and environment: The disease triangle. Pythopathologia Mediterr. 2019, 58, 17–37. [Google Scholar] [CrossRef]
- Wang, Y.M.; Ostendorf, B.; Pagay, V. Detecting Virus Infections in Red and White Winegrape Canopies Using Proximal Hyperspectral Sensing. Sensors 2023, 23, 2851. [Google Scholar] [CrossRef]
- Müller, E.; Lipps, H.-P.; Walg, O. Der Winzer. Weinbau, 4th ed.; Wollgrasweg 41; Eugen Ulmer KG: Stuttgart, Germany, 2019. [Google Scholar]
- van Leeuwen, C.; Destrac-Irvine, A.; Dubernet, M.; Duchêne, E.; Gowdy, M.; Marguerit, E.; Pieri, P.; Parker, A.; de Rességuier, L.; Ollat, N. An Update on the Impact of Climate Change in Viticulture and Potential Adaptations. Agronomy 2019, 9, 514–533. [Google Scholar] [CrossRef]
- Dougherty, P.H. The Geography of Wine: Regions, Terroir and Techniques; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Gade, D.W. Tradition, territory and terroir in French viniculture. Ann. Assoc. Geogr. 2004, 94, 848–867. [Google Scholar] [CrossRef]
- Arnó, J.; Escolà, A.; Vallès, J.M.; Llorens, J.; Sanz, R.; Masip, J. Leaf area index estimation in vineyards using a ground based lidar scanner. Precis. Agric. 2013, 14, 290–306. [Google Scholar] [CrossRef]
- Caruso, G.; Tozzini, L.; Rallo, G.; Primicerio, J.; Moriondo, M.; Palai, G. Estimating biophysical and geometrical parameters of grapevine canopies (‘sangiovese’) by an unmanned aerial vehicle (uav) and vis-nir cameras. Vitis 2017, 56, 63–70. [Google Scholar] [CrossRef]
- Bramley, R.; Le Moigne, M.; Evain, S.; Ouzman, J.; Florin, L.; Fadaili, E.; Hinze, C.; Cerovic, Z.G. On-the-go sensing of grape berry anthocyanins during commercial harvest: Development and prospects. Aust. J. Grape Wine Res. 2011, 17, 316–326. [Google Scholar] [CrossRef]
- Cortell, J.M.; Sivertsen, H.K.; Kennedy, J.A.; Heymann, H. Influence of vine vigour on Pinot noir fruit composition, wine chemical analysis, and wine sensory attributes. Am. J. Enol. Vitic. 2008, 59, 1–10. [Google Scholar] [CrossRef]
- Gatti, M.; Squeri, C.; Garavani, A.; Vercesi, A.; Dosso, P.; Diti, I.; Poni, S. Effects of variable rate nitrogen application on cv. Barbera Perform. Veg. Growth Leaf Nutr. Status-Am. J. Enol. Vitic. 2018, 69, 196–209. [Google Scholar]
- Pena-Neira, A.; Duenas, M.; Duarte, A.; Hernandez, T.; Estrella, I.; Loyola, E. Effects of ripening stages and of plant vegetative vigour on the phenolic composition of grapes (*Vitis vinifera* L.) cv. Cabernet Sauvignon in the Maipo Valley (Chile). Vitis 2017, 43, 51–57. [Google Scholar]
- Bonilla, I.; Martinez de Toda, F.; Martinez-Casasnovas, J.A. Unexpected relationships between vine vigour and grape composition in warm climate conditions. J. Int. Sci. Vigne 2016, 49, 127–136. [Google Scholar]
- Bellvert, J.; Zarco-Tejada, P.J.; Girona, J.; Fereres, E. Mapping Crop Water Stress Index in A “Pinot Noir” Vineyard: Comparing Ground Measurements with Thermal Remote Sensing Imagery from Unmanned Aerial Vehicle. Precis. Vitic. 2013, 15, 361–376. [Google Scholar] [CrossRef]
- Panten, K.; Bramley, R.G.V. Whole-of-block experimentation for evaluating a change to canopy management intended to enhance wine quality. Aust. J. Grape Wine Res. 2012, 18, 147–157. [Google Scholar] [CrossRef]
- Dorin, B.; Reynolds, A.G.; Lee, H.-S.; Carrey, M.; Shemrock, A.; Shabanian, M. Detecting cool-climate Riesling vineyard variation using unmanned aerial vehicles and proximal sensors. Drone Syst. Appl. 2024, 12, 1–18. [Google Scholar] [CrossRef]
- Rey-Caramés, C.; Diago, M.P.; Martín, M.P.; Lobo, A.; Tardaguila, J. Using RPAS Multi-Spectral Imagery to Characterize Vigour, Leaf Development, Yield Components and Berry Composition Variability within a Vineyard. Remote Sens. 2015, 7, 14458–14481. [Google Scholar] [CrossRef]
- Ballesteros, R.; Intrigliolo, D.S.; Ortega, J.F.; Ramírez-Cuesta, J.M.; Buesa, I.; Moreno, M.A. Vineyard yield estimation by combining remote sensing, computer vision and artificial neural network techniques. Precis. Agric. 2020, 21, 1242–1262. [Google Scholar] [CrossRef]
- Romero, M.; Luo, Y.; Su, B.; Fuentes, S. Vineyard water status estimation using multispectral imagery from an UAV platform and machine learning algorithms for irrigation scheduling management. Comput. Electron. Agric. 2018, 147, 109–117. [Google Scholar] [CrossRef]
- Soubry, I.; Patias, P.; Tsioukas, V. Monitoring Vineyards with UAV and multisensor for the assessment of water stress and grape maturity. J. Unmanned Veh. Syst. 2017, 5, 37–50. [Google Scholar] [CrossRef]
- Wan, L.; Cen, H.; Zhu, J.; Zhang, J.; Zhu, Y.; Sun, D. Grain yield prediction of rice using multitemporal UAV-based RGB and multispectral images and model transfer-a case study of small farmlands in the South of China. Agric. For. Meteorol. 2020, 291, 108096. [Google Scholar] [CrossRef]
- Ji, Y.; Chen, Z.; Cheng, Q.; Liu, R.; Li, M.; Yan, X. Estimation of plant height and yield based on UAV imagery in faba bean (Vicia fabia L.). Plant Methods 2022, 18, 26. [Google Scholar] [CrossRef] [PubMed]
- Mathenge, M.; Sonneveld, B.G.J.S.; Broerse, J.E.W. Application of GIS in Agriculture in Promoting Evidence-Informed Decision Making for Improving Agriculture Sustainability: A Systematic Review. Sustainability 2022, 14, 9974–9988. [Google Scholar] [CrossRef]
- Mathews, A.J. Applying Geospatial Tools and Techniques to Viticulture. Geography Compass 2013, 7, 22–34. [Google Scholar] [CrossRef]
- Moral, F.J.; Rebollo, F.J.; Paniagua, L.L.; García-Martín, A. A GIS-based multivariate clustering for characterization and ecoregion mapping from a viticultural perspective. Span. J. Agric. Res. 2016, 14, 10. [Google Scholar] [CrossRef]
- Ferrer, M.; Echeverría, G.; Pereyra, G.; Neves, G.G.; Pan, D.; Mirás-Avalos, J.M. Mapping Vineyard vigour using airborne remote sensing: Relations with yield, berry composition and sanitary status under humid climate conditions. Precis. Agric. 2020, 21, 178–197. [Google Scholar] [CrossRef]
- Albetis, J.; Jacquin, A.; Goulard, M.; Poilvé, H.; Rousseau, J.; Clenet, H.; Dedieu, G.; Duthoit, S. On the potential of UAV Multispectral Imagery to Detect Flavescence dorée and Grapevine Trunk Diseases. Remote Sens. 2019, 11, 23. [Google Scholar] [CrossRef]
- Vanegas, F.; Bratanov, D.; Powell, K.; Weiss, J.; Gonzalez, F. A Novel Methodology for Improving Plant Pest Surveillance in Vineyards and Crop Using UAV-based Hyperspectral and Spatial Data. Sensors 2018, 18, 260. [Google Scholar] [CrossRef] [PubMed]
- Helman, D.; Bahat, I.; Netzer, Y.; Ben-Gal, A.; Alchanatis, V.; Peeters, A.; Cohen, Y. Using Time Series of High-Resolution Planet Satellite Images to Monitor Grapevine Stem Water Potential in Commercial Vineyards. Remote Sens. 2018, 10, 1615–1636. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G.; Major, D.J. A vegetation Index which minimizes soil brightness effects on LAI and APAR estimation. In Proceedings of the 12th Canadian Symposium on Remote Sensing Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 10–14 July 1989; 1989; pp. 1355–1358. [Google Scholar]
- Borgogno-Mondino, E.; Novello, V.; Lessio, A.; de Palma, L. Describing the spatio-temporal variability of vines and soil by satelitte-based spectral indices: A case study in Apulia (South Italy). Int. J. Appl. Earth Obs. Geoinformatics 2018, 68, 42–50. [Google Scholar] [CrossRef]
- Heralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. Syst. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Stanton, J.M. Galton, Pearson and Peas: A Brief History of Linear Regression for Statistics Instructors. J. Stat. Educ. 2001, 9, 1–13. [Google Scholar] [CrossRef]
- Nichol, J.E.; Sarker, M.L.R. Improved biomass estimation using the texture parameters of two high-resolution optical sensors. IEEE Trans. Geosci. Remote Sens. 2010, 49, 930–948. [Google Scholar] [CrossRef]
- Sassu, A.; Ghiani, L.; Salvati, L.; Mercenaro, L.; Deidda, A.; Gambella, F. Integrating UAVs and Canopy Height Models in Vineyard Management: A Time-Space Approach. Remote Sens. 2022, 14, 140–143. [Google Scholar] [CrossRef]
- Otsu, N.A. A threshold Selection Method from Gray Level Histograms. IEEE Trans. Syst. Man Cybern 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Junges, A.H.; Fontana, D.C.; Anzanello, R.; Bremm, C. Normalized Difference Vegetation Index obtained by ground-based remote sensing to characterize vine cycle in Rio Grande do Sul, Brazil. Ciênca Agrotecnologia 2017, 41, 543–553. [Google Scholar] [CrossRef]
- Whiteside, T.G.; Boggs, G.S.; Maier, S.W. Comparing object-based and pixel-based classification for mapping savannas. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 884–893. [Google Scholar] [CrossRef]
- Adams, R.; Bischof, L. Seeded Region Growing. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 641–647. [Google Scholar] [CrossRef]
- Lemenkova, P. Object Based Image Segmentation Algorithm of SAGA GIS for Detecting Urban Spaces in Yaoundé, Cameroon. Cent. Eur. J. Geogr. Sustain. Dev. 2020, 2, 38–51. [Google Scholar] [CrossRef]
- Lemenkova, P. SAGA GIS for information extraction on presence and conditions of vegetation of northern coast of Iceland bbased on nthe Landsat TM. Acta Biol. Marisiensis 2020, 3, 10–21. [Google Scholar] [CrossRef]
- Hossain, M.D.; Chen, D. Segmentation for Object-Based Image Analysis (OBIA): A Review of algorithms and challenges from remote sensing perspective. ISPRS J. Photogramm. Remote Sens. 2019, 150, 115–134. [Google Scholar] [CrossRef]
- Drǎguţ, L.; Tiede, D.; Levick, S.R. ESP: A tool to estimate scale parameter for multiresolution image segmentation of remotely sensed data. Int. J. Geogr. Inf. Sci. 2010, 24, 859–871. [Google Scholar] [CrossRef]
- Singla, S.; Eldawy, A. Raptor Zonal Statitics: Fully Distributed Zonal Statistics of Big Raster+ Vector Data. In Proceedings of the IEEE International Conference on Big Data (Big Data), Atlanta, GA, USA, 10–13 December 2020; IEEE: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Wu, Z.; Wang, S.; Sun, H.; Senthilnath, J. Modified Red Blue Vegetation Index for Chlorophyll Estimation and Yield Prediction of Maize from Visible Images Captured by UAV. Sensors 2020, 20, 5055–5070. [Google Scholar] [CrossRef] [PubMed]
- Naidu, G.; Zuva, T.; Sibanda, E. A Review of Evaluation Metrics in Machine Learning. Artif. Intell. Appl. Netw. Syst. 2023, 724, 15–25. [Google Scholar]
- Sitaula, C.; Basnet, A.; Mainali, A.; Shahi, T.B. Deep Learning based methods for sentiment analysis on Nepali COVID-19 related tweets. Comput. Intell. Neurosci. 2021, 2021, 2158184. [Google Scholar] [CrossRef] [PubMed]
- Rakshit, H.; Zadeh, P.B. A New Approach to Classify Drones Using a Deep Convolutional Neural Network. Drones 2024, 8, 319. [Google Scholar] [CrossRef]
- Miller, C.; Portlock, T.; Nyaga, D.M.; O’sullivan, J.M. A review of model evaluation metrics for machine learning in genetics and genomics. Front. Bioinform. 2024, 4, 1457619. [Google Scholar] [CrossRef] [PubMed]
- Ye, S.; Pontius, R.G., Jr.; Rakshit, R. A review of accuracy assessment for object-based image analysis: From per-pixel to per-polygon approaches. ISPRS J. Photogramm. Remote Sens. 2018, 141, 137–147. [Google Scholar] [CrossRef]
- Ez-zahouani, B.; Teodoro, A.; El Kharki, O.; Jianhua, L. Remote sensing imagery segmentation in object-based analysis: A review of methods, optimization, and quality evaluation over the past 20 years. Remote Sens. Appl. Soc. Environ. 2023, 32, 101032. [Google Scholar] [CrossRef]
- Michez, A.; Lejeune, P.; Bauwens, S.; Herinaina, A.A.L.; Blaise, Y.; Castro-Muἧoz, E. Mapping and monitoring of biomass and grazing in pasture with an unmanned aerial system. Remote Sens. 2019, 11, 473–476. [Google Scholar] [CrossRef]
- Shu, M.; Wang, Z.; Guo, W.; Qiao, H.; Fu, Y.; Guo, Y.; Wang, L.; Ma, Y.; Gu, X. Effects of Variety and Growth Stage on UAV Multispectral Estimation of Plant Nitrogen Content of Winter Wheat. Agriculture 2024, 14, 1775. [Google Scholar] [CrossRef]
- Gillot, J.M.; Michelin, J.; Hadjard, D.; Houot, S. An accurate method for predicting spatial variability of maize yield from UAV-based plant height estimation: A tool for monitoring agronomic field experiments. Precis. Agric. 2021, 22, 897–921. [Google Scholar] [CrossRef]
- Karakizi, C.; Oikonomou, M.; Karantzalos, K. Spectral discrimination and reflectance properties of various vine varieties from satellite, UAV and proximate sensors. The international Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2015, 40, 31–37. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Hartling, S.; Esposito, F.; Fritschi, F.B. Soybean yield prediction from UAV using multimodal data fusion and deep learning. Remote Sens. 2020, 237, 111599. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Li, J.; Guo, X.; Wang, S.; Lu, J. Estimating biomass of winter oilseed rape using vegetation indices and texture metrics derived from UAV multispectral images. Comput. Electron. Agric. 2019, 166, 105026. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, Y.; Feng, H.; Chen, R.; Bian, M.; Ma, Y.; Yue, J.; Yang, G. Estimating potato above-ground biomass based on spectral and spatial features extracted from high-definition digital camera images. Comput. Electron. Agric. 2024, 213, 108229. [Google Scholar] [CrossRef]
- Zheng, H.B.; Cheng, T.; Zhou, M.; Li, D.; Yao, X.; Tian, Y.C.; Cao, W.X.; Zhu, Y. Improved estimation of rice aboveground biomass combining textural and spectral analysis of UAV-Imagery. Precis. Agric. 2019, 20, 611–629. [Google Scholar] [CrossRef]
- Yue, J.; Yang, G.; Tian, Q.; Feng, H.; Xu, K.; Zhou, C. Estimate of winter-wheat above-ground biomass based on UAV ultrahigh-ground-resolution image textures and vegetation indices. Photogramm. Remote Sens. 2019, 150, 226–244. [Google Scholar] [CrossRef]
- Yue, J.; Yang, G.; Li, C.; Li, Z.; Wang, Y.; Feng, H.; Xu, B. Estimation of Winter Wheat Above-Ground Biomass Using Unmanned Aerial Vehicle-Based Snapshot Hyperspectral Sensor and Crop Height Improved Models. Remote Sens. 2017, 9, 708–726. [Google Scholar] [CrossRef]
- Li, B.; Xu, X.; Zhang, L.; Han, J.; Bian, C.; Li, G.; Liu, J.; Jin, L. Above-ground biomass estimation and yield prediction in potato by using UAV-based RGB and hyperspectral imaging. ISPRS J. Photogramm. Remote Sens. 2020, 162, 161–172. [Google Scholar] [CrossRef]
- Wang, C.; Nie, S.; Xi, X.; Luo, S.; Sun, X. Estimating the biomass of maize with hyperspectral and LiDAR data. Remote Sens. 2016, 9, 11. [Google Scholar] [CrossRef]
- Zha, H.; Miao, Y.; Wang, T.; Li, Y.; Sun, J.Z.W.; Feng, Z.; Kusnierek, K. Improving unmanned aerial vehicle remote sensing-based nitrogen nutrition index prediction with machine learning. Remote Sens. 2020, 12, 215–226. [Google Scholar] [CrossRef]
- Grüner, E.; Wachendorf, M.; Astor, T. The potential of UAV-borne spectral and textural information for predicting aboveground biomass and N fixation in legume-grass mixture. PLoS ONE 2020, 15, e0234703. [Google Scholar] [CrossRef] [PubMed]
- Yoosefzadeh-Najafabadi, M.; Earl, H.J.; Tulpan, D.; Sulik, J.; Eskandari, M. Application of machine learning algorithms in plant and breeding: Predicting yield from hyperspectral reflectance in soybean. Fron. Plant Sci. 2021, 11, 2169. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Yang, G.; Wang, J.; Song, X.; Feng, H. Winter wheat biomass estimation based on spectral indices, band depth analysis and partial least regression using hyperspectral measurements. Comput. Electron. Agric. 2014, 100, 51–59. [Google Scholar] [CrossRef]
- Wang, F.; Yang, M.; Ma, L.; Zhang, T.; Qin, W.; Li, W.; Zhang, Y.; Sun, Z.; Wang, Z.; Li, F.; et al. Estimation of above-ground biomass of winter wheat based on consumer-grade multi-spectral UAV. Remote Sens. 2022, 14, 1271. [Google Scholar] [CrossRef]
- Duan, B.; Liu, Y.; Gong, Y.; Peng, Y.; Wu, X.; Zhu, R.; Fang, S. Remote estimation of rice LAI based on Fourier spectrum texture from UAV image. Plant Methods 2019, 15, 124–135. [Google Scholar] [CrossRef] [PubMed]
- Geipel, J.; Link, J.; Claupein, W. Combined spectral-and spatial modeling of corn yield based on aerial images and crop surface models acquired with an unmanned aircraft system. Remote Sens. 2014, 6, 10335–10355. [Google Scholar] [CrossRef]
- Zhou, X.; Zheng, H.; Xu, X.; He, J.; Ge, X.; Yao, X. Predicting grain yield of rice using multi-temporal vegetation indices from UAV-based multispectral and digital imagery. ISPRS J. Photogramm. 2017, 130, 246–255. [Google Scholar] [CrossRef]
- Kerkech, M.; Hafiane, A.; Canals, R. Deep learning approach with colorimetric spaces and vegetation indices for vine diseases detection in UAV images. Comput. Electron. Agric. 2018, 155, 237–243. [Google Scholar] [CrossRef]
- Prabhakara, K.; Hively, W.D.; McCarthy, G.W. Evaluating the relationship between biomass, percent groundcover and remote sensing indices across six winter cover crop fields in Maryland, United States. Int. J. Appl. Earth Obs. Geoinformatics 2015, 39, 88–102. [Google Scholar] [CrossRef]
- Maimaitijang, M.; Ghulam, A.; Sidike, P.; Hartling, S.; Maimaitijang, M.; Peterson, K.; Shavers, E.; Fishman, J.; Peterson, J.; Kadam, S.; et al. Unmanned Aerial System (UAS)-based phenotyping of soybean using multi-sensor data fusion and extreme learning machine. ISPRS J. Photogramm. Remote Sens. 2017, 134, 43–58. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices overcome the saturation problem in biomass estimation. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
- Heege, H.J.; Reusch, S.; Thiessen, E. Prospects and results for optical systems for site-specific on the-o control of nitrogen-top dressing in Germany. Precis. Agric. 2008, 9, 115–131. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L.; Wang, L. Evaluation of morphological texture features for mangrove forest mapping and species discrimination using multispectral IKONOS imagery. IEEE Geosci. Remote Sens. Lett. 2009, 6, 393–397. [Google Scholar] [CrossRef]
- Pádua, L.; Matese, A.; Di Gennaro, S.F.; Morais, R.; Peres, E.; Sousa, J.J. Vineyard Classification using OBIA on UAV-based RGB and multispectral data: A case study in different wine regions. Comput. Electron. 2022, 196, 106905. [Google Scholar] [CrossRef]
- Willkomm, M.; Bolten, A.; Bareth, G. Non-Destructive Monitoring of Rice by Hyperspectral in-Field Spectrometry and UAV-Based Remote Sensing: Case Study of Field-Grown Rice in North Rhine-Westphalia, Germany. In Proceedings of the 2016 XXIII ISPRS Congress, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Acorsi, M.G.; das Dores Abati Miranda, F.; Martello, M.; Smaniotto, D.A.; Sartor, L.R. Estimating Biomass of Black Oat Using UAV-Based RGB Imaging. Agronomy 2019, 9, 344–357. [Google Scholar] [CrossRef]
- Bendig, J.; Bolten, A.; Bennertz, S.; Broscheit, J.; Eichfuss, S.; Bareth, G. Estimating biomass of barley using crop surface models (CSMs) drived from UAV-based RGB imaging. Remote Sens. 2014, 6, 10395–10412. [Google Scholar] [CrossRef]
- Shu, M.; Mengyuan, S.; Qizhou, D.; Xiaohong, Y.; Baoguo, L.; Yuntao, M. Estimating the maize above-ground biomass by contructing the tridimensional concept model based UAV-based digital and multi-spectral images. Field Crop Res. 2022, 282, 108491. [Google Scholar] [CrossRef]
- Bah, M.D.; Hafiane, A.; Canals, R. Deep learning with unsupervised data labeling for weed detection in line crops in UAV images. Remote Sens. 2018, 10, 1690–1711. [Google Scholar] [CrossRef]
- Zhang, J.; Chang, T.; Shi, L.; Wang, W. Combining spectral-and texture features of UAV hyperspectral images for leaf nitrogen content monitoring in winter wheat. Int. J. Remote Sens. 2022, 43, 2335–2356. [Google Scholar] [CrossRef]
- Schuhmacher, P.; Mislimshoeva, B.; Brenning, A.; Zandler, H.; Brandt, M.; Samimi, C.; Koellner, T. Do Red Edge and Texture Attributes from High-Resolution Satellite Data Improve Wood Volume Estimation in a Semi-Arid Mountainous Region? Remote Sens. 2016, 8, 540–558. [Google Scholar] [CrossRef]
- Wengert, M.; Piepho, H.-P.; Astor, T.; Graß, R.; Wijesingha, J. Assesing spatial variability of barley whole crop biomass yield and leaf area index in silvooarable agroforestry systems using UAV-borne remote sensing. Remote Sens. 2021, 13, 2751–2774. [Google Scholar] [CrossRef]
- Colombo, R.; Bellingeri, D.; Fasolini, D.; Marino, C.M. Retrieval of leaf area index in different vegetation types using high resolution satellite data. Remote Sens. Environ. 2003, 86, 120–131. [Google Scholar] [CrossRef]
- Tilly, N.; Aasen, H.; Bareth, G. Fusion of plant height and vegetation indices for the estimation of barley biomass. Remote Sens. 2015, 7, 11449–11480. [Google Scholar] [CrossRef]
- Possoch, M.; Bieker, S.; Hoffmeister, D.; Bolten, A.; Schellberg, J.; Bareth, G. Multi-temporal crop surface models combined with the RGB vegetation index from UAV-based images for forage monitoring in grassland. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 991–998. [Google Scholar] [CrossRef]
- Kwak, G.-H.; Park, N.-W. Impact of Texture Information on Crop Classification with Machine Learning and UAV Images. Appl. Sci. 2019, 9, 643–659. [Google Scholar] [CrossRef]
- Viljanen, N.; Honkavaara, E.; Näsi, R.; Hakala, T.; Niemeläinen, O.; Kaivosoja, J. A novel machine learning method for estimating biomass of grass swards using photogrammetric canopy height model, images and vegetation indices captured by a drone. Agriculture 2018, 5, 70–97. [Google Scholar] [CrossRef]
- Näsi, R.; Viljanen, N.; Kaivosoja, J.; Alhonoja, K.; Hakala, T.; Markelin, L.; Honkavaara, E. Estimating biomass and nitrogen amount of barley and grass using UAV and aircraft based spectral and photogrammetric 3D features. Remote Sens. 2018, 10, 1082–1113. [Google Scholar] [CrossRef]
- Moeckel, T.; Safari, H.; Reddersen, B.; Fricke, T.; Wachendorf, M. Fusion of ultrasonic and spectral sensor data for improving the estimation of biomass in grasslands with heterogeneous sward structure. Remote Sens. 2017, 9, 98–111. [Google Scholar] [CrossRef]
- Lu, N.; Zhou, J.; Han, Z.; Li, D.; Cao, Q.; Yao, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cheng, T. Improved estimation of aboveground biomass in wheat from RGB imagery and point cloud data acquired with low-cost unmanned aerial vehicle system. Plant Methods 2019, 15, 17. [Google Scholar] [CrossRef] [PubMed]
- Adugna, T.; Xu, W.; Fan, J. Comparison of Random Forest and Support Vector Machine Classifiers for Regional Land Cover Mapping Using Coarse Resolution FY-3C Images. Remote Sens. 2022, 14, 574–595. [Google Scholar] [CrossRef]
- Sheykhousma, M.; Mahdianpari, M.; Mohammadimanesh, F.; Ghamisi, P.; Homayouni, S. Support Vector Machine Vs Random Forest for Remote Sensing Image Classification: A Meta-Analysis and Systematic Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6308–6325. [Google Scholar]
- Talukdar, S.; Singha, P.; Mahato, S.; Shahfahad; Pal, S.; Liou, Y.-A.; Rahman, A. Land-Use Land-Cover Classification by Machine Learning Classifiers for Satellite Observations-A Review. Remote Sens. 2020, 12, 1135–1158. [Google Scholar] [CrossRef]
- Shao, G.; Tang, L.; Zhang, H. Introducing Image Classification Efficacies. IEEE Access 2016, 4, 134809–134816. [Google Scholar] [CrossRef]
- Zhen, Z.; Chen, S.; Yin, T.; Chavanon, E.; Lauret, N.; Guilleux, J.; Henke, M.; Qin, W.; Cao, L.; Li, J.; et al. Using the Negative Soil Adjustment Factor of Soil Adjusted Vegetation Index (SAVI) to Resist Saturation Effects and Estimate Leaf Area Index (LAI) in Dense Vegetation Areas. Sensors 2021, 21, 2115–2128. [Google Scholar] [CrossRef] [PubMed]
- Keshtkar, H.; Voigt, W.; Alizadeh, E. Land-cover classification and analysis of change using machine-learning classifiers and multi temporal remote sensing imagery. Arab. J. Geosci. 2017, 10, 154–168. [Google Scholar] [CrossRef]
- Abdi, A.M. Land cover and land use classification performance of machine learning algorithms in a boreal landscape using Sentinel-2 data. GIScience Remote Sens. 2020, 57, 1–20. [Google Scholar] [CrossRef]



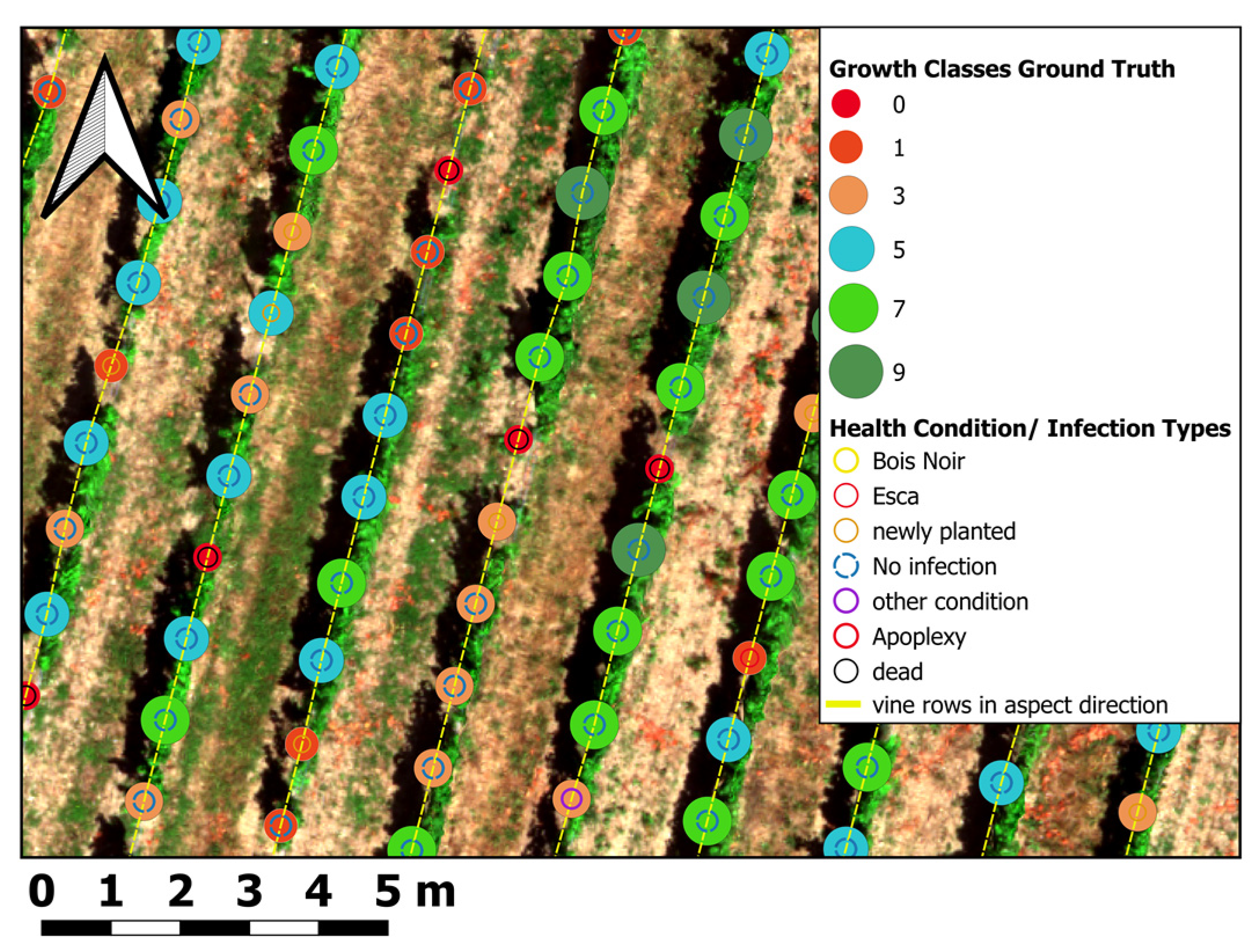




| Growth Class | Growth Description | Additive | Description | INS |
|---|---|---|---|---|
| APO/0 | Apoplexy/Death/Missing stem | E | Esca symptoms | 0.5-4.5 |
| 1 | Almost dead | S | Blackwood disease (Bois Noir) | 0.5–4.5 |
| 3 | Very weak growth | ES | Esca and Bois Noir | 0.5–4.5 |
| 5 | Medium growth | P | Infection with Peronospora | 0.5–4.5 |
| 7 | Medium to good growth | N | New planted vine/vines | 0.5–4.5 |
| 9 | Excellent-to-excessive growth | NA | Re-expulled from the trunk after APO or other damage | 0.5–4.5 |
| Spectral Band | Center Wavelength (nm) | Bandwidth FWHM (nm) |
|---|---|---|
| Blue (1) | 475 | 32 |
| Green (2) | 560 | 27 |
| Red (3) | 668 | 16 |
| Red Edge (4) | 717 | 12 |
| Near Infrared (5) | 842 | 57 |
| ID | Spectral Indices | Source Reference | Abbreviation |
|---|---|---|---|
| 1 | Normalized Difference Vegetation Index | [72] | NDVI |
| 2 | Normalized Difference Red Edge Index | [73] | NDREI |
| 3 | Optimized Soil Adjusted Vegetation Index | [74] | OSAVI |
| 4 | Green Normalized Difference Vegetation Index | [75] | GNDVI |
| 5 | Transformed Soil Adjusted Vegetation Index | [76] | TSAVI |
| 6 | Normalized Difference Water Index | [77] | NDWI |
| ID F.I. | Height and Volume Measures | Name |
|---|---|---|
| 1 | Mean Height | CHMmean |
| 2 | Median Height | CHMmedian |
| 3 | Minimum Height | CHMmin |
| 4 | Maximum Height | CHMmax |
| 5 | Standard Deviation Height | CHMstd |
| 6 | Variance | CHMvar |
| 7 | Aggregated Pixel Volume | CHM Volume |
| S.N. | Texture Measure | Formula |
|---|---|---|
| 1. | Mean (ME) | |
| 2. | Variance (VAR) | |
| 3. | Homogeneity (HOM) | |
| 4. | Contrast (CON) | |
| 5. | Dissimilarity (DIS) | |
| 6. | Entropy (ENT) | |
| 7. | Angular Second Moment (ASM) | |
| 8. | Correlation (COR) |
| ID Input Feature Group | Abbreviation | Input Features |
|---|---|---|
| 1. spectral features fitted to growth class ground truth | sp | n = 6 NDVI + NDVIRE + OSAVI + GNDVI + NDWI + TSAVI |
| 2. structural features fitted to growth class ground truth | str | n = 4 CHM(mean) + CHM(max) + CHM(std) + CHM(Volume) |
| 3. texture features fitted to growth class ground truth | tex | n = 4 Contrast + Correlation + Entropy + Angular Second Moment |
| 4. spectral and structural features fitted to growth class ground truth | sp + str/sp-str | n = 10 NDVI + NDVIRE + OSAVI + TSAVI + GNDVI + NDWI+ CHM(mean) + CHM(max) + CHM(std) + CHM(Volume) |
| 5. spectral and texture features fitted to growth class ground truth | sp + tex/sp-tex | n = 10 NDVI + NDVIRE + OSAVI + GNDVI + NDWI + TSAVI + Contrast + Correlation + Entropy+ Angular Second Moment |
| 6. structural and texture features fitted to growth class ground truth | str + tex/str-tex | n = 8 CHM(mean) + CHM(max) + CHM(std) + CHM(Volume) + Contrast + Correlation + Entropy + Angular Second Moment |
| 7. spectral, structural, and texture features fitted to growth class ground truth | sp + str + tex/sp-str-tex | n = 14 NDVI + NDVIRE + OSAVI + GNDVI + NDWI + TSAVI + CHM(mean) + CHM(max) + CHM(std) + CHM(Volume) + Contrast + Correlation + Entropy + Angular Second Moment |
| Machine Learning Classifiers | Pre-Processing of Input Features | Train–Test Split | Parameter for Hyperparameter Tuning |
|---|---|---|---|
| SVM (Support Vector Machines) | - selection of features - eliminating NoData values - standard scaling of the input features | repeated-k-fold-cross-validation splits = 5, repeats = 5 (n = 25), random state = 1, jobs = −1 with hyperparameter tuning (grid search) | kernel: [linear, rbf]; c: 0.001, 0.01, 0.1, 1, 10, 15, 20, 100, 1000]: gamma: [0.001, 0.01, 0.1, 1, 10] |
| RFC (Random Forest Classifier) | - selection of features - eliminating NoData values - standard scaling of the input features | repeated-k-fold-cross-validation splits = 5, repeats = 5 (n = 25), random state = 1, jobs = −1 with hyperparameter tuning (grid search) | n_estimators: [25, 50, 100, 150, 300, 500], max_features: [sqrt, log2, none], max_depth: [3, 6, 9, 15, 20, 30], max_leaf nodes: [3, 6, 9] max_samples: [2, 4, 6] min_samples_leaf: [1, 2, 4] criterion: [entropy, gini] |
| Train Data | Test Data | |||||||
|---|---|---|---|---|---|---|---|---|
| Model Type | Accuracy | F1-Weighted | Accuracy std. | F1-Weighted std. | Accuracy | F1-Weighted | Accuracy std. | F1-Weighted std. |
| RF 1 | 31.51% | 22.25% | 2% | 4.40% | 30.41% | 20.98% | 2.79% | 4.93% |
| RF 2 | 41.58% | 32.66% | 3% | 5.29% | 40.04% | 31.57% | 3.33% | 5.59% |
| RF 3 | 34.10% | 29.10% | 2% | 5.31% | 33.17% | 28.32% | 2.84% | 6.90% |
| RF 4 | 37.38% | 34.11% | 4% | 5.51% | 37.38% | 33.05% | 3.99% | 6.27% |
| RF 5 | 35.07% | 27.20% | 3% | 3.24% | 33.23% | 26.79% | 4.23% | 4.38% |
| RF 6 | 39.96% | 27.73% | 3% | 5.14% | 38.86% | 26.65% | 3.65% | 4.82% |
| RF 7 | 38.00% | 31.63% | 2% | 4.53% | 36.77% | 30.01% | 4.37% | 6.30% |
| SVM 1 | 50.48% | 46.76% | 1% | 4.89% | 40.65% | 37.48% | 3.16% | 3.40% |
| SVM 2 | 50.34% | 51.23% | 2% | 2.41% | 47.38% | 46.21% | 1.89% | 2.76% |
| SVM 3 | 40.13% | 52.49% | 2% | 2.64% | 37.98% | 47.72% | 2.56% | 2.90% |
| SVM 4 | 51.75% | 49.63% | 2% | 1.63% | 47.42% | 45.86% | 2.78% | 3.12% |
| SVM 5 | 50.13% | 35.68% | 3% | 1.67% | 44.21% | 33.59% | 1.92% | 2.44% |
| SVM 6 | 51.05% | 47.38% | 2% | 3.47% | 47.57% | 42.39% | 2.69% | 2.97% |
| SVM 7 | 53.66% | 50.11% | 2% | 2.27% | 48.51% | 45.50% | 2.22% | 3.16% |
| GC | 0 GP | 1 GP | 3 GP | 5 GP | 7 GP | 9 GP | UA |
|---|---|---|---|---|---|---|---|
| 0 GL | 29.28 | 34.25 | 27.62 | 6.63 | 2.21 | 0.00 | 29.28 |
| 1 GL | 14.77 | 36.29 | 29.11 | 15.61 | 4.22 | 0.00 | 36.29 |
| 3 GL | 3.69 | 10.82 | 35.88 | 44.59 | 5.01 | 0.00 | 35.88 |
| 5 GL | 0.00 | 1.08 | 16.81 | 65.73 | 16.16 | 0.22 | 65.73 |
| 7 GL | 0.30 | 0.30 | 2.72 | 39.58 | 57.10 | 0.00 | 57.10 |
| 9 GL | 0.00 | 0.00 | 0.00 | 9.09 | 81.82 | 9.09 | 9.09 |
| PA | 60.95 | 43.86 | 32.00 | 36.27 | 34.29 | 18.92 | SVM 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dillner, R.P.; Wimmer, M.A.; Porten, M.; Udelhoven, T.; Retzlaff, R. Combining a Standardized Growth Class Assessment, UAV Sensor Data, GIS Processing, and Machine Learning Classification to Derive a Correlation with the Vigour and Canopy Volume of Grapevines. Sensors 2025, 25, 431. https://doi.org/10.3390/s25020431
Dillner RP, Wimmer MA, Porten M, Udelhoven T, Retzlaff R. Combining a Standardized Growth Class Assessment, UAV Sensor Data, GIS Processing, and Machine Learning Classification to Derive a Correlation with the Vigour and Canopy Volume of Grapevines. Sensors. 2025; 25(2):431. https://doi.org/10.3390/s25020431
Chicago/Turabian StyleDillner, Ronald P., Maria A. Wimmer, Matthias Porten, Thomas Udelhoven, and Rebecca Retzlaff. 2025. "Combining a Standardized Growth Class Assessment, UAV Sensor Data, GIS Processing, and Machine Learning Classification to Derive a Correlation with the Vigour and Canopy Volume of Grapevines" Sensors 25, no. 2: 431. https://doi.org/10.3390/s25020431
APA StyleDillner, R. P., Wimmer, M. A., Porten, M., Udelhoven, T., & Retzlaff, R. (2025). Combining a Standardized Growth Class Assessment, UAV Sensor Data, GIS Processing, and Machine Learning Classification to Derive a Correlation with the Vigour and Canopy Volume of Grapevines. Sensors, 25(2), 431. https://doi.org/10.3390/s25020431







