Image Representation-Driven Knowledge Distillation for Improved Time-Series Interpretation on Wearable Sensor Data
Abstract
1. Introduction
- We introduce the integration of image representations into the KD framework and conduct a comparative analysis between methods that employ image representations and those that do not.
- We perform KD using a single or multiple teachers with different image representations and a diverse capacity of teachers to identify which approach and combination provide the most benefit.
- We clarify the relationships between representation richness and model compactness, providing insights for designing efficient, high-performance wearable-sensor recognition systems.
- We demonstrate the effectiveness of image representation-driven KD strategies in diverse perspectives, including analysis of noises, generalizability, and compatibility with distillation on wearable sensor data. We investigate both small- and large-scale datasets, ensuring consistent and trustworthy observations across varying dataset sizes.
2. Background
2.1. Persistence Image Extraction by Topological Data Analysis
2.2. Gramian Angular Field Image Extraction
2.3. Knowledge Distillation
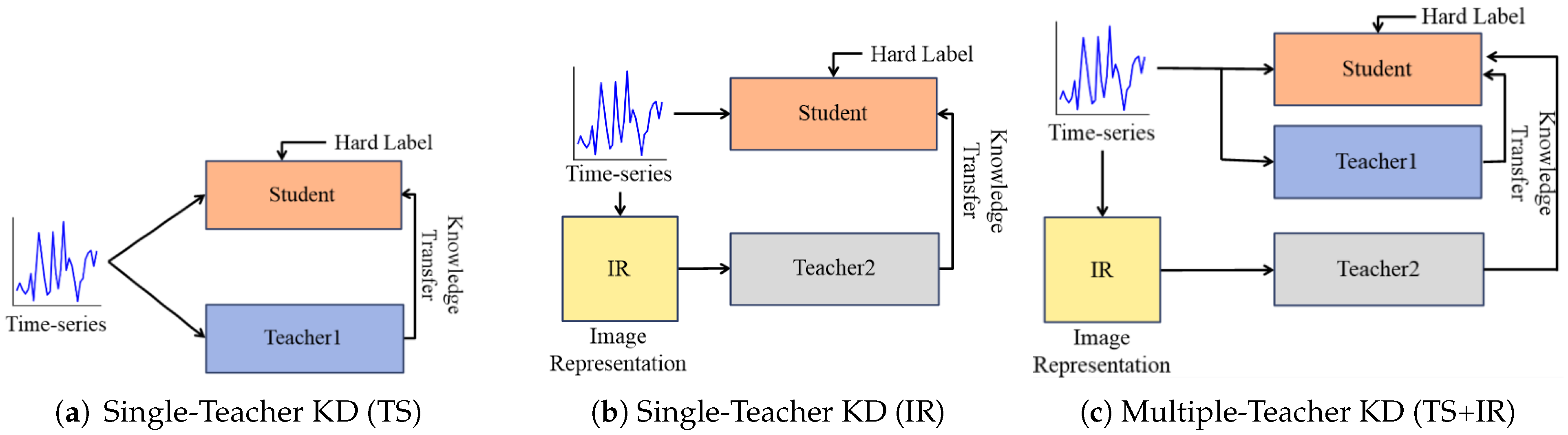
3. Strategies Leveraging Image Representations in KD
3.1. Leveraging IR with a Single Teacher
3.2. Leveraging IR with Multiple Teachers
4. Experiments
4.1. Dataset Description and Settings
4.1.1. Dataset Description
4.1.2. Experimental Settings
4.2. Analysis of Different Strategies and Combinations
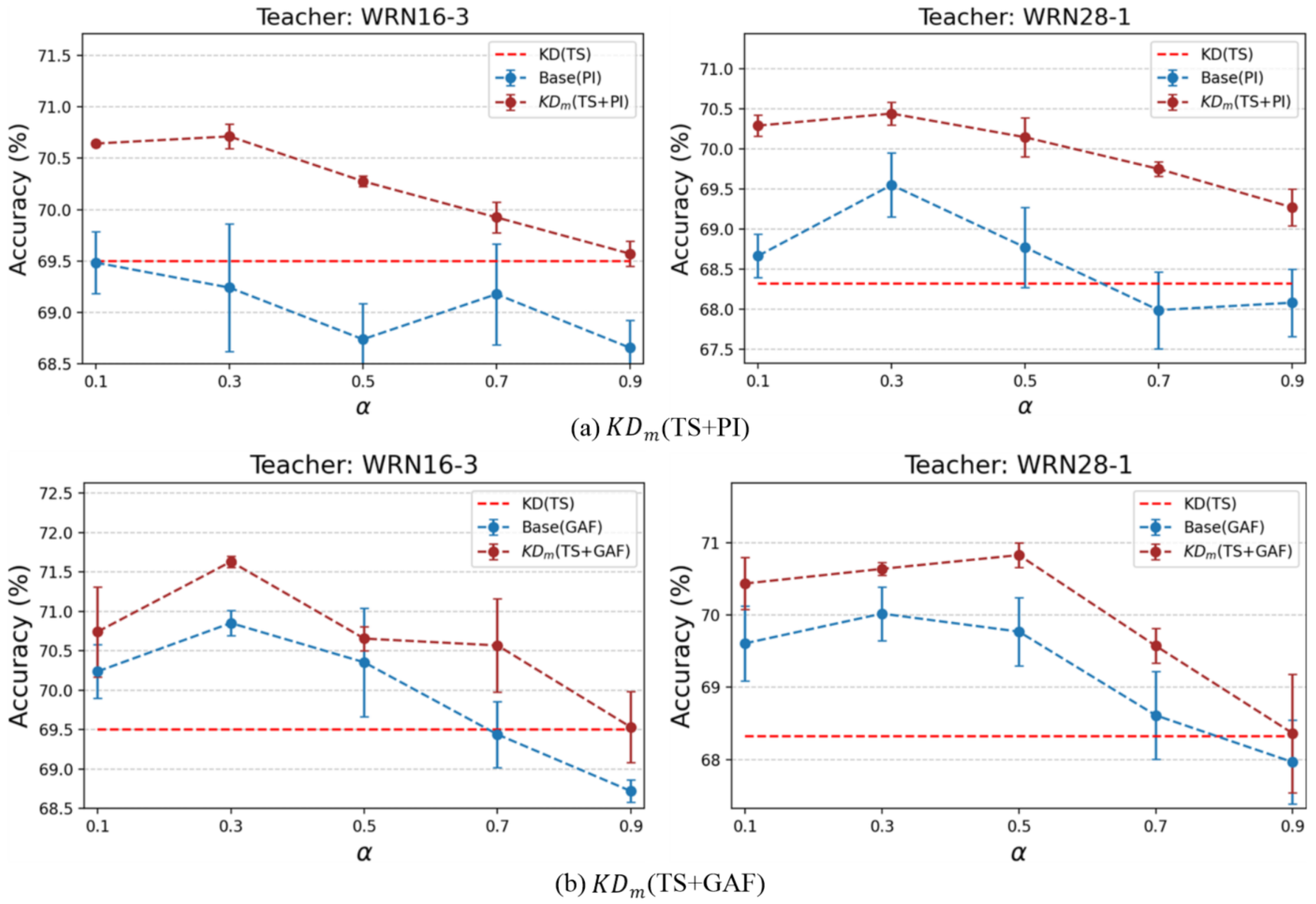
4.2.1. Single and Multiple Teachers
4.2.2. Different Capacities of Teachers
4.3. Analysis on Tolerance to Noises
4.4. Analysis of Sensitivity and Compatibility
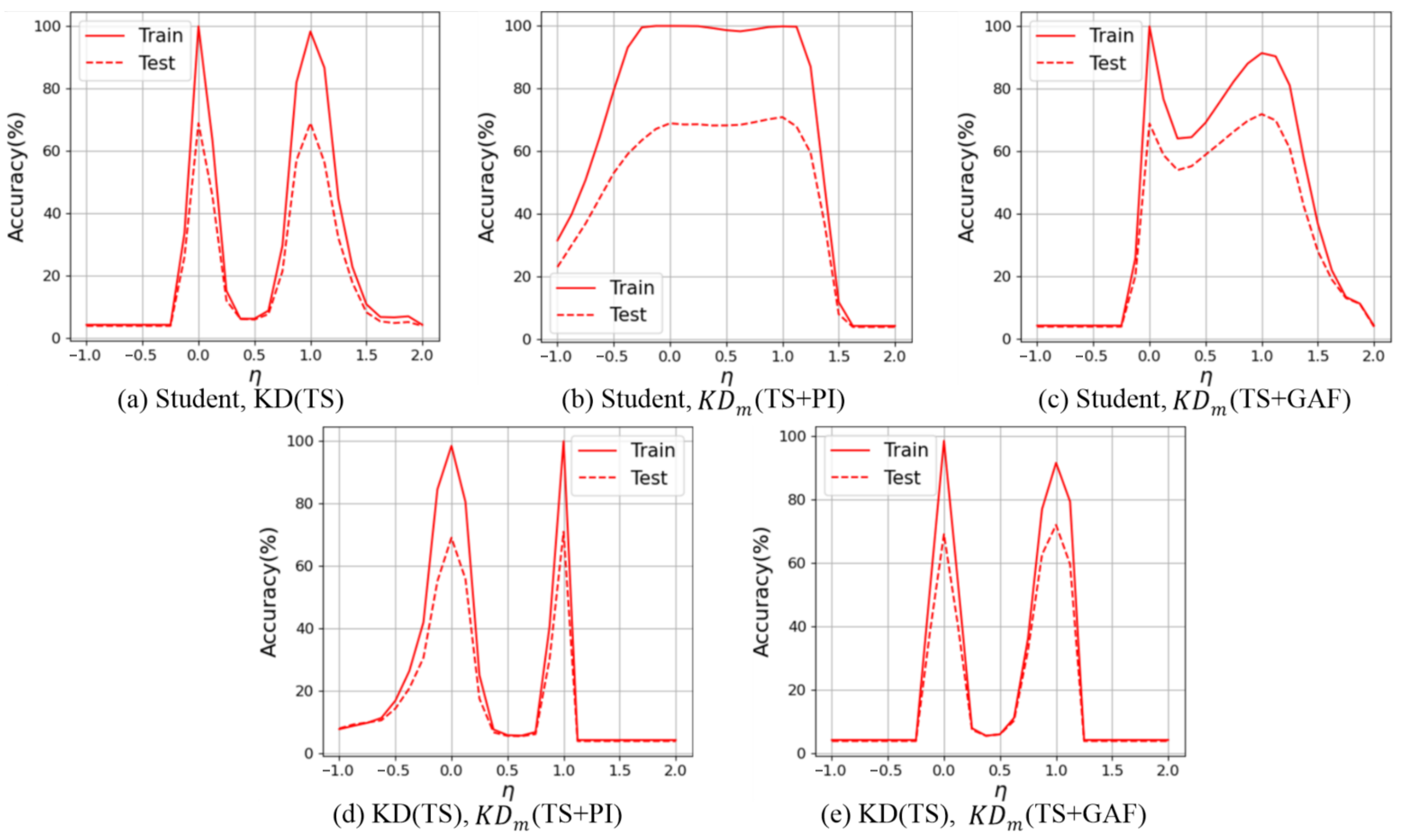
4.4.1. Sensitivity Analysis
4.4.2. Distillation Compatibility
4.5. Processing Time
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Patel, S.; Park, H.; Bonato, P.; Chan, L.; Rodgers, M. A review of wearable sensors and systems with application in rehabilitation. J. Neuroeng. Rehabil. 2012, 9, 21. [Google Scholar] [CrossRef]
- Morita, P.P.; Sahu, K.S.; Oetomo, A. Health monitoring using smart home technologies: Scoping review. JMIR mHealth uHealth 2023, 11, e37347. [Google Scholar] [CrossRef]
- Porciuncula, F.; Roto, A.V.; Kumar, D.; Davis, I.; Roy, S.; Walsh, C.J.; Awad, L.N. Wearable movement sensors for rehabilitation: A focused review of technological and clinical advances. Pm&r 2018, 10, S220–S232. [Google Scholar]
- Gu, T.; Tang, M. Indoor Abnormal Behavior Detection for the Elderly: A Review. Sensors 2025, 25, 3313. [Google Scholar] [CrossRef] [PubMed]
- Nweke, H.F.; Teh, Y.W.; Al-Garadi, M.A.; Alo, U.R. Deep learning algorithms for human activity recognition using mobile and wearable sensor networks: State of the art and research challenges. Expert Syst. Appl. 2018, 105, 233–261. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Y.; Zhang, S.; Shahabi, F.; Xia, S.; Deng, Y.; Alshurafa, N. Deep learning in human activity recognition with wearable sensors: A review on advances. Sensors 2022, 22, 1476. [Google Scholar] [CrossRef]
- Gupta, S. Deep learning based human activity recognition (HAR) using wearable sensor data. Int. J. Inf. Manag. Data Insights 2021, 1, 100046. [Google Scholar] [CrossRef]
- Shajari, S.; Kuruvinashetti, K.; Komeili, A.; Sundararaj, U. The emergence of AI-based wearable sensors for digital health technology: A review. Sensors 2023, 23, 9498. [Google Scholar] [CrossRef]
- Qin, Z.; Zhang, Y.; Meng, S.; Qin, Z.; Choo, K.K.R. Imaging and fusing time series for wearable sensor-based human activity recognition. Inf. Fusion 2020, 53, 80–87. [Google Scholar] [CrossRef]
- Zebhi, S. Human activity recognition using wearable sensors based on image classification. IEEE Sens. J. 2022, 22, 12117–12126. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Harer, J. Computational Topology: An Introduction; American Mathematical Soc.: Providence, RI, USA, 2010. [Google Scholar]
- Adams, H.; Emerson, T.; Kirby, M.; Neville, R.; Peterson, C.; Shipman, P.; Chepushtanova, S.; Hanson, E.; Motta, F.; Ziegelmeier, L. Persistence images: A stable vector representation of persistent homology. J. Mach. Learn. Res. 2017, 18, 1–35. [Google Scholar]
- Wang, Y.; Behroozmand, R.; Johnson, L.P.; Bonilha, L.; Fridriksson, J. Topological signal processing and inference of event-related potential response. J. Neurosci. Methods 2021, 363, 109324. [Google Scholar] [CrossRef]
- Wang, Z.; Oates, T. Imaging time-series to improve classification and imputation. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Buenos Aires, Argentina, 25–31 July 2015; pp. 3939–3945. [Google Scholar]
- Nawar, A.; Rahman, F.; Krishnamurthi, N.; Som, A.; Turaga, P. Topological descriptors for parkinson’s disease classification and regression analysis. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 793–797. [Google Scholar]
- Som, A.; Choi, H.; Ramamurthy, K.N.; Buman, M.P.; Turaga, P. Pi-net: A deep learning approach to extract topological persistence images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 834–835. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. In Proceedings of the NeurIPS Deep Learning and Representation Learning Workshop, Montreal, QC, Canada, 11 December 2015; Volume 2. [Google Scholar]
- Gou, J.; Yu, B.; Maybank, S.J.; Tao, D. Knowledge distillation: A survey. Int. J. Comput. Vis. 2021, 129, 1789–1819. [Google Scholar] [CrossRef]
- Jeon, E.S.; Choi, H.; Shukla, A.; Wang, Y.; Lee, H.; Buman, M.P.; Turaga, P. Topological persistence guided knowledge distillation for wearable sensor data. Eng. Appl. Artif. Intell. 2024, 130, 107719. [Google Scholar] [CrossRef]
- Ni, J.; Sarbajna, R.; Liu, Y.; Ngu, A.H.; Yan, Y. Cross-modal knowledge distillation for vision-to-sensor action recognition. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 4448–4452. [Google Scholar]
- Han, H.; Kim, S.; Choi, H.S.; Yoon, S. On the Impact of Knowledge Distillation for Model Interpretability. In Proceedings of the International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; pp. 12389–12410. [Google Scholar]
- Zeng, S.; Graf, F.; Hofer, C.; Kwitt, R. Topological attention for time series forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 24871–24882. [Google Scholar]
- Krim, H.; Gentimis, T.; Chintakunta, H. Discovering the whole by the coarse: A topological paradigm for data analysis. IEEE Signal Process. Mag. 2016, 33, 95–104. [Google Scholar] [CrossRef]
- Perea, J.A.; Harer, J. Sliding windows and persistence: An application of topological methods to signal analysis. Found. Comput. Math. 2015, 15, 799–838. [Google Scholar] [CrossRef]
- Edelsbrunner.; Letscher.; Zomorodian. Topological persistence and simplification. Discret. Comput. Geom. 2002, 28, 511–533. [Google Scholar] [CrossRef]
- Cohen-Steiner, D.; Edelsbrunner, H.; Harer, J. Stability of persistence diagrams. In Proceedings of the Annual Symposium on Computational Geometry, Pisa, Italy, 6–8 June 2005; pp. 263–271. [Google Scholar]
- Wang, Z.; Oates, T. Encoding time series as images for visual inspection and classification using tiled convolutional neural networks. In Proceedings of the Workshops at the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–29 January 2015; pp. 91–96. [Google Scholar]
- Liu, Y.; Wang, K.; Li, G.; Lin, L. Semantics-aware adaptive knowledge distillation for sensor-to-vision action recognition. IEEE Trans. Image Process. 2021, 30, 5573–5588. [Google Scholar] [CrossRef]
- Yuan, Z.; Yang, Z.; Ning, H.; Tang, X. Multiscale knowledge distillation with attention based fusion for robust human activity recognition. Sci. Rep. 2024, 14, 12411. [Google Scholar] [CrossRef]
- Iwanski, J.S.; Bradley, E. Recurrence plots of experimental data: To embed or not to embed? Chaos Interdiscip. J. Nonlinear Sci. 1998, 8, 861–871. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, K.; Turaga, P. Recurrence textures for human activity recognition from compressive cameras. In Proceedings of the IEEE International Conference on Image Processing, Orlando, FL, USA, 30 September–3 October 2012; pp. 1417–1420. [Google Scholar]
- Cena, C.; Bucci, S.; Balossino, A.; Chiaberge, M. A Self-Supervised Task for Fault Detection in Satellite Multivariate Time Series. arXiv 2024, arXiv:2407.02861. [Google Scholar] [CrossRef]
- Ben Said, A.; Abdel-Salam, A.S.G.; Hazaa, K.A. Performance prediction in online academic course: A deep learning approach with time series imaging. Multimed. Tools Appl. 2024, 83, 55427–55445. [Google Scholar] [CrossRef]
- Wen, L.; Ye, Y.; Zuo, L. GAF-Net: A new automated segmentation method based on multiscale feature fusion and feedback module. Pattern Recognit. Lett. 2025, 187, 86–92. [Google Scholar] [CrossRef]
- Buciluǎ, C.; Caruana, R.; Niculescu-Mizil, A. Model compression. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 535–541. [Google Scholar]
- Jeon, E.S.; Choi, H.; Shukla, A.; Wang, Y.; Buman, M.P.; Turaga, P. Topological Knowledge Distillation for Wearable Sensor Data. In Proceedings of the Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 31 October–2 November 2022; pp. 837–842. [Google Scholar] [CrossRef]
- Wang, Q.; Lohit, S.; Toledo, M.J.; Buman, M.P.; Turaga, P. A statistical estimation framework for energy expenditure of physical activities from a wrist-worn accelerometer. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Orlando, FL, USA, 16–20 August 2016; pp. 2631–2635. [Google Scholar]
- Jeon, E.S.; Som, A.; Shukla, A.; Hasanaj, K.; Buman, M.P.; Turaga, P. Role of Data Augmentation Strategies in Knowledge Distillation for Wearable Sensor Data. IEEE Internet Things J. 2022, 9, 12848–12860. [Google Scholar] [CrossRef]
- Reiss, A.; Stricker, D. Introducing a new benchmarked dataset for activity monitoring. In Proceedings of the International Symposium on Wearable Computers, Newcastle, UK, 18–22 June 2012; pp. 108–109. [Google Scholar]
- Jordao, A.; Nazare Jr, A.C.; Sena, J.; Schwartz, W.R. Human activity recognition based on wearable sensor data: A standardization of the state-of-the-art. arXiv 2018, arXiv:1806.05226. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Wide Residual Networks. In Proceedings of the British Machine Vision Conference (BMVC), York, UK, 19–22 September 2016. [Google Scholar]
- Cho, J.H.; Hariharan, B. On the Efficacy of Knowledge Distillation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4794–4802. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Paying more attention to attention: Improving the performance of convolutional neural networks via attention transfer. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Tung, F.; Mori, G. Similarity-preserving knowledge distillation. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1365–1374. [Google Scholar]
- Chen, D.; Mei, J.P.; Zhang, H.; Wang, C.; Feng, Y.; Chen, C. Knowledge distillation with the reused teacher classifier. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11933–11942. [Google Scholar]
- Huang, T.; You, S.; Wang, F.; Qian, C.; Xu, C. Knowledge distillation from a stronger teacher. Adv. Neural Inf. Process. Syst. 2022, 35, 33716–33727. [Google Scholar]
- Giakoumoglou, N.; Stathaki, T. Discriminative and Consistent Representation Distillation. arXiv 2024, arXiv:2407.11802. [Google Scholar]
- Miles, R.; Mikolajczyk, K. Understanding the role of the projector in knowledge distillation. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 4233–4241. [Google Scholar]
- You, S.; Xu, C.; Xu, C.; Tao, D. Learning from multiple teacher networks. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1285–1294. [Google Scholar]
- Kwon, K.; Na, H.; Lee, H.; Kim, N.S. Adaptive knowledge distillation based on entropy. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 7409–7413. [Google Scholar]
- Zhang, H.; Chen, D.; Wang, C. Confidence-aware multi-teacher knowledge distillation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 4498–4502. [Google Scholar]
- Wang, X.; Wang, C. Time series data cleaning: A survey. IEEE Access 2019, 8, 1866–1881. [Google Scholar] [CrossRef]
- Wen, Q.; Sun, L.; Yang, F.; Song, X.; Gao, J.; Wang, X.; Xu, H. Time Series Data Augmentation for Deep Learning: A Survey. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Montreal, QC, Canada, 19–26 August 2021; pp. 4653–4660. [Google Scholar]
- Goodfellow, I.J.; Vinyals, O.; Saxe, A.M. Qualitatively Characterizing Neural Network Optimization Problems. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Li, H.; Xu, Z.; Taylor, G.; Studer, C.; Goldstein, T. Visualizing the loss landscape of neural nets. In Proceedings of the Advances in Neural Information Processing Systems, NeurIPS 2018, Montreal, QC, Canada, 2–8 December 2018; Volume 31. [Google Scholar]
- Rosenberg, A.; Hirschberg, J. V-measure: A conditional entropy-based external cluster evaluation measure. In Proceedings of the Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning (EMNLP-CoNLL), Prague, Czech Republic, 28 June 2007; pp. 410–420. [Google Scholar]
- Gao, Y.; He, Y.; Li, X.; Zhao, B.; Lin, H.; Liang, Y.; Zhong, J.; Zhang, H.; Wang, J.; Zeng, Y.; et al. An empirical study on low gpu utilization of deep learning jobs. In Proceedings of the IEEE/ACM International Conference on Software Engineering, Lisbon, Portugal, 14–20 April 2024; pp. 1–13. [Google Scholar]
- Zhang, H.; Huang, J. Challenging GPU Dominance: When CPUs Outperform for On-Device LLM Inference. arXiv 2025, arXiv:2505.06461. [Google Scholar] [CrossRef]






| DB | Teachers | Student | FLOPs | # of Params | Compression Ratio | ||||
|---|---|---|---|---|---|---|---|---|---|
| Teacher1 | Teacher2 | Student | Teacher1 | Teacher2 | Student | ||||
| (TS) | (PI/GAF) | (TS) | (TS) | (PI/GAF) | (TS) | ||||
| GENEActiv | WRN16-1 | WRN16-1 | 11.03 M | 108.97 M | 11.03 M | 0.06 M | 0.18 M | 0.06 M | 25.93% |
| WRN16-3 | 93.95 M | 898.52 M | 0.54 M | 1.55 M | 2.94% | ||||
| WRN28-1 | 22.22 M | 224.28 M | 0.13 M | 0.37 M | 12.36% | ||||
| WRN28-3 | 192.01 M | 1923.93 M | 1.12 M | 3.29 M | 1.39% | ||||
| PAMAP2 | WRN16-1 | WRN16-1 | 2.39 M | 131.02 M | 2.39 M | 0.06 M | 0.18 M | 0.06 M | 25.88% |
| WRN16-3 | 19.00 M | 921.03 M | 0.54 M | 1.56 M | 3.01% | ||||
| WRN28-1 | 4.64 M | 246.56 M | 0.13 M | 0.37 M | 12.52% | ||||
| WRN28-3 | 38.64 M | 1947.13 M | 1.12 M | 3.30 M | 1.43% | ||||
| Model | Teacher1 | WRN16-1 | WRN16-3 | WRN28-1 | WRN28-3 | |
| (Time Series) | (67.66) | (68.89) | (68.63) | (69.23) | ||
| Teacher2 | WRN16-1 | WRN16-3 | WRN28-1 | WRN28-3 | ||
| (PI) | (58.64) | (59.80) | (59.45) | (59.69) | ||
| (GAF) | (63.32) | (64.03) | (64.00) | (65.39) | ||
| Student | WRN16-1 | |||||
| (Time Series) | (67.66 ± 0.45) | |||||
| Single Teacher | GAF | KD | 70.32 | 70.37 | 69.52 | 69.77 |
| ±0.07 | ±0.03 | ±0.09 | ±0.09 | |||
| PI | KD | 67.83 | 68.76 | 68.51 | 68.46 | |
| ±0.17 | ±0.73 | ±0.01 | ±0.28 | |||
| Time Series | KD | 69.71 | 69.50 | 68.32 | 68.58 | |
| ±0.38 | ±0.10 | ±0.63 | ±0.66 | |||
| AT | 68.21 | 69.79 | 68.09 | 67.73 | ||
| ±0.64 | ±0.36 | ±0.24 | ±0.27 | |||
| SP | 67.20 | 67.85 | 68.71 | 67.39 | ||
| ±0.36 | ±0.24 | ±0.46 | ±0.49 | |||
| SimKD | 69.39 | 69.89 | 68.92 | 68.80 | ||
| ±0.18 | ±0.11 | ±0.40 | ±0.38 | |||
| DIST | 68.20 | 69.71 | 69.23 | 68.18 | ||
| ±0.28 | ±0.15 | ±0.19 | ±0.60 | |||
| Projector | 69.64 | 70.28 | 69.43 | 69.09 | ||
| ±0.53 | ±0.38 | ±0.47 | ±0.38 | |||
| DCD | 70.56 | 70.17 | 70.05 | 69.22 | ||
| ±0.12 | ±0.2 | ±0.41 | ±0.35 | |||
| Multiple Teachers | TS + PI | AVER | 68.99 | 68.74 | 68.77 | 69.02 |
| ±0.76 | ±0.35 | ±0.70 | ±0.50 | |||
| EBKD | 68.43 | 69.24 | 68.45 | 67.50 | ||
| ±0.25 | ±0.25 | ±0.73 | ±0.40 | |||
| CA-MKD | 69.33 | 69.80 | 69.61 | 68.81 | ||
| ±0.61 | ±0.16 | ±0.57 | ±0.79 | |||
| Base | 69.09 | 69.24 | 69.55 | 69.42 | ||
| ±0.37 | ±0.62 | ±0.41 | ±0.58 | |||
| Ann | 70.15 | 70.71 | 70.44 | 69.97 | ||
| ±0.03 | ±0.12 | ±0.10 | ±0.06 | |||
| TS + GAF | AVER | 69.93 | 70.35 | 69.76 | 69.93 | |
| ±0.76 | ±0.35 | ±0.70 | ±0.50 | |||
| EBKD | 68.85 | 67.84 | 68.51 | 68.25 | ||
| ±0.41 | ±0.20 | ±0.67 | ±0.68 | |||
| CA-MKD | 70.48 | 69.98 | 69.64 | 70.01 | ||
| ±0.86 | ±0.32 | ±0.56 | ±0.25 | |||
| Base | 70.39 | 70.85 | 70.01 | 69.39 | ||
| ±0.45 | ±0.16 | ±0.37 | ±0.13 | |||
| Ann | 70.88 | 71.63 | 70.63 | 70.64 | ||
| ±0.13 | ±0.24 | ±0.35 | ±0.40 | |||
| Method | Window Length | |||||
| 1000 | 500 | |||||
| LS | WRN16-1 | 89.29 ± 0.32 | 86.83 ± 0.15 | |||
| WRN16-3 | 89.53 ± 0.15 | 87.95 ± 0.25 | ||||
| WRN16-8 | 89.31 ± 0.21 | 87.29 ± 0.17 | ||||
| KD Method | Teacher Model | |||||
| WRN16-1 | WRN16-3 | WRN16-1 | WRN16-3 | |||
| Single Teacher | Time Series | ESKD | 89.79 ± 0.32 | 89.88 ± 0.07 | 87.44 ± 0.53 | 88.16 ± 0.15 |
| Full KD | 88.78 ± 0.72 | 89.84 ± 0.21 | 86.28 ± 1.02 | 87.05 ± 0.19 | ||
| AT | 90.10 ± 0.49 | 90.32 ± 0.09 | 87.25 ± 0.22 | 87.60 ± 0.22 | ||
| SP | 87.08 ± 0.56 | 88.47 ± 0.19 | 87.65 ± 0.11 | 87.69 ± 0.18 | ||
| SimKD | 90.25 ± 0.22 | 90.47 ± 0.32 | 87.24 ± 0.09 | 88.16 ± 0.37 | ||
| DIST | 90.18 ± 0.31 | 90.20 ± 0.39 | 87.62 ± 0.02 | 87.05 ± 0.31 | ||
| DCD | 89.72 ± 0.91 | 90.20 ± 0.39 | 87.82 ± 0.80 | 88.06 ± 0.75 | ||
| Projector | 90.01 ± 0.70 | 90.23 ± 0.36 | 87.75 ± 0.90 | 87.93 ± 0.72 | ||
| Multiple Teachers | TS + PI | AVER | 90.01 ± 0.46 | 90.06 ± 0.33 | 87.53 ± 0.16 | 87.05 ± 0.37 |
| EBKD | 90.35 ± 0.12 | 89.82 ± 0.14 | 87.51 ± 0.41 | 87.66 ± 0.28 | ||
| CA-MKD | 90.01 ± 0.28 | 90.13 ± 0.34 | 87.14 ± 0.25 | 88.04 ± 0.26 | ||
| Base | 90.22 ± 0.73 | 89.98 ± 0.16 | 88.52 ± 0.68 | 87.85 ± 0.51 | ||
| Ann | 90.44 ± 0.16 | 90.71 ± 0.15 | 88.18 ± 0.12 | 88.26 ± 0.24 | ||
| TS + GAF | AVER | 90.32 ± 0.94 | 90.18 ± 0.83 | 88.44 ± 0.03 | 88.13 ± 0.76 | |
| EBKD | 89.55 ± 0.52 | 89.91 ± 1.04 | 87.91 ± 0.18 | 88.07 ± 0.52 | ||
| CA-MKD | 90.25 ± 1.06 | 91.28 ± 0.58 | 87.74 ± 0.44 | 88.00 ± 0.25 | ||
| Base | 90.44 ± 0.18 | 90.58 ± 0.11 | 88.31 ± 0.71 | 88.71 ± 0.24 | ||
| Ann | 91.14 ± 0.12 | 91.84 ± 0.24 | 88.79 ± 0.20 | 88.93 ± 0.39 | ||
| Model | Teacher1 | WRN16-1 | WRN16-3 | WRN28-1 | WRN28-3 | |
| (Time Series) | (85.27) | (85.80) | (84.81) | (84.46) | ||
| Teacher2 | WRN16-1 | WRN16-3 | WRN28-1 | WRN28-3 | ||
| (PI) | (86.93) | (87.23) | (87.45) | (87.88) | ||
| (GAF) | (81.44) | (82.29) | (81.90) | (82.98) | ||
| Student | WRN16-1 | |||||
| (Time Series) | (82.99±2.50) | |||||
| Single Teacher | GAF | KD | 87.57 | 85.03 | 85.57 | 85.42 |
| ±2.06 | ±2.34 | ±2.58 | ±2.43 | |||
| PI | KD | 85.04 | 86.68 | 85.08 | 85.39 | |
| ±2.58 | ±2.19 | ±2.44 | ±2.35 | |||
| TS | KD | 85.96 | 86.50 | 84.92 | 86.26 | |
| ±2.19 | ±2.21 | ±2.45 | ±2.40 | |||
| DCD | 85.58 | 85.29 | 83.91 | 85.69 | ||
| ±2.29 | ±2.45 | ±2.56 | ±2.56 | |||
| Projector | 86.61 | 85.07 | 84.59 | 86.78 | ||
| ±2.04 | ±2.32 | ±2.53 | ±2.26 | |||
| Multiple Teachers | TS + PI | Base | 85.91 | 86.18 | 85.54 | 86.04 |
| ±2.32 | ±2.37 | ±2.26 | ±2.24 | |||
| Ann | 86.09 | 87.12 | 85.89 | 86.33 | ||
| ±2.33 | ±2.26 | ±2.26 | ±2.30 | |||
| TS + GAF | Base | 87.22 | 86.56 | 84.66 | 86.41 | |
| ±2.23 | ±2.21 | ±2.51 | ±2.32 | |||
| Ann | 88.69 | 87.57 | 86.58 | 86.77 | ||
| ±1.83 | ±2.08 | ±2.33 | ±2.31 | |||
| Method | Architecture Difference | ||||||||||||
| Depth | Width | Depth + Width | |||||||||||
| Teacher1 (Time Series) | WRN | WRN | WRN | WRN | WRN | WRN | WRN | WRN | WRN | WRN | WRN | WRN | |
| 16-1 | 16-1 | 28-1 | 40-1 | 16-1 | 16-3 | 28-1 | 28-3 | 28-1 | 28-3 | 40-1 | 16-1 | ||
| 0.06M | 0.06M | 0.1M | 0.2M | 0.06M | 0.5M | 0.1M | 1.1M | 0.1M | 1.1M | 0.2M | 0.06M | ||
| (67.66) | (67.66) | (68.63) | (69.05) | (67.66) | (68.89) | (68.63) | (69.23) | (68.63) | (69.23) | (69.05) | (67.66) | ||
| Teacher2 | WRN | WRN | WRN | WRN | WRN | WRN | WRN | WRN | WRN | WRN | WRN | WRN | |
| 28-1 | 40-1 | 16-1 | 16-1 | 16-3 | 16-1 | 28-3 | 28-1 | 16-3 | 40-1 | 28-3 | 28-3 | ||
| 0.1M | 0.6M | 0.2M | 0.2M | 1.6M | 0.2M | 3.3M | 0.4M | 1.6M | 0.6M | 3.3M | 3.3M | ||
| (PI) | (59.45) | (59.67) | (58.64) | (58.64) | (59.80) | (58.64) | (59.69) | (59.45) | (59.80) | (59.67) | (59.69) | (59.69) | |
| (GAF) | (64.00) | (64.35) | (63.32) | (63.32) | (64.03) | (63.32) | (65.39) | (64.00) | (64.03) | (64.35) | (65.39) | (65.39) | |
| Student (Time Series) | WRN16-1 | ||||||||||||
| 0.06M ( 67.66±0.45) | |||||||||||||
| TS + PI | Base | 68.71 | 68.41 | 67.89 | 68.33 | 68.77 | 68.92 | 68.26 | 69.09 | 68.04 | 68.29 | 68.90 | 68.15 |
| ±0.36 | ±0.27 | ±0.27 | ±0.17 | ±0.43 | ±0.79 | ±0.13 | ±0.59 | ±0.24 | ±0.27 | ±0.50 | ±0.23 | ||
| Ann | 69.95 | 69.86 | 70.34 | 70.56 | 69.68 | 71.06 | 70.28 | 69.95 | 70.28 | 69.87 | 70.49 | 69.65 | |
| ±0.05 | ±0.07 | ±0.14 | ±0.04 | ±0.14 | ±0.02 | ±0.08 | ±0.07 | ±0.13 | ±0.23 | ±0.05 | ±0.04 | ||
| (2.29) | (2.20) | (2.68) | (2.90) | (2.02) | (3.40) | (2.62) | (2.29) | (2.62) | (2.21) | (2.83) | (1.99) | ||
| TS + GAF | Base | 70.57 | 70.18 | 69.48 | 70.37 | 70.58 | 71.07 | 70.02 | 69.86 | 69.68 | 69.69 | 70.19 | 69.97 |
| ±0.52 | ±0.76 | ±0.19 | ±0.18 | ±0.49 | ±0.36 | ±0.10 | ±0.68 | ±0.38 | ±0.58 | ±0.4 | ±0.49 | ||
| Ann | 70.90 | 71.53 | 70.48 | 70.83 | 71.32 | 70.92 | 70.42 | 70.87 | 70.57 | 70.43 | 71.39 | 70.99 | |
| ±0.30 | ±0.68 | ±0.43 | ±0.25 | ±0.14 | ±0.22 | ±0.22 | ±0.74 | ±0.60 | ±0.56 | ±0.50 | ±0.71 | ||
| (3.24) | (3.87) | (2.82) | (3.17) | (3.66) | (3.26) | (2.76) | (3.21) | (2.91) | (2.77) | (3.73) | (3.33) | ||
| Model | Learning from Scratch | KD | ||||||
|---|---|---|---|---|---|---|---|---|
| TS (1D) | PImage (2D) | GAF Image (2D) | TS | PI | GAF | (TS+PI) | (TS+GAF) | |
| WRN28-3 | WRN16-3 | WRN16-3 | ||||||
| Accuracy (%) | 69.42 | 59.90 | 64.04 | 69.50 | 68.76 | 70.37 | 70.71 | 71.63 |
| GPU (s) | 22.23 | 126.48 (PIs on CPU) | 5.39 (GAFs on CPU) | 15.03 | ||||
| +16.31 (model) | +16.31 (model) | |||||||
| CPU (s) | 29.63 | 126.48 (PIs on CPU) | 5.39 (GAFs on CPU) | 13.57 | ||||
| +29.94 (model) | +29.94 (model) | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, J.C.; Buman, M.P.; Turaga, P.; Jeon, E.S. Image Representation-Driven Knowledge Distillation for Improved Time-Series Interpretation on Wearable Sensor Data. Sensors 2025, 25, 6396. https://doi.org/10.3390/s25206396
Jeong JC, Buman MP, Turaga P, Jeon ES. Image Representation-Driven Knowledge Distillation for Improved Time-Series Interpretation on Wearable Sensor Data. Sensors. 2025; 25(20):6396. https://doi.org/10.3390/s25206396
Chicago/Turabian StyleJeong, Jae Chan, Matthew P. Buman, Pavan Turaga, and Eun Som Jeon. 2025. "Image Representation-Driven Knowledge Distillation for Improved Time-Series Interpretation on Wearable Sensor Data" Sensors 25, no. 20: 6396. https://doi.org/10.3390/s25206396
APA StyleJeong, J. C., Buman, M. P., Turaga, P., & Jeon, E. S. (2025). Image Representation-Driven Knowledge Distillation for Improved Time-Series Interpretation on Wearable Sensor Data. Sensors, 25(20), 6396. https://doi.org/10.3390/s25206396







