Measurement of Force and Position Using a Cantilever Beam and Multiple Strain Gauges: Sensing Principles and Design Considerations
Highlights
- Novel sensor concept uses strain gauges on a cantilever beam to simultaneously measure force and position.
- Sensor is highly linear, with accuracy primarily based on the applied load.
- The sensor can be designed to fit a wide variety of measurement ranges.
- The durable, compact design is suitable for rugged field and robotics applications.
Abstract
1. Introduction
2. Operating Principles
3. Analysis of Sensor Performance
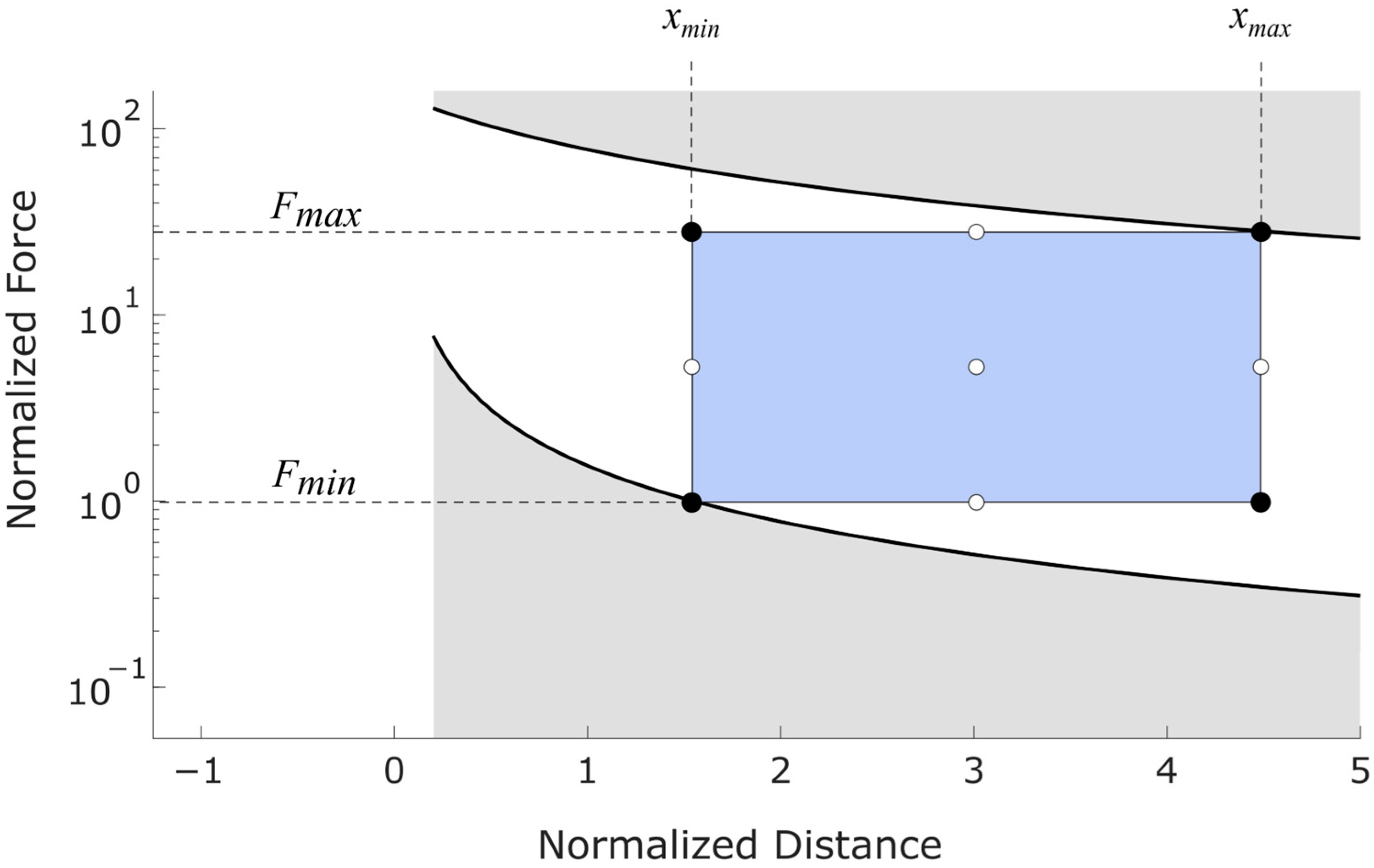
3.1. Sensor Design Limits
3.1.1. Maximum and Minimum Moment
3.1.2. Maximum Moment and Strain
3.1.3. Minimum Moment and Strain
3.1.4. Operational Limits
3.1.5. Relationship Between Physical Design and Measurement Limits
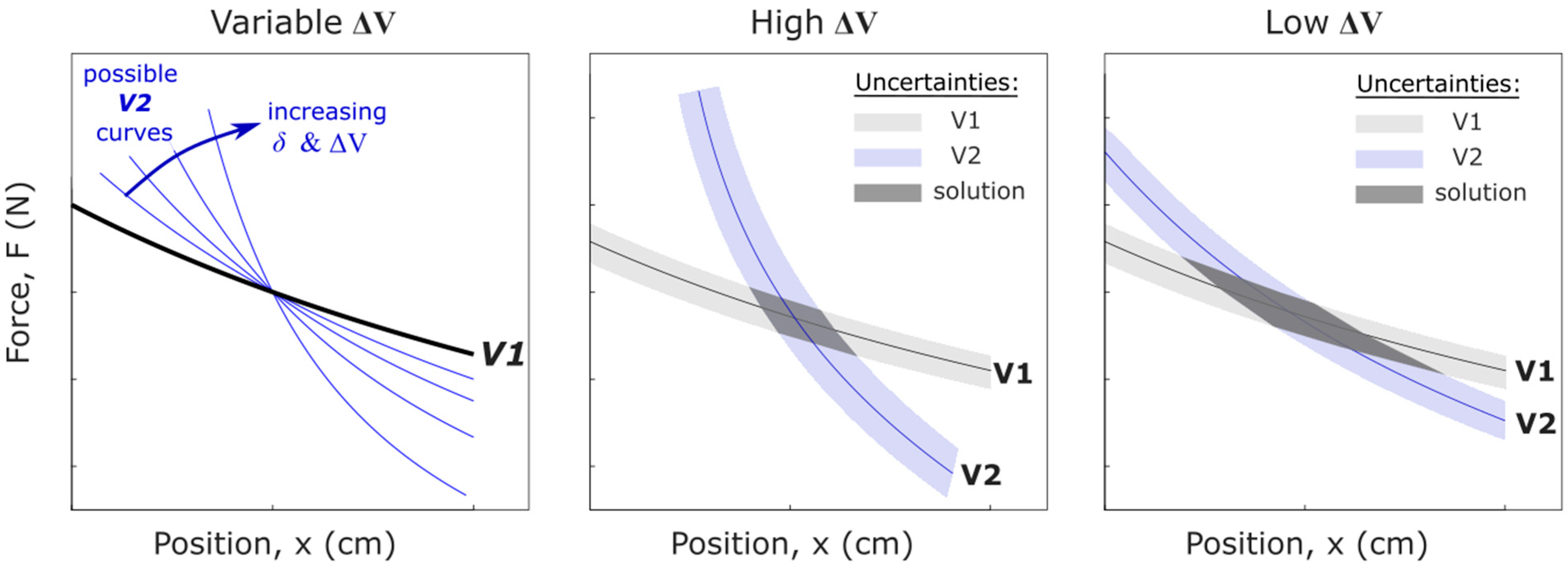
3.2. Voltage Disparity and Sensor Accuracy
3.3. Calibration and Prediction
4. Prototypes, Experiments, and Simulations
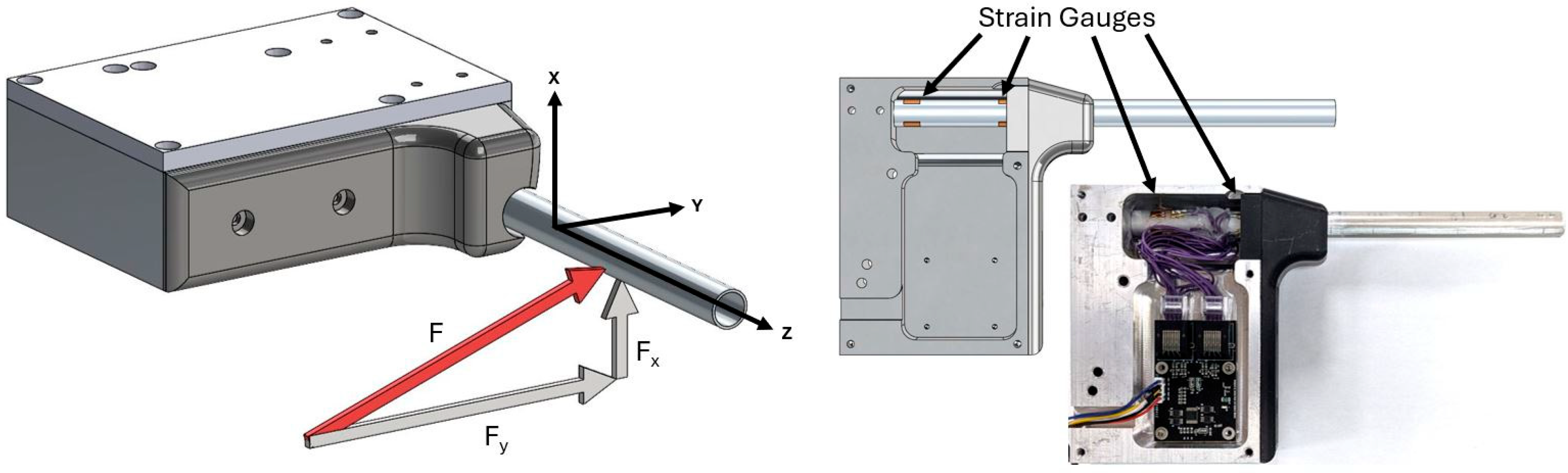
4.1. Prototype Construction
4.2. Prototype Calibration and Measurement
4.2.1. Data Collection
4.2.2. Calibration Data
4.2.3. Measurement and Validation Data
4.2.4. Influence of Strain Gauge Spacing
4.3. Simulations for Assessing Variation in Performance Across the Operational Range
5. Results
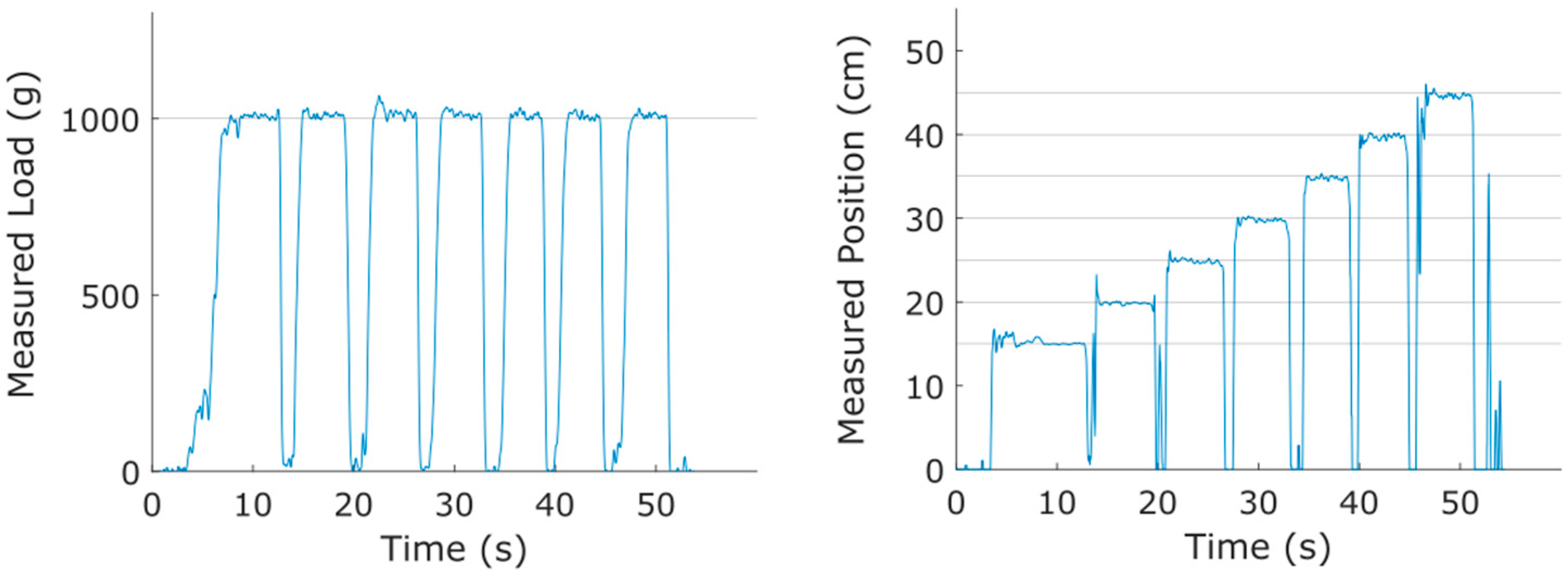
5.1. Illustration of Sensor Data
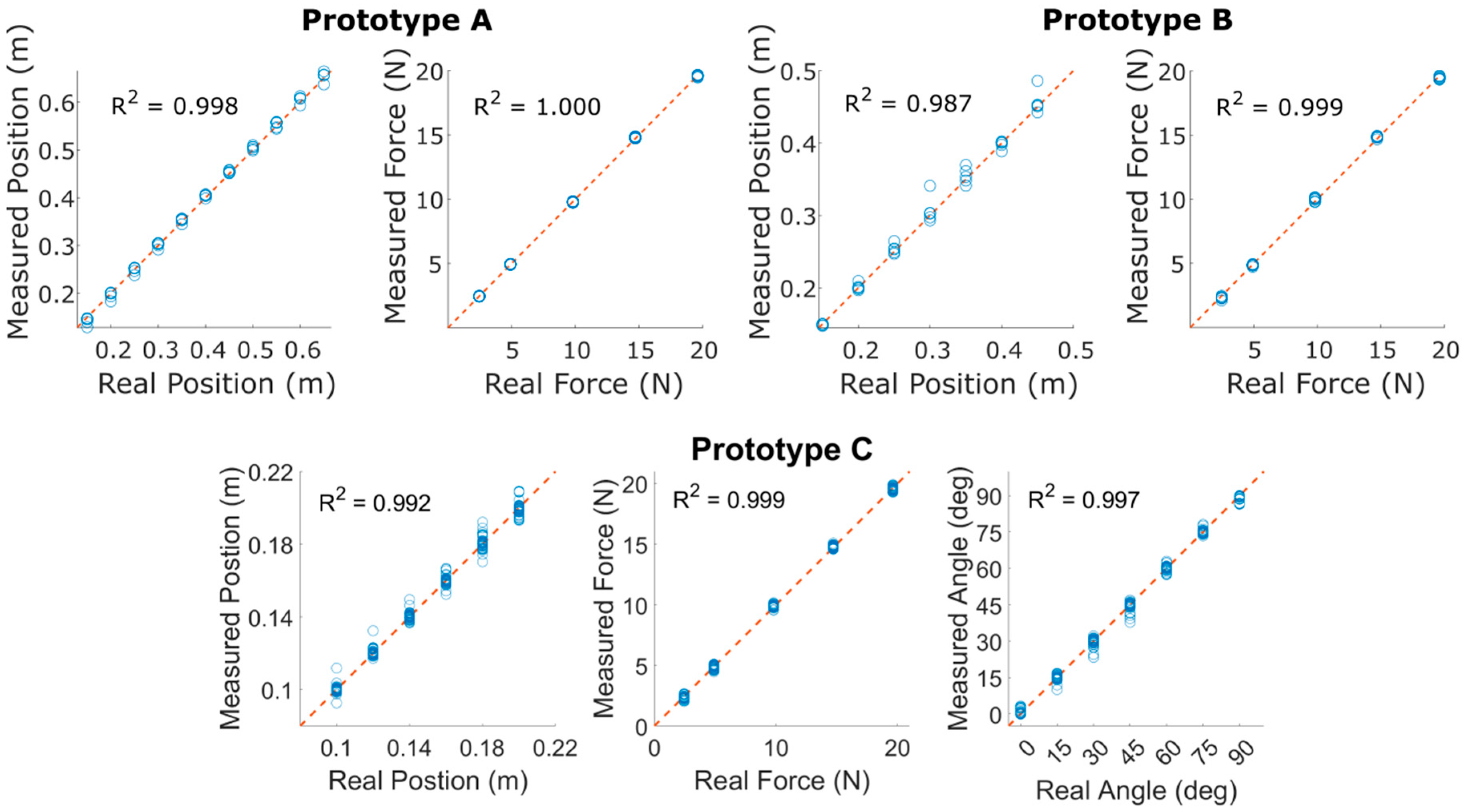
5.2. Calibration Results
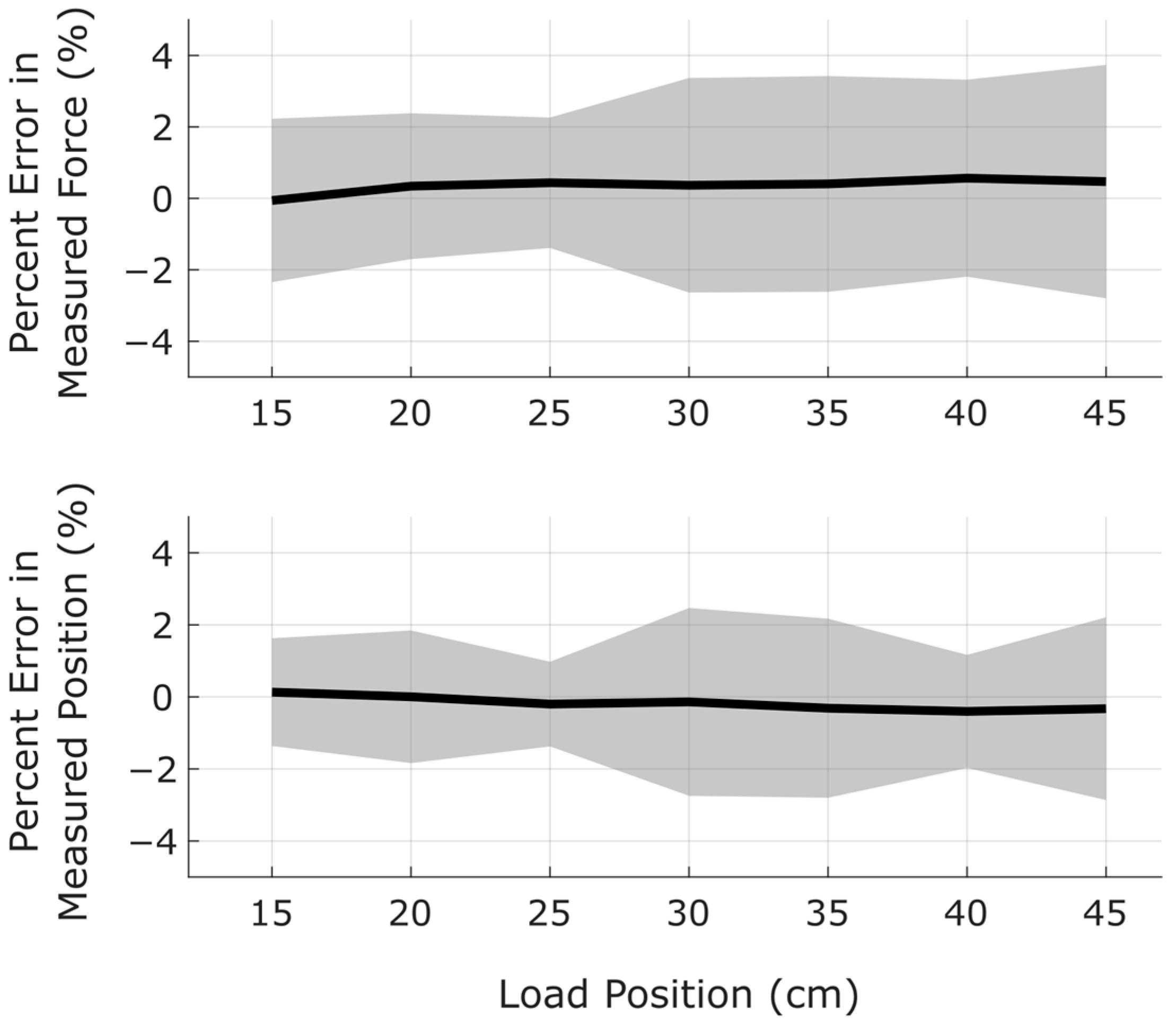
5.3. Measurement Predictions
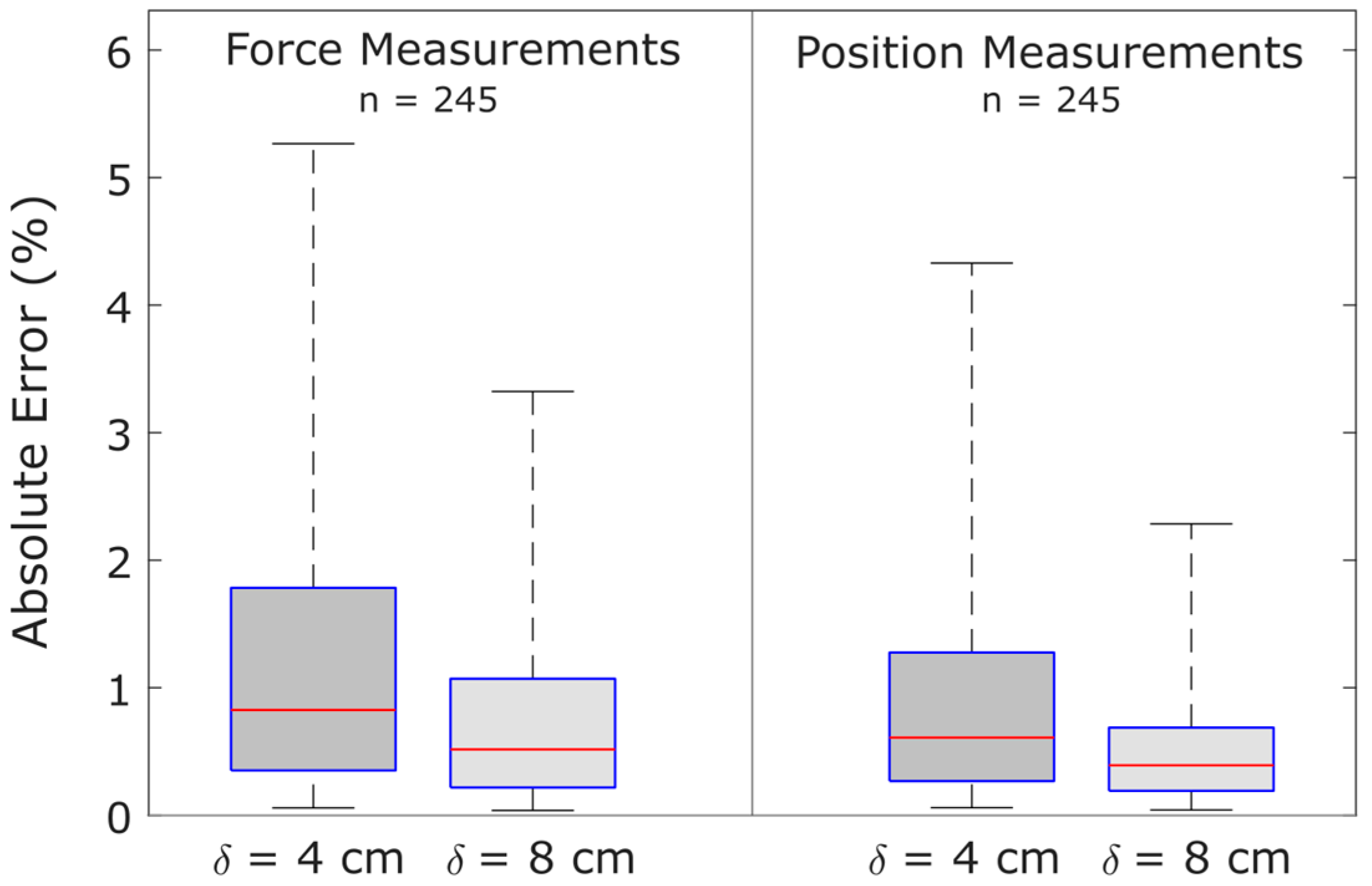
5.4. Influence of Strain Gauge Spacing on Measurement Accuracy
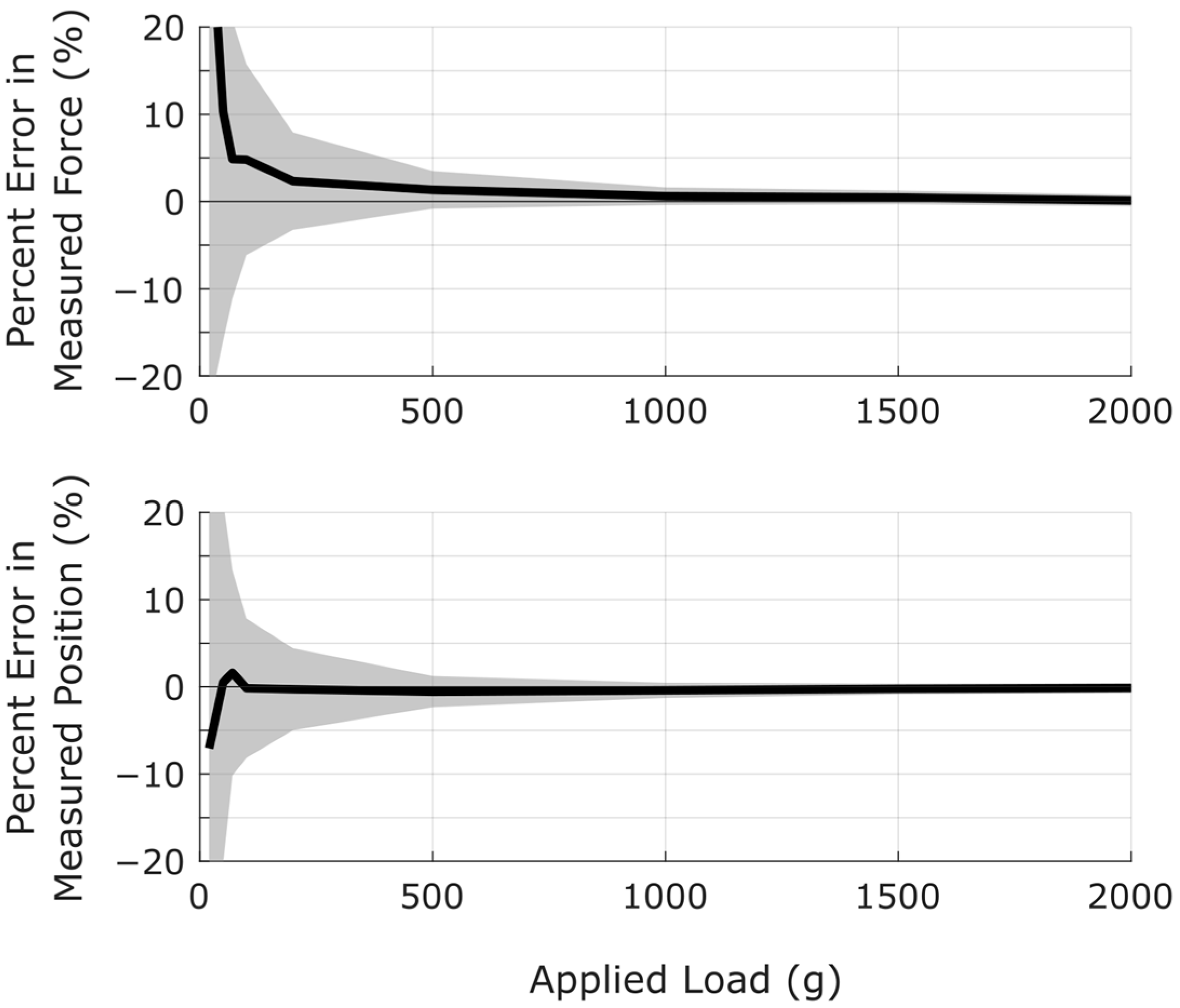
5.5. Performance as a Function of Applied Load and Position
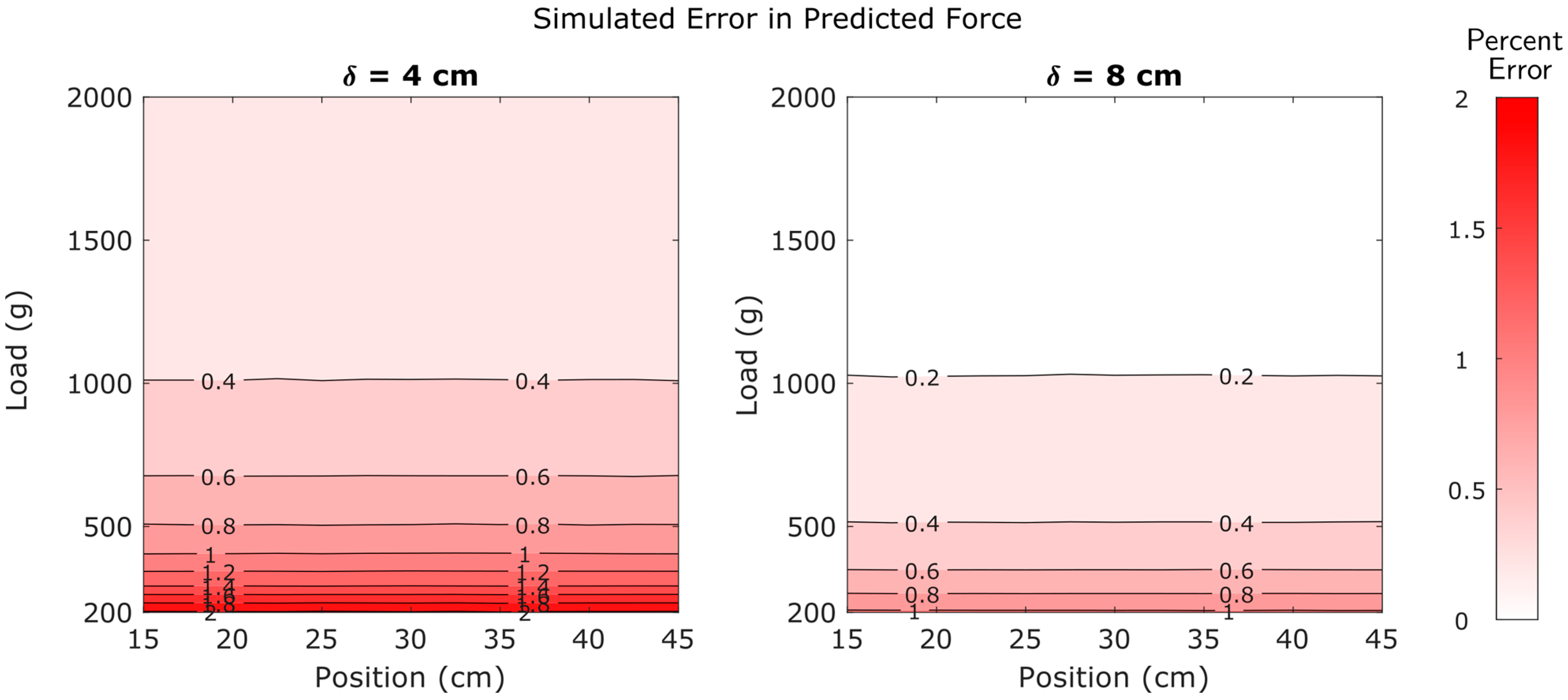
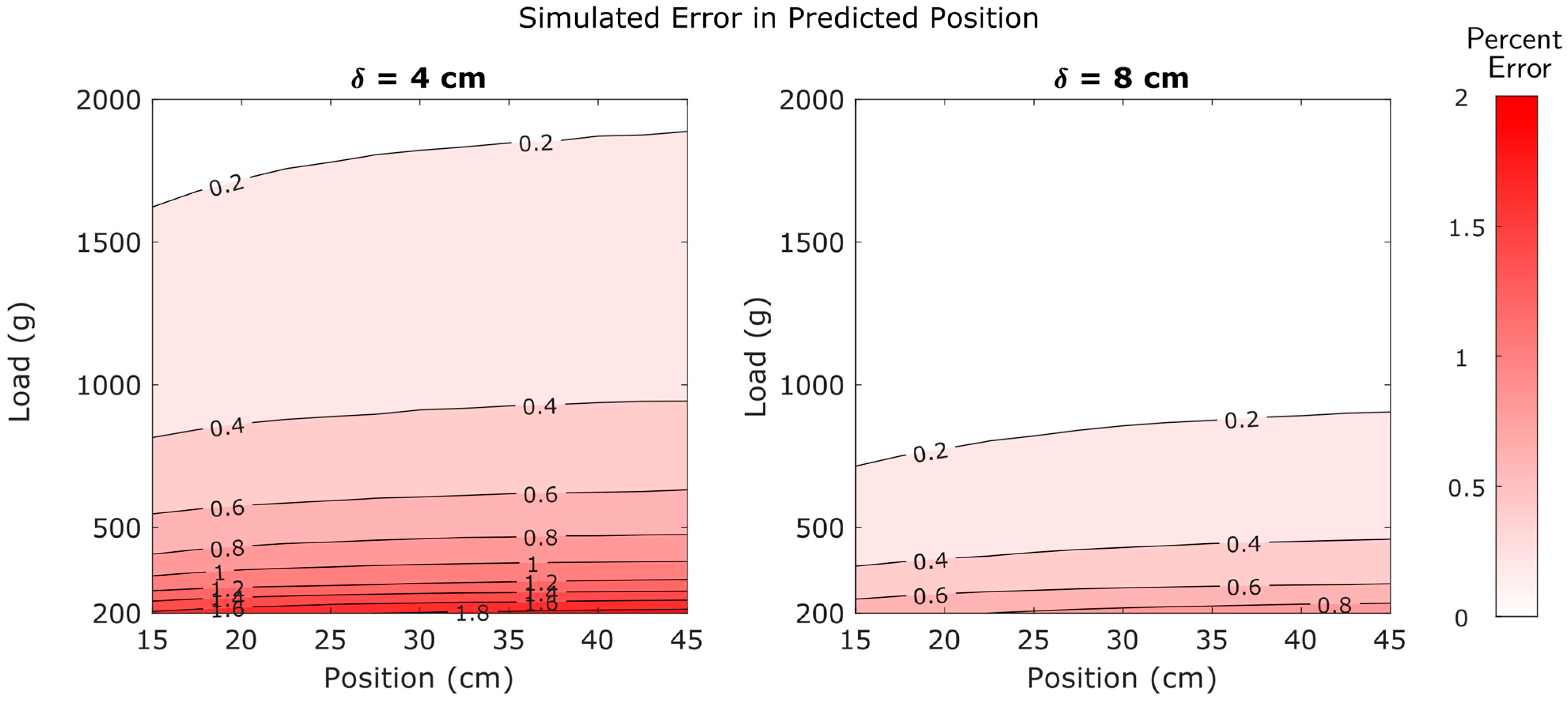
5.6. Simulation Results
6. Discussion
6.1. Synthesizing Results
6.2. Potential Applications
6.3. Assumptions and Limitations
6.3.1. Linearity Assumptions
6.3.2. Limitations in Error Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kamble, V.; Shinde, V.; Kittur, J. Overview of Load Cells. J. Mech. Mech. Eng. 2020, 6, 22–29. [Google Scholar]
- Joo, J.W.; Na, K.S.; Kang, D.I. Design and evaluation of a six-component load cell. Measurement 2002, 32, 125–133. [Google Scholar] [CrossRef]
- Muller, I.; de Brito, R.M.; Pereira, C.E.; Brusamarello, V. Load cells in force sensing analysis—Theory and a novel application. IEEE Instrum. Meas. Mag. 2010, 13, 15–19. [Google Scholar] [CrossRef]
- Mastinu, G.; Gobbi, M.; Previati, G. A New Six-axis Load Cell. Part I: Design. Exp. Mech. 2011, 51, 373–388. [Google Scholar] [CrossRef]
- Chang, Y.-S.; Lin, T.-C. An Optimal G-shaped Load Cell for Two-range Loading. Eng. Agric. Environ. Food 2013, 6, 172–176. [Google Scholar] [CrossRef]
- Zou, L.; Ge, C.; Wang, Z.J.; Cretu, E.; Li, X. Novel Tactile Sensor Technology and Smart Tactile Sensing Systems: A Review. Sensors 2017, 17, 2653. [Google Scholar] [CrossRef]
- Yang, T.; Xie, D.; Li, Z.; Zhu, H. Recent advances in wearable tactile sensors: Materials, sensing mechanisms, and device performance. Mater. Sci. Eng. R Rep. 2017, 115, 1–37. [Google Scholar] [CrossRef]
- Chu, Z.; Sarro, P.M.; Middelhoek, S. Silicon Three-axial Tactile Sensor. In Proceedings of the International Solid-State Sensors and Actuators Conference—TRANSDUCERS ’95, Stockholm, Sweden, 25–29 June 1995; pp. 656–659. [Google Scholar] [CrossRef]
- Ge, C.; Wang, Z.; Liu, Z.; Wu, T.; Wang, S.; Ren, X.; Chen, D.; Zhao, J.; Hu, P.; Zhang, J. A Capacitive and Piezoresistive Hybrid Sensor for Long-Distance Proximity and Wide-Range Force Detection in Human–Robot Collaboration. Adv. Intell. Syst. 2022, 4, 2100213. [Google Scholar] [CrossRef]
- Chuang, C.-H.; Li, T.-H.; Chou, I.-C.; Teng, Y.-J. Piezoelectric tactile sensor for submucosal tumor detection in endoscopy. Sens. Actuators Phys. 2016, 244, 299–309. [Google Scholar] [CrossRef]
- Dargahi, J. A piezoelectric tactile sensor with three sensing elements for robotic, endoscopic and prosthetic applications. Sens. Actuators Phys. 2000, 80, 23–30. [Google Scholar] [CrossRef]
- Wisitsoraat, A.; Patthanasetakul, V.; Lomas, T.; Tuantranont, A. Low cost thin film based piezoresistive MEMS tactile sensor. Sens. Actuators Phys. 2007, 139, 17–22. [Google Scholar] [CrossRef]
- Shikida, M.; Shimizu, T.; Sato, K.; Itoigawa, K. Active tactile sensor for detecting contact force and hardness of an object. Sens. Actuators Phys. 2003, 103, 213–218. [Google Scholar] [CrossRef]
- da Silva, J.G.; de Carvalho, A.A.; da Silva, D.D. A strain gauge tactile sensor for finger-mounted applications. IEEE Trans. Instrum. Meas. 2002, 51, 18–22. [Google Scholar] [CrossRef]
- Weiner, P.; Neef, C.; Shibata, Y.; Nakamura, Y.; Asfour, T. An Embedded, Multi-Modal Sensor System for Scalable Robotic and Prosthetic Hand Fingers. Sensors 2020, 20, 101. [Google Scholar] [CrossRef]
- Choi, B.; Choi, H.R.; Kang, S. Development of tactile sensor for detecting contact force and slip. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 2638–2643. [Google Scholar] [CrossRef]
- Park, M.; Bok, B.-G.; Ahn, J.-H.; Kim, M.-S. Recent Advances in Tactile Sensing Technology. Micromachines 2018, 9, 321. [Google Scholar] [CrossRef]
- Alea, M.D.; Safa, A.; Giacomozzi, F.; Adami, A.; Temel, I.R.; Rosa, M.A. A Fingertip-Mimicking 12 × 16 200 μm-Resolution e-skin Taxel Readout Chip with per-Taxel Spiking Readout and Embedded Receptive Field Processing. IEEE Trans. Biomed. Circuits Syst. 2024, 18, 1308–1320. [Google Scholar] [CrossRef]
- Sygulla, F.; Ellensohn, F.; Hildebrandt, A.-C.; Wahrmann, D.; Rixen, D. A flexible and low-cost tactile sensor for robotic applications. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 58–63. [Google Scholar] [CrossRef]
- Liu, W.; Gu, C.; Zeng, R.; Yu, P.; Fu, X. A Novel Inverse Solution of Contact Force Based on a Sparse Tactile Sensor Array. Sensors 2018, 18, 351. [Google Scholar] [CrossRef] [PubMed]
- Pannen, T.J.; Puhlmann, S.; Brock, O. A Low-Cost, Easy-to-Manufacture, Flexible, Multi-Taxel Tactile Sensor and its Application to In-Hand Object Recognition. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 10939–10944. [Google Scholar] [CrossRef]
- Crottet, D.; Maeder, T.; Fritschy, D.; Bleuler, H.; Nolte, L.-P.; Pappas, I.P. Development of a force amplitude- and location-sensing device designed to improve the ligament balancing procedure in TKA. IEEE Trans. Biomed. Eng. 2005, 52, 1609–1611. [Google Scholar] [CrossRef]
- Matsumoto, S.; Tajima, M.; Fukunaga, H. Impact Force Identification of Aluminum Plates Using Strain Sensors. Struct. Eng. Earthq. Eng. 2005, 22, 175s–184s. [Google Scholar] [CrossRef]
- Patel, R.; Cox, R.; Correll, N. Integrated proximity, contact and force sensing using elastomer-embedded commodity proximity sensors. Auton. Robot. 2018, 42, 1443–1458. [Google Scholar] [CrossRef]
- Pi, C.-H.; Tsai, I.-F.; Ou, K.-S.; Chen, K.-S. A one-dimensional touch panel based on strain sensing. Mechatronics 2012, 22, 802–810. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Wu, M.-F.; Guo, S.-H.; Chen, K.-S. Realization and performance assessment of a force-sensing based smart floor panel for indoor localization applications. Sens. Actuators Phys. 2019, 285, 468–481. [Google Scholar] [CrossRef]
- Payo, I.; Feliu, V. Strain gauges based sensor system for measuring 3-D deflections of flexible beams. Sens. Actuators Phys. 2014, 217, 81–94. [Google Scholar] [CrossRef]
- Figliola, R.S.; Beasley, D.E. Theory and Design for Mechanical Measurements, 5th ed.; Wiley: New York, NY, USA, 2010. [Google Scholar]
- Jenkins, C.; Khanna, S. Mechanics of Materials: A Modern Integration of Mechanics and Materials in Structural Design. In Mechanics of Materials: A Modern Integration of Mechanics and Materials in Structural Design, 1st ed.; Academic Press: Salt Lake City, UT, USA, 2005; p. 356. [Google Scholar]
- Adam, G.; Boudaoud, M.; Reynaud, V.; Agnus, J.; Cappelleri, D.J.; Clévy, C. An Overview of Microrobotic Systems for Microforce Sensing. Annu. Rev. Control Robot. Auton. Syst. 2024, 7, 359–383. [Google Scholar] [CrossRef]
- Cevantes, J.E.M.; Méndez, J.V.M.; León, H.F.M.; Arce, M.Á.A.; Acevedo, S.M.; Vázquez, H.E. Si3N4 Young’s modulus measurement from microcantilever beams using a calibrated stylus profiler. Superf. Vacío 2017, 30, 10–13. [Google Scholar] [CrossRef]
- Peiner, E.; Doering, L.; Balke, M.; Christ, A. Silicon cantilever sensor for micro-/nanoscale dimension and force metrology. Microsyst. Technol. 2008, 14, 441–451. [Google Scholar] [CrossRef]
- Hoffmann, K. An Introduction to Measurement Using Strain Gages; Hottinger Baldwin: Darmstadt, Germany, 1989; pp. 126–130. [Google Scholar]
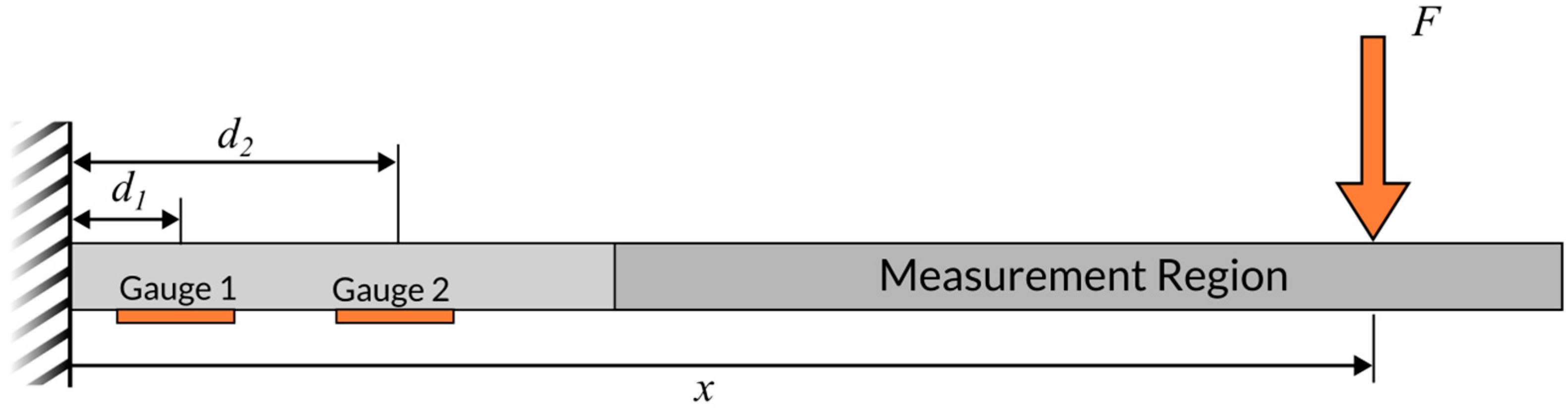






| Prototype | A | B | C |
|---|---|---|---|
| Beam Profile | Rectangular | Rectangular | Tubular |
| Material | 6061 Alum. | 2024 Alum. | 6061 Alum. |
| Length (cm) | 80 | 45 | 20 |
| Width/Diameter (cm) | 5 | 1.27 | 1.27 |
| Height (A, B) (cm) | 0.318 | 1.27 | n/a |
| Tube Wall Thickness (C) (cm) | n/a | n/a | 0.165 |
| Bridge 1 Position (cm) | 2 | 2 | 2 |
| Bridge 2 position (cm) | 12 | 6 | 7 |
| Bridge 3 Position (cm) | n/a | 10 | n/a |
| Prototype | Masses (g) | Positions (cm) |
|---|---|---|
| A | 250, 500, 1000, 1500, 2000 | 15, 20, 25, … 65 |
| B | 20, 50, 70, 100, 300, 500, 1500, 2000, 2500, 3000 | 15, 20, 25, … 45 |
| C | 250, 500, 1000, 1500, 2000 | 10, 12, 14, … 20 |
| Prototype | A | B | Cx | Cy |
|---|---|---|---|---|
| Bridge Type | Full | Half | Half | Half |
| Bridge 1 (4 pts) | 0.99990 | 1.00000 | 0.99997 | 0.99993 |
| Bridge 1 (9 pts) | 0.99942 | 0.99999 | 0.99980 | 0.99966 |
| Bridge 2 (4 pts) | 0.99984 | 1.00000 | 0.99999 | 0.99996 |
| Bridge 2 (9 pts) | 0.99917 | 0.99992 | 0.99976 | 0.99974 |
| Prototype | A | B | C |
|---|---|---|---|
| Position | 2.110 | 1.754 | 0.970 |
| Force | 0.643 | 2.351 | 1.542 |
| Angle | n/a | n/a | 2.618 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, C.T.; Smith, K.; Shamo, C.L.; Porter, J.; Steele, K.; Ludlow, N.D.; Hall, R.W.; Holst, M.G.; Williams, A.R.; Cook, D.D. Measurement of Force and Position Using a Cantilever Beam and Multiple Strain Gauges: Sensing Principles and Design Considerations. Sensors 2025, 25, 6561. https://doi.org/10.3390/s25216561
Noh CT, Smith K, Shamo CL, Porter J, Steele K, Ludlow ND, Hall RW, Holst MG, Williams AR, Cook DD. Measurement of Force and Position Using a Cantilever Beam and Multiple Strain Gauges: Sensing Principles and Design Considerations. Sensors. 2025; 25(21):6561. https://doi.org/10.3390/s25216561
Chicago/Turabian StyleNoh, Carter T., Kenneth Smith, Christian L. Shamo, Jordan Porter, Kirsten Steele, Nathan D. Ludlow, Ryan W. Hall, Maeson G. Holst, Alex R. Williams, and Douglas D. Cook. 2025. "Measurement of Force and Position Using a Cantilever Beam and Multiple Strain Gauges: Sensing Principles and Design Considerations" Sensors 25, no. 21: 6561. https://doi.org/10.3390/s25216561
APA StyleNoh, C. T., Smith, K., Shamo, C. L., Porter, J., Steele, K., Ludlow, N. D., Hall, R. W., Holst, M. G., Williams, A. R., & Cook, D. D. (2025). Measurement of Force and Position Using a Cantilever Beam and Multiple Strain Gauges: Sensing Principles and Design Considerations. Sensors, 25(21), 6561. https://doi.org/10.3390/s25216561






