Estimation of Pressure Pain in the Lower Limbs Using Electrodermal Activity, Tissue Oxygen Saturation, and Heart Rate Variability
Abstract
:1. Introduction
1.1. Electrodermal Activity (EDA)
1.2. Heart Rate Variablity (HRV)
1.3. Tissue Oxygen Saturation (StO2)
1.4. The Purpose of the Study
2. Materials and Methods
2.1. Experiments
2.2. Equipments
- Pneumatic Cuffs and Pressure-Applying Devices
- EDA
- ECG
- Near-Infrared Spectroscopy (NIRS).
2.3. Method
2.4. Data Processing
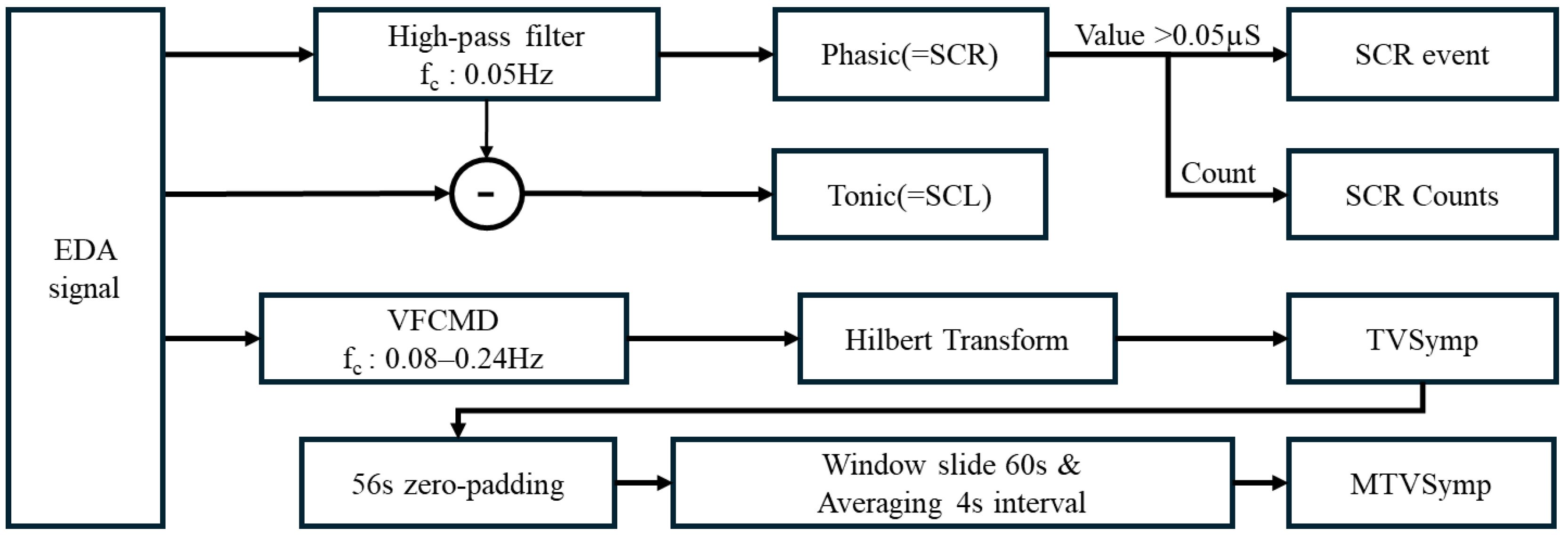
2.4.1. EDA Signal Processing
2.4.2. HRV Signal Processing
2.4.3. StO2 Signal Processing
2.5. Statistics
2.6. Regression
2.7. Machine Learning
3. Results
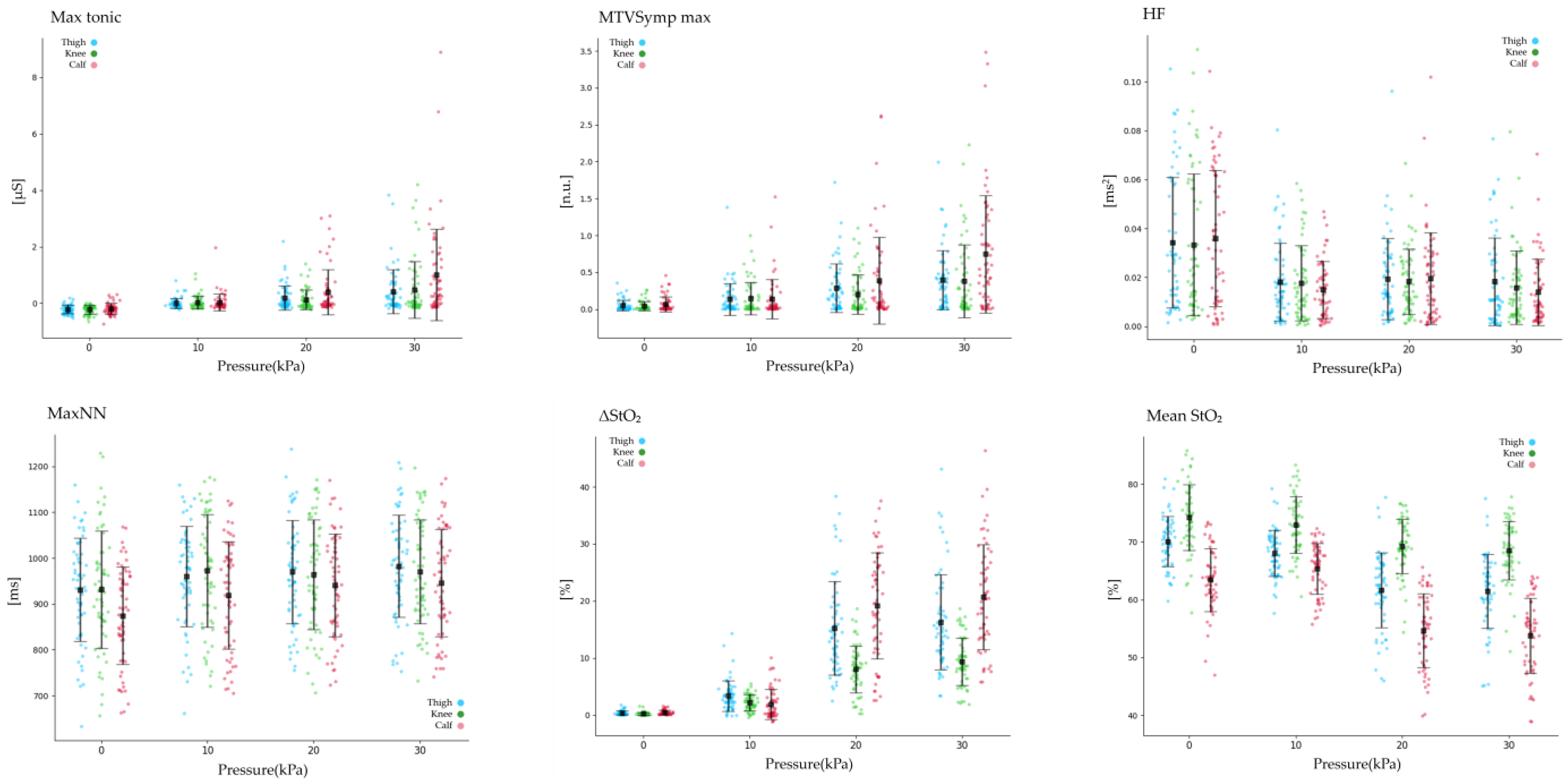
3.1. Statistical Analysis of EDA and StO2
3.2. Statistical Analysis of HRV
3.3. Regression
3.4. Machine Learning Classification
4. Discussion
4.1. Pain and Biosignal
4.2. Differences Among the Thigh, Knee, and Calf
4.3. Regression and Classification Model with BioSignal
5. Limitation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Features | Position | Pressure Intensity | Pain Level | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 kPa | 10 kPa | 20 kPa | 30 kPa | No Pain | Low | Moderate | High | ||
| Max phasic [μS] | Thigh | 0.1 ± 0.14 | 0.26 ± 0.410 | 0.52 ± 0.620 | 0.7 ± 0.7 | 0.13 ± 0.19 | 0.34 ± 0.6 | 0.45 ± 0.4 | 1 ± 0. |
| Knee | 0.07 ± 0.11 | 0.24 ± 0.3 | 0.35 ± 0.4 | 0.68 ± 0.9 | 0.08 ± 0.1 | 0.27 ± 0.38 | 0.34 ± 0.4 | 1.06 ± 1.0 | |
| Calf | 0.13 ± 0.19 | 0.23 ± 0.44 | 0.7 ± 1.0 | 1.24 ± 1.3 | 0.14 ± 0.2 | 0.23 ± 0.5 | 0.79 ± 1.1 | 1.3 ± 1.3 | |
| Mean Phasic [μS] | Thigh | 0 ± 0.001 | 0.001 ± 0.00 | 0.002 ± 0.00 | 0.002 ± 0.00 | 0 ± 0.001 | 0.001 ± 0.00 | 0.001 ± 0.00 | 0.003 ± 0.00 |
| Knee | 0 ± 0.001 | 0.001 ± 0.00 | 0.002 ± 0.0 | 0.002 ± 0.00 | 0 ± 0.001 | 0.001 ± 0.002 | 0.001 ± 0.002 | 0.003 ± 0.004 | |
| Calf | 0 ± 0.001 | 0.001 ± 0.001 | 0.002 ± 0.00 | 0.003 ± 0.00 | 0 ± 0.001 | 0.001 ± 0.00 | 0.002 ± 0.00 | 0.003 ± 0.00 | |
| Std phasic [μS] | Thigh | 0.02 ± 0.03 | 0.04 ± 0.05 | 0.07 ± 0.0 | 0.1 ± 0.1 | 0.02 ± 0.04 | 0.04 ± 0.07 | 0.06 ± 0.0 | 0.15 ± 0.1 |
| Knee | 0.02 ± 0.03 | 0.04 ± 0.05 | 0.05 ± 0.0 | 0.11 ± 0.1 | 0.02 ± 0.03 | 0.04 ± 0.06 | 0.05 ± 0.0 | 0.17 ± 0.1 | |
| Calf | 0.03 ± 0.05 | 0.03 ± 0.05 | 0.1 ± 0.1 | 0.21 ± 0.2 | 0.03 ± 0.04 | 0.03 ± 0.05 | 0.12 ± 0.1 | 0.22 ± 0.2 | |
| Mean SCR event [μS] | Thigh | 0.05 ± 0.1 | 0.11 ± 0.1 | 0.28 ± 0.3 | 0.37 ± 0.4 | 0.06 ± 0.11 | 0.16 ± 0.28 | 0.24 ± 0.2 | 0.53 ± 0.4 |
| Knee | 0.04 ± 0.09 | 0.11 ± 0.1 | 0.19 ± 0. | 0.36 ± 0.5 | 0.04 ± 0.0 | 0.13 ± 0.2 | 0.18 ± 0.2 | 0.57 ± 0.6 | |
| Calf | 0.07 ± 0.13 | 0.09 ± 0.1 | 0.46 ± 0.8 | 0.71 ± 0. | 0.07 ± 0.1 | 0.09 ± 0.19 | 0.55 ± 0. | 0.74 ± 0.6 | |
| Std SCR event [μS] | Thigh | 0.04 ± 0.06 | 0.08 ± 0. | 0.2 ± 0.2 | 0.27 ± 0.3 | 0.05 ± 0.08 | 0.12 ± 0.24 | 0.16 ± 0.1 | 0.38 ± 0.3 |
| Knee | 0.03 ± 0.05 | 0.08 ± 0.14 | 0.12 ± 0.1 | 0.24 ± 0.3 | 0.03 ± 0.0 | 0.09 ± 0.15 | 0.12 ± 0.1 | 0.36 ± 0. | |
| Calf | 0.06 ± 0.08 | 0.07 ± 0.1 | 0.28 ± 0. | 0.47 ± 0.5 | 0.05 ± 0.0 | 0.08 ± 0.18 | 0.32 ± 0.5 | 0.49 ± 0.5 | |
| Max SCR event [μS] | Thigh | 0.12 ± 0.19 | 0.28 ± 0.3 | 0.64 ± 0.8 | 0.88 ± 1.0 | 0.16 ± 0.26 | 0.37 ± 0.68 | 0.56 ± 0.5 | 1.28 ± 1.2 |
| Knee | 0.1 ± 0.16 | 0.26 ± 0.4 | 0.4 ± 0.5 | 0.82 ± 1. | 0.1 ± 0.17 | 0.3 ± 0.44 | 0.4 ± 0.4 | 1.27 ± 1. | |
| Calf | 0.17 ± 0.26 | 0.25 ± 0.4 | 0.91 ± 1. | 1.63 ± 1.8 | 0.18 ± 0. | 0.23 ± 0.48 | 1.04 ± 1.4 | 1.71 ± 1. | |
| SCR counts [ea] | Thigh | 1.5 ± 2.59 | 3.6 ± 5.97 | 4.72 ± 6. | 5.67 ± 5.9 | 1.94 ± 3.86 | 3.34 ± 5.45 | 4.75 ± 5.2 | 6.64 ± 7.5 |
| Knee | 0.8 ± 1.27 | 2.4 ± 3.62 | 2.97 ± 4. | 4.4 ± 5.2 | 0.89 ± 1.64 | 2.22 ± 3.32 | 3.43 ± 4.3 | 6.29 ± 6.0 | |
| Calf | 0.72 ± 1.06 | 2.58 ± 4.74 | 3.55 ± 4.3 | 6.55 ± 7.3 | 1.55 ± 3.57 | 1.53 ± 2.99 | 3.79 ± 4.4 | 6.97 ± 7.2 | |
| Mean Tonic [μS] | Thigh | −0.33 ± 0.17 | −0.14 ± 0.0 | −0.14 ± 0.0 | −0.13 ± 0.0 | −0.27 ± 0.17 | −0.15 ± 0.0 | −0.14 ± 0.0 | −0.12 ± 0.0 |
| Knee | −0.32 ± 0.17 | −0.14 ± 0.0 | −0.13 ± 0.0 | −0.12 ± 0.1 | −0.27 ± 0.17 | −0.13 ± 0.0 | −0.13 ± 0.0 | −0.12 ± 0.1 | |
| Calf | −0.32 ± 0.2 | −0.13 ± 0.0 | −0.11 ± 0.0 | −0.08 ± 0.1 | −0.25 ± 0.19 | −0.12 ± 0.0 | −0.11 ± 0.0 | −0.08 ± 0.1 | |
| Std Tonic [μS] | Thigh | 0.07 ± 0.05 | 0.06 ± 0.05 | 0.1 ± 0. | 0.15 ± 0.1 | 0.07 ± 0.05 | 0.07 ± 0.07 | 0.09 ± 0.08 | 0.21 ± 0.2 |
| Knee | 0.06 ± 0.05 | 0.07 ± 0.06 | 0.09 ± 0.08 | 0.17 ± 0.2 | 0.06 ± 0.05 | 0.07 ± 0.07 | 0.08 ± 0.08 | 0.26 ± 0.2 | |
| Calf | 0.08 ± 0.06 | 0.07 ± 0.06 | 0.15 ± 0. | 0.29 ± 0.3 | 0.07 ± 0.05 | 0.05 ± 0.0 | 0.17 ± 0. | 0.3 ± 0.3 | |
| TVSymp max [n.u.] | Thigh | 0.06 ± 0.07 | 0.16 ± 0.2 | 0.33 ± 0.3 | 0.45 ± 0.4 | 0.08 ± 0.11 | 0.22 ± 0.3 | 0.3 ± 0.2 | 0.61 ± 0.5 |
| Knee | 0.04 ± 0.07 | 0.16 ± 0.2 | 0.23 ± 0. | 0.42 ± 0.5 | 0.06 ± 0.1 | 0.18 ± 0.2 | 0.22 ± 0.2 | 0.65 ± 0.5 | |
| Calf | 0.08 ± 0.11 | 0.15 ± 0. | 0.45 ± 0.6 | 0.81 ± 0.8 | 0.09 ± 0.1 | 0.16 ± 0.35 | 0.51 ± 0.7 | 0.85 ± 0.8 | |
| TVSymp mean [n.u.] | Thigh | 0.02 ± 0.03 | 0.02 ± 0.04 | 0.05 ± 0.0 | 0.07 ± 0.0 | 0.02 ± 0.03 | 0.03 ± 0.05 | 0.04 ± 0.0 | 0.1 ± 0.1 |
| Knee | 0.01 ± 0.02 | 0.02 ± 0.04 | 0.03 ± 0.0 | 0.07 ± 0.1 | 0.01 ± 0.02 | 0.03 ± 0.04 | 0.03 ± 0.05 | 0.12 ± 0.1 | |
| Calf | 0.02 ± 0.04 | 0.02 ± 0.03 | 0.06 ± 0.1 | 0.14 ± 0.1 | 0.02 ± 0.0 | 0.02 ± 0.03 | 0.07 ± 0.1 | 0.14 ± 0.1 | |
| TVSymp std [n.u.] | Thigh | 0.02 ± 0.02 | 0.03 ± 0.0 | 0.06 ± 0.0 | 0.08 ± 0.0 | 0.02 ± 0.02 | 0.04 ± 0.07 | 0.06 ± 0.0 | 0.12 ± 0. |
| Knee | 0.01 ± 0.02 | 0.03 ± 0.05 | 0.04 ± 0.0 | 0.09 ± 0.1 | 0.01 ± 0.0 | 0.03 ± 0.05 | 0.04 ± 0.0 | 0.14 ± 0.1 | |
| Calf | 0.02 ± 0.03 | 0.03 ± 0.05 | 0.09 ± 0.1 | 0.17 ± 0.1 | 0.02 ± 0.0 | 0.03 ± 0.05 | 0.1 ± 0.1 | 0.17 ± 0.1 | |
| MTVSymp mean [n.u.] | Thigh | 0.02 ± 0.03 | 0.02 ± 0.04 | 0.05 ± 0.0 | 0.07 ± 0.0 | 0.02 ± 0.03 | 0.03 ± 0.05 | 0.04 ± 0.0 | 0.1 ± 0.1 |
| Knee | 0.01 ± 0.02 | 0.02 ± 0.0 | 0.03 ± 0.0 | 0.07 ± 0.1 | 0.01 ± 0.0 | 0.03 ± 0.04 | 0.03 ± 0.05 | 0.12 ± 0.1 | |
| Calf | 0.02 ± 0.04 | 0.02 ± 0.03 | 0.06 ± 0.1 | 0.14 ± 0.1 | 0.02 ± 0.0 | 0.02 ± 0.03 | 0.07 ± 0.12 | 0.14 ± 0.1 | |
| MTVSymp std [n.u.] | Thigh | 0.01 ± 0.02 | 0.03 ± 0.0 | 0.06 ± 0.0 | 0.08 ± 0.0 | 0.02 ± 0.02 | 0.04 ± 0.06 | 0.05 ± 0.0 | 0.11 ± 0.0 |
| Knee | 0.01 ± 0.02 | 0.03 ± 0.05 | 0.04 ± 0.0 | 0.08 ± 0.1 | 0.01 ± 0.0 | 0.03 ± 0.05 | 0.04 ± 0.0 | 0.13 ± 0.1 | |
| Calf | 0.02 ± 0.03 | 0.03 ± 0.05 | 0.08 ± 0.1 | 0.16 ± 0.1 | 0.02 ± 0.0 | 0.03 ± 0.05 | 0.1 ± 0.1 | 0.17 ± 0.1 | |
| MeanNN [ms] | Thigh | 830.2 ± 87.7 | 837.3 ± 86.8 | 844.9 ± 85.4 | 849.9 ± 82.5 | 828.6 ± 86.1 | 850.3 ± 91.0 | 841.8 ± 79.0 | 853.8 ± 87.4 |
| Knee | 831.1 ± 99. | 841.1 ± 96. | 841.2 ± 91.8 | 843.1 ± 89.3 | 827.7 ± 95.6 | 852.5 ± 88.7 | 841 ± 92.3 | 844 ± 102.8 | |
| Calf | 826.9 ± 89.5 | 801.5 ± 94.7 | 822.5 ± 91. | 821.3 ± 90. | 787.2 ± 86. | 839.8 ± 103 | 817.7 ± 89.3 | 812.9 ± 91. | |
| MinNN [ms] | Thigh | 725.5 ± 70.7 | 719.1 ± 69.9 | 725.8 ± 67.3 | 721.6 ± 63.3 | 718.5 ± 67 | 723.6 ± 76.4 | 726.9 ± 63.8 | 725.7 ± 64.3 |
| Knee | 729 ± 86. | 716 ± 75.8 | 719.3 ± 75.4 | 721 ± 68.4 | 721.4 ± 78 | 719.9 ± 76.9 | 722.91 ± 75.6 | 720.5 ± 76.1 | |
| Calf | 619.9 ± 79.1 | 686.2 ± 66. | 707.9 ± 76. | 698.9 ± 68. | 693.7 ± 70. | 706.1 ± 79.5 | 703.21 ± 73 | 696.2 ± 7 | |
| MeanHR [bpm] | Thigh | 73.13 ± 8.29 | 72.47 ± 8.05 | 71.74 ± 7.41 | 71.28 ± 7.2 | 73.23 ± 8.05 | 71.42 ± 8.25 | 71.92 ± 6.97 | 71.03 ± 7.62 |
| Knee | 73.29 ± 9. | 72.31 ± 8.71 | 72.23 ± 8.4 | 71.99 ± | 73.48 ± 8.7 | 71.19 ± 8.05 | 72.25 ± 8.46 | 72.18 ± 9.3 | |
| Calf | 74.26 ± 9.1 | 75.92 ± 9.1 | 73.87 ± 8. | 73.95 ± 8.2 | 77.16 ± 8.7 | 72.6 ± 9. | 74.24 ± 8.1 | 74.74 ± 8.4 | |
| MinHR [bpm] | Thigh | 65.45 ± 8.57 | 63.35 ± 7.9 | 62.69 ± 7.4 | 61.89 ± 7.3 | 64.94 ± 8.38 | 62.5 ± 8.04 | 62.48 ± 6.89 | 62.27 ± 8.04 |
| Knee | 65.64 ± 9. | 62.69 ± 8.35 | 63.24 ± 8.21 | 62.63 ± 7.3 | 65.17 ± 8.9 | 62.04 ± 7.4 | 63.35 ± 8.2 | 62.2 ± 8.0 | |
| Calf | 69.69 ± 8.9 | 66.39 ± 8. | 64.72 ± 7.97 | 64.39 ± 8.1 | 66.7 ± 9.0 | 63.61 ± 8.4 | 64.99 ± 7.8 | 65.27 ± 8.2 | |
| MaxHR [bpm] | Thigh | 83.49 ± 8.27 | 84.23 ± 8.28 | 83.39 ± 7.91 | 83.79 ± 7.39 | 84.24 ± 7.91 | 83.86 ± 9.22 | 83.17 ± 7.31 | 83.31 ± 7.36 |
| Knee | 83.46 ± 10.11 | 84.73 ± 9.0 | 84.33 ± 8.91 | 83.97 ± 8. | 84.13 ± 9.1 | 84.31 ± 9.29 | 83.89 ± 8.73 | 84.22 ± 9.32 | |
| Calf | 86.84 ± 10.1 | 88.25 ± 8. | 85.72 ± 9.1 | 86.68 ± 8. | 87.39 ± 9.0 | 86.05 ± 9.95 | 86.2 ± 8.67 | 86.12 ± 9.09 | |
| RMSSD [ms] | Thigh | 36.32 ± 17.3 | 37.17 ± 16.56 | 37.77 ± 16.39 | 39.44 ± 17.29 | 37.31 ± 18.08 | 38.05 ± 18.58 | 37.7 ± 14.02 | 37.97 ± 16.56 |
| Knee | 36.93 ± 22.5 | 39.92 ± 21.0 | 38.67 ± 21.18 | 39.31 ± 21.12 | 38.58 ± 23.76 | 41.55 ± 20.92 | 35.59 ± 17.7 | 40.24 ± 21.9 | |
| Calf | 27.7 ± 11.9 | 32.0 ± 14. | 34.4 ± 15. | 34.9 ± 16. | 29.3 ± 14.1 | 42.2 ± 20.8 | 30.8 ± 10.9 | 31.7 ± 12.0 | |
| SDNN [ms] | Thigh | 46.66 ± 19.73 | 47.83 ± 18.57 | 47.24 ± 18.79 | 50.99 ± 21.25 | 48.17 ± 20.31 | 48.67 ± 19.36 | 47.97 ± 19.21 | 47.93 ± 19.45 |
| Knee | 48.46 ± 20.95 | 51.64 ± 21.41 | 47.67 ± 19.46 | 50.24 ± 18.74 | 48.58 ± 20.58 | 52.19 ± 21.11 | 47.65 ± 19.95 | 50.98 ± 17.74 | |
| Calf | 40.17 ± 16.5 | 44.7 ± 16.8 | 46.01 ± 17.8 | 48.04 ± 18.3 | 41.61 ± 17.5 | 50.54 ± 15.41 | 45.32 ± 18.32 | 45.46 ± 17.47 | |
| pNN50 [%] | Thigh | 17.06 ± 17.12 | 17.9 ± 17.41 | 18.24 ± 16.67 | 20.2 ± 17.55 | 18.1 ± 18.26 | 17.97 ± 18.27 | 18.61 ± 15.05 | 18.98 ± 16.96 |
| Knee | 16.07 ± 17.92 | 20.04 ± 20.8 | 18.32 ± 19.85 | 18.64 ± 19.49 | 18.19 ± 20.5 | 21.14 ± 21.4 | 15 ± 16.15 | 19.91 ± 19.02 | |
| Calf | 9.39 ± 12. | 13.35 ± 15. | 14.22 ± 15.8 | 14.43 ± 16. | 10.99 ± 14.6 | 23.5 ± 21. | 11.4 ± 10.2 | 11.23 ± 11 | |
| pNN20 [%] | Thigh | 51.77 ± 19.21 | 55.01 ± 19.07 | 55.99 ± 16.93 | 57.28 ± 17.9 | 53.2 ± 19.6 | 55.02 ± 18.2 | 56.78 ± 16.35 | 56.03 ± 19.44 |
| Knee | 50.68 ± 20.04 | 55.32 ± 18.6 | 53.48 ± 19.67 | 55.25 ± 17.75 | 52.3 ± 21.1 | 57.18 ± 16.7 | 52.06 ± 17.32 | 54.62 ± 19.88 | |
| Calf | 43.05 ± 20. | 49.33 ± 20. | 51.4 ± 18. | 51.54 ± 17. | 44.6 ± 2 | 59.71 ± 19. | 48.1 ± 17. | 49.2 ± 16.1 | |
| LF [ms2] | Thigh | 0.022 ± 0.015 | 0.016 ± 0.014 | 0.018 ± 0.014 | 0.016 ± 0.01 | 0.02 ± 0.015 | 0.017 ± 0.014 | 0.017 ± 0.014 | 0.016 ± 0.011 |
| Knee | 0.021 ± 0.016 | 0.018 ± 0.013 | 0.021 ± 0.014 | 0.017 ± 0.013 | 0.02 ± 0.014 | 0.017 ± 0.012 | 0.02 ± 0.016 | 0.017 ± 0.013 | |
| Calf | 0.023 ± 0.015 | 0.017 ± 0.01 | 0.02 ± 0.016 | 0.016 ± 0.012 | 0.02 ± 0.014 | 0.017 ± 0.012 | 0.02 ± 0.016 | 0.017 ± 0.013 | |
| HFn [n.u.] | Thigh | 0.55 ± 0.24 | 0.43 ± 0.2 | 0.44 ± 0.2 | 0.43 ± 0.2 | 0.51 ± 0.25 | 0.43 ± 0.22 | 0.42 ± 0.21 | 0.46 ± 0.24 |
| Knee | 0.56 ± 0.2 | 0.4 ± 0.2 | 0.4 ± 0.2 | 0.41 ± 0.2 | 0.48 ± 0.26 | 0.47 ± 0.22 | 0.34 ± 0.2 | 0.39 ± 0.2 | |
| Calf | 0.53 ± 0.2 | 0.39 ± 0.2 | 0.4 ± 0.2 | 0.4 ± 0.2 | 0.48 ± 0.26 | 0.47 ± 0.22 | 0.34 ± 0.2 | 0.39 ± 0.2 | |
| LFn [n.u.] | Thigh | 0.42 ± 0.24 | 0.39 ± 0.2 | 0.4 ± 0.2 | 0.41 ± 0.23 | 0.4 ± 0.24 | 0.4 ± 0.2 | 0.41 ± 0.2 | 0.41 ± 0.23 |
| Knee | 0.42 ± 0.2 | 0.44 ± 0.2 | 0.45 ± 0.2 | 0.44 ± 0.2 | 0.44 ± 0.26 | 0.39 ± 0.19 | 0.48 ± 0. | 0.44 ± 0.19 | |
| Calf | 0.44 ± 0.2 | 0.45 ± 0.2 | 0.44 ± 0.2 | 0.43 ± 0.19 | 0.44 ± 0.26 | 0.39 ± 0.19 | 0.48 ± 0.2 | 0.44 ± 0.19 | |
| LFHF [n.u.] | Thigh | 1.65 ± 2.92 | 2.09 ± 4.08 | 2.01 ± 3.71 | 3.31 ± 7.28 | 1.96 ± 3.87 | 2.05 ± 3.57 | 2.27 ± 4.59 | 3.31 ± 7.87 |
| Knee | 1.33 ± 1.55 | 3.35 ± 6.5 | 2.37 ± 3.6 | 2 ± 2.4 | 4.5 ± 13.3 | 1.64 ± 2.31 | 3.48 ± 6.3 | 2.13 ± 2.69 | |
| Calf | 3.21 ± 7.74 | 4.79 ± 14.9 | 2.86 ± 5.75 | 2.15 ± 2.71 | 4.5 ± 13.3 | 1.64 ± 2.31 | 3.48 ± 6.3 | 2.13 ± 2.69 | |
| Max StO2 [%] | Thigh | 70.42 ± 4.58 | 70.75 ± 3.9 | 70.41 ± 4.3 | 70.83 ± 4.14 | 70.62 ± 4.71 | 70.78 ± 3.92 | 70.39 ± 4.15 | 70.69 ± 3.55 |
| Knee | 74.46 ± 5.5 | 74.75 ± 5.0 | 75.06 ± 5. | 75.24 ± 5.1 | 75.18 ± 5.2 | 75.29 ± 5.6 | 73.96 ± 4.5 | 75.13 ± 5.8 | |
| Calf | 63.7 ± 5.21 | 67.61 ± 3.9 | 65.29 ± 4. | 65.01 ± 4. | 65.46 ± 5.08 | 66.82 ± 4.9 | 64.89 ± 4.29 | 64.82 ± 4.29 | |
| Std StO2 [%] | Thigh | 0.23 ± 0.19 | 0.89 ± 0.6 | 4.36 ± 2.7 | 4.65 ± 2.8 | 0.4 ± 0.39 | 2.01 ± 2.3 | 4.51 ± 2.8 | 4.73 ± 2. |
| Knee | 0.13 ± 0.12 | 0.55 ± 0.2 | 1.81 ± 0.9 | 2.07 ± 1.0 | 0.24 ± 0.21 | 1.11 ± 0.7 | 1.91 ± 1.0 | 2.04 ± 1.1 | |
| Calf | 0.27 ± 0.2 | 1.29 ± 0.7 | 6.36 ± 2.7 | 6.72 ± 2. | 0.52 ± 0.4 | 2.57 ± 1.8 | 6.49 ± 2.7 | 6.99 ± 2.8 | |
| VAS | Pressure | ||||||
|---|---|---|---|---|---|---|---|
| Feature | Thigh | Knee | Calf | Feature | Thigh | Knee | Calf |
| Std StO2 | 0.801 | 0.778 | 0.854 | Std StO2 | 0.838 | 0.845 | 0.861 |
| ΔStO2 | 0.813 | 0.747 | 0.805 | ΔStO2 | 0.845 | 0.831 | 0.793 |
| Max Tonic | 0.619 | 0.595 | 0.636 | Max Tonic | 0.619 | 0.534 | 0.634 |
| Mean StO2 | −0.6 | −0.476 | −0.681 | Mean StO2 | −0.593 | −0.420 | −0.591 |
| TVSymp max | 0.555 | 0.529 | 0.59 | TVSymp max | 0.479 | 0.41 | 0.497 |
| MTVSymp max | 0.559 | 0.528 | 0.592 | MTVSymp max | 0.48 | 0.409 | 0.499 |
| Max phasic | 0.556 | 0.533 | 0.579 | Max phasic | 0.487 | 0.414 | 0.489 |
| Max SCR event | 0.521 | 0.523 | 0.566 | Mean Tonic | 0.439 | 0.422 | 0.492 |
| TVSymp std | 0.522 | 0.498 | 0.558 | Max SCR event | 0.452 | 0.398 | 0.482 |
| MTVSymp std | 0.527 | 0.500 | 0.562 | TVSymp std | 0.43 | 0.365 | 0.452 |
| Mean SCR event | 0.505 | 0.497 | 0.559 | MTVSymp std | 0.436 | 0.369 | 0.458 |
| Std phasic | 0.474 | 0.465 | 0.517 | Mean SCR event | 0.417 | 0.364 | 0.457 |
| SCR counts | 0.431 | 0.483 | 0.508 | SCR counts | 0.371 | 0.355 | 0.452 |
| TVSymp mean | 0.423 | 0.42 | 0.473 | Std phasic | 0.372 | 0.317 | 0.402 |
| MTVSymp mean | 0.422 | 0.417 | 0.472 | Mean phasic | 0.35 | 0.281 | 0.409 |
| Std SCR event | 0.444 | 0.423 | 0.417 | Std SCR event | 0.395 | 0.305 | 0.336 |
| Mean Tonic | 0.369 | 0.382 | 0.431 | TVSymp mean | 0.314 | 0.26 | 0.354 |
| Mean phasic | 0.376 | 0.328 | 0.399 | MTVSymp mean | 0.313 | 0.258 | 0.352 |
| Std Tonic | 0.276 | 0.28 | 0.31 | HF | −0.233 | −0.208 | −0.256 |
| HF | −0.156 | −0.232 | −0.195 | Std Tonic | 0.194 | 0.141 | 0.212 |
| HFn | −0.117 | −0.262 | −0.169 | HFn | −0.17 | −0.205 | −0.177 |
| MinHR | −0.114 | −0.145 | −0.151 | MinHR | −0.148 | −0.093 | −0.219 |
| MaxNN | 0.114 | 0.145 | 0.151 | MaxNN | 0.148 | 0.093 | 0.219 |
| LFHF | 0.058 | 0.222 | 0.108 | LF | −0.122 | −0.079 | −0.152 |
| MeanHR | −0.072 | −0.107 | −0.104 | pNN20 | 0.122 | 0.066 | 0.141 |
| MeanNN | 0.072 | 0.107 | 0.104 | LFHF | 0.088 | 0.137 | 0.1 |
| LFn | 0.004 | 0.159 | 0.038 | RMSSD | 0.091 | 0.045 | 0.171 |
| RMSSD | 0.045 | 0.048 | 0.107 | MeanHR | −0.077 | −0.047 | −0.137 |
| pNN20 | 0.077 | 0.04 | 0.08 | MeanNN | 0.077 | 0.047 | 0.137 |
| pNN50 | 0.033 | 0.051 | 0.09 | pNN50 | 0.082 | 0.043 | 0.151 |
| LF | −0.084 | 0.013 | −0.075 | SDNN | 0.054 | 0.011 | 0.151 |
| SDNN | −0.022 | 0.049 | 0.085 | Max StO2 | 0.019 | 0.05 | 0.034 |
| Max StO2 | 0.014 | −0.043 | −0.071 | LFn | −0.005 | 0.047 | 0.01 |
| MaxHR | −0.029 | −0.028 | −0.009 | MinNN | −0.011 | −0.021 | 0.029 |
| MinNN | 0.029 | 0.028 | 0.009 | MaxHR | 0.011 | 0.021 | −0.029 |
References
- Ralfs, L.; Hoffmann, N.; Weidner, R. Method and Test Course for the Evaluation of Industrial Exoskeletons. Appl. Sci. 2021, 11, 9614. [Google Scholar] [CrossRef]
- Daly, W.C.; Voo, L.; Rosenbaum-Chou, T.; Arabian, A.P.; Boone, D.P. Socket Pressure and Discomfort in Upper-Limb Prostheses. JPO J. Prosthet. Orthot. 2014, 26, 99–106. [Google Scholar] [CrossRef]
- Meyer, J.T.; Gassert, R.; Lambercy, O. An Analysis of Usability Evaluation Practices and Contexts of Use in Wearable Robotics. J. Neuroeng. Rehabil. 2021, 18, 170. [Google Scholar] [CrossRef]
- Wilson, N. Drug and opioid-involved overdose deaths—United States, 2017–2018. Mmwr. Morb. Mortal. Wkly. Rep. 2020, 69, 290–297. [Google Scholar] [CrossRef]
- Rudd, R.A.; Seth, P.; David, F.; Scholl, L. Increases in Drug and Opioid-Involved Overdose Deaths-United States, 2010–2015. MMWR. Morb. Mortal. Wkly. Rep. 2016, 65, 1445–1452. [Google Scholar] [CrossRef] [PubMed]
- Sehgal, N.; Manchikanti, L.; Smith, H.S. Prescription opioid abuse in chronic pain: A review of opioid abuse predictors and strategies to curb opioid abuse. Pain Physician 2012, 15, ES67. [Google Scholar] [CrossRef]
- Posada-Quintero, H.F.; Kong, Y.; Nguyen, K.; Tran, C.; Beardslee, L.; Chen, L.; Guo, T.; Cong, X.; Feng, B.; Chon, K.H. Using electrodermal activity to validate multilevel pain stimulation in healthy volunteers evoked by thermal grills. Am. J. Physiol. Integr. Comp. Physiol. 2020, 319, R366–R375. [Google Scholar] [CrossRef]
- Posada-Quintero, H.F.; Kong, Y.; Chon, K.H. Objective Pain Stimulation Intensity and Pain Sensation Assessment Using Machine Learning Classification and Regression Based on Electrodermal Activity. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 2021, 321, R186–R196. [Google Scholar] [CrossRef]
- Kong, Y.; Posada-Quintero, H.F.; Chon, K.H. Real-Time High-Level Acute Pain Detection Using a Smartphone and a Wrist-Worn Electrodermal Activity Sensor. Sensors 2021, 21, 3956. [Google Scholar] [CrossRef]
- Aziz, S.; Khan, M.U.; Hirachan, N.; Chetty, G.; Goecke, R.; Fernandez-Rojas, R. “Where does it hurt?”: Exploring EDA Signals to Detect and Localise Acute Pain. In Proceedings of the 2023 45th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Sydney, NSW, Australia, 24–27 July 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Szpak, A.; Loetscher, T.; Churches, O.; Thomas, N.A.; Spence, C.J.; Nicholls, M.E.R. Keeping your distance: Attentional withdrawal in individuals who show physiological signs of social discomfort. Neuropsychologia 2015, 70, 462–467. [Google Scholar] [CrossRef]
- Jang, E.-H.; Park, B.-J.; Park, M.-S.; Kim, S.-H.; Sohn, J.-H. Analysis of physiological signals for recognition of boredom, pain, and surprise emotions. J. Physiol. Anthr. 2015, 34, 25. [Google Scholar] [CrossRef]
- Boucsein, W. Electrodermal Activity; Springer: Boston, MA, USA, 2012; ISBN 978-1-4614-1125-3. [Google Scholar] [CrossRef]
- Boucsein, W.; Fowles, D.C.; Grimnes, S.; Ben-Shakhar, G.; Roth, W.T.; Dawson, M.E.; Filion, D.L.; Society for Psychophysiological Research Ad Hoc Committee on Electrodermal Measures. Publication recommendations for electrodermal measurements. Psychophysiology 2012, 49, 1017–1034. [Google Scholar] [CrossRef]
- Braithwaite, J.J.; Watson, D.G.; Jones, R.; Rowe, M. A guide for analysing electrodermal activity (EDA) & skin conductance responses (SCRs) for psychological experiments. Psychophysiology 2015, 49, 1017–1034. [Google Scholar]
- Kim, J.H.; Jeon, G.R.; Son, J.M.; Baik, S.W.; Kim, Y.J.; Kim, S.S. Electrodermal Activity at the Left Palm and Finger in Accordance with the Pressure Stimuli Applied to the Left Scapula. J. Sens. Sci. Technol. 2016, 25, 235–242. [Google Scholar] [CrossRef]
- Posada-Quintero, H.F.; Florian, J.P.; Orjuela-Cañón, A.D.; Aljama-Corrales, T.; Charleston-Villalobos, S.; Chon, K.H. Power Spectral Density Analysis of Electrodermal Activity for Sympathetic Function Assessment. Ann. Biomed. Eng. 2016, 44, 3124–3135. [Google Scholar] [CrossRef]
- Posada-Quintero, H.F.; Florian, J.P.; Orjuela-Cañón, Á.D.; Chon, K.H. Highly sensitive index of sympathetic activity based on time-frequency spectral analysis of electrodermal activity. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2016, 311, R582–R591. [Google Scholar] [CrossRef]
- Kong, Y.; Posada-Quintero, H.; Chon, K. Sensitive physiological indices of pain based on differential characteristics of electrodermal activity. IEEE Trans. Biomed. Eng. 2021, 68, 3122–3130. [Google Scholar] [CrossRef]
- Forte, G.; Troisi, G.; Pazzaglia, M.; De Pascalis, V.; Casagrande, M. Heart Rate Variability and Pain: A Systematic Review. Brain Sci. 2022, 12, 153. [Google Scholar] [CrossRef]
- Koenig, J.; Jarczok, M.N.; Ellis, R.; Hillecke, T.; Thayer, J. Heart rate variability and experimentally induced pain in healthy adults: A systematic review. Eur. J. Pain 2013, 18, 301–314. [Google Scholar] [CrossRef]
- Petersen, K.K.; Andersen, H.H.; Tsukamoto, M.; Tracy, L.; Koenig, J.; Arendt-Nielsen, L. The effects of propranolol on heart rate variability and quantitative, mechanistic, pain profiling: A randomized placebo-controlled crossover study. Scand. J. Pain. 2018, 18, 479–489. [Google Scholar] [CrossRef]
- Sclocco, R.; Beissner, F.; Desbordes, G.; Polimeni, J.; Wald, L.; Kettner, N.W.; Kim, J.; Garcia, R.G.; Renvall, V.; Bianchi, A.M.; et al. Neuroimaging brainstem circuitry supporting cardiovagal response to pain: A combined heart rate variability/ultrahigh-field (7 T) functional magnetic resonance imaging study. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150189. [Google Scholar] [CrossRef]
- Tracy, L.M.; Koenig, J.; Georgiou-Karistianis, N.; Gibson, S.J.; Giummarra, M.J. Heart rate variability is associated with thermal heat pain threshold in males, but not females. Int. J. Psychophysiol. 2018, 131, 37–43. [Google Scholar] [CrossRef]
- Pollatos, O.; Füstös, J.; Critchley, H.D. On the generalised embodiment of pain: How interoceptive sensitivity modulates cutaneous pain perception. Pain 2012, 153, 1680–1686. [Google Scholar] [CrossRef]
- Terkelsen, A.J.; Mølgaard, H.; Hansen, J.; Finnerup, N.B.; Krøner, K.; Jensen, T.S. Heart rate variability in complex regional pain syndrome during rest and mental and orthostatic stress. Anesthesiology 2012, 116, 133–146. [Google Scholar] [CrossRef]
- Kermavnar, T.; Power, V.; De Eyto, A.; O’Sullivan, L.W. Computerized Cuff Pressure Algometry as Guidance for Circumferential Tissue Compression for Wearable Soft Robotic Applications: A Systematic Review. Soft Robot. 2018, 5, 1–16. [Google Scholar] [CrossRef]
- Linnenberg, C.; Reimeir, B.; Eberle, R.; Weidner, R. The Influence of Circular Physical Human–Machine Interfaces of Three Shoulder Exoskeletons on Tissue Oxygenation. Appl. Sci. 2023, 13, 10534. [Google Scholar] [CrossRef]
- Kermavnar, T.; O’Sullivan, K.J.; de Eyto, A.; O’Sullivan, L.W. Discomfort/pain and tissue oxygenation at the lower limb during circumferential compression: Application to soft exoskeleton design. Hum. Factors 2020, 62, 475–488. [Google Scholar] [CrossRef]
- Kermavnar, T.; O’Sullivan, K.J.; de Eyto, A.; O’Sullivan, L.W. The effect of simulated circumferential soft exoskeleton compression at the knee on discomfort and pain. Ergonomics 2020, 63, 618–628. [Google Scholar] [CrossRef]
- Nam, Y.; Yang, S.; Kim, J.; Koo, B.; Song, S.; Kim, Y. Quantification of Comfort for the Development of Binding Parts in a Standing Rehabilitation Robot. Sensors 2023, 23, 2206. [Google Scholar] [CrossRef]
- Kim, Y.; Han, I.; Jung, J.; Yang, S.; Lee, S.; Koo, B.; Ahn, S.; Nam, Y.; Song, S.H. Measurements of Electrodermal Activity, Tissue Oxygen Saturation, and Visual Analog Scale for Different Cuff Pressures. Sensors 2024, 24, 917. [Google Scholar] [CrossRef]
- Wassenaar, E.B.; Van den Brand, J.G. Reliability of near-infrared spectroscopy in people with dark skin pigmentation. J. Clin. Monit. Comput. 2005, 19, 195–199. [Google Scholar] [CrossRef]
- Shuler, M.S.; Reisman, W.M.; Whitesides, T.E.; Kinsey, T.L.; Hammerberg, E.M.; Davila, M.G.; Moore, T.J. Near-Infrared Spectroscopy in Lower Extremity Trauma. J. Bone Jt. Surg. 2009, 91, 1360–1368. [Google Scholar] [CrossRef]
- Ostrov, L.; Grimsby, G.; Menon, V.; Keays, M.; Sheth, K.; Granberg, C.; Baker, L. The effect of race and skin color on near-infrared spectroscopy readings in pediatric patients with unilateral acute scrotum. J. Urol. 2015, 193, e467. [Google Scholar] [CrossRef]
- Makowski, D.; Pham, T.; Lau, Z.J.; Brammer, J.C.; Lespinasse, F.; Pham, H.; Schölzel, C.; Chen, S.H.A. NeuroKit2: A Python toolbox for neurophysiological signal processing. Behav. Res. Methods 2021, 53, 1689–1696. [Google Scholar] [CrossRef]
- Caruelle, D.; Gustafsson, A.; Shams, P.; Lervik-Olsen, L. The use of electrodermal activity (EDA) measurement to understand consumer emotions—A literature review and a call for action. J. Bus. Res. 2019, 104, 146–160. [Google Scholar] [CrossRef]
- Pham, T.; Lau, Z.J.; Chen, S.H.A.; Makowski, D. Heart Rate Variability in Psychology: A Review of HRV Indices and an Analysis Tutorial. Sensors 2021, 21, 3998. [Google Scholar] [CrossRef]
- Razali, N.M.; Wah, Y.B. Power comparisons of shapiro-wilk, kolmogorov-smirnov, lilliefors and anderson-darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Bland, M. An Introduction to Medical Statistics; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Zimmerman, D.W.; Zumbo, B.D. Relative power of the wilcoxon test, the friedman test, and repeated-measures anova on ranks. J. Exp. Educ. 1993, 62, 75–86. [Google Scholar] [CrossRef]
- Armitage, P.; Berry, G.; Matthews, J.N.S. (Eds.) Statistical Methods in Medical Research, 4th ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2013; ISBN 978-1-118-70258-1. [Google Scholar]
- Vu, D.H.; Muttaqi, K.M.; Agalgaonkar, A. A variance inflation factor and backward elimination based robust regression model for forecasting monthly electricity demand using climatic variables. Appl. Energy 2015, 140, 385–394. [Google Scholar] [CrossRef]
- Douzas, G.; Bacao, F.; Last, F. Improving imbalanced learning through a heuristic oversampling method based on k-means and SMOTE. Inf. Sci. 2018, 465, 1–20. [Google Scholar] [CrossRef]
- Treister, R.; Kliger, M.; Zuckerman, G.; Aryeh, I.G.; Eisenberg, E. Differentiating between heat pain intensities: The combined effect of multiple autonomic parameters. Pain 2012, 153, 1807–1814. [Google Scholar] [CrossRef]
- Tracy, L.M.; Ioannou, L.; Baker, K.S.; Gibson, S.J.; Georgiou-Karistianis, N.; Giummarra, M.J. Meta-analytic evidence for decreased heart rate variability in chronic pain implicating parasympathetic nervous system dysregulation. Pain 2016, 157, 7–29. [Google Scholar] [CrossRef]
- Jiang, M.; Mieronkoski, R.; Syrjälä, E.; Anzanpour, A.; Terävä, V.; Rahmani, A.M.; Salanterä, S.; Aantaa, R.; Hagelberg, N.; Liljeberg, P. Acute pain intensity monitoring with the classification of multiple physiological parameters. J. Clin. Monit. Comput. 2019, 33, 493–507. [Google Scholar] [CrossRef] [PubMed]
- Polianskis, R.; Graven-Nielsen, T.; Arendt-Nielsen, L. Spatial and temporal aspects of deep tissue pain assessed by cuff algometry. Pain 2002, 100, 19–26. [Google Scholar] [CrossRef]
- Meeuse, J.J.; Löwik, M.S.; Löwik, S.A.; Aarden, E.; van Roon, A.M.; Gans, R.O.; van Wijhe, M.; Lefrandt, J.D.; Reyners, A.K. Heart rate variability parameters do not correlate with pain intensity in healthy volunteers. Pain Med. 2013, 14, 1192–1201. [Google Scholar] [CrossRef]
- Neziri, A.Y.; Curatolo, M.; Nüesch, E.; Scaramozzino, P.; Andersen, O.K.; Arendt-Nielsen, L.; Jüni, P. Factor analysis of responses to thermal, electrical, and mechanical painful stimuli supports the importance of multi-modal pain assessment. Pain 2011, 152, 1146–1155. [Google Scholar] [CrossRef] [PubMed]
- Graven-Nielsen, T.; Vaegter, H.B.; Finocchietti, S.; Handberg, G.; Arendt-Nielsen, L. Assessment of musculoskeletal pain sensitivity and temporal summation by cuff pressure algometry: A reliability study. Pain 2015, 156, 2193–2202. [Google Scholar] [CrossRef] [PubMed]
- Finocchietti, S.; Takahashi, K.; Okada, K.; Watanabe, Y.; Graven-Nielsen, T.; Mizumura, K. Deformation and pressure propagation in deep tissue during mechanical painful pressure stimulation. Med. Biol. Eng. Comput. 2013, 51, 113–122. [Google Scholar] [CrossRef]
- Finocchietti, S.; Mørch, C.D.; Arendt-Nielsen, L.; Graven-Nielsen, T. Effects of adipose thickness and muscle hardness on pressure pain sensitivity. Clin. J. Pain 2011, 27, 735–745. [Google Scholar] [CrossRef]
- Fischer, A.A. Pressure algometry over normal muscles. Standard values, validity and reproducibility of pressure threshold. Pain 1987, 30, 115–126. [Google Scholar] [CrossRef]
- Melia, M.; Geissler, B.; König, J.; Ottersbach, H.J.; Umbreit, M.; Letzel, S.; Muttray, A. Pressure pain thresholds: Subject factors and the meaning of peak pressures. Eur. J. Pain 2019, 23, 167–182. [Google Scholar] [CrossRef]
- Lemming, D.; Börsbo, B.; Sjörs, A.; Lind, E.B.; Arendt-Nielsen, L.; Graven-Nielsen, T.; Gerdle, B. Cuff pressure pain detection is associated with both sex and physical activity level in nonathletic healthy subjects. Pain Med. 2017, 18, 1573–1581. [Google Scholar] [CrossRef]
- Manafi-Khanian, B.; Arendt-Nielsen, L.; Graven-Nielsen, T. An MRI-based leg model used to simulate biomechanical phenomena during cuff algometry: A finite element study. Med. Biol. Eng. Comput. 2016, 54, 315–324. [Google Scholar] [CrossRef]
- Lopez-Martinez, D.; Picard, R. Continuous Pain Intensity Estimation from Autonomic Signals with Recurrent Neural Networks. In Proceedings of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018. [Google Scholar] [CrossRef]
- Gary, C.S.; Iskandarova, A.; Abadeer, A.I.; Yohe, G.J.; Giladi, A.M. Performance of Near-Infrared Spectroscopy in Detecting Acute Tourniquet-Induced Upper-Extremity Ischemia Across Different Skin Phenotypes. J. Hand Surg. Am. 2023, 48, 612–623. [Google Scholar] [CrossRef]
- Cowen, R.; Stasiowska, M.K.; Laycock, H.; Bantel, C. Assessing pain objectively: The use of physiological markers. Anaesthesia 2015, 70, 828–847. [Google Scholar] [CrossRef]
- Nielsen, C.S.; Stubhaug, A.; Price, D.D.; Vassend, O.; Czajkowski, N.; Harris, J.R. Individual differences in pain sensitivity: Genetic and environmental contributions. Pain 2008, 136, 21–29. [Google Scholar] [CrossRef]
- Fillingim, R.B. Individual differences in pain: Understanding the mosaic that makes pain personal. Pain 2016, 158, S11. [Google Scholar] [CrossRef]
- Haefeli, M.; Elfering, A. Pain assessment. Eur. Spine J. 2006, 15 (Suppl. 1), S17–S24. [Google Scholar] [CrossRef]
- Chiarotto, A.; Maxwell, L.J.; Ostelo, R.W.; Boers, M.; Tugwell, P.; Terwee, C.B. Measurement properties of visual analogue scale, numeric rating scale, and pain severity subscale of the brief pain inventory in patients with low back pain: A systematic review. J. Pain 2019, 20, 245–263. [Google Scholar] [CrossRef]
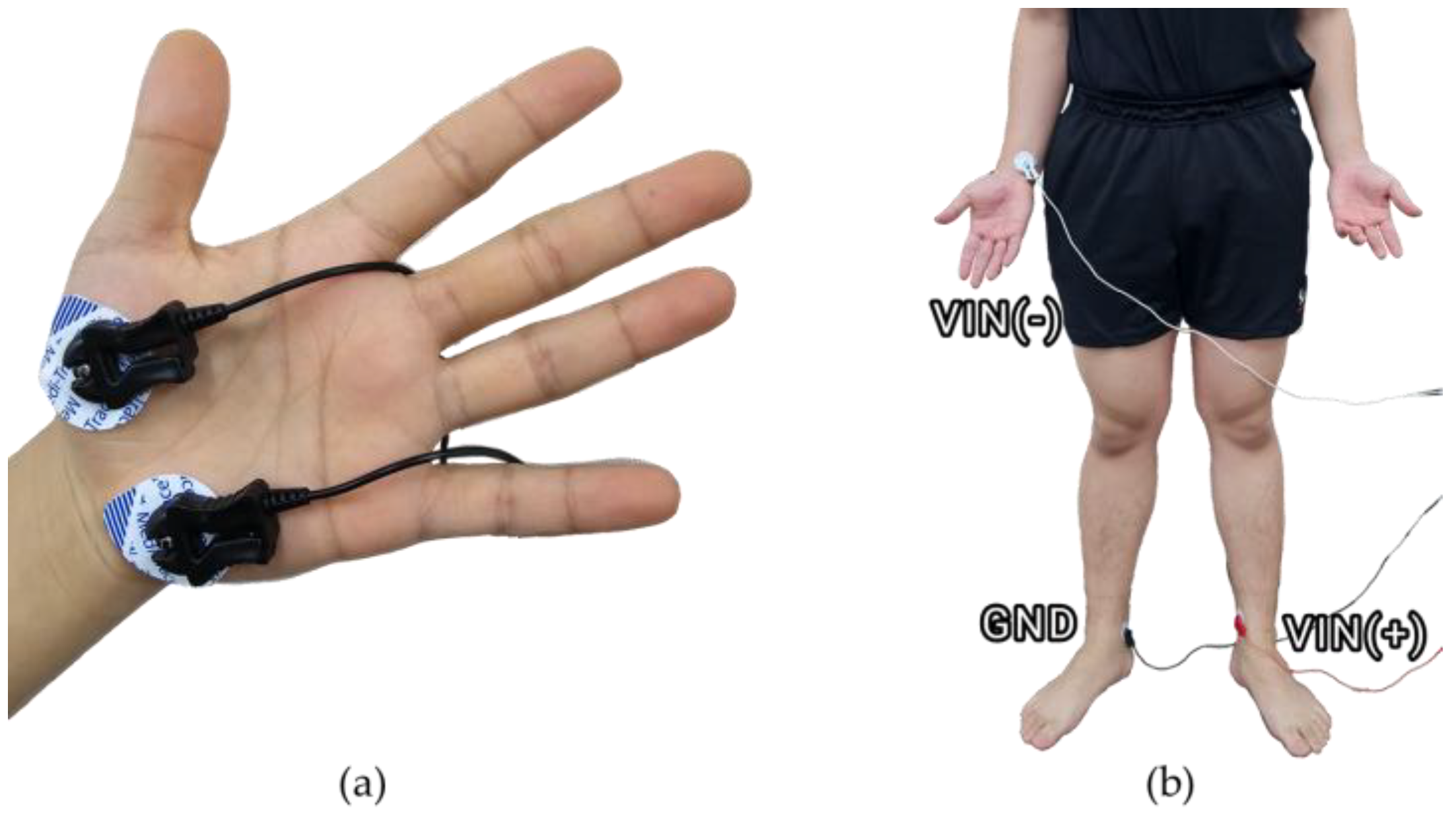
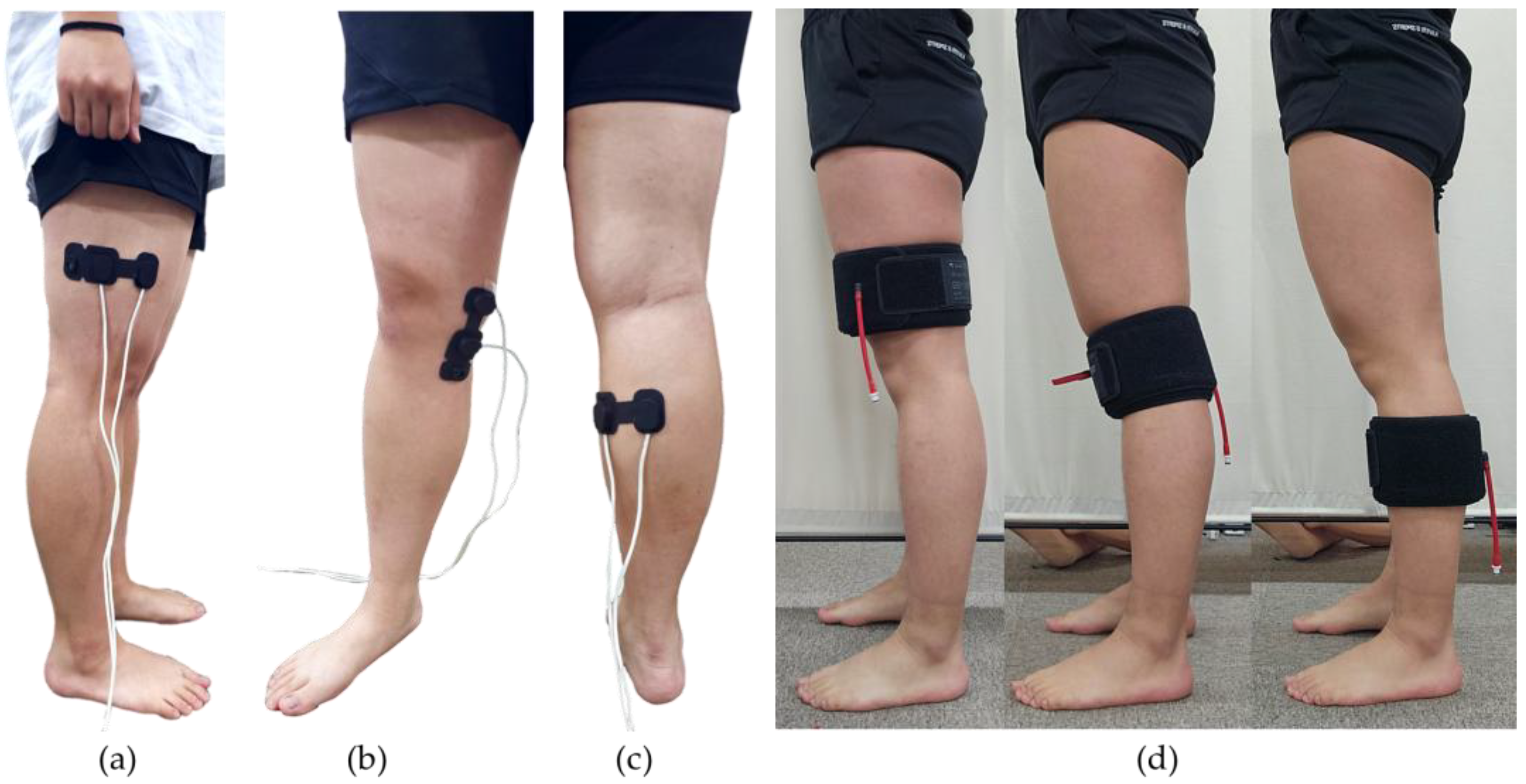



| Thigh | The 2/3 position between the greater trochanter and the lateral epicondyle |
| Knee | The position between the medial epicondyle and medial condyle |
| Calf | The muscle belly of the medial gastrocnemius |
| Classifiers | Parameters | Values |
|---|---|---|
| Support Vector Machine | C | 1, 10, 100, 1000 |
| Gamma | 0.0001, 0.001, 0.01, 0.1 | |
| Degree (poly) | 2, 3, 4 | |
| Logistic Regression | Solver | Newton-CG, LBFGS, |
| Random Forest | Criterion | Gini, Entropy |
| Multi-layer perceptron | Hidden Layer | 1, 2, 3 (Hidden unit: 100) |
| Activation | Logistic, tanh, relu | |
| Solvers | Adam, Stochastic gradient descent | |
| Learning rate | 0.0001, 0.001, 0.01 | |
| K-nearest neighbors | K | 3, 5, 7, 9 |
| Features | Position | Pressure Intensity | Pain Level | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 kPa | 10 kPa | 20 kPa | 30 kPa | No Pain | Low | Moderate | High | ||
| Max Tonic [μS] | Thigh | −0.22 ± 0.15 | 0 ± 0.1 | 0.2 ± 0.4 | 0.41 ± 0.7 | −0.16 ± 0.18 | 0.04 ± 0.2 | 0.15 ± 0. | 0.68 ± 0.9 |
| Knee | −0.22 ± 0.15 | 0.03 ± 0.2 | 0.13 ± 0.3 | 0.48 ± | −0.17 ± 0.18 | 0.06 ± 0.2 | 0.1 ± 0.3 | 0.84 ± 1.1 | |
| Calf | −0.19 ± 0.19 | 0.03 ± 0. | 0.4 ± 0.8 | 1.01 ± 1.6 | −0.12 ± 0.21 | 0.03 ± 0.3 | 0.43 ± 0.7 | 1.07 ± 1.6 | |
| MTVSymp max [n.u.] | Thigh | 0.05 ± 0.07 | 0.14 ± 0.2 | 0.29 ± 0.3 | 0.39 ± 0. | 0.06 ± 0.09 | 0.19 ± 0.3 | 0.27 ± 0.2 | 0.54 ± 0.4 |
| Knee | 0.04 ± 0.06 | 0.14 ± 0.22 | 0.2 ± 0.2 | 0.38 ± 0. | 0.05 ± 0.0 | 0.16 ± 0.23 | 0.19 ± 0.2 | 0.6 ± 0.5 | |
| Calf | 0.07 ± 0.1 | 0.14 ± 0.27 | 0.39 ± 0.5 | 0.75 ± 0.7 | 0.08 ± 0.1 | 0.14 ± 0.31 | 0.44 ± 0.6 | 0.78 ± 0.7 | |
| MaxNN [ms] | Thigh | 931 ± 112.4 | 961 ± 109. | 970 ± 112. | 982 ± 111. | 938.2 ± 113 | 974.2 ± 114.3 | 971.4 ± 103 | 978.4 ± 120 |
| Knee | 932 ± 128.0 | 973 ± 122. | 964 ± 119. | 971 ± 113. | 937.5 ± 126 | 980.2 ± 111 | 962.4 ± 120 | 980.1 ± 12 | |
| Calf | 874.3 ± 10 | 919.2 ± 11 | 940.6 ± 11 | 946.3 ± 11 | 937.8 ± 112 | 958.3 ± 117.3 | 936 ± 110.1 | 933.7 ± 11 | |
| HF [ms2] | Thigh | 0.034 ± 0.027 | 0.018 ± 0.01 | 0.019 ± 0.01 | 0.018 ± 0.01 | 0.029 ± 0.025 | 0.019 ± 0.01 | 0.019 ± 0.01 | 0.019 ± 0.01 |
| Knee | 0.033 ± 0.029 | 0.018 ± 0.01 | 0.018 ± 0.01 | 0.016 ± 0.01 | 0.028 ± 0.02 | 0.02 ± 0.012 | 0.017 ± 0.02 | 0.014 ± 0.014 | |
| Calf | 0.036 ± 0.028 | 0.015 ± 0.01 | 0.02 ± 0.01 | 0.014 ± 0.01 | 0.028 ± 0.02 | 0.02 ± 0.01 | 0.016 ± 0.0 | 0.014 ± 0.01 | |
| ΔStO2 [%] | Thigh | 0.39 ± 0.34 | 3.36 ± 2. | 15.24 ± 8.1 | 16.3 ± 8.3 | 1.15 ± 1.54 | 7.09 ± 7.0 | 15.75 ± 8.4 | 16.87 ± 7.7 |
| Knee | 0.24 ± 0.2 | 2.19 ± 1.3 | 8.05 ± 4.0 | 9.41 ± 4.1 | 0.87 ± 1.14 | 4.93 ± 3.9 | 8.34 ± 4.4 | 9.29 ± 4.4 | |
| Calf | 0.47 ± 0.3 | 1.89 ± 2.5 | 19.19 ± 9.2 | 20.68 ± 9. | 0.81 ± 1.26 | 5.65 ± 6.4 | 19.8 ± 9.5 | 21.53 ± 8.7 | |
| Std StO2 [%] | Thigh | 0.23 ± 0.19 | 0.89 ± 0.6 | 4.36 ± 2.7 | 4.65 ± 2.8 | 0.4 ± 0.39 | 2.01 ± 2.3 | 4.51 ± 2.8 | 4.73 ± 2. |
| Knee | 0.13 ± 0.12 | 0.55 ± 0.2 | 1.81 ± 0.9 | 2.07 ± 1.0 | 0.24 ± 0.21 | 1.11 ± 0.7 | 1.91 ± 1.0 | 2.04 ± 1.1 | |
| Calf | 0.27 ± 0.2 | 1.29 ± 0.7 | 6.36 ± 2.7 | 6.72 ± 2. | 0.52 ± 0.4 | 2.57 ± 1.8 | 6.49 ± 2.7 | 6.99 ± 2.8 | |
| VAS | Thigh | 0 ± 0 | 0.85 ± 1.0 | 4.23 ± 1.4 | 6.35 ± 1.8 | 0 ± 0 | 1.86 ± 0.8 | 4.66 ± 0.8 | 7.79 ± 0.7 |
| Knee | 0 ± 0 | 0.86 ± | 4.25 ± 1.2 | 6.71 ± 1.7 | 0 ± 0 | 2.04 ± 0.8 | 5.06 ± 0.7 | 7.99 ± 0.8 | |
| Calf | 0 ± 0 | 0.65 ± 0. | 4.72 ± 1. | 7.94 ± 1.4 | 0 ± 0 | 1.85 ± 0.9 | 4.89 ± 0.7 | 8.22 ± 0.8 | |
| Regression Model: VAS Prediction | |||
| Body Part | R2 | RMSE | Regression Equation |
| Thigh | 0.554 | 1.925 | VAS = −1.969 + (1.647 × Max Tonic) + (0.042 × MeanHR) + (0.186 × ΔStO2) |
| Knee | 0.643 | 1.798 | VAS = 1.616 + (13.943 × TVSymp mean) + (−2.519 × HFn) + (0.394 × ΔStO2) |
| Calf | 0.668 | 1.969 | VAS = 1.001 + (0.121 × SCR counts) + (−14.585 × HF) + (0.211 × ΔStO2 |
| Regression Model: Pressure Prediction | |||
| Thigh | 0.597 | 7.121 | Pressure = 29.856 + (21.487 × Mean Tonic) + (−0.025 × MinNN) + (0.784 × ΔStO2) |
| Knee | 0.687 | 6.245 | Pressure = 8.714 + (1238.511 × Mean phasic) + (−8.118 × HFn) + (1.758 × Δ StO2) |
| Calf | 0.668 | 6.516 | Pressure = 11.409 + (15.880 × Mean Tonic) + (−70.098 × HF) + (2.081 × Std StO2) |
| Classifier | Pain Level | Pressure Intensity | ||||
|---|---|---|---|---|---|---|
| Thigh | Knee | Calf | Thigh | Knee | Calf | |
| L-SVM | 0.657 | 0.690 | 0.776 | 0.729 | 0.778 | 0.780 |
| P-SVM | 0.629 | 0.704 | 0.713 | 0.720 | 0.750 | 0.750 |
| LR | 0.657 | 0.690 | 0.776 | 0.708 | 0.729 | 0.783 |
| RF | 0.757 | 0.803 | 0.882 | 0.729 | 0.778 | 0.833 |
| MLP | 0.800 | 0.746 | 0.881 | 0.708 | 0.750 | 0.813 |
| KNN | 0.714 | 0.803 | 0.803 | 0.708 | 0.729 | 0.750 |
| Feature Set (Count of Combinations) | Mean Accuracy ± Standard Deviation | ||
|---|---|---|---|
| Thigh | Knee | Calf | |
| EDA (16) | 0.397 ± 0.076 | 0.364 ± 0.071 | 0.425 ± 0.059 |
| HRV (15) | 0.353 ± 0.054 | 0.324 ± 0.050 | 0.346 ± 0.062 |
| StO2 (4) | 0.439 ± 0.086 | 0.500 ± 0.147 | 0.523 ± 0.136 |
| EDA+HRV (240) | 0.495 ± 0.058 | 0.468 ± 0.055 | 0.516 ± 0.054 |
| EDA+StO2 (60) | 0.545 ± 0.082 | 0.587 ± 0.084 | 0.660 ± 0.071 |
| HRV+StO2 (51) | 0.550 ± 0.104 | 0.567 ± 0.090 | 0.602 ± 0.095 |
| EDA+HRV+StO2 (767) | 0.599 ± 0.072 | 0.632 ± 0.076 | 0.693 ± 0.075 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Pyo, S.; Lee, S.; Park, C.; Song, S. Estimation of Pressure Pain in the Lower Limbs Using Electrodermal Activity, Tissue Oxygen Saturation, and Heart Rate Variability. Sensors 2025, 25, 680. https://doi.org/10.3390/s25030680
Kim Y, Pyo S, Lee S, Park C, Song S. Estimation of Pressure Pain in the Lower Limbs Using Electrodermal Activity, Tissue Oxygen Saturation, and Heart Rate Variability. Sensors. 2025; 25(3):680. https://doi.org/10.3390/s25030680
Chicago/Turabian StyleKim, Youngho, Seonggeon Pyo, Seunghee Lee, Changeon Park, and Sunghyuk Song. 2025. "Estimation of Pressure Pain in the Lower Limbs Using Electrodermal Activity, Tissue Oxygen Saturation, and Heart Rate Variability" Sensors 25, no. 3: 680. https://doi.org/10.3390/s25030680
APA StyleKim, Y., Pyo, S., Lee, S., Park, C., & Song, S. (2025). Estimation of Pressure Pain in the Lower Limbs Using Electrodermal Activity, Tissue Oxygen Saturation, and Heart Rate Variability. Sensors, 25(3), 680. https://doi.org/10.3390/s25030680







