Dynamic Stability Analysis and Optimization of Multi-Vehicle Systems in Heterogeneous Connected Traffic
Abstract
:1. Introduction
2. Analysis of Car-Following Characteristics in Mixed-Traffic Flow
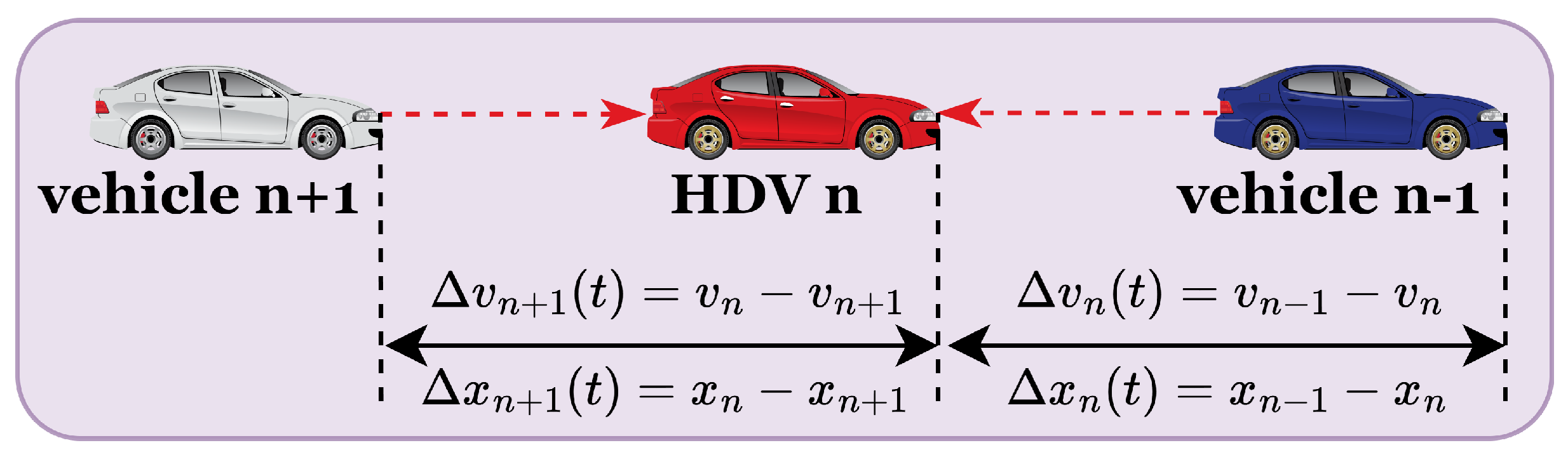
2.1. Car-Following Model for HDVs
2.2. Car-Following Model for CAVs
2.3. Car-Following Model for CHVs
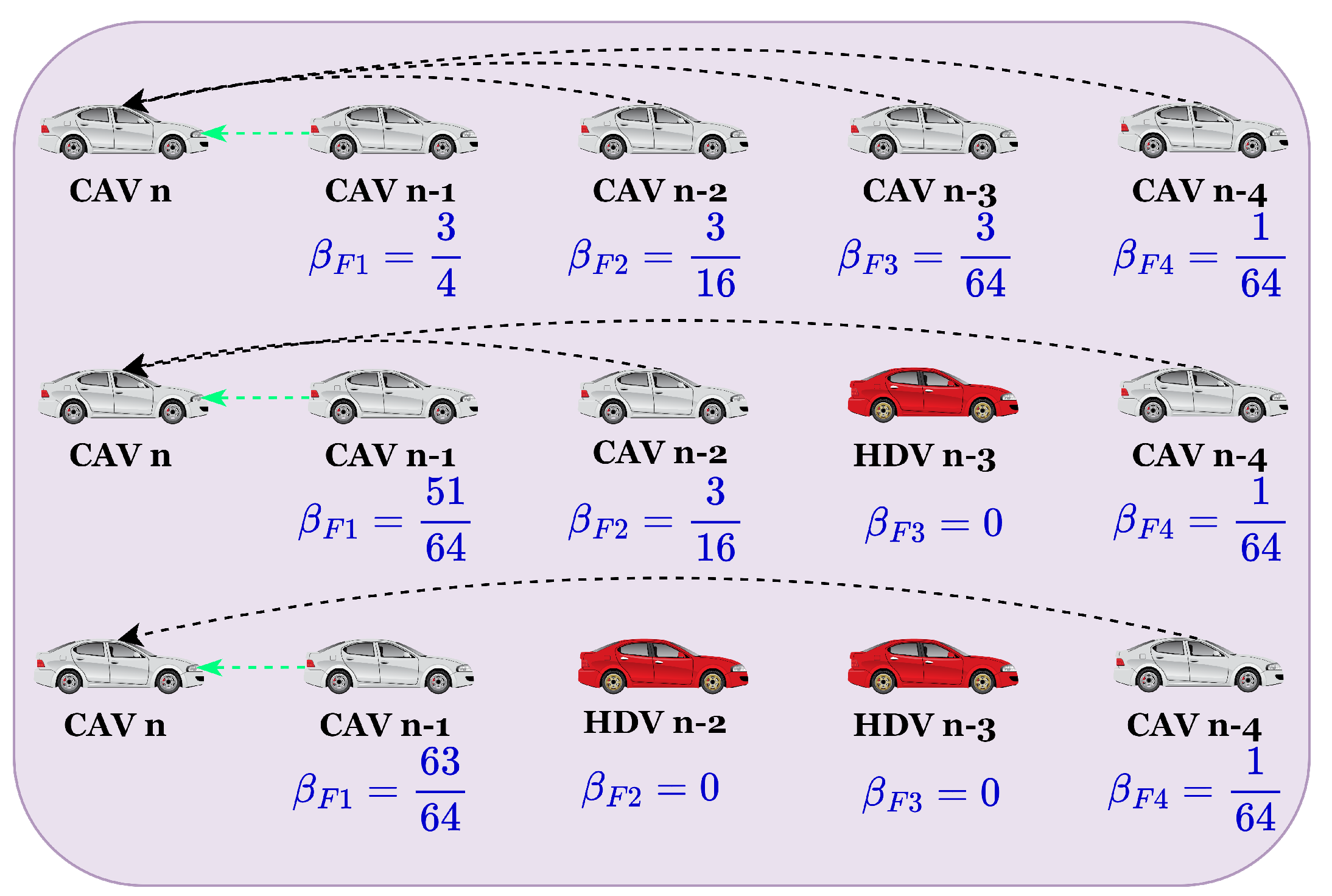
2.4. Car-Following Models Considering Degradation Scenarios
- CAVs with both the front and rear vehicles being CVs. The car-following models is given by Equation (8).
- HDVs following other vehicles. The car-following models is given by Equation (7).
- CAVs with both the front and rear vehicles being HDVs. The target CAV is positioned between two HDVs, and the CAV degrades to function as an AV. In this degraded state, the vehicle relies solely on onboard sensors to obtain information from multiple surrounding vehicles. Consequently, Equation (8) is simplified to the following expression to account for this degradation:
- CAVs with only the preceding vehicle as an HDV. The target CAV has an HDV immediately ahead and a non-HDV vehicle behind, the CAV degrades to function as an AV relative to the vehicle in front. In this degraded state, it relies on onboard sensors to gather information from multiple preceding vehicles, while utilizing V2V communication to acquire data from multiple following vehicles. As a result, Equation (8) simplifies to the following form to reflect this degradation:
- CAVs with only the following vehicle as an HDV. The CAV degrades to function as an AV relative to the vehicle behind. In this scenario, it relies solely on onboard sensors to gather information from multiple following vehicles, while utilizing V2V communication to obtain data from multiple preceding vehicles. As a result, Equation (8) simplifies to the following form to reflect this degradation:
- CHVs following other vehicles. The car-following models are given by Equation (11).
3. Stability Analysis
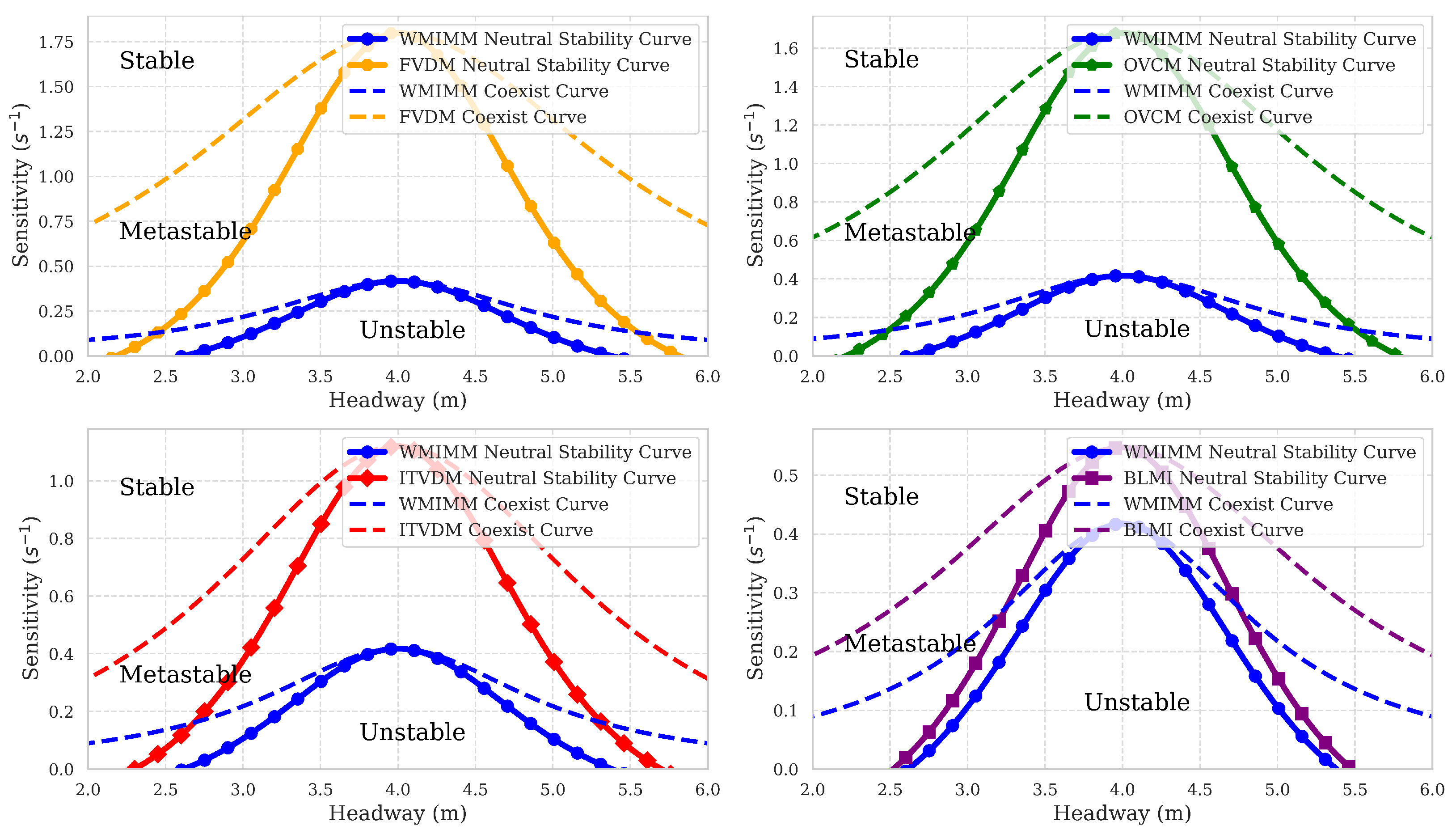
3.1. Linear Stability Analysis
3.2. Nonlinear Stability Analysis
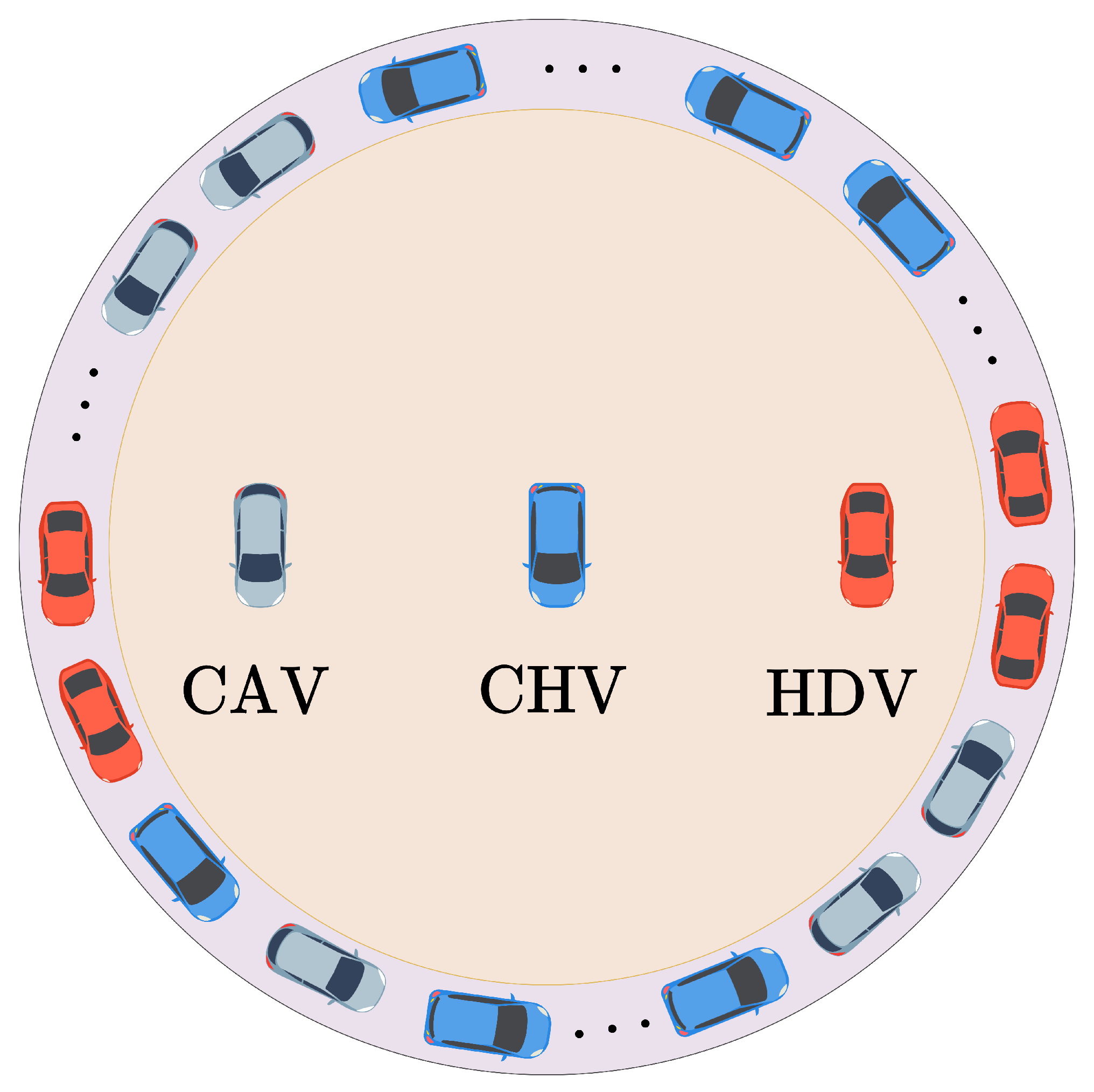
4. Numerical Simulations
4.1. Sensitivity Analysis of Parameters of WMIMM Model in Ring Road Scenario
4.1.1. Velocity Fluctuations Influenced by
4.1.2. Velocity Fluctuations Influenced by
4.1.3. Velocity Fluctuations Influenced by q
4.1.4. Velocity Fluctuations Influenced by
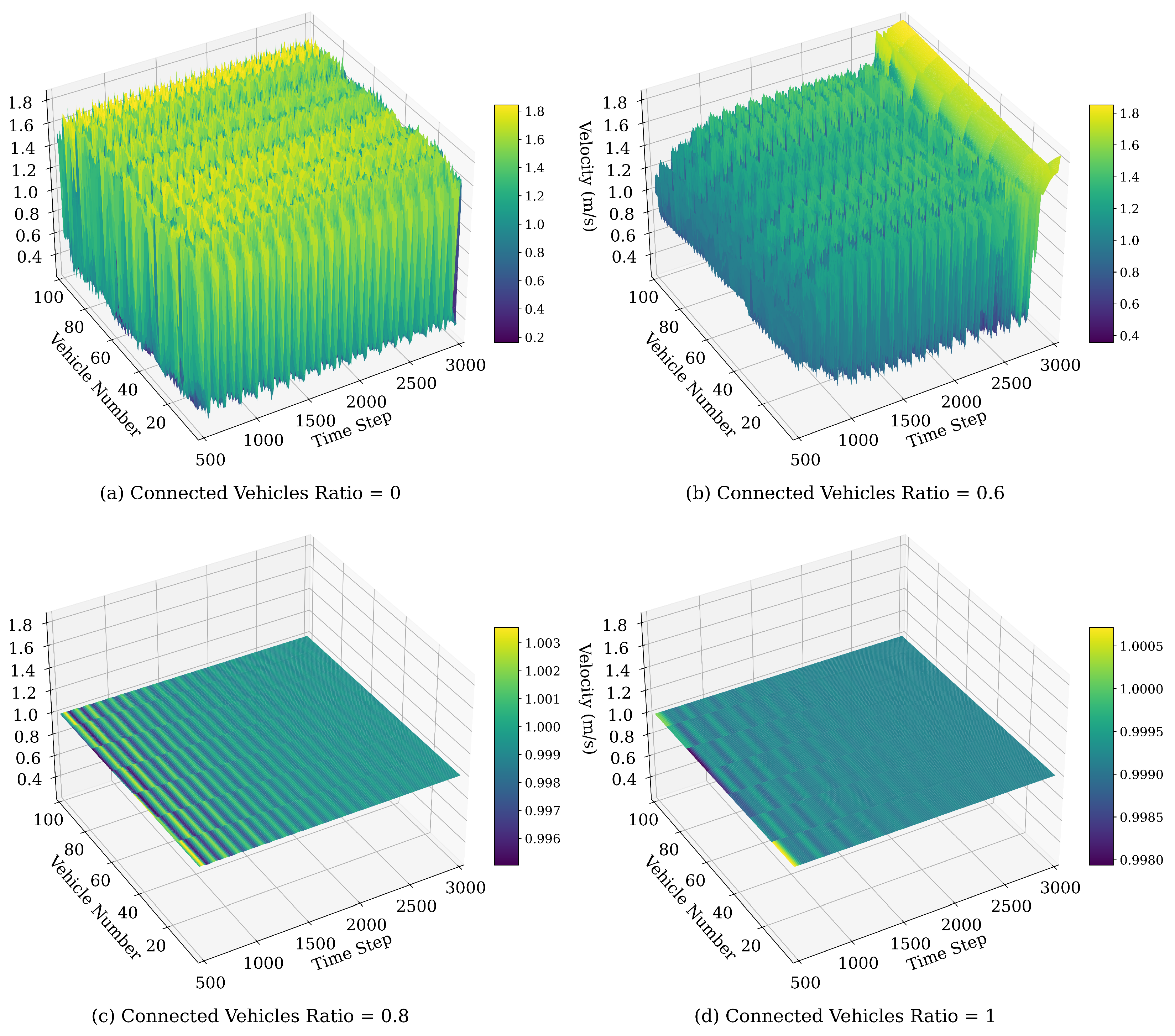
4.1.5. Velocity Fluctuations Influenced by the Ratio of CVs
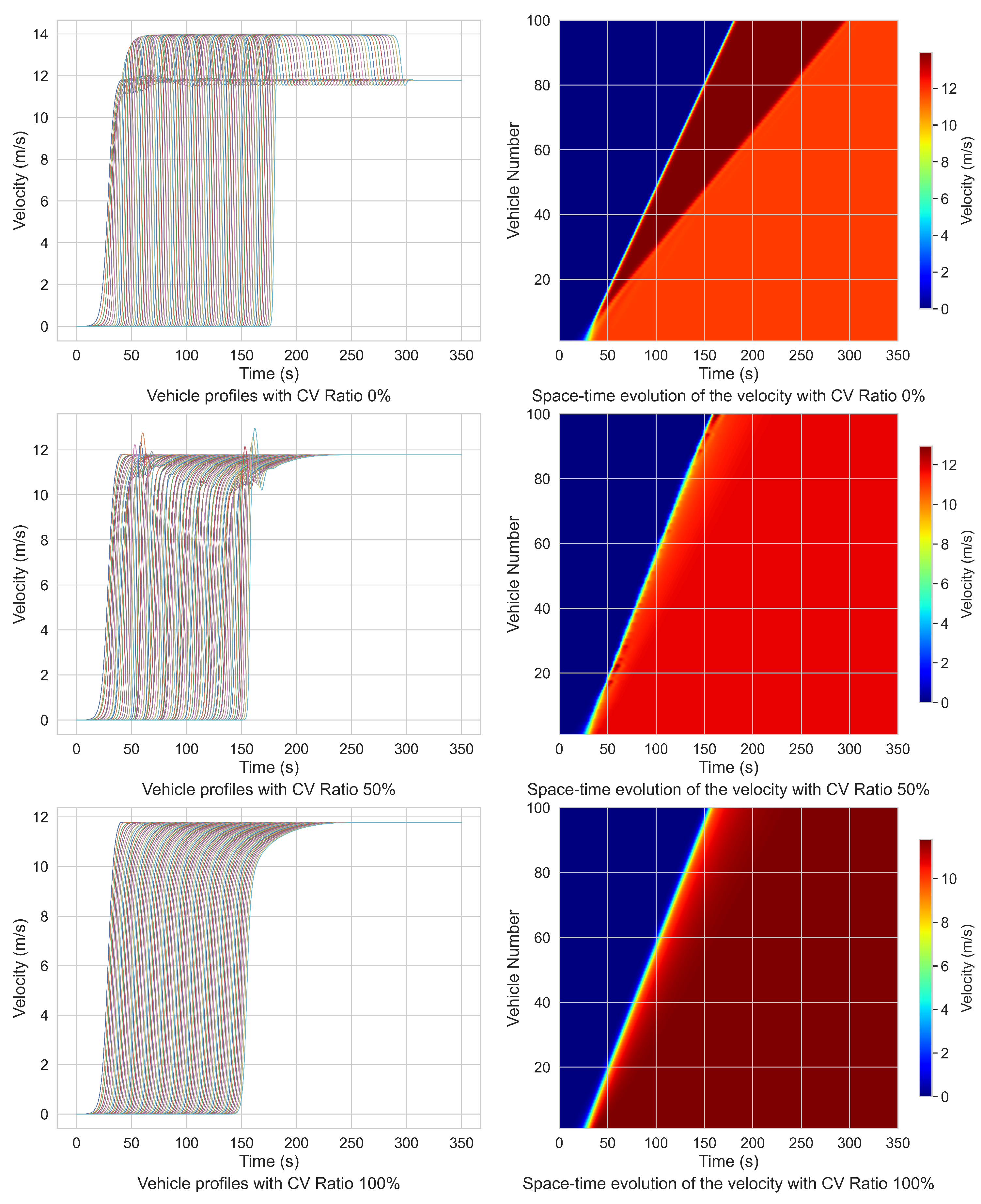
4.2. Braking and Start-Up Scenarios in Mixed Traffic
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, L.; An, B.; Wang, Z.; Gan, J.; Qu, X.; Ran, B. Stability analysis and numerical simulation of a car-following model considering safety potential field and V2X communication: A focus on influence weight of multiple vehicles. Phys. A Stat. Mech. Its Appl. 2024, 640, 129706. [Google Scholar] [CrossRef]
- Pan, Y.; Wu, Y.; Xu, L.; Xia, C.; Olson, D.L. The impacts of connected autonomous vehicles on mixed traffic flow: A comprehensive review. Phys. A Stat. Mech. Its Appl. 2024, 635, 129454. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, L.; Qu, X.; Ran, B. PACC: A platoon-based adaptive cruise control strategy based on leader-following information topology to mitigate traffic oscillations under CAV environment. Phys. A Stat. Mech. Its Appl. 2024, 654, 130117. [Google Scholar] [CrossRef]
- Yin, J.; Cao, P.; Li, Z.; Li, L.; Li, Z.; Li, D. Modelling the fundamental diagram of traffic flow mixed with connected vehicles based on the risk potential field. IET Intell. Transp. Syst. 2024, 18, 1616–1631. [Google Scholar] [CrossRef]
- Zong, F.; Yue, S.; Zeng, M.; He, Z.; Ngoduy, D. Platoon or individual: An adaptive car-following control of connected and automated vehicles. Chaos Solitons Fractals 2025, 191, 115850. [Google Scholar] [CrossRef]
- Li, L.; Gan, J.; Cui, C.; Ma, H.; Qu, X.; Wang, Q.; Ran, B. Potential field-based modeling and stability analysis of heterogeneous traffic flow. Appl. Math. Model. 2024, 125, 485–508. [Google Scholar] [CrossRef]
- Singh, N.; Kumar, K. A new car following model based on weighted average velocity field. Phys. Scr. 2024, 99, 055244. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, W.; Bai, H.; Jiang, R.; Ding, H.; Wei, L. A sigmoid-based car-following model to improve acceleration stability in traffic oscillation and following failure in free flow. IEEE Trans. Intell. Transp. Syst. 2024, 25, 9039–9057. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, M.; Hao, W. Energy-optimal car-following model for connected automated vehicles considering traffic flow stability. Energy 2024, 298, 131333. [Google Scholar] [CrossRef]
- Wu, X.; Xiao, X. An improved stochastic car-following model considering the complete state information of multiple preceding vehicles under connected vehicles environment. Phys. A Stat. Mech. Its Appl. 2024, 644, 129845. [Google Scholar] [CrossRef]
- Redhu, P.; Yadav, D.; Siwach, V. A novel car-following model incorporating advance reaction time with passing. Eur. Phys. J. Plus 2024, 139, 557. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Y.; Zhao, H.; Huang, X.; Ou, Y.; Peeta, S. The effects of communication topology on mixed traffic flow: Modelling and analysis. Transp. B Transp. Dyn. 2024, 12, 2422373. [Google Scholar] [CrossRef]
- Wang, Q.; Xie, N.; Hou, D.; Huang, Z.; Li, Z. Effects of adaptive cruise control and cooperative adaptive cruise control on traffic flow. China J. Highw. Transp. 2019, 32, 188–197. [Google Scholar]
- Xie, D.F.; Zhao, X.M.; He, Z. Heterogeneous traffic mixing regular and connected vehicles: Modeling and stabilization. IEEE Trans. Intell. Transp. Syst. 2018, 20, 2060–2071. [Google Scholar] [CrossRef]
- Jiang, Y.; Ren, T.; Ma, Y.; Wu, Y.; Yao, Z. Traffic safety evaluation of mixed traffic flow considering the maximum platoon size of connected automated vehicles. Phys. A Stat. Mech. Its Appl. 2023, 612, 128452. [Google Scholar] [CrossRef]
- Guo, M.; Bai, Y.; Li, X.; Zhou, W.; Wang, C.; Ma, X.; Gao, H.; Xiao, Y. Freeway capacity modeling and analysis for traffic mixed with human-driven and connected automated vehicles considering driver behavior characteristics. Phys. A Stat. Mech. Its Appl. 2023, 623, 128894. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Y.; Zhao, H.; Hu, S.; Wang, Y. Evaluating Stability and Performance in Mixed Traffic: A Theoretical and Co-Simulation Approach. IEEE Trans. Intell. Transp. Syst. 2024, 25, 16978–16988. [Google Scholar] [CrossRef]
- Dong, J.; Gao, Z.; Luo, D.; Wang, J.; Chen, L. Impact of beyond-line-of-sight connectivity on the capacity and stability of mixed traffic flow: An analytical and numerical investigation. Phys. A Stat. Mech. Its Appl. 2024, 635, 129502. [Google Scholar] [CrossRef]
- Yao, Z.; Ma, Y.; Ren, T.; Jiang, Y. Impact of the heterogeneity and platoon size of connected vehicles on the capacity of mixed traffic flow. Appl. Math. Model. 2024, 125, 367–389. [Google Scholar] [CrossRef]
- Shen, J.; Zhao, J.D.; Liu, H.Q.; Jiang, R.; Yu, Z.X. Effects of connected automated vehicle on stability and energy consumption of heterogeneous traffic flow system. Chin. Phys. B 2024, 33, 030504. [Google Scholar] [CrossRef]
- Jiang, Y.; Tan, L.; Xiao, G.; Wu, Y.; Yao, Z. Platoon-aware cooperative lane-changing strategy for connected automated vehicles in mixed traffic flow. Phys. A Stat. Mech. Its Appl. 2024, 640, 129689. [Google Scholar] [CrossRef]
- Hosen, M.Z.; Hossain, M.A.; Tanimoto, J. Traffic model for the dynamical behavioral study of a traffic system imposing push and pull effects. Phys. A Stat. Mech. Its Appl. 2024, 645, 129816. [Google Scholar] [CrossRef]
- Zong, T.; Li, Y.; Qin, Y. Enhancing stability of traffic flow mixed with connected automated vehicles via enabling partial regular vehicles with vehicle-to-vehicle communication function. Phys. A Stat. Mech. Its Appl. 2024, 641, 129750. [Google Scholar] [CrossRef]
- Yu, W.; Ngoduy, D.; Hua, X.; Wang, W. On the stability of a heterogeneous platoon-based traffic system with multiple anticipations in the presence of connected and automated vehicles. Transp. Res. Part C Emerg. Technol. 2023, 157, 104389. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, H. Stabilizing mixed cooperative adaptive cruise control traffic flow to balance capacity using car-following model. J. Intell. Transp. Syst. 2023, 27, 57–79. [Google Scholar] [CrossRef]
- Qin, Y.; Luo, Q.; Wang, H. Stability analysis and connected vehicles management for mixed traffic flow with platoons of connected automated vehicles. Transp. Res. Part C Emerg. Technol. 2023, 157, 104370. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Z.; Yao, Z.; Jiang, Y. Analysis of mixed traffic flow with different lane management strategy for connected automated vehicles: A fundamental diagram method. Expert Syst. Appl. 2024, 254, 124340. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, H.; Cong, H.; Wu, Y.; Yao, Z. Fundamental diagram of mixed traffic flow of CAVs with different connectivity and automation levels. Phys. A Stat. Mech. Its Appl. 2024, 646, 129904. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.; Xu, C. An Adaptive Control Framework for Mixed Autonomy Traffic Platoon. Arab. J. Sci. Eng. 2024, 49, 13409–13427. [Google Scholar] [CrossRef]
- Wang, S.T.; Zhu, W.X.; Ma, X.L. Mixed traffic system with multiple vehicle types and autonomous vehicle platoon: Modeling, stability analysis and control strategy. Phys. A Stat. Mech. Its Appl. 2023, 632, 129293. [Google Scholar] [CrossRef]
- Jiang, R.; Wu, Q.; Zhu, Z. Full velocity difference model for a car-following theory. Phys. Rev. E 2001, 64, 017101. [Google Scholar] [CrossRef]
- Peng, G.; Lu, W.; He, H.; Gu, Z. Nonlinear analysis of a new car-following model accounting for the optimal velocity changes with memory. Commun. Nonlinear Sci. Numer. Simul. 2016, 40, 197–205. [Google Scholar] [CrossRef]
- Wang, L.; Horn, B.K. On the stability analysis of mixed traffic with vehicles under car-following and bilateral control. IEEE Trans. Autom. Control 2019, 65, 3076–3083. [Google Scholar] [CrossRef]
- Gong, H.; Liu, H.; Wang, B.H. An asymmetric full velocity difference car-following model. Phys. A Stat. Mech. Its Appl. 2008, 387, 2595–2602. [Google Scholar] [CrossRef]
- Bando, M.; Hasebe, K.; Nakayama, A.; Shibata, A.; Sugiyama, Y. Dynamical model of traffic congestion and numerical simulation. Phys. Rev. E 1995, 51, 1035. [Google Scholar] [CrossRef] [PubMed]
- Ma, M.; Ma, G.; Liang, S. Density waves in car-following model for autonomous vehicles with backward looking effect. Appl. Math. Model. 2021, 94, 1–12. [Google Scholar] [CrossRef]
- Ma, M.; Wang, W.; Liang, S.; Xiao, J.; Wu, C. Improved car-following model for connected vehicles considering backward-looking effect and motion information of multiple vehicles. J. Transp. Eng. Part A Syst. 2023, 149, 04022148. [Google Scholar] [CrossRef]
- Yadav, S.; Redhu, P. Driver’s attention effect in car-following model with passing under V2V environment. Nonlinear Dyn. 2023, 111, 13245–13261. [Google Scholar] [CrossRef]
- Yadav, S.; Redhu, P. Impact of driving prediction on headway and velocity in car-following model under V2X environment. Phys. A Stat. Mech. Its Appl. 2024, 635, 129493. [Google Scholar] [CrossRef]
- Peng, J.; Shangguan, W.; Chai, L.; Qiu, W. Car-following model and optimization strategy for connected and automated vehicles under mixed traffic environment. J. Traffic Transp. Eng. 2023, 23, 232–247. [Google Scholar]




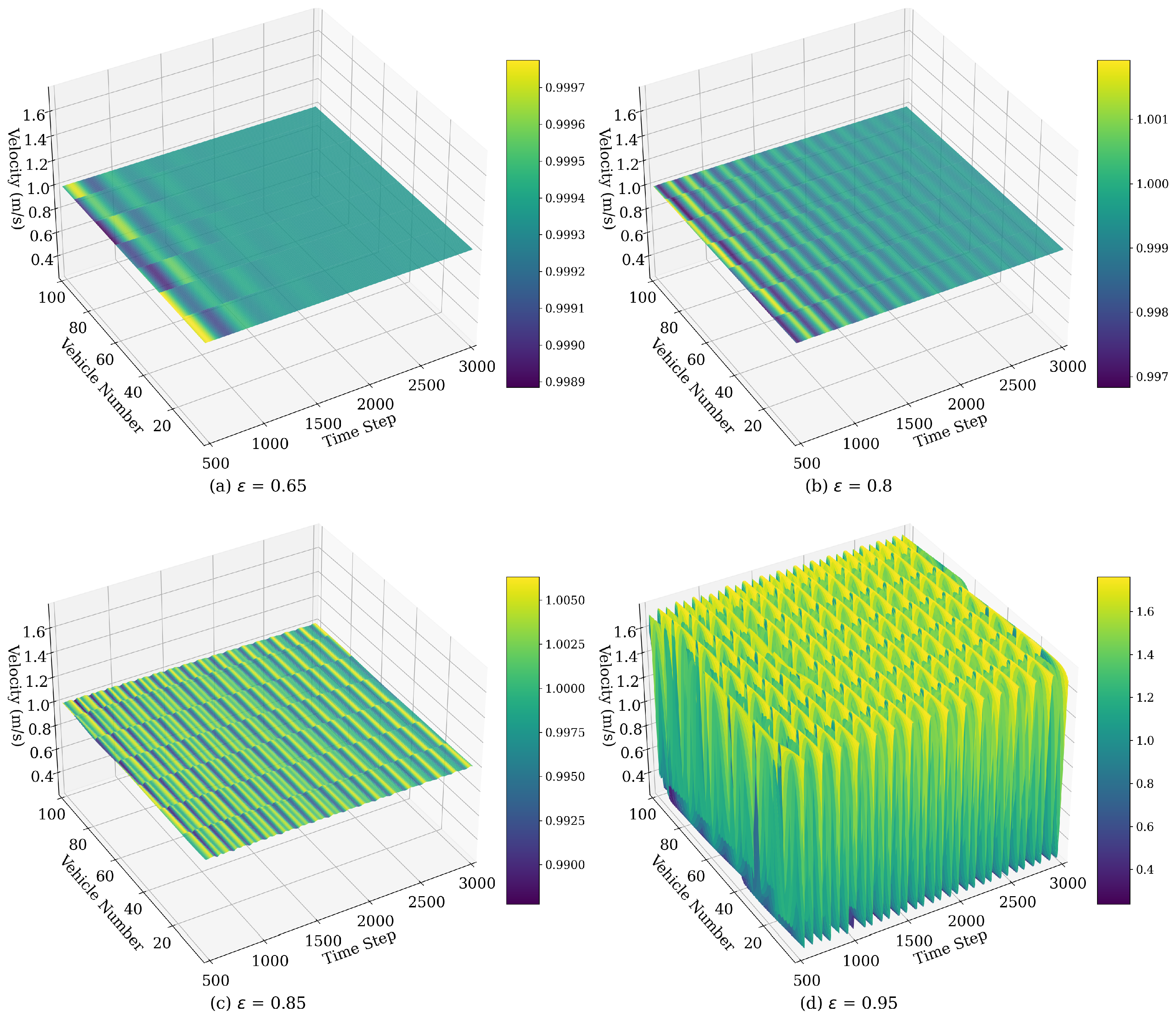
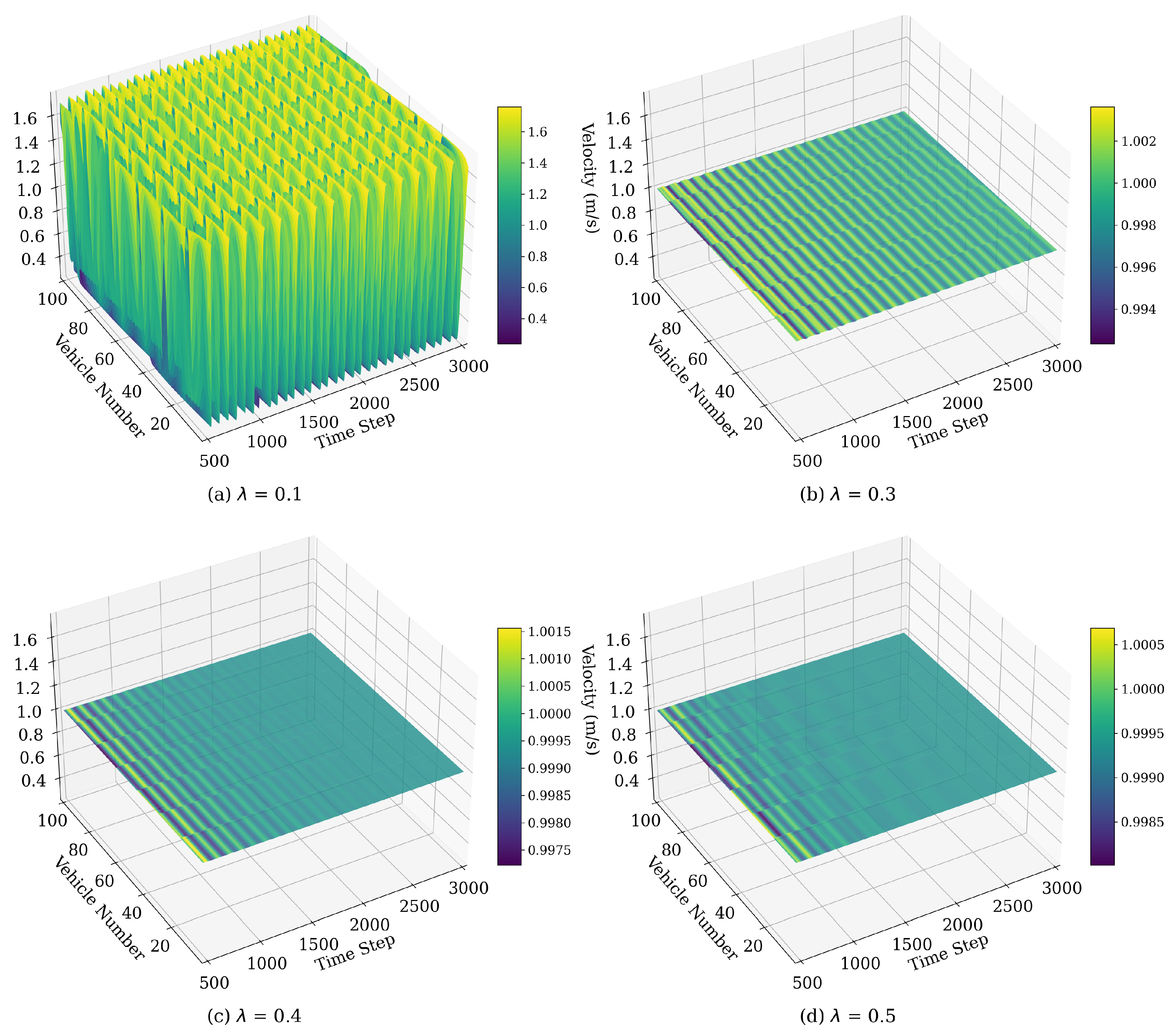
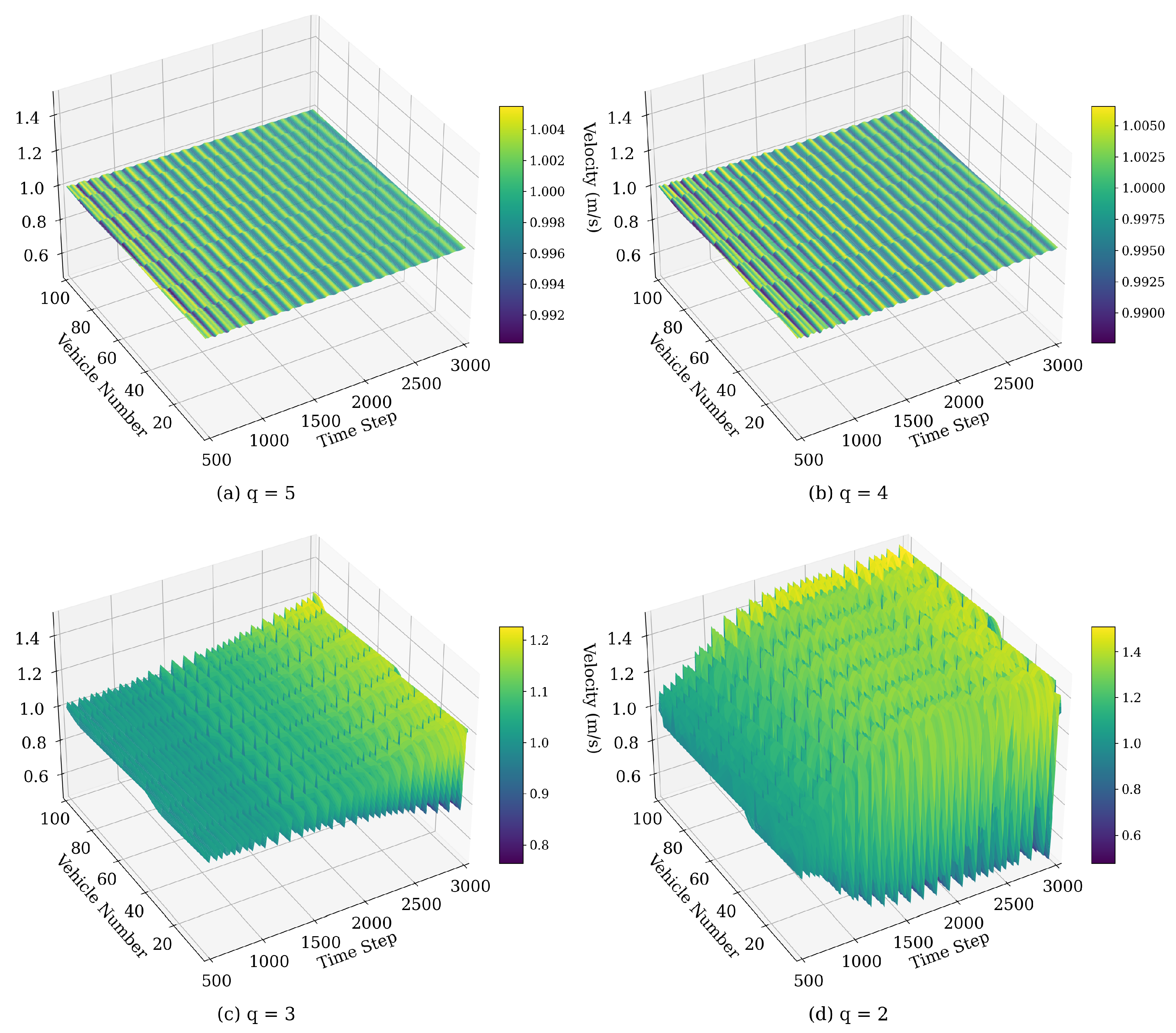
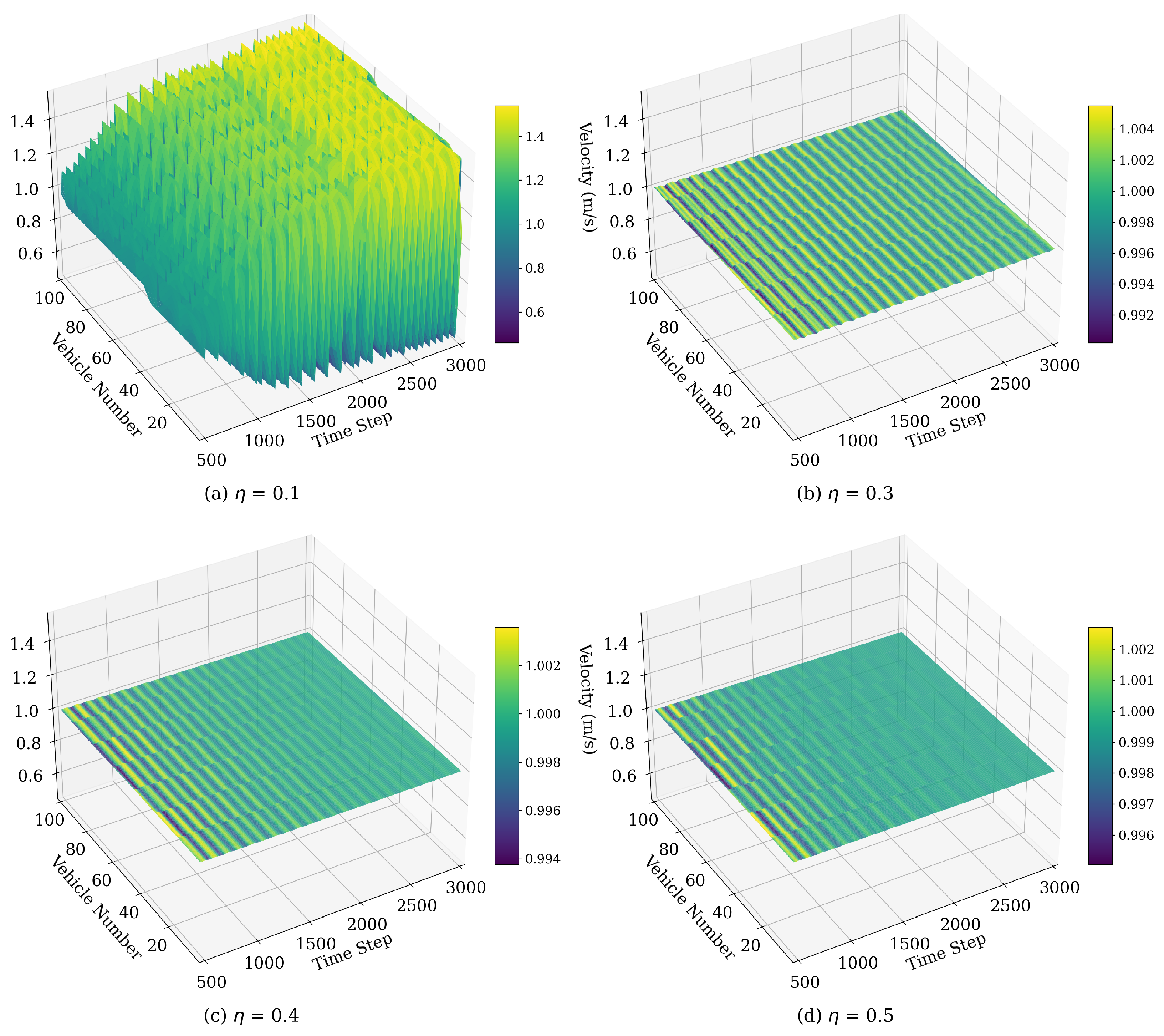

| Model | |||||
|---|---|---|---|---|---|
| FVDM | |||||
| OVCM | |||||
| ITVDM | |||||
| BLMI | |||||
| WMIMM |
| Parameter Names and Symbols | Values and Ranges |
|---|---|
| Safe Headway Distance | |
| Time Step | |
| Optimal Velocity Sensitivity Coefficient | |
| Optimal Velocity Weight of Multiple Vehicles | |
| Velocity Difference Sensitivity Coefficient | |
| Optimal Velocity Memory Sensitivity Coefficient | |
| Number of Preceding Vehicles q | |
| Number of Rear Vehicles p | 2 |
| Acceleration Sensitivity Coefficient of Multiple Vehicles |
| CV Ratio | Average Acceleration | Wave Velocity |
|---|---|---|
| 0 | ||
| 50 | ||
| 100 |
| CV Ratio | Average Acceleration | Wave Velocity |
|---|---|---|
| 0 | ||
| 50 | ||
| 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Qu, D. Dynamic Stability Analysis and Optimization of Multi-Vehicle Systems in Heterogeneous Connected Traffic. Sensors 2025, 25, 727. https://doi.org/10.3390/s25030727
Wang T, Qu D. Dynamic Stability Analysis and Optimization of Multi-Vehicle Systems in Heterogeneous Connected Traffic. Sensors. 2025; 25(3):727. https://doi.org/10.3390/s25030727
Chicago/Turabian StyleWang, Tao, and Dayi Qu. 2025. "Dynamic Stability Analysis and Optimization of Multi-Vehicle Systems in Heterogeneous Connected Traffic" Sensors 25, no. 3: 727. https://doi.org/10.3390/s25030727
APA StyleWang, T., & Qu, D. (2025). Dynamic Stability Analysis and Optimization of Multi-Vehicle Systems in Heterogeneous Connected Traffic. Sensors, 25(3), 727. https://doi.org/10.3390/s25030727






