Three-Dimensional Visualization Using Proportional Photon Estimation Under Photon-Starved Conditions
Abstract
1. Introduction
2. Theory
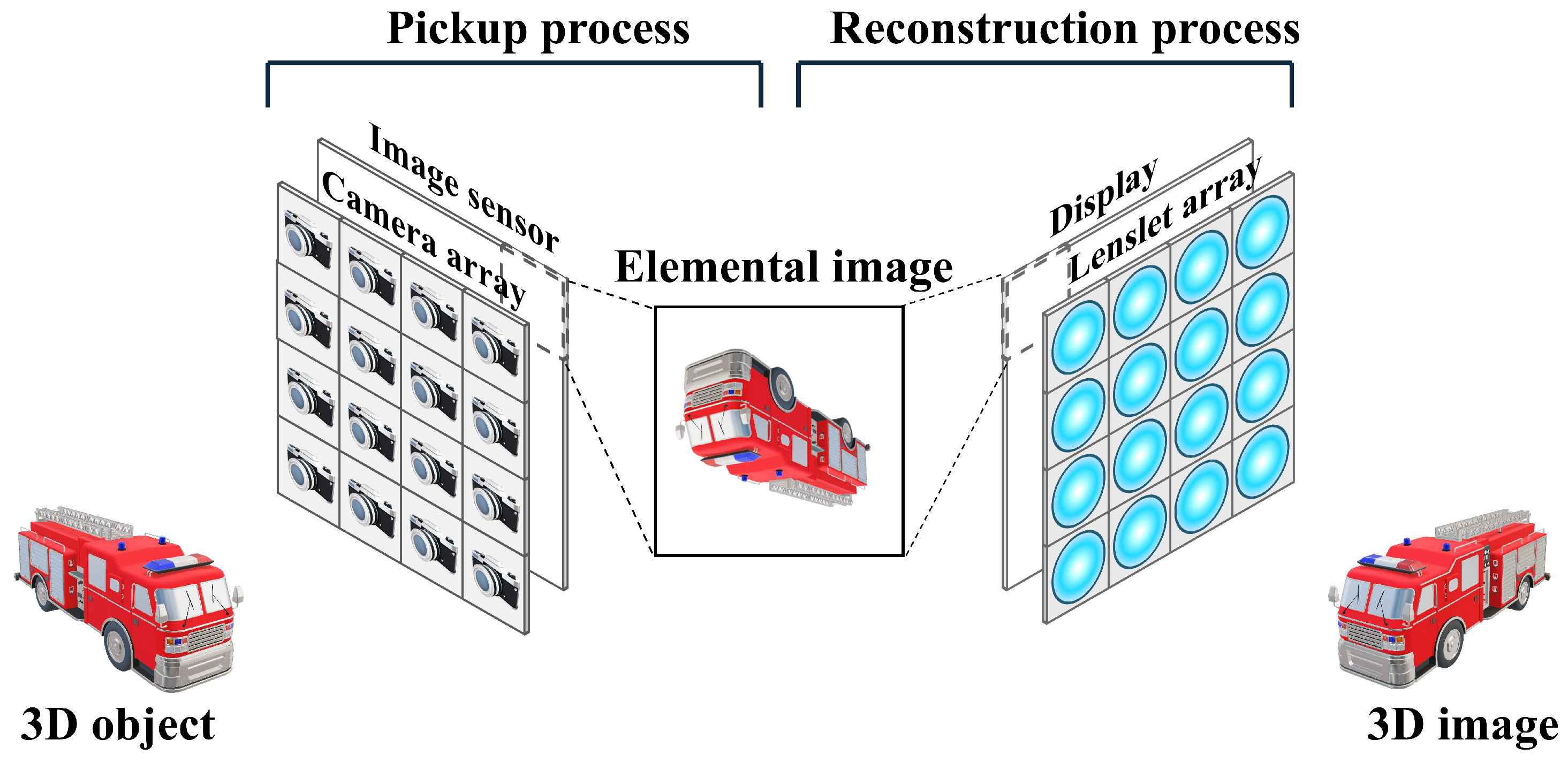
2.1. Integral Imaging
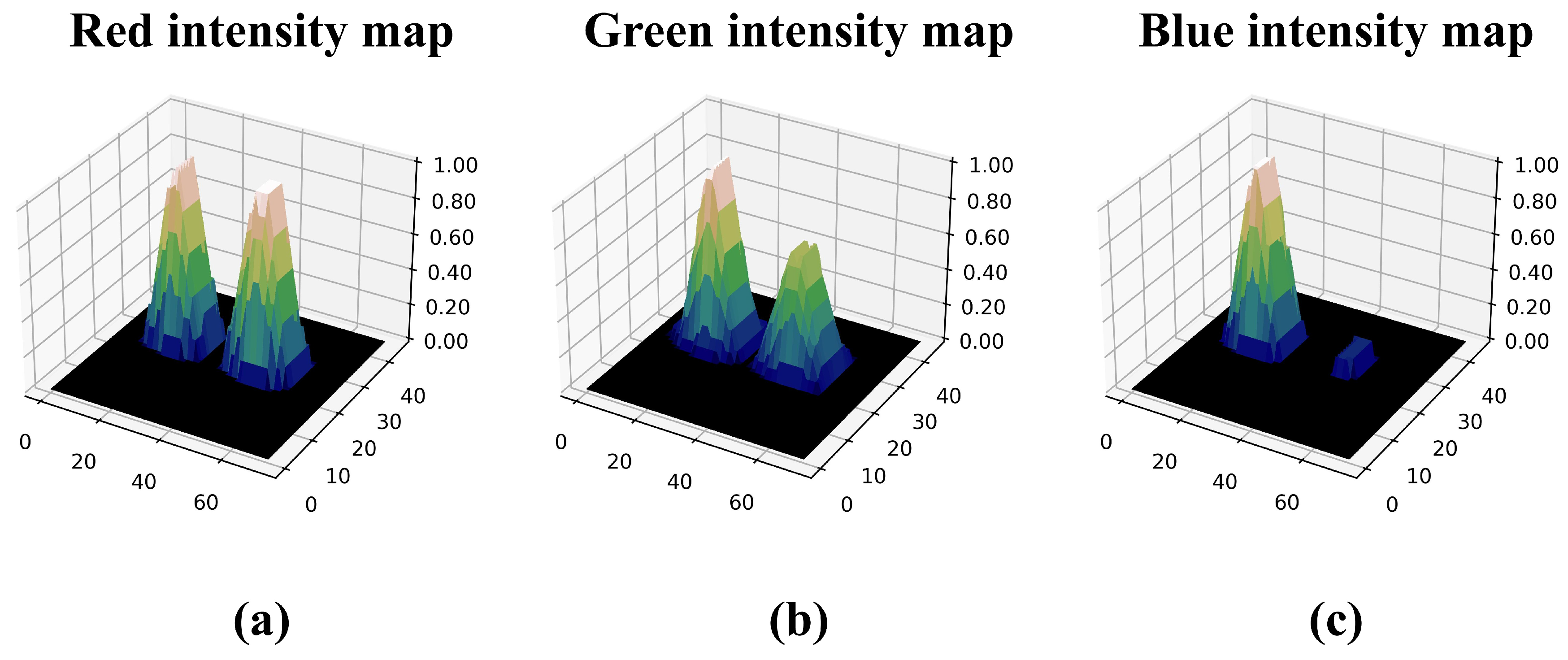
2.2. Photon-Counting Integral Imaging
3. Three-Dimensional Reconstruction by Proportional Estimation of Photon-Counting Method Under Photon-Starved Conditions
3.1. Proportional Photon-Counting Imaging (PPCI)
3.2. Proportional Estimation Integral Imaging (PEII)
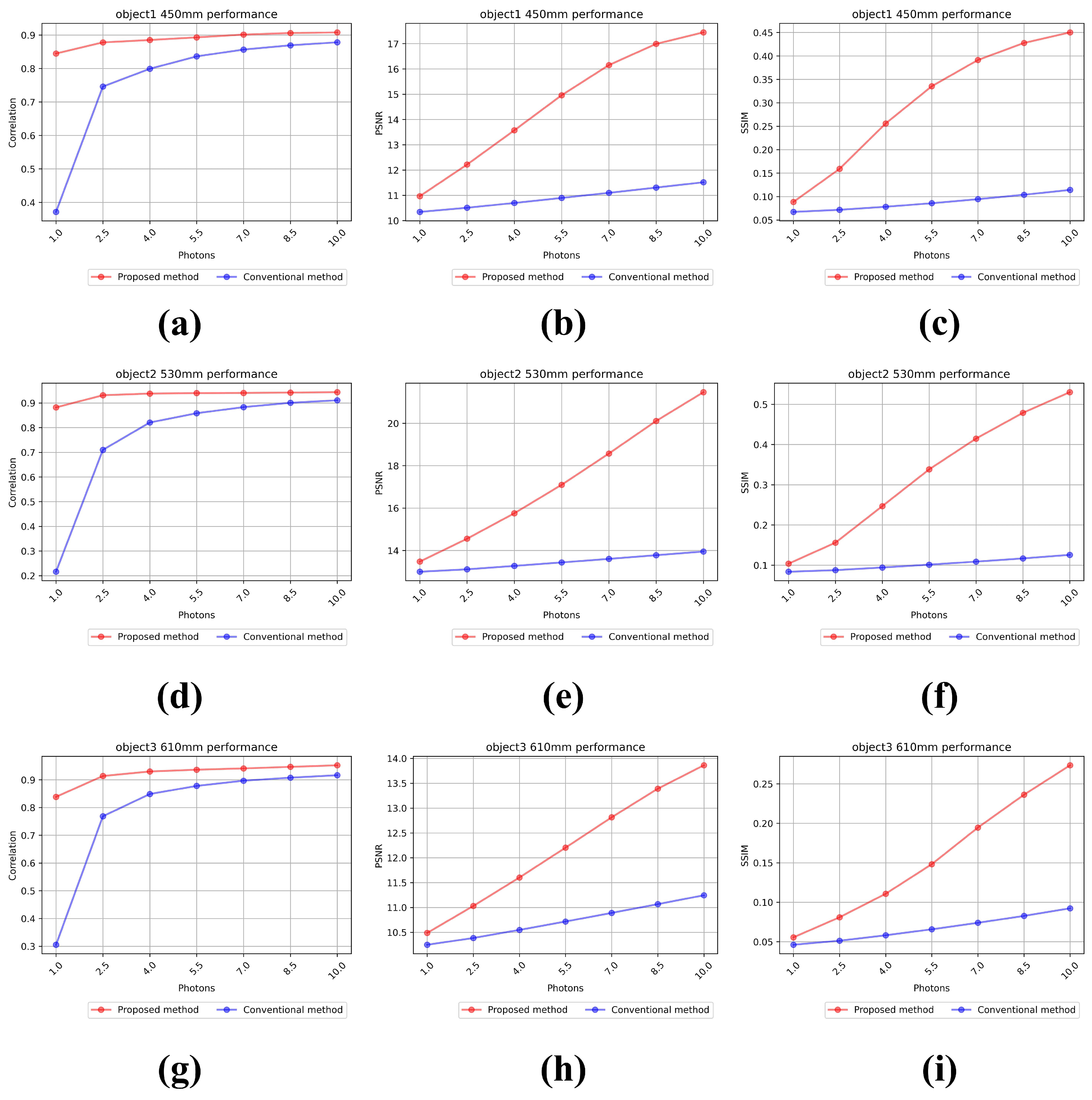
4. Experimental Setup and Results
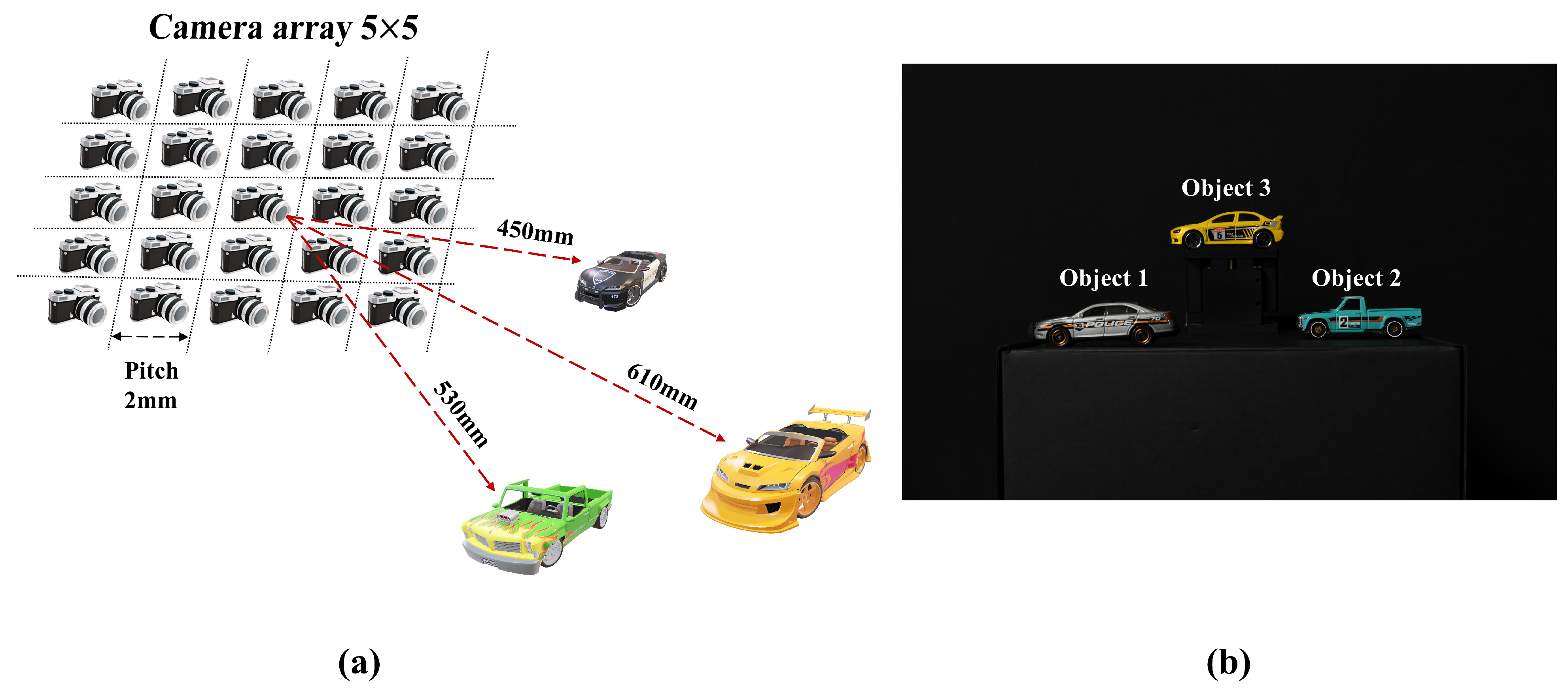
4.1. Experimental Setup
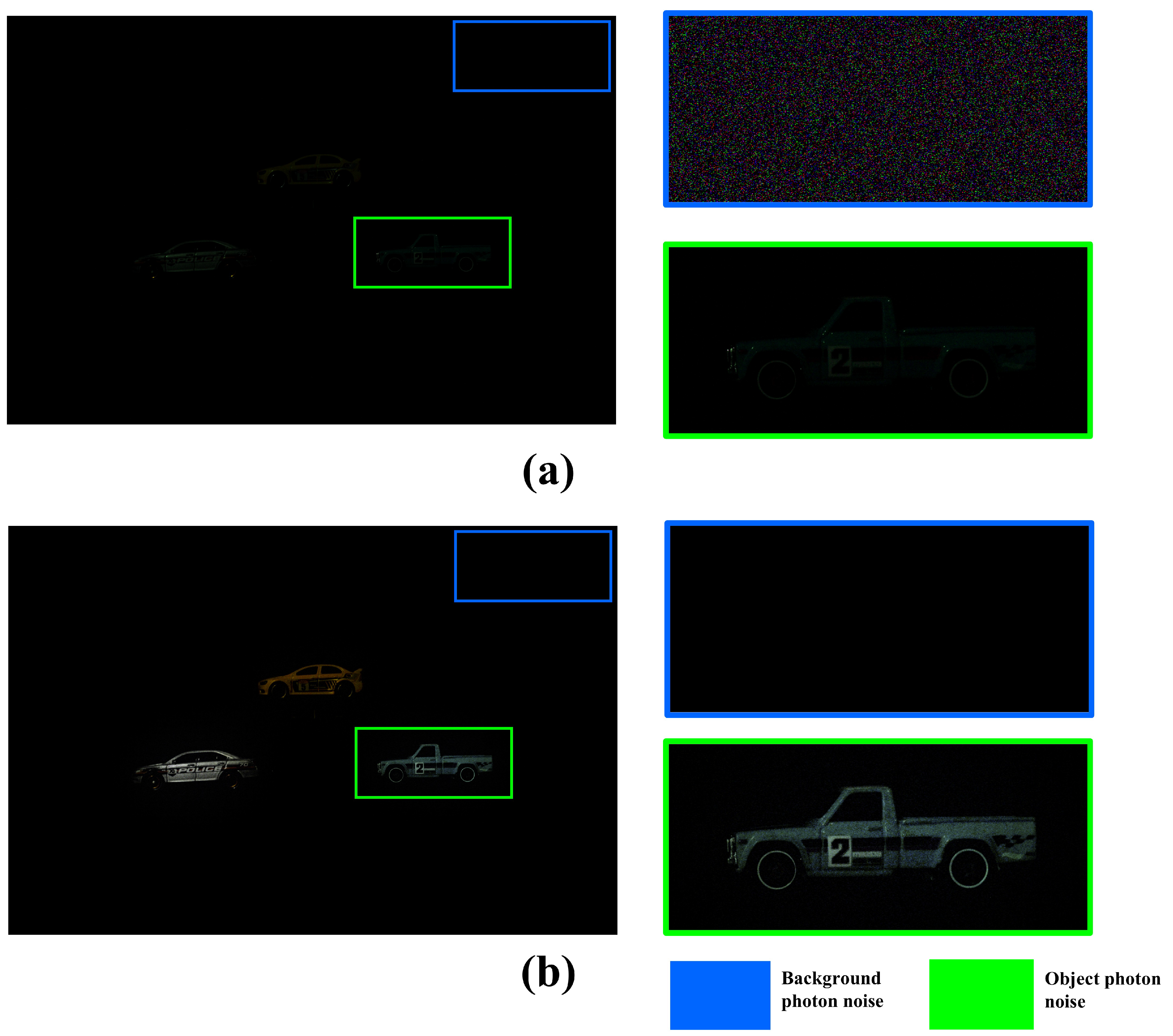
4.2. Result
4.2.1. Result of Reconstructing the 2D Elemental Image
4.2.2. The Result of Reconstructing the 3D Image
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jang, J.S.; Javidi, B. Three-dimensional integral imaging of micro-objects. Opt. Lett. 2004, 29, 1230–1232. [Google Scholar] [CrossRef] [PubMed]
- Javidi, B.; Moon, I.; Yeom, S. Three-dimensional identification of biological microorganism using integral imaging. Opt. Express 2006, 14, 12096–12108. [Google Scholar] [CrossRef]
- Carmigniani, J.; Furht, B.; Anisetti, M.; Ceravolo, P.; Damiani, E.; Ivkovic, M. Augmented reality technologies, systems and applications. Multimed. Tools Appl. 2011, 51, 341–377. [Google Scholar] [CrossRef]
- Li, Y.; Ibanez-Guzman, J. Lidar for autonomous driving: The principles, challenges, and trends for automotive lidar and perception systems. IEEE Signal Process. Mag. 2020, 37, 50–61. [Google Scholar] [CrossRef]
- Willemink, M.J.; Persson, M.; Pourmorteza, A.; Pelc, N.J.; Fleischmann, D. Photon-counting CT: Technical principles and clinical prospects. Radiology 2018, 289, 293–312. [Google Scholar] [CrossRef]
- Lippmann, G. Epreuves reversibles donnant la sensation du relief. J. Phys. Theor. Appl. 1908, 7, 821–825. [Google Scholar] [CrossRef]
- Cho, M.; Daneshpanah, M.; Moon, I.; Javidi, B. Three-dimensional optical sensing and visualization using integral imaging. Proc. IEEE 2010, 99, 556–575. [Google Scholar]
- Park, J.H.; Hong, K.; Lee, B. Recent progress in three-dimensional information processing based on integral imaging. Appl. Opt. 2009, 48, H77–H94. [Google Scholar] [CrossRef]
- Xiao, X.; Javidi, B.; Martinez-Corral, M.; Stern, A. Advances in three-dimensional integral imaging: Sensing, display, and applications. Appl. Opt. 2013, 52, 546–560. [Google Scholar] [CrossRef]
- Jang, J.S.; Javidi, B. Three-dimensional synthetic aperture integral imaging. Opt. Lett. 2002, 27, 1144–1146. [Google Scholar] [CrossRef]
- Piao, Y.; Xing, L.; Zhang, M.; Lee, B.G. Three-dimensional reconstruction of far and large objects using synthetic aperture integral imaging. Opt. Lasers Eng. 2017, 88, 153–161. [Google Scholar] [CrossRef]
- Hong, S.H.; Jang, J.S.; Javidi, B. Three-dimensional volumetric object reconstruction using computational integral imaging. Opt. Express 2004, 12, 483–491. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.H.; Javidi, B. Three-dimensional visualization of partially occluded objects using integral imaging. J. Disp. Technol. 2005, 1, 354. [Google Scholar] [CrossRef]
- Cho, B.; Kopycki, P.; Martinez-Corral, M.; Cho, M. Computational volumetric reconstruction of integral imaging with improved depth resolution considering continuously non-uniform shifting pixels. Opt. Lasers Eng. 2018, 111, 114–121. [Google Scholar] [CrossRef]
- Yeom, S.; Javidi, B.; Watson, E. Three-dimensional distortion-tolerant object recognition using photon-counting integral imaging. Opt. Express 2007, 15, 1513–1533. [Google Scholar] [CrossRef]
- Yeom, S.; Javidi, B.; Watson, E. Photon counting passive 3D image sensing for automatic target recognition. Opt. Express 2005, 13, 9310–9330. [Google Scholar] [CrossRef]
- Tavakoli, B.; Javidi, B.; Watson, E. Three dimensional visualization by photon counting computational integral imaging. Opt. Express 2008, 16, 4426–4436. [Google Scholar] [CrossRef]
- Kim, H.W.; Cho, M.; Lee, M.C. Three-Dimensional (3D) Visualization under Extremely Low Light Conditions Using Kalman Filter. Sensors 2023, 23, 7571. [Google Scholar] [CrossRef]
- Xiao, X.; Javidi, B. 3D photon counting integral imaging with unknown sensor positions. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2012, 29, 767–771. [Google Scholar] [CrossRef]
- Myung, I.J. Tutorial on maximum likelihood estimation. J. Math. Psychol. 2003, 47, 90–100. [Google Scholar] [CrossRef]
- Guillaume, M.; Melon, P.; Réfrégier, P.; Llebaria, A. Maximum-likelihood estimation of an astronomical image from a sequence at low photon levels. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 1998, 15, 2841–2848. [Google Scholar] [CrossRef]
- Lantz, E.; Blanchet, J.L.; Furfaro, L.; Devaux, F. Multi-imaging and Bayesian estimation for photon counting with EMCCDs. Mon. Not. R. Astron. Soc. 2008, 386, 2262–2270. [Google Scholar] [CrossRef]
- Bassett, R.; Deride, J. Maximum a posteriori estimators as a limit of Bayes estimators. Math. Program 2019, 174, 129–144. [Google Scholar] [CrossRef]
- Ha, J.U.; Kim, H.W.; Cho, M.; Lee, M.C. A Method for Visualization of Images by Photon-Counting Imaging Only Object Locations under Photon-Starved Conditions. Electronics 2023, 13, 38. [Google Scholar] [CrossRef]
- Yoo, J.C.; Han, T.H. Fast normalized cross-correlation. CSSP 2009, 28, 819–843. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 4th ed.; Pearson: New York, NY, USA, 2018. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]













| Setup | Nikon D850 | |
|---|---|---|
| Resolution | 4128 × 2752 | |
| Camera array | 5 × 5 | |
| Pitch | 2 mm | |
| Sensor size | 35.9 × 23.9 mm | |
| Kernel size | 500 × 500 | |
| Focal length | 50 mm | |
| ISO | 400 | |
| Shutter speed | Normal | 1.6 s |
| Extremely low-light | 1/5 s | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ha, J.-U.; Kim, H.-W.; Cho, M.; Lee, M.-C. Three-Dimensional Visualization Using Proportional Photon Estimation Under Photon-Starved Conditions. Sensors 2025, 25, 893. https://doi.org/10.3390/s25030893
Ha J-U, Kim H-W, Cho M, Lee M-C. Three-Dimensional Visualization Using Proportional Photon Estimation Under Photon-Starved Conditions. Sensors. 2025; 25(3):893. https://doi.org/10.3390/s25030893
Chicago/Turabian StyleHa, Jin-Ung, Hyun-Woo Kim, Myungjin Cho, and Min-Chul Lee. 2025. "Three-Dimensional Visualization Using Proportional Photon Estimation Under Photon-Starved Conditions" Sensors 25, no. 3: 893. https://doi.org/10.3390/s25030893
APA StyleHa, J.-U., Kim, H.-W., Cho, M., & Lee, M.-C. (2025). Three-Dimensional Visualization Using Proportional Photon Estimation Under Photon-Starved Conditions. Sensors, 25(3), 893. https://doi.org/10.3390/s25030893






