Impact of Running Clothes on Accuracy of Smartphone-Based 2D Joint Kinematic Assessment During Treadmill Running Using OpenPifPaf
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
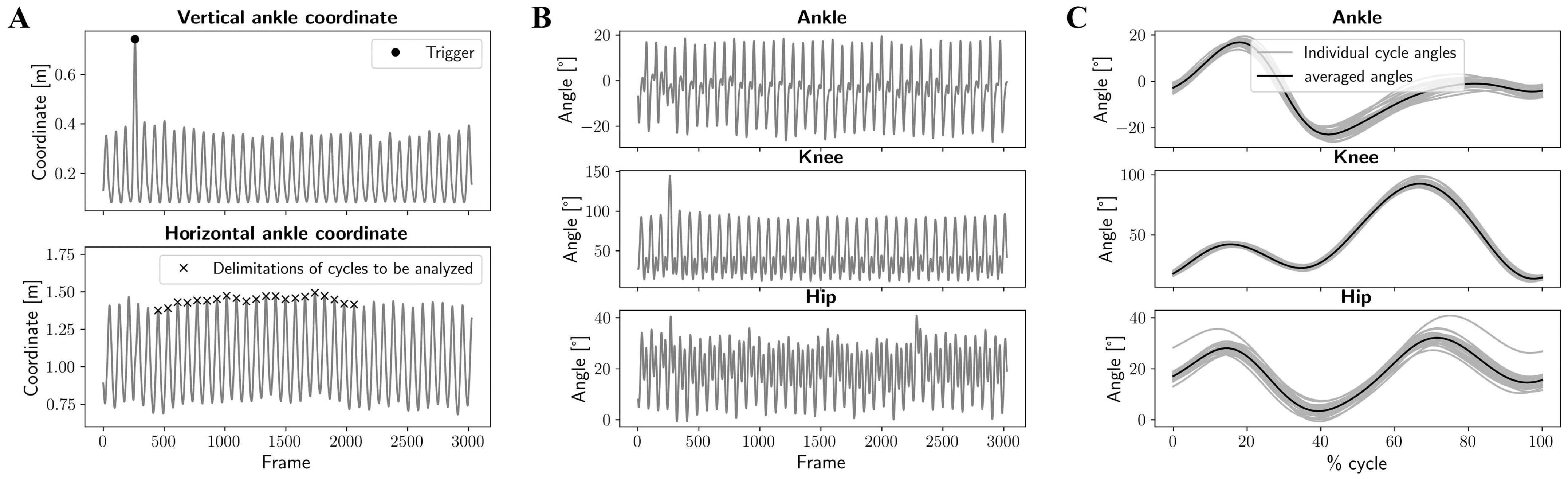
2.2. Procedure
2.3. Data Processing
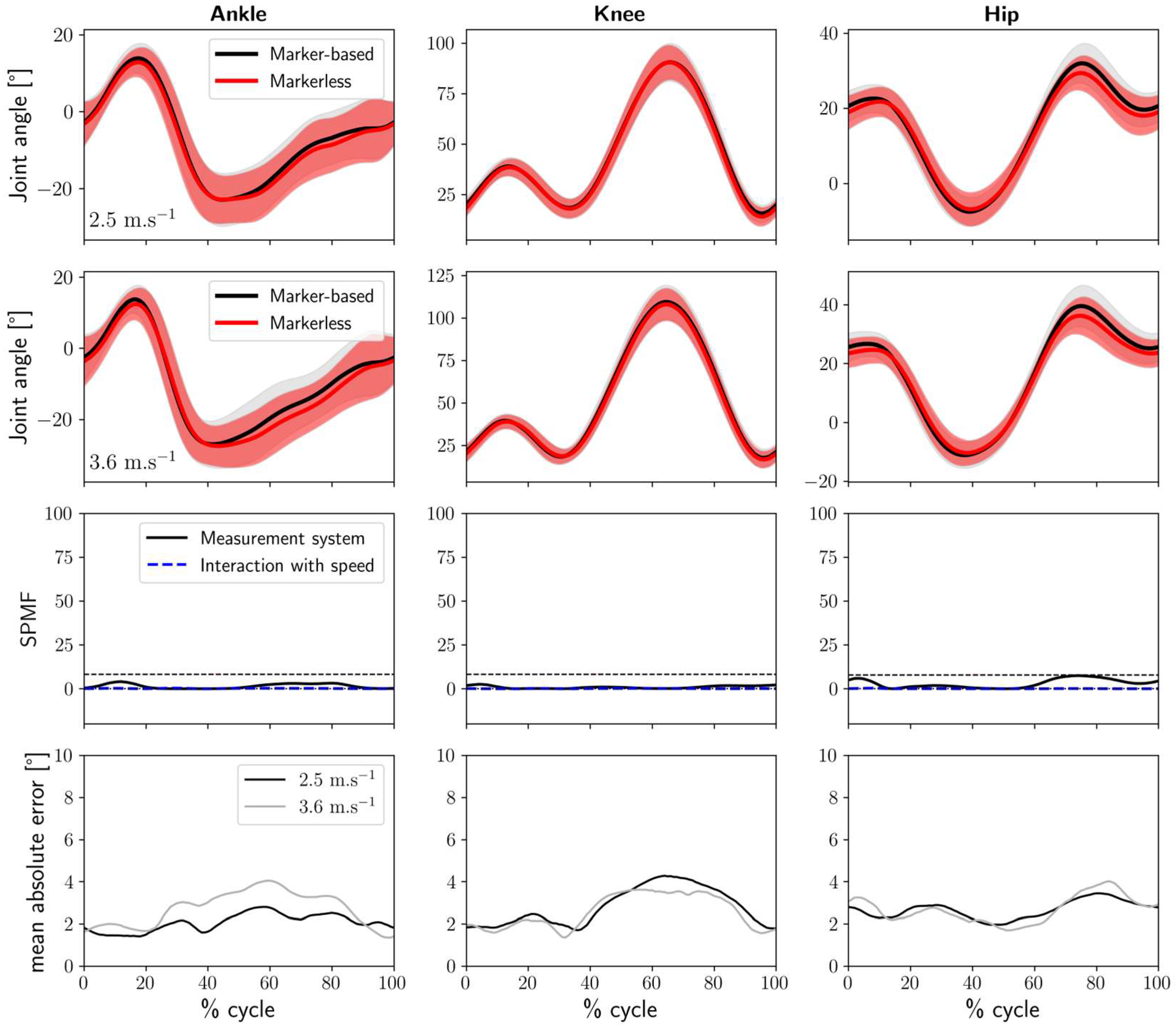
2.4. Statistical Analysis
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, D.; Brellenthin, A.G.; Thompson, P.D.; Sui, X.; Lee, I.-M.; Lavie, C.J. Running as a Key Lifestyle Medicine for Longevity. Prog. Cardiovasc. Dis. 2017, 60, 45–55. [Google Scholar] [CrossRef] [PubMed]
- Fredette, A.; Roy, J.-S.; Perreault, K.; Dupuis, F.; Napier, C.; Esculier, J.-F. The Association Between Running Injuries and Training Parameters: A Systematic Review. J. Athl. Train. 2022, 57, 650–671. [Google Scholar] [CrossRef] [PubMed]
- Cavanagh, P.R.; Lafortune, M.A. Ground Reaction Forces in Distance Running. J. Biomech. 1980, 13, 397–406. [Google Scholar] [CrossRef] [PubMed]
- Van Hooren, B.; Goudsmit, J.; Restrepo, J.; Vos, S. Real-Time Feedback by Wearables in Running: Current Approaches, Challenges and Suggestions for Improvements. J. Sports Sci. 2020, 38, 214–230. [Google Scholar] [CrossRef] [PubMed]
- Sanders, T.L.; Maradit Kremers, H.; Bryan, A.J.; Larson, D.R.; Dahm, D.L.; Levy, B.A.; Stuart, M.J.; Krych, A.J. Incidence of Anterior Cruciate Ligament Tears and Reconstruction: A 21-Year Population-Based Study. Am. J. Sports Med. 2016, 44, 1502–1507. [Google Scholar] [CrossRef]
- Kotsifaki, R.; Korakakis, V.; King, E.; Barbosa, O.; Maree, D.; Pantouveris, M.; Bjerregaard, A.; Luomajoki, J.; Wilhelmsen, J.; Whiteley, R. Aspetar Clinical Practice Guideline on Rehabilitation after Anterior Cruciate Ligament Reconstruction. Br. J. Sports Med. 2023, 57, 500–514. [Google Scholar] [CrossRef] [PubMed]
- Rambaud, A.J.M.; Ardern, C.L.; Thoreux, P.; Regnaux, J.-P.; Edouard, P. Criteria for Return to Running after Anterior Cruciate Ligament Reconstruction: A Scoping Review. Br. J. Sports Med. 2018, 52, 1437–1444. [Google Scholar] [CrossRef]
- Pairot-de-Fontenay, B.; Willy, R.W.; Elias, A.R.C.; Mizner, R.L.; Dubé, M.-O.; Roy, J.-S. Running Biomechanics in Individuals with Anterior Cruciate Ligament Reconstruction: A Systematic Review. Sports Med. 2019, 49, 1411–1424. [Google Scholar] [CrossRef] [PubMed]
- Andriacchi, T.P.; Mündermann, A. The Role of Ambulatory Mechanics in the Initiation and Progression of Knee Osteoarthritis. Curr. Opin. Rheumatol. 2006, 18, 514–518. [Google Scholar] [CrossRef]
- Paterno, M.V.; Schmitt, L.C.; Ford, K.R.; Rauh, M.J.; Myer, G.D.; Huang, B.; Hewett, T.E. Biomechanical Measures during Landing and Postural Stability Predict Second Anterior Cruciate Ligament Injury after Anterior Cruciate Ligament Reconstruction and Return to Sport. Am. J. Sports Med. 2010, 38, 1968–1978. [Google Scholar] [CrossRef] [PubMed]
- Sigward, S.M.; Lin, P.; Pratt, K. Knee Loading Asymmetries during Gait and Running in Early Rehabilitation Following Anterior Cruciate Ligament Reconstruction: A Longitudinal Study. Clin. Biomech. 2016, 32, 249–254. [Google Scholar] [CrossRef] [PubMed]
- Ancillao, A.; Tedesco, S.; Barton, J.; O’Flynn, B. Indirect Measurement of Ground Reaction Forces and Moments by Means of Wearable Inertial Sensors: A Systematic Review. Sensors 2018, 18, 2564. [Google Scholar] [CrossRef]
- Benson, L.C.; Räisänen, A.M.; Clermont, C.A.; Ferber, R. Is This the Real Life, or Is This Just Laboratory? A Scoping Review of IMU-Based Running Gait Analysis. Sensors 2022, 22, 1722. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Zhang, Q.; Chai, H.; Li, Y. Obtaining Lower-Body Euler Angle Time Series in an Accurate Way Using Depth Camera Relying on Optimized Kinect CNN. Measurement 2022, 188, 110461. [Google Scholar] [CrossRef]
- Pagnon, D.; Domalain, M.; Reveret, L. Pose2Sim: An End-to-End Workflow for 3D Markerless Sports Kinematics—Part 2: Accuracy. Sensors 2022, 22, 2712. [Google Scholar] [CrossRef] [PubMed]
- Young, F.; Mason, R.; Morris, R.; Stuart, S.; Godfrey, A. Internet-of-Things-Enabled Markerless Running Gait Assessment from a Single Smartphone Camera. Sensors 2023, 23, 696. [Google Scholar] [CrossRef] [PubMed]
- Cronin, N.J. Using Deep Neural Networks for Kinematic Analysis: Challenges and Opportunities. J. Biomech. 2021, 123, 110460. [Google Scholar] [CrossRef] [PubMed]
- Scataglini, S.; Abts, E.; Van Bocxlaer, C.; Van Den Bussche, M.; Meletani, S.; Truijen, S. Accuracy, Validity, and Reliability of Markerless Camera-Based 3D Motion Capture Systems versus Marker-Based 3D Motion Capture Systems in Gait Analysis: A Systematic Review and Meta-Analysis. Sensors 2024, 24, 3686. [Google Scholar] [CrossRef] [PubMed]
- D’Haene, M.; Chorin, F.; Colson, S.S.; Guérin, O.; Zory, R.; Piche, E. Validation of a 3D Markerless Motion Capture Tool Using Multiple Pose and Depth Estimations for Quantitative Gait Analysis. Sensors 2024, 24, 7105. [Google Scholar] [CrossRef]
- Van Hooren, B.; Pecasse, N.; Meijer, K.; Essers, J.M.N. The Accuracy of Markerless Motion Capture Combined with Computer Vision Techniques for Measuring Running Kinematics. Scand. J. Med. Sci. Sports 2023, 33, 966–978. [Google Scholar] [CrossRef] [PubMed]
- Haberkamp, L.D.; Garcia, M.C.; Bazett-Jones, D.M. Validity of an Artificial Intelligence, Human Pose Estimation Model for Measuring Single-Leg Squat Kinematics. J. Biomech. 2022, 144, 111333. [Google Scholar] [CrossRef]
- Cao, Z.; Hidalgo, G.; Simon, T.; Wei, S.-E.; Sheikh, Y. OpenPose: Realtime Multi-Person 2D Pose Estimation Using Part Affinity Fields. arXiv 2019. [Google Scholar] [CrossRef] [PubMed]
- Uhlrich, S.D.; Falisse, A.; Kidziński, Ł.; Muccini, J.; Ko, M.; Chaudhari, A.S.; Hicks, J.L.; Delp, S.L. OpenCap: Human Movement Dynamics from Smartphone Videos. PLoS Comput. Biol. 2023, 19, e1011462. [Google Scholar] [CrossRef]
- Kreiss, S.; Bertoni, L.; Alahi, A. OpenPifPaf: Composite Fields for Semantic Keypoint Detection and Spatio-Temporal Association. arXiv 2021. [Google Scholar] [CrossRef]
- Kreiss, S.; Bertoni, L.; Alahi, A. PifPaf: Composite Fields for Human Pose Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 11969–11978. [Google Scholar]
- Zheng, C.; Wu, W.; Chen, C.; Yang, T.; Zhu, S.; Shen, J.; Kehtarnavaz, N.; Shah, M. Deep Learning-Based Human Pose Estimation: A Survey. ACM Comput. Surv. 2024, 56, 1–37. [Google Scholar] [CrossRef]
- Lambricht, N.; Englebert, A.; Pitance, L.; Fisette, P.; Detrembleur, C. Quantifying Performance and Joint Kinematics in Functional Tasks Crucial for Anterior Cruciate Ligament Rehabilitation Using Smartphone Video and Pose Detection. Knee 2025, 52, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Sarafianos, N.; Boteanu, B.; Ionescu, B.; Kakadiaris, I.A. 3D Human Pose Estimation: A Review of the Literature and Analysis of Covariates. Comput. Vis. Image Underst. 2016, 152, 1–20. [Google Scholar] [CrossRef]
- Horsak, B. Repeatability and Minimal Detectable Change Including Clothing Effects for Smartphone-Based 3D Markerless Motion Capture. J. Biomech. 2024, 175, 112281. [Google Scholar] [CrossRef] [PubMed]
- Kanko, R.M.; Outerleys, J.B.; Laende, E.K.; Selbie, W.S.; Deluzio, K.J. Comparison of Concurrent and Asynchronous Running Kinematics and Kinetics From Marker-Based and Markerless Motion Capture Under Varying Clothing Conditions. J. Appl. Biomech. 2024, 40, 129–137. [Google Scholar] [CrossRef]
- Keller, V.T.; Outerleys, J.B.; Kanko, R.M.; Laende, E.K.; Deluzio, K.J. Clothing Condition Does Not Affect Meaningful Clinical Interpretation in Markerless Motion Capture. J. Biomech. 2022, 141, 111182. [Google Scholar] [CrossRef] [PubMed]
- Davis, R.B.; Õunpuu, S.; Tyburski, D.; Gage, J.R. A Gait Analysis Data Collection and Reduction Technique. Hum. Mov. Sci. 1991, 10, 575–587. [Google Scholar] [CrossRef]
- Pataky, T.C. One-Dimensional Statistical Parametric Mapping in Python. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 295–301. [Google Scholar] [CrossRef]
- Novacheck, T.F. The Biomechanics of Running. Gait Posture 1998, 7, 77–95. [Google Scholar] [CrossRef] [PubMed]
- McGinley, J.L.; Baker, R.; Wolfe, R.; Morris, M.E. The Reliability of Three-Dimensional Kinematic Gait Measurements: A Systematic Review. Gait Posture 2009, 29, 360–369. [Google Scholar] [CrossRef]
- Stenum, J.; Rossi, C.; Roemmich, R.T. Two-Dimensional Video-Based Analysis of Human Gait Using Pose Estimation. PLoS Comput. Biol. 2021, 17, e1008935. [Google Scholar] [CrossRef]
- Horsak, B.; Eichmann, A.; Lauer, K.; Prock, K.; Krondorfer, P.; Siragy, T.; Dumphart, B. Concurrent Validity of Smartphone-Based Markerless Motion Capturing to Quantify Lower-Limb Joint Kinematics in Healthy and Pathological Gait. J. Biomech. 2023, 159, 111801. [Google Scholar] [CrossRef] [PubMed]
- Mathis, A.; Mamidanna, P.; Cury, K.M.; Abe, T.; Murthy, V.N.; Mathis, M.W.; Bethge, M. DeepLabCut: Markerless Pose Estimation of User-Defined Body Parts with Deep Learning. Nat. Neurosci. 2018, 21, 1281–1289. [Google Scholar] [CrossRef] [PubMed]
- Wouda, F.J.; Giuberti, M.; Bellusci, G.; Maartens, E.; Reenalda, J.; Van Beijnum, B.-J.F.; Veltink, P.H. On the Validity of Different Motion Capture Technologies for the Analysis of Running. In Proceedings of the 2018 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob), Enschede, The Netherlands, 26–29 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1175–1180. [Google Scholar]
- Okahisa, T.; Matsuura, T.; Tomonari, K.; Komatsu, K.; Yokoyama, K.; Iwase, J.; Yamada, M.; Sairyo, K. Between-Day Reliability and Minimum Detectable Change of the Conventional Gait Model 2 and Plug-in Gait Model during Running. Gait Posture 2023, 100, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Wilken, J.M.; Rodriguez, K.M.; Brawner, M.; Darter, B.J. Reliability and Minimal Detectible Change Values for Gait Kinematics and Kinetics in Healthy Adults. Gait Posture 2012, 35, 301–307. [Google Scholar] [CrossRef] [PubMed]
- Kadaba, M.P.; Ramakrishnan, H.K.; Wootten, M.E. Measurement of Lower Extremity Kinematics during Level Walking. J. Orthop. Res. 1990, 8, 383–392. [Google Scholar] [CrossRef]
- Mousavi, S.H.; Hijmans, J.M.; Moeini, F.; Rajabi, R.; Ferber, R.; van der Worp, H.; Zwerver, J. Validity and Reliability of a Smartphone Motion Analysis App for Lower Limb Kinematics during Treadmill Running. Phys. Ther. Sport 2020, 43, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Dingenen, B.; Barton, C.; Janssen, T.; Benoit, A.; Malliaras, P. Test-Retest Reliability of Two-Dimensional Video Analysis during Running. Phys. Ther. Sport 2018, 33, 40–47. [Google Scholar] [CrossRef]
- Bramah, C.; Preece, S.J.; Gill, N.; Herrington, L. The Between-Day Repeatability, Standard Error of Measurement and Minimal Detectable Change for Discrete Kinematic Parameters during Treadmill Running. Gait Posture 2021, 85, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Della Croce, U.; Leardini, A.; Chiari, L.; Cappozzo, A. Human Movement Analysis Using Stereophotogrammetry. Part 4: Assessment of anatomical landmark misplacement and its effects on joint kinematics. Gait Posture 2005, 21, 226–237. [Google Scholar] [CrossRef] [PubMed]
- Leardini, A.; Chiari, L.; Croce, U.D.; Cappozzo, A. Human Movement Analysis Using Stereophotogrammetry. Part 3. Soft tissue artifact assessment and compensation. Gait Posture 2005, 21, 212–225. [Google Scholar] [CrossRef] [PubMed]


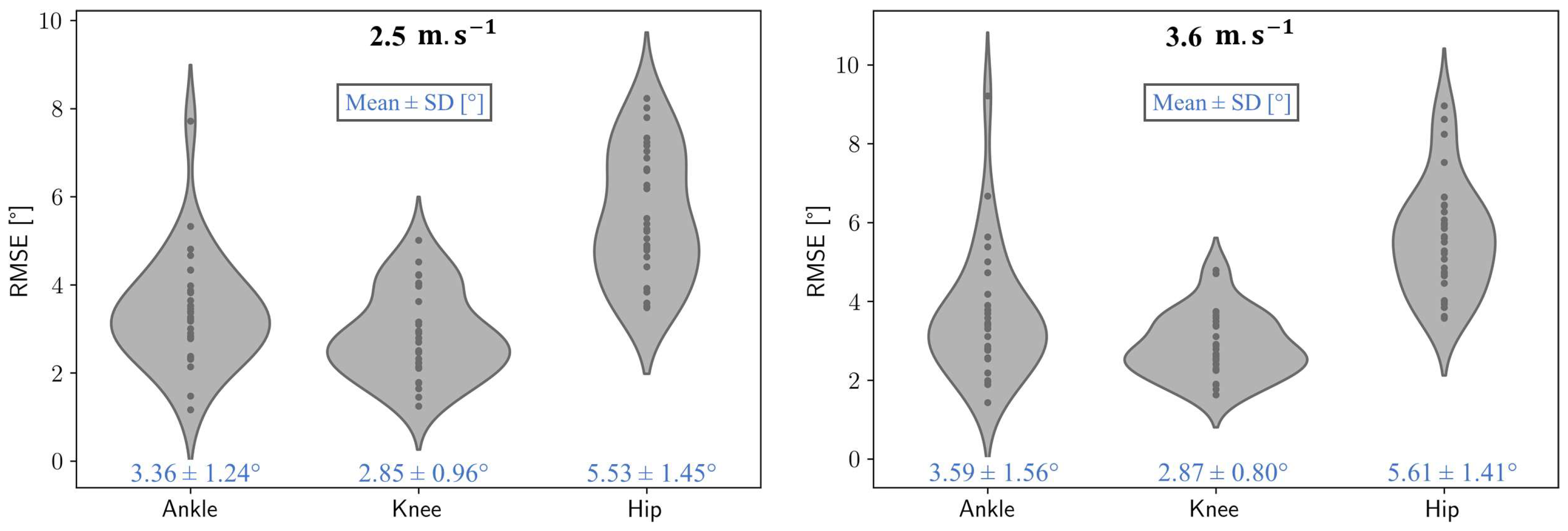
| Speed | 2.5 m.s−1 | 3.6 m.s−1 |
|---|---|---|
| Marker-based vs. markerless in Lab clothing condition | ||
| Ankle | 3.36 ± 1.24° | 3.59 ± 1.56° |
| Knee | 2.85 ± 0.96° | 2.87 ± 0.80° |
| Hip | 5.53 ± 1.45° | 5.61 ± 1.41° |
| Markerless in Lab clothing vs. Running clothes conditions | ||
| Ankle | 2.06 ± 0.88° | 2.72 ± 1.81° |
| Knee | 2.80 ± 1.75° | 2.58 ± 1.42° |
| Hip | 2.66 ± 1.35° | 2.68 ± 1.27° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lambricht, N.; Englebert, A.; Nguyen, A.P.; Fisette, P.; Pitance, L.; Detrembleur, C. Impact of Running Clothes on Accuracy of Smartphone-Based 2D Joint Kinematic Assessment During Treadmill Running Using OpenPifPaf. Sensors 2025, 25, 934. https://doi.org/10.3390/s25030934
Lambricht N, Englebert A, Nguyen AP, Fisette P, Pitance L, Detrembleur C. Impact of Running Clothes on Accuracy of Smartphone-Based 2D Joint Kinematic Assessment During Treadmill Running Using OpenPifPaf. Sensors. 2025; 25(3):934. https://doi.org/10.3390/s25030934
Chicago/Turabian StyleLambricht, Nicolas, Alexandre Englebert, Anh Phong Nguyen, Paul Fisette, Laurent Pitance, and Christine Detrembleur. 2025. "Impact of Running Clothes on Accuracy of Smartphone-Based 2D Joint Kinematic Assessment During Treadmill Running Using OpenPifPaf" Sensors 25, no. 3: 934. https://doi.org/10.3390/s25030934
APA StyleLambricht, N., Englebert, A., Nguyen, A. P., Fisette, P., Pitance, L., & Detrembleur, C. (2025). Impact of Running Clothes on Accuracy of Smartphone-Based 2D Joint Kinematic Assessment During Treadmill Running Using OpenPifPaf. Sensors, 25(3), 934. https://doi.org/10.3390/s25030934







