Shake Table Tests on Scaled Masonry Building: Comparison of Performance of Various Micro-Electromechanical System Accelerometers (MEMS) for Structural Health Monitoring
Abstract
:1. Introduction
2. Materials and Methods
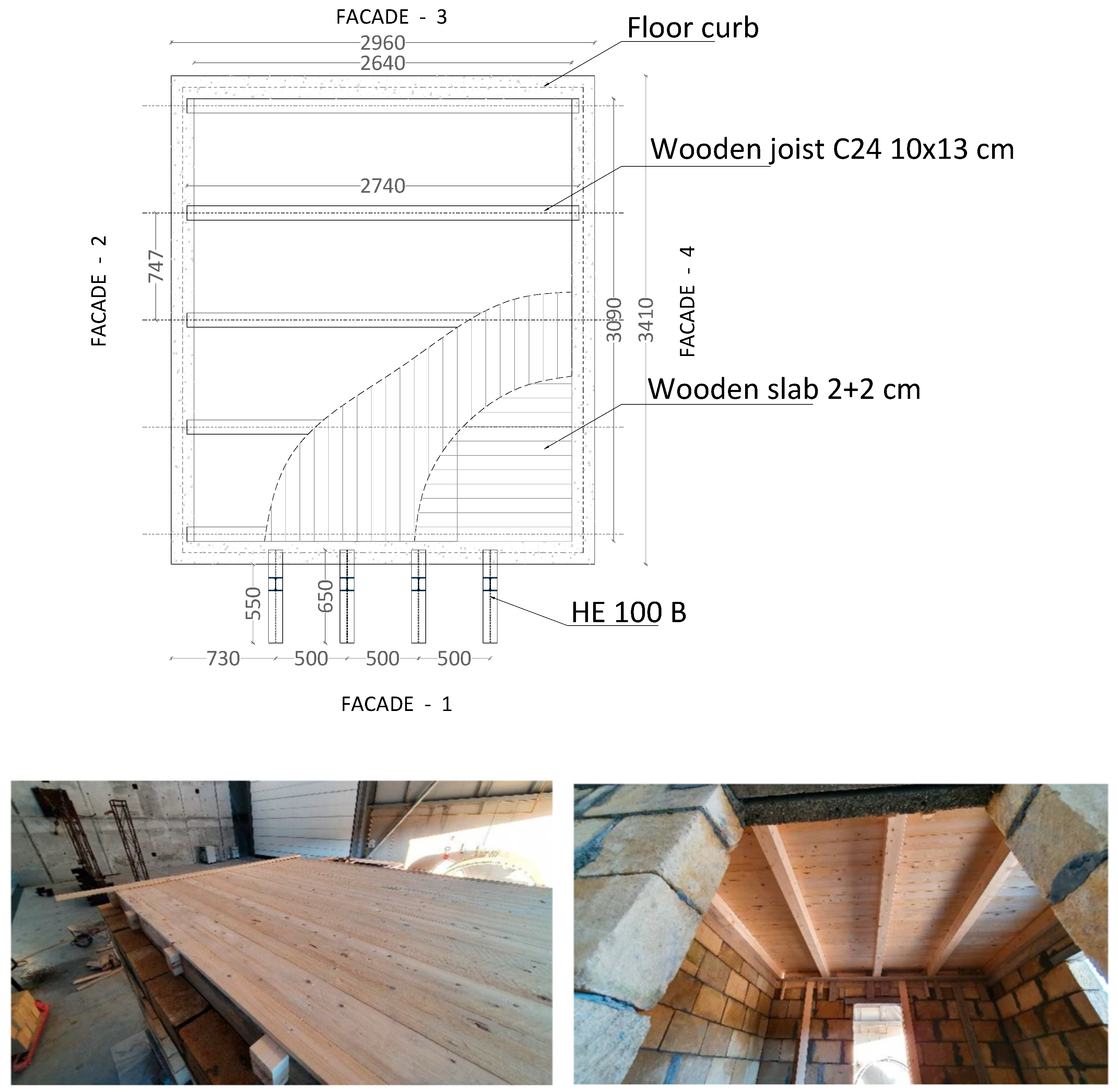
2.1. Building Characteristics
2.2. Test Facility
2.3. Instrumentation
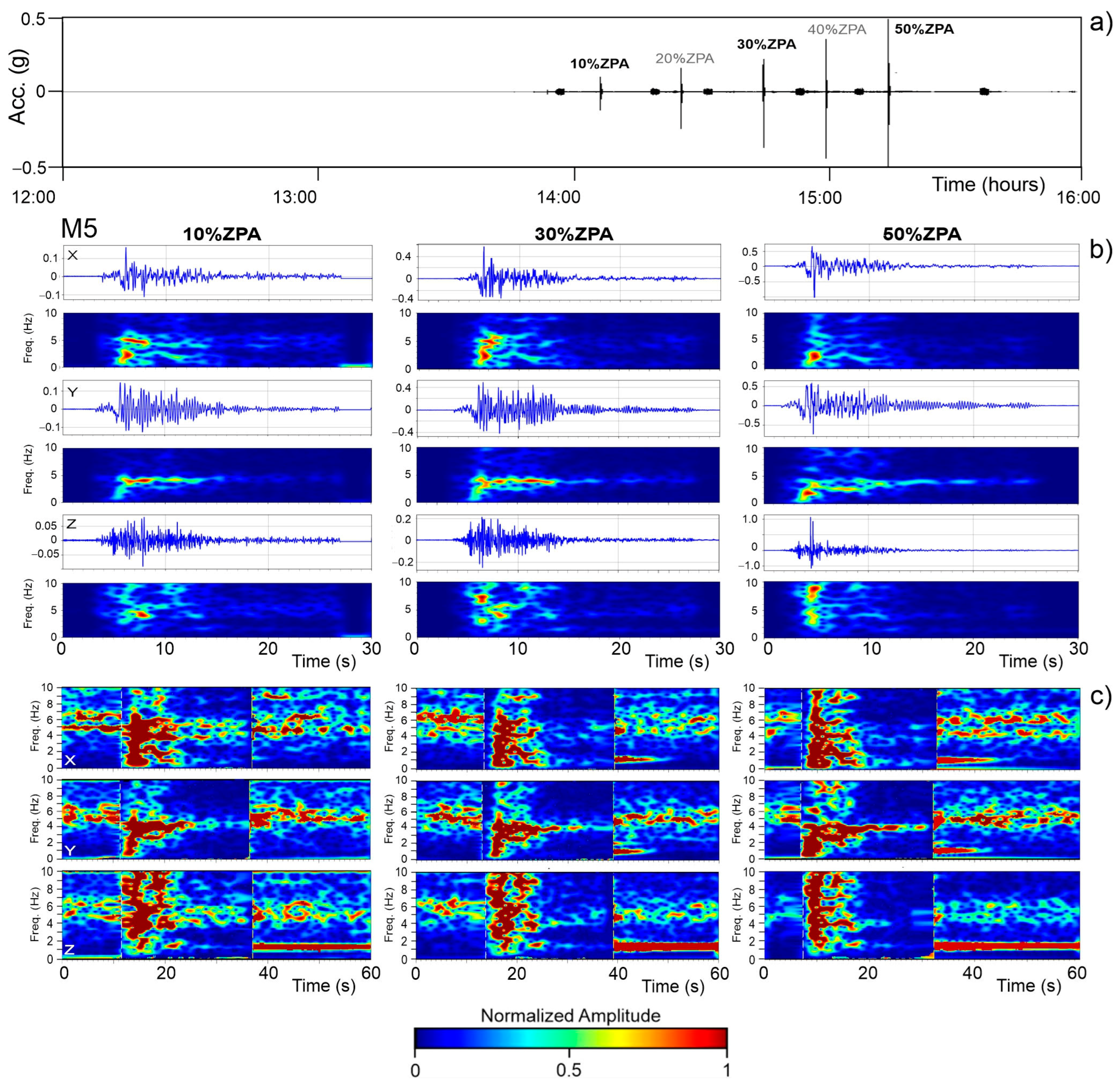
2.4. Test Sequence
- Environmental noise when the shaking table was not operating.
- Three-direction broadband noise excitation by reproducing on the shaking table a three-component, uncorrelated Gaussian random noise in frequency ranges from 0.25 Hz to 60 Hz, with an RMS amplitude equal to 0.03 g.
3. Results
3.1. Analysis of Horizontal-to-Vertical Spectral Ratio (HVSR) of Ambient Noise
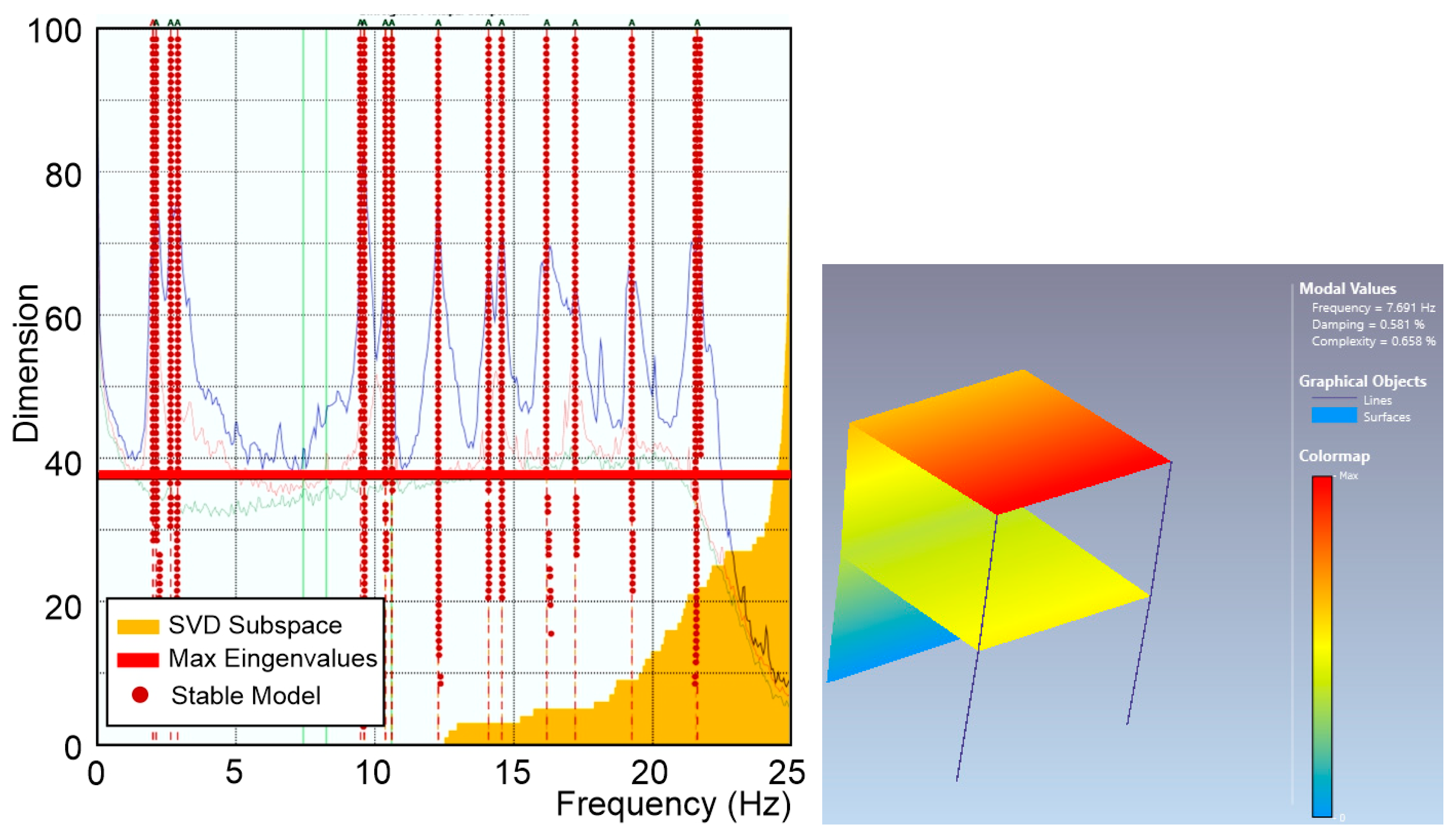
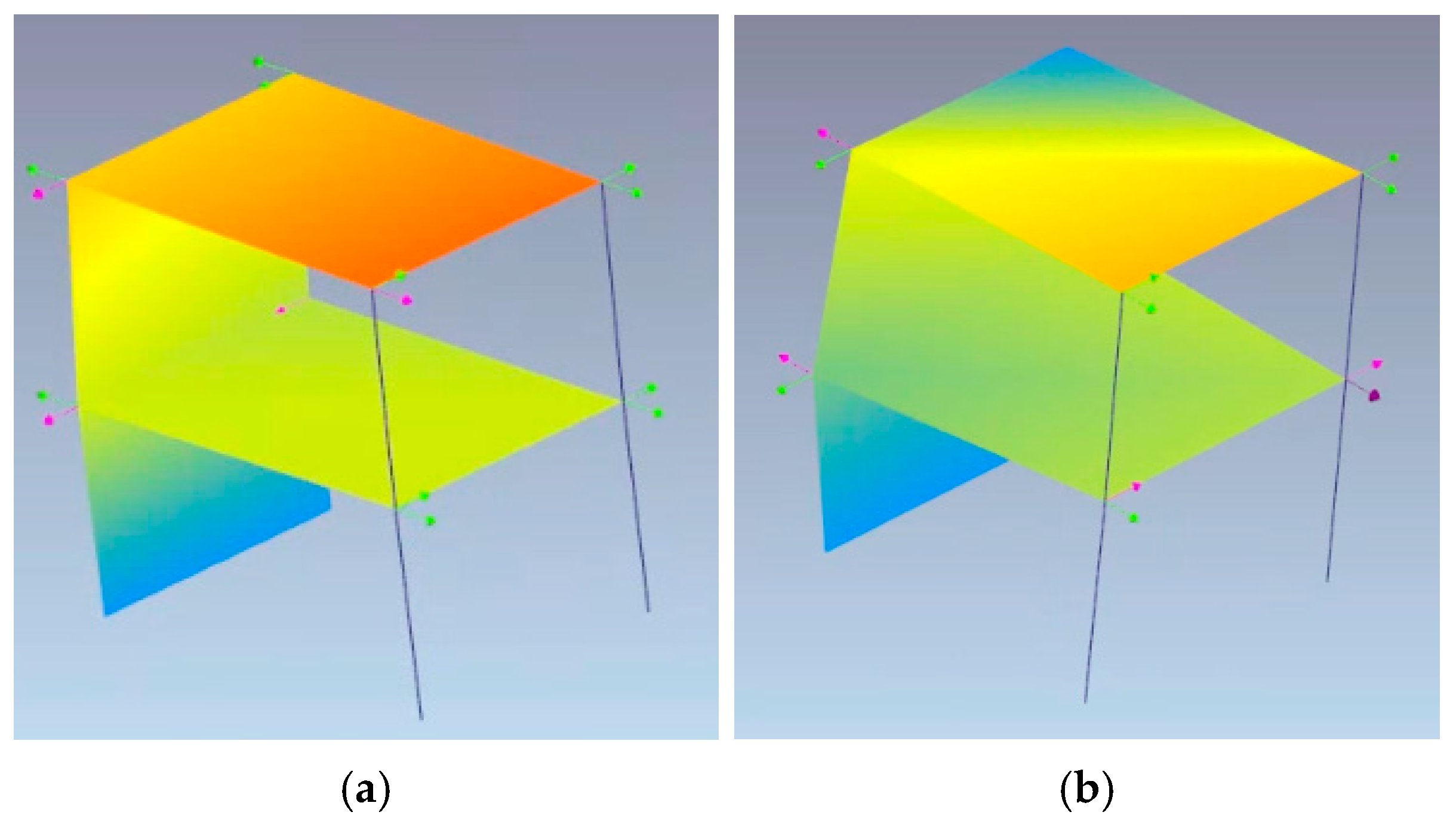
3.2. Structural Dynamic Behaviour
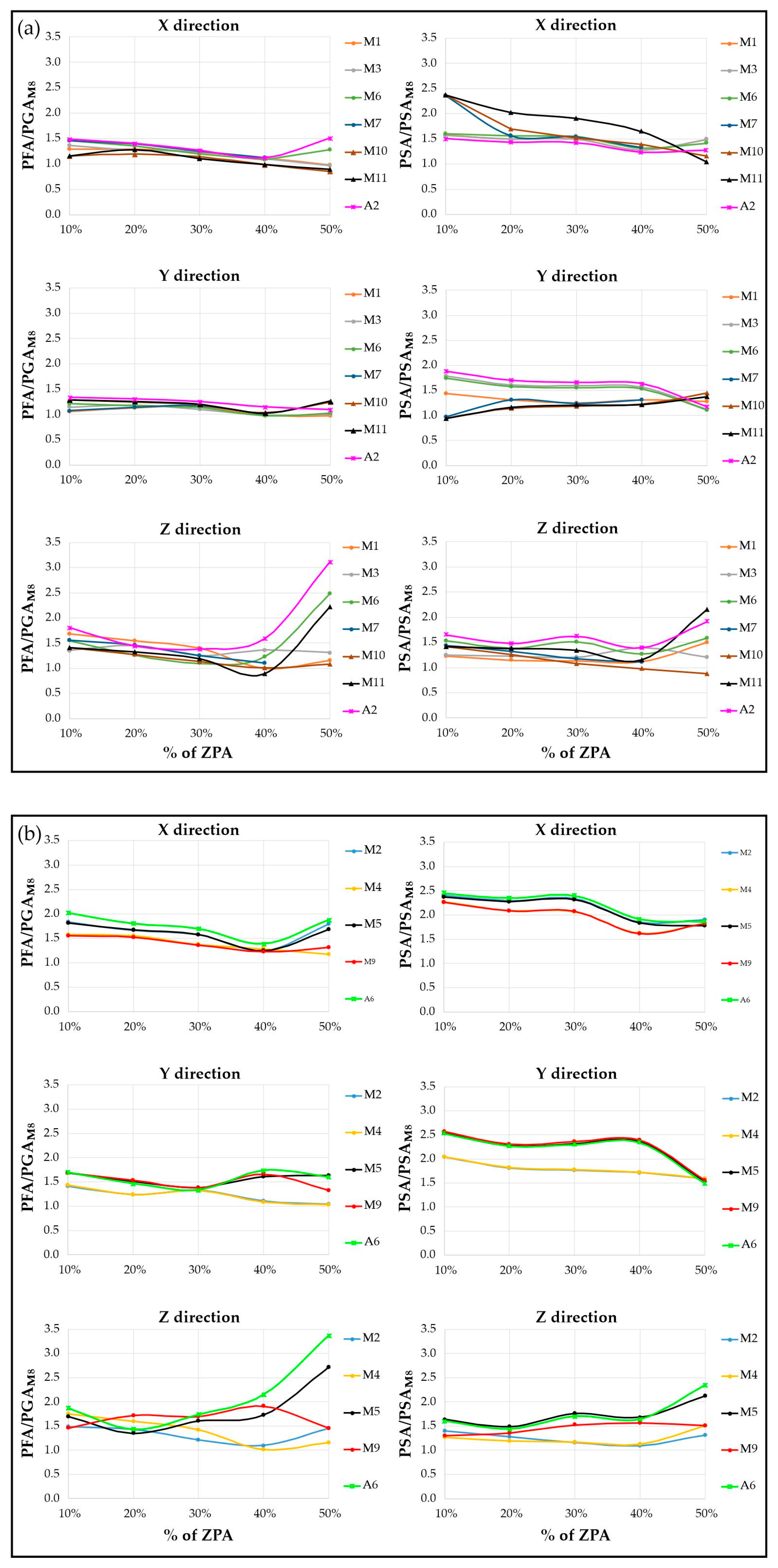
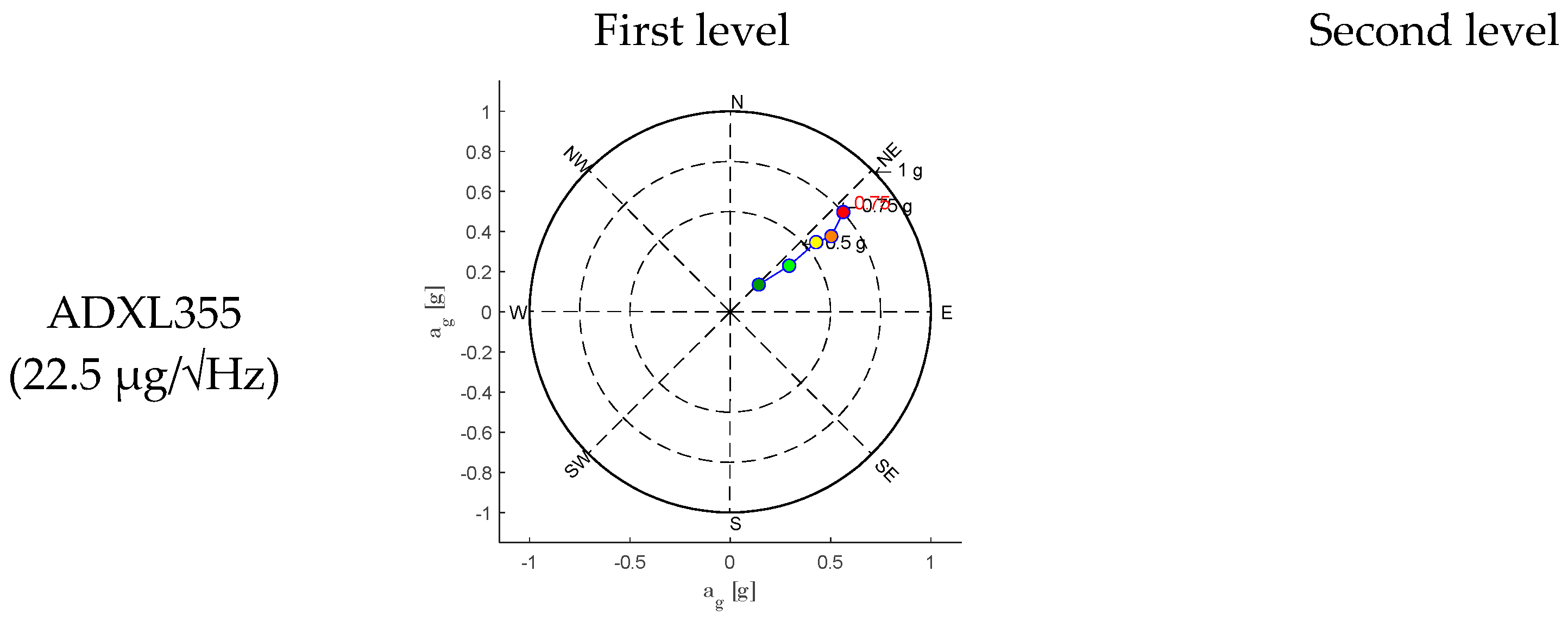
3.3. Strong Motion Parameters
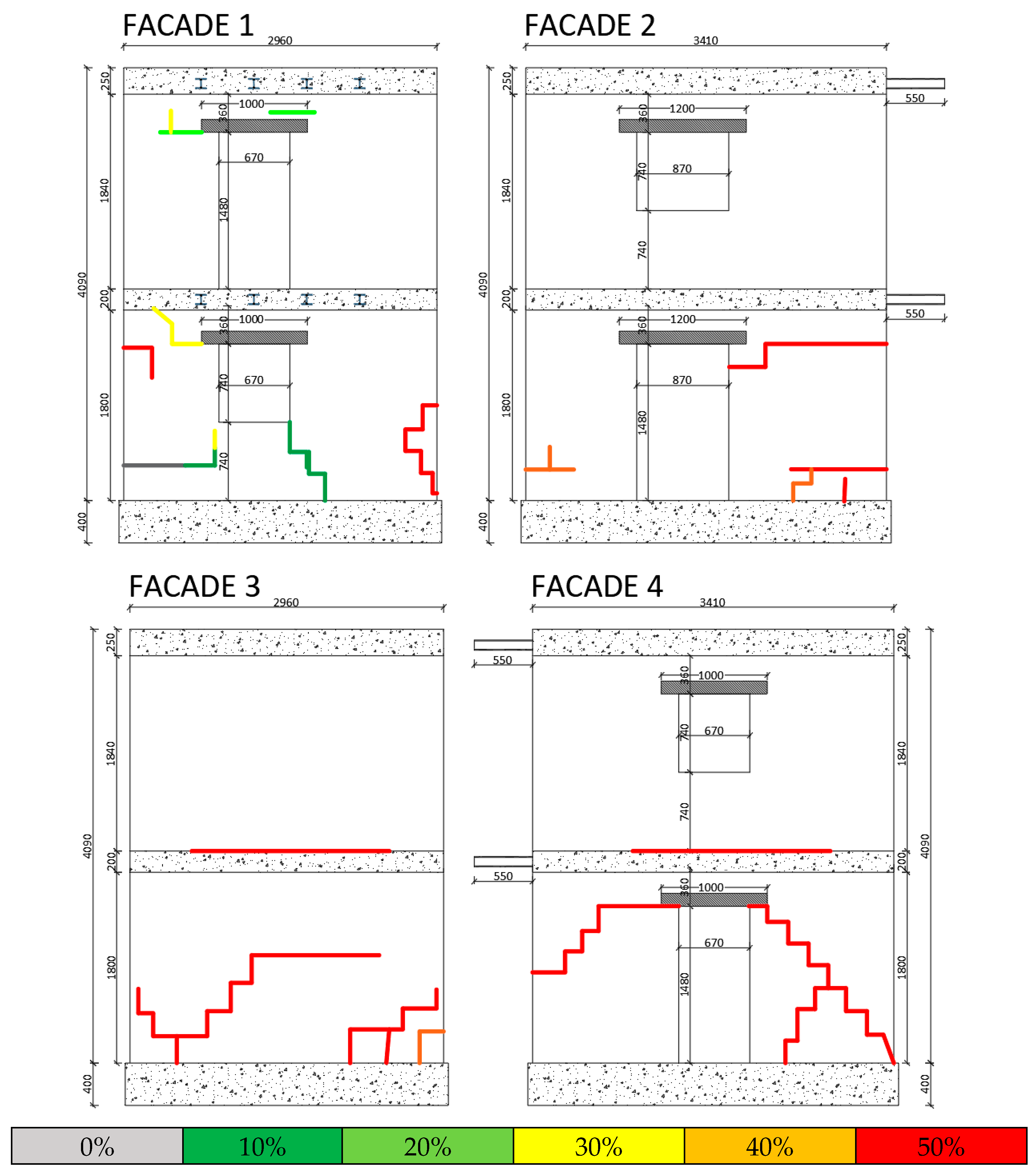
3.4. Damage Distribution
4. Conclusions
- All the MEMS sensors used during the experiment demonstrated their ability to accurately measure the dynamic response during seismic excitation. Instead, their suitability for Operational Modal Analysis (OMA) under noisy conditions, such as during the experiment, varies significantly due to their self-noise characteristics.
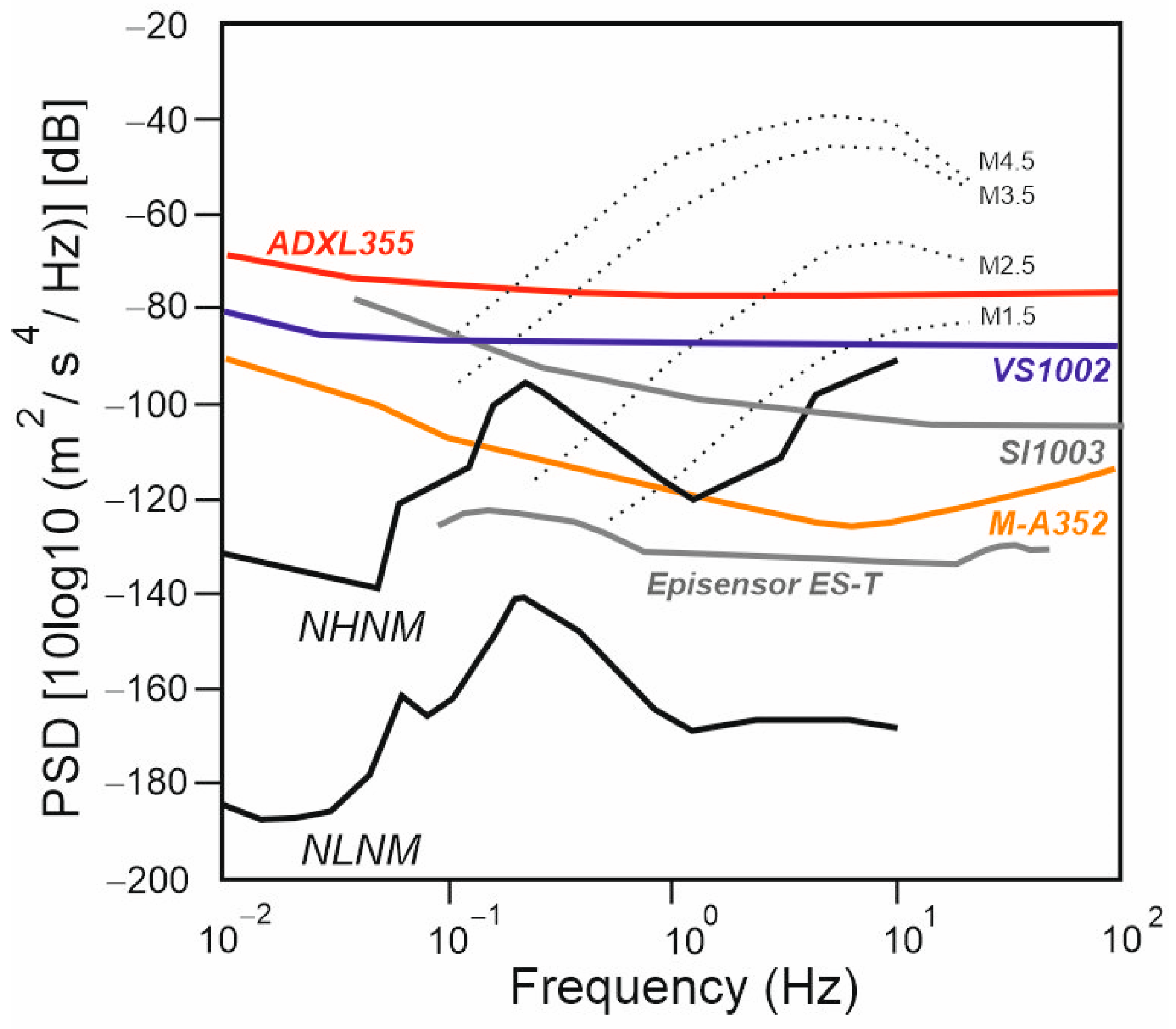
- Overall, also for the piezoelectric sensors, the self-noise could become a crucial factor in very-low-ambient-noise environments and for OMA applications, affecting the quality of the results. Therefore, we retain that both piezoelectric and MEMS (micro-electromechanical systems) accelerometers with self-noise levels below 1 µg/√Hz—or preferably below 0.5 µg/√Hz—are recommended for effective OMA in environments with very low noise. In general, ultra-low sensor self-noise minimizes the interference from environmental noise, allowing for the more precise identification of modal frequencies and damage detection.
- For MEMS sensors with self-noise greater than 1 µg/√Hz, their performance, as mentioned above, in very-low-noise conditions may be significantly compromised and mask the acceleration signal. Additionally, other noise sources like wiring and electronic components can further degrade the measurement quality. However, in SHM applications in environments with high noise levels, such as busy bridges, footbridges, or civil structures exposed to strong winds, these sensors may still provide adequate performance.
- The OMA identified a frequency decrement during the tests. The extensive OMA campaign and the comparison between several sensors confirmed the necessity to engage sensors with a low (or ultra-low) noise density if the frequency identification is needed, both before and after a seismic event for real applications. A suggested value of less than 1 µg/√Hz—or preferably below 0.5 µg/√Hz—may be appropriate for the analysis of stiff masonry structures. This aspect is crucial if a reliable estimation of damage has to be carried out after an event under ambient noise conditions.
- The results obtained from the Stockwell transform are coherent with the expected dynamic behaviour of the structure and the impact of seismic loading. Indeed, a shift in lateral modes to lower frequencies can indicate reduced stiffness in the horizontal direction, whereas increased energy at higher frequencies in the Z component could be attributed to vertical accelerations and structural rigidity in the vertical direction. It also indicates localized damage affecting the sensor’s response to seismic inputs, as higher frequencies are generated by local and global rocking of the masonry structure.
- The acceleration response maintains the same proportion among the components for the first, second, and third loading steps. This aspect can be interpreted as an elastic response condition of the structure under incremental loads. From this step onwards, and more evidently in the subsequent step, the maximum recorded acceleration shows significant variations in orientation. This phenomenon may be related to the disassembly of the masonry structure due to damage. This is consistent with the conditions observed during the experimental test, where cracking patterns emerged from the fourth loading step. The crack pattern survey, conducted after each experimental test and reported in Figure 16, illustrates that at the fourth step (40% of the load), large cracks corresponding to the vertical alignment of station M5 are evident. In the subsequent step (50%), a widespread crack pattern significantly affects the in-plane resistance of the panel and, in general, the masonry piers. This results in higher out-of-plane accelerations.
- It is evident that the amplification of motion with respect to the ground decreases as the intensity of the seismic input increases, suggesting a progressive change in the structure’s damping behaviour. The height and sharpness of the peaks in the normalized response spectra decrease, suggesting a change in the structure’s ability to dissipate seismic energy, potentially indicating higher damping.
- The eccentricity between mass and stiffness centres due to the presence of solid walls (facade 3) led to an unequally distributed damage pattern. This response closely mirrors real cases, where structural irregularities lead to the damage of the structural elements with different mechanisms. As a result, the shear and flexural failures of the masonry walls define the damage at 50% of the target input level. The damage significantly affected the specimen’s dynamic behaviour, as identified by most of the sensors. It is worth noting that some differences have been identified in the acceleration peaks captured by each sensor type.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Clementi, F.; Formisano, A.; Milani, G.; Ubertini, F. Structural Health Monitoring of Architectural Heritage: From the past to the Future Advances. Int. J. Arch. Herit. 2021, 15, 1–4. [Google Scholar] [CrossRef]
- Patanè, D.; Yang, W.; Occhipinti, G.; Cannizzaro, F.; Oriti, C.; Caliò, I. MonVia Project, development and application of a new sensor box. In Proceedings of the 10th International Operational Modal Analysis Conference (IOMAC 2024), Naples, Italy, 21–24 May 2024. [Google Scholar]
- Farrar, C.R.; Worden, K. Structural Health Monitoring—A Machine Learning Perspective; John Wiley & Sons, Ltd.: Oxford, UK, 2013. [Google Scholar]
- Iacono, F.L.; Navarra, G.; Oliva, M. Structural monitoring of “Himera” viaduct by low-cost MEMS sensors: Characterization and preliminary results. Meccanica 2017, 52, 3221–3236. [Google Scholar] [CrossRef]
- Rainieri, C.; Fabbrocino, G. Operational Modal Analysis of Civil Engineering Structures—An Introduction and Guide for Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Friswell, M.I.; Mottershead, J.E. Finite Element Model Updating in Structural Dynamics; Springer Science & Business Media: New York, NY, USA, 1995. [Google Scholar]
- Iacono, F.L.; Navarra, G.; Orlando, C.; Ricciardello, A. Continuous particle swarm optimization for model updating of structures from experimental modal analysis. Mater. Res. Proc. 2023, 26, 467–472. [Google Scholar]
- Liu, H.-F.; Luo, Z.-C.; Hu, Z.-K.; Yang, S.-Q.; Tu, L.-C.; Zhou, Z.-B.; Kraft, M. A review of high-performance MEMS sensors for resource exploration and geophysical applications. Pet. Sci. 2022, 19, 2631–2648. [Google Scholar] [CrossRef]
- Zhu, L.; Fu, Y.; Chow, R.; Spencer, B.F.; Park, J.W.; Mechitov, K. Development of a High-Sensitivity Wireless Accelerometer for Structural Health Monitoring. Sensors 2018, 18, 262. [Google Scholar] [CrossRef] [PubMed]
- Fertitta, G.; Yang, W.; Costanza, A.; Martino, C.; Macaluso, F.; Patanè, D. Design and test of a Smart Sensor Box for structural and seismological monitoring with a high-performance QMEMS accelerometer. In Proceedings of the 2024 IEEE International Workshop on Metrology for Industry 4.0 & IoT (MetroInd4.0 & IoT), Florence, Italy, 29–31 May 2024. [Google Scholar]
- Ribeiro, R.R.; Lameiras, R. Evaluation of low-cost MEMS accelerometers for SHM: Frequency anddamping identification of civil structures. Lat. Am. J. Solids Struct. 2019, 16, e203. [Google Scholar] [CrossRef]
- Longo, S. Analisi Dimensionale e Modellistica Fisica. Principi e Applicazioni Alle Scienze Ingegneristiche; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Fossetti, M.; Iacono, F.L.; Minafò, G.; Navarra, G.; Tesoriere, G. A new large scale laboratory: The LEDA research centre (Laboratory of Earthquake engineering and Dynamic Analysis). In Proceedings of the International Conference on Advances in Experimental Structural Engineering (AESE 2017), Pavia, Italy, 6–8 September 2017. [Google Scholar]
- Lo Iacono, F.; Navarra, G.; Oliva, M.; Cascone, D. Experimental investigation of the dynamic performances of the LEDA shaking tables system. In Proceedings of the AIMETA 2017—Proceedings of the 23rd Conference of the Italian Association of Theo-retical, Salerno, Italy, 4–7 September 2017. [Google Scholar]
- Barone, G.; Iacono, F.L.; Navarra, G.; Palmeri, A. A novel analytical model of power spectral density function coherent with earthquake response spectra. In Proceedings of the UNCECOMP 2015—1st ECCOMAS Thematic Conference on Uncertainty Quantification in Computational Sciences and Engineering, Hersonissos, Crete, Greece, 25–27 May 2015. [Google Scholar]
- Cacciola, P. A stochastic approach for generating spectrum compatible fully nonstationary earthquakes. Comput. Struct. 2010, 88, 889–901. [Google Scholar] [CrossRef]
- Unruh, J.F.; Kana, D.D. An iterative procedure for the generation of consistent power/response spectrum. Nucl. Eng. Des. 1981, 66, 427–435. [Google Scholar] [CrossRef]
- UNI ENV 1998: 2005; Eurocode 8: Design of Structures for Earthquake Resistance Part 1: General Rules, Seismic Actions and Rules for Buildings. CEN Central Secretariat Brussels: Belgium, Germany, 2005.
- Pentaris, F.P. A novel horizontal to vertical spectral ratio approach in a wired structural health monitoring system. J. Sensors Sens. Syst. 2014, 3, 145–165. [Google Scholar] [CrossRef]
- Moisidi, M.; Vallianatos, F.; Gallipoli, M.R. Assessing the Main Frequencies of Modern and Historical Buildings Using Ambient Noise Recordings: Case Studies in the Historical Cities of Crete (Greece). Heritage 2018, 1, 171–188. [Google Scholar] [CrossRef]
- Wathelet, M.; Chatelain, J.-L.; Cornou, C.; Di Giulio, G.; Guillier, B.; Ohrnberger, M.; Savvaidis, A. Geopsy: A User-Friendly Open-Source Tool Set for Ambient Vibration Processing. Seism. Res. Lett. 2020, 91, 1878–1889. [Google Scholar] [CrossRef]
- Alguhane, T.M.; Fayed, M.N.; Hussin, A.; Ismail, A.M. Simplified Equations for Estimating the Period of Vibration of Ksa Existing Building Using Ambient vibration testing. J. Multidiscip. Eng. Sci. Technol. 2016, 3, 4335–4343. [Google Scholar]
- NTC18. NTC Normativa Tecnica Per le Costruzionii-DM 14 Gennaio 2018; Ministero Delle Infrastrutture e dei Trasporti: Rome, Italy, 2018. [Google Scholar]
- American Society of Civil Engineers Standard Committee. ASCE/SEI 7-05; Minimum Design Loads for Buildings and Other Structures; American Society of Civil Engineers: Reston, VA, USA, 2005. [Google Scholar]
- Van Overschee, P.; de Moor, B. Subspace Identification for Linear Systems—Theory, Implementation, Applications; Kluwer Academic Publishers: Dordrecht, The Netherland, 1996. [Google Scholar]
- SVIBS. ARTeMIS Modal Help V3; SVIBS: Aalborg, Denmark.
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: The S transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Pianese, G.; Petrovic, B.; Parolai, S.; Paolucci, R. Identification of the nonlinear seismic response of buildings by a combined Stockwell Transform and deconvolution interferometry approach. Bull. Earthq. Eng. 2018, 16, 3103–3126. [Google Scholar] [CrossRef]
- Ditommaso, R.; Iacovino, C.; Auletta, G.; Parolai, S.; Ponzo, F.C. Damage Detection and Localization on Real Structures Subjected to Strong Motion Earthquakes Using the Curvature Evolution Method: The Navelli (Italy) Case Study. Appl. Sci. 2021, 11, 6496. [Google Scholar] [CrossRef]











| Masses | Floor 1 [kg] | Floor 2 [kg] | Balconies [kg] |
|---|---|---|---|
| G1 prototype | 10,659 | 7223 | 65 |
| G1 model | 7106 | 4815 | 43 |
| Additional mass G1 | 3553 | 2408 | 22 |
| (G2 + Ψ2Q) × A | 1192 | 746 | 191 |
| Total additional mass | 4745 | 3154 | 213 |
| Actual additional mass | 4809 | 3150 | 221 |
| System Characteristics | Single Tables (Each) | Connected Tables |
|---|---|---|
| Dimensions | 4 m × 4 m | 10 m × 4 m |
| Nominal maximum payload | 60 t | 100 t |
| Frequency range | 0.01 ÷ 60 Hz | 0.01 ÷ 60 Hz |
| Max displacement | X and Y: ±0.4 m, Z: ±0.25 m | X and Y: ±0.4 m, Z: ±0.25 m |
| Max velocity | X and Y: ±2.2 m/s, Z: ±1.5 m/s | X and Y: ±1.1 m/s, Z: ±0.75 m/s |
| Max acceleration (at max payload) | X and Y: ±1.5 g, Z: ±1.0 g | X and Y: ±1.05 g, Z: ±0.7 g |
| Company | Product | Type | N. of Axes | Noise Floor [µg/√Hz] | Sensitivity [mV/g] | Sensitivity [µg/LSB] | Full-Scale Range Dynamic Range | Bandwidth |
|---|---|---|---|---|---|---|---|---|
| Seiko-Epson | M-A352 (1) | Digital 32-bit MEMS | 3 | 0.2 at 0.5–30 Hz | 0.06 | ±15 g > 140 dB | 0–460 Hz | |
| Safran-Colibyis | SI1003 | Analog MEMS | 1 | 0.7 | 900 | ±3 g 108.5 dB (0.1–100 Hz) | 0–500 Hz | |
| Safran-Colibrys | VS1002 (1) | Analog MEMS | 1 | 7 | 1350 | ±2 g 108.5 dB (0.1–100 Hz) | 0–700 Hz | |
| Analog Device | ADXL355 (1) | Digital 20-bit MEMS | 3 | 22.5 Hz at ±2 g | 3.9 at ± 2 g | ±2 g to ±8 g~90 dB (±2 g) | 1–1000 Hz | |
| PCB Piezotronics | 3711B1110G (2) | Analog MEMS | 1 | 107.9 | 1000 | ±10 g | 0–1000 Hz | |
| PCB Piezotronics | 393B04 (1) | Analog piezoelectric | 1 | 0.3 at 1 Hz 0.1 at 10 Hz | 1000 | ±5 g | 0.06–450 Hz | |
| PCB Piezotronics | T333B50 (1) | Analog piezoelectric | 1 | 15 at 1 Hz 3.8 at 10 Hz 1.1 at 100 Hz | 1000 | ±5 g | 0.5–3000 Hz | |
| PCB Piezotronics | 356A17 (1) | Analog piezoelectric | 3 | 18 at 1 Hz 6 at 10 Hz 2 at 100 Hz | 500 | ±10 g | 0.5–3000 Hz | |
| Kinemetrics | Episensor ES-T | Force balance | 3 | 0.06 at 1 Hz (±0.25 g) | 10,000 | ±0.25 g to ±4 g 155 dB | DC–200 Hz |
| Graphical Representation | Station Code | F | L | V | Model | Sampling Rate [Hz] |
|---|---|---|---|---|---|---|
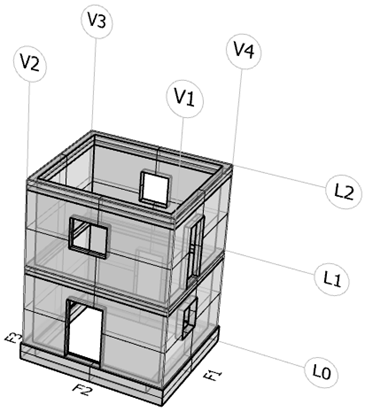  | M1 | 3 | 1 | 3 | M-A352 | 200 |
| M2 | 3 | 2 | 2 | M-A352 | 200 | |
| M3 | 1 | 1 | 4 | M-A352 | 200 | |
| M4 | 3 | 2 | 3 | M-A352 | 200 | |
| M5 | 1 | 2 | 1 | M-A352 | 200 | |
| M6 | 1 | 1 | 1 | M-A352 | 200 | |
| M7 | 3 | 1 | 2 | M-A352 | 200 | |
| M8 | - | 0 | - | M-A352 | 200 | |
| M9 | 1 | 2 | 4 | M-A352 | 200 | |
| M10 | 2 | 1 | 2 | ADXL355 | 125 | |
| M11 | 2 | 1 | 1 | ADXL355 | 125 | |
| M12 | - | 0 | - | ADXL355 | 125 | |
| W1 | 2 | 1 | 1 | VS1002 | 1000 | |
| W2 | 2 | 1 | 2 | VS1002 | 1000 | |
| W3 | 4 | 1 | 3 | VS1002 | 1000 | |
| W4 | 4 | 1 | 4 | VS1002 | 1000 | |
| W5 | 2 | 2 | 1 | VS1002 | 1000 | |
| W6 | 2 | 2 | 2 | VS1002 | 1000 | |
| W7 | 4 | 2 | 3 | VS1002 | 1000 | |
| W8 | 4 | 2 | 4 | VS1002 | 1000 | |
| A1 | 1 | 1 | 4 | 356A17 | 1000 | |
| A2 | 1 | 1 | 1 | 356A17 | 1000 | |
| A3 | 3 | 1 | 2 | 356A17 | 1000 | |
| A4 | 3 | 1 | 3 | 356A17 | 1000 | |
| A5 | 1 | 2 | 4 | 356A17 | 1000 | |
| A6 | 1 | 2 | 1 | 356A17 | 1000 | |
| A7 | 3 | 2 | 2 | 356A17 | 1000 | |
| A8 | 3 | 2 | 3 | 356A17 | 1000 | |
| F2 | 2 | 1 | - | T333B50 | 1000 | |
| F3 | 3 | 1 | - | T333B50 | 1000 | |
| F4 | 4 | 1 | - | T333B50 | 1000 | |
| F6 | 2 | 2 | - | T333B50 | 1000 | |
| F7 | 3 | 2 | - | T333B50 | 1000 | |
| F8 | 4 | 2 | - | T333B50 | 1000 | |
| S1 | 0 | 1 | 1 | 393B04 | 1000 | |
| S2 | 0 | 2 | 1 | 393B04 | 1000 | |
| AccGDL | - | Shake table | - | 3711B1110G | 1000 |
| Type of Excitation | Intensity [g] | Direction |
|---|---|---|
| WN | 0.03 (RMS) | X |
| WN | 0.04 (RMS) | X |
| WN | 0.03 (RMS) | Y |
| WN | 0.04 (RMS) | Y |
| WN | 0.015 (RMS) | Z |
| WN | 0.03 (RMS) | Z |
| WN | 0.04 (RMS) | XYZ |
| EQ | 0.05 (PGA) | XYZ |
| WN | 0.03 (RMS) | XYZ |
| EQ | 0.1 (PGA) | XYZ |
| WN | 0.03 (RMS) | XYZ |
| EQ | 0.2 (PGA) | XYZ |
| WN | 0.03 (RMS) | XYZ |
| EQ | 0.3 (PGA) | XYZ |
| WN | 0.03 (RMS) | XYZ |
| EQ | 0.4 (PGA) | XYZ |
| WN | 0.03 (RMS) | XYZ |
| EQ | 0.5 (PGA) | XYZ |
| WN | 0.03 (RMS) | XYZ |
| Formula | C | a | Fundamental Frequency f [Hz] of the Full-Scale Building | Fundamental Frequency f [Hz] of the Specimen | |
|---|---|---|---|---|---|
| Alguhane et al. [22] (D = 2.96 m) | 0.07 | 0.5 | 4.91 | 6.01 | |
| Alguhane et al. [22] (D = 3.41 m) | 0.07 | 0.5 | 5.27 | 6.46 | |
| EUROCODE 8 [18]-NTC18 [23] | 0.05 | 0.75 | 5.13 | 6.29 | |
| ASCE 7-10 [24] | 0.0488 | 0.75 | 5.26 | 6.44 | |
| Alguhane et al. [22] | 0.042 | 0.75 | 6.11 | 7.49 |
| Sensor | Mode 1 | Mode 2 | Mode 3 |
|---|---|---|---|
| M-A352 before the hydraulic pumps’ activation |  7.584 Hz |  8.301 Hz |  9.823 Hz |
| M-A352 during the hydraulic pumps’ activation |  7.050 Hz |  7.549 Hz |  9.875 Hz |
| PCB356A17during the hydraulic pumps’ activation |  6.871 Hz |  7.208 Hz |  8.768 Hz |
| M-A352 Before the Hydraulic Pumps’ Activation | ||||
| 7.584 Hz | 8.301 Hz | 9.823 Hz | ||
| M-A352 during the hydraulic pumps’ activation | 7.050 Hz | 0.9411 | ||
| 7.549 Hz | 0.829 | |||
| 9.875 Hz | 0.8339 | |||
| M-A352 During the Hydraulic Pumps’ Activation | ||||
| 7.050 Hz | 7.549 Hz | 9.875 Hz | ||
| PCB356A17 during the hydraulic pumps’ activation | 6.871 Hz | 0.4955 | ||
| 7.208 Hz | 0.419 | |||
| 8.768 Hz | 0.344 | |||
| Chunk of Data | Frequency f1 [Hz] | Damping [%] | Complexity [%] |
|---|---|---|---|
| 01_R1345_1355 | 6.98 | 4.44 | 4.34 |
| Seismic action at 10% of the PGA max | |||
| 04_R1407_1417 | 6.46 | 8.05 | 17.47 |
| Seismic action at 20% of the PGA max | |||
| 07_R1433_1444 | 6.44 | 6.30 | 33.61 |
| Seismic action at 30% of the PGA max | |||
| 09_R1445_1451 | 5.75 | 6.72 | 26.66 |
| Seismic action at 40% of the PGA max | |||
| 12_R1500_1505 | 5.001 | 0.207 | 23.868 |
| Seismic action at 50% of the PGA max | |||
| 15_R1514_1520 | 5.014 | 7.468 | 40.055 |
| Station Code | F | L | V | Noise Density [µg/√Hz] | Sampling Rate [Hz] | X | Y | Z |
|---|---|---|---|---|---|---|---|---|
| M6 | 1 | 1 | 1 | 0.2 | 200 | z | x | y |
| M5 | 1 | 2 | 1 | 0.2 | 200 | z | x | y |
| W1 | 2 | 1 | 1 | 7 | 1000 | x | y | - |
| W5 | 2 | 2 | 1 | 7 | 1000 | x | y | - |
| M11 | 2 | 1 | 1 | 25 | 200 | x | -z | y |
| A2 | 1 | 1 | 1 | 18-6-2 @ 1-10-100 Hz | 1000 | X | Y | Z |
| A6 | 1 | 2 | 1 | 18-6-2 @ 1-10-100 Hz | 1000 | X | Y | Z |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Occhipinti, G.; Lo Iacono, F.; Tusa, G.; Costanza, A.; Fertitta, G.; Lodato, L.; Macaluso, F.; Martino, C.; Mugnos, G.; Oliva, M.; et al. Shake Table Tests on Scaled Masonry Building: Comparison of Performance of Various Micro-Electromechanical System Accelerometers (MEMS) for Structural Health Monitoring. Sensors 2025, 25, 1010. https://doi.org/10.3390/s25041010
Occhipinti G, Lo Iacono F, Tusa G, Costanza A, Fertitta G, Lodato L, Macaluso F, Martino C, Mugnos G, Oliva M, et al. Shake Table Tests on Scaled Masonry Building: Comparison of Performance of Various Micro-Electromechanical System Accelerometers (MEMS) for Structural Health Monitoring. Sensors. 2025; 25(4):1010. https://doi.org/10.3390/s25041010
Chicago/Turabian StyleOcchipinti, Giuseppe, Francesco Lo Iacono, Giuseppina Tusa, Antonio Costanza, Gioacchino Fertitta, Luigi Lodato, Francesco Macaluso, Claudio Martino, Giuseppe Mugnos, Maria Oliva, and et al. 2025. "Shake Table Tests on Scaled Masonry Building: Comparison of Performance of Various Micro-Electromechanical System Accelerometers (MEMS) for Structural Health Monitoring" Sensors 25, no. 4: 1010. https://doi.org/10.3390/s25041010
APA StyleOcchipinti, G., Lo Iacono, F., Tusa, G., Costanza, A., Fertitta, G., Lodato, L., Macaluso, F., Martino, C., Mugnos, G., Oliva, M., Storni, D., Alessandroni, G., Navarra, G., & Patanè, D. (2025). Shake Table Tests on Scaled Masonry Building: Comparison of Performance of Various Micro-Electromechanical System Accelerometers (MEMS) for Structural Health Monitoring. Sensors, 25(4), 1010. https://doi.org/10.3390/s25041010







