Analysis of Kinect-Based Human Motion Capture Accuracy Using Skeletal Cosine Similarity Metrics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Experimental Scenarios
2.2.1. Static Test Protocol
2.2.2. Dynamic Test Protocol
2.3. Description and Visualization of Human Pose Data
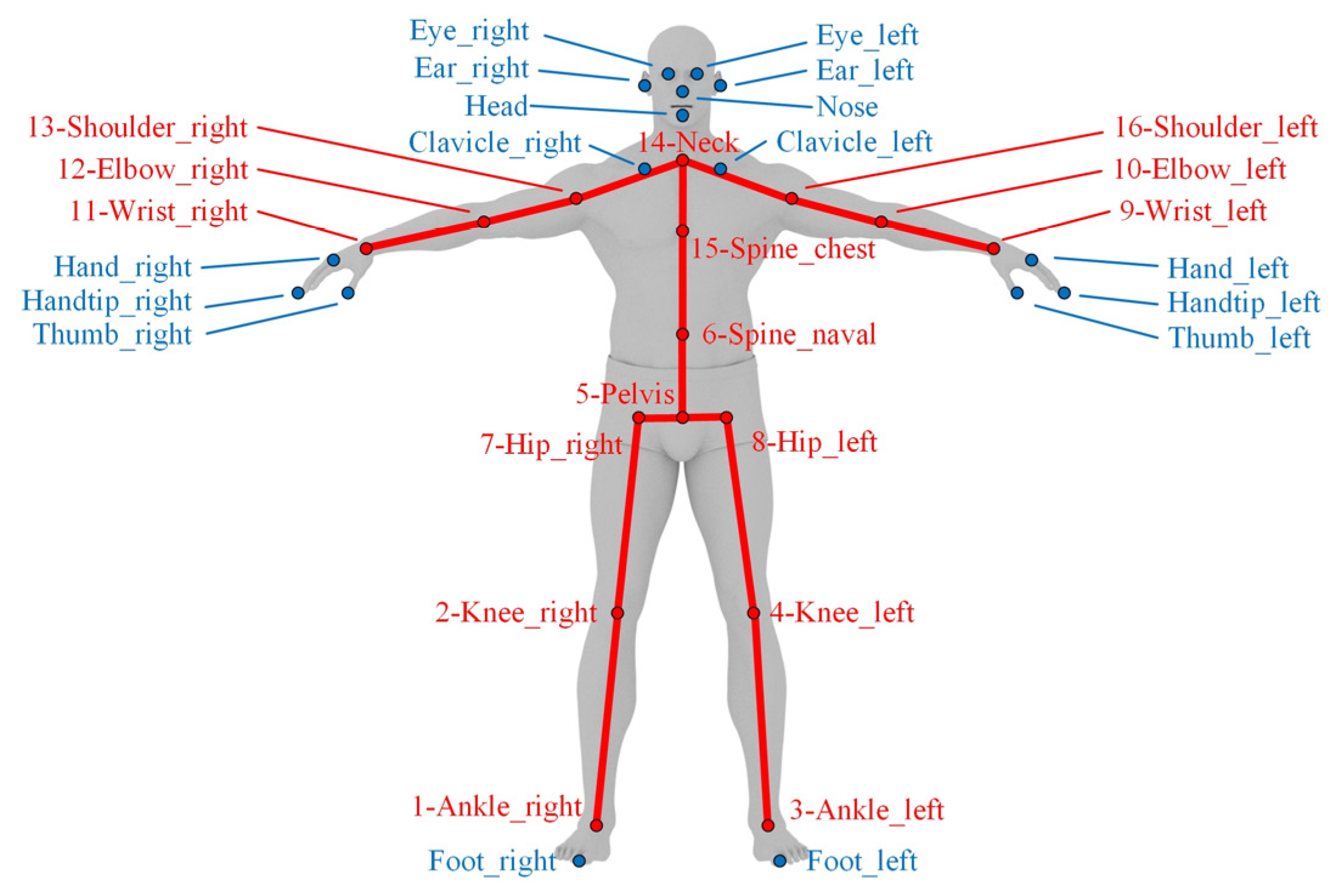
2.3.1. Selection of Joint Nodes
2.3.2. Ensuring Data Quality of Skeletal Nodes
- Stable testing conditions: The experiments were conducted in an enclosed indoor space with minimal natural light, primarily illuminated by indoor light sources. These sources consisted of LED lights uniformly distributed across the ceiling. The walls were painted white, the floor was wood-textured, and the primary testing area featured adhesive floor markers. The lighting remained constant throughout all experiments. This setup ensured consistent diffuse lighting conditions, similar to typical well-lit indoor environments.
- Specific design of experimental apparatus: In the experimental area, a thin, graduated carpet was fixed to the floor in front of Kinect to visually indicate the distance between any given position and the Kinect. The mannequin used in static experiments was mounted on a mobile stand equipped with counterweights, allowing for convenient and precise adjustments to its position and orientation, thereby enabling corresponding adjustments to the mannequin subject. Curtains were also employed to occlude external light sources that could potentially compromise the measurement accuracy of Visualeyez.
- Experimental data extraction: The data acquisition frequency of the Kinect was set to 30 Hz, while that of the Visualeyez was set to 60 Hz. In static test tasks, the Kinect continuously acquired 500 frames of valid data, which were directly averaged. The Visualeyez, on the other hand, continuously acquired over 1000 frames of data, from which, after preliminary screening and filtering, 100 high-quality frames were selected for averaging. In dynamic test tasks, if the Visualeyez software momentarily failed to effectively detect a visual marker due to occlusion or other factors, the last valid data point corresponding to that marker was used as the current data record. This approach aimed to maximize the integrity of data during dynamic testing. Through this processing, the data for each skeletal node obtained from both devices were refined to minimize the influence of environmental disturbances, such as random infrared interference and occlusion.
- Synchronization of experimental data: Compared to static tests, data acquired from the two devices in dynamic tests required further temporal synchronization. To ensure low-latency data processing, the software systems of the two testing devices were operated on separate computer systems, both of which exhibited startup delays. This presented challenges for strict hardware-based synchronization. Consequently, an offline data synchronization method based on timestamps and pose comparison was adopted. Specifically, we first selected the most recent 500 frames of valid data acquired by the Kinect and designated the first frame as the Kinect’s starting frame. Then, based on the timestamp, the Visualeyez data frame closest in time to the Kinect’s starting frame was identified. Next, within a range of 60 frames before and after this identified Visualeyez frame, the frame exhibiting the closest human pose to the starting data was selected and designated as the Visualeyez starting frame. Through this process, the starting points of the two data sequences were aligned. Subsequently, all data frames were matched based on their respective actual time intervals. The method used to assess the similarity of human posture will be described in the following section.
2.3.3. Visualization of the Human Skeleton
2.4. Motion Capture Data Correction
2.5. Evaluation Method for Motion Capture Data
3. Results
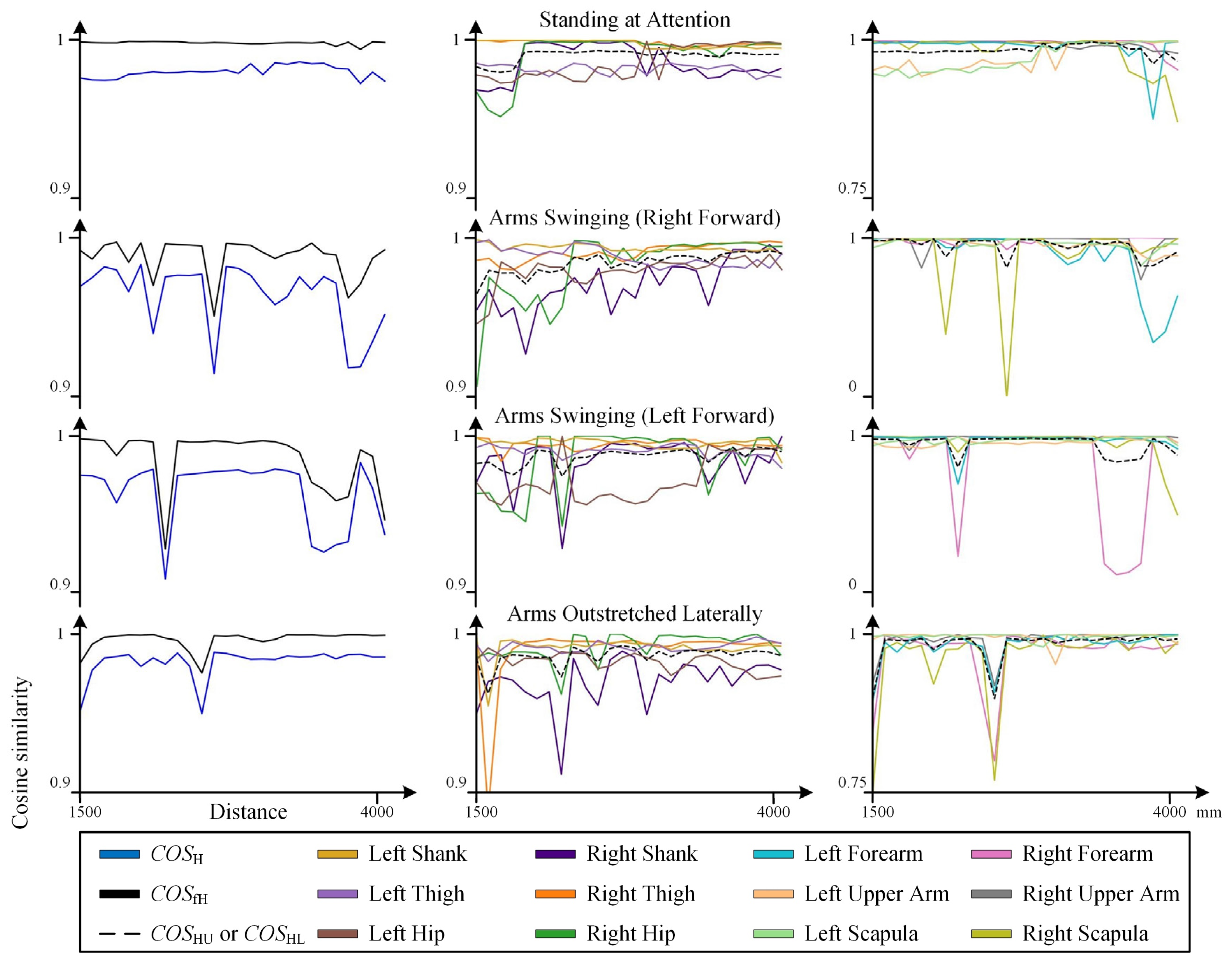
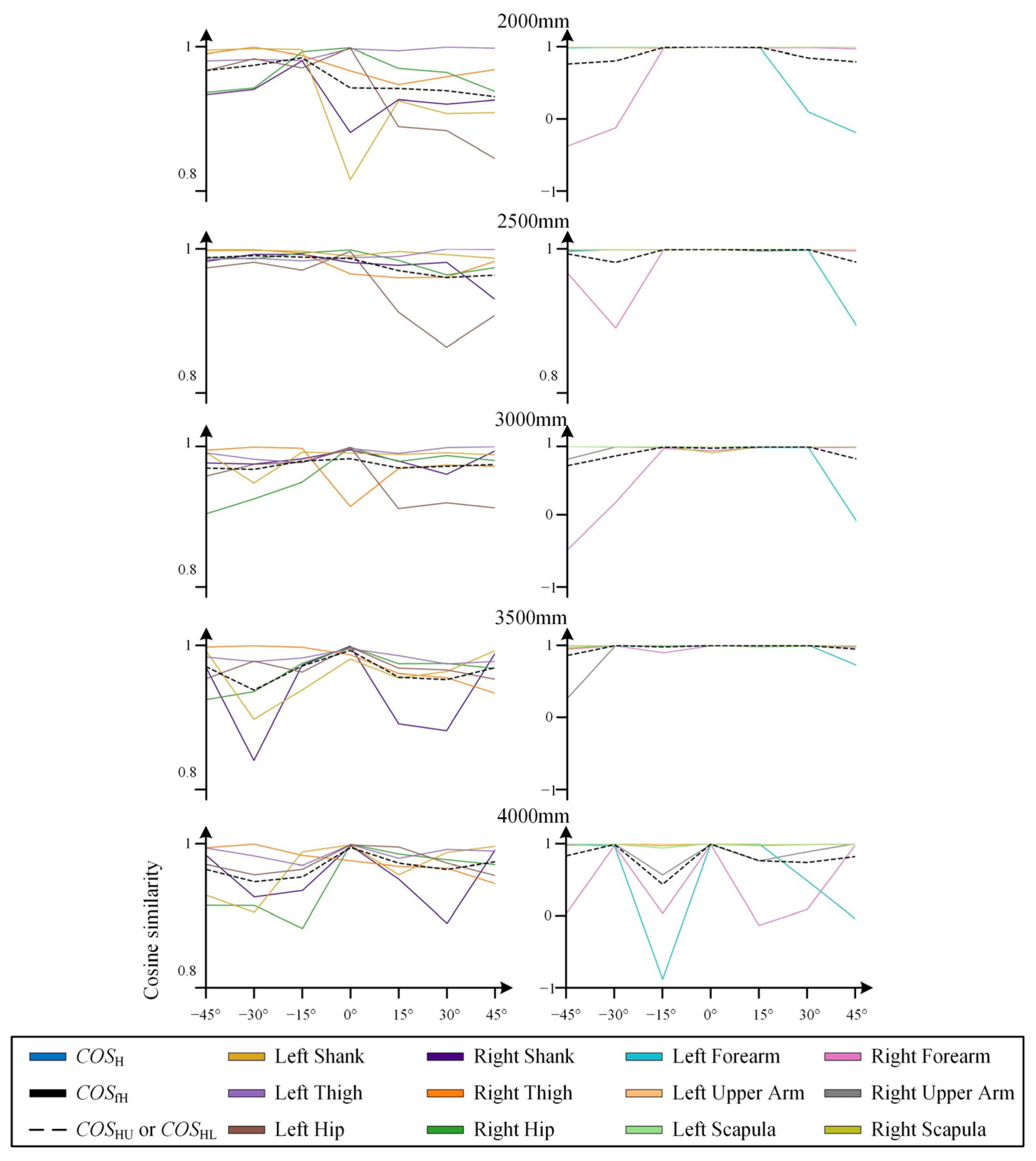
3.1. Results of Static Tests
3.1.1. Cosine Similarity Data
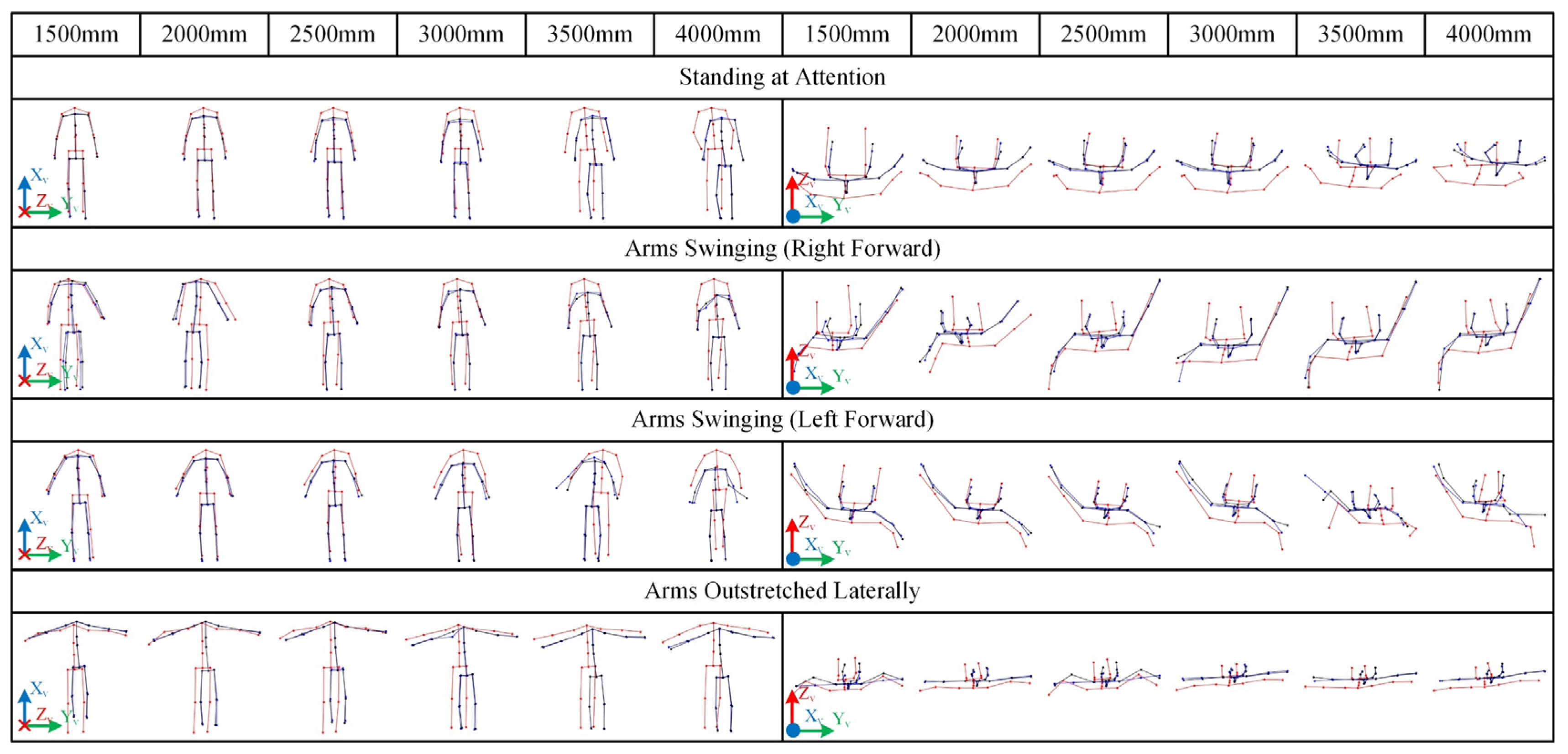
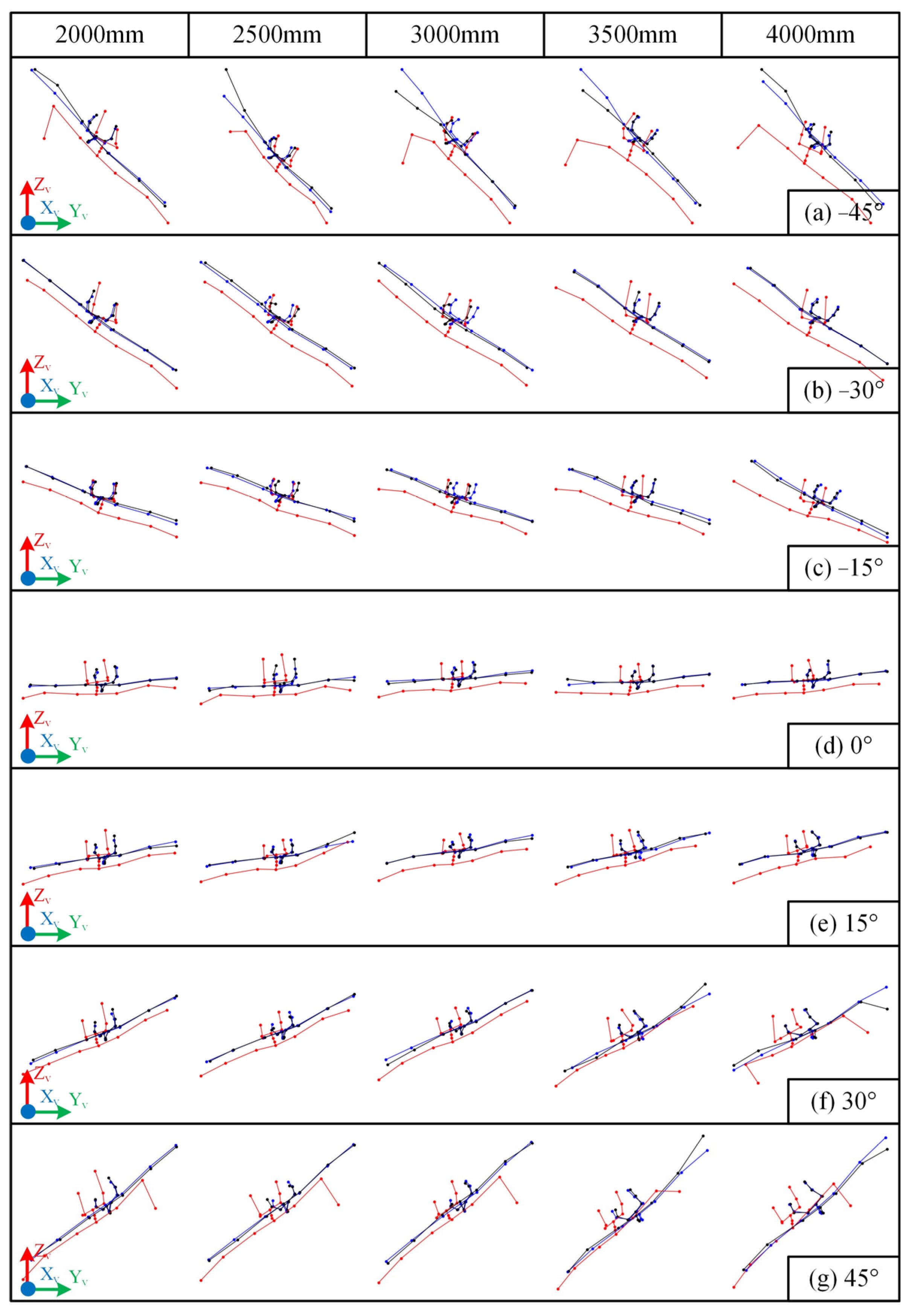
3.1.2. Visualized Skeletal Data
3.2. Analysis of Static Test Results
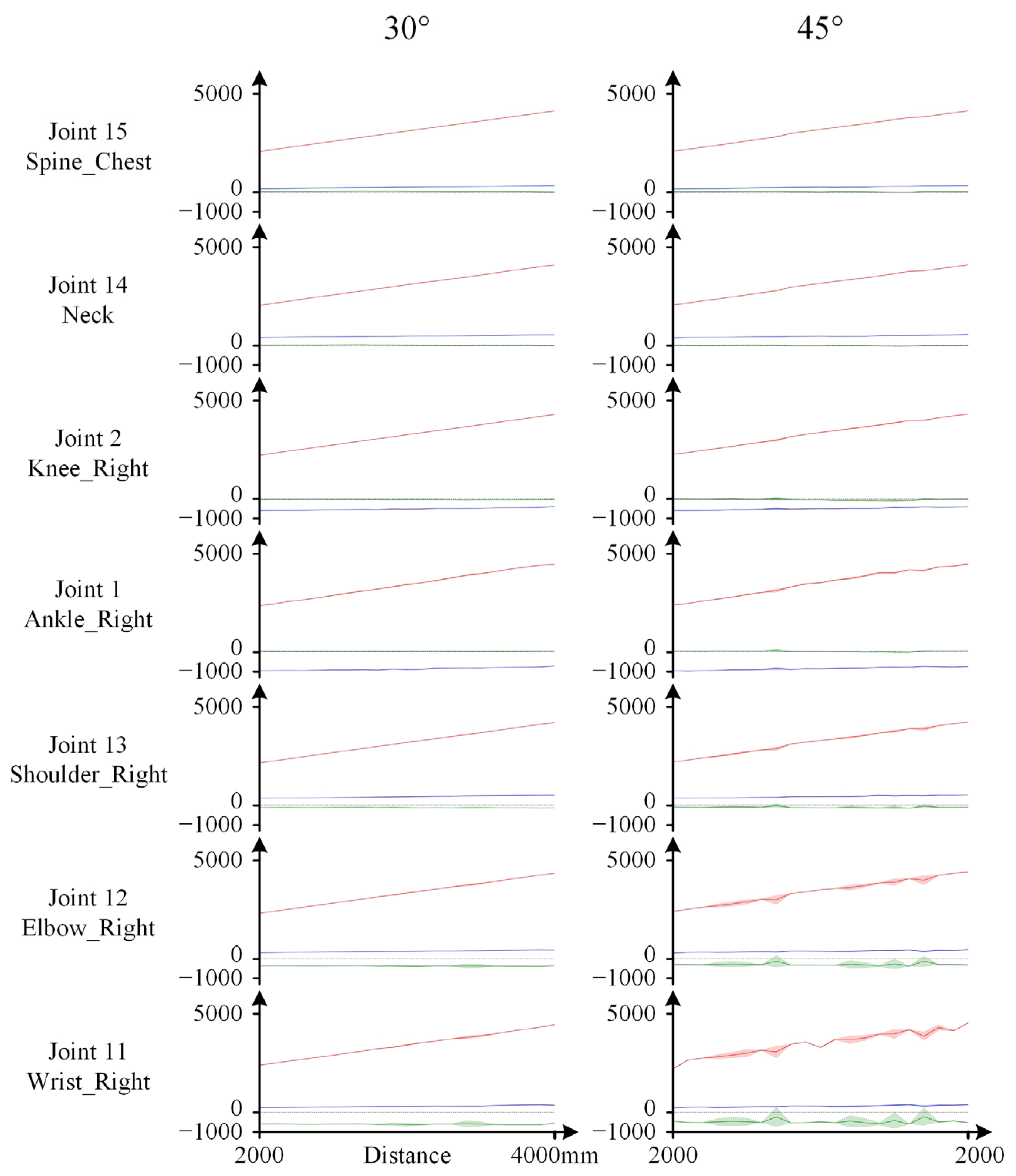
3.2.1. Data Accuracy Analysis
3.2.2. Effectiveness of Data Correction
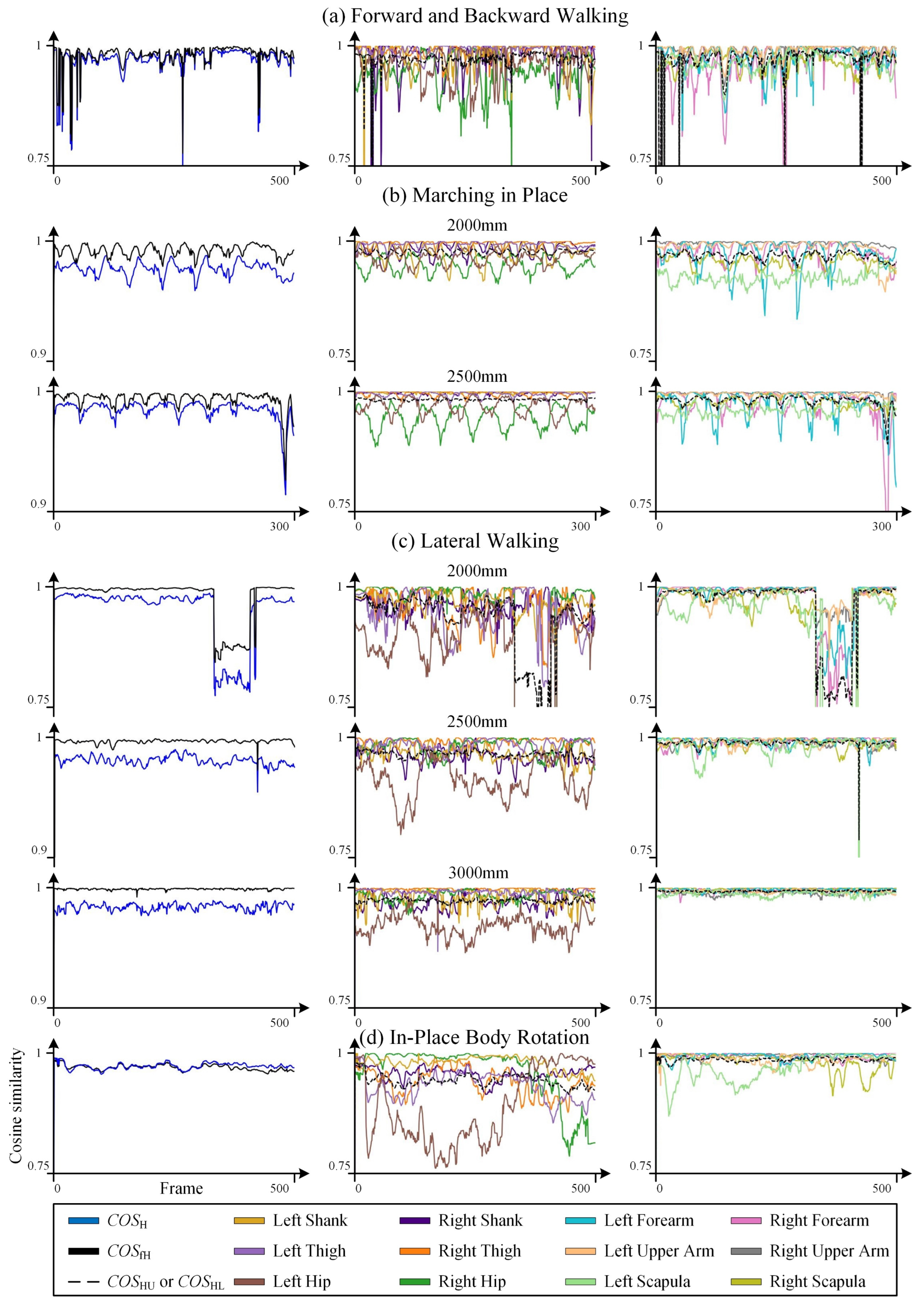
3.3. Results of Dynamic Tests
3.4. Analysis of Dynamic Tests
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Distance (mm) | Node Index (i) | Node Name | Kinect Measurements | Visualeyez Measurements | Corrected Kinect Values | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
(mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | |||
| 1500 | 1 | Ankle_Right | −1181.91 | −79.75 | 1565.90 | −945.49 | 9.29 | 1352.81 | −966.19 | 8.06 | 1490.07 |
| 2 | Knee_Right | −762.39 | −76.92 | 1351.41 | −645.44 | −14.54 | 1305.08 | −663.76 | −20.16 | 1398.85 | |
| 3 | Ankle_Left | −1171.43 | 143.46 | 1577.87 | −947.15 | 189.16 | 1400.66 | −970.04 | 194.94 | 1506.22 | |
| 4 | Knee_Left | −747.49 | 154.39 | 1384.04 | −643.39 | 197.34 | 1313.86 | −660.91 | 203.10 | 1393.28 | |
| 5 | Pelvis | −272.35 | 17.07 | 1302.66 | −237.66 | 85.70 | 1243.17 | −248.41 | 84.80 | 1274.80 | |
| 6 | Spine_Naval | −64.36 | 11.12 | 1239.58 | 77.10 | 55.12 | 1187.34 | 70.21 | 52.67 | 1209.00 | |
| 7 | Hip_Right | −278.87 | −82.18 | 1290.54 | −235.36 | 1.53 | 1238.37 | −246.64 | −4.78 | 1273.75 | |
| 8 | Hip_Left | −265.12 | 127.14 | 1316.11 | −221.42 | 159.01 | 1260.53 | −232.98 | 163.02 | 1289.47 | |
| 9 | Wrist_Left | 217.50 | 753.55 | 1218.26 | 275.09 | 759.95 | 1311.03 | 263.01 | 757.06 | 1297.46 | |
| 10 | Elbow_Left | 276.75 | 506.28 | 1341.67 | 301.80 | 507.06 | 1285.75 | 306.25 | 513.11 | 1377.20 | |
| 11 | Wrist_Right | 136.45 | −690.55 | 1082.30 | 172.24 | −632.04 | 1212.12 | 180.39 | −628.13 | 1208.42 | |
| 12 | Elbow_Right | 245.52 | −507.94 | 1273.79 | 249.26 | −382.55 | 1222.50 | 258.53 | −403.27 | 1326.40 | |
| 13 | Shoulder_Right | 284.20 | −189.53 | 1152.06 | 357.67 | −103.52 | 1232.79 | 358.65 | −112.37 | 1233.73 | |
| 14 | Neck | 367.47 | 5.60 | 1168.39 | 408.86 | 47.26 | 1227.52 | 413.65 | 48.41 | 1244.67 | |
| 15 | Spine_Chest | 104.77 | 4.85 | 1200.00 | 199.85 | 49.11 | 1173.96 | 197.29 | 45.50 | 1190.52 | |
| 16 | Shoulder_Left | 284.85 | 215.78 | 1171.49 | 358.02 | 215.53 | 1237.51 | 358.60 | 226.91 | 1243.46 | |
| 2000 | 1 | Ankle_Right | −1016.73 | −125.23 | 1971.81 | −920.77 | −5.35 | 1873.28 | −915.52 | −14.01 | 1901.04 |
| 2 | Knee_Right | −622.24 | −105.71 | 1795.11 | −619.80 | −29.72 | 1825.31 | −616.54 | −33.76 | 1842.45 | |
| 3 | Ankle_Left | −1008.72 | 56.36 | 1988.34 | −922.10 | 175.26 | 1918.26 | −917.52 | 160.04 | 1927.88 | |
| 4 | Knee_Left | −614.77 | 88.59 | 1823.68 | −588.03 | 182.16 | 1832.79 | −585.62 | 173.24 | 1835.99 | |
| 5 | Pelvis | −171.81 | −9.58 | 1780.61 | −211.96 | 69.96 | 1762.81 | −209.90 | 68.89 | 1759.34 | |
| 6 | Spine_Naval | 21.34 | −9.79 | 1729.99 | 102.54 | 37.97 | 1707.32 | 104.79 | 39.16 | 1706.74 | |
| 7 | Hip_Right | −175.64 | −100.41 | 1766.37 | −209.87 | −14.81 | 1759.38 | −207.30 | −16.10 | 1755.45 | |
| 8 | Hip_Left | −167.56 | 91.15 | 1796.40 | −196.20 | 143.03 | 1778.89 | −194.73 | 142.01 | 1776.99 | |
| 9 | Wrist_Left | 263.87 | 726.84 | 1725.54 | 297.23 | 742.99 | 1823.48 | 288.25 | 742.88 | 1812.57 | |
| 10 | Elbow_Left | 321.61 | 474.87 | 1748.98 | 327.25 | 491.17 | 1800.85 | 326.41 | 494.07 | 1795.62 | |
| 11 | Wrist_Right | 139.72 | −711.43 | 1628.11 | 197.53 | −648.90 | 1740.66 | 181.54 | −641.17 | 1755.08 | |
| 12 | Elbow_Right | 298.69 | −508.78 | 1680.13 | 274.45 | −399.28 | 1748.29 | 282.42 | −403.92 | 1744.10 | |
| 13 | Shoulder_Right | 342.82 | −197.11 | 1665.62 | 382.95 | −120.35 | 1755.42 | 381.05 | −117.76 | 1754.38 | |
| 14 | Neck | 418.65 | −17.57 | 1666.19 | 434.28 | 30.41 | 1748.57 | 437.31 | 32.63 | 1751.23 | |
| 15 | Spine_Chest | 178.09 | −11.68 | 1699.94 | 225.62 | 31.75 | 1694.56 | 228.14 | 34.32 | 1698.10 | |
| 16 | Shoulder_Left | 339.89 | 175.64 | 1672.99 | 383.64 | 198.84 | 1755.97 | 381.10 | 199.85 | 1751.66 | |
| 2500 | 1 | Ankle_Right | −1060.83 | −152.40 | 2542.82 | −896.70 | −25.53 | 2397.84 | −919.05 | −27.20 | 2479.15 |
| 2 | Knee_Right | −640.00 | −142.17 | 2343.19 | −594.88 | −49.29 | 2351.18 | −622.53 | −50.99 | 2390.42 | |
| 3 | Ankle_Left | −1045.13 | 26.53 | 2584.71 | −896.53 | 154.42 | 2448.32 | −919.27 | 148.08 | 2540.50 | |
| 4 | Knee_Left | −631.37 | 61.69 | 2384.41 | −593.07 | 162.40 | 2365.70 | −621.28 | 161.03 | 2400.63 | |
| 5 | Pelvis | −155.17 | −42.60 | 2326.97 | −186.89 | 50.98 | 2292.21 | −203.52 | 49.17 | 2313.24 | |
| 6 | Spine_Naval | 50.90 | −43.01 | 2265.70 | 128.16 | 18.96 | 2237.43 | 116.72 | 17.69 | 2250.44 | |
| 7 | Hip_Right | −158.93 | −140.87 | 2314.97 | −184.96 | −33.98 | 2287.68 | −200.93 | −41.23 | 2310.82 | |
| 8 | Hip_Left | −150.99 | 66.39 | 2340.28 | −170.90 | 123.50 | 2310.15 | −188.23 | 127.56 | 2329.06 | |
| 9 | Wrist_Left | 331.05 | 678.31 | 2242.97 | 337.60 | 720.33 | 2368.43 | 324.83 | 717.11 | 2337.98 | |
| 10 | Elbow_Left | 386.29 | 441.51 | 2380.56 | 353.28 | 469.49 | 2340.65 | 355.47 | 473.84 | 2444.42 | |
| 11 | Wrist_Right | 247.05 | −747.45 | 2113.13 | 219.94 | −670.37 | 2262.48 | 219.23 | −663.67 | 2240.85 | |
| 12 | Elbow_Right | 350.42 | −560.28 | 2298.51 | 300.10 | −419.90 | 2273.81 | 305.66 | −443.84 | 2379.75 | |
| 13 | Shoulder_Right | 397.92 | −243.96 | 2185.47 | 407.49 | −141.17 | 2285.11 | 402.10 | −151.02 | 2281.42 | |
| 14 | Neck | 478.36 | −51.11 | 2199.62 | 460.13 | 9.30 | 2281.55 | 464.91 | 9.77 | 2294.06 | |
| 15 | Spine_Chest | 218.20 | −44.62 | 2226.38 | 251.19 | 12.35 | 2226.67 | 245.02 | 12.04 | 2232.58 | |
| 16 | Shoulder_Left | 404.24 | 159.23 | 2204.88 | 409.50 | 178.08 | 2291.34 | 407.40 | 188.78 | 2290.65 | |
| 3000 | 1 | Ankle_Right | −852.08 | −175.45 | 2945.98 | −863.94 | −50.71 | 2905.30 | −855.01 | −38.38 | 2887.33 |
| 2 | Knee_Right | −469.95 | −171.32 | 2800.78 | −573.06 | −74.61 | 2859.93 | −565.23 | −64.76 | 2847.92 | |
| 3 | Ankle_Left | −847.49 | 18.44 | 2967.13 | −874.69 | 128.28 | 2958.82 | −865.47 | 144.84 | 2933.34 | |
| 4 | Knee_Left | −460.19 | 24.55 | 2850.29 | −541.29 | 136.12 | 2875.86 | −532.86 | 144.18 | 2869.76 | |
| 5 | Pelvis | −42.88 | −69.37 | 2806.34 | −165.84 | 25.53 | 2803.62 | −160.51 | 33.18 | 2799.22 | |
| 6 | Spine_Naval | 137.46 | −70.52 | 2750.90 | 147.82 | −6.32 | 2750.15 | 151.66 | −0.08 | 2742.88 | |
| 7 | Hip_Right | −47.41 | −155.23 | 2793.38 | −163.57 | −59.57 | 2798.66 | −158.42 | −50.15 | 2795.13 | |
| 8 | Hip_Left | −37.86 | 25.84 | 2820.70 | −150.30 | 98.17 | 2822.96 | −143.88 | 103.89 | 2816.72 | |
| 9 | Wrist_Left | 390.15 | 630.44 | 2756.54 | 359.58 | 696.72 | 2878.24 | 357.00 | 691.69 | 2859.47 | |
| 10 | Elbow_Left | 426.71 | 387.99 | 2762.76 | 374.98 | 444.69 | 2852.62 | 373.64 | 441.40 | 2837.05 | |
| 11 | Wrist_Right | 313.27 | −776.63 | 2623.61 | 242.92 | −695.69 | 2775.43 | 242.49 | −681.90 | 2752.12 | |
| 12 | Elbow_Right | 379.16 | −544.15 | 2681.01 | 320.50 | −445.11 | 2786.35 | 318.57 | −431.34 | 2772.94 | |
| 13 | Shoulder_Right | 439.92 | −252.98 | 2695.11 | 353.53 | −165.63 | 2795.52 | 418.14 | −157.43 | 2798.10 | |
| 14 | Neck | 511.48 | −84.14 | 2684.57 | 482.28 | −15.80 | 2793.51 | 480.22 | −12.73 | 2787.55 | |
| 15 | Spine_Chest | 284.53 | −73.24 | 2717.53 | 271.50 | −12.78 | 2738.84 | 272.92 | −7.32 | 2731.24 | |
| 16 | Shoulder_Left | 458.51 | 102.08 | 2711.38 | 430.74 | 149.87 | 2805.81 | 429.59 | 150.24 | 2803.92 | |
| 3500 | 1 | Ankle_Right | −843.76 | −188.58 | 3469.32 | −847.25 | −48.32 | 3422.10 | −852.46 | −44.75 | 3417.18 |
| 2 | Knee_Right | −449.80 | −191.14 | 3328.33 | −555.82 | −73.82 | 3375.94 | −558.44 | −74.12 | 3375.36 | |
| 3 | Ankle_Left | −831.07 | −13.75 | 3492.16 | −856.42 | 131.37 | 3474.51 | −860.17 | 131.94 | 3472.68 | |
| 4 | Knee_Left | −437.04 | 0.81 | 3365.65 | −522.68 | 136.17 | 3392.06 | −524.96 | 133.40 | 3388.72 | |
| 5 | Pelvis | −11.58 | −88.51 | 3321.31 | −148.71 | 23.03 | 3320.42 | −148.51 | 21.76 | 3321.30 | |
| 6 | Spine_Naval | 173.23 | −92.70 | 3265.50 | 165.49 | −10.89 | 3266.01 | 166.10 | −14.41 | 3265.16 | |
| 7 | Hip_Right | −17.71 | −176.22 | 3307.60 | −146.40 | −62.23 | 3314.63 | −147.10 | −63.18 | 3315.69 | |
| 8 | Hip_Left | −4.78 | 8.77 | 3336.52 | −131.41 | 95.26 | 3337.56 | −130.91 | 93.92 | 3340.30 | |
| 9 | Wrist_Left | 462.71 | 624.60 | 3279.20 | 381.98 | 690.61 | 3394.92 | 396.50 | 688.59 | 3390.20 | |
| 10 | Elbow_Left | 487.60 | 374.90 | 3274.94 | 395.81 | 437.69 | 3370.75 | 401.00 | 433.47 | 3363.19 | |
| 11 | Wrist_Right | 366.77 | −829.63 | 3213.35 | 255.05 | −700.46 | 3288.55 | 261.28 | −715.02 | 3342.78 | |
| 12 | Elbow_Right | 420.85 | −581.35 | 3206.38 | 335.94 | −450.80 | 3306.32 | 337.30 | −460.17 | 3312.98 | |
| 13 | Shoulder_Right | 487.41 | −284.03 | 3200.72 | 441.76 | −172.73 | 3314.69 | 436.29 | −179.48 | 3310.70 | |
| 14 | Neck | 555.48 | −110.10 | 3194.40 | 499.63 | −22.98 | 3310.59 | 500.56 | −30.42 | 3306.36 | |
| 15 | Spine_Chest | 323.87 | −98.02 | 3232.18 | 288.13 | −18.27 | 3255.94 | 289.48 | −24.07 | 3253.74 | |
| 16 | Shoulder_Left | 505.21 | 81.12 | 3221.72 | 449.92 | 143.06 | 3322.03 | 448.67 | 136.11 | 3321.07 | |
| 4000 | 1 | Ankle_Right | −801.31 | −253.34 | 3978.51 | −825.34 | −81.38 | 3935.26 | −839.44 | −76.18 | 3932.71 |
| 2 | Knee_Right | −406.94 | −248.46 | 3836.56 | −532.70 | −106.28 | 3889.84 | −543.99 | −101.20 | 3883.49 | |
| 3 | Ankle_Left | −788.13 | −90.61 | 4027.84 | −833.97 | 95.88 | 3989.49 | −846.31 | 101.13 | 4022.95 | |
| 4 | Knee_Left | −402.93 | −46.36 | 3880.45 | −501.10 | 101.16 | 3911.69 | −513.32 | 111.99 | 3907.12 | |
| 5 | Pelvis | 27.92 | −141.49 | 3834.27 | −126.30 | −9.39 | 3836.04 | −133.38 | −9.89 | 3841.33 | |
| 6 | Spine_Naval | 214.01 | −136.95 | 3781.66 | 187.21 | −42.88 | 3781.51 | 182.55 | −43.00 | 3789.03 | |
| 7 | Hip_Right | 25.93 | −229.41 | 3819.62 | −123.78 | −95.23 | 3830.22 | −130.47 | −96.22 | 3834.03 | |
| 8 | Hip_Left | 30.12 | −44.00 | 3850.51 | −109.25 | 62.14 | 3856.45 | −117.22 | 63.12 | 3862.03 | |
| 9 | Wrist_Left | 470.53 | 591.76 | 3800.17 | 405.81 | 656.28 | 3925.66 | 400.75 | 671.15 | 3919.20 | |
| 10 | Elbow_Left | 519.99 | 345.26 | 3795.94 | 418.25 | 402.75 | 3895.16 | 415.55 | 415.50 | 3898.40 | |
| 11 | Wrist_Right | 341.20 | −814.03 | 3663.16 | 276.58 | −734.50 | 3795.31 | 252.30 | −705.27 | 3793.28 | |
| 12 | Elbow_Right | 446.42 | −594.31 | 3700.88 | 356.54 | −484.36 | 3812.61 | 348.79 | −470.21 | 3821.30 | |
| 13 | Shoulder_Right | 563.46 | −315.18 | 3711.85 | 463.59 | −206.19 | 3825.51 | 465.35 | −201.60 | 3828.89 | |
| 14 | Neck | 598.04 | −136.93 | 3715.04 | 521.04 | −56.24 | 3825.01 | 520.23 | −48.70 | 3836.17 | |
| 15 | Spine_Chest | 365.04 | −134.83 | 3748.48 | 309.80 | −50.18 | 3769.54 | 306.80 | −48.97 | 3777.93 | |
| 16 | Shoulder_Left | 562.55 | 53.83 | 3740.89 | 481.37 | 101.56 | 3838.78 | 472.11 | 117.71 | 3847.18 | |
| Orientation (°) | Node Index (i) | Node Name | Kinect Measurements | Visualeyez Measurements | Corrected Kinect Values | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
(mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | |||
| −45° | 1 | Ankle_Right | −1002.88 | 32.67 | 1944.30 | −912.39 | −49.86 | 1903.94 | −913.48 | −30.96 | 1915.92 |
| 2 | Knee_Right | −611.03 | −31.96 | 1789.64 | −617.12 | −87.00 | 1869.38 | −619.78 | −80.45 | 1859.18 | |
| 3 | Ankle_Left | −1019.26 | 123.63 | 1807.77 | −933.89 | 107.49 | 1814.97 | −934.16 | 114.50 | 1832.25 | |
| 4 | Knee_Left | −610.39 | 112.46 | 1704.93 | −613.17 | 76.26 | 1739.73 | −609.15 | 81.33 | 1740.91 | |
| 5 | Pelvis | −171.08 | 29.98 | 1717.98 | −231.22 | −35.49 | 1747.50 | −229.53 | −32.78 | 1757.14 | |
| 6 | Spine_Naval | 17.85 | 4.95 | 1669.41 | 93.81 | −85.34 | 1720.11 | 95.79 | −87.21 | 1724.48 | |
| 7 | Hip_Right | −171.88 | −51.81 | 1757.03 | −227.17 | −101.16 | 1801.83 | −226.21 | −93.19 | 1807.13 | |
| 8 | Hip_Left | −170.19 | 120.68 | 1674.68 | −219.66 | 28.57 | 1707.60 | −216.79 | 30.60 | 1722.37 | |
| 9 | Wrist_Left | 197.28 | 500.94 | 1114.13 | 239.60 | 474.76 | 1266.09 | 247.25 | 478.59 | 1239.42 | |
| 10 | Elbow_Left | 264.65 | 346.36 | 1306.31 | 276.56 | 286.76 | 1443.42 | 284.31 | 285.30 | 1430.12 | |
| 11 | Wrist_Right | 244.73 | −421.35 | 1742.77 | 239.95 | −514.38 | 2250.50 | 252.38 | −489.63 | 2255.87 | |
| 12 | Elbow_Right | 314.49 | −350.70 | 1981.76 | 298.73 | −341.52 | 2079.83 | 328.91 | −321.21 | 2197.32 | |
| 13 | Shoulder_Right | 361.22 | −152.56 | 1747.47 | 383.80 | −143.28 | 1857.09 | 386.83 | −136.40 | 1870.65 | |
| 14 | Neck | 409.08 | −27.55 | 1613.72 | 424.83 | −43.35 | 1739.21 | 431.27 | −45.70 | 1746.07 | |
| 15 | Spine_Chest | 172.57 | −8.29 | 1644.84 | 219.83 | −93.25 | 1712.80 | 219.86 | −97.72 | 1716.92 | |
| 16 | Shoulder_Left | 323.62 | 106.88 | 1485.11 | 370.54 | 60.56 | 1632.37 | 375.35 | 53.35 | 1633.43 | |
| −30° | 1 | Ankle_Right | −1027.16 | −6.46 | 2005.28 | −912.53 | −63.77 | 1902.22 | −912.58 | −48.33 | 1945.99 |
| 2 | Knee_Right | −628.36 | −48.36 | 1844.79 | −616.33 | −97.55 | 1861.02 | −618.37 | −87.02 | 1863.72 | |
| 3 | Ankle_Left | −1035.24 | 125.13 | 1843.72 | −932.03 | 104.59 | 1837.98 | −935.44 | 117.76 | 1849.36 | |
| 4 | Knee_Left | −623.73 | 113.94 | 1726.69 | −611.69 | 83.66 | 1758.95 | −613.72 | 95.90 | 1760.02 | |
| 5 | Pelvis | −182.53 | 21.48 | 1738.70 | −230.55 | −29.99 | 1749.61 | −231.45 | −16.89 | 1750.38 | |
| 6 | Spine_Naval | 9.69 | −6.01 | 1692.63 | 94.73 | −79.55 | 1716.96 | 94.49 | −65.33 | 1715.91 | |
| 7 | Hip_Right | −188.09 | −65.68 | 1767.53 | −227.40 | −103.37 | 1793.43 | −228.21 | −89.90 | 1789.75 | |
| 8 | Hip_Left | −176.37 | 118.14 | 1706.73 | −218.23 | 39.54 | 1720.44 | −219.07 | 53.82 | 1726.17 | |
| 9 | Wrist_Left | 223.48 | 574.36 | 1211.85 | 244.81 | 546.26 | 1355.94 | 235.99 | 569.39 | 1348.24 | |
| 10 | Elbow_Left | 275.81 | 383.91 | 1380.07 | 280.29 | 332.42 | 1500.62 | 277.64 | 352.66 | 1494.91 | |
| 11 | Wrist_Right | 227.67 | −531.99 | 2026.58 | 239.14 | −580.10 | 2177.82 | 241.67 | −583.75 | 2174.6 | |
| 12 | Elbow_Right | 314.40 | −426.56 | 1950.92 | 299.25 | −384.63 | 2025.80 | 298.35 | −377.30 | 2021.02 | |
| 13 | Shoulder_Right | 356.32 | −182.46 | 1756.34 | 384.42 | −159.90 | 1843.82 | 386.61 | −147.36 | 1842.95 | |
| 14 | Neck | 406.71 | −39.92 | 1638.10 | 425.76 | −43.83 | 1743.00 | 427.29 | −28.59 | 1743.18 | |
| 15 | Spine_Chest | 166.07 | −24.46 | 1666.99 | 221.24 | −85.02 | 1707.89 | 221.79 | −72.08 | 1706.12 | |
| 16 | Shoulder_Left | 327.91 | 118.67 | 1530.04 | 372.93 | 79.53 | 1652.55 | 374.77 | 98.46 | 1651.75 | |
| −15° | 1 | Ankle_Right | −942.66 | −81.31 | 1901.17 | −912.67 | −81.43 | 1889.45 | −896.32 | −62.12 | 1890.94 |
| 2 | Knee_Right | −555.20 | −95.50 | 1787.27 | −616.96 | −106.27 | 1843.09 | −606.35 | −90.28 | 1829.14 | |
| 3 | Ankle_Left | −934.45 | 115.29 | 1857.14 | −930.04 | 98.13 | 1874.26 | −916.18 | 119.70 | 1878.45 | |
| 4 | Knee_Left | −551.72 | 93.39 | 1743.29 | −609.89 | 95.19 | 1794.02 | −598.06 | 111.90 | 1794.09 | |
| 5 | Pelvis | −136.24 | 9.08 | 1744.51 | −229.85 | −15.51 | 1754.82 | −222.57 | 3.19 | 1751.84 | |
| 6 | Spine_Naval | 43.26 | −5.66 | 1696.18 | 94.88 | −58.69 | 1711.41 | 100.99 | −38.06 | 1707.85 | |
| 7 | Hip_Right | −138.47 | −75.06 | 1761.87 | −227.96 | −97.95 | 1777.76 | −220.05 | −78.65 | 1771.85 | |
| 8 | Hip_Left | −133.76 | 102.39 | 1725.26 | −216.37 | 59.28 | 1745.58 | −209.05 | 78.55 | 1746.32 | |
| 9 | Wrist_Left | 281.34 | 640.75 | 1414.72 | 255.48 | 637.33 | 1528.04 | 275.03 | 651.59 | 1582.82 | |
| 10 | Elbow_Left | 311.36 | 418.12 | 1505.85 | 287.28 | 393.16 | 1611.74 | 291.95 | 413.50 | 1628.86 | |
| 11 | Wrist_Right | 284.02 | −687.56 | 1889.89 | 229.53 | −662.53 | 2023.94 | 235.90 | −657.39 | 2019.26 | |
| 12 | Elbow_Right | 318.46 | −454.31 | 1821.72 | 294.19 | −435.84 | 1933.16 | 277.73 | −427.49 | 1937.79 | |
| 13 | Shoulder_Right | 348.34 | −184.93 | 1707.01 | 383.02 | −172.12 | 1815.31 | 385.52 | −154.98 | 1804.95 | |
| 14 | Neck | 410.80 | −36.42 | 1623.69 | 426.52 | −34.47 | 1748.00 | 430.28 | −15.48 | 1748.50 | |
| 15 | Spine_Chest | 188.19 | −16.37 | 1662.91 | 221.63 | −62.53 | 1702.20 | 226.70 | −43.22 | 1697.91 | |
| 16 | Shoulder_Left | 343.78 | 139.67 | 1575.41 | 375.68 | 108.79 | 1691.75 | 379.76 | 128.73 | 1701.92 | |
| 0° | 1 | Ankle_Right | −1016.73 | −125.23 | 1971.81 | −910.77 | −5.35 | 1873.28 | −905.52 | −14.01 | 1901.04 |
| 2 | Knee_Right | −622.24 | −105.71 | 1795.11 | −619.80 | −29.72 | 1825.31 | −616.54 | −33.76 | 1842.45 | |
| 3 | Ankle_Left | −1008.72 | 56.36 | 1988.34 | −922.10 | 175.26 | 1918.26 | −917.52 | 160.04 | 1927.88 | |
| 4 | Knee_Left | −614.77 | 88.59 | 1823.68 | −588.03 | 182.16 | 1832.79 | −585.62 | 173.24 | 1835.99 | |
| 5 | Pelvis | −171.81 | −9.58 | 1780.61 | −211.96 | 69.96 | 1762.81 | −209.90 | 68.89 | 1759.34 | |
| 6 | Spine_Naval | 21.34 | −9.79 | 1729.99 | 102.54 | 37.97 | 1707.32 | 104.79 | 39.16 | 1706.74 | |
| 7 | Hip_Right | −175.64 | −100.41 | 1766.37 | −209.87 | −14.81 | 1759.38 | −207.30 | −16.10 | 1755.45 | |
| 8 | Hip_Left | −167.56 | 91.15 | 1796.40 | −196.20 | 143.03 | 1778.89 | −194.73 | 142.01 | 1776.99 | |
| 9 | Wrist_Left | 263.87 | 726.84 | 1725.54 | 297.23 | 742.99 | 1823.48 | 288.25 | 742.88 | 1812.57 | |
| 10 | Elbow_Left | 321.61 | 474.87 | 1748.98 | 327.25 | 491.17 | 1800.85 | 326.41 | 494.07 | 1795.62 | |
| 11 | Wrist_Right | 139.72 | −711.43 | 1628.11 | 197.53 | −648.90 | 1740.66 | 181.54 | −641.17 | 1755.08 | |
| 12 | Elbow_Right | 298.69 | −508.78 | 1680.13 | 274.45 | −399.28 | 1748.29 | 282.42 | −403.92 | 1744.10 | |
| 13 | Shoulder_Right | 342.82 | −197.11 | 1665.62 | 382.95 | −120.35 | 1755.42 | 381.05 | −117.76 | 1754.38 | |
| 14 | Neck | 418.65 | −17.57 | 1666.19 | 434.28 | 30.41 | 1748.57 | 437.31 | 32.63 | 1751.23 | |
| 15 | Spine_Chest | 178.09 | −11.68 | 1699.94 | 225.62 | 31.75 | 1694.56 | 228.14 | 34.32 | 1698.10 | |
| 16 | Shoulder_Left | 339.89 | 175.64 | 1672.99 | 383.64 | 198.84 | 1755.97 | 381.10 | 199.85 | 1751.66 | |
| 15° | 1 | Ankle_Right | −984.67 | −121.62 | 1882.06 | −929.25 | −26.82 | 1825.63 | −927.29 | −34.47 | 1851.35 |
| 2 | Knee_Right | −595.03 | −109.03 | 1707.27 | −634.96 | −41.66 | 1777.48 | −636.81 | −36.43 | 1774.68 | |
| 3 | Ankle_Left | −974.33 | 60.96 | 1990.39 | −930.93 | 142.59 | 1893.71 | −924.32 | 146.16 | 1935.49 | |
| 4 | Knee_Left | −592.47 | 83.01 | 1810.49 | −612.19 | 157.37 | 1840.44 | −606.64 | 157.57 | 1837.52 | |
| 5 | Pelvis | −153.99 | −5.12 | 1751.85 | −233.15 | 78.98 | 1744.09 | −229.19 | 85.16 | 1739.42 | |
| 6 | Spine_Naval | 33.73 | −1.54 | 1691.71 | 90.07 | 43.08 | 1685.89 | 94.77 | 53.49 | 1685.95 | |
| 7 | Hip_Right | −154.85 | −95.62 | 1743.78 | −234.93 | −1.03 | 1722.72 | −231.39 | 4.01 | 1717.35 | |
| 8 | Hip_Left | −153.04 | 95.24 | 1760.79 | −219.39 | 149.73 | 1772.24 | −215.18 | 156.45 | 1770.56 | |
| 9 | Wrist_Left | 228.25 | 722.38 | 1771.50 | 240.26 | 731.07 | 1880.25 | 251.22 | 739.53 | 1840.89 | |
| 10 | Elbow_Left | 298.19 | 476.90 | 1748.38 | 278.60 | 480.96 | 1831.46 | 286.02 | 490.25 | 1818.82 | |
| 11 | Wrist_Right | 273.34 | −723.05 | 1474.17 | 296.09 | −653.51 | 1632.49 | 320.39 | −629.03 | 1625.09 | |
| 12 | Elbow_Right | 316.36 | −480.41 | 1555.63 | 310.44 | −409.42 | 1673.01 | 350.78 | −378.84 | 1689.04 | |
| 13 | Shoulder_Right | 358.32 | −179.00 | 1620.47 | 378.35 | −116.20 | 1714.08 | 377.62 | −103.38 | 1717.54 | |
| 14 | Neck | 424.77 | 0.88 | 1623.38 | 426.06 | 44.12 | 1730.31 | 432.48 | 56.47 | 1735.69 | |
| 15 | Spine_Chest | 186.90 | 0.31 | 1654.60 | 215.67 | 41.38 | 1672.70 | 221.02 | 52.58 | 1671.88 | |
| 16 | Shoulder_Left | 357.27 | 190.75 | 1659.61 | 381.81 | 194.42 | 1747.79 | 387.72 | 205.48 | 1752.88 | |
| 30° | 1 | Ankle_Right | −961.56 | −127.33 | 1843.05 | −930.58 | −13.37 | 1796.87 | −924.88 | −14.38 | 1828.54 |
| 2 | Knee_Right | −584.75 | −90.11 | 1672.12 | −635.62 | −19.11 | 1747.83 | −636.64 | −16.27 | 1742.99 | |
| 3 | Ankle_Left | −943.11 | 46.52 | 1997.76 | −930.74 | 135.16 | 1904.42 | −920.25 | 142.21 | 1944.43 | |
| 4 | Knee_Left | −574.94 | 85.26 | 1818.96 | −611.52 | 158.80 | 1857.32 | −605.24 | 165.05 | 1856.77 | |
| 5 | Pelvis | −152.81 | −10.48 | 1724.53 | −232.25 | 102.16 | 1748.15 | −230.40 | 107.45 | 1750.23 | |
| 6 | Spine_Naval | 33.21 | −2.09 | 1678.98 | 91.12 | 77.99 | 1684.94 | 94.33 | 79.62 | 1686.50 | |
| 7 | Hip_Right | −155.77 | −94.38 | 1697.00 | −234.66 | 29.75 | 1708.09 | −234.70 | 35.17 | 1709.94 | |
| 8 | Hip_Left | −149.54 | 82.55 | 1755.07 | −217.69 | 163.87 | 1792.63 | −213.86 | 168.67 | 1796.54 | |
| 9 | Wrist_Left | 245.88 | 556.86 | 1635.89 | 247.38 | 697.02 | 2043.84 | 258.79 | 711.82 | 1912.97 | |
| 10 | Elbow_Left | 286.85 | 435.28 | 1849.49 | 282.86 | 465.68 | 1935.11 | 288.07 | 464.29 | 1934.20 | |
| 11 | Wrist_Right | 241.91 | −654.73 | 1367.10 | 290.47 | −587.02 | 1462.72 | 316.28 | −565.36 | 1494.09 | |
| 12 | Elbow_Right | 293.88 | −425.33 | 1458.58 | 306.85 | −360.10 | 1562.81 | 324.58 | −366.68 | 1579.94 | |
| 13 | Shoulder_Right | 356.87 | −151.10 | 1569.83 | 377.42 | −86.35 | 1675.26 | 379.49 | −88.08 | 1675.85 | |
| 14 | Neck | 414.21 | 18.92 | 1619.28 | 427.06 | 64.93 | 1731.18 | 430.84 | 62.95 | 1736.03 | |
| 15 | Spine_Chest | 183.30 | 2.68 | 1648.34 | 216.77 | 78.71 | 1672.56 | 220.64 | 81.01 | 1672.99 | |
| 16 | Shoulder_Left | 355.78 | 190.08 | 1696.86 | 383.68 | 206.97 | 1784.32 | 390.44 | 206.70 | 1791.37 | |
| 45° | 1 | Ankle_Right | −988.68 | −122.79 | 1823.42 | −931.72 | 8.07 | 1767.61 | −925.22 | 7.84 | 1774.56 |
| 2 | Knee_Right | −604.83 | −72.16 | 1657.31 | −636.24 | 11.19 | 1720.32 | −633.59 | 17.25 | 1715.18 | |
| 3 | Ankle_Left | −965.66 | 6.29 | 1993.24 | −930.76 | 125.95 | 1908.22 | −919.36 | 109.26 | 1939.91 | |
| 4 | Knee_Left | −588.76 | 65.84 | 1824.38 | −610.89 | 157.01 | 1869.75 | −603.10 | 161.93 | 1870.89 | |
| 5 | Pelvis | −164.75 | −11.89 | 1695.88 | −231.34 | 124.34 | 1752.69 | −228.31 | 129.73 | 1751.49 | |
| 6 | Spine_Naval | 24.49 | 1.23 | 1652.35 | 92.25 | 112.53 | 1687.45 | 95.75 | 118.38 | 1683.65 | |
| 7 | Hip_Right | −169.19 | −89.72 | 1653.51 | −234.20 | 63.86 | 1696.64 | −232.17 | 67.97 | 1698.83 | |
| 8 | Hip_Left | −159.82 | 74.42 | 1742.87 | −216.72 | 173.34 | 1810.98 | −212.65 | 179.41 | 1806.20 | |
| 9 | Wrist_Left | 223.74 | 467.21 | 1706.84 | 252.34 | 625.12 | 2188.58 | 258.00 | 628.87 | 2177.64 | |
| 10 | Elbow_Left | 302.89 | 368.26 | 1921.51 | 286.44 | 426.35 | 2026.10 | 290.77 | 430.41 | 2010.70 | |
| 11 | Wrist_Right | 225.72 | −545.64 | 1161.43 | 285.49 | −481.78 | 1310.37 | 287.23 | −484.87 | 1321.89 | |
| 12 | Elbow_Right | 291.07 | −379.30 | 1341.14 | 303.53 | −285.62 | 1463.11 | 303.46 | −261.94 | 1466.59 | |
| 13 | Shoulder_Right | 343.78 | −133.40 | 1511.05 | 377.11 | −47.77 | 1640.17 | 376.33 | −36.74 | 1635.05 | |
| 14 | Neck | 413.13 | 14.64 | 1600.52 | 427.54 | 85.08 | 1731.03 | 429.60 | 93.46 | 1721.73 | |
| 15 | Spine_Chest | 177.98 | 6.12 | 1627.35 | 217.77 | 115.14 | 1675.48 | 221.16 | 121.32 | 1671.19 | |
| 16 | Shoulder_Left | 365.38 | 170.77 | 1709.64 | 385.60 | 210.49 | 1817.69 | 391.93 | 216.10 | 1807.59 | |
| Distance | 1500 mm | 2000 mm | 2500 mm | 3000 mm | 3500 mm | 4000 mm | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Orientation | ||||||||||||
| 0° | 0.4283 | 0.7327 | 0.7127 | 0.9849 | 0.4168 | 0.6579 | 0.7698 | 0.9214 | 0.8127 | 0.9796 | 0.7872 | 0.9841 |
| Distance | 2000 mm | 2500 mm | 3000 mm | 3500 mm | 4000 mm | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Orientation | ||||||||||
| −45° | −0.1362 | 0.9853 | −0.0504 | 0.9845 | −0.0363 | 0.9728 | 0.5672 | 0.9507 | −0.0368 | 0.9596 |
| −30° | 0.0724 | 0.8493 | 0.7436 | 0.9243 | 0.7660 | 0.9375 | 0.7504 | 0.9226 | 0.0286 | 0.7229 |
| −15° | 0.7112 | 0.9653 | 0.7313 | 0.9527 | 0.7427 | 0.9732 | 0.7343 | 0.9569 | −0.0776 | 0.9753 |
| 0° | 0.7127 | 0.9849 | 0.4168 | 0.6579 | 0.7698 | 0.9214 | 0.8127 | 0.9796 | 0.7872 | 0.9841 |
| 15° | 0.7928 | 0.9726 | 0.8122 | 0.9888 | 0.7561 | 0.9526 | 0.6730 | 0.9290 | 0.5998 | 0.9351 |
| 30° | −0.1009 | 0.9770 | −0.0833 | 0.9667 | 0.1693 | 0.9267 | 0.6941 | 0.9531 | 0.7011 | 0.9866 |
| 45° | −0.2969 | 0.8619 | 0.5375 | 0.9203 | 0.2850 | 0.2859 | 0.1841 | 0.6947 | 0.0205 | −0.0486 |
| Test Scenario | Distance (mm) | ||
|---|---|---|---|
| Forward and backward walking | - | 0.9744 | 0.9781 |
| Lateral walking | 2000 | 0.9003 | 0.9162 |
| 2500 | 0.9762 | 0.9960 | |
| 3000 | 0.9820 | 0.9961 | |
| Marching in place | 2000 | 0.9770 | 0.9949 |
| 2500 | 0.9814 | 0.9875 | |
| In-place body rotation | 2000 | 0.9625 | 0.9681 |
References
- Ren, Z.; Yuan, J.; Meng, J.; Zhang, Z. Robust Part-Based Hand Gesture Recognition Using Kinect Sensor. IEEE Trans. Multimed. 2013, 15, 1110–1120. [Google Scholar] [CrossRef]
- Du, G.; Zhang, P.; Mai, J.; Li, S. Markerless Kinect-Based Hand Tracking for Robot Teleoperation. Int. J. Adv. Robot. Syst. 2012, 9, 36–44. [Google Scholar] [CrossRef]
- Ramos, J.; Kim, S. Dynamic Locomotion Synchronization of Bipedal Robot and Human Operator via Bilateral Feedback Teleoperation. Sci. Robot. 2019, 4, eaav4282. [Google Scholar] [CrossRef] [PubMed]
- Kofman, J.; Wu, X.; Luu, T.J.; Verma, S. Teleoperation of a Robot Manipulator Using a Vision-Based Human-Robot Interface. IEEE Trans. Ind. Electron. 2005, 52, 1206–1219. [Google Scholar] [CrossRef]
- Verma, S. Vision-Based Markerless 3D Human-Arm Tracking. Master’s Thesis, University of Ottawa, Ottawa, ON, Canada, 2005. [Google Scholar]
- Tölgyessy, M.; Dekan, M.; Chovanec, Ľ.; Hubinský, P. Evaluation of the Azure Kinect and Its Comparison to Kinect v1 and Kinect v2. Sensors 2021, 21, 413. [Google Scholar] [CrossRef]
- Xing, Q.J.; Shen, Y.Y.; Cao, R.; Zong, S.X.; Zhao, S.X.; Shen, Y.F. Functional Movement Screen Dataset Collected with Two Azure Kinect Depth Sensors. Sci. Data 2022, 9, 104. [Google Scholar] [CrossRef] [PubMed]
- Microsoft. About Azure Kinect DK. Microsoft Learn. Available online: https://learn.microsoft.com/previous-versions/azure/kinect-dk/about-azure-kinect-dk (accessed on 25 December 2024).
- Amprimo, G.; Masi, G.; Priano, L.; Azzaro, C.; Galli, F.; Pettiti, G.; Mauro, A.; Ferraris, C. Assessment Tasks and Virtual Exergames for Remote Monitoring of Parkinson’s Disease: An Integrated Approach Based on Azure Kinect. Sensors 2022, 22, 8173. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Li, C.; Wu, C.; Zhao, C.; Sun, J.; Peng, H.; Hu, X.; Hu, B. A Gait Assessment Framework for Depression Detection Using Kinect Sensors. IEEE Sens. J. 2021, 21, 3260–3270. [Google Scholar] [CrossRef]
- Bertram, J.; Krüger, T.; Röhling, H.M.; Jelusic, A.; Mansow-Model, S.; Schniepp, R.; Wuehr, M.; Otte, K. Accuracy and Repeatability of the Microsoft Azure Kinect for Clinical Measurement of Motor Function. PLoS ONE 2023, 18, e0279697. [Google Scholar] [CrossRef] [PubMed]
- Bärligea, A.; Hase, K.; Yoshida, M. Simulation of Human Movement in Zero Gravity. Sensors 2024, 24, 1770. [Google Scholar] [CrossRef] [PubMed]
- Nascimento, H.; Mujica, M.; Benoussaad, M. Collision Avoidance in Human-Robot Interaction Using Kinect Vision System Combined with Robot’s Model and Data. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 10293–10298. [Google Scholar] [CrossRef]
- Zhang, J.; Li, P.; Zhu, T.; Zhang, W.A.; Liu, S. Human Motion Capture Based on Kinect and IMUs and Its Application to Human-Robot Collaboration. In Proceedings of the 2020 5th International Conference on Advanced Robotics and Mechatronics (ICARM), Shenzhen, China, 18–21 December 2020; pp. 392–397. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, D.; Cai, L. Deep Learning-Based Upper Limb Functional Assessment Using a Single Kinect v2 Sensor. Sensors 2020, 20, 1903. [Google Scholar] [CrossRef]
- An, J.; Cheng, X.; Wang, Q.; Chen, H.; Li, J.; Li, S. Human Action Recognition Based on Kinect. J. Phys. Conf. Ser. 2020, 1693, 012190. [Google Scholar] [CrossRef]
- Park, B.-K.D.; Jung, H.; Ebert, S.M.; Corner, B.D.; Reed, M.P. Efficient Model-Based Anthropometry under Clothing Using Low-Cost Depth Sensors. Sensors 2024, 24, 1350. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.-L.; Chang, C.-C.; Li, L.; Xu, X. A Simple Method to Optimally Select Upper-Limb Joint Angle Trajectories from Two Kinect Sensors during the Twisting Task for Posture Analysis. Sensors 2022, 22, 7662. [Google Scholar] [CrossRef] [PubMed]
- Saputra, A.A.; Besari, A.R.A.; Kubota, N. Human Joint Skeleton Tracking Using Multiple Kinect Azure. In Proceedings of the 2022 International Electronics Symposium (IES), Surabaya, Indonesia, 9–11 August 2022. [Google Scholar] [CrossRef]
- Ryselis, K.; Petkus, T.; Blažauskas, T.; Maskeliūnas, R.; Damaševičius, R. Multiple Kinect Based System to Monitor and Analyze Key Performance Indicators of Physical Training. Hum.-Centric Comput. Inf. Sci. 2020, 10, 51. [Google Scholar] [CrossRef]
- Eichler, N.; Hel-Or, H.; Shimshoni, I. Spatio-Temporal Calibration of Multiple Kinect Cameras Using 3D Human Pose. Sensors 2022, 22, 8900. [Google Scholar] [CrossRef] [PubMed]
- Yeung, L.F.; Yang, Z.; Cheng, K.C.; Du, D.; Tong, R.K.Y. Effects of Camera Viewing Angles on Tracking Kinematic Gait Patterns Using Azure Kinect, Kinect v2 and Orbbec Astra Pro v2. Gait Posture 2021, 87, 19–26. [Google Scholar] [CrossRef]
- Bilesan, A.; Behzadipour, S.; Tsujita, T.; Komizunai, S.; Konno, A. Markerless Human Motion Tracking Using Microsoft Kinect SDK and Inverse Kinematics. In Proceedings of the 2019 12th Asian Control Conference (ASCC), Kitakyushu, Japan, 9–12 June 2019; pp. 504–509. [Google Scholar]
- Bilesan, A.; Komizunai, S.; Tsujita, T.; Konno, A. Improved 3D Human Motion Capture Using Kinect Skeleton and Depth Sensor. J. Robot. Mechatron. 2021, 33, 1408–1422. [Google Scholar] [CrossRef]
- Beshara, P.; Anderson, D.B.; Pelletier, M.; Walsh, W.R. The Reliability of the Microsoft Kinect and Ambulatory Sensor-Based Motion Tracking Devices to Measure Shoulder Range-of-Motion: A Systematic Review and Meta-Analysis. Sensors 2021, 21, 8186. [Google Scholar] [CrossRef]
- Kurillo, G.; Hemingway, E.; Cheng, M.L.; Cheng, L. Evaluating the Accuracy of the Azure Kinect and Kinect v2. Sensors 2022, 22, 2469. [Google Scholar] [CrossRef]
- Büker, L.; Quinten, V.; Hackbarth, M.; Hellmers, S.; Diekmann, R.; Hein, A. How the Processing Mode Influences Azure Kinect Body Tracking Results. Sensors 2023, 23, 878. [Google Scholar] [CrossRef] [PubMed]
- Jamali, Z.; Behzadipour, S. Quantitative Evaluation of Parameters Affecting the Accuracy of Microsoft Kinect in Gait Analysis. In Proceedings of the 23rd Iranian Conference on Biomedical Engineering (ICBME), Tehran, Iran, 24–25 November 2016; pp. 306–311. [Google Scholar] [CrossRef]
- Martiš, P.; Košutzká, Z.; Kranzl, A. A Step Forward Understanding Directional Limitations in Markerless Smartphone-Based Gait Analysis: A Pilot Study. Sensors 2024, 24, 3091. [Google Scholar] [CrossRef] [PubMed]
- Thomas, J.; Hall, J.B.; Bliss, R.; Guess, T.M. Comparison of Azure Kinect and Optical Retroreflective Motion Capture for Kinematic and Spatiotemporal Evaluation of the Sit-to-Stand Test. Gait Posture 2022, 94, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Steinebach, T.; Grosse, E.H.; Glock, C.H.; Wakula, J.; Lunin, A. Accuracy Evaluation of Two Markerless Motion Capture Systems for Measurement of Upper Extremities: Kinect V2 and Captiv. Hum. Factors Ergon. Manuf. Serv. Ind. 2020, 30, 315–327. [Google Scholar] [CrossRef]
- Antico, M.; Balletti, N.; Laudato, G.; Lazich, A.; Notarantonio, M.; Oliveto, R.; Ricciardi, S.; Scalabrino, S.; Simeone, J. Postural Control Assessment via Microsoft Azure Kinect DK: An Evaluation Study. Comput. Methods Programs Biomed. 2021, 209, 106324. [Google Scholar] [CrossRef] [PubMed]
- Milosevic, B.; Leardini, A.; Farella, E. Kinect and Wearable Inertial Sensors for Motor Rehabilitation Programs at Home: State of the Art and an Experimental Comparison. BioMed. Eng. OnLine 2020, 19, 25. [Google Scholar] [CrossRef]
- Pfister, A.; West, A.M.; Bronner, S.; Noah, J.A. Comparative Abilities of Microsoft Kinect and Vicon 3D Motion Capture for Gait Analysis. J. Med. Eng. Technol. 2014, 38, 274–280. [Google Scholar] [CrossRef]
- Holland, M. Visual Puppeteering Using the Vizualeyez: 3D Motion Capture System. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2018. [Google Scholar]
- Oztop, E.; Lin, L.-H.; Kawato, M.; Cheng, G. Extensive Human Training for Robot Skill Synthesis: Validation on a Robotic Hand. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 1788–1793. [Google Scholar] [CrossRef]
- PTI Phoenix Technologies Inc. Visualeyez III VZ10K/VZ10K5 Trackers. Available online: https://www.ptiphoenix.com/products/trackers/VZ10K_VZ10K5 (accessed on 25 December 2024).
- Sosa-León, V.A.L.; Schwering, A. Evaluating Automatic Body Orientation Detection for Indoor Location from Skeleton Tracking Data to Detect Socially Occupied Spaces Using the Kinect v2, Azure Kinect, and Zed 2i. Sensors 2022, 22, 3798. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Bao, T.; Jia, W.; Ma, S.; Yuan, J. Towards a More Practical Data-Driven Biped Walking Control. In Proceedings of the 2021 IEEE International Conference on Robotics and Biomimetics (ROBIO), Sanya, China, 27–31 December 2021; pp. 1058–1064. [Google Scholar] [CrossRef]
- Cao, Z.; Bao, T.; Ren, Z.; Fan, Y.; Deng, K.; Jia, W. Real-Time Stylized Humanoid Behavior Control through Interaction and Synchronization. Sensors 2022, 22, 1457. [Google Scholar] [CrossRef] [PubMed]

| Pose | Orientation (°) | Distance Range (mm) | Distance Interval (mm) | Number of Sub-Tests |
|---|---|---|---|---|
| Standing at attention | 0 | [1500, 4000] | 100 | 26 |
| ±30 | [1500, 4000] | 500 | 12 | |
| ±45 | [1500, 4000] | 500 | 12 | |
| Arms swinging (Left forward) | 0 | [1500, 4000] | 100 | 26 |
| Arms swinging (Right forward) | 0 | [1500, 4000] | 100 | 26 |
| Arms Outstretched laterally 1 | 0 | [1500, 4000] | 100 | 26 |
| ±15 | [2000, 4000] | 500 | 10 | |
| ±30 | [2000, 4000] | 500 | 10 | |
| ±45 | [2000, 4000] | 500 | 10 |
| Action 1 | Orientation (°) | Distance Range (mm) | Distance Interval (mm) | Number of Sub-Tests |
|---|---|---|---|---|
| Marching in place | 0 | [1500, 3500] | 500 | 5 |
| Forward and backward walking | 0 | [1500, 3500] | - | 3 |
| Lateral walking | 0 | [1500, 3500] | 500 | 5 |
| In-place body rotation | [−15,15] | 2000 | - | 1 |
| Skeletal Segment Index (j) | Skeletal Segment Name | Terminating Node (i) | Originating Node (i) | Weight (Pelvis Weight = 1) | Normalized Weight () |
|---|---|---|---|---|---|
| 1 | Right Shank | Ankle_Right (1) | Knee_Right (2) | 10 | 0.130 |
| 2 | Right Thigh | Knee_Right (2) | Hip_Right (7) | 5 | 0.065 |
| 3 | Left Shank | Ankle_Left (3) | Knee_Left (4) | 10 | 0.130 |
| 4 | Left Thigh | Knee_Left (4) | Hip_Left (8) | 5 | 0.065 |
| 5 | Pelvis | Pelvis (5) | Pelvis (5) | 1 | 0.013 |
| 6 | Lumbar Spine | Spine_Naval (6) | Pelvis (5) | 1 | 0.013 |
| 7 | Right Hip | Hip_Right (7) | Pelvis (5) | 3 | 0.039 |
| 8 | Left Hip | Hip_Left (8) | Pelvis (5) | 3 | 0.039 |
| 9 | Left Forearm | Wrist_Left (9) | Elbow_Left (10) | 10 | 0.130 |
| 10 | Left Upper Arm | Elbow_Left (10) | Shoulder_Left (16) | 5 | 0.065 |
| 11 | Right Forearm | Wrist_Right (11) | Elbow_Right (12) | 10 | 0.130 |
| 12 | Right Upper Arm | Elbow_Right (12) | Shoulder_Right (13) | 5 | 0.065 |
| 13 | Right Scapula | Shoulder_Right (13) | Neck (14) | 3 | 0.039 |
| 14 | Cervical Spine | Neck (14) | Spine_Chest (15) | 2 | 0.025 |
| 15 | Thoracic Spine | Spine_Chest (15) | Spine_Naval (6) | 1 | 0.013 |
| 16 | Left Scapula | Shoulder_Left (16) | Neck (14) | 3 | 0.039 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, W.; Wang, H.; Chen, Q.; Bao, T.; Sun, Y. Analysis of Kinect-Based Human Motion Capture Accuracy Using Skeletal Cosine Similarity Metrics. Sensors 2025, 25, 1047. https://doi.org/10.3390/s25041047
Jia W, Wang H, Chen Q, Bao T, Sun Y. Analysis of Kinect-Based Human Motion Capture Accuracy Using Skeletal Cosine Similarity Metrics. Sensors. 2025; 25(4):1047. https://doi.org/10.3390/s25041047
Chicago/Turabian StyleJia, Wenchuan, Hanyang Wang, Qi Chen, Tianxu Bao, and Yi Sun. 2025. "Analysis of Kinect-Based Human Motion Capture Accuracy Using Skeletal Cosine Similarity Metrics" Sensors 25, no. 4: 1047. https://doi.org/10.3390/s25041047
APA StyleJia, W., Wang, H., Chen, Q., Bao, T., & Sun, Y. (2025). Analysis of Kinect-Based Human Motion Capture Accuracy Using Skeletal Cosine Similarity Metrics. Sensors, 25(4), 1047. https://doi.org/10.3390/s25041047







