A Multimodal Deep Learning Approach to Intraoperative Nociception Monitoring: Integrating Electroencephalogram, Photoplethysmography, and Electrocardiogram
Abstract
:1. Introduction
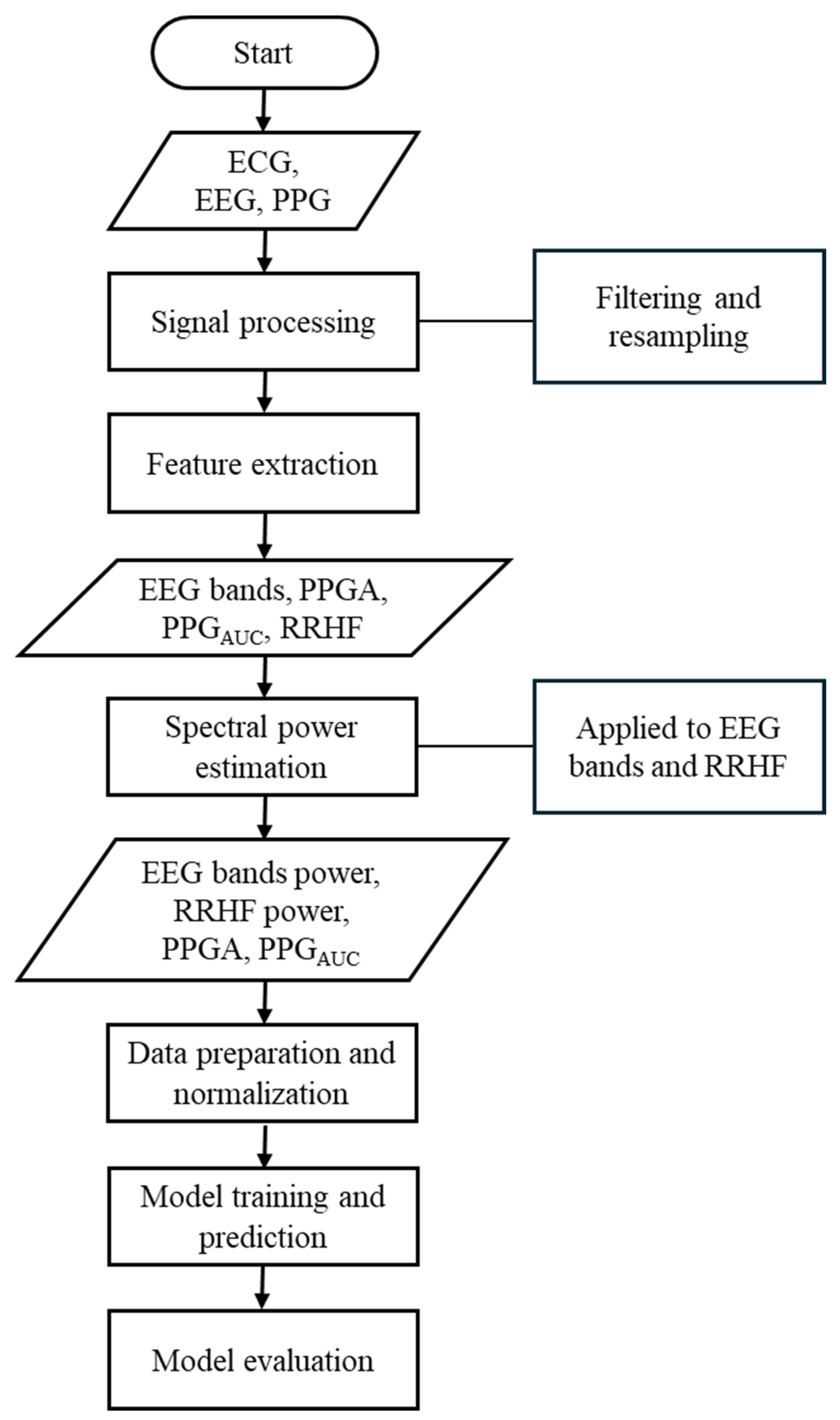
2. Materials and Methods
2.1. Data Collection
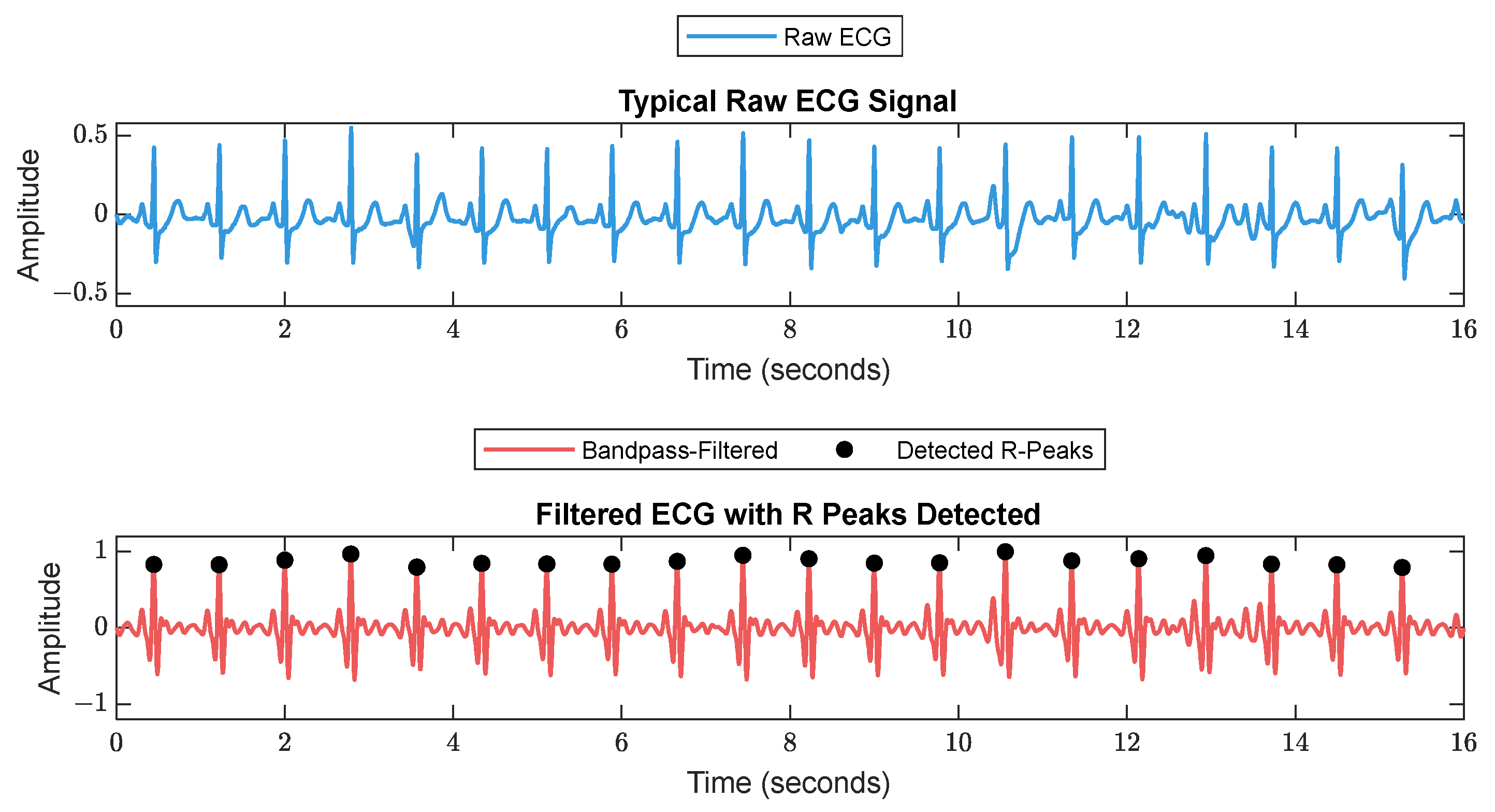
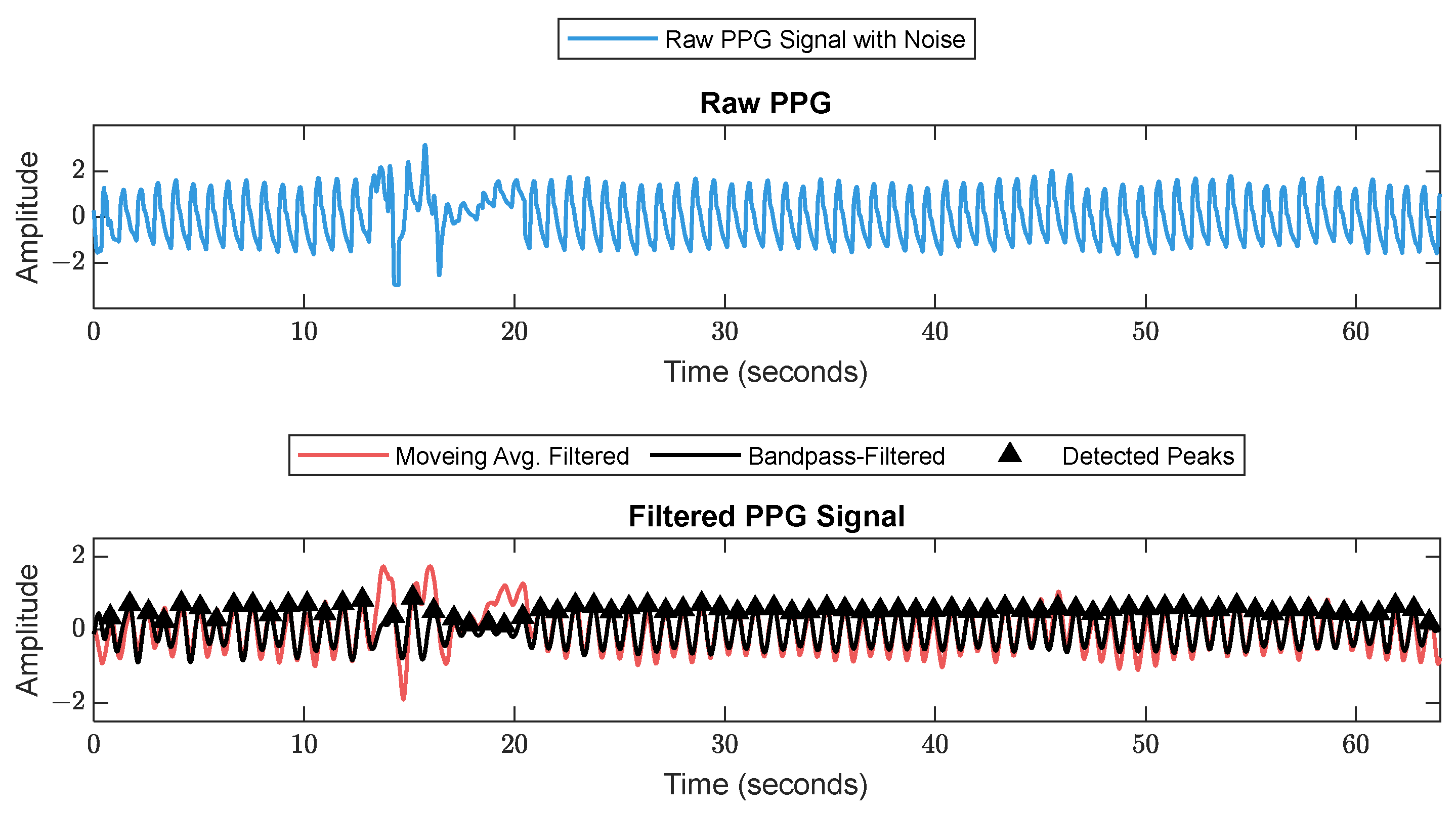
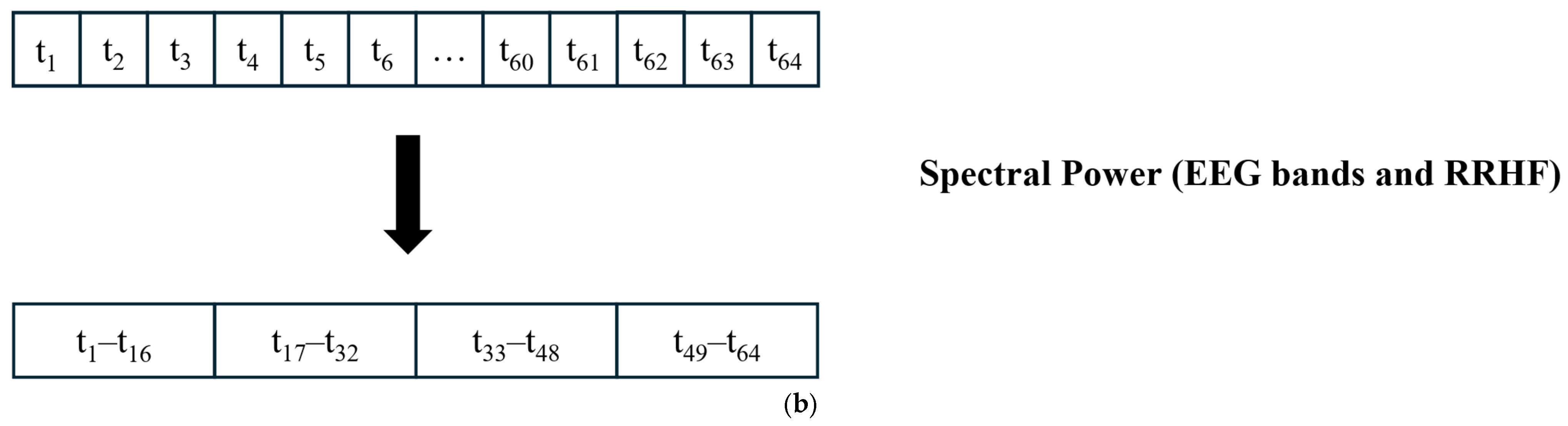
2.2. Signal Processing and Feature Extraction
- Delta: 0.5–3.5.
- Theta: 4–7.5.
- Alpha: 8–12.
- Beta: 13–30.
- Gamma: 30.5–48.
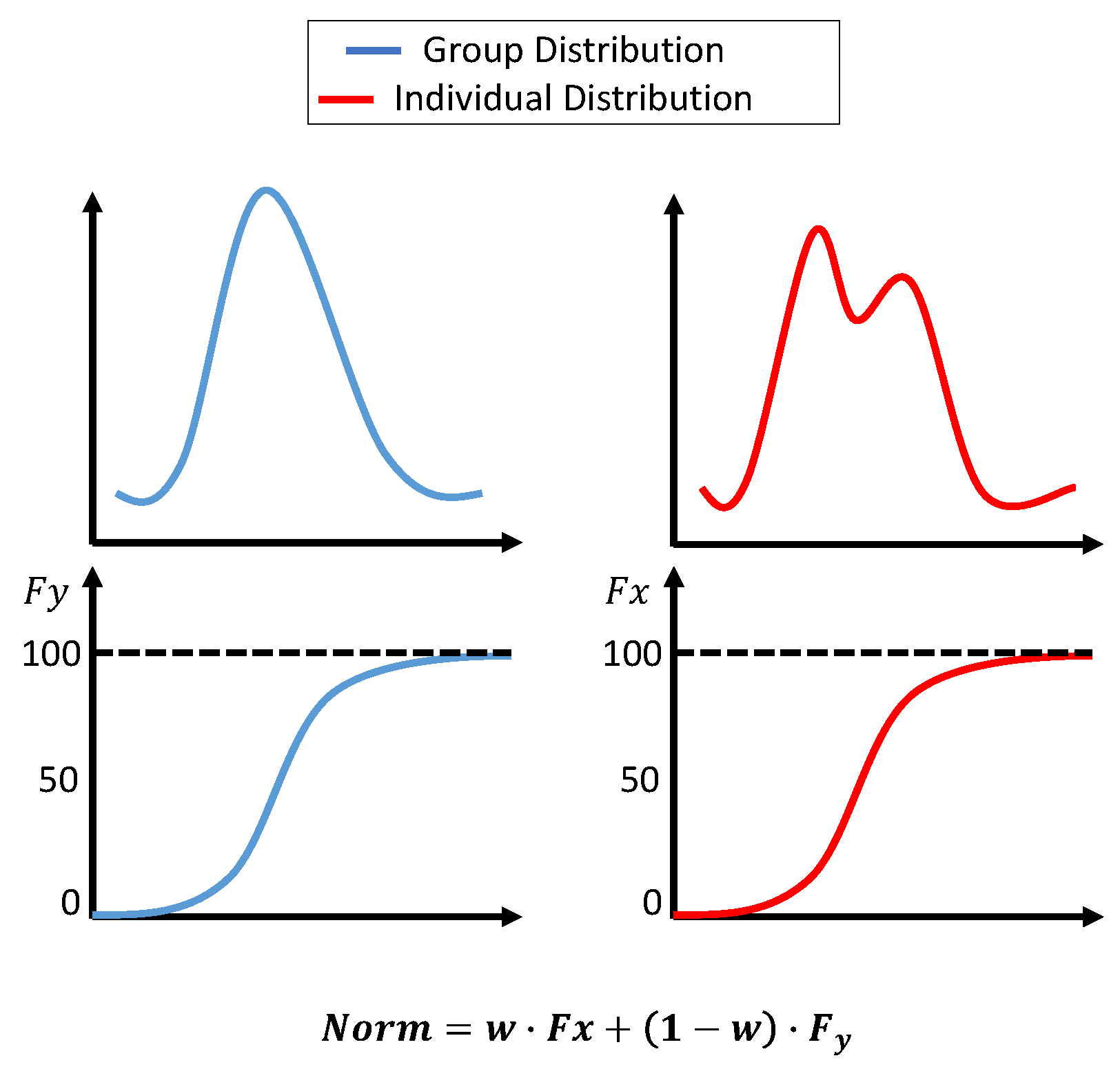
2.3. Normalization
- Xnorm is the normalized value of .
- is the cumulative probability of in the individual dataset (from the beginning of the surgery until the current value).
- is the cumulative probability of in the group dataset.
- is the weight for the individual dataset, adjusted based on t, which is the window number. starts at 0 and smoothly adjusts to 0.7 over the segments.
- Xnorm is the normalized value of .
- is the collected data from the beginning of the surgery to the current time.
- is the group dataset.
- Xnorm is the normalized value of .
- is the collected data from the beginning of the surgery to the current time.
- is the group dataset.
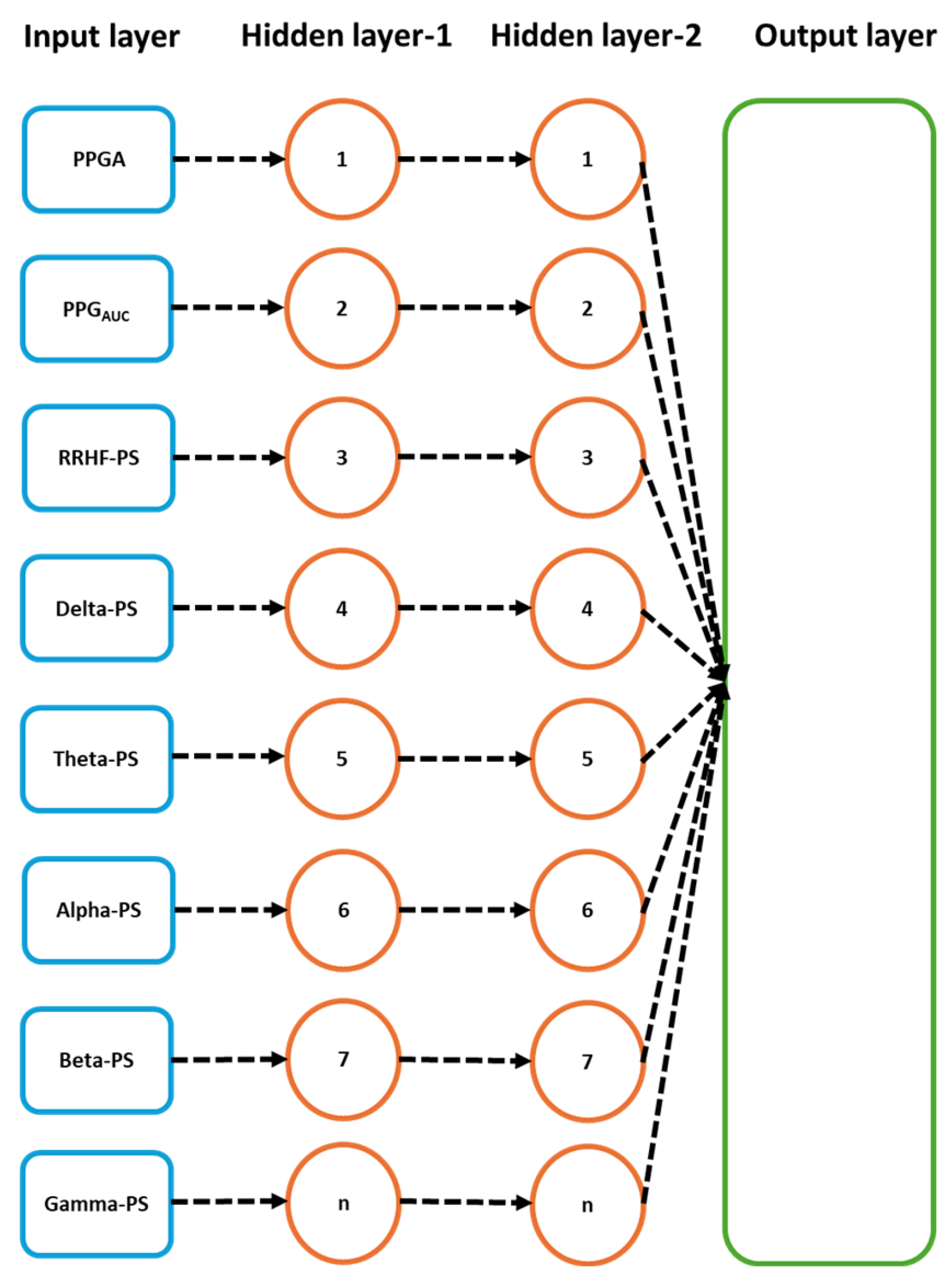
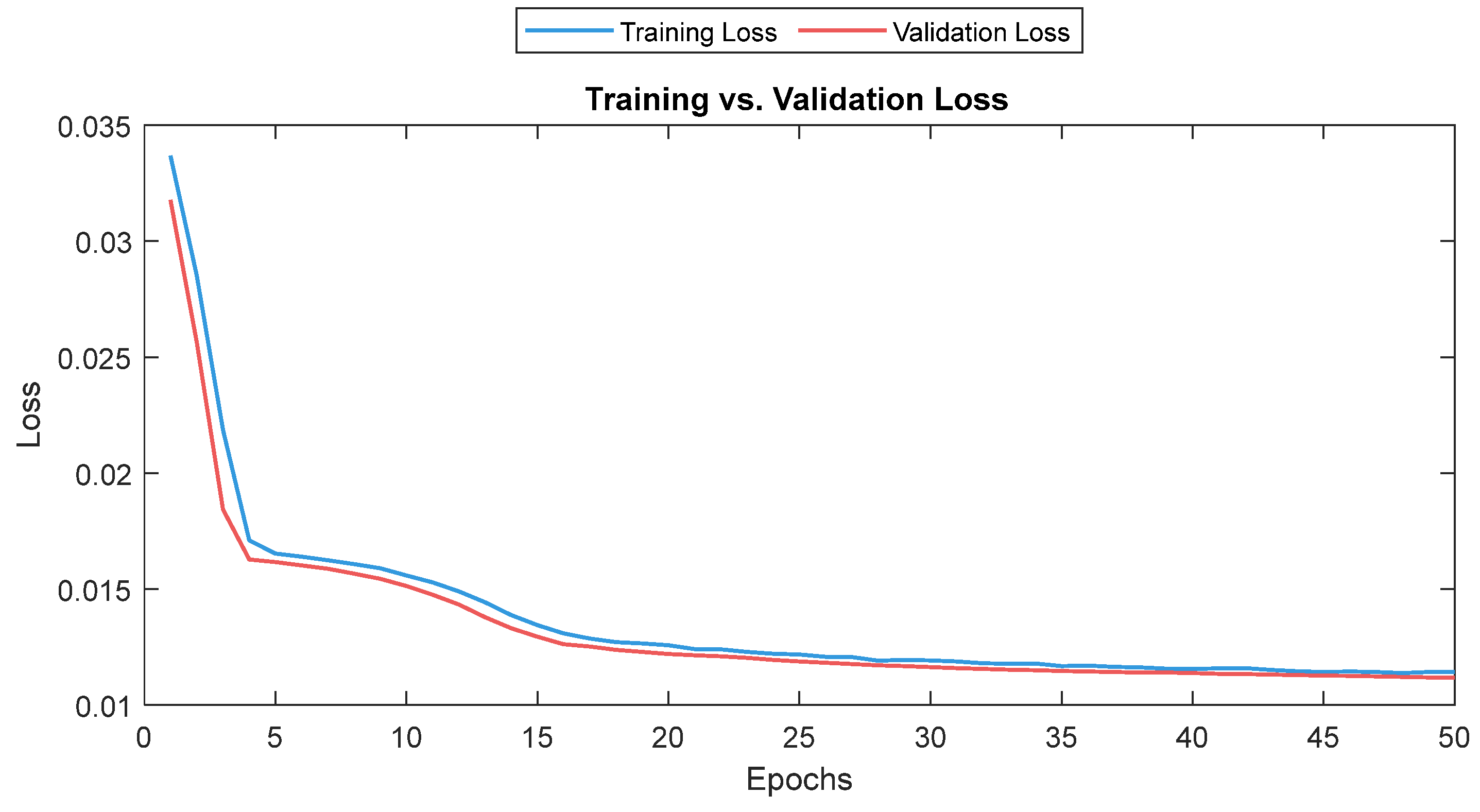
2.4. Deep Learning Training
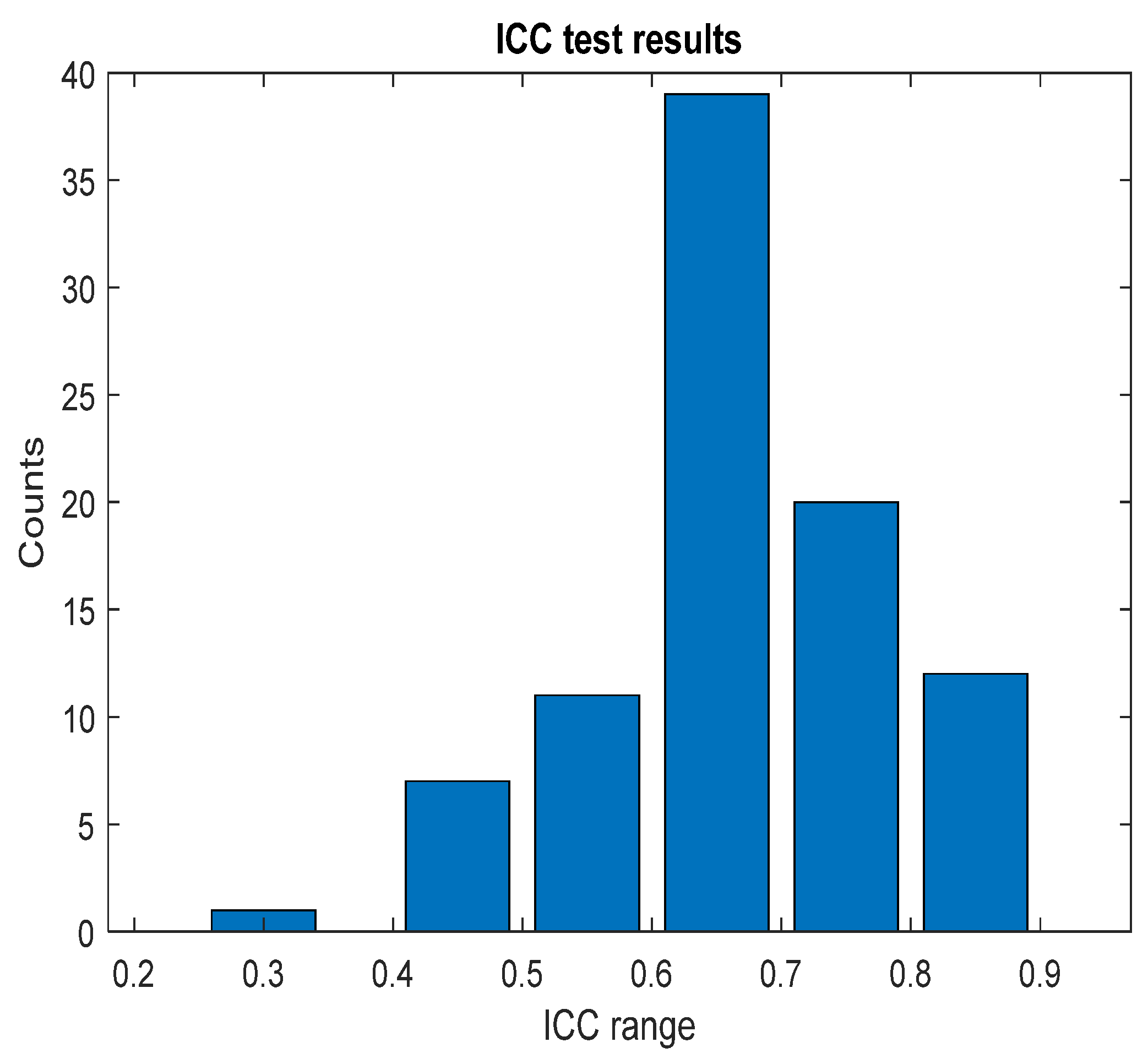
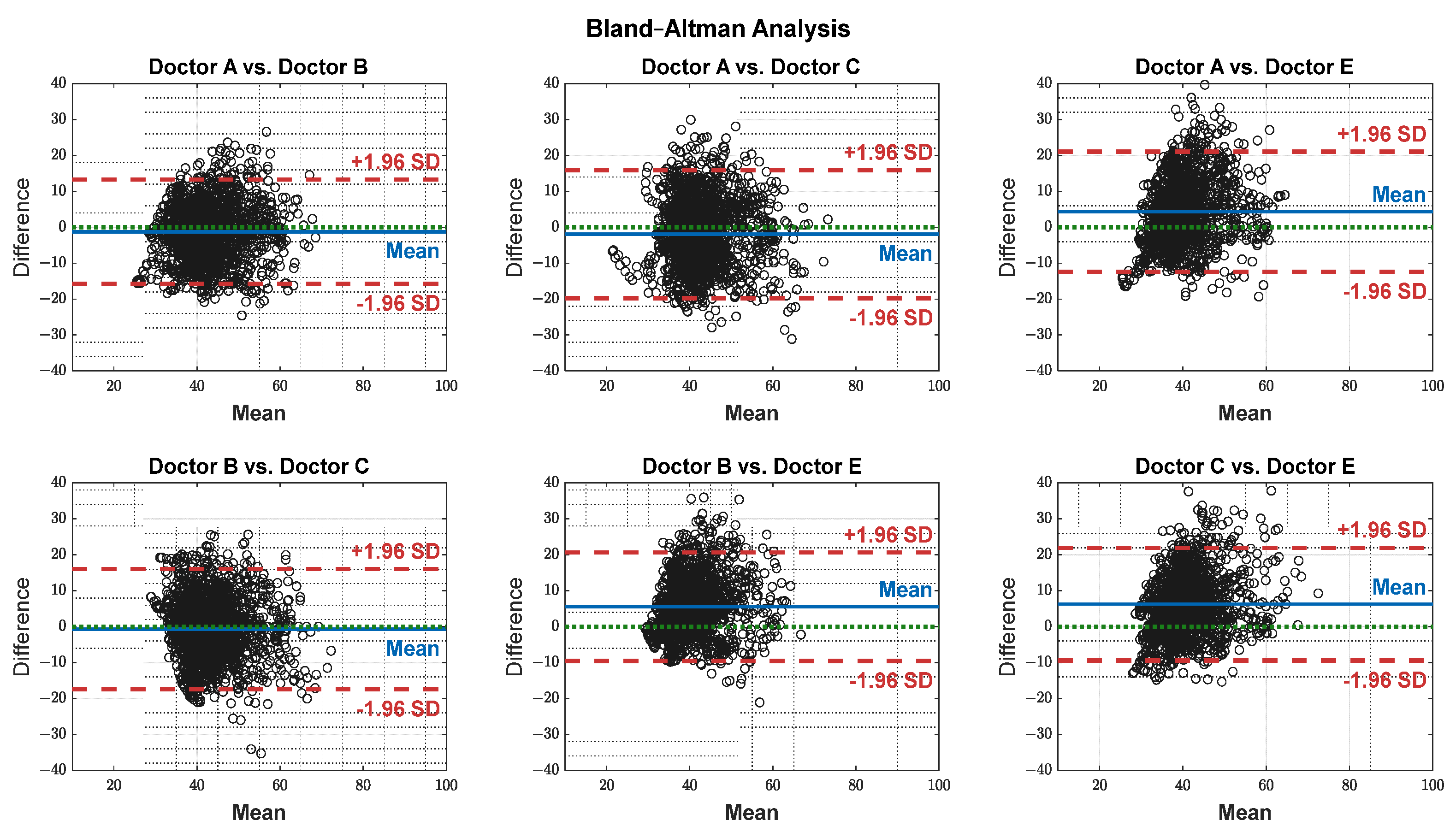
2.5. Statistical Analysis
3. Results
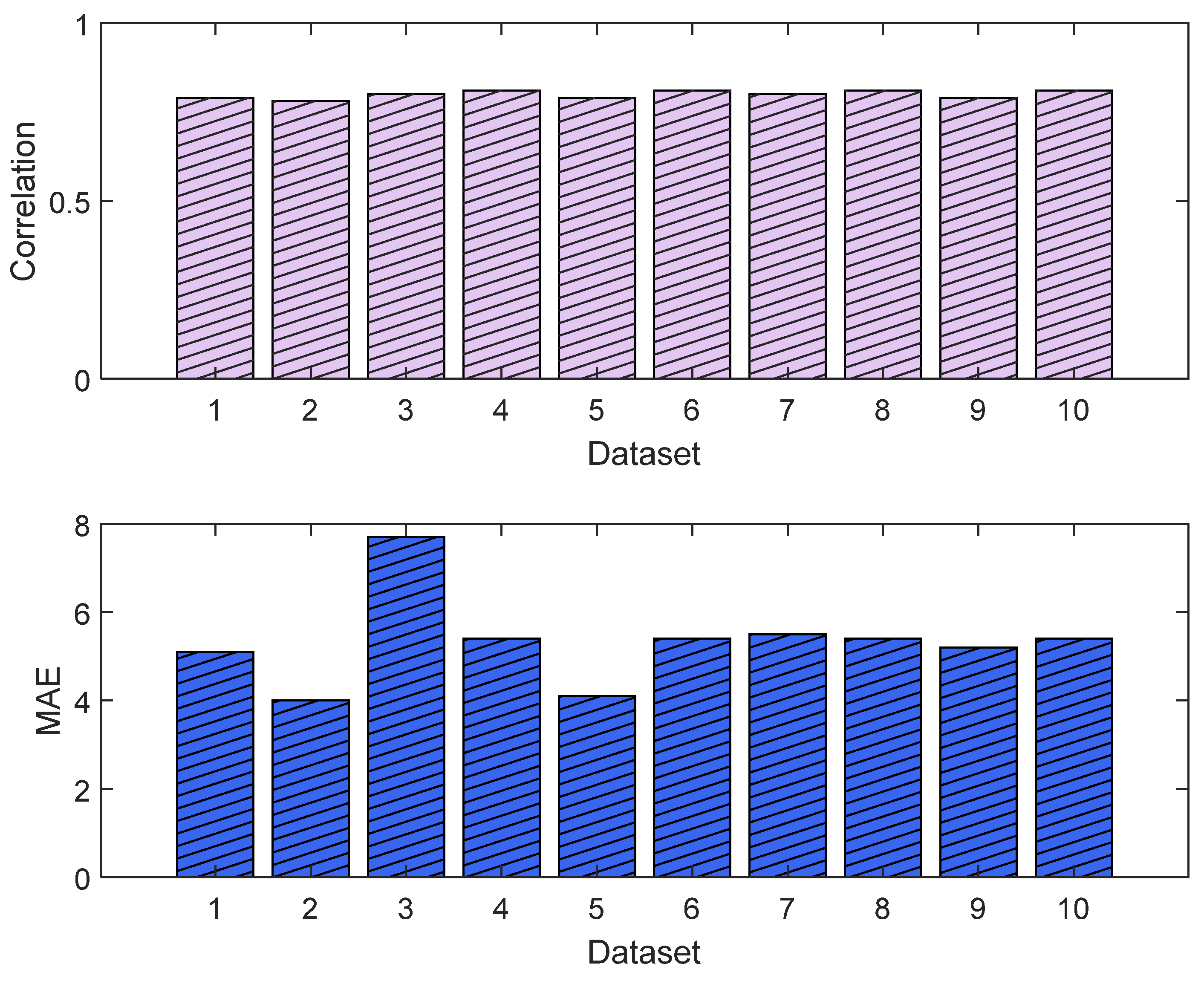
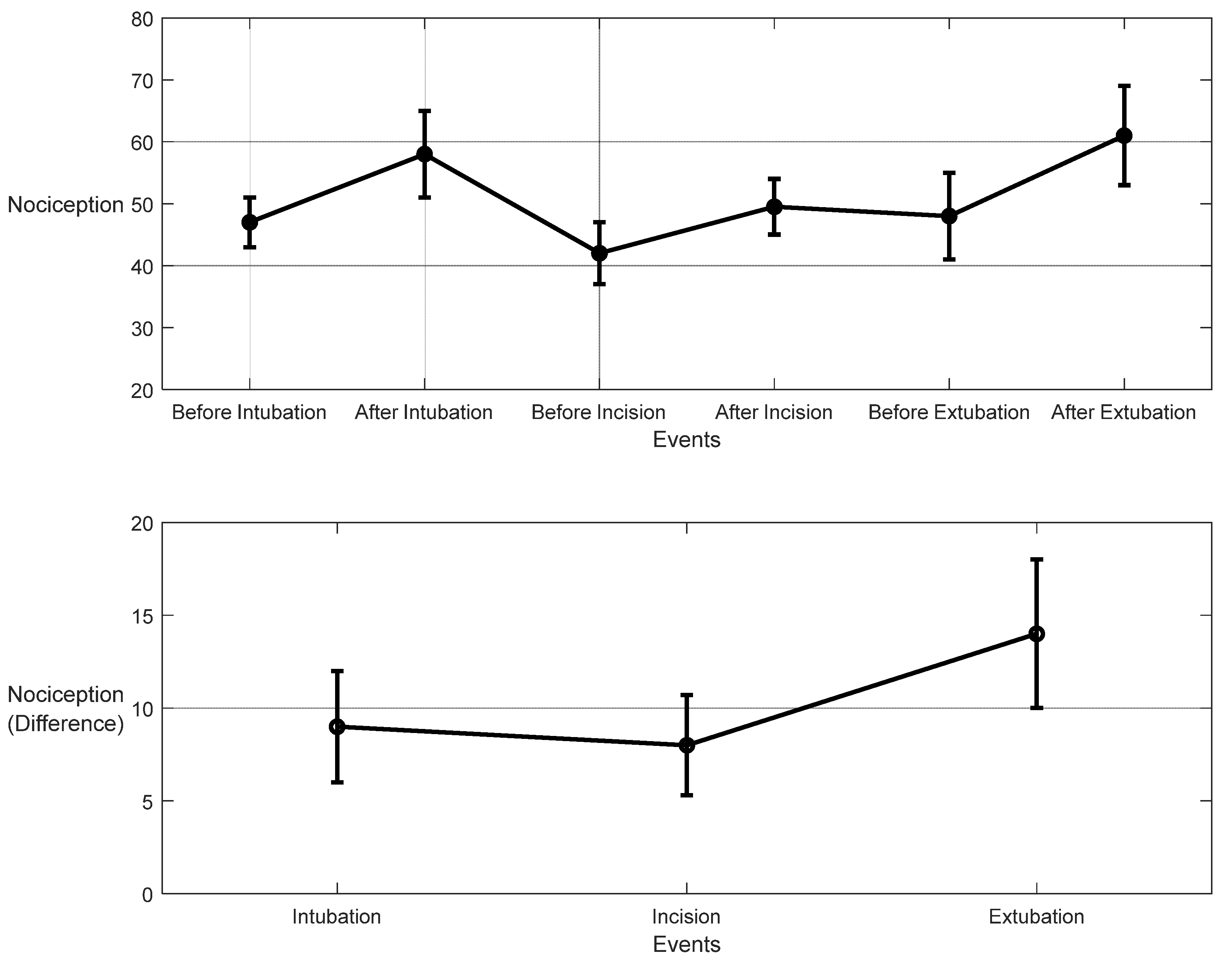
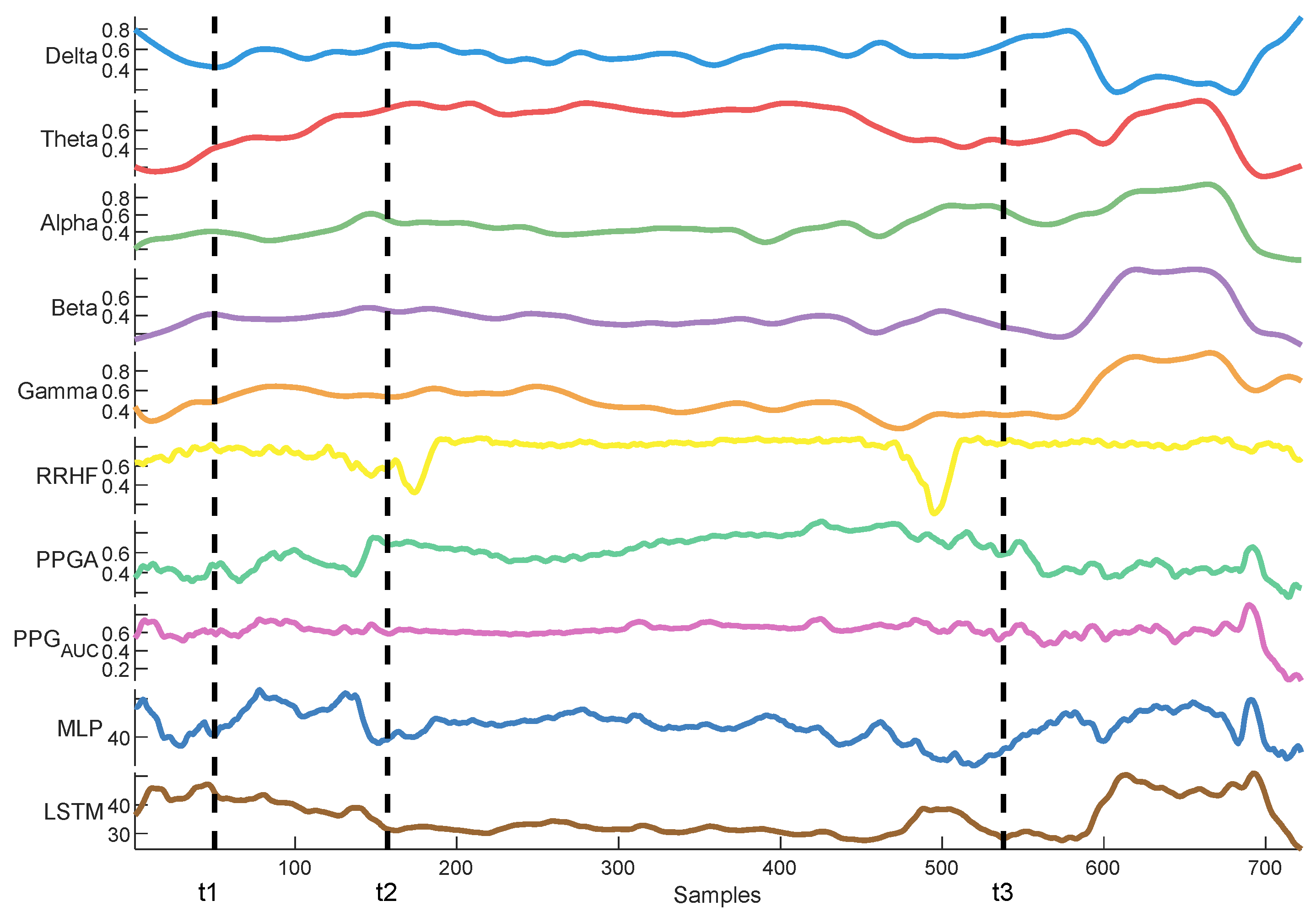
3.1. NOA
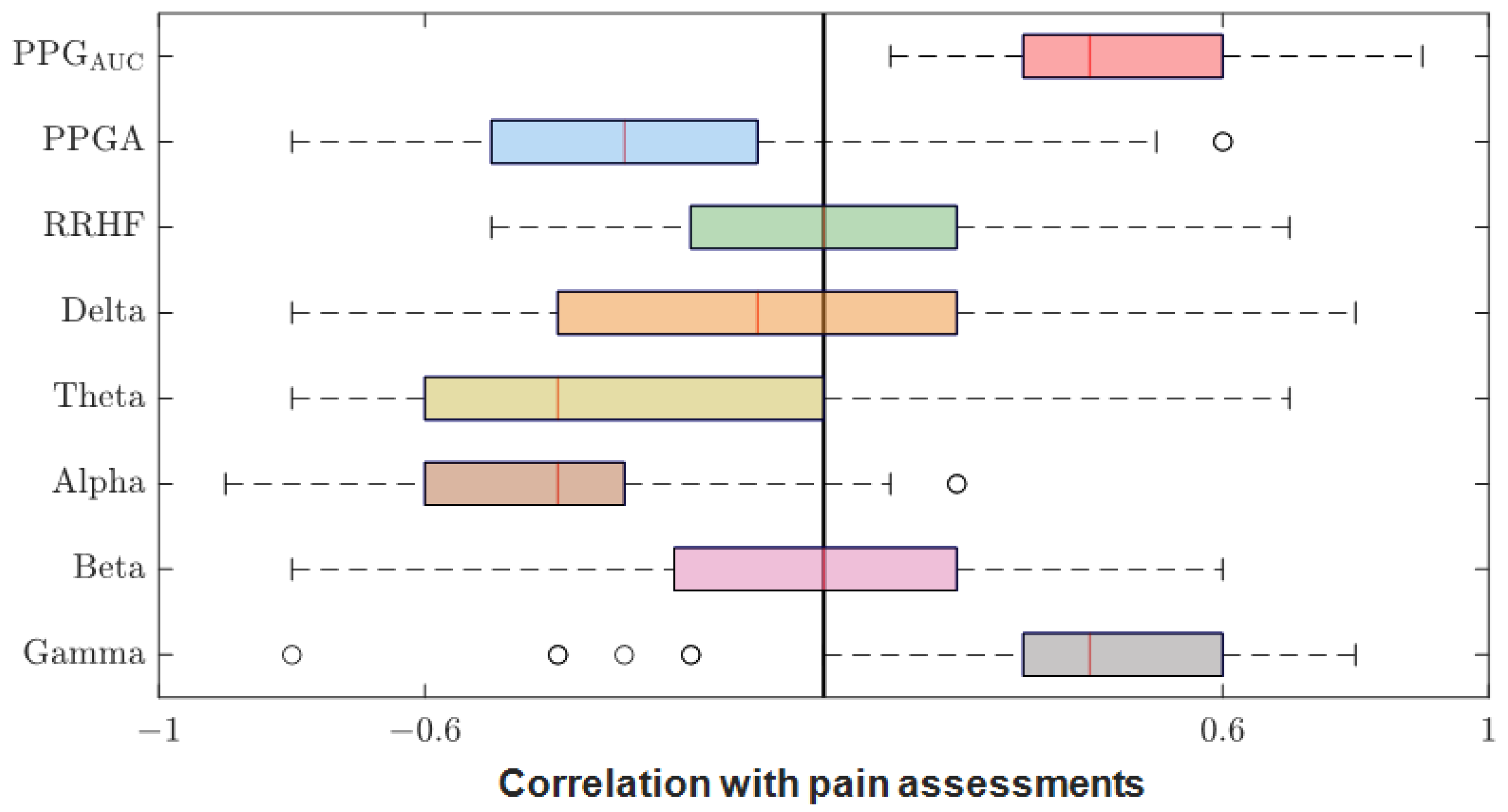
3.2. Parameter Correlations
3.3. Parameter Normalization
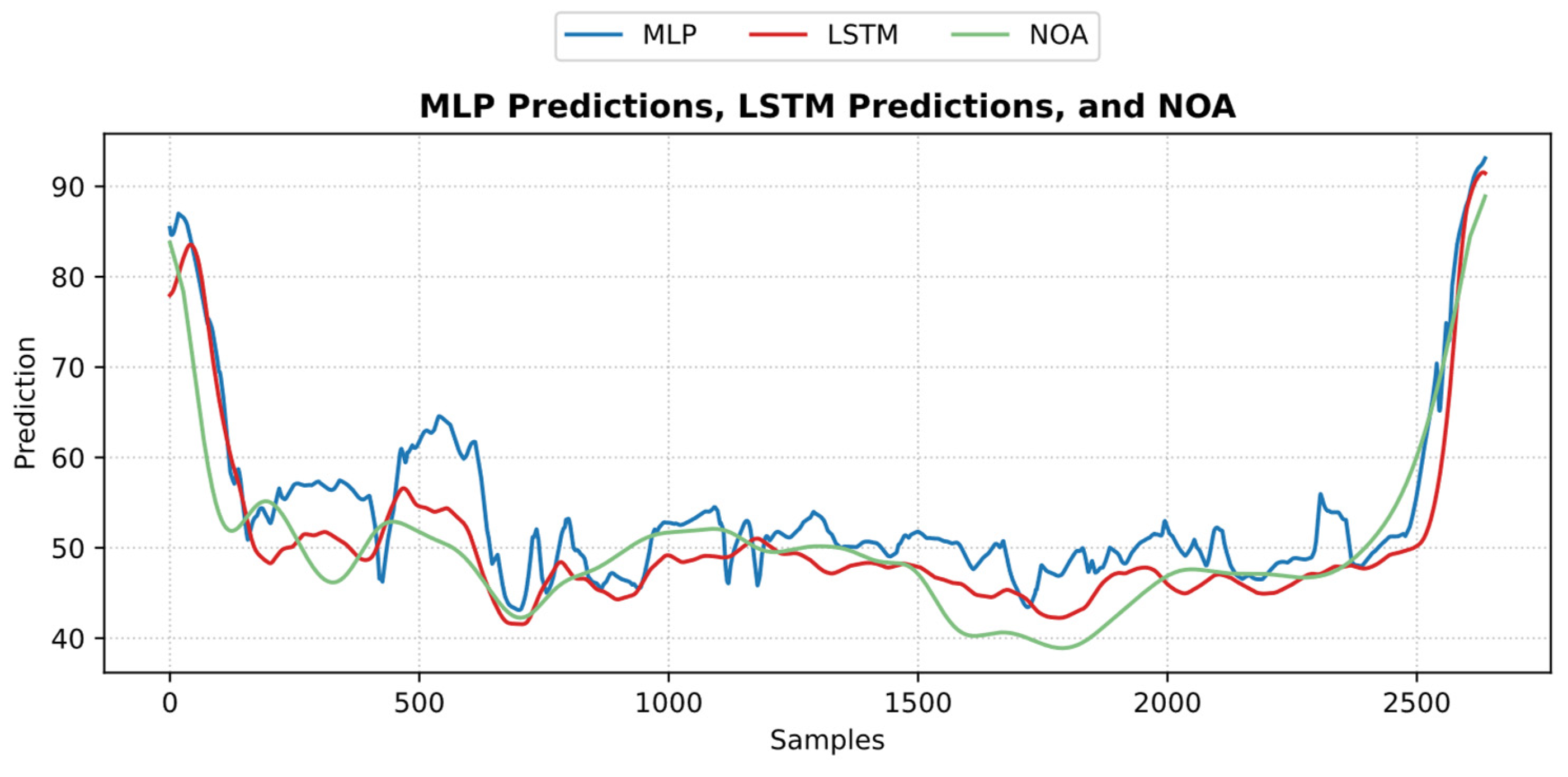
3.4. Pain/Nociception Models
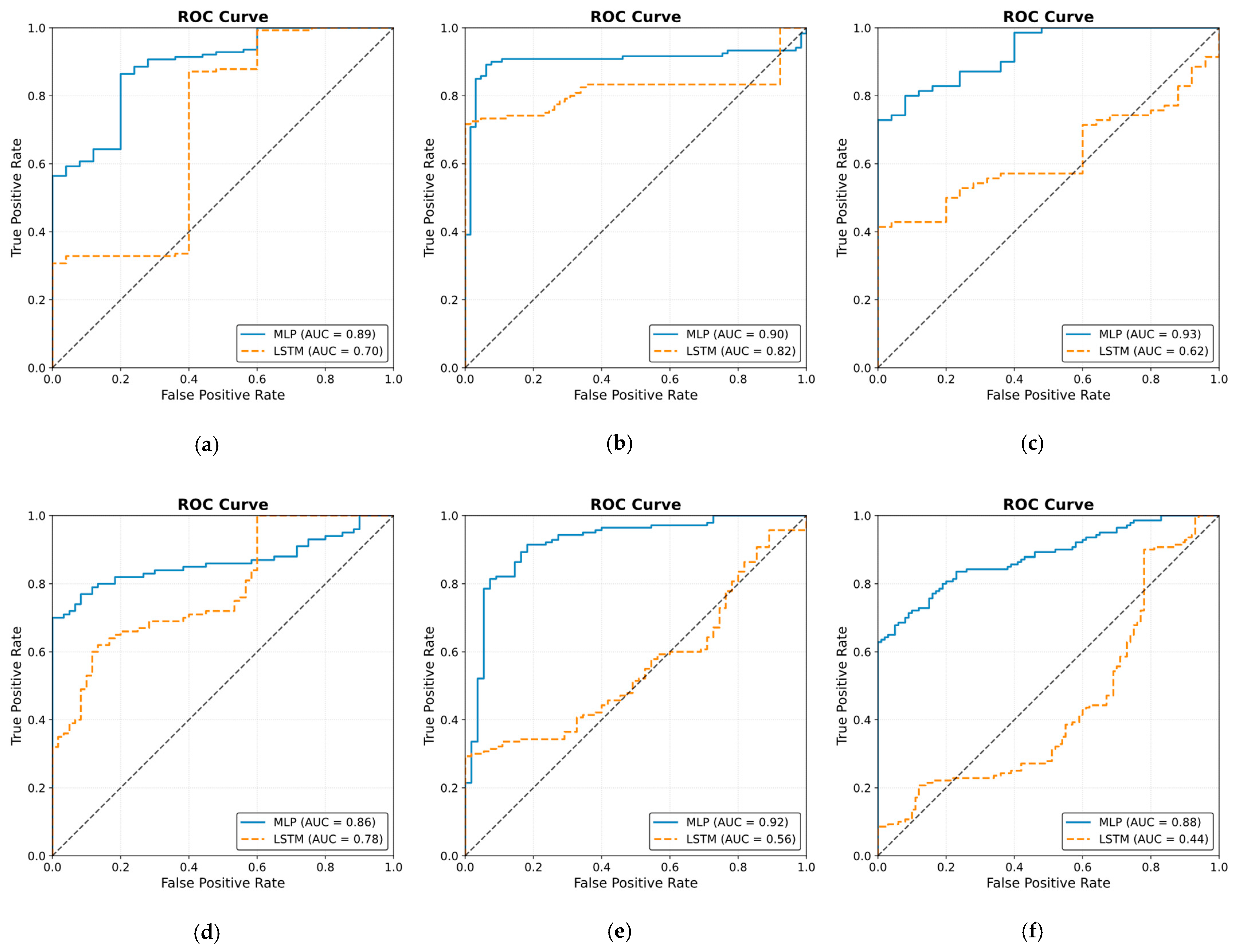
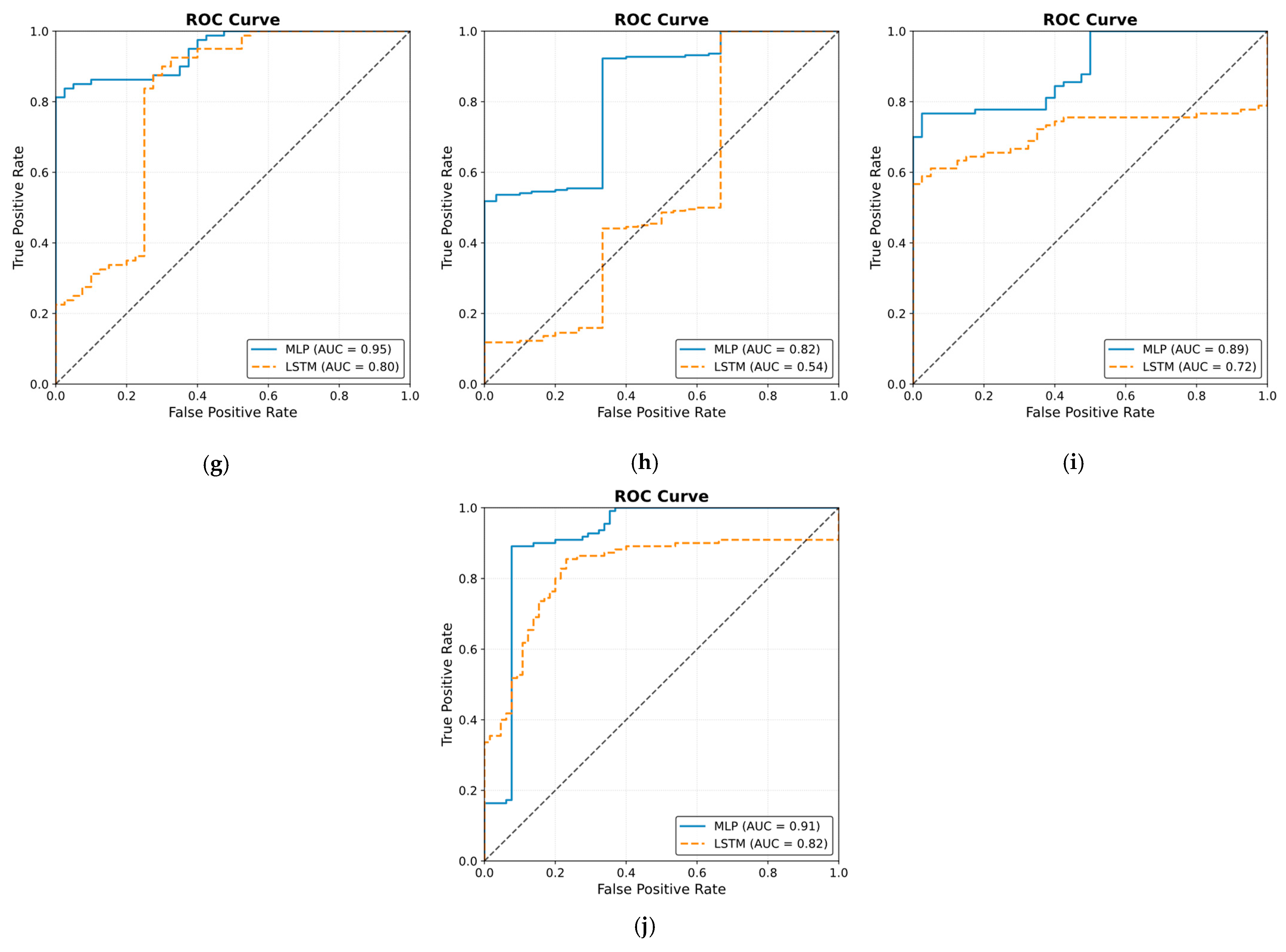
3.4.1. MLP Model
3.4.2. LSTM Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Loeser, J.D.; Treede, R.D. The Kyoto protocol of IASP Basic Pain Terminology. Pain 2008, 137, 473–477. [Google Scholar] [CrossRef] [PubMed]
- Schlereth, T.; Birklein, F. The sympathetic nervous system and pain. Neuromol. Med. 2008, 10, 141–147. [Google Scholar] [CrossRef] [PubMed]
- Huiku, M.; Uutela, K.; van Gils, M.; Korhonen, I.; Kymalainen, M.; Merilainen, P.; Paloheimo, M.; Rantanen, M.; Takala, P.; Viertio-Oja, H.; et al. Assessment of surgical stress during general anaesthesia. Br. J. Anaesth. 2007, 98, 447–455. [Google Scholar] [CrossRef] [PubMed]
- Gruenewald, M.; Ilies, C. Monitoring the nociception-anti-nociception balance. Best Pract. Res. Clin. Anaesthesiol. 2013, 27, 235–247. [Google Scholar] [CrossRef]
- Logier, R.; Jeanne, M.; Tavernier, B. Method and Device for Assessing Pain in Human Being. European Patent N 04370029.3, 20 September 2004. [Google Scholar]
- Jeanne, M.; Logier, R.; De Jonckheere, J.; Tavernier, B. Validation of a graphic measurement of heart rate variability to assess analgesia/nociception balance during general anesthesia. In Proceedings of the 31st Annual International Conference of the IEEE EMBS, Minneapolis, MN, USA, 2–6 September 2009; Volume 2009, pp. 1840–1843. [Google Scholar] [CrossRef]
- Wheeler, P.; Hoffman, W.E.; Baughman, V.L.; Koenig, H. Response entropy increases during painful stimulation. J. Neurosurg. Anesthesiol. 2005, 17, 86–90. [Google Scholar] [CrossRef]
- Coleman, R.M.; Tousignant-Laflamme, Y.; Ouellet, P.; Parenteau-Goudreault, É.; Cogan, J.; Bourgault, P. The Use of the Bispectral Index in the Detection of Pain in Mechanically Ventilated Adults in the Intensive Care Unit: A Review of the Literature. Pain Res. Manag. 2015, 20, e33–e37. [Google Scholar] [CrossRef]
- Garcia, P.S.; Kreuzer, M.; Hight, D.; Sleigh, J.W. Effects of noxious stimulation on the electroencephalogram during general anaesthesia: A narrative review and approach to analgesic titration. Br. J. Anaesth. 2021, 126, 445–457. [Google Scholar] [CrossRef]
- Jensen, E.W.; Valencia, J.F.; Lopez, A.; Anglada, T.; Agusti, M.; Ramos, Y.; Serra, R.; Jospin, M.; Pineda, P.; Gambus, P. Monitoring hypnotic effect and nociception with two EEG-derived indices, qCON and qNOX, during general anaesthesia. Acta Anaesthesiol. Scand. 2014, 58, 933–941. [Google Scholar] [CrossRef]
- Ben-Israel, N.; Kliger, M.; Zuckerman, G.; Katz, Y.; Edry, R. Monitoring the nociception level: A multi-parameter approach. J. Clin. Monit. Comput. 2013, 27, 659–668. [Google Scholar] [CrossRef]
- Rantanen, M.; Yli-Hankala, A.; van Gils, M.; Ypparila-Wolters, H.; Takala, P.; Huiku, M.; Kymalainen, M.; Seitsonen, E.; Korhonen, I. Novel multiparameter approach for measurement of nociception at skin incision during general anaesthesia. Br. J. Anaesth. 2006, 96, 367–376. [Google Scholar] [CrossRef]
- Baliki, M.N.; Apkarian, A.V. Nociception, Pain, Negative Moods, and Behavior Selection. Neuron 2015, 87, 474–491. [Google Scholar] [CrossRef] [PubMed]
- Lichtner, G.; Auksztulewicz, R.; Velten, H.; Mavrodis, D.; Scheel, M.; Blankenburg, F.; von Dincklage, F. Nociceptive activation in spinal cord and brain persists during deep general anaesthesia. Br. J. Anaesth. 2018, 121, 291–302. [Google Scholar] [CrossRef] [PubMed]
- Garland, E.L. Pain processing in the human nervous system: A selective review of nociceptive and biobehavioral pathways. Prim. Care 2012, 39, 561–571. [Google Scholar] [CrossRef]
- Hartley, C.; Poorun, R.; Goksan, S.; Worley, A.; Boyd, S.; Rogers, R.; Ali, T.; Slater, R. Noxious stimulation in children receiving general anaesthesia evokes an increase in delta frequency brain activity. Pain 2014, 155, 2368–2376. [Google Scholar] [CrossRef]
- Ekman, A.; Flink, R.; Sundman, E.; Eriksson, L.I.; Brudin, L.; Sandin, R. Neuromuscular block and the electroencephalogram during sevoflurane anaesthesia. Neuroreport 2007, 18, 1817–1820. [Google Scholar] [CrossRef]
- Kox, W.J.; von Heymann, C.; Heinze, J.; Prichep, L.S.; John, E.R.; Rundshagen, I. Electroencephalographic mapping during routine clinical practice: Cortical arousal during tracheal intubation? Anesth. Analg. 2006, 102, 825–831. [Google Scholar] [CrossRef]
- Ropcke, H.; Rehberg, B.; Koenen-Bergmann, M.; Bouillon, T.; Bruhn, J.; Hoeft, A. Surgical stimulation shifts EEG concentration-response relationship of desflurane. Anesthesiology 2001, 94, 390–399. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar]
- Park, Y.-S.; Lek, S. Artificial neural networks: Multilayer perceptron for ecological modeling. In Developments in Environmental Modelling; Elsevier: Amsterdam, The Netherlands, 2016; Volume 28, pp. 123–140. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Pan, J.; Tompkins, W.J. A real-time QRS detection algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef]
- Scholkmann, F.; Boss, J.; Wolf, M. An efficient algorithm for automatic peak detection in noisy periodic and quasi-periodic signals. Algorithms 2012, 5, 588–603. [Google Scholar] [CrossRef]
- Charlton, P.H.; Kotzen, K.; Mejia-Mejia, E.; Aston, P.J.; Budidha, K.; Mant, J.; Pettit, C.; Behar, J.A.; Kyriacou, P.A. Detecting beats in the photoplethysmogram: Benchmarking open-source algorithms. Physiol. Meas. 2022, 43, 085007. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef]
- Cicchetti, D.V. Guidelines, criteria, and rules of thumb for evaluating normed and standardized assessment instruments in psychology. Psychol. Assess. 1994, 6, 284. [Google Scholar] [CrossRef]
- Jean, W.-H.; Sutikno, P.; Fan, S.-Z.; Abbod, M.F.; Shieh, J.-S. Comparison of Deep Learning Algorithms in Predicting Expert Assessments of Pain Scores during Surgical Operations Using Analgesia Nociception Index. Sensors 2022, 22, 5496. [Google Scholar] [CrossRef]
- Abdel Deen, O.M.T.; Jean, W.-H.; Fan, S.-Z.; Abbod, M.F.; Shieh, J.-S. Pain scores estimation using surgical pleth index and long short-term memory neural networks. Artif. Life Robot. 2023, 28, 600–608. [Google Scholar] [CrossRef]
- Melia, U.; Gabarron, E.; Agustí, M.; Souto, N.; Pineda, P.; Fontanet, J.; Vallverdu, M.; Jensen, E.W.; Gambus, P. Comparison of the qCON and qNOX indices for the assessment of unconsciousness level and noxious stimulation response during surgery. J. Clin. Monit. Comput. 2017, 31, 1273–1281. [Google Scholar] [CrossRef]
- Anders, M.; Anders, B.; Dreismickenbecker, E.; Hight, D.; Kreuzer, M.; Walter, C.; Zinn, S. EEG responses to standardised noxious stimulation during clinical anaesthesia: A pilot study. BJA Open 2023, 5, 100118. [Google Scholar] [CrossRef]
- Hight, D.F.; Gaskell, A.L.; Kreuzer, M.; Voss, L.J.; García, P.S.; Sleigh, J.W. Transient electroencephalographic alpha power loss during maintenance of general anaesthesia. Br. J. Anaesth. 2019, 122, 635–642. [Google Scholar] [CrossRef]
- Hagihira, S.; Takashina, M.; Mori, T.; Ueyama, H.; Mashimo, T. Electroencephalographic bicoherence is sensitive to noxious stimuli during isoflurane or sevoflurane anesthesia. J. Am. Soc. Anesthesiol. 2004, 100, 818–825. [Google Scholar] [CrossRef]
- Kochs, E.; Bischoff, P.; Pichlmeier, U.; Schulte am Esch, J. Surgical stimulation induces changes in brain electrical activity during isoflurane/nitrous oxide anesthesia. A topographic electroencephalographic analysis. Anesthesiology 1994, 80, 1026–1034. [Google Scholar] [CrossRef]
- Rundshagen, I.; Schröder, T.; Heinze, J.; Prichep, L.; John, E.; Kox, W. Topographic electroencephalography: Endotracheal intubation during anaesthesia with propofol/fentanyl. Anasthesiol. Intensivmed. Notfallmedizin Schmerzther. AINS 2005, 40, 633–639. [Google Scholar] [CrossRef]












| NTUH | ECKH | |||
|---|---|---|---|---|
| Range | Mean ± SD | Range | Mean ± SD | |
| Age (yr) | 22–78 | 48 ± 12 | 40–67 | 57 ± 10 |
| Weight (kg) | 40–160 | 59 ± 14 | 41–93 | 68 ± 18 |
| Height (cm) | 138–185 | 157 ± 7 | 150–189 | 166 ± 15 |
| Fentanyl IV (µg) | 50–205 | 117 ± 42 | 50–100 | 80 ± 27 |
| Propofol IV (mg) | 50–250 | 124 ± 30 | 90–200 | 122 ± 45 |
| Hidden Layers | Neurons | Batch Size | Epochs | Learning Rate | Optimizer | Activation (Output) | |
|---|---|---|---|---|---|---|---|
| MLP | 2 | 50/30 | 125 | 50 | 0.001 | Adam | ReLU |
| LSTM | 2 | 100/200 | 256 | 50 | 0.0001 | Adam | ReLU |
| Group1 | Group2 | SD | Bias | Agreement (%) |
|---|---|---|---|---|
| A | B | 7.40 | −1.22 | 95.00 |
| A | C | 9.11 | −1.92 | 96.00 |
| A | E | 8.52 | 4.32 | 95.00 |
| B | C | 8.55 | −0.7 | 95.00 |
| B | E | 7.70 | 5.55 | 95.01 |
| C | E | 8.01 | 6.25 | 95.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdel Deen, O.M.T.; Fan, S.-Z.; Shieh, J.-S. A Multimodal Deep Learning Approach to Intraoperative Nociception Monitoring: Integrating Electroencephalogram, Photoplethysmography, and Electrocardiogram. Sensors 2025, 25, 1150. https://doi.org/10.3390/s25041150
Abdel Deen OMT, Fan S-Z, Shieh J-S. A Multimodal Deep Learning Approach to Intraoperative Nociception Monitoring: Integrating Electroencephalogram, Photoplethysmography, and Electrocardiogram. Sensors. 2025; 25(4):1150. https://doi.org/10.3390/s25041150
Chicago/Turabian StyleAbdel Deen, Omar M. T., Shou-Zen Fan, and Jiann-Shing Shieh. 2025. "A Multimodal Deep Learning Approach to Intraoperative Nociception Monitoring: Integrating Electroencephalogram, Photoplethysmography, and Electrocardiogram" Sensors 25, no. 4: 1150. https://doi.org/10.3390/s25041150
APA StyleAbdel Deen, O. M. T., Fan, S.-Z., & Shieh, J.-S. (2025). A Multimodal Deep Learning Approach to Intraoperative Nociception Monitoring: Integrating Electroencephalogram, Photoplethysmography, and Electrocardiogram. Sensors, 25(4), 1150. https://doi.org/10.3390/s25041150







