Three-Component Accelerometer Based on Distributed Optical Fiber Sensing
Abstract
:1. Introduction
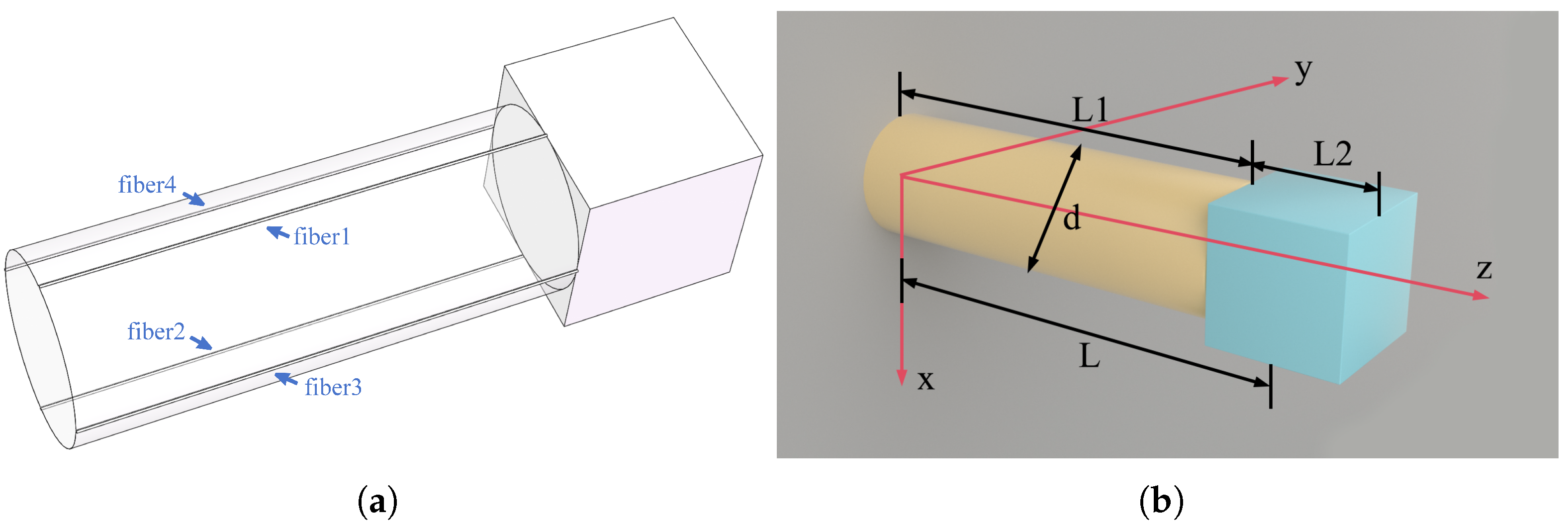
2. Three-Component Sensing Unit
2.1. Structure Design
2.2. Mechanical Model
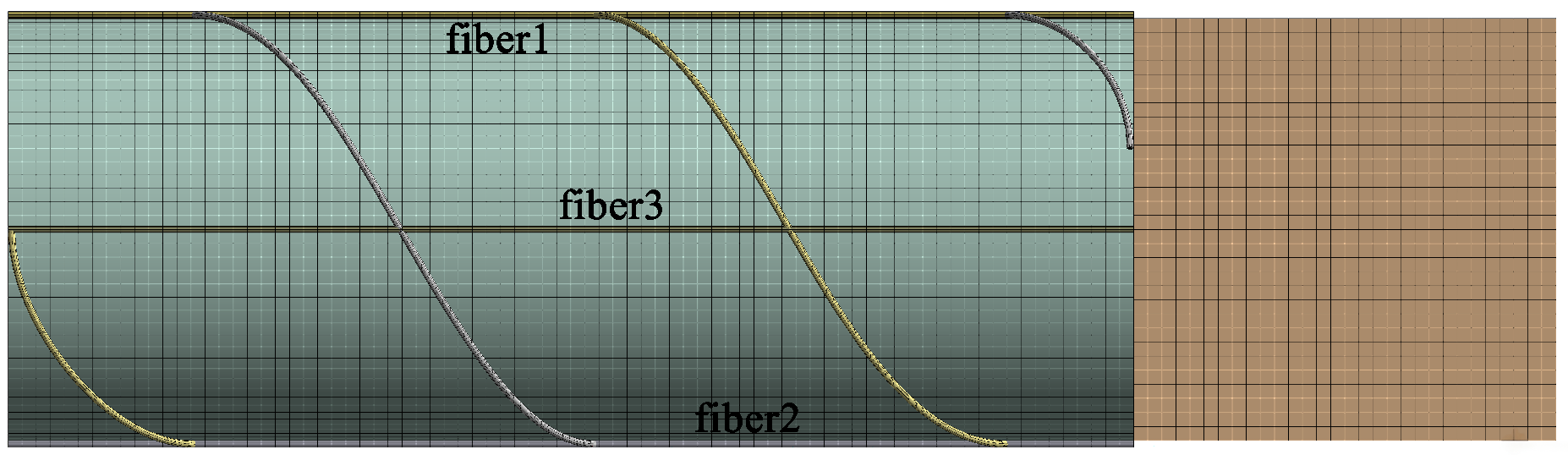
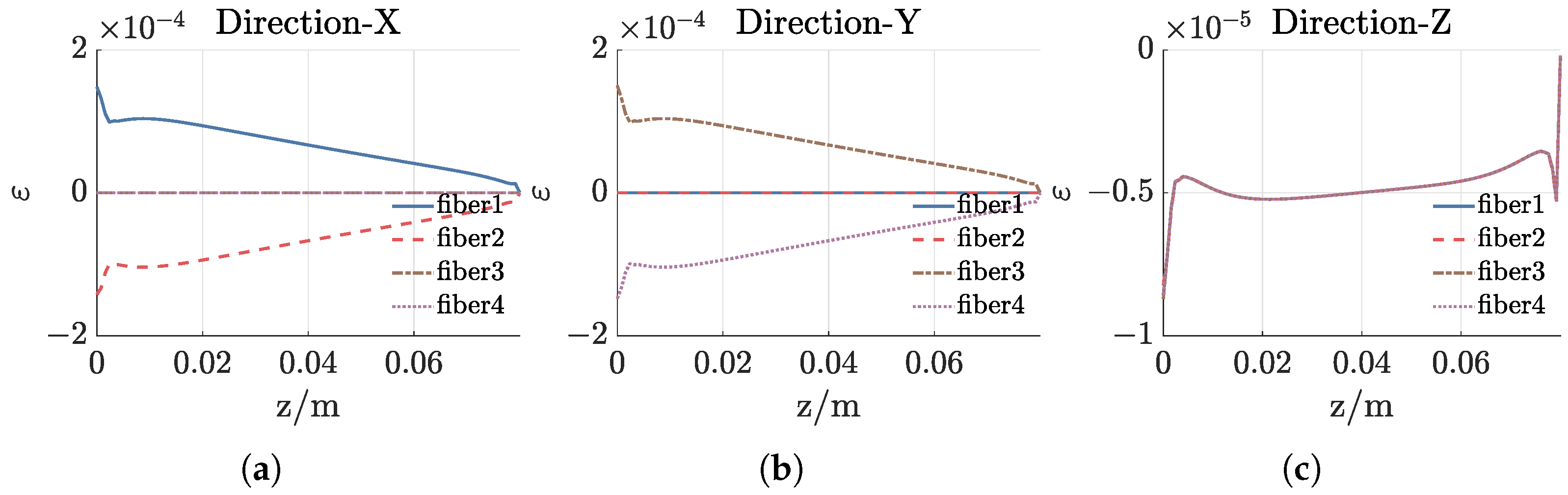
2.3. Finite Element Analysis
3. Dynamic Strain Demodulation System
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, H.; Zhou, P.; Xie, Z.; Gong, X.; Yang, Y.; Yuan, W. Theoretical modeling for a six-DOF vortex inertial sensor and experimental verification. J. Microelectromech. Syst. 2013, 22, 1100–1108. [Google Scholar] [CrossRef]
- Amarasinghe, R.; Dao, D.V.; Toriyama, T.; Sugiyama, S. Development of miniaturized 6-axis accelerometer utilizing piezoresistive sensing elements. Sens. Actuators A Phys. 2007, 134, 310–320. [Google Scholar] [CrossRef]
- Abdul-Wahed, A.M.; Mahmoud, M.A. Vibratory ring six-axis motion sensor. Microsyst. Technol. 2015, 21, 2133–2144. [Google Scholar] [CrossRef]
- Gonzalez-Herraez, M.; Fernandez-Ruiz, M.R.; Magalhaes, R.; Costa, L.; Martins, H.F.; Becerril, C.; Martin-Lopez, S.; Williams, E.; Zhan, Z.; Vantilho, R. Distributed acoustic sensing for seismic monitoring. In Proceedings of the Optical Fiber Communication Conference (OFC) 2021, Washington, DC, USA, 6–11 June 2021; p. Tu1L.2. [Google Scholar] [CrossRef]
- He, Z.; Liu, Q. Optical fiber distributed acoustic sensors: A review. J. Light. Technol. 2021, 39, 3671–3686. [Google Scholar] [CrossRef]
- Chen, D.; Liu, Q.; Fan, X.; He, Z. Distributed fiber-optic acoustic sensor with enhanced response bandwidth and high signal-to-noise ratio. J. Light. Technol. 2017, 35, 2037–2043. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Z.; Chang, T.; Yu, M.; Chen, J.; Zheng, G.; Cui, H.L. Seismic observation and analysis based on three-component fiber optic seismometer. IEEE Access 2019, 8, 1374–1382. [Google Scholar] [CrossRef]
- Wang, D.; Wu, Y.; Song, Y.; Wang, Y.; Zhu, L. High sensitivity fiber optic acceleration sensor based on Fabry-Perot interferometer. Opt. Fiber Technol. 2022, 72, 102989. [Google Scholar] [CrossRef]
- Chen, J.; Chang, T.; Yang, Y.; Gao, W.; Wang, Z.; Cui, H.L. Ultra-low-frequency tri-component fiber optic interferometric accelerometer. IEEE Sens. J. 2018, 18, 8367–8374. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, M.; Xiong, L.; Zhou, X.; Li, C. Fiber Bragg grating based acceleration sensors: A review. Sens. Rev. 2021, 41, 101–122. [Google Scholar] [CrossRef]
- Shan-chao, J.; Jing, W.; Qing-mei, S.; Qing-lin, Y.; Li-jun, W. Study of Three-Component FBG Vibration Sensor for Simultaneous Measurement of Vibration, Temperature, and Verticality. J. Sens. 2015, 2015, 382865. [Google Scholar] [CrossRef]
- Li, T.; Shi, C.; Tan, Y.; Li, R.; Zhou, Z.; Ren, H. A diaphragm type fiber Bragg grating vibration sensor based on transverse property of optical fiber with temperature compensation. IEEE Sens. J. 2016, 17, 1021–1029. [Google Scholar] [CrossRef]
- Fan, W.; Wen, J.; Gao, H.; Qiao, X. Low-frequency fiber Bragg grating accelerometer based on diaphragm-type cantilever. Opt. Fiber Technol. 2022, 70, 102888. [Google Scholar] [CrossRef]
- Teng, Y.; Zhang, B.; Qiu, Z.; Hu, X.; He, Z. High-sensitivity dual-FBG acceleration sensor for low frequency vibration measurement. J. Opt. 2024, 53, 2361–2373. [Google Scholar] [CrossRef]
- Qiu, Z.; Mai, M.; Teng, Y.; Wang, X.; Ma, J. Bearing-based FBG acceleration sensor for low-frequency vibration measurement. Measurement 2024, 228, 114322. [Google Scholar] [CrossRef]
- Reghuprasad, A.E.; Colombero, C.; Godio, A. Serially connected cantilever beam-based FBG accelerometers: Design, optimization and testing. Sensors 2023, 23, 3188. [Google Scholar] [CrossRef]
- Nguyen, T.T.V.; Le, H.D.; Hsu, H.C.; Nguyen, C.N.; Chiang, C.C. A symmetrical dual-mass block fiber Bragg grating vibration sensor based on a V-shaped flexible hinge. Sens. Actuators A Phys. 2023, 364, 114815. [Google Scholar] [CrossRef]
- Song, H.; Wang, Q.; Liu, M.; Cai, Q. A novel fiber Bragg grating vibration sensor based on orthogonal flexure hinge structure. IEEE Sens. J. 2020, 20, 5277–5285. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, M.; Hong, L.; Li, C.; Zhou, Z. Design and optimization of an FBG accelerometer based on single-notch circular flexure hinge for medium-frequency vibration measurement. IEEE Sens. J. 2022, 22, 20303–20311. [Google Scholar] [CrossRef]
- Qu, Z.; Lu, P.; Zhang, W.; Xiong, W.; Liu, D.; Zhang, J. Miniature tri-axis accelerometer based on fiber optic Fabry-Pérot interferometer. Opt. Express 2022, 30, 23227–23237. [Google Scholar] [CrossRef] [PubMed]
- Teng, Y.; Ge, L.; Fan, X.; Ge, C.; Ma, J. Dual straight-wing FBG accelerometer for low-frequency vibration measurement. Opt. Commun. 2024, 563, 130590. [Google Scholar] [CrossRef]
- Xiong, L.; Guo, Y.; Zhou, W.; Chen, M.; Zhou, X. Fiber Bragg grating-based three-axis vibration sensor. IEEE Sens. J. 2021, 21, 25749–25757. [Google Scholar] [CrossRef]
- Qiu, Z.; Zhang, Y. Three-Dimensional low-frequency earthquake monitoring vibration sensor based on FBG. IEEE Trans. Instrum. Meas. 2024, 73, 1–9. [Google Scholar] [CrossRef]
- Zhu, W.; Liu, G.; Qin, H.; Liu, R. Development of fiber Bragg grating vibration sensor for bidirectional monitoring of thin rod cantilever beam. Measurement 2025, 242, 115979. [Google Scholar] [CrossRef]
- Mo, L.; Zheng, J.; Shen, S.; Song, X.; Sun, W. A novel three-component fiber-optic geophone for distributed acoustic sensing system. IEEE Sens. J. 2023, 24, 329–336. [Google Scholar] [CrossRef]
- Zhou, R.; Chen, F.; Li, S.; Wang, R.; Qiao, X. Three-dimensional vector accelerometer using a multicore fiber inscribed with three FBGs. J. Light. Technol. 2021, 39, 3244–3250. [Google Scholar] [CrossRef]
- Ning, I.L.C.; Sava, P. High-resolution multi-component distributed acoustic sensing. Geophys. Prospect. 2018, 66, 1111–1122. [Google Scholar] [CrossRef]
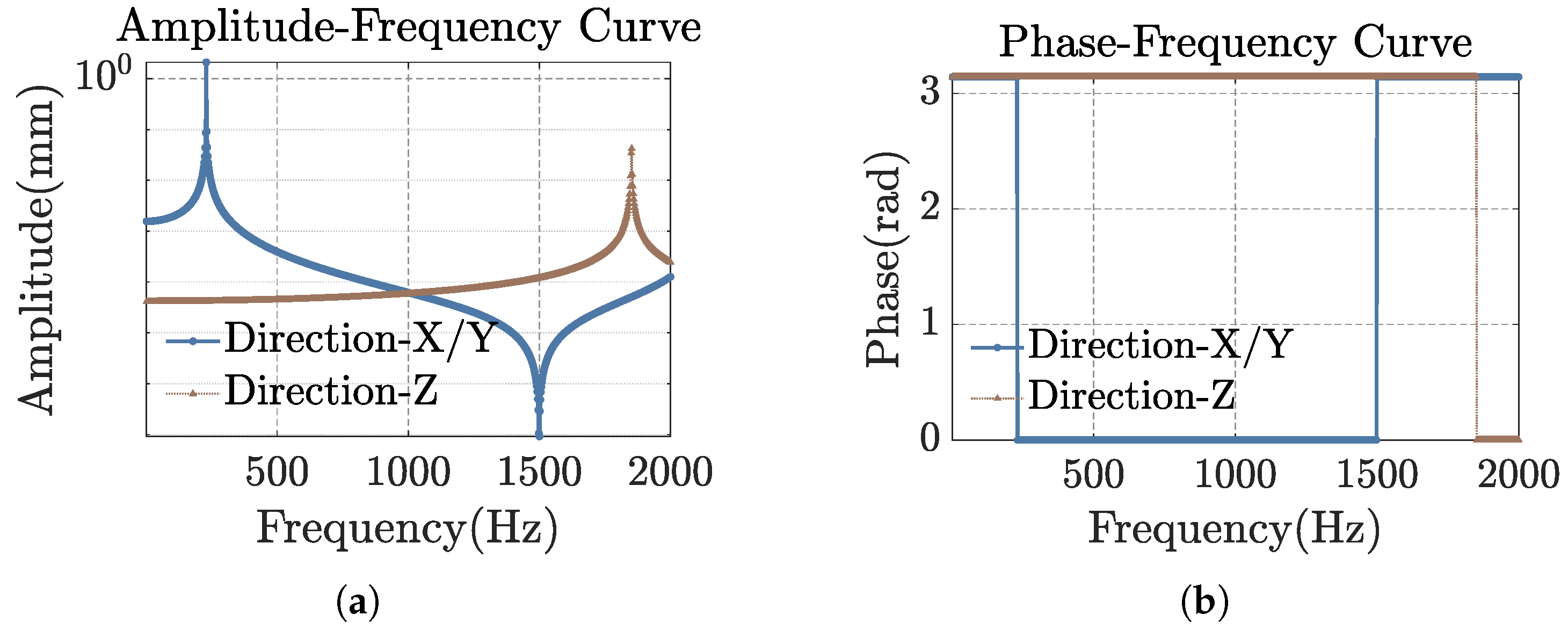
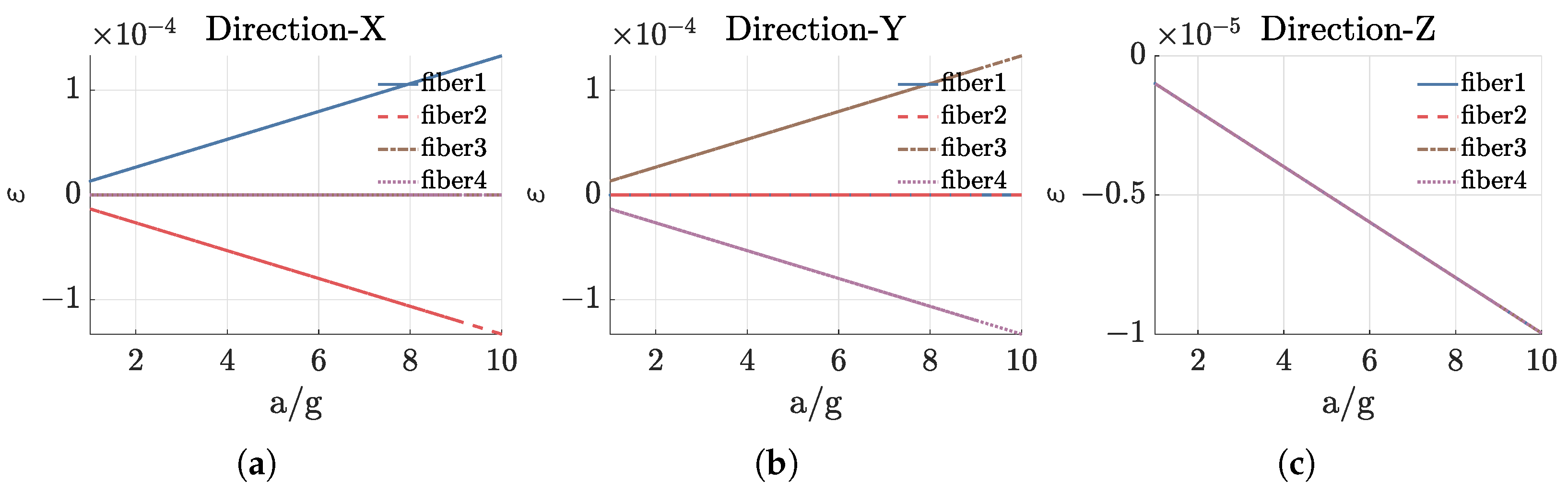
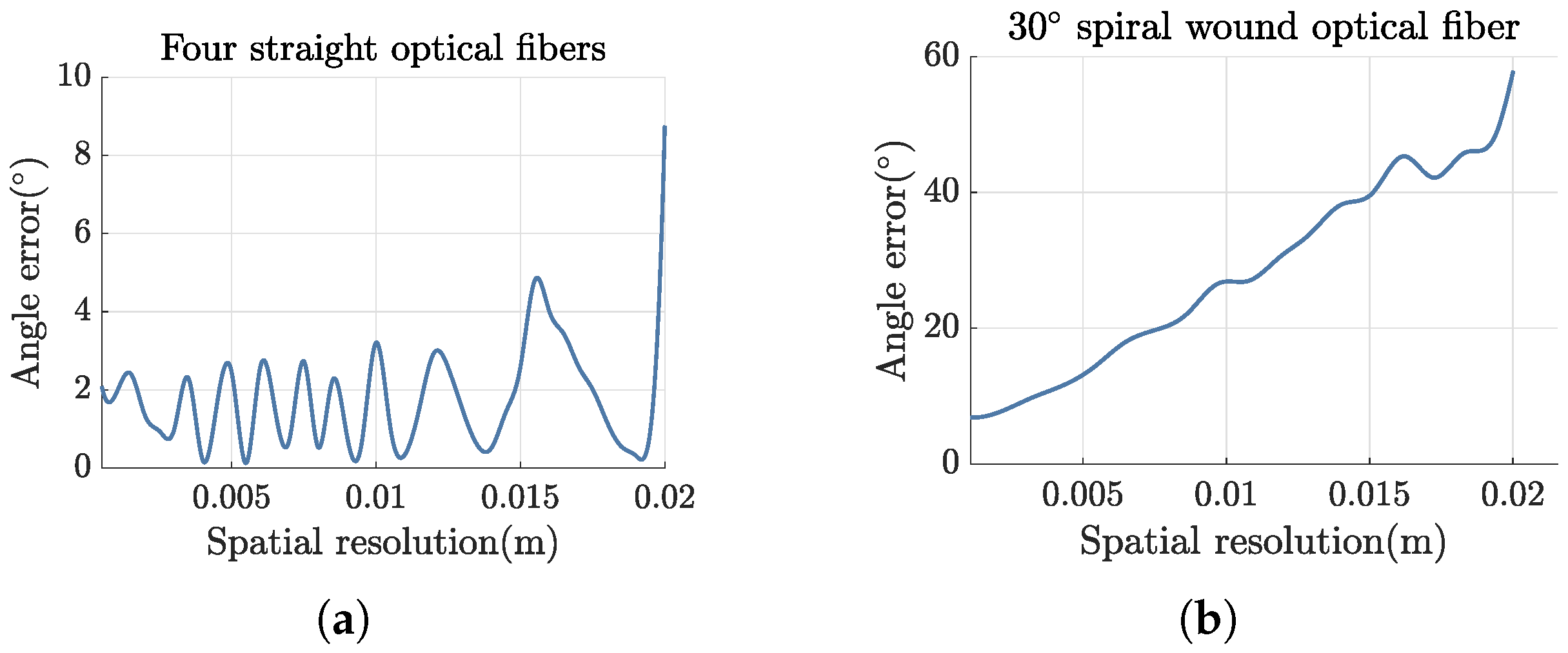



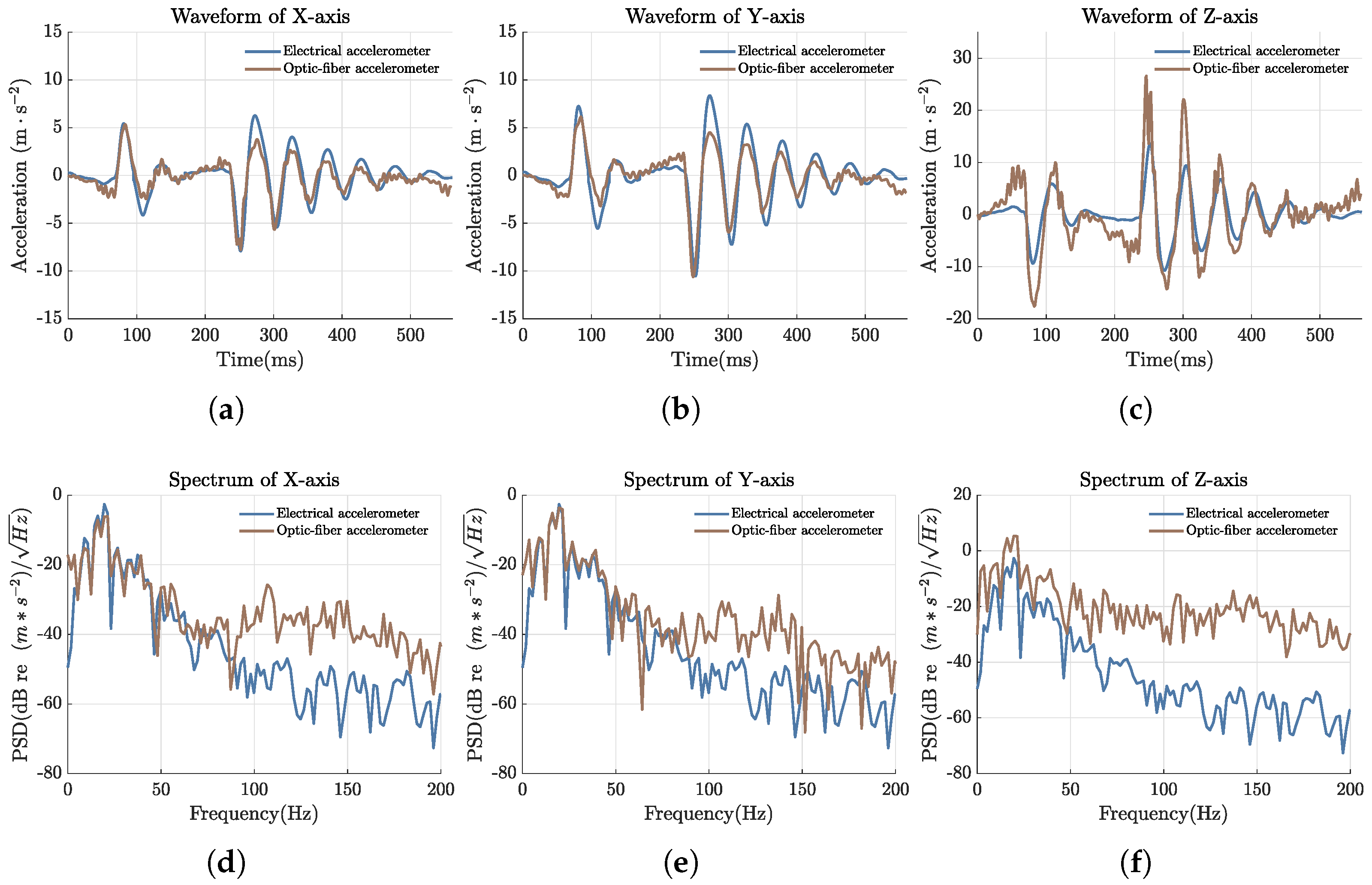
| Order | First | Second | Third | Fourth | Fifth | Sixth |
|---|---|---|---|---|---|---|
| Resonance frequency (Hz) | 230.08 | 230.08 | 953.2 | 1851.1 | 2143.4 | 2143.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Liu, Q.; Niu, R.; He, Z. Three-Component Accelerometer Based on Distributed Optical Fiber Sensing. Sensors 2025, 25, 997. https://doi.org/10.3390/s25040997
Zhang Z, Liu Q, Niu R, He Z. Three-Component Accelerometer Based on Distributed Optical Fiber Sensing. Sensors. 2025; 25(4):997. https://doi.org/10.3390/s25040997
Chicago/Turabian StyleZhang, Zongxiao, Qingwen Liu, Rongrong Niu, and Zuyuan He. 2025. "Three-Component Accelerometer Based on Distributed Optical Fiber Sensing" Sensors 25, no. 4: 997. https://doi.org/10.3390/s25040997
APA StyleZhang, Z., Liu, Q., Niu, R., & He, Z. (2025). Three-Component Accelerometer Based on Distributed Optical Fiber Sensing. Sensors, 25(4), 997. https://doi.org/10.3390/s25040997






