Trade-Off Analysis for Array Configurations of Chipless RFID Sensor Tag Designs
Abstract
1. Introduction
- Experimental validation of the performance of chipless RFID tags using linear and planar array configurations.
- Examination of detectability highlights trade-offs between tag identification range and angular coverage.
- Comprehensive analysis elucidates trade-offs among parameters such as linear detectability, spherical detectability, RCS, and Q-factor.
- Providing guidance for optimising the design and operation of chipless RFID tags based on planar array configurations.
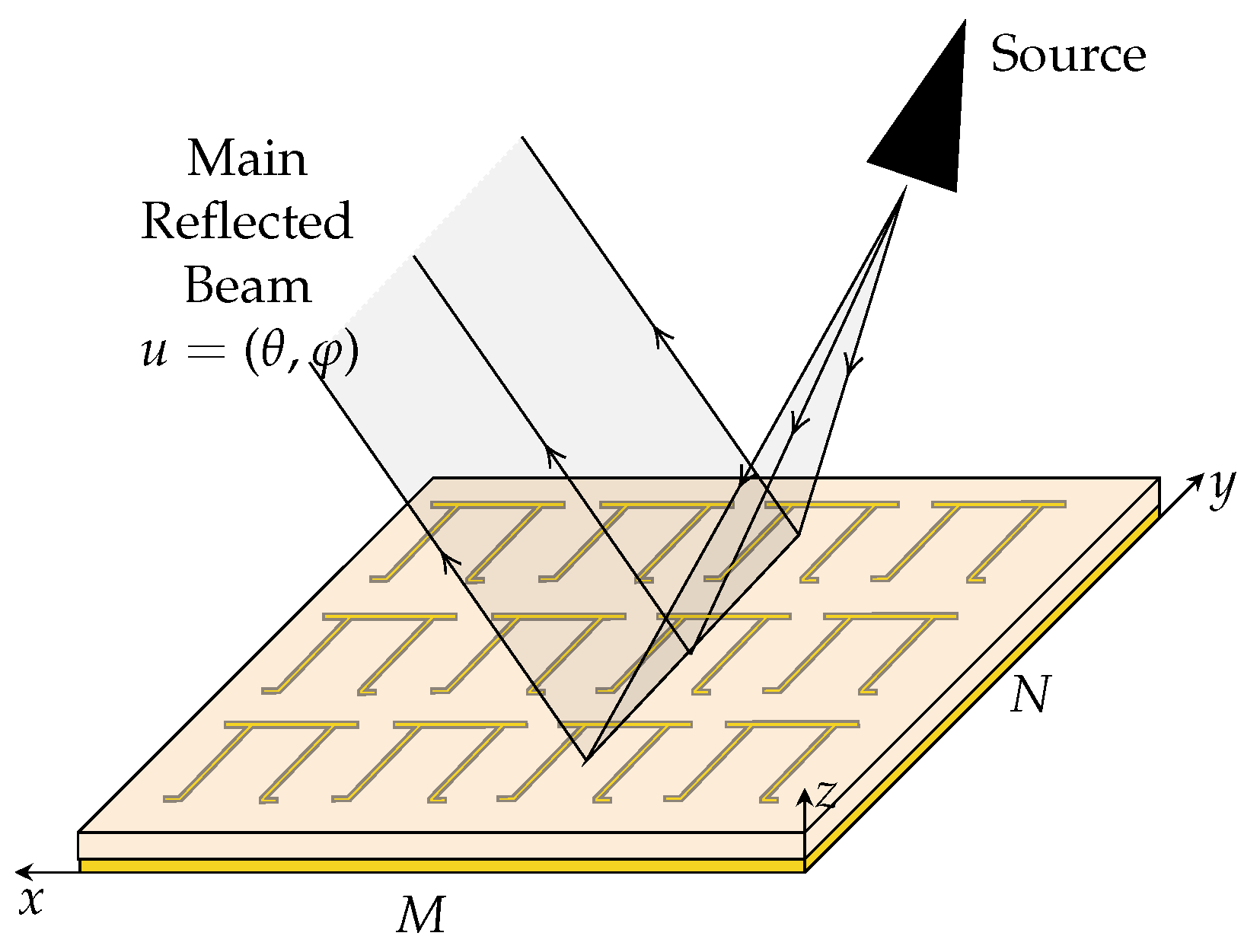
2. RCS of Chipless RFID Arrays
2.1. RCS Modelling
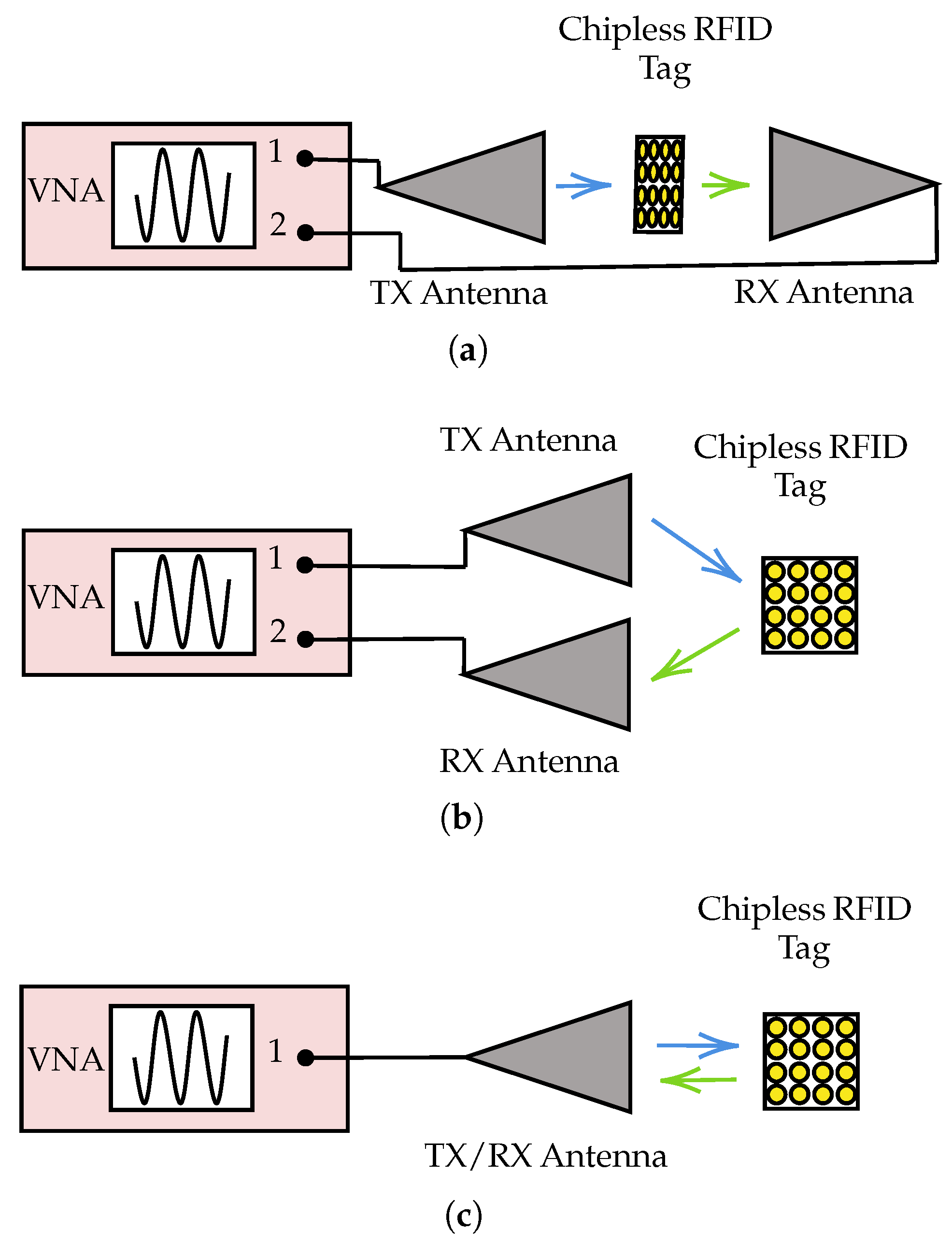
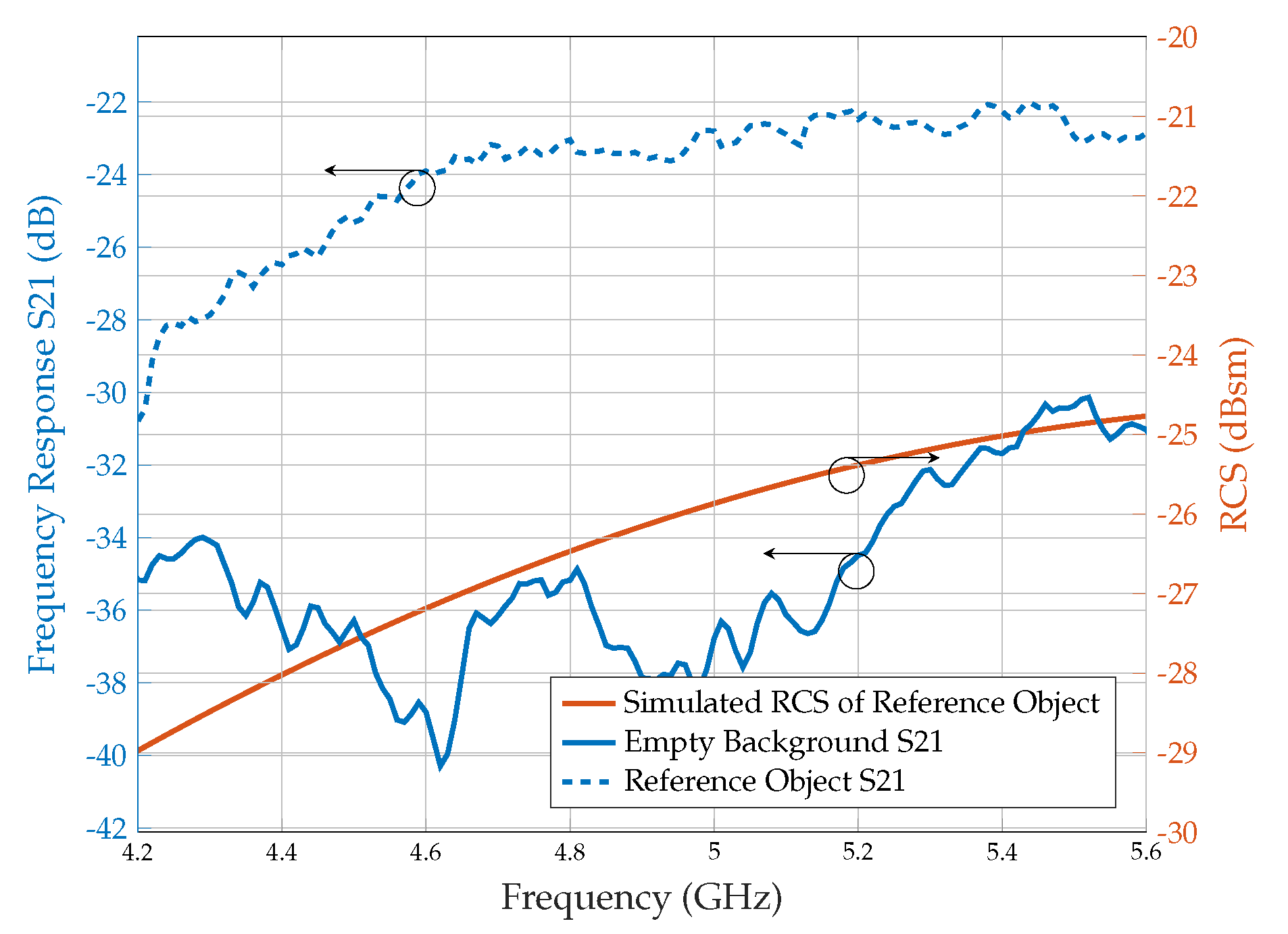
2.2. RCS Measurement Techniques
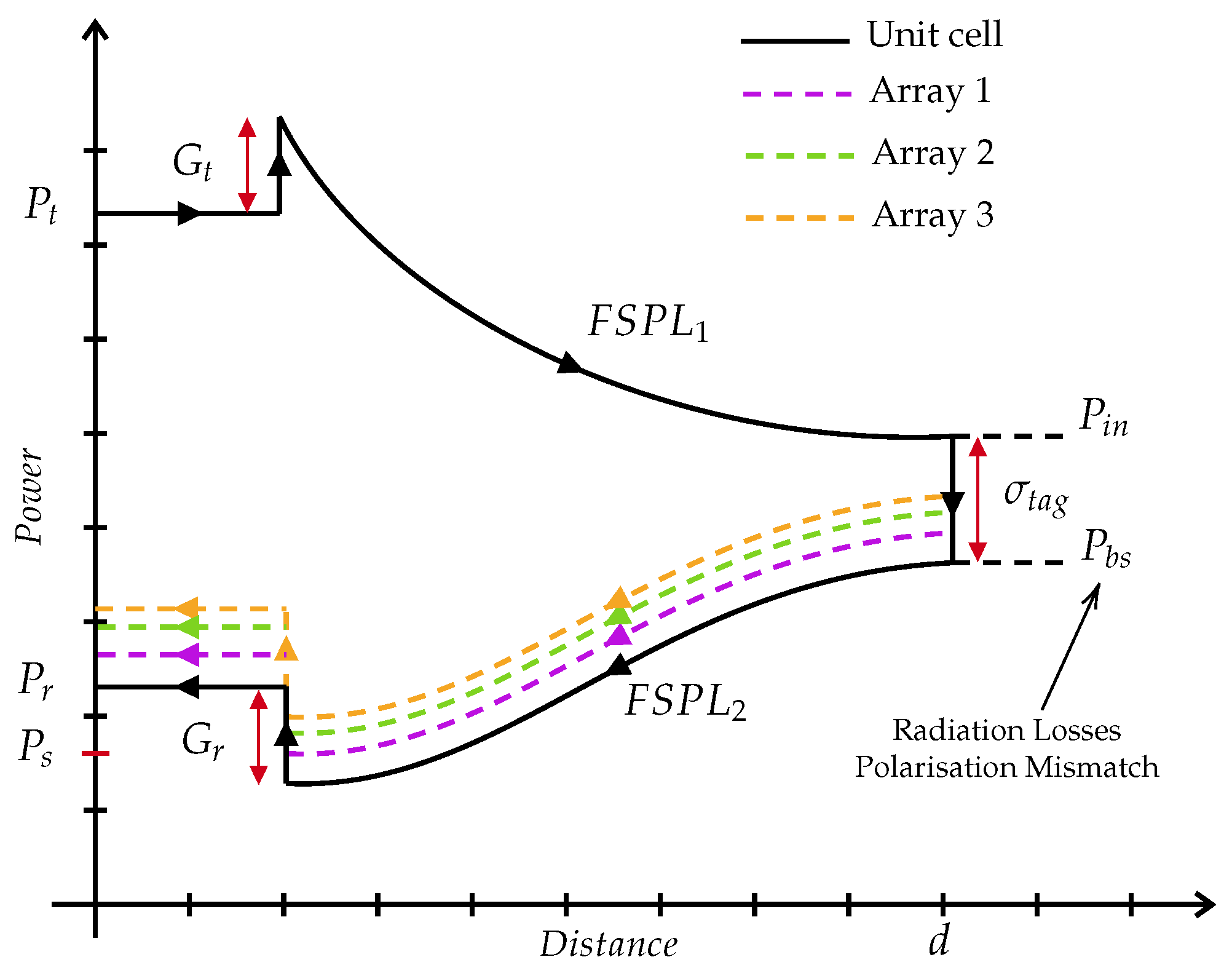
3. Link Budget of Chipless RFID Arrays
The Role of Chipless RFID Arrays in Link Budget
4. Chipless RFID Array Design
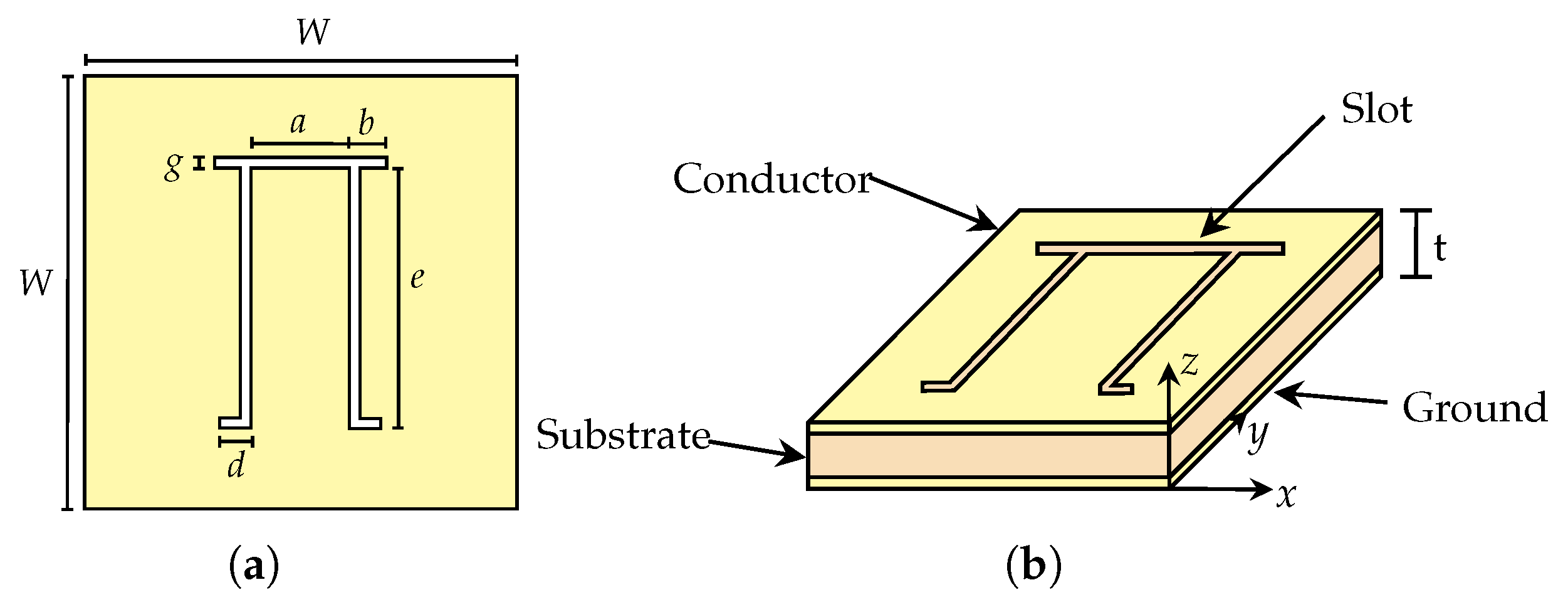
4.1. Unit Cell Tag
| Ref. | Resonator Type | Resonance Frequency (GHz) | Simulated Q-Factor |
|---|---|---|---|
| without Ground Plane | |||
| [25] | U-shaped Slot Resonator | 4.372 | 329 |
| [28] | Asymmetric Circular Split Ring Resonator | 5.760 | 182 |
| [29] | Slot Ring Resonator | 4.352 | 125 |
| [30] | Cobweb Resonator | 4.504 | 111 |
| [31] | ELC Resonator | 9.249 | 178 |
| with Ground Plane | |||
| [23] | Square Resonator | 4.597 | 159 |
| [32] | Tip Loaded Dipole Resonator | 5.461 | 229 |
| [33] | Triangular Patch Resonator | 5.308 | 128 |
| This work | Pi-shaped Resonator | 4.780 | 4515 |
4.2. Linear Array Tags
4.3. Planar Array Tags
5. Simulation Study of Array Configurations
5.1. RCS Analysis
Structural and Antenna Mode RCS of Array Configurations
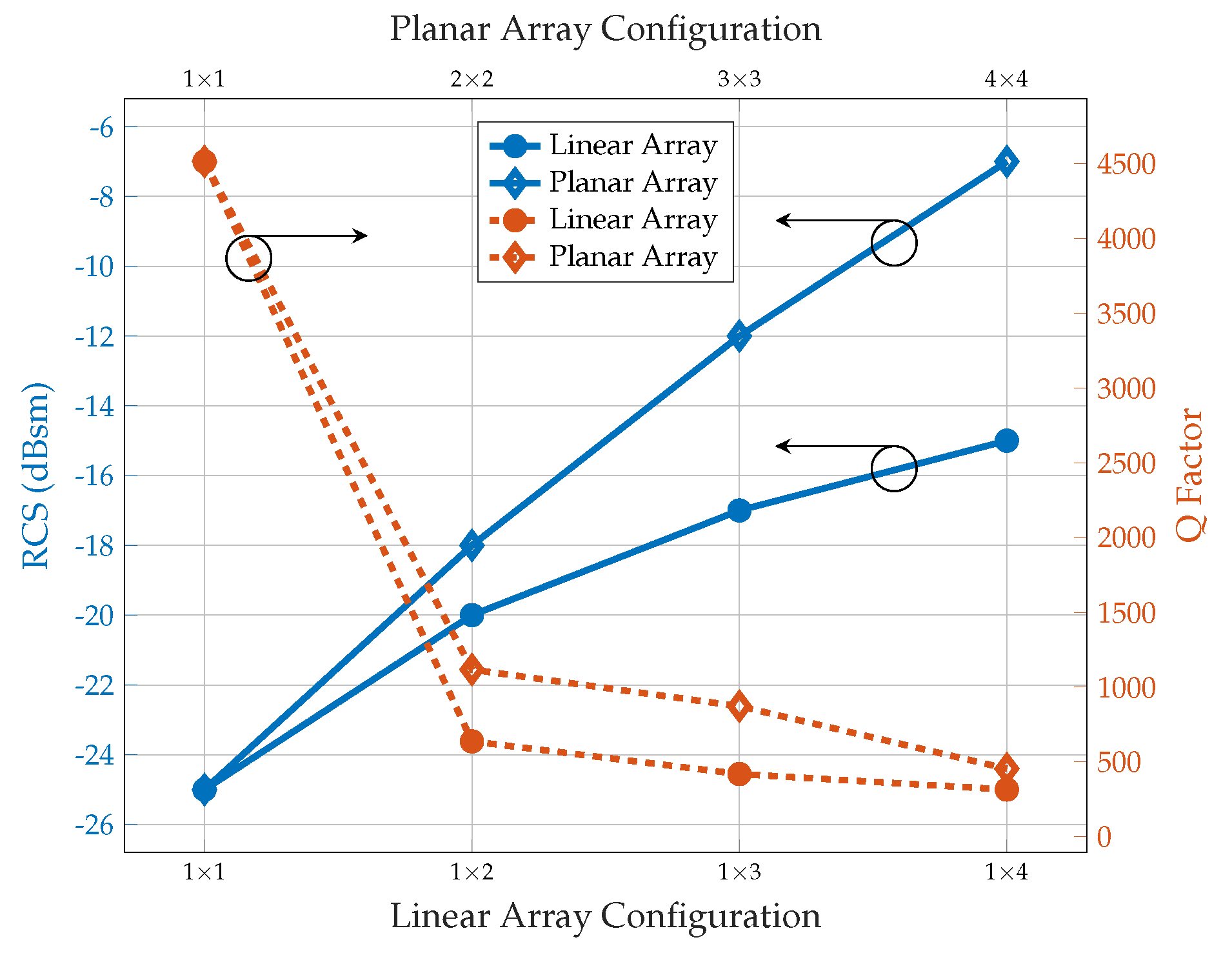
5.2. Q-Factor Analysis
6. Experimental Validation and Discussion
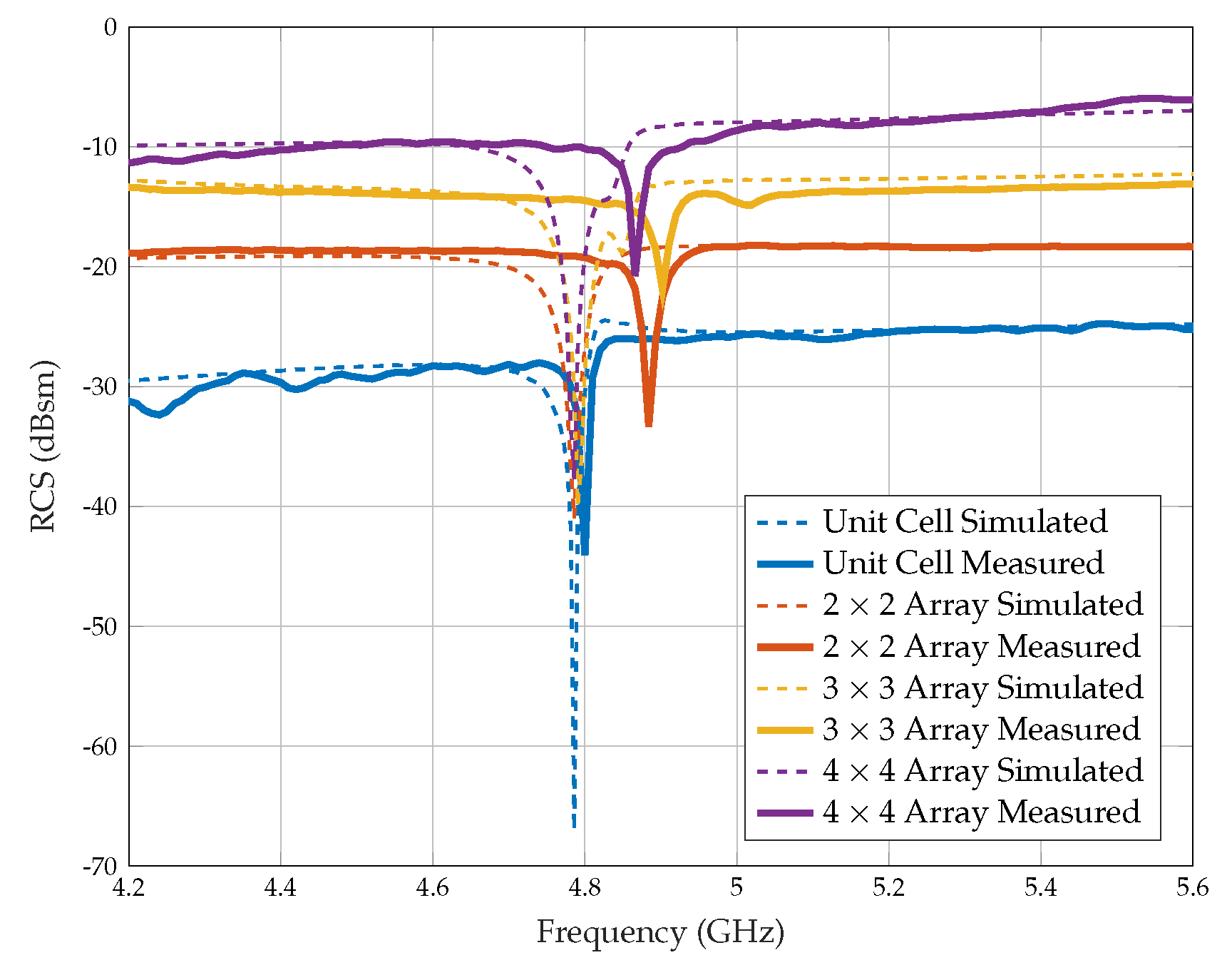
6.1. RCS of Planar Array Configurations
6.2. Detectability of Planar Array Configurations
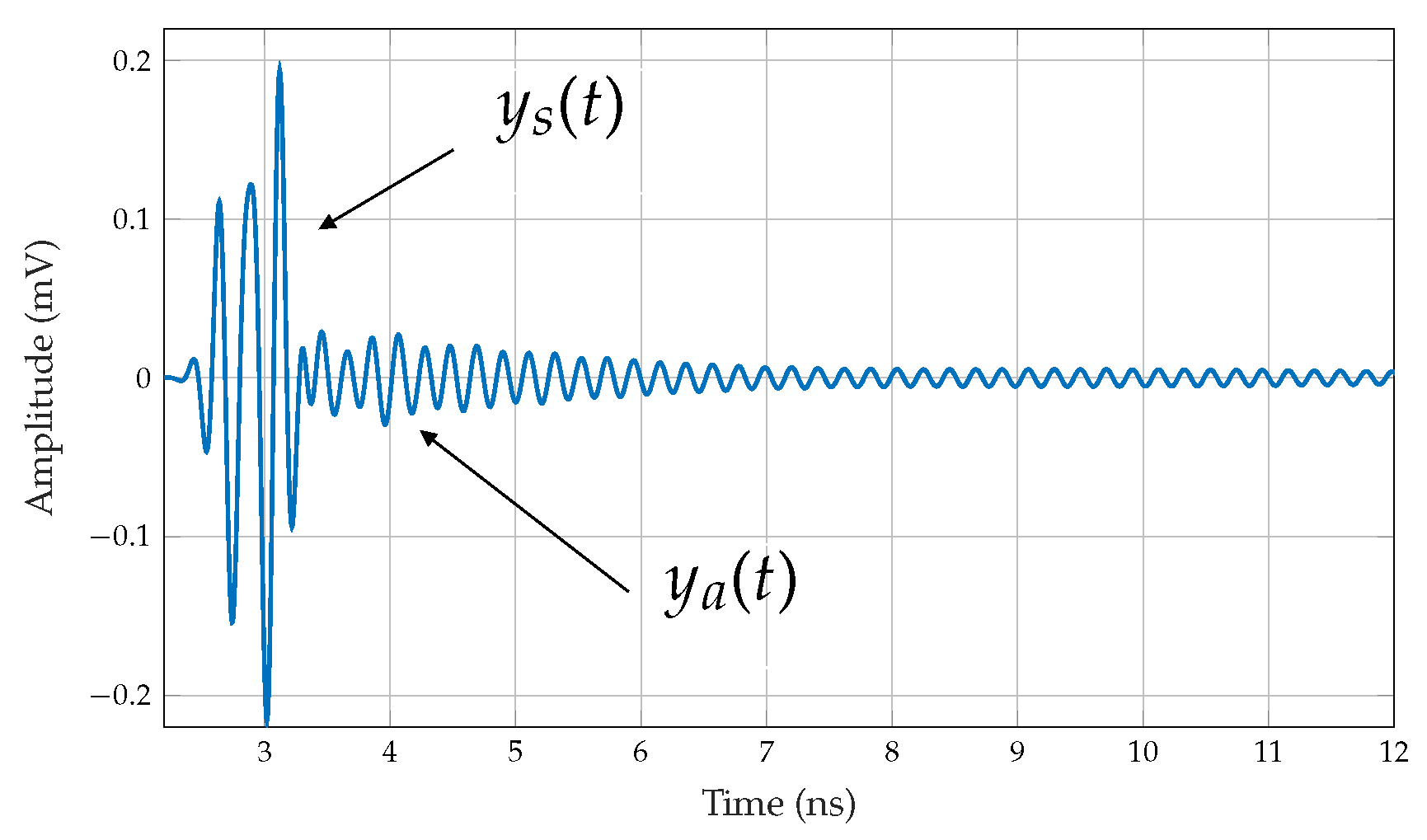
6.2.1. Linear Detectability
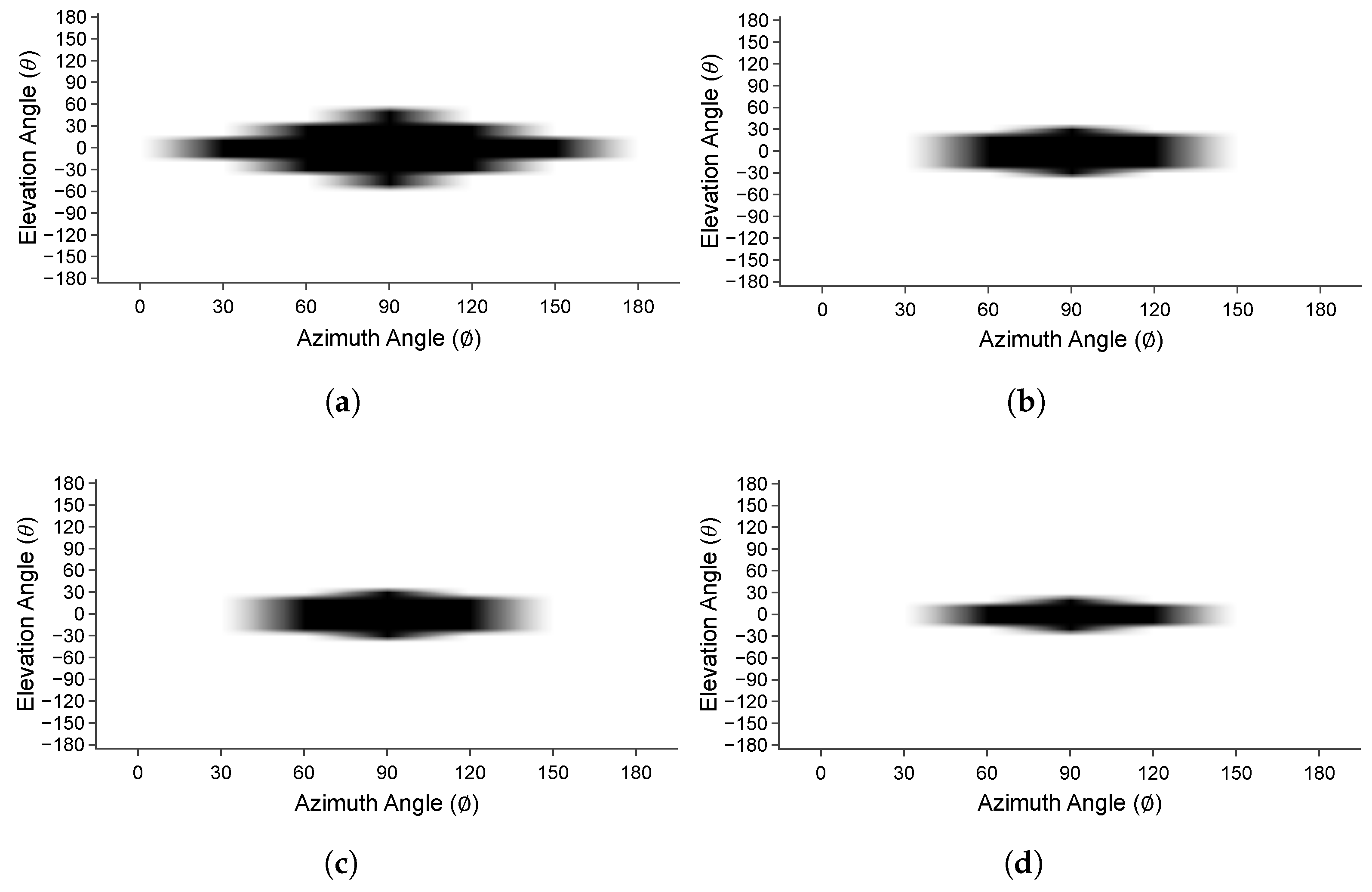
6.2.2. Spherical Detectability
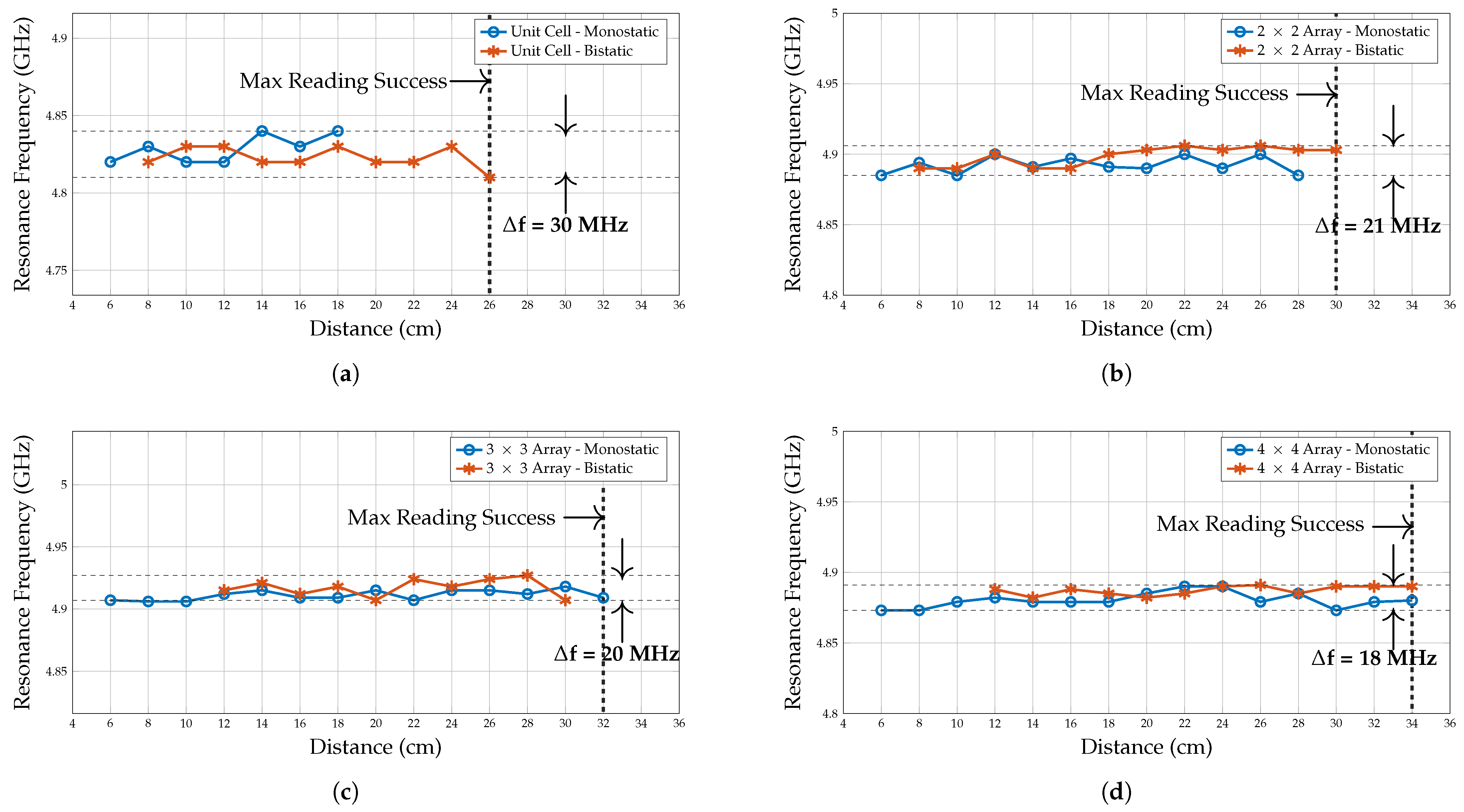
6.3. Q-Factor of Planar Array Configurations
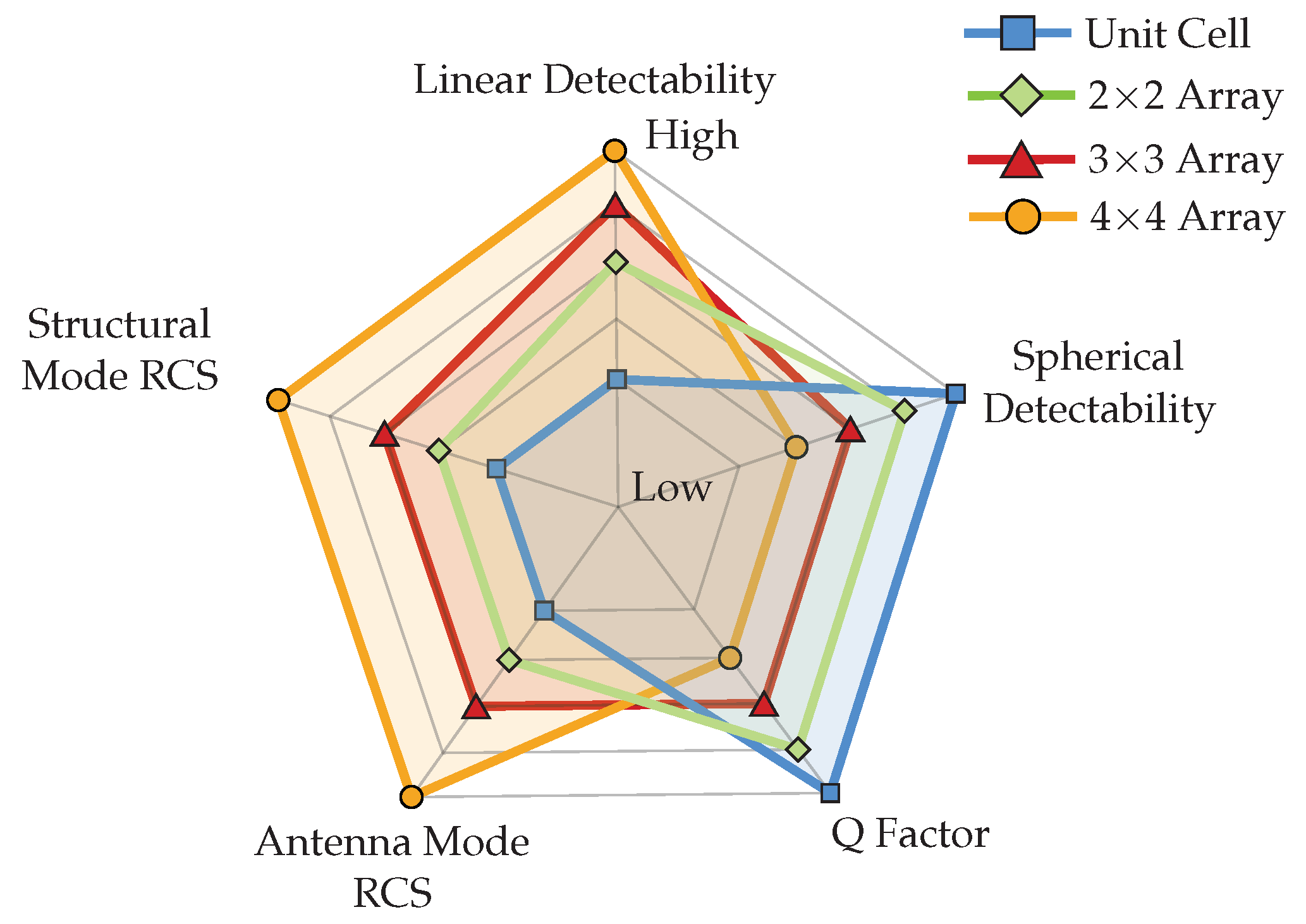
7. Trade-Off Analysis
7.1. Linear Detectability vs. Spherical Detectability
7.2. RCS vs. Q-Factor
7.3. Optimising Trade-Offs
7.4. Future Optimised Array Design Considerations
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Delen, D.; Sharda, R.; Hardgrave, B.C. The promise of RFID-based sensors in the perishables supply chain. IEEE Wirel. Commun. 2011, 18, 82–88. [Google Scholar] [CrossRef]
- Li, A.; Li, J.; Zhang, Y.; Han, D.; Li, T.; Zhang, Y. Secure UHF RFID Authentication with Smart Devices. IEEE Trans. Wirel. Commun. 2023, 22, 4520–4533. [Google Scholar] [CrossRef]
- Tan, W.C.; Sidhu, M.S. Review of RFID and IoT integration in supply chain management. Oper. Res. Perspect. 2022, 9, 100229. [Google Scholar] [CrossRef]
- Subrahmannian, A.; Behera, S.K. Chipless RFID Sensors for IoT-Based Healthcare Applications: A Review of State of the Art. IEEE Trans. Instrum. Meas. 2022, 71, 8003920. [Google Scholar] [CrossRef]
- Vena, A.; Perret, E.; Kaddour, D.; Baron, T. Toward a Reliable Chipless RFID Humidity Sensor Tag Based on Silicon Nanowires. IEEE Trans. Microw. Theory Tech. 2016, 64, 2977–2985. [Google Scholar] [CrossRef]
- Zuo, J.; Feng, J.; Gameiro, M.G.; Tian, Y.; Liang, J.; Wang, Y.; Ding, J.; He, Q. RFID-based sensing in smart packaging for food applications: A review. Future Foods 2022, 6, 100198. [Google Scholar] [CrossRef]
- Liu, G.; Wang, Q.A.; Jiao, G.; Dang, P.; Nie, G.; Liu, Z.; Sun, J. Review of Wireless RFID Strain Sensing Technology in Structural Health Monitoring. Sensors 2023, 23, 6925. [Google Scholar] [CrossRef] [PubMed]
- Herrojo, C.; Paredes, F.; Mata-Contreras, J.; Martín, F. Chipless-RFID: A Review and Recent Developments. Sensors 2019, 19, 3385. [Google Scholar] [CrossRef]
- Menon, S.K.; Donelli, M. Development of Enhanced Range, High Q, Passive, Chipless RFID Tags for Continuous Monitoring and Sensing Applications. Electronics 2022, 11, 127. [Google Scholar] [CrossRef]
- Rance, O.; Siragusa, R.; Lemaître-Auger, P.; Perret, E. Toward RCS Magnitude Level Coding for Chipless RFID. IEEE Trans. Microw. Theory Tech. 2016, 64, 2315–2325. [Google Scholar] [CrossRef]
- Karmaker, N.C. Tag, You’re It Radar Cross Section of Chipless RFID Tags. IEEE Microw. Mag. 2016, 17, 64–74. [Google Scholar] [CrossRef]
- Karmakar, N.C.; Amin, E.; Saha, J.K. Chipless RFID Sensors; John Wiley & Sons: Nashville, TN, USA, 2016. [Google Scholar]
- Pouzin, A.; Vuong, T.P.; Tedjini, S.; Perdereau, J.; Dreux, L. Measurement of Radar Cross Section for Passive UHF RFID Tags. In Proceedings of the Second European Conference on Antennas and Propagation, EuCAP 2007, Edinburgh, UK, 11–16 November 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Polivka, M.; Svanda, M.; Machac, J. Chipless RFID tag with an improved RCS response. In Proceedings of the 2014 44th European Microwave Conference, Rome, Italy, 6–9 October 2014; pp. 770–773. [Google Scholar] [CrossRef]
- Borgese, M.; Genovesi, S.; Manara, G.; Costa, F. Radar Cross Section of Chipless RFID Tags and BER Performance. IEEE Trans. Antennas Propag. 2021, 69, 2877–2886. [Google Scholar] [CrossRef]
- Ding, D.; Shi, G.; Li, K.; Wu, W.; Tang, X.; Yin, B. Passive ammonia detection sensor based on a ZnO/TiO2-loaded chipless RFID sensor circularly polarized array. Sens. Actuators Phys. 2025, 383, 116247. [Google Scholar] [CrossRef]
- Trzebiatowski, K.; Kalista, W.; Kulas, L.; Nyka, K. RCS Enhancement of Millimeter-Wave LTCC Van Atta Arrays with 3-D Printed Lenses for Chipless RFID Applications. IEEE Antennas Wirel. Propag. Lett. 2025, 24, 309–313. [Google Scholar] [CrossRef]
- Fodop Sokoudjou, J.J.; Villa-González, F.; García-Cardarelli, P.; Díaz, J.; Valderas, D.; Ochoa, I. Chipless RFID Tag Implementation and Machine-Learning Workflow for Robust Identification. IEEE Trans. Microw. Theory Tech. 2023, 71, 5147–5159. [Google Scholar] [CrossRef]
- Abbas, H.T.; Abdullah, H.H.; Mohanna, M.A.H.; Mansour, H.A.; Shehata, G.S. High RCS compact orientation independent chipless RFID tags based on slot ring resonators (SRR). In Proceedings of the 2018 35th National Radio Science Conference (NRSC), Cairo, Egypt, 20–22 March 2018; pp. 69–76. [Google Scholar] [CrossRef]
- Kumar, C.S.; Patre, S.R. Array of chipless RFID sensor tag for wireless detection of crack on large metallic surface. In Proceedings of the 2021 IEEE International Conference on RFID Technology and Applications (RFID-TA), Delhi, India, 6–8 October 2021; pp. 142–144. [Google Scholar] [CrossRef]
- El-Hadidy, M.; Lasantha, L.; Khan, S.I.; Sayed, Y.E.; Karmakar, N.C. Improved RCS Chipless RFID Tag Array for Long Reading Range. In Proceedings of the 2023 33rd International Conference Radioelektronika (RADIOELEKTRONIKA), Pardubice, Czech Republic, 19–20 April 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Singh, H.; Jha, R.M. Radar Cross Section of Phased Antenna Arrays. In Active Radar Cross Section Reduction: Theory and Applications; Cambridge University Press: Cambridge, UK, 2015; pp. 65–125. [Google Scholar]
- Shahid, L.; Shahid, H.; Riaz, M.A.; Naqvi, S.I.; Khan, M.J.; Khan, M.S.; Amin, Y.; Loo, J. Chipless RFID Tag for Touch Event Sensing and Localization. IEEE Access 2020, 8, 502–513. [Google Scholar] [CrossRef]
- Griffin, J.D.; Durgin, G.D. Complete Link Budgets for Backscatter-Radio and RFID Systems. IEEE Antennas Propag. Mag. 2009, 51, 11–25. [Google Scholar] [CrossRef]
- Huang, N.; Chen, J.; Ma, Z. High-Q Slot Resonator Used in Chipless Tag Design. Electronics 2021, 10, 1119. [Google Scholar] [CrossRef]
- Daliri, A.; Galehdar, A.; Rowe, W.S.; John, S.; Wang, C.H.; Ghorbani, K. Quality factor effect on the wireless range of microstrip patch antenna strain sensors. Sensors 2014, 14, 595–605. [Google Scholar] [CrossRef]
- Babaeian, F.; Karmakar, N.C. Time and Frequency Domains Analysis of Chipless RFID Back-Scattered Tag Reflection. IoT 2020, 1, 109–127. [Google Scholar] [CrossRef]
- Athauda, T.; Karmakar, N.C. The Realization of Chipless RFID Resonator for Multiple Physical Parameter Sensing. IEEE Internet Things J. 2019, 6, 5387–5396. [Google Scholar] [CrossRef]
- Islam, M.A.; Yap, Y.; Karmakar, N.C.; Azad, A. Compact Printable Orientation Independent Chipless RFID Tag. Prog. Electromagn. Res. 2012, 33, 55–66. [Google Scholar] [CrossRef]
- Khan, A.; Riaz, M.; Shahid, H.; Amin, Y.; Tenhunen, H.; Loo, J. Design of a Cobweb Shape Chipless RFID Tag. Microw. J. 2021, 64, 90. [Google Scholar]
- Dhouibi, A.; Burokur, S.N.; de Lustrac, A.; Priou, A. Study and analysis of an electric Z-shaped meta-atom. Adv. Electromagn. 2012, 1, 64–70. [Google Scholar] [CrossRef]
- Marindra, A.M.J.; Tian, G.Y. Chipless RFID Sensor Tag for Metal Crack Detection and Characterization. IEEE Trans. Microw. Theory Tech. 2018, 66, 2452–2462. [Google Scholar] [CrossRef]
- Mekki, K.; Necibi, O.; Dinis, H.; Mendes, P.; Gharsallah, A. Investigation on the chipless RFID tag with a UWB pulse using a UWB IR-based reader. Int. J. Microw. Wirel. Technol. 2021, 14, 166–175. [Google Scholar] [CrossRef]
- Baliarda, C.; Romeu, J.; Cardama, A. The Koch monopole: A small fractal antenna. IEEE Trans. Antennas Propag. 2000, 48, 1773–1781. [Google Scholar] [CrossRef]
- Babaeian, F.; Karmakar, N.C. Development of Cross-Polar Orientation-Insensitive Chipless RFID Tags. IEEE Trans. Antennas Propag. 2020, 68, 5159–5170. [Google Scholar] [CrossRef]
- Babaeian, F.; Karmakar, N. A High Gain Dual Polarised Ultra-Wideband Array of Antenna for Chipless RFID Applications. IEEE Access 2018, 6, 73702–73712. [Google Scholar] [CrossRef]
- Ali, Z.; Perret, E. Compact Measurement Apparatus for 3D Spherical Read Range Characterization of Chipless RFID. IEEE Access 2023, 11, 53643–53653. [Google Scholar] [CrossRef]

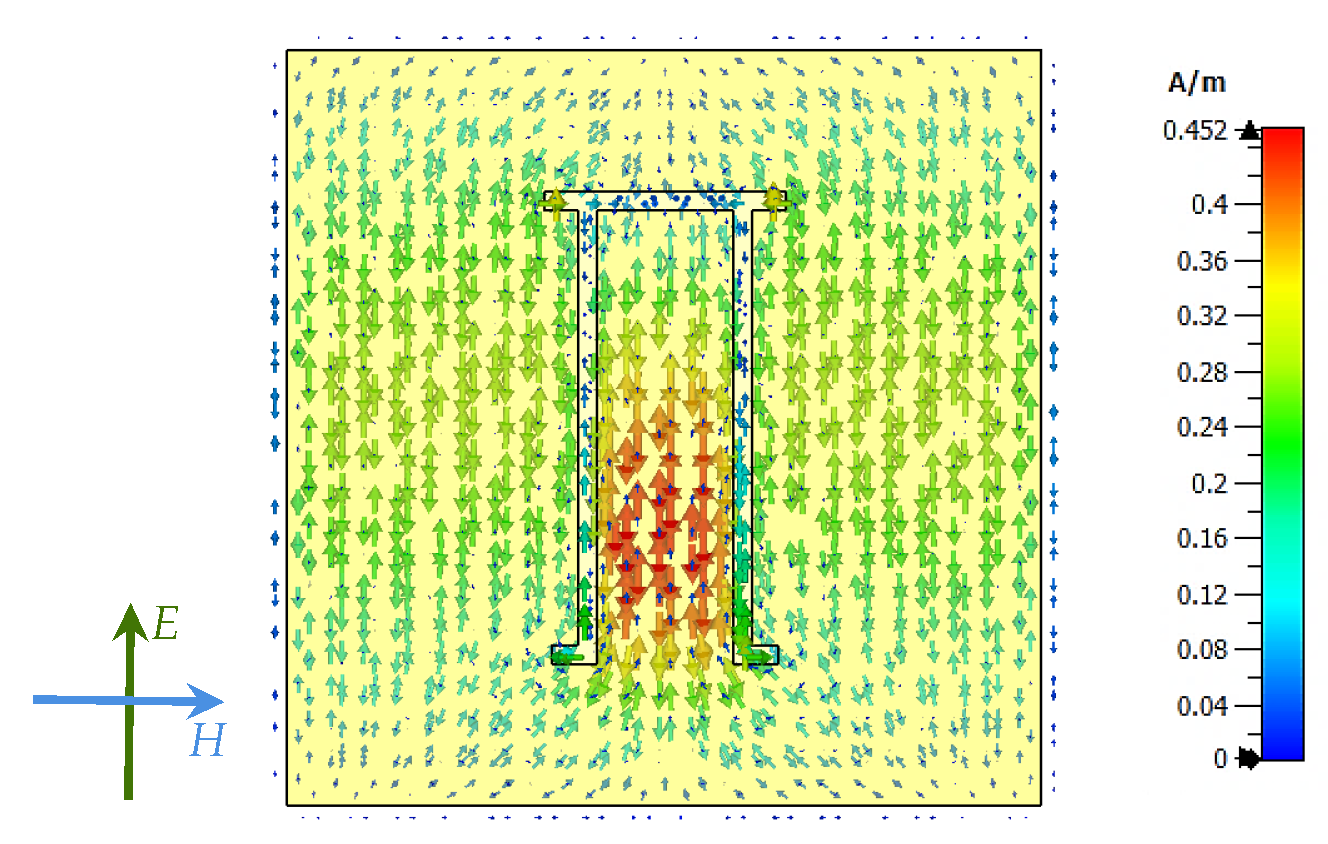

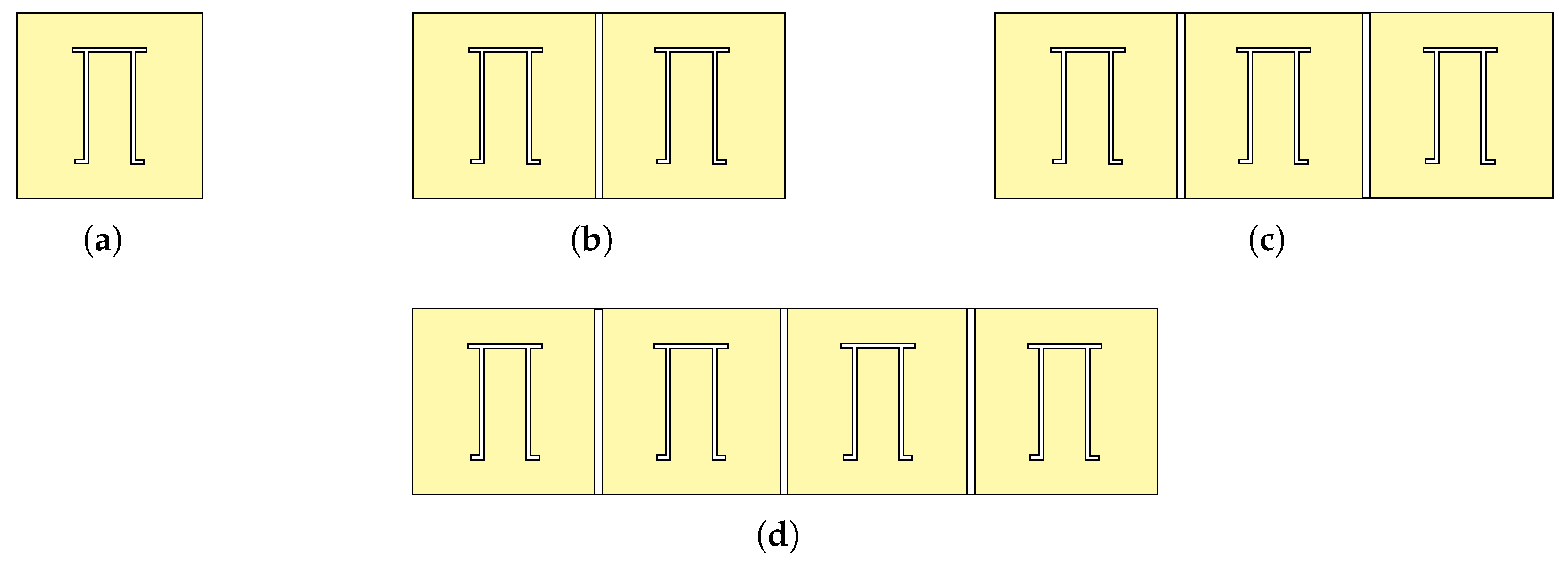
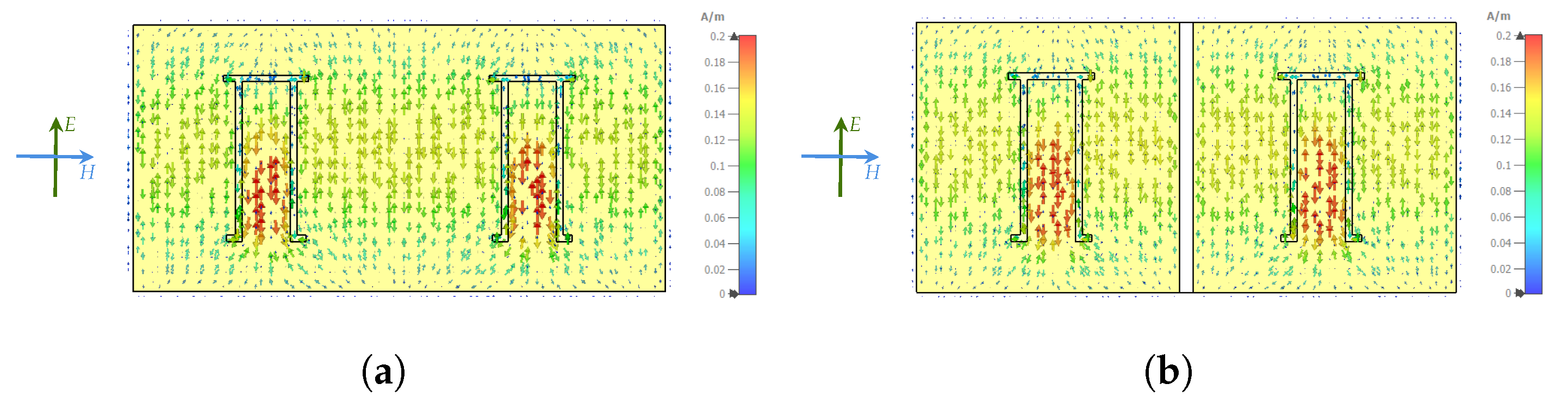
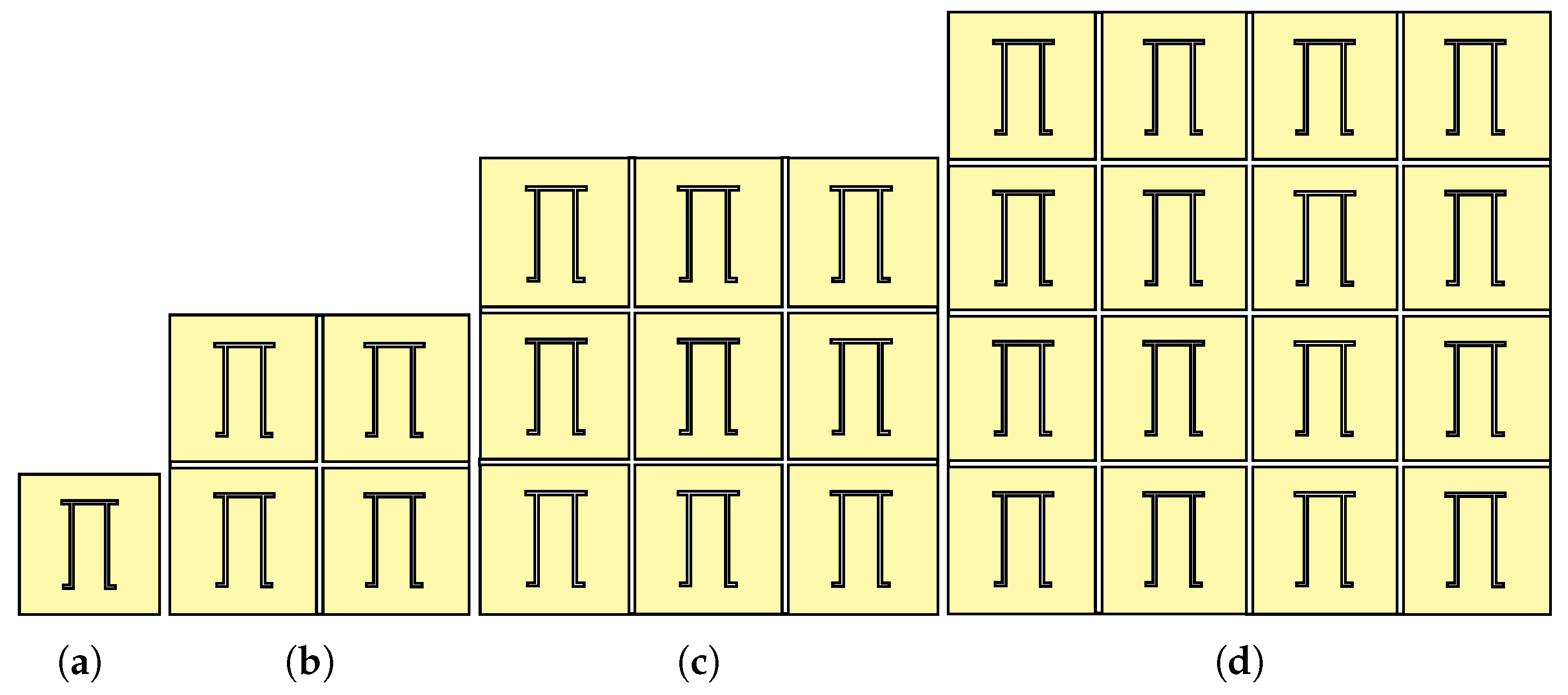

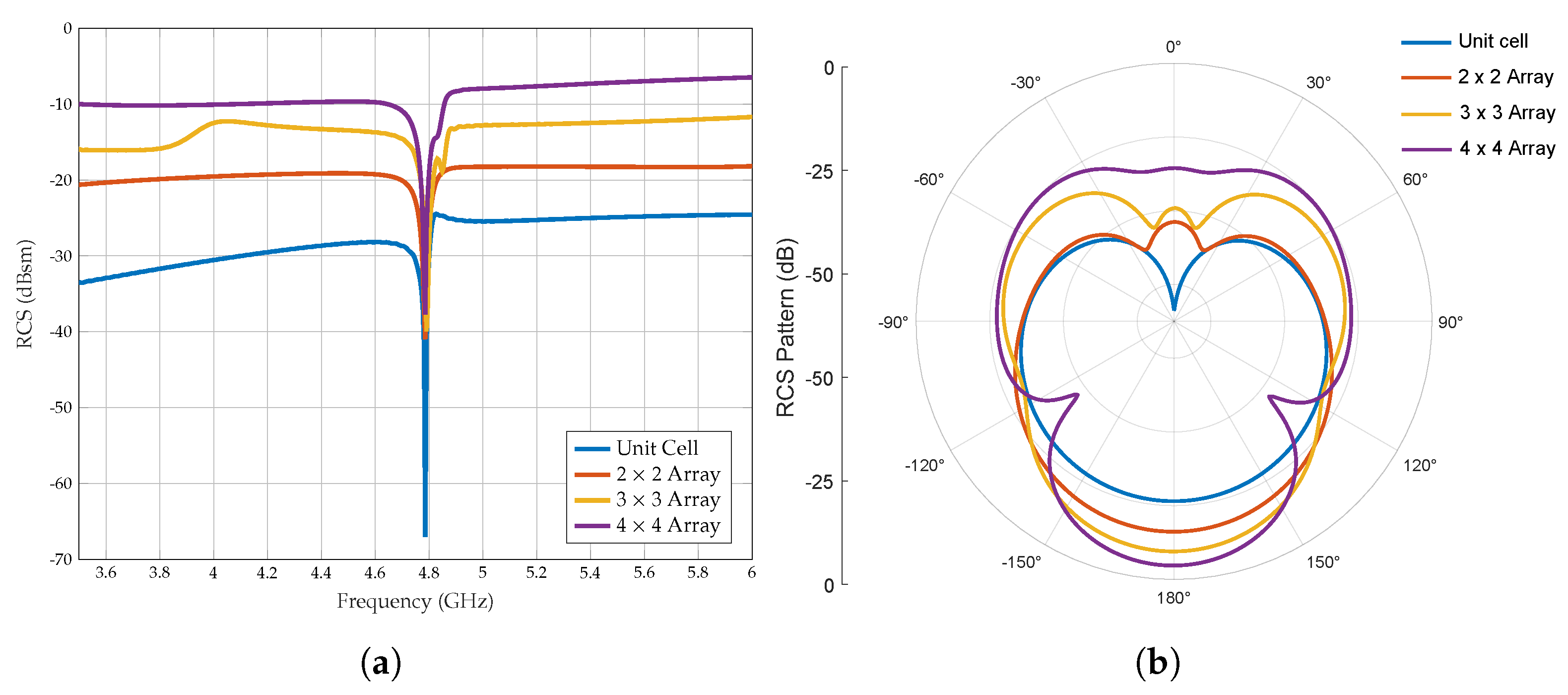







| Resonator Configuration | RCS Level (dBsm) | Normalised RCS Level (dBsm/Cells) | Resonance Frequency (GHz) | Simulated Q-Factor |
|---|---|---|---|---|
| Unit cell | −25 | −25.00 | 4.78 | 4515 |
| Array | −20 | −10.00 | 4.75 | 637 |
| Array | −17 | −5.77 | 4.75 | 418 |
| Array | −15 | −9.02 | 4.75 | 314 |
| Resonator Configuration | RCS Level (dBsm) | Normalised RCS Level (dBsm/Cells) | Resonance Frequency (GHz) | Simulated Q-Factor |
|---|---|---|---|---|
| Unit cell | −25 | −25.00 | 4.78 | 4515 |
| Array | −18 | −24.02 | 4.78 | 1117 |
| Array | −12 | −21.54 | 4.79 | 872 |
| Array | −7 | −19.04 | 4.78 | 454 |
| Resonator Configuration | Simulated | Measured | ΔRCS (dBsm) | Δf (GHz) | ΔQ | ||||
|---|---|---|---|---|---|---|---|---|---|
| RCS Level | Resonance Freq. (GHz) | Q Factor | RCS Level | Resonance Freq. (GHz) | Q Factor | ||||
| Unit cell | −25 | 4.78 | 4515 | −25 | 4.80 | 1224 | 0 | −0.02 | −3291 |
| Array | −18 | 4.78 | 1117 | −18 | 4.88 | 784 | 0 | −0.10 | −333 |
| Array | −12 | 4.79 | 872 | −13 | 4.90 | 525 | +1 | −0.11 | −347 |
| Array | −7 | 4.78 | 454 | −8 | 4.86 | 359 | +1 | −0.08 | −95 |
| Resonator Configuration | Measured | Simulated Resonance Frequency (GHz) | Δf (GHz) | |
|---|---|---|---|---|
| Distance (m) | Resonance Frequency (GHz) | |||
| Array | 0.65 | 4.88 | 4.78 | +0.10 |
| 1.30 | 4.89 | 4.78 | +0.11 | |
| Array | 1.00 | 4.88 | 4.78 | +0.10 |
| 3.00 | 4.89 | 4.78 | +0.11 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lasantha, L.; Ray, B.; Karmakar, N. Trade-Off Analysis for Array Configurations of Chipless RFID Sensor Tag Designs. Sensors 2025, 25, 1653. https://doi.org/10.3390/s25061653
Lasantha L, Ray B, Karmakar N. Trade-Off Analysis for Array Configurations of Chipless RFID Sensor Tag Designs. Sensors. 2025; 25(6):1653. https://doi.org/10.3390/s25061653
Chicago/Turabian StyleLasantha, Likitha, Biplob Ray, and Nemai Karmakar. 2025. "Trade-Off Analysis for Array Configurations of Chipless RFID Sensor Tag Designs" Sensors 25, no. 6: 1653. https://doi.org/10.3390/s25061653
APA StyleLasantha, L., Ray, B., & Karmakar, N. (2025). Trade-Off Analysis for Array Configurations of Chipless RFID Sensor Tag Designs. Sensors, 25(6), 1653. https://doi.org/10.3390/s25061653







