An Adaptive Grid Generation Approach to Pipeline Leakage Rapid Localization Based on Time Reversal
Abstract
:1. Introduction
2. Description of the Principle
2.1. The Signal Adjustment Computation
- a1.
- Adjust the NPW signals captured by the two PZT sensors.
- a2.
- Derive parameter .
2.2. The Adaptive Grid Generation Computation
- b1:
- Set up the sizes of the initial grid and the initial monitoring area. Generate the initial grid and save their positions.
- b2:
- At the saved grid, calculate the localization functional value based on the parameter determined by Equation (12) and ref. [48].
- b3:
- Resize the grid to half of the previous grid size.
- b4:
- Resize the monitoring area. The center of the new monitoring area is the position of the maximum localization functional value obtained in step b2, and the range of the new monitoring area is set as the previous grid size.
- b5:
- Generate new grids at the new monitoring area by using the new grid size, and save the new grids’ positions.
- b6:
- Repeat step b2–step b5 until the maximum localization functional value of the latest monitoring area equals the sum of the maximum of the acquired signals.
2.3. Conventional TR Localization Computation Based on the Adaptive Grids
- c1:
- Calculate and plot the maximum energy distribution curve according to the original acquired NPW signals by using the conventional TR localization method [35] at all the saved grids.
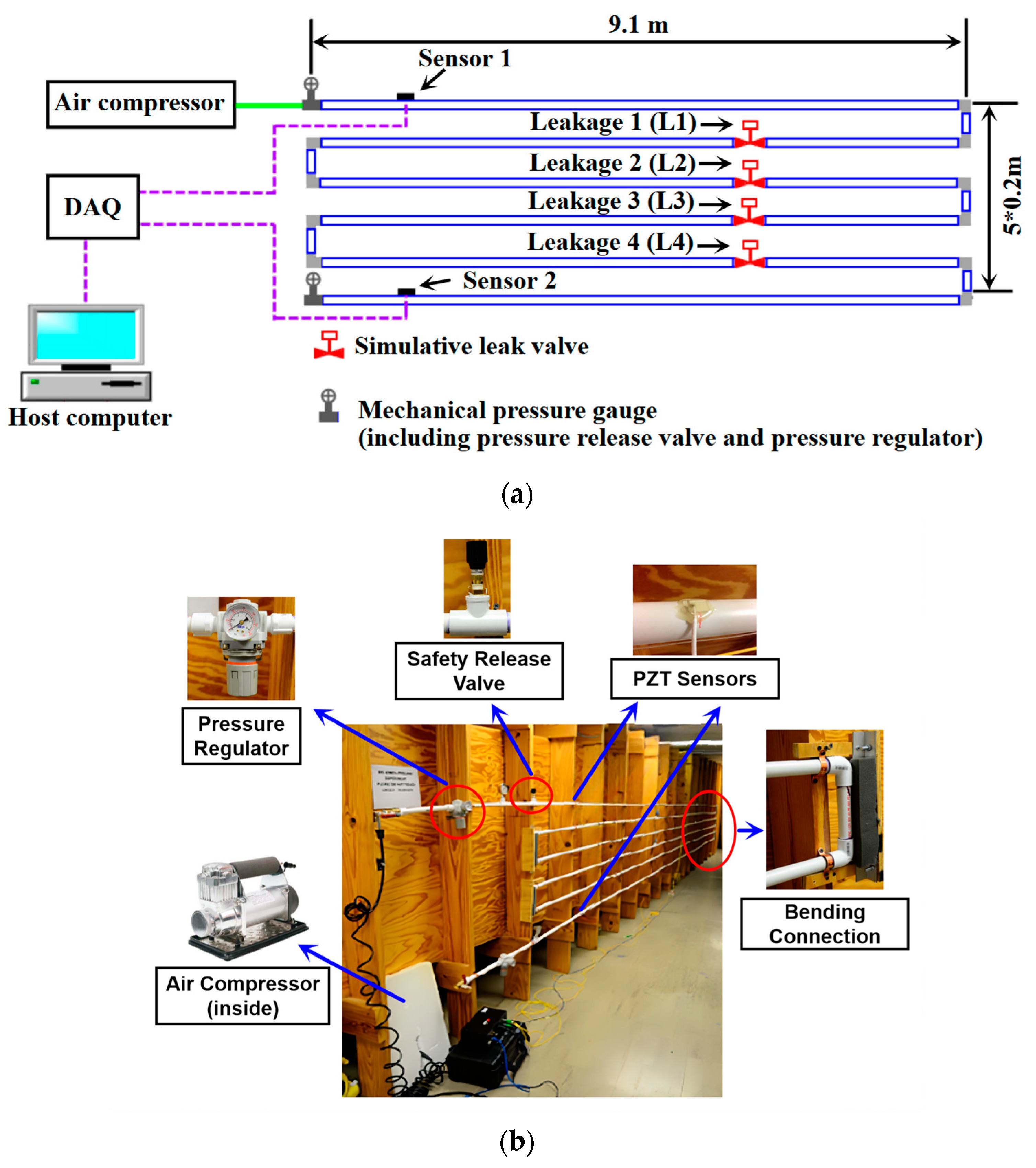
3. Experiment
4. Adaptive Grid Generation
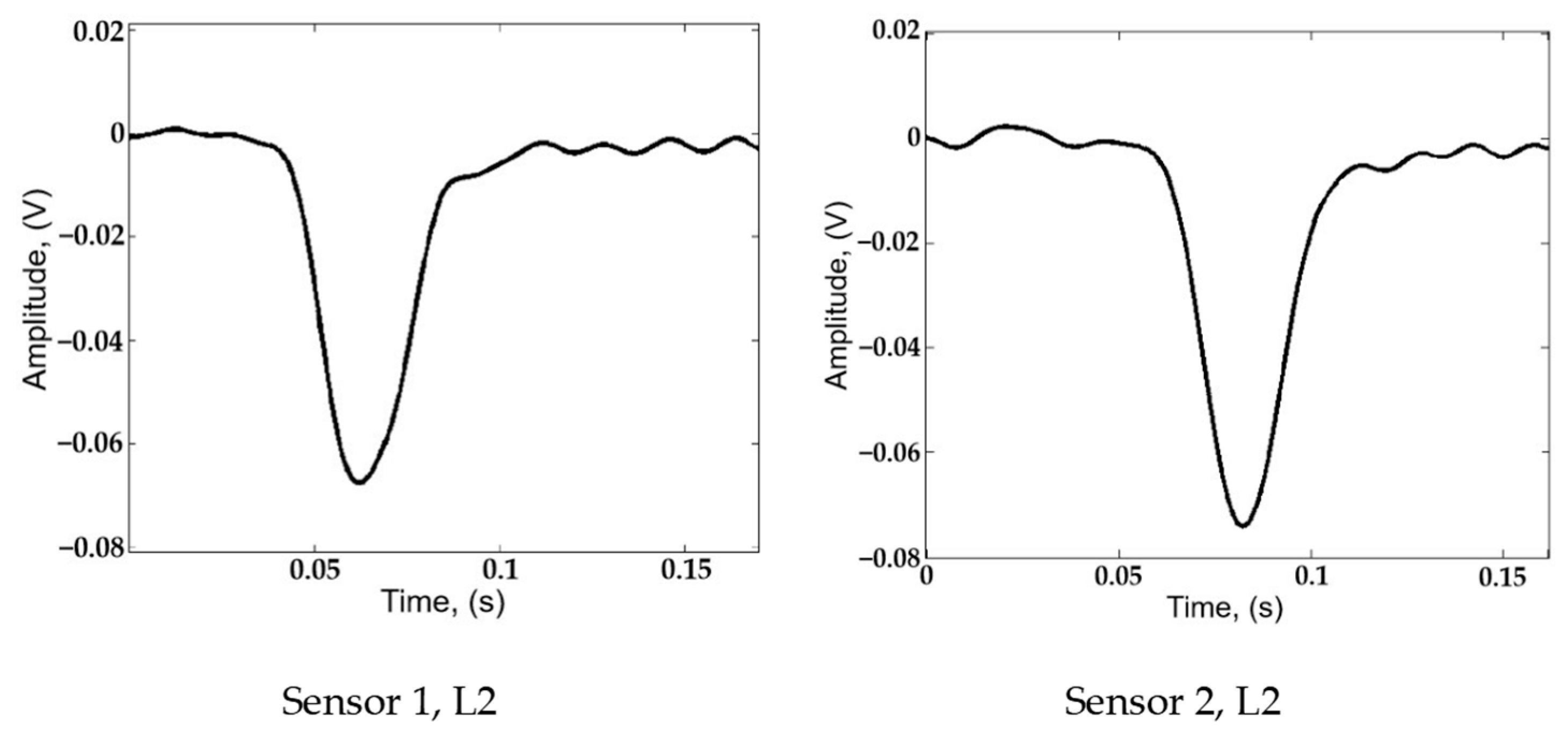
4.1. The Signal Adjustment
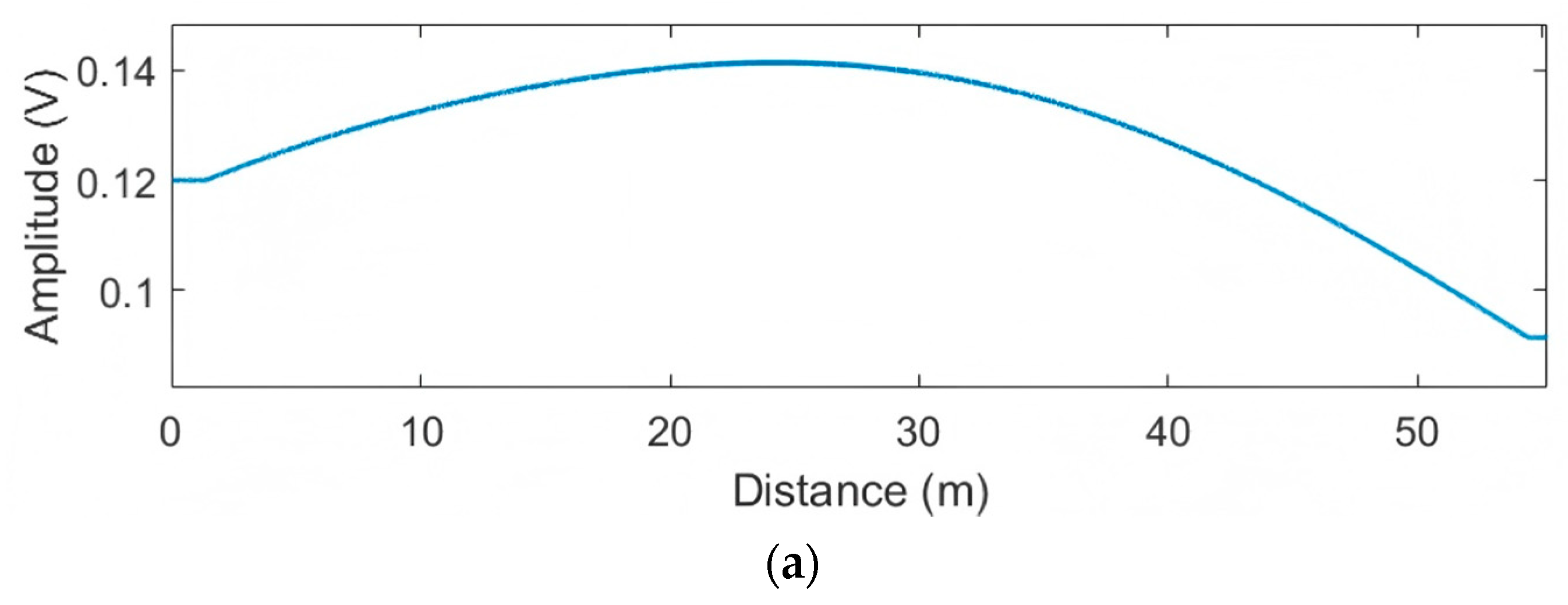
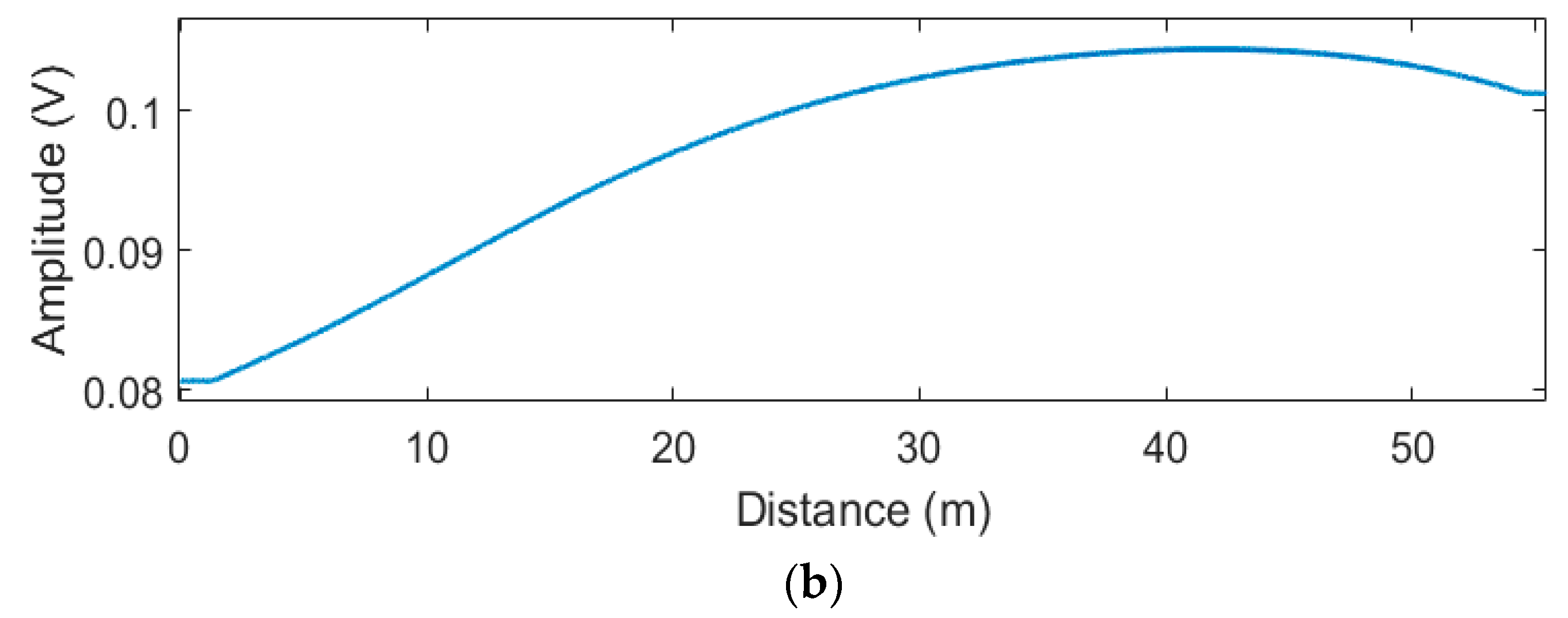
4.2. The Adaptive Grid
5. Leakage Localization Results and Comparison
5.1. Leak Localization Results
5.2. Comparison of Leak Localization Cost
6. Discussion
6.1. Discussion About Initial Grid Size
6.2. Discussion About the Ratio of the New Grid Size to the Previous Grid Size
6.3. Analysis of Localization Error
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CS | Compressive Sensing |
| NPW | Negative Pressure Wave |
| PZT | Lead Zirconate Titanate |
| PVC | Polyvinyl Chloride |
| SHM | Structural Health Monitoring |
| TR | Time Reversal |
| VMD | Variational Mode Decomposition |
References
- Liao, X.; Yan, Q.; Zhang, Y.; Zhong, H.; Qi, M.; Wang, C. An innovative deep neural network coordinating with percussion-based technique for automatic detection of concrete cavity defects. Constr. Build. Mater. 2023, 400, 132700. [Google Scholar] [CrossRef]
- Kudela, P.; Radzienski, M.; Ostachowicz, W.; Yang, Z. Structural Health Monitoring system based on a concept of Lamb wave focusing by the piezoelectric array. Mech. Syst. Signal Process. 2018, 108, 21–32. [Google Scholar] [CrossRef]
- Ge, B.; Kim, S. Probabilistic service life prediction updating with inspection information for RC structures subjected to coupled corrosion and fatigue. Eng. Struct. 2021, 238, 112260. [Google Scholar] [CrossRef]
- Lin, J.; Liu, H.; Huang, S.; Nie, Z.; Ma, H. Structural damage detection with canonical correlation analysis using limited sensors. J. Sound Vib. 2022, 538, 117243. [Google Scholar] [CrossRef]
- Wang, X.; Yue, Q.; Liu, X. Bolted lap joint loosening monitoring and damage identification based on acoustic emission and machine learning. Mech. Syst. Signal Process. 2024, 220, 111690. [Google Scholar] [CrossRef]
- Gorski, J.; Dziedziech, K.; Klepka, A. A hybrid approach for damage detection and localisation using modulation transfer and vibroacoustic modulation. Mech. Syst. Signal Process. 2024, 210, 111180. [Google Scholar] [CrossRef]
- Qin, X.; Lv, S.; Xu, C.; Xie, J.; Jia, L.; Sui, Q.; Jiang, M. Implications of liquid impurities filled in breaking cracks on nonlinear acoustic modulation response: Mechanisms, phenomena and potential applications. Mech. Syst. Signal Process. 2023, 200, 110550. [Google Scholar] [CrossRef]
- Lee, Y.F.; Lu, Y. Identification of fatigue crack under vibration by nonlinear guided waves. Mech. Syst. Signal Process. 2022, 163, 108138. [Google Scholar] [CrossRef]
- Xue, Q.; Xu, S.; Li, A.; Wang, Y. Local–overall buckling behavior of corroded intermediate compression-bending H-section steel columns. Eng. Struct. 2024, 308, 118025. [Google Scholar] [CrossRef]
- Yuan, H.; Han, F.; Theofanous, M. Experimental behaviour of hybrid carbon steel—Stainless steel bolted connections subjected to electrochemical corrosion. Thin-Walled Struct. 2024, 199, 111794. [Google Scholar] [CrossRef]
- Tong, T.; Hua, J.; Du, D.; Gao, F.; Lin, J. Bolt looseness detection in lap joint based on phase change of Lamb waves. Mech. Syst. Signal Process. 2025, 223, 111840. [Google Scholar] [CrossRef]
- Liu, P.; Wang, X.; Wang, Y.; Zhu, J.; Ji, X. Research on percussion-based bolt looseness monitoring under noise interference and insufficient samples. Mech. Syst. Signal Process. 2024, 208, 111013. [Google Scholar] [CrossRef]
- Huang, J.; Liu, J.; Gong, H.; Deng, X. Multimodal loosening detection for threaded fasteners based on multiscale cross fuzzy entropy. Mech. Syst. Signal Process. 2023, 186, 109834. [Google Scholar] [CrossRef]
- Huo, L.; Cheng, H.; Kong, Q.; Chen, X. Bond-Slip Monitoring of Concrete Structures Using Smart Sensors—A Review. Sensors 2019, 19, 1231. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Zheng, Y.; Song, G.; Chen, D.; Ye, Y. Identification of the structural damage mechanism of BFRP bars reinforced concrete beams using smart transducers based on time reversal method. Constr. Build. Mater. 2019, 220, 615–627. [Google Scholar] [CrossRef]
- Zheng, D.; Kou, J.; Wei, H.; Zhang, T.; Guo, H. Experimental study on flexural behavior of damaged concrete beams strengthened with high ductility concrete under repeated load. Eng. Struct. 2023, 274, 115203. [Google Scholar] [CrossRef]
- Meng, H.; Yang, W.; Yang, X. Real-Time Damage Monitoring of Double-Tube Concrete Column Under Axial Force. Arab. J. Sci. Eng. 2022, 47, 12711–12728. [Google Scholar] [CrossRef]
- He, S.; Zhang, G.; Song, G. Design of a networking stress wave communication method along pipelines. Mech. Syst. Signal Process. 2022, 164, 108192. [Google Scholar] [CrossRef]
- Yin, J.; Chen, S.; Wong, V.K.; Yao, K. Thermal Sprayed Lead-Free Piezoelectric Ceramic Coatings for Ultrasonic Structural Health Monitoring. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 3070–3080. [Google Scholar] [CrossRef]
- Ben Seghier, M.E.A.; Mohamed, O.A.; Ouaer, H. Machine learning-based Shapley additive explanations approach for corroded pipeline failure mode identification. Structures 2024, 65, 106653. [Google Scholar] [CrossRef]
- Shuai, Y.; Zhang, Y.; Shuai, J.; Xie, D.; Zhu, X.; Zhang, Z. A novel framework for predicting the burst pressure of energy pipelines with clustered corrosion defects. Thin-Walled Struct. 2024, 205, 112413. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Zhou, T.; Wang, T.; Li, J. A Novel Pipeline Corrosion Monitoring Method Based on Piezoelectric Active Sensing and CNN. Sensors 2023, 23, 855. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, X.; Li, W. Hidden Markov models for pipeline damage detection using piezoelectric transducers. J. Civ. Struct. Health Monit. 2021, 11, 745–755. [Google Scholar] [CrossRef]
- Tran, V.Q.C.; Le, D.V.; Yntema, D.R.; Havinga, P.J.M. A Review of Inspection Methods for Continuously Monitoring PVC Drinking Water Mains. IEEE Internet Things J. 2022, 9, 14336–14354. [Google Scholar] [CrossRef]
- Yuan, J.; Mao, W.; Hu, C.; Zheng, J.; Zheng, D.; Yang, Y. Leak detection and localization techniques in oil and gas pipeline: A bibliometric and systematic review. Eng. Fail. Anal. 2023, 146, 107060. [Google Scholar] [CrossRef]
- Martins, J.C.; Seleghim Jr, P. Assessment of the performance of acoustic and mass balance methods for leak detection in pipelines for transporting liquids. J. Fluids Eng. Trans. ASME 2010, 132, 0114011–0114018. [Google Scholar] [CrossRef]
- Nguyen, D.-T.; Nguyen, T.-K.; Ahmad, Z.; Kim, J.-M. A Reliable Pipeline Leak Detection Method Using Acoustic Emission with Time Difference of Arrival and Kolmogorov–Smirnov Test. Sensors 2023, 23, 9296. [Google Scholar] [CrossRef] [PubMed]
- Abuhatira, A.A.; Salim, S.M.; Vorstius, J.B. CFD-FEA based model to predict leak-points in a 90-degree pipe elbow. Eng. Comput. 2023, 39, 3941–3954. [Google Scholar] [CrossRef]
- Liping, F.; Lingya, M.; Cuiwei, L.; Yuxing, L. Experimental study on the amplitude characteristics and propagation velocity of dynamic pressure wave for the leakage of gas-liquid two-phase intermittent flow in pipelines. Int. J. Press. Vessel. Pip. 2021, 193, 104457. [Google Scholar] [CrossRef]
- Waqar, M.; Memon, A.M.; Louati, M.; Ghidaoui, M.S.; Alhems, L.M.; Meniconi, S.; Brunone, B.; Capponi, C. Pipeline leak detection using hydraulic transients and domain-guided machine learning. Mech. Syst. Signal Process. 2025, 224, 111967. [Google Scholar] [CrossRef]
- Wang, J.; Ren, L.; Jia, Z.; Jiang, T.; Wang, G.X. A novel pipeline leak detection and localization method based on the FBG pipe-fixture sensor array and compressed sensing theory. Mech. Syst. Signal Process. 2022, 169, 108669. [Google Scholar] [CrossRef]
- Lang, X. Leak Localization Method for Pipeline Based on Fusion Signal. IEEE Sens. J. 2021, 21, 3271–3277. [Google Scholar] [CrossRef]
- Hu, X.; Ma, D.; Song, Q.; Chen, G.; Wang, R.; Zhang, H. Negative Pressure Wave-Based Method for Abnormal Signal Location in Energy Transportation System. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, Y.; Yang, Y.; Zhou, J.; Shi, L. Research on Noise Reduction Method for Leakage Signal of Water Supply Pipeline. IEEE Access 2024, 12, 71406–71418. [Google Scholar] [CrossRef]
- Ing, R.K.; Quieffin, N.; Catheline, S.; Fink, M. In solid localization of finger impacts using acoustic time-reversal process. Appl. Phys. Lett. 2005, 87, 204104. [Google Scholar] [CrossRef]
- He, J.; Wu, X.; Guan, X. An enhanced ultrasonic method for monitoring and predicting stress loss in multi-layer structures via vibro-acoustic modulation. Mech. Syst. Signal Process. 2024, 208, 110984. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Wang, T.; Lu, G.; Peng, Y. Study on pipeline corrosion monitoring based on piezoelectric active time reversal method. Smart Mater. Struct. 2023, 32, 054003. [Google Scholar] [CrossRef]
- Cheng, Z.H.; Ma, M.L.; Liang, F.; Zhao, D.; Wang, B.Z. Low Complexity Time Reversal Imaging Methods Based on Truncated Time Reversal Operator. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–14. [Google Scholar] [CrossRef]
- Huo, L.; Li, C.; Jiang, T.; Li, H.-N. Feasibility Study of Steel Bar Corrosion Monitoring Using a Piezoceramic Transducer Enabled Time Reversal Method. Appl. Sci. 2018, 8, 2304. [Google Scholar] [CrossRef]
- Cai, J.; Shi, L.; Yuan, S.; Shao, Z. High spatial resolution imaging for structural health monitoring based on virtual time reversal. Smart Mater. Struct. 2011, 20, 055018. [Google Scholar] [CrossRef]
- Shi, G.; Nehorai, A. A relationship between time-reversal imaging and maximum-likelihood scattering estimation. IEEE Trans. Signal Process. 2007, 55, 4707–4711. [Google Scholar]
- Mukherjee, S.; Udpa, L.; Udpa, S.; Rothwell, E.J. Target Localization Using Microwave Time-Reversal Mirror in Reflection Mode. IEEE Trans. Antennas Propag. 2017, 65, 820–828. [Google Scholar] [CrossRef]
- Liao, T.H.; Hsieh, P.C.; Chen, F.C. Subwavelength target detection using ultrawideband time-reversal techniques with a multilayered dielectric slab. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 835–838. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, J.; Zhang, X. Adaptive Compressive Sensing: An Optimization Method for Pipeline Magnetic Flux Leakage Detection. Sustainability 2023, 15, 14591. [Google Scholar] [CrossRef]
- Li, J.; Wang, C.; Zheng, Q.; Qian, Z. Leakage Localization for Long Distance Pipeline Based on Compressive Sensing. IEEE Sens. J. 2019, 19, 6795–6801. [Google Scholar] [CrossRef]
- Li, P.; Wang, X.; Jiang, C.; Bi, H.; Liu, Y.; Yan, W.; Zhang, C.; Dong, T.; Sun, Y. Advanced transformer model for simultaneous leakage aperture recognition and localization in gas pipelines. Reliab. Eng. Syst. Saf. 2024, 241, 109685. [Google Scholar] [CrossRef]
- Cheng, J.; Jiang, Z.; Wu, H.; Zhang, X. Water Pipeline Leak Detection Method Based on Transfer Learning. Water 2025, 17, 368. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, J.; Song, Y.; Peng, C.; Song, G. A time reversal based pipeline leakage localization method with the adjustable resolution. IEEE Access 2018, 6, 26993–27000. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, M.; Yin, X.; Huang, Z.; Wang, L. Debonding detection of reinforced concrete (RC) beam with near-surface mounted (NSM) pre-stressed carbon fiber reinforced polymer (CFRP) plates using embedded piezoceramic smart aggregates (SAs). Appl. Sci. 2020, 10, 50. [Google Scholar] [CrossRef]
- Meshkinzar, A.; Al-Jumaily, A.M. Cylindrical Piezoelectric PZT Transducers for Sensing and Actuation. Sensors 2023, 23, 3042. [Google Scholar] [CrossRef]
- Safaei, M.; Sodano, H.A.; Anton, S.R. A review of energy harvesting using piezoelectric materials: State-of-the-art a decade later (2008–2018). Smart Mater. Struct. 2019, 28, 113001. [Google Scholar] [CrossRef]
- Luo, A.; Gu, S.; Guo, X.; Xu, W.; Wang, Y.; Zhong, G.; Lee, C.; Wang, F. AI-enhanced backpack with double frequency-up conversion vibration energy converter for motion recognition and extended battery life. Nano Energy 2024, 131, 110302. [Google Scholar] [CrossRef]
- Liu, T.; Huang, Y.; Zou, D.; Teng, J.; Li, B. Exploratory study on water seepage monitoring of concrete structures using piezoceramic based smart aggregates. Smart Mater. Struct. 2013, 22, 065002. [Google Scholar] [CrossRef]
- Rimašauskienė, R.; Jūrėnas, V.; Radzienski, M.; Rimašauskas, M.; Ostachowicz, W. Experimental analysis of active–passive vibration control on thin-walled composite beam. Compos. Struct. 2019, 223, 110975. [Google Scholar] [CrossRef]
- Zhao, N.; Huo, L.; Song, G. A nonlinear ultrasonic method for real-time bolt looseness monitoring using PZT transducer–enabled vibro-acoustic modulation. J. Intell. Mater. Syst. Struct. 2020, 31, 364–376. [Google Scholar] [CrossRef]
- Du, G.; Kong, Q.; Wu, F.; Ruan, J.; Song, G. An experimental feasibility study of pipeline corrosion pit detection using a piezoceramic time reversal mirror. Smart Mater. Struct. 2016, 25, 037002. [Google Scholar] [CrossRef]
- Kong, Q.; Robert, R.; Silva, P.; Mo, Y. Cyclic crack monitoring of a reinforced concrete column under simulated pseudo-dynamic loading using piezoceramic-based smart aggregates. Appl. Sci. 2016, 6, 341. [Google Scholar] [CrossRef]
- Porn, S.; Nasser, H.; Coelho, R.F.; Belouettar, S.; Deraemaeker, A. Level set based structural optimization of distributed piezoelectric modal sensors for plate structures. Int. J. Solids Struct. 2016, 80, 348–358. [Google Scholar] [CrossRef]
- Wu, A.; He, S.; Ren, Y.; Wang, N.; Ho, S.C.M.; Song, G. Design of a new stress wave-based pulse position modulation (PPM) communication system with piezoceramic transducers. Sensors 2019, 19, 558. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, G.; Wang, Y.; Ren, B.; Zhou, H.; Xie, A.; Xie, W. Design of a networking bolted joints monitoring method based on PZT. Smart Mater. Struct. 2023, 32, 064003. [Google Scholar] [CrossRef]
- Zhu, J.; Ren, L.; Ho, S.-C.; Jia, Z.; Song, G. Gas pipeline leakage detection based on PZT sensors. Smart Mater. Struct. 2017, 26, 025022. [Google Scholar] [CrossRef]
- Jia, Z.-G.; Ren, L.; Li, H.-N.; Ho, S.-C.; Song, G.-B. Experimental study of pipeline leak detection based on hoop strain measurement. Struct. Control Health Monit. 2015, 22, 799–812. [Google Scholar] [CrossRef]
- Benkherouf, A.; Allidina, A. Leak detection and location in gas pipelines. IEE Proc. D—Control. Theory Appl. 1988, 135, 142–148. [Google Scholar] [CrossRef]

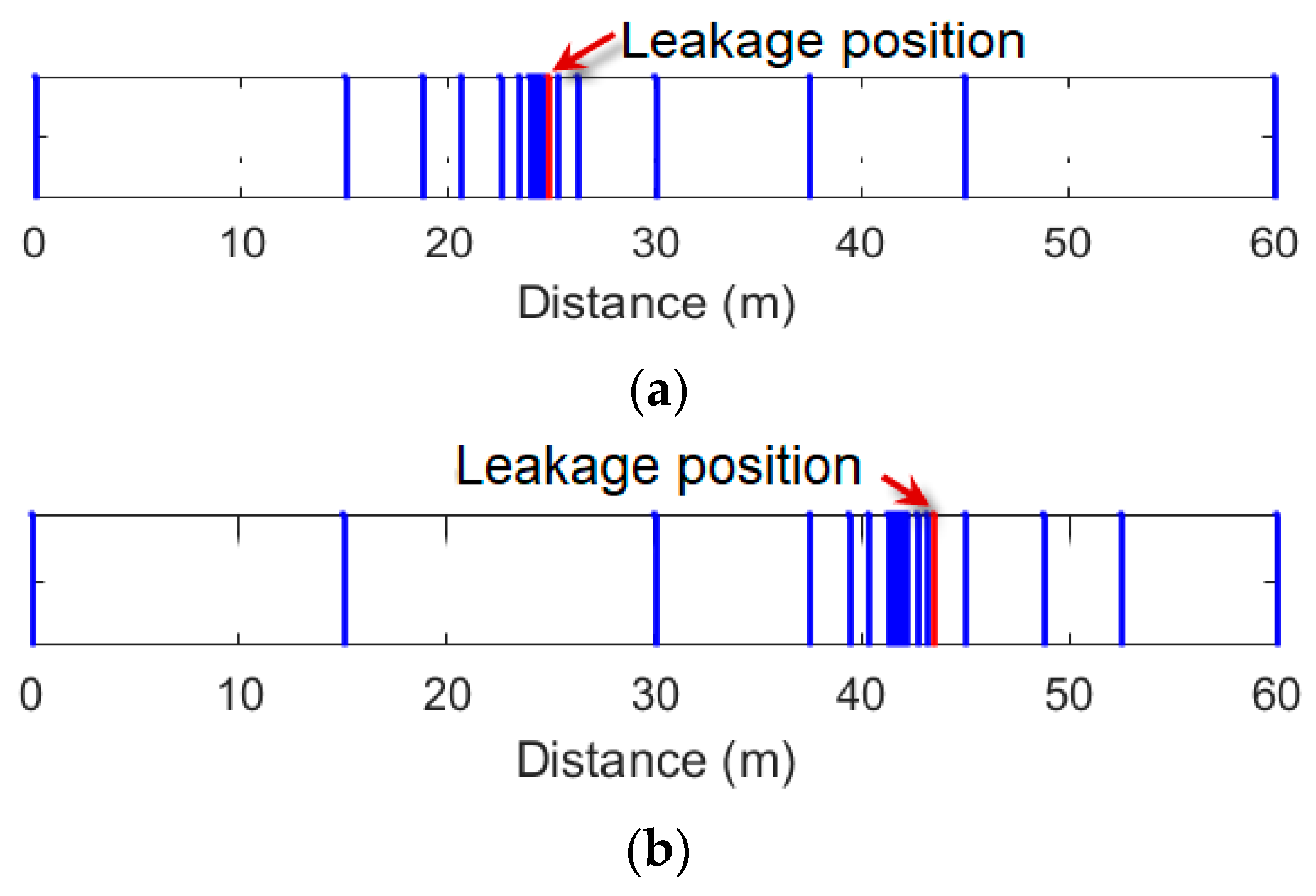
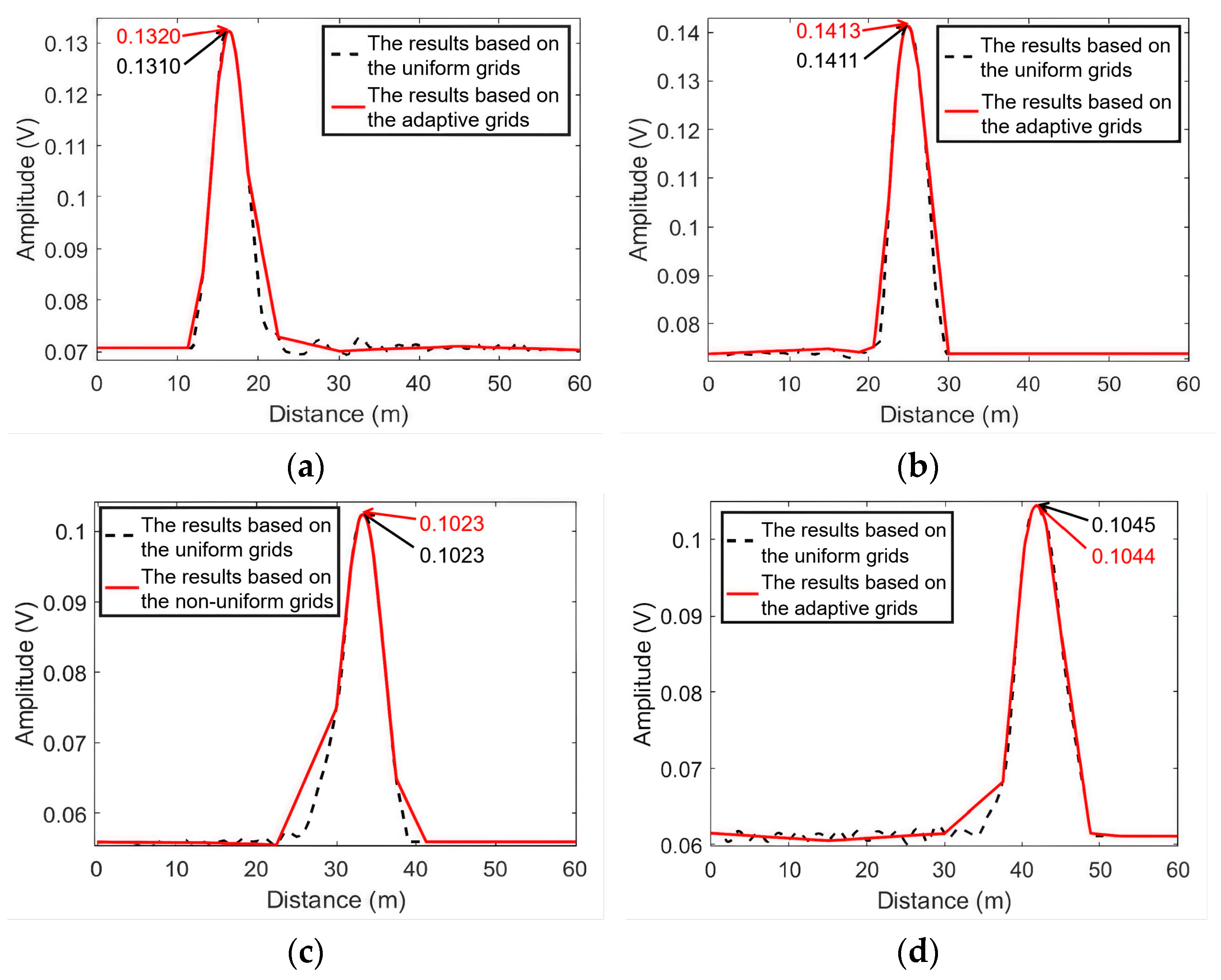
| Parameters | Symbol |
|---|---|
| The locations of the leakage | |
| The resolution adjustment parameter | |
| Convolution operation | |
| Attenuation coefficient | |
| NPW propagation time from to | |
| m | Forward propagation fields measured via the experiment |
| Adjusted time function | |
| Ideal impulse | |
| The localization functional value function | |
| The maximum energy distribution value function | |
| Negative pressure wave signal at leakage | |
| Sensor-captured signal from sensor n to | |
| The localization background functions | |
| The starting point of the monitoring area | |
| The end point of the monitoring area |
| Leakage Valve | Leakage 1 (L1) | Leakage 2 (L2) | Leakage 3 (L3) | Leakage 4 (L4) |
|---|---|---|---|---|
| Location from inlet (m) | 15.55 | 24.84 | 34.21 | 43.47 |
| PZT Sensors | Sensor 1 | Sensor 2 |
|---|---|---|
| Location from inlet (m) | 1.32 | 54.46 |
| Parameters | Value |
|---|---|
| Relative Dielectric Constant | 1900 |
| Electromechanical Coupling Factor | 0.72 (k33) |
| Piezoelectric Charge Constant (10 − 12 C/N or 10 − 12 m/V) | 400 (d33) |
| Piezoelectric Voltage Constant (10 − 3 Vm/N or 10 − 3 m2/C) | 24.8 (g33) |
| Leakage | Grid Size | Conventional TR Localization Time | Number of Grids |
|---|---|---|---|
| L1 | 0.01 m | 89.944 s | 5581 |
| L2 | 0.01 m | 88.384 s | 5581 |
| L3 | 0.01 m | 89.487 s | 5581 |
| L4 | 0.01 m | 87.759 s | 5581 |
| Leakage | L1 | L2 | L3 | L4 |
|---|---|---|---|---|
| Signal adjustment time | 1.093 s | 1.161 s | 1.205 s | 1.154 s |
| Adaptive grid generation time | 0.51 s | 0.357 s | 0.464 s | 0.362 s |
| Conventional TR localization time | 0.505 s | 0.355 s | 0.5 s | 0.362 s |
| Total time | 2.108 s | 1.873 s | 2.169 s | 1.878 s |
| Number of grids | 33 | 21 | 30 | 21 |
| Grids Type | Uniform Grids | Grids Based on Proposed Method |
|---|---|---|
| Maximum total computational time | 89.944 s | 2.169 s |
| Minimum total computational time | 87.759 s | 1.873 s |
| Average total computational time | 88.894 s | 2.007 s |
| Number of grids | All 5581 | 21–33 |
| Test | Leakage 1 (15.55 m) | Leakage 2 (24.84 m) | Leakage 3 (34.21 m) | Leakage 4 (43.47 m) |
|---|---|---|---|---|
| Result#1 | 16.41 m | 24.38 m | 33.75 m | 41.25 m |
| Result#2 | 16.87 m | 24.38 m | 33.75 m | 41.25 m |
| Result#3 | 16.35 m | 24.38 m | 33.28 m | 41.25 m |
| Result#4 | 16.05 m | 24.38 m | 33.28 m | 41.25 m |
| Result#5 | 16.87 m | 24.38 m | 33.75 m | 41.25 m |
| Test | Leakage 1 (15.55 m) | Leakage 2 (24.84 m) | Leakage 3 (34.21 m) | Leakage 4 (43.47 m) |
|---|---|---|---|---|
| Result#1 | 16.25 m | 25 m | 33.75 m | 42.5 m |
| Result#2 | 16.25 m | 25 m | 33.75 m | 41.9 m |
| Result#3 | 16.33 m | 25 m | 33.13 m | 42.5 m |
| Result#4 | 16.09 m | 25 m | 33.13 m | 42.5 m |
| Result#5 | 16.25 m | 25 m | 33.75 m | 42.5 m |
| Leakage | L1 | L2 | L3 | L4 |
|---|---|---|---|---|
| Signal adjustment time | 1.125 s | 1.234 s | 1.277 s | 1.287 s |
| Adaptive grid generation time | 0.366 s | 0.391 s | 0.398 s | 0.382 s |
| Conventional TR localization time | 0.325 s | 0.417 s | 0.325 s | 0.368 s |
| Test | Leakage 1 (15.55 m) | Leakage 2 (24.84 m) | Leakage 3 (34.21 m) | Leakage 4 (43.47 m) |
|---|---|---|---|---|
| Result#1 | 16.67 m | 24.88 m | 33.33 m | 41.67 m |
| Result#2 | 16.67 m | 25 m | 33.33 m | 41.85 m |
| Result#3 | 16.36 m | 25 m | 33.33 m | 41.67 m |
| Result#4 | 16.30 m | 25 m | 33.33 m | 41.67 m |
| Result#5 | 16.67 m | 25 m | 33.33 m | 41.67 m |
| Leakage | L1 | L2 | L3 | L4 |
|---|---|---|---|---|
| Signal adjustment time | 1.082 s | 1.154 s | 1.158 s | 1.240 s |
| Adaptive grid generation time | 0.426 s | 0.411 s | 0.364 s | 0.411 s |
| Conventional TR localization time | 0.442 s | 0.436 s | 0.379 s | 0.429 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, H.; Yang, Y.; Zhou, H.; Zhang, G.; Ren, B.; Yuan, Y. An Adaptive Grid Generation Approach to Pipeline Leakage Rapid Localization Based on Time Reversal. Sensors 2025, 25, 1753. https://doi.org/10.3390/s25061753
Wang Y, Chen H, Yang Y, Zhou H, Zhang G, Ren B, Yuan Y. An Adaptive Grid Generation Approach to Pipeline Leakage Rapid Localization Based on Time Reversal. Sensors. 2025; 25(6):1753. https://doi.org/10.3390/s25061753
Chicago/Turabian StyleWang, Yu, Haoyang Chen, Yang Yang, Haoyu Zhou, Guangmin Zhang, Bin Ren, and Yufei Yuan. 2025. "An Adaptive Grid Generation Approach to Pipeline Leakage Rapid Localization Based on Time Reversal" Sensors 25, no. 6: 1753. https://doi.org/10.3390/s25061753
APA StyleWang, Y., Chen, H., Yang, Y., Zhou, H., Zhang, G., Ren, B., & Yuan, Y. (2025). An Adaptive Grid Generation Approach to Pipeline Leakage Rapid Localization Based on Time Reversal. Sensors, 25(6), 1753. https://doi.org/10.3390/s25061753






