Time-Impact Optimal Trajectory Planning for Wafer-Handling Robotic Arms Based on the Improved Snake Optimization Algorithm
Abstract
1. Introduction
- (1)
- In the area of intelligent optimization methods, the following improvements have been made to the SO algorithm.
- The Tent Chaotic Map initializes populations, instead of randomly generating populations with ‘rand’ functions.
- Dynamic learning factors, integrated with random perturbations, replace static learning factors.
- A cosine annealing learning rate scheme is employed for the adaptive updating of individual positions.
- The Bayesian method is utilized to optimize thresholds, surpassing the reliance on empirical thresholds.
- (2)
- In the area of trajectory planning, the following improvements have been made to the S-shaped speed curve.
- The interpolated arc transition supplants the abrupt right-angle transition.
- The continuous single-segment start–stop mechanism supersedes the segmented start–stop mechanism.
2. Materials and Methods
2.1. The Structure Parameters of the Wafer-Handling Robotic Arms
2.2. The Mathematical Model of Multiple Objective Function
2.3. The Construction of Trajectory Planning
2.3.1. The Explanation of S-Shaped Speed Curve
2.3.2. The Improvement of the S-Shaped Speed Curve
2.4. Improved Snake Optimization Algorithm
2.4.1. Initialization Population of a Tent Chaotic Map
2.4.2. Dynamic Learning Factor with Random Noise
2.4.3. Cosine Annealing Learning Rate
2.4.4. The Bayesian Method to Find the Optimization Threshold
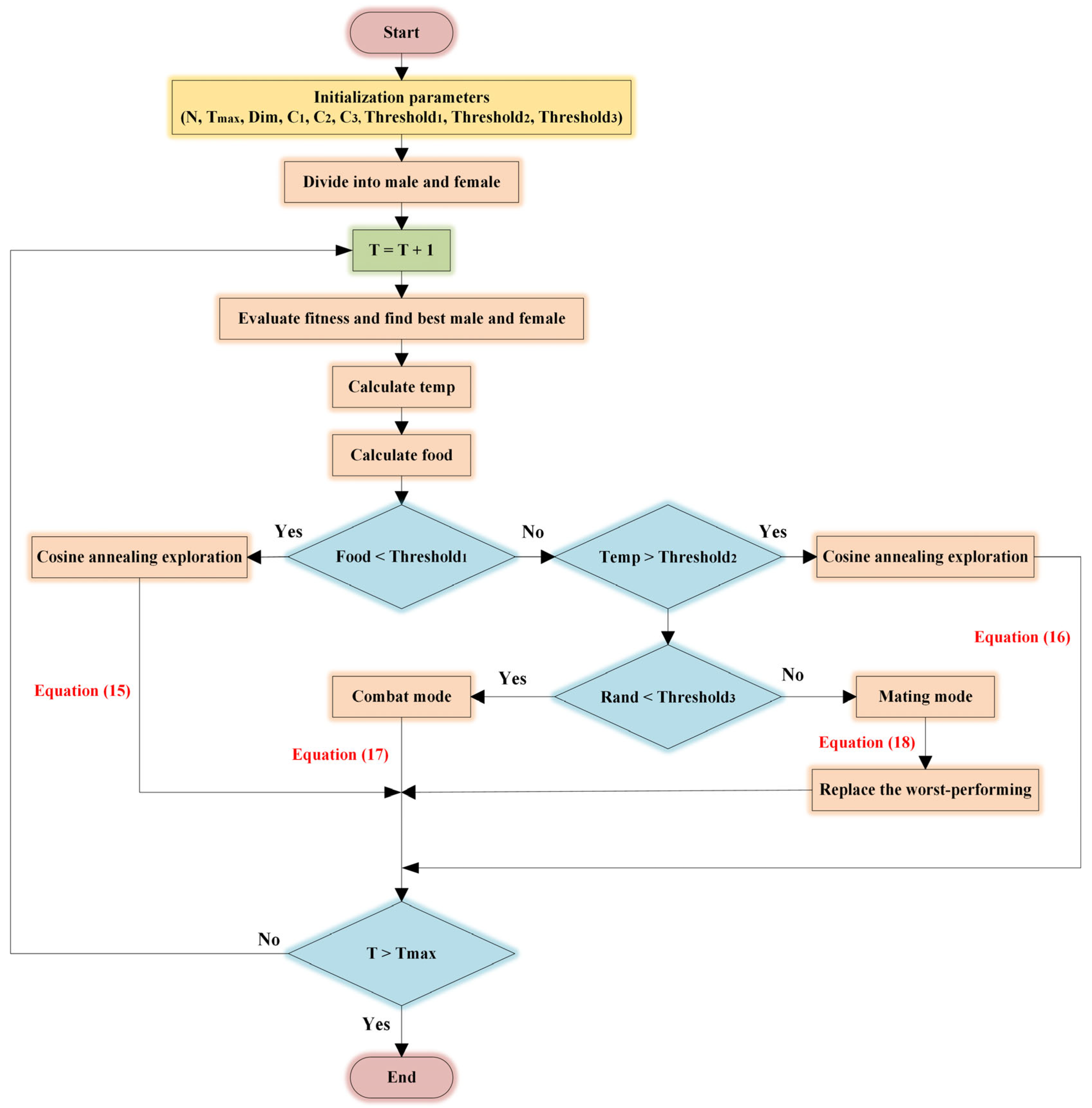
2.4.5. ISO Algorithm Steps
3. Results
3.1. Ability Test and Analysis for ISO
3.1.1. Parameter Settings and Simulation Results
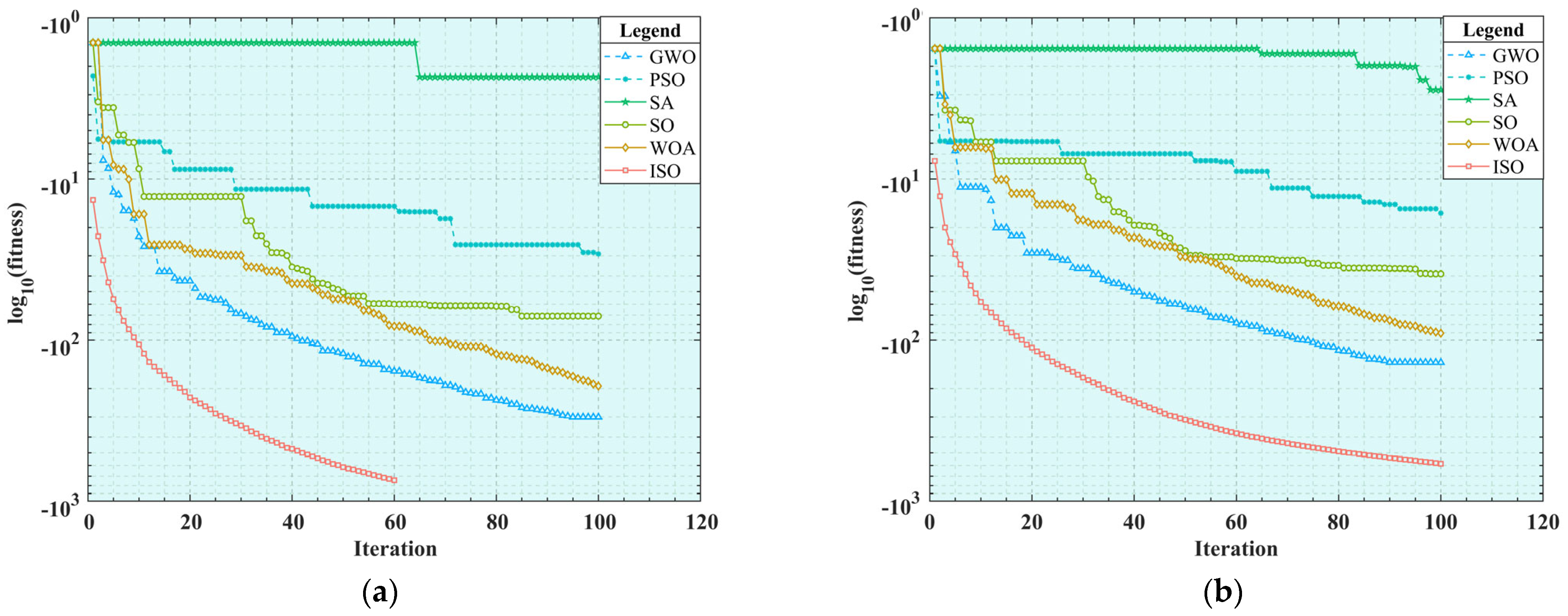
3.1.2. Simulation Result Analysis
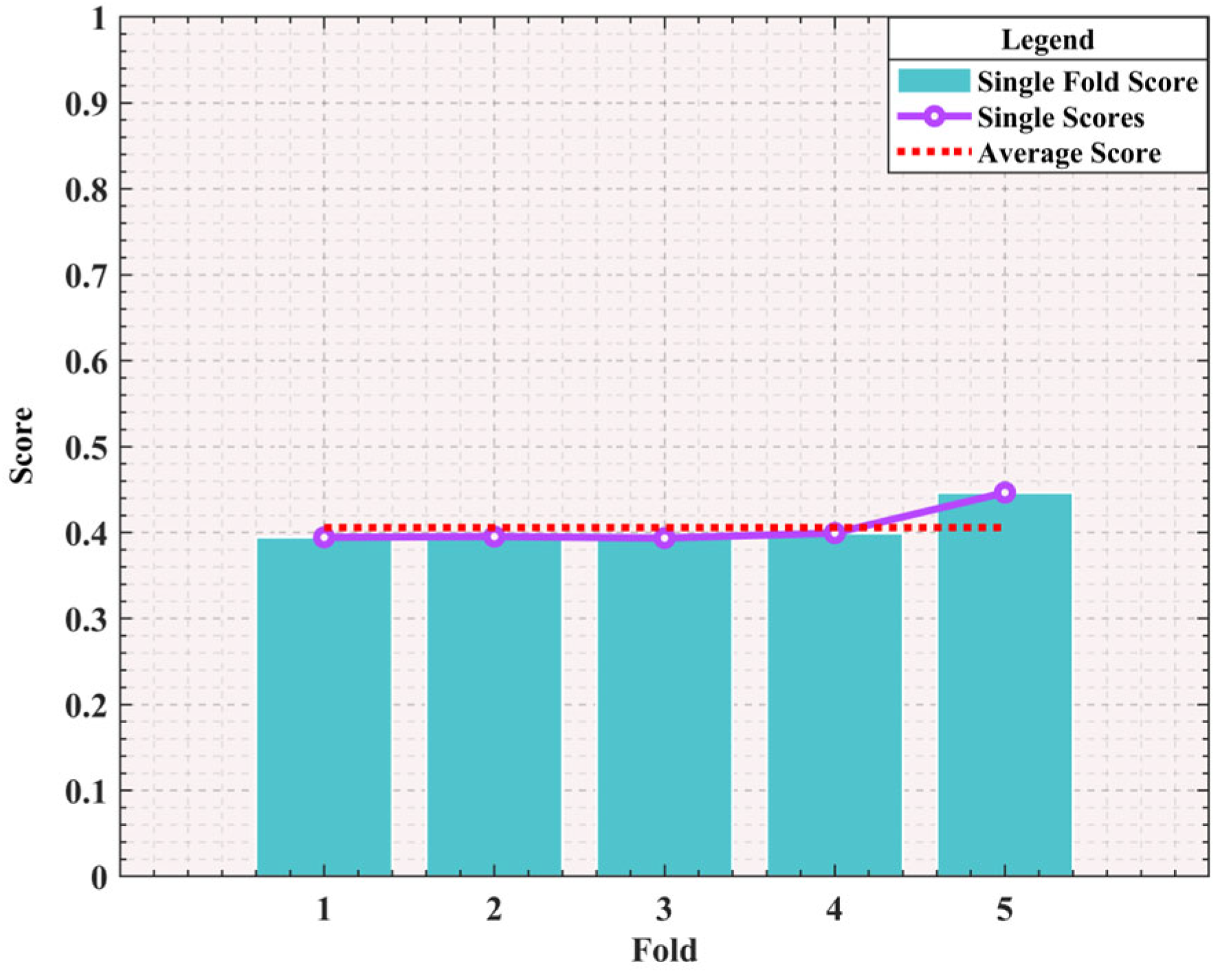
3.1.3. The Friedman Test
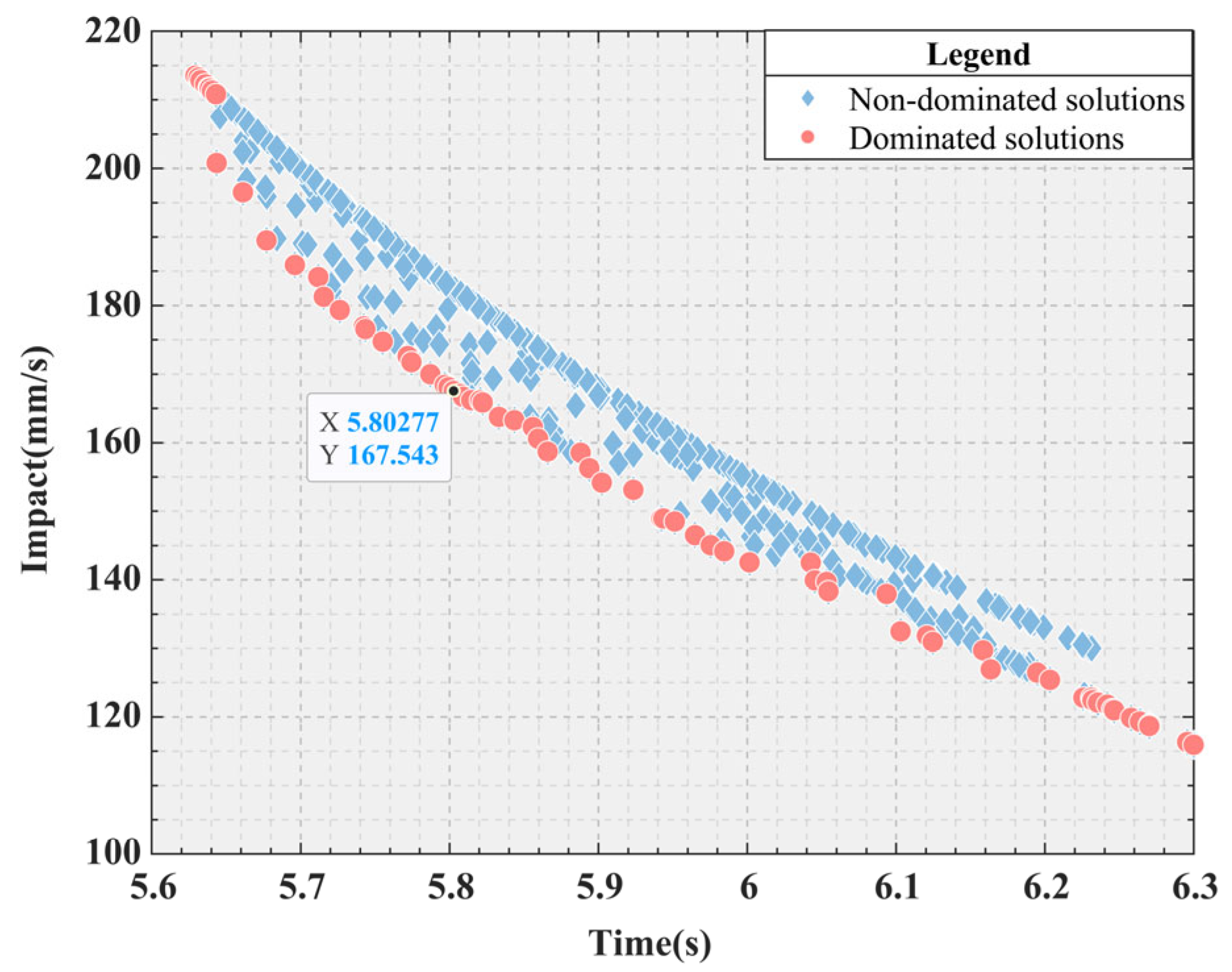
3.2. Time-Jerk Optimal Trajectory Planning Based on ISO
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pu, Q.C.; Xu, X.R.; Li, Q.Q.; Zhang, H. Robotic Arm Time-Jerk Optimal Trajectory Based on Improved Dingo Optimization. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 198. [Google Scholar] [CrossRef]
- Zhang, S.B.; Xia, Q.X.; Chen, M.X.; Cheng, S.Z. Multi-Objective Optimal Trajectory Planning for Robotic Arms Using Deep Reinforcement Learning. Sensors 2023, 23, 5974. [Google Scholar] [CrossRef] [PubMed]
- Ye, J.T.; Hao, L.N.; Cheng, H.T. Multi-Objective Optimal Trajectory Planning for Robot Manipulator Attention to End-Effector Path Limitation. Robotica 2024, 42, 1761–1780. [Google Scholar] [CrossRef]
- Lu, Z.K.; You, Z.C.; Xia, B.H. Time Optimal Trajectory Planning of Robotic Arm Based on Improved Sand Cat Swarm Optimization Algorithm. Appl. Intell. 2025, 55, 323. [Google Scholar] [CrossRef]
- Shrivastava, A.; Dalla, V.K. Strategy of Smooth Motion Planning of Multi-Axes Space Manipulator Avoiding Dynamic Singularity in Cartesian Space. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 278. [Google Scholar] [CrossRef]
- Tagliavini, A.; Bianco, C.G. A Smooth Orientation Planner for Trajectories in the Cartesian Space. IEEE Rob. Autom. Lett. 2023, 8, 2606–2613. [Google Scholar] [CrossRef]
- Lin, J.J.; Rickert, M.; Knoll, A. Parameterizable and Jerk-Limited Trajectories with Blending for Robot Motion Planning and Spherical Cartesian Waypoints. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 13982–13988. [Google Scholar]
- Xiao, P.F.; Ju, H.H.; Li, Q.D. Point-to-point Trajectory Planning for Space Robots Based on Jerk Constraints. Rev. Sci. Instrum. 2021, 92, 09450. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Z. Research on Joint Space Trajectory Planning of SCARA Robot Based on SimMechanics. In Proceedings of the 2019 Electronic and Automation Control Conference (ITNEC), Chongqing, China, 15–17 March 2019; pp. 1446–1450. [Google Scholar]
- Luo, L.; Guo, T.B.; Cui, K.K.; Zhang, Q. Trajectory Planning in Robot Joint Space Based on Improved Quantum Particle Swarm Optimization Algorithm. Appl. Sci. 2023, 13, 7031. [Google Scholar] [CrossRef]
- Wu, G.L.; Zhang, N. Kinematically Constrained Jerk-Continuous S-Curve Trajectory Planning in Joint Space for Industrial Robots. Electronics 2023, 12, 1135. [Google Scholar] [CrossRef]
- Hu, Y.H.; Zhang, S.L.; Chen, Y.H. Trajectory Planning Method of 6-DOF Modular Manipulator Based on Polynomial Interpolation. J. Comput. Methods Sci. 2023, 23, 1589–1600. [Google Scholar] [CrossRef]
- Chen, G.R.; Ma, M.; Guo, S.; Hou, B.W.; Wang, J.Z. An Easy-implemented Optimization Method of Trajectory Planning Based on Polynomial Interpolation. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 2802–2807. [Google Scholar]
- Shrivastava, A.; Dalla, V.K. Multi-Segment Trajectory Tracking of the Redundant Space Robot for Smooth Motion Planning Based on Interpolation of Linear Polynomials with Parabolic Blend. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 9255–9269. [Google Scholar] [CrossRef]
- Cong, Y.Z.; Jiang, C.R.; Liu, H.; Du, H.B.; Gan, Y.H.; Jiang, C.H. Research on Trajectory Planning Method of Dual-Arm Robot Based on ROS. In Proceedings of the 2020 Chinese Automation Congress (CAC), Xi’an, China, 6–8 November 2020; pp. 2616–2621. [Google Scholar]
- Ayazbay, A.A.; Gani, B.; Sandugash, O.; Konrad, G.; Algazy, Z. Trajectory Planning, Kinematics, and Experimental Validation of a 3D-Printed Delta Robot Manipulator. Mech. Eng. Robot. Res. 2024, 13, 113–125. [Google Scholar] [CrossRef]
- Wang, G.R.; Xu, F.; Zhou, Z.K.; Pang, Z.H. S-Velocity Profile of Industrial Robot Based on NURBS Curve and Slerp Interpolation. Processes 2022, 10, 2195. [Google Scholar] [CrossRef]
- Patle, B.K.; Chen, S.L.; Singh, A.; Kashyap, S.K. Optimal Trajectory Planning of the Industrial Robot Using Hybrid S-Curve-PSO Approach. Rob. Intell. Autom. 2023, 43, 153–174. [Google Scholar] [CrossRef]
- Wu, N.K.; Jia, D.Y.; Li, Z.Q.; He, Z.H. Trajectory Planning of Robotic Arm Based on Particle Swarm Optimization Algorithm. Appl. Sci. 2024, 14, 8234. [Google Scholar] [CrossRef]
- Du, Y.X.; Chen, Y.H. Time Optimal Trajectory Planning Algorithm for Robotic Manipulator Based on Locally Chaotic Particle Swarm Optimization. Chin. J. Electron. 2022, 31, 906–914. [Google Scholar] [CrossRef]
- Luo, L.; Guo, T.B.; Zhang, Q. Optimal Trajectory Planning for Robotic Arm Based on Improved Dynamic Multi-Population Particle Swarm Optimization Algorithm. Int. J. Adv. Comput. Sci. Appl. 2024, 15, 710–718. [Google Scholar]
- Zhong, F.F.; Liu, G.P.; Lu, Z.Y.; Hu, L.Y.; Han, Y.Y.; Xiao, Y.S.; Zhang, X.R. Dynamic Parameter Identification Based on Improved Particle Swarm Optimization and Comprehensive Excitation Trajectory for 6R Robotic Arm. Ind. Robot 2024, 51, 148–166. [Google Scholar] [CrossRef]
- Liang, B.Q.; Lin, X.Z.; Liu, G.H.; Lei, J. Trajectory Analysis and Optimization of Sea Buckthorn Fruit Vibration Separation Manipulator Based on IPSO Algorithm. Sci. Rep. 2023, 13, 20124. [Google Scholar] [CrossRef]
- Lu, Z.G.; Wang, X. Mechanical Arm Trajectory Planning Based on B-Spline and Whale Optimization Algorithm. J. Northeast. Univ. 2024, 45, 683–689. [Google Scholar]
- Qie, X.H.; Kang, C.F.; Zong, S.C.; Chen, S.J. Trajectory Planning and Simulation Study of Redundant Robotic Arm for Upper Limb Rehabilitation Based on Back Propagation Neural Network and Genetic Algorithm. Sensors 2022, 22, 4071. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Zhao, J.B.; Wang, J.Z. An Improved Snake Optimization Algorithm and Its Application in Manipulator Trajectory Planning. In Proceedings of the 2023 35th Chinese Control and Decision Conference (CCDC), Yichang, China, 20–22 May 2023; pp. 4306–4313. [Google Scholar]
- Lu, S.Y.; He, Q.; Wang, Y.M.; Li, Y.B. Enhanced Snake Optimization Algorithm for Mobile Robot Path Planning. Trans. Microsyst. Technol. 2023, 42, 127–133. [Google Scholar]
- Liang, X.M.; Shi, L.Y.; Long, W. Improved Snake Optimization Algorithm for Solving Constrained Optimization Problems. Comput. Eng. Appl. 2024, 60, 76–87. [Google Scholar]
- Li, Q.L.; Ma, Q.H.; Weng, X. Dynamic Path Planning for Mobile Robots Based on Artificial Potential Field Enhanced Improved Multiobjective Snake Optimization. J. Field Rob. 2024, 41, 1843–1863. [Google Scholar] [CrossRef]
- Jin, R.Y.; Rocco, P.; Geng, Y.H. Cartesian Trajectory Planning of Space Robots Using a Multi-Objective Optimization. Aerosp. Sci. Technol. 2021, 108, 106360. [Google Scholar] [CrossRef]
- Zhang, X.C.; Chao, Y.S.; Li, C.Y.; Zhou, J.L. Multi-Objective Trajectory Planning for Industrial Robots Based on Machine Learning. Mod. Manuf. Eng. 2024, 2, 31–37. [Google Scholar]
- Zhu, H.L.; Xiao, W.B.; Zhou, H.; Li, X.R. Parameter Extraction of Photovoltaic Cells Based on Chaotic Adaptive Weight Improved Snake Optimization Algorithm. Laser Optoelectron. Process 2024, 61, 1525002. [Google Scholar]
- Fu, H.; Shi, H.F.; Xu, Y.S.; Shao, J.Y. Research on Gas Outburst Prediction Model Based on Multiple Strategy Fusion Improved Snake Optimization Algorithm with Temporal Convolutional Network. IEEE Access 2022, 10, 117973–117984. [Google Scholar] [CrossRef]
- Liu, J.; Deng, Y.H.; Liu, Y.L.; Chen, L.L.; Hu, Z.Z.; Wei, P.Y.; Li, Z.B. A Logistic-tent Chaotic Mapping Levenberg Marquardt Algorithm for Improving Positioning Accuracy of Grinding Robot. Sci. Rep. 2024, 14, 9649. [Google Scholar] [CrossRef]
- Zheng, W.D.; Ai, Y.B.; Zhang, W.D. Improved Snake Optimizer Using Sobol Sequential Nonlinear Factors and Different Learning Strategies and Its Applications. Mathematics 2024, 12, 1708. [Google Scholar] [CrossRef]
- Huang, Y.; Liang, F.C.; Fan, C.L.; Song, Z.F. Improved Particle Swarm Optimization Algorithm with Random Mutation and Perception. J. Northwest. Polytech. Univ. 2023, 41, 428–438. [Google Scholar] [CrossRef]
- Zhang, C.; Shao, Y.C.; Sun, H.J.; Xing, L.; Zhao, Q.; Song, Z.F. The WuC-Adam Algorithm Based on Joint Improvement of Warmup and Cosine Annealing Algorithms. Math Biosci. Eng. 2024, 21, 1270–1285. [Google Scholar] [CrossRef]
- Liu, X.; Tian, M.; Zhou, J.; Liang, J.Y. An Efficient Coverage Method for SEMWSNs Based on Adaptive Chaotic Gaussian Variant Snake Optimization Algorithm. Math. Biosci. Eng. 2023, 20, 3191–3215. [Google Scholar] [CrossRef] [PubMed]
- Shan, Q.Y.; Jin, H.W.; Jie, C. Gearbox Fault Diagnosis Method Based on PSM-BN. IEEE Access 2024, 12, 39876–39886. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A Novel Meta-Heuristic Optimization Algorithm. Knowl. Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Shi, W.J.; He, Z.; Tang, W.; Liu, W.F.; Ma, Z.Y. Path Planning of Multi-Robot Systems with Boolean Specifications Based on Simulated Annealing. IEEE Rob. Autom. Lett. 2022, 7, 6091–6098. [Google Scholar] [CrossRef]
- Zhao, Y.T.; Gan, L.; Li, W.G.; Liu, A. Path Planning of Spot Welding Robot Based on Multi-Objective Grey Wolf Algorithm. J. Intell. Fuzzy Syst. 2021, 41, 6181–6189. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Gholizadeh, H.A. A Comprehensive Survey: Whale Optimization Algorithm and Its Applications. Swarm Evol. Comput. 2019, 48, 1–24. [Google Scholar] [CrossRef]

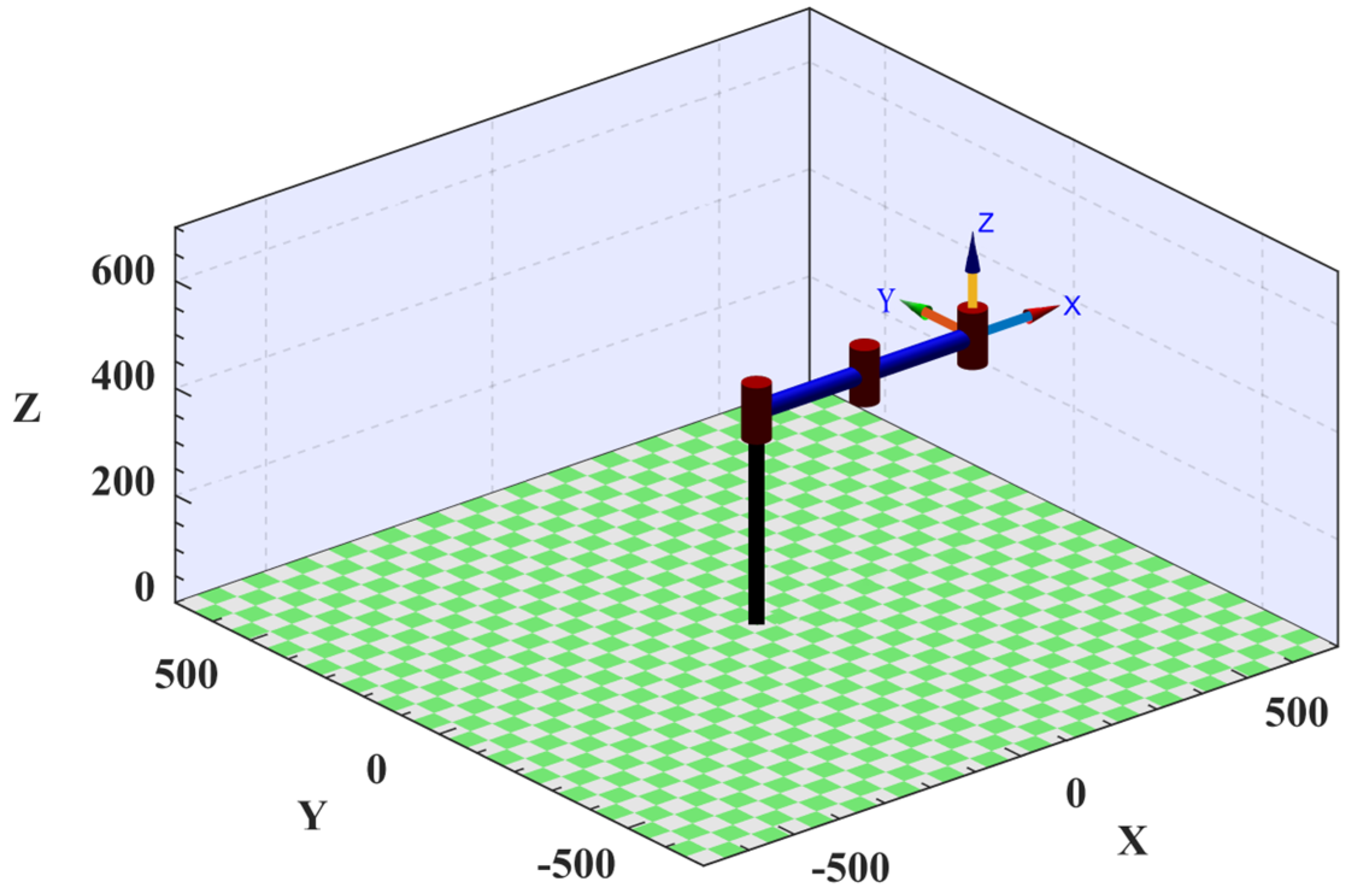


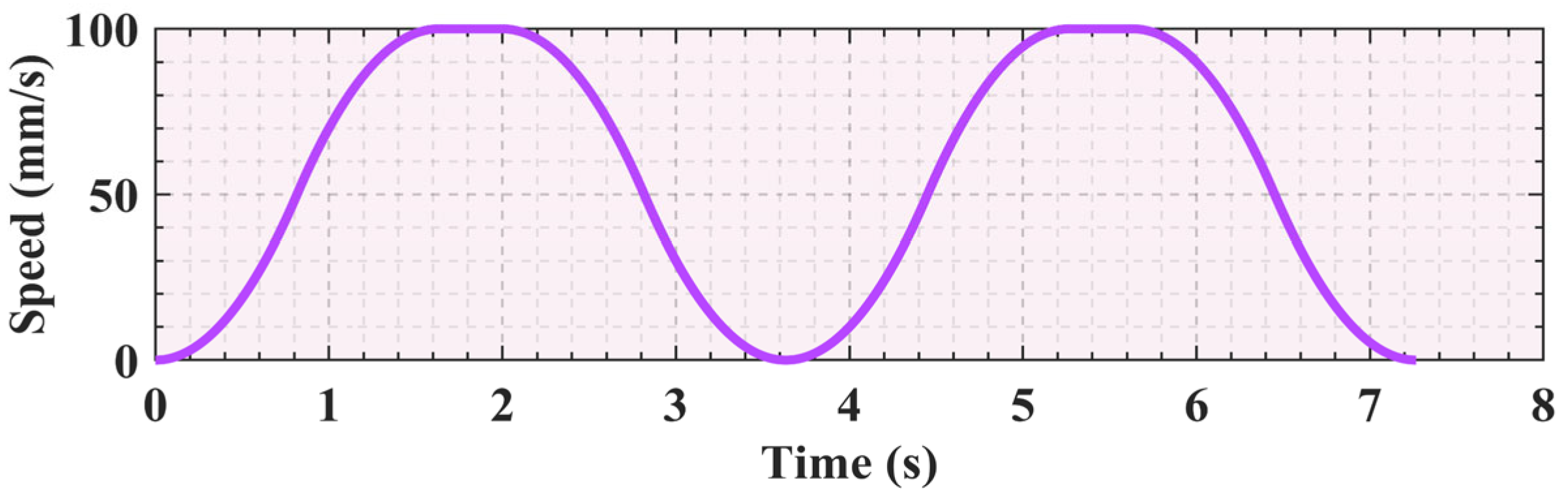




| Linki | ai/mm | αi/(°) | di/mm | θi (/°) | Range of θi/(°) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 400 | 0 | −120–120 |
| 2 | 0 | 238.4 | 0 | 0 | −120–120 |
| 3 | 0 | 238.4 | 0 | 0 | −120–120 |
| Starting Point | Intermediate Point | Ending Point |
|---|---|---|
| (400, 0, 400) | (200, 0, 400) | (200, 200, 400) |
| v_ p0 (mm/s) | v_ p1 (mm/s) | v_ p2 (mm/s) | vmax (mm/s) | amax (mm/s2) | jmax (mm/s3) | r (mm) |
|---|---|---|---|---|---|---|
| 0 | 100 | 0 | 100 | 100 | 100 | 30 |
| 1: Initialize parameters 2: Initialize the population using the Tent Chaotic Map as Equation (13) 3: Divide population into Nm and Nf using Equations (10) and (11) 4: while (T < Tmax) do 5: Evaluate the fitness and identify the best female and male 6: Calculate the iteration temperature and food quantity Equation (14) 7: if (Food < threshold1) then 8: Cosine annealing exploration using Equation (15) 9: else if (Temp > threshold2) then |
| 10: Cosine annealing exploration using Equation (16) 11: else 12: if (rand < threshold3) then 13: Enter Fight Mode using Equation (17) 14: else 15: Enter Mating Mode using Equation (18) 16: Replace the worst-performing female and male 17: end if 18: end if 19: end while 20: Return the optimal solution |
| Function | Range | Min |
|---|---|---|
| [−100,100] | 0 | |
| [−10,10] | 0 | |
| [−100,100] | 0 | |
| [−100,100] | 0 | |
| [−128,128] | 0 | |
| [−5.12,5.12] | 0 | |
| [−600,600] | 0 | |
| [−50,50] | 0 |
| Algorithm | Parameter Settings |
| SO | Theshold1 = 0.25, Theshold2 = 0.6, Theshold3 = 0.6, C1 = 0.5, C2 = 0.05, C3 = 2 |
| SA | Temp = 100, Tempmin = 0.01, alpha = 0.95 |
| PSO | w = 0.9, c1 = 2, c2 = 2, Vmax = 0.3 ∗ ub, Vmin = 0.3 ∗ lb |
| GWO | r1 = r2 = rand |
| WOA | r1 = r2 = rand, p = rand, b = 1 |
| ISO | sigma = 0.1, alphamin = 0.01, alphamax = 1.0, etamax = 0.01, etamin = 0.001 |
| Function | SO | SA | PSO | GWO | WOA | ISO | |
|---|---|---|---|---|---|---|---|
| F1 | MEAN | 8.27 × 10−40 | 7.30 × 10−2 | 3.04 × 10−12 | 6.24 × 10−105 | 8.40 × 10−79 | 0 |
| STD | 2.51 × 10−39 | 2.27 × 10−1 | 6.51 × 10−12 | 2.79 × 10−104 | 2.10 × 10−78 | 0 | |
| F2 | MEAN | 3.95 × 10−21 | 4.26 × 10−2 | 1.38 × 10−7 | 8.55 × 10−57 | 2.95 × 10−40 | 9.14 × 10−214 |
| STD | 5.26 × 10−21 | 2.87 × 10−2 | 2.22 × 10−7 | 3.13 × 10−56 | 7.95 × 10−40 | 0 | |
| F3 | MEAN | 2.16 × 10−39 | 3.85 × 10−2 | 6.47 × 10−12 | 6.66 × 10−107 | 2.18 × 10−79 | 0 |
| STD | 7.04 × 10−39 | 8.37 × 10−2 | 2.16 × 10−11 | 2.98 × 10−106 | 6.74 × 10−79 | 0 | |
| F4 | MEAN | 2.01 × 10−20 | 1.34 × 10−1 | 1.38 × 10−6 | 1.27 × 10−53 | 8.56 × 10−40 | 2.27 × 10−213 |
| STD | 3.54 × 10−20 | 9.71 × 10−2 | 2.36 × 10−6 | 3.93 × 10−53 | 2.64 × 10−39 | 0 | |
| F5 | MEAN | 7.01 × 10−4 | 6.64 × 10−1 | 1.77 × 10−3 | 5.21 × 10−4 | 7.33 × 10−4 | 1.75 × 10−4 |
| STD | 7.23 × 10−4 | 8.91 × 10−1 | 1.26 × 10−3 | 5.08 × 10−4 | 7.05 × 10−4 | 2.72 × 10−4 | |
| F6 | MEAN | 0 | 1.79 × 10−2 | 2.39 × 10−12 | 0 | 0 | 0 |
| STD | 0 | 3.42 × 10−2 | 3.35 × 10−12 | 0 | 0 | 0 | |
| F7 | MEAN | 0 | 1.67 × 10−2 | 6.15 × 10−12 | 0 | 0 | 0 |
| STD | 0 | 3.42 × 10−2 | 3.35 × 10−12 | 0 | 0 | 0 | |
| F8 | MEAN | 1.74 × 101 | 1.10 × 109 | 4.41 × 101 | 1.24 × 100 | 8.13 × 10−1 | 2.06 × 10−1 |
| STD | 3.32 × 101 | 1.35 × 108 | 2.59 × 101 | 4.26 × 10−1 | 3.08 × 10−1 | 2.03 × 10−1 | |
| Algorithm | SO | SA | PSO | GWO | WOA | ISO |
|---|---|---|---|---|---|---|
| Mean rank | 3.5 | 6 | 5 | 2.25 | 2.875 | 1.375 |
| STD rank | 3.75 | 6 | 4.875 | 2.25 | 2.75 | 1.375 |
| v_ p0 (mm/s) | v_ p1 (mm/s) | v_ p2 (mm/s) | vmax (mm/s) | r1 (mm) | Bayesian Evaluations | Bayesian Threshold | Tmax | Dim | N | lb | ub |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 100 | 0 | 100 | 30 | 10 | [0.05,0.8] | 100 | 2 | 20 | [80,120] | [80,120] |
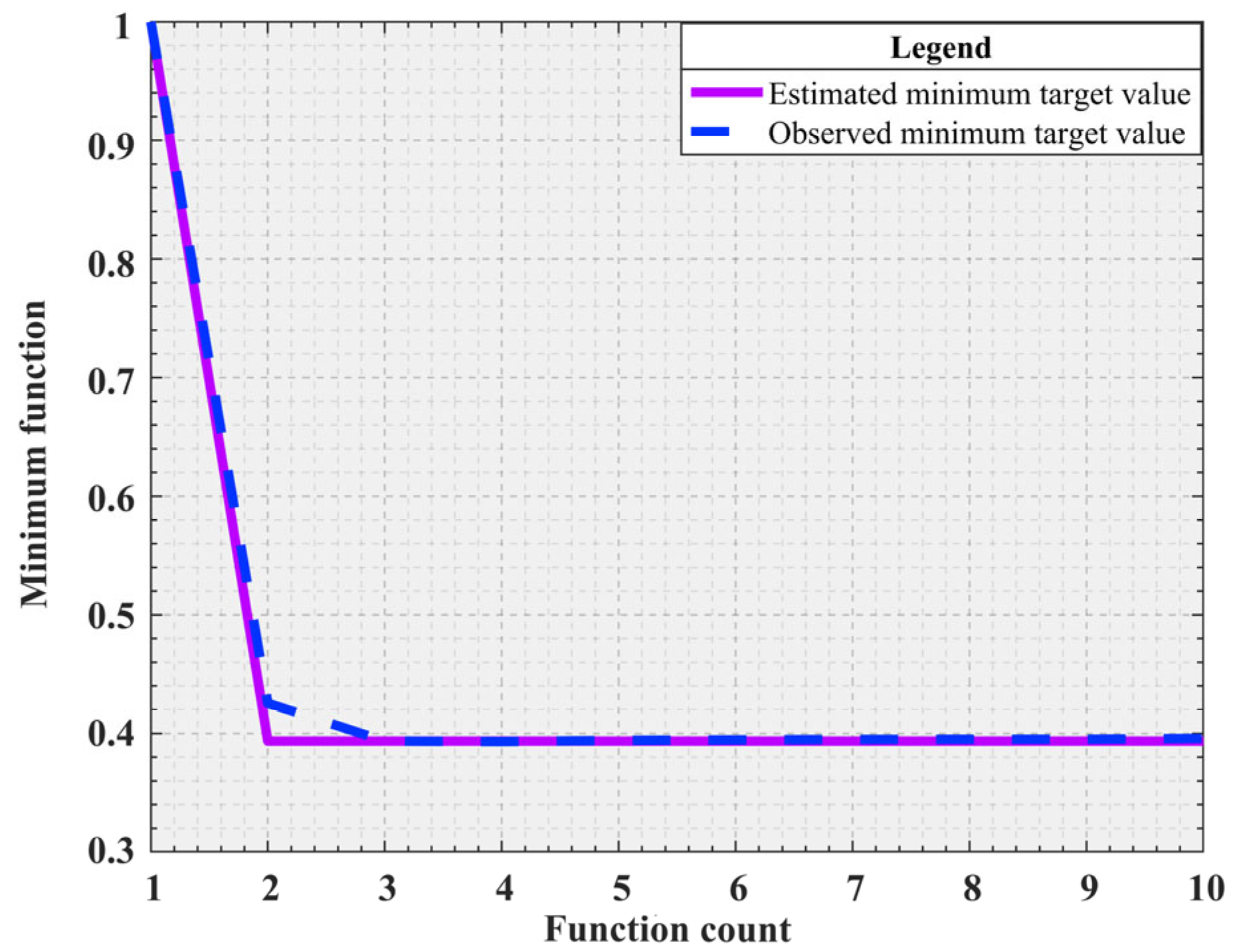
| Iteration | Objective | BestSoFar (Observed) | BestSoFar (Estimated) | Threshold1 | Threshold2 | Threshold3 |
|---|---|---|---|---|---|---|
| 1 | — | — | — | 0.4227 | 0.7616 | 0.5225 |
| 2 | 0.3936 | 0.3936 | 0.4255 | 0.0989 | 0.7764 | 0.5705 |
| 3 | 0.3952 | 0.3936 | 0.3936 | 0.1721 | 0.7210 | 0.7933 |
| 4 | 0.3969 | 0.3936 | 0.3932 | 0.0752 | 0.4968 | 0.5437 |
| 5 | 0.3953 | 0.3936 | 0.3942 | 0.1403 | 0.6057 | 0.7633 |
| 6 | 0.3991 | 0.3936 | 0.3946 | 0.0500 | 0.5764 | 0.5441 |
| 7 | 0.3957 | 0.3936 | 0.3949 | 0.1485 | 0.5278 | 0.4003 |
| 8 | 0.3969 | 0.3936 | 0.3951 | 0.1113 | 0.7425 | 0.4637 |
| 9 | 0.3955 | 0.3936 | 0.3951 | 0.1592 | 0.7106 | 0.7313 |
| 10 | 0.3979 | 0.3936 | 0.3958 | 0.1587 | 0.6833 | 0.6341 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Y.; Yu, J. Time-Impact Optimal Trajectory Planning for Wafer-Handling Robotic Arms Based on the Improved Snake Optimization Algorithm. Sensors 2025, 25, 1872. https://doi.org/10.3390/s25061872
Ji Y, Yu J. Time-Impact Optimal Trajectory Planning for Wafer-Handling Robotic Arms Based on the Improved Snake Optimization Algorithm. Sensors. 2025; 25(6):1872. https://doi.org/10.3390/s25061872
Chicago/Turabian StyleJi, Yujie, and Jiale Yu. 2025. "Time-Impact Optimal Trajectory Planning for Wafer-Handling Robotic Arms Based on the Improved Snake Optimization Algorithm" Sensors 25, no. 6: 1872. https://doi.org/10.3390/s25061872
APA StyleJi, Y., & Yu, J. (2025). Time-Impact Optimal Trajectory Planning for Wafer-Handling Robotic Arms Based on the Improved Snake Optimization Algorithm. Sensors, 25(6), 1872. https://doi.org/10.3390/s25061872






