A Perspective Distortion Correction Method for Planar Imaging Based on Homography Mapping
Abstract
:1. Introduction
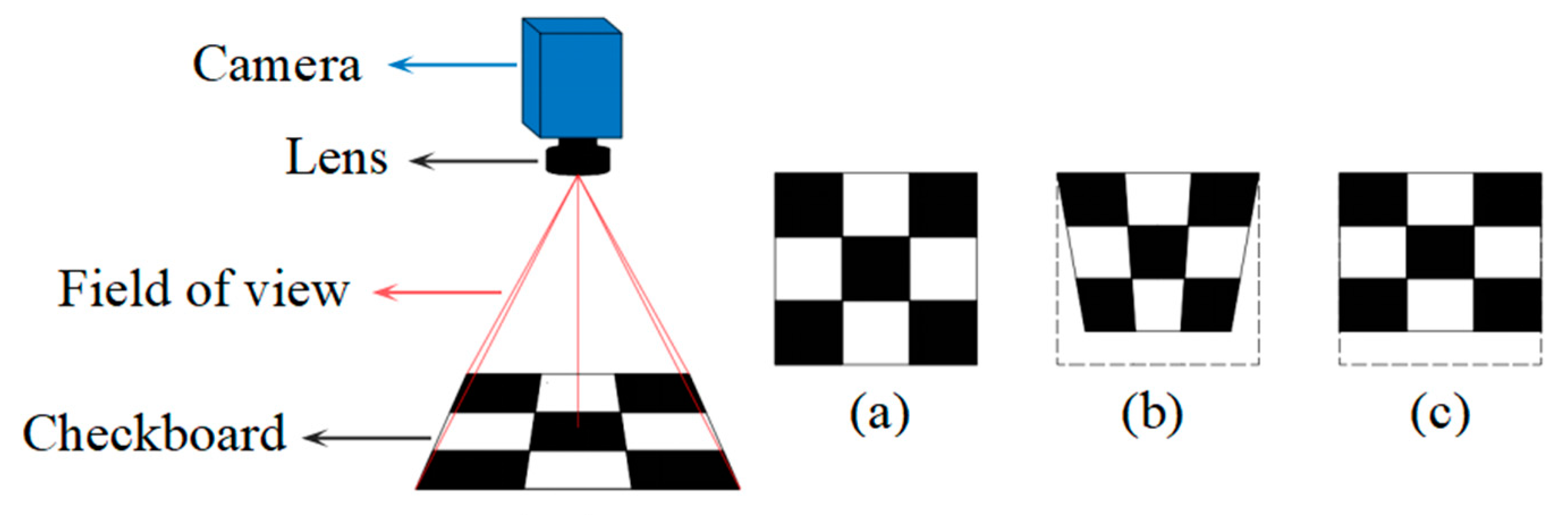
2. Perspective Distortion Analysis
2.1. Analysis from Extrinsic Parameters
2.2. Analysis from Intrinsic Parameters
3. Proposed Method
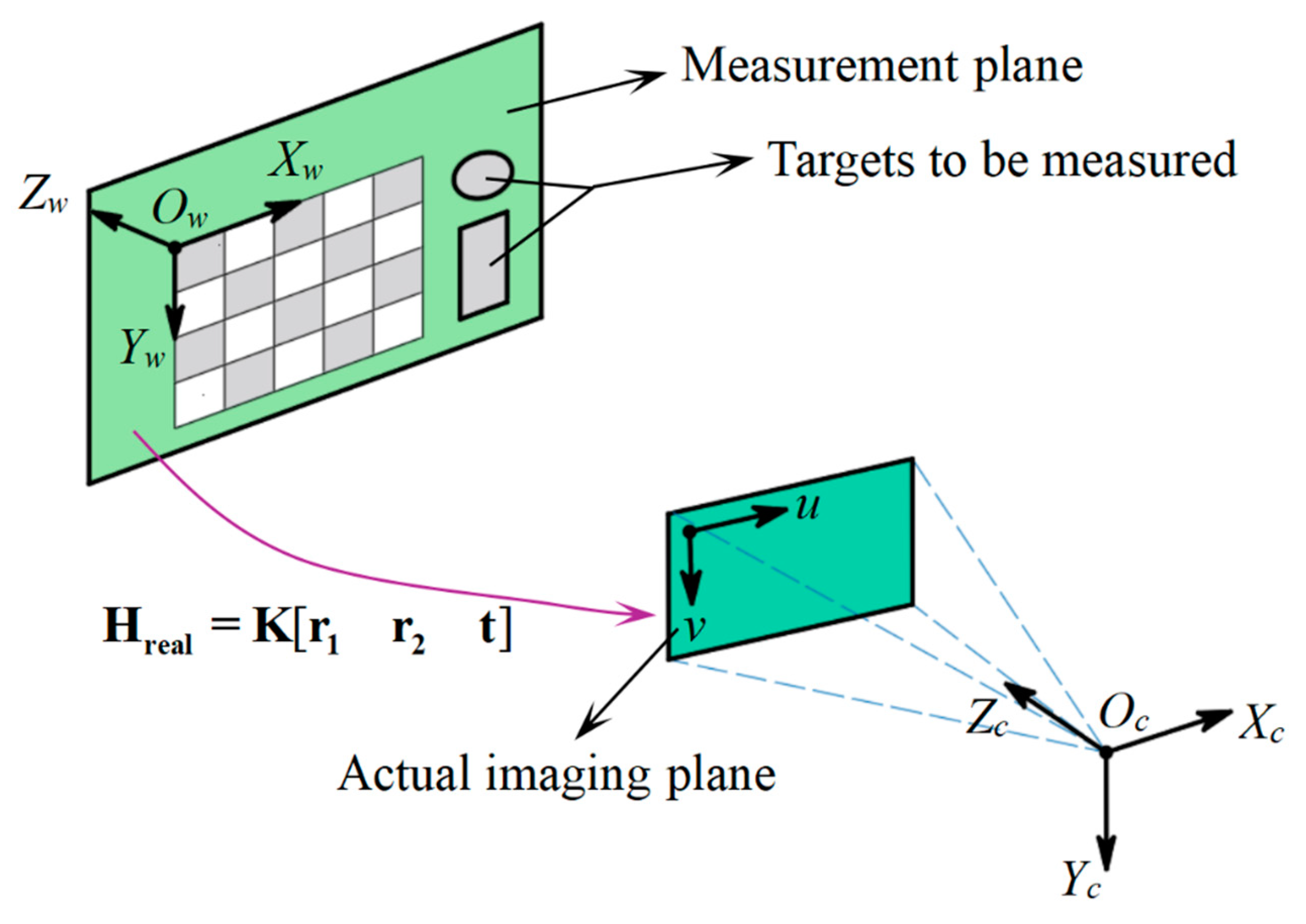
3.1. Model Construction
3.2. Model Calibration
3.2.1. Calibration of the Actual Homography Matrix
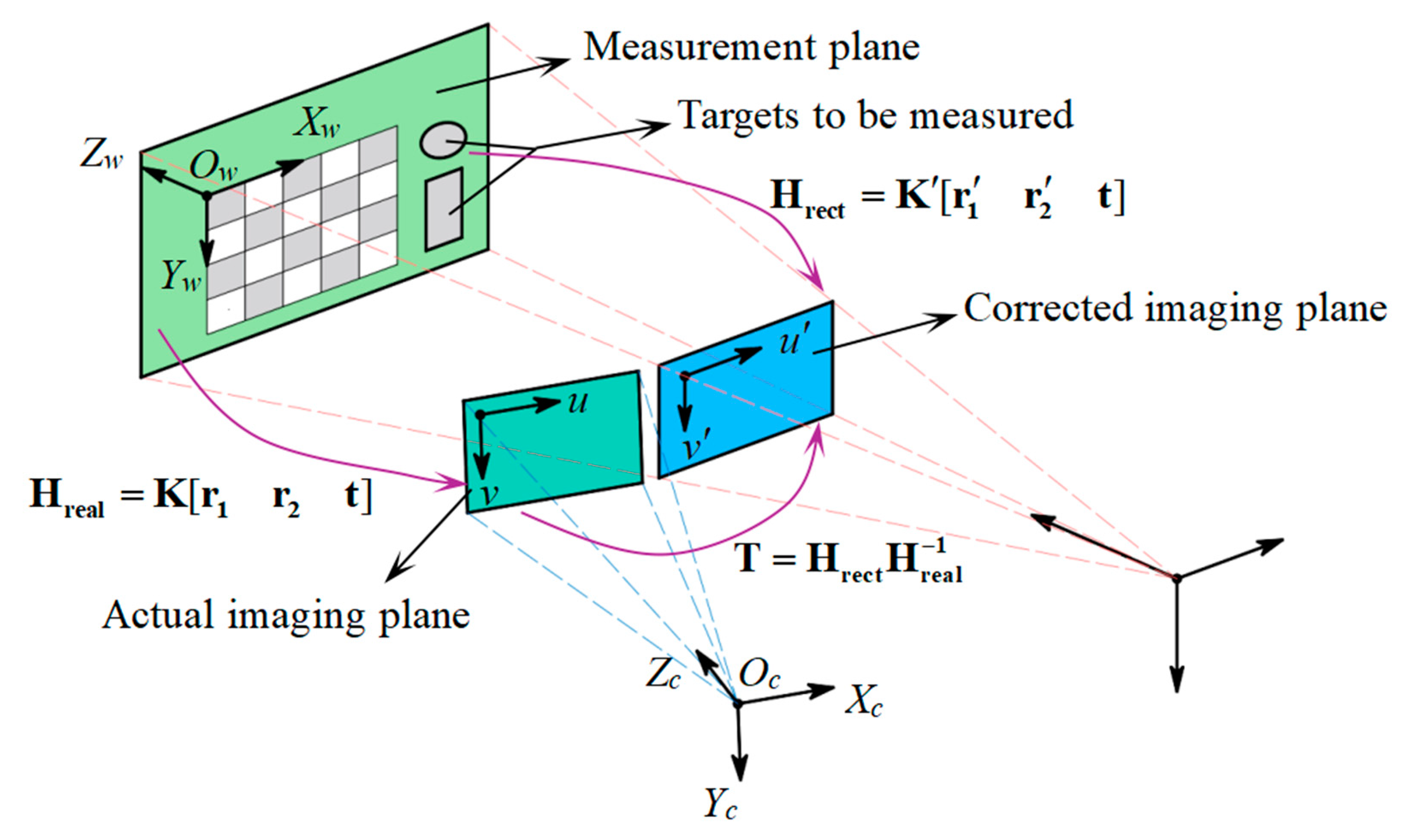
3.2.2. Generation of the Corrected Homography Matrix
- Intrinsic parameter adjustment:
- Extrinsic parameter adjustment:
3.2.3. Calibration
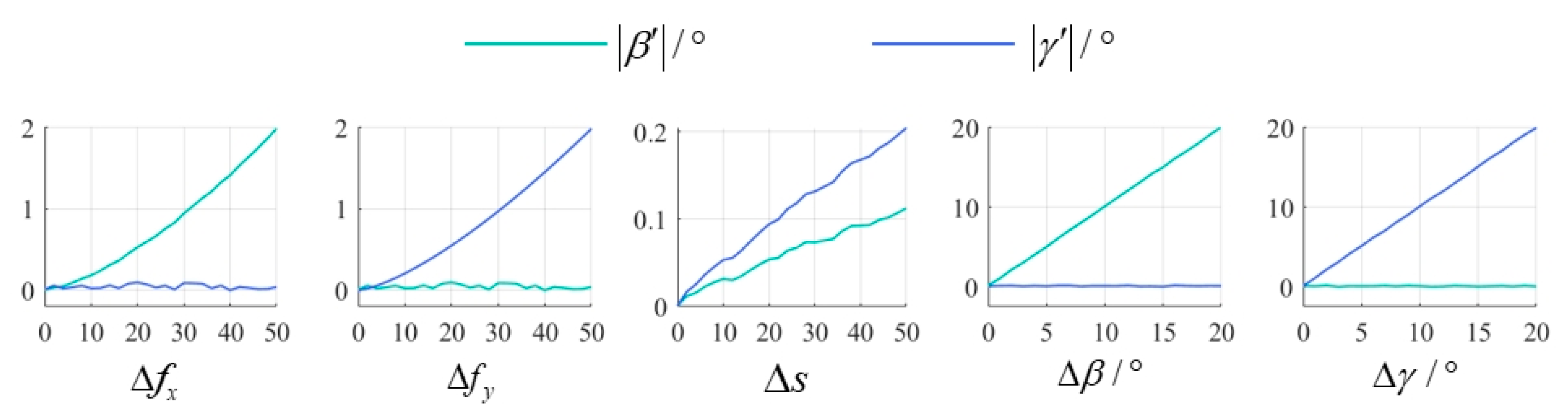
3.2.4. Method to Improve Calibration Accuracy
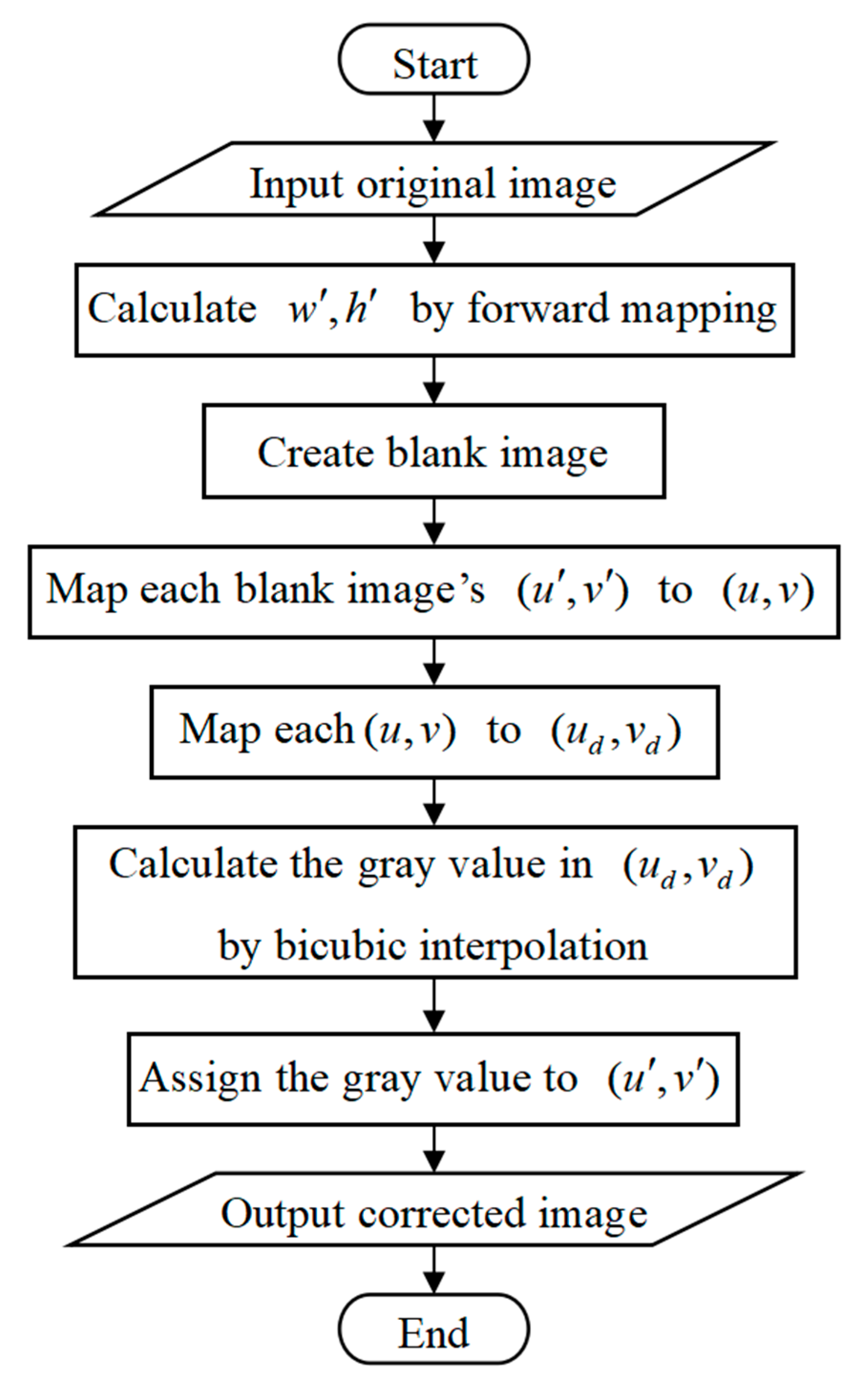
3.2.5. Algorithm Design
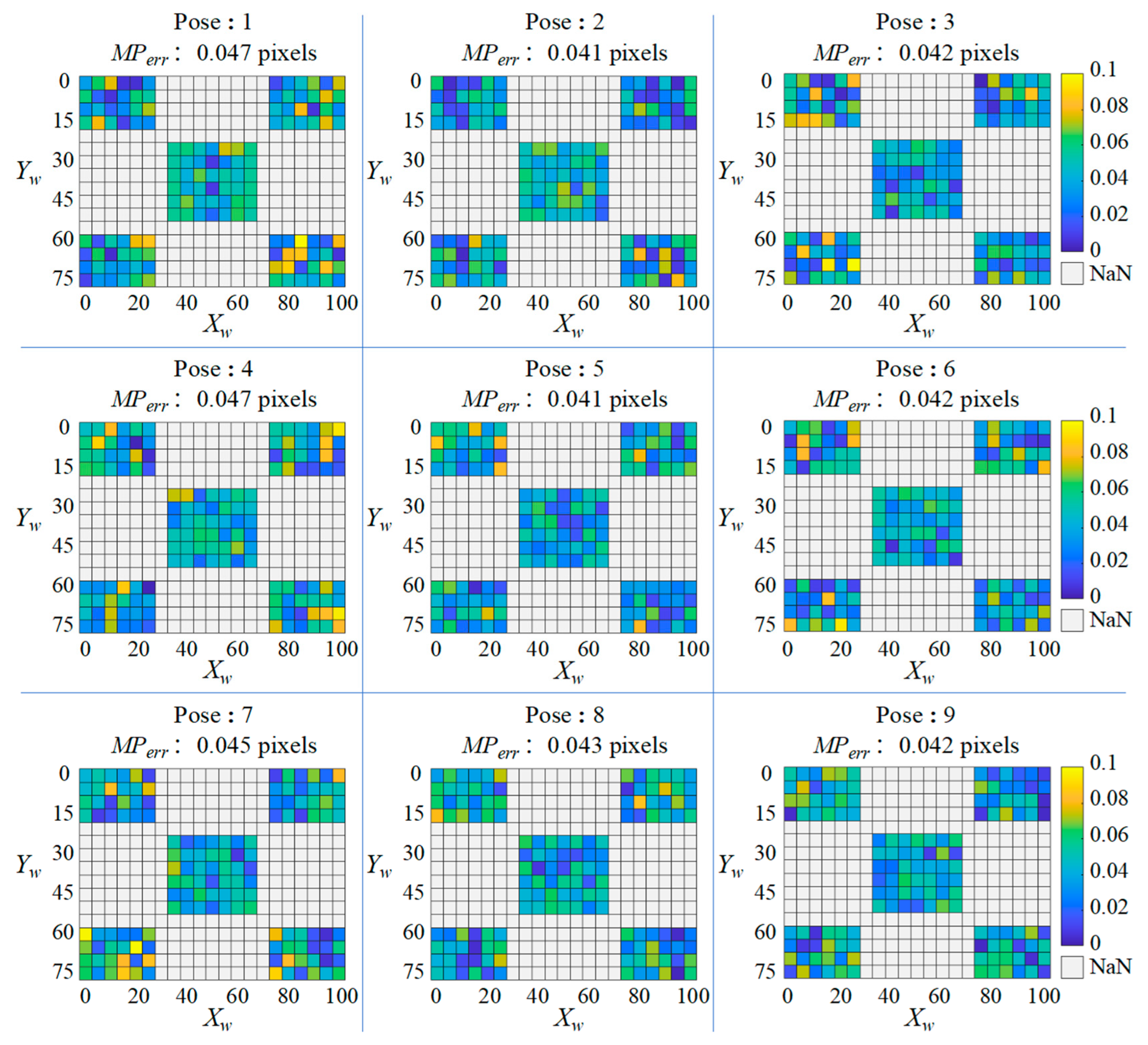
4. Experiment
4.1. Experiment Design
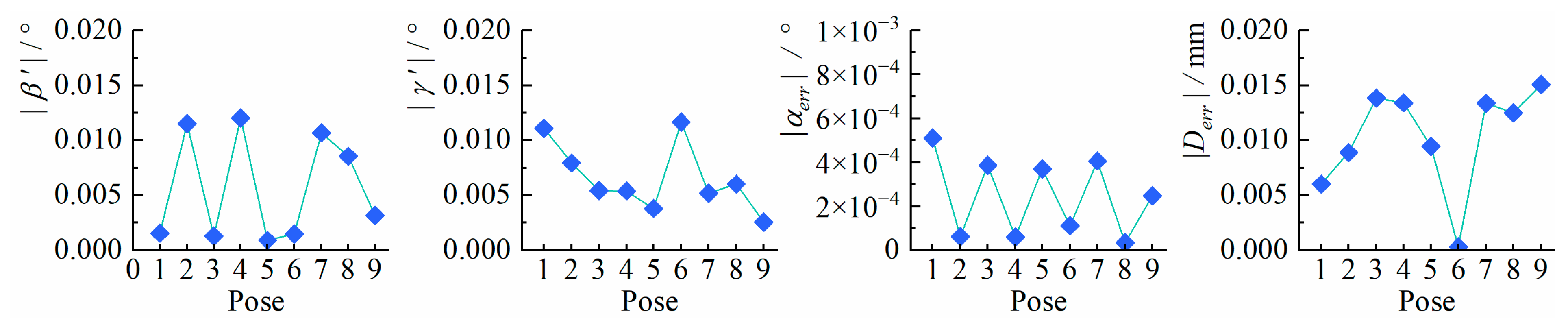
4.2. Results and Evaluations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Zhang, C.; Hu, C. Research on Aeroengine Detection Technology Based on Machine Vision; SPIE: Beijing, China, 2023; Volume 12963. [Google Scholar]
- Javaid, M.; Haleem, A.; Singh, R.P.; Rab, S.; Suman, R. Exploring impact and features of machine vision for progressive industry 4.0 culture. Sens. Int. 2022, 3, 100132. [Google Scholar] [CrossRef]
- Nogueira, V.V.E.; Barca, L.F.; Pimenta, T.C. A Cost-Effective Method for Automatically Measuring Mechanical Parts Using Monocular Machine Vision. Sensors 2023, 23, 5994. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Wang, X.; Xin, Y.; Luo, Y. Sub-pixel dimensional and vision measurement method of eccentricity for annular parts. Appl. Opt. 2022, 61, 1531–1538. [Google Scholar] [CrossRef]
- Fang, S.; Yang, L.; Tang, J.; Guo, W.; Zeng, C.; Shao, P. Visual measurement of lateral relative displacement of wheel-rail of high-speed train under earthquake. Eng. Struct. 2024, 305, 117736. [Google Scholar] [CrossRef]
- Wang, X.; Li, F.; Du, Q.; Zhang, Y.; Wang, T.; Fu, G.; Lu, C. Micro-amplitude vibration measurement using vision-based magnification and tracking. Measurement 2023, 208, 112464. [Google Scholar] [CrossRef]
- Sun, Y. Analysis for center deviation of circular target under perspective projection. Eng. Comput. 2019, 36, 2403–2413. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.; Zhang, Y.; Xu, K. Effects of camera external parameters error on measurement accuracy in monocular vision. Measurement 2024, 229, 114413. [Google Scholar] [CrossRef]
- Fang, L.; Shi, Z.L.; Li, C.X.; Liu, Y.P.; Zhao, E.B. Geometric transformation modeling for line-scan images under different camera poses. Opt. Eng. 2022, 61, 10103. [Google Scholar] [CrossRef]
- Li, X.; Liu, W.; Pan, Y.; Ma, J.; Wang, F. A Knowledge-Driven Approach for 3D High Temporal-Spatial Measurement of an Arbitrary Contouring Error of CNC Machine Tools Using Monocular Vision. Sensors 2019, 19, 744. [Google Scholar] [CrossRef]
- Liu, F.; Li, J.; Yang, Q.; Gao, P.; Ni, Y.; Wang, L. Monocular spatial geometrical measurement method based on local geometric elements associated with out-of-view datum. Measurement 2023, 214, 112828. [Google Scholar] [CrossRef]
- Poyraz, A.G.; Kaçmaz, M.; Gürkan, H.; Dirik, A.E. Sub-Pixel counting based diameter measurement algorithm for industrial Machine vision. Measurement 2024, 225, 114063. [Google Scholar] [CrossRef]
- Liu, S.; Ge, Y.; Wang, S.; He, J.; Kou, Y.; Bao, H.; Tan, Q.; Li, N. Vision measuring technology for the position degree of a hole group. Appl. Opt. 2023, 62, 869–879. [Google Scholar] [CrossRef]
- Chen, L.; Zhong, G.; Han, Z.; Li, Q.; Wang, Y.; Pan, H. Binocular visual dimension measurement method for rectangular workpiece with a precise stereoscopic matching algorithm. Meas. Sci. Technol. 2022, 34, 035010. [Google Scholar] [CrossRef]
- Le, K.; Yuan, Y. Based on the Geometric Characteristics of Binocular Imaging for Yarn Remaining Detection. Sensors 2025, 25, 339. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Yin, H. A Monocular Vision-Based Framework for Power Cable Cross-Section Measurement. Energies 2019, 12, 3034. [Google Scholar] [CrossRef]
- Miao, J.; Tan, Q.; Liu, S.; Bao, H.; Li, X. Vision measuring method for the involute profile of a gear shaft. Appl. Opt. 2020, 59, 4183–4190. [Google Scholar] [CrossRef]
- Wang, L.C.; Dong, J.H.; Cheng, Q.Y.; Shang, Y.J.; Geng, S.Q. Velocity measurement of moving target based on rotating mirror high speed camera. Opt. Eng. 2023, 62, 17. [Google Scholar] [CrossRef]
- Santana-Cedrés, D.; Gomez, L.; Alemán-Flores, M.; Salgado, A.; Esclarín, J.; Mazorra, L.; Alvarez, L. Automatic correction of perspective and optical distortions. Comput. Vis. Image Underst. 2017, 161, 1–10. [Google Scholar] [CrossRef]
- Lin, J.; Peng, J. Adaptive inverse perspective mapping transformation method for ballasted railway based on differential edge detection and improved perspective mapping model. Digit. Signal Process. 2023, 135, 103944. [Google Scholar] [CrossRef]
- Merino-Gracia, C.; Mirmehdi, M.; Sigut, J.; González-Mora, J.L. Fast perspective recovery of text in natural scenes. Image Vis. Comput. 2013, 31, 714–724. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, Q.; Jing, G.; Bai, S. Circular saw core localization in the quenching process using machine vision. Opt. Laser Technol. 2023, 161, 109111. [Google Scholar] [CrossRef]
- Zhao, X.; Du, H.; Yu, D. Improving Measurement Accuracy of Deep Hole Measurement Instruments through Perspective Transformation. Sensors 2024, 24, 3158. [Google Scholar] [CrossRef]
- Li, X.Y.; Zhang, B.; Liao, J.; Sander, P. Document Rectification and Illumination Correction using a Patch-based CNN. ACM Trans. Graph. (TOG) 2019, 38, 1–11. [Google Scholar] [CrossRef]
- Li, Y.; Wright, B.; Hameiri, Z. Deep learning-based perspective distortion correction for outdoor photovoltaic module images. Sol. Energy Mater. Sol. Cells 2024, 277, 113107. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]







| Parameters Names | Parameters Values |
|---|---|
| Pixel resolution | 2592 × 1944 |
| Pixel size | 2.2 μm × 2.2 μm |
| Size of imaging chip | 2592 × 2.2 = 5.702 mm |
| 1944 × 2.2 = 4.276 mm | |
| Focal length | 12 mm |
| Focus distance | 520 mm |
| Image distance | 1/(1/12 − 1/520) = 12.283 mm |
| Visual field | 520 × 5.702/12.283 = 241.394 mm |
| 520 × 4.276/12.283 = 181.024 mm | |
| Pixel precision | 520 × 2.2/12.283 = 93.137 μm/pixel |
| Parameters Names | Parameters Values |
|---|---|
| (1262.928, 960.322) | |
| 5497.031 | |
| 5497.245 | |
| 0.041 | |
| −0.077 | |
| 0.305 | |
| 0.00047 | |
| −0.00011 |
| Pose | α/° | β/° | γ/° | t3/mm |
|---|---|---|---|---|
| 1 | −0.198 | −16.987 | −0.316 | 521.447 |
| 2 | −0.897 | −8.157 | −0.350 | 523.331 |
| 3 | −0.579 | 13.439 | −0.240 | 494.681 |
| 4 | −0.113 | 29.971 | −0.132 | 464.244 |
| 5 | 1.287 | −1.827 | −33.269 | 470.868 |
| 6 | −0.238 | −1.384 | −16.685 | 495.230 |
| 7 | −0.364 | −1.990 | 6.645 | 522.048 |
| 8 | −1.330 | −1.699 | 30.047 | 512.587 |
| 9 | 4.653 | 7.897 | −8.376 | 491.392 |
| Pose | α′/° | β′/° | γ′/° | |
|---|---|---|---|---|
| 1 | −0.199 | 0.002 | −0.011 | 521.453 |
| 2 | −0.897 | −0.012 | −0.008 | 523.340 |
| 3 | −0.579 | 0.001 | 0.005 | 494.695 |
| 4 | −0.113 | 0.012 | −0.005 | 464.258 |
| 5 | 1.287 | −0.001 | −0.004 | 470.858 |
| 6 | −0.238 | 0.001 | −0.011 | 495.230 |
| 7 | −0.364 | −0.010 | −0.005 | 522.061 |
| 8 | −1.330 | −0.008 | 0.006 | 512.599 |
| 9 | 4.653 | −0.018 | −0.001 | 491.407 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Ding, Y.; Cui, K.; Li, J.; Xu, Q.; Mei, J. A Perspective Distortion Correction Method for Planar Imaging Based on Homography Mapping. Sensors 2025, 25, 1891. https://doi.org/10.3390/s25061891
Wang C, Ding Y, Cui K, Li J, Xu Q, Mei J. A Perspective Distortion Correction Method for Planar Imaging Based on Homography Mapping. Sensors. 2025; 25(6):1891. https://doi.org/10.3390/s25061891
Chicago/Turabian StyleWang, Chen, Yabin Ding, Kai Cui, Jianhui Li, Qingpo Xu, and Jiangping Mei. 2025. "A Perspective Distortion Correction Method for Planar Imaging Based on Homography Mapping" Sensors 25, no. 6: 1891. https://doi.org/10.3390/s25061891
APA StyleWang, C., Ding, Y., Cui, K., Li, J., Xu, Q., & Mei, J. (2025). A Perspective Distortion Correction Method for Planar Imaging Based on Homography Mapping. Sensors, 25(6), 1891. https://doi.org/10.3390/s25061891









