Development and In-Field Validation of an Autonomous Soil Mechanical Resistance Sensor
Abstract
:1. Introduction
2. Materials and Methods
2.1. Integration with Autonomous Robot Platform
2.2. Automated Penetrometer
2.2.1. Hardware
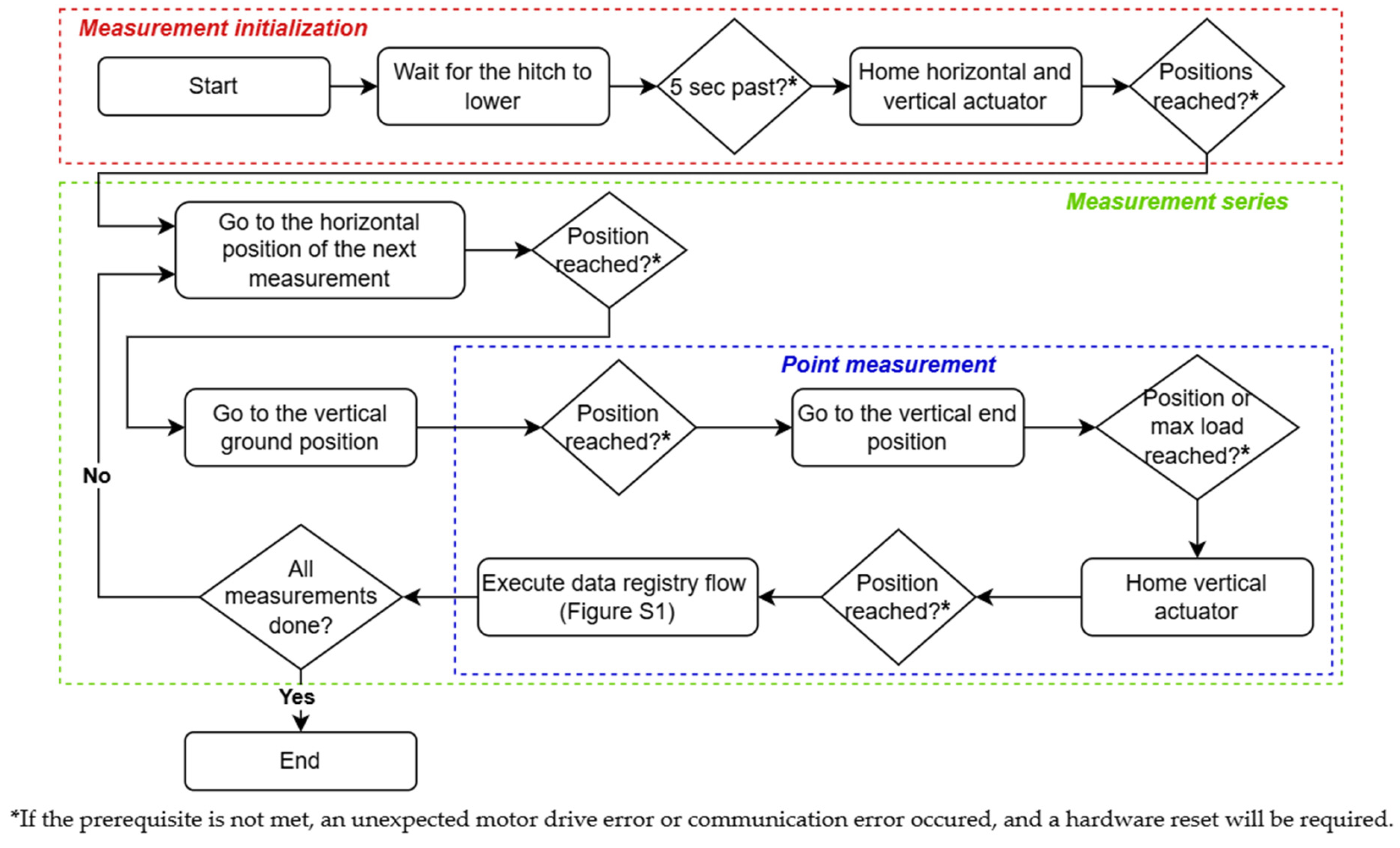
2.2.2. Programmable Logic Controller Program
2.2.3. Data Registry
2.2.4. Task Map Execution
2.3. Calibration and Validation Under Controlled Conditions
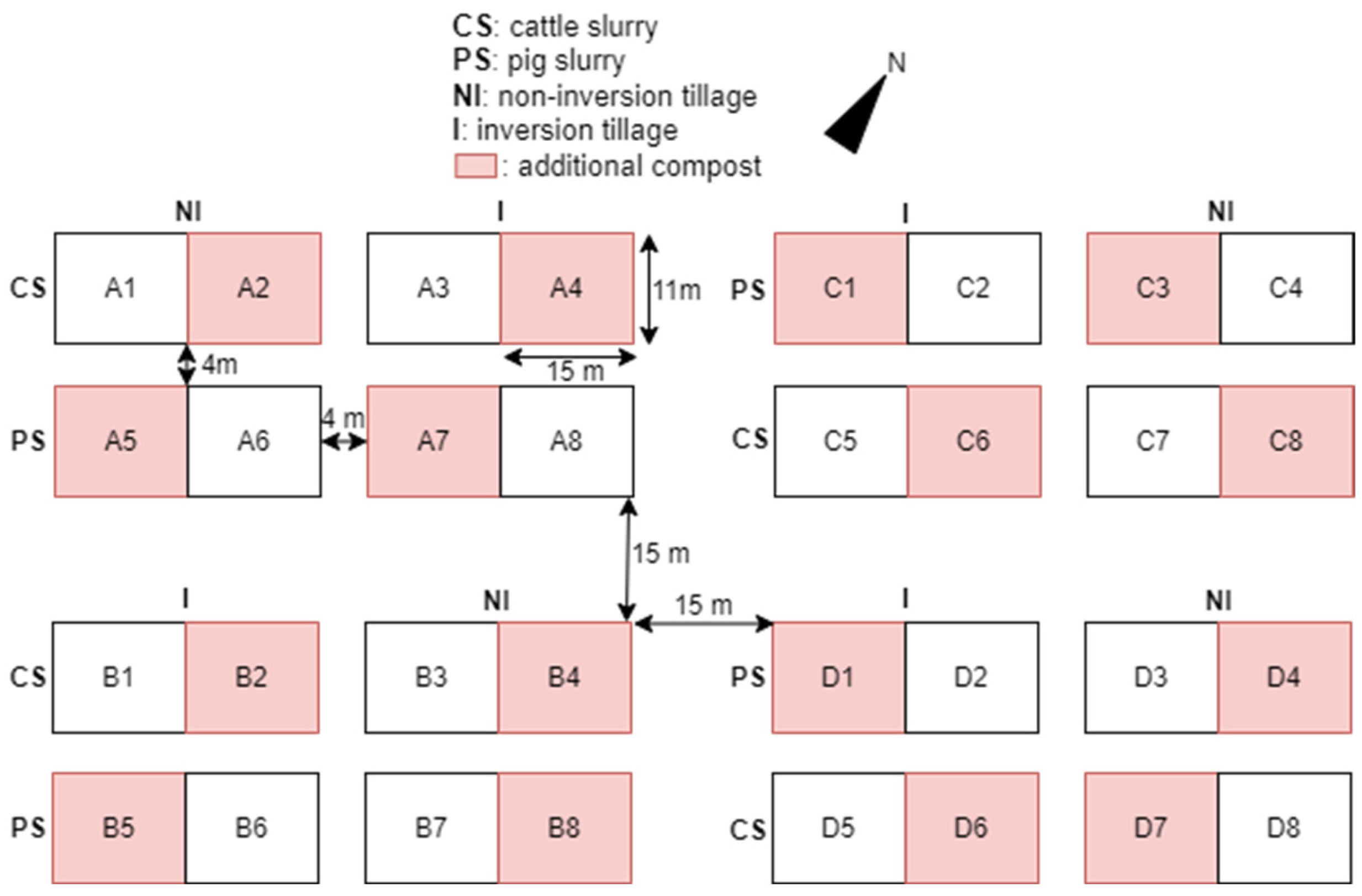
2.4. Field Validation
2.5. Data Processing and Analysis
3. Results and Discussion
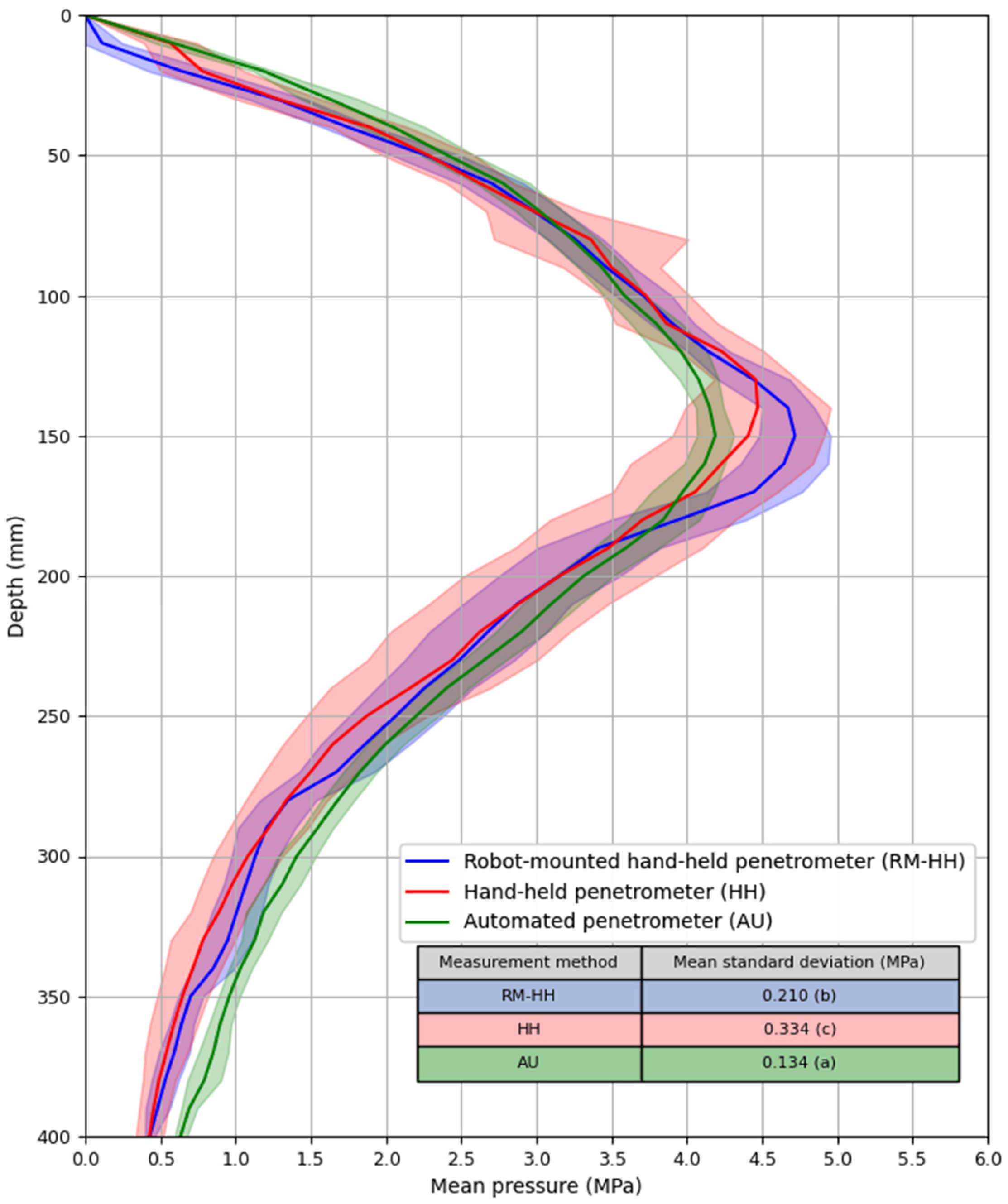
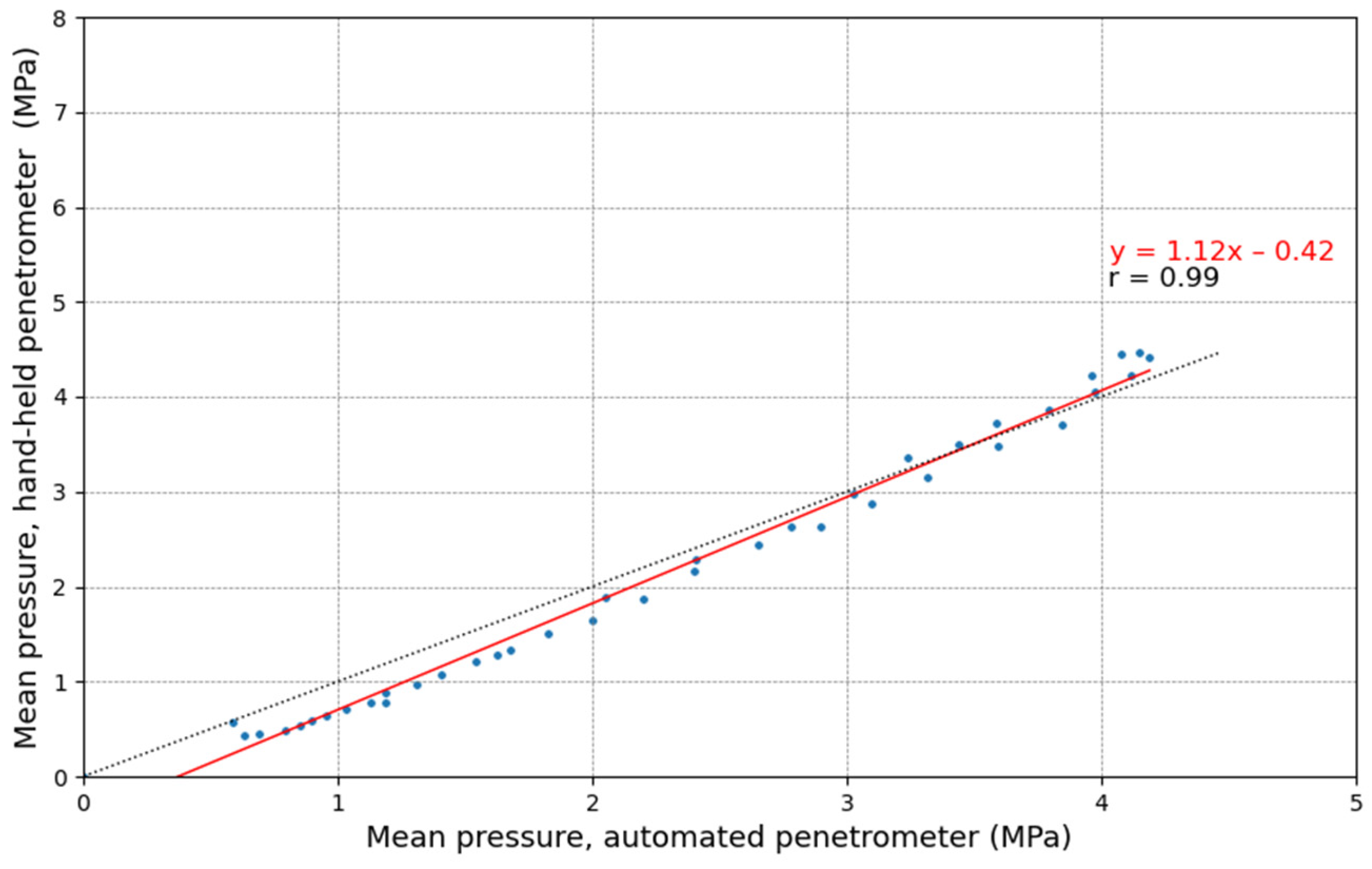
3.1. Calibration and Validation Under Controlled Conditions
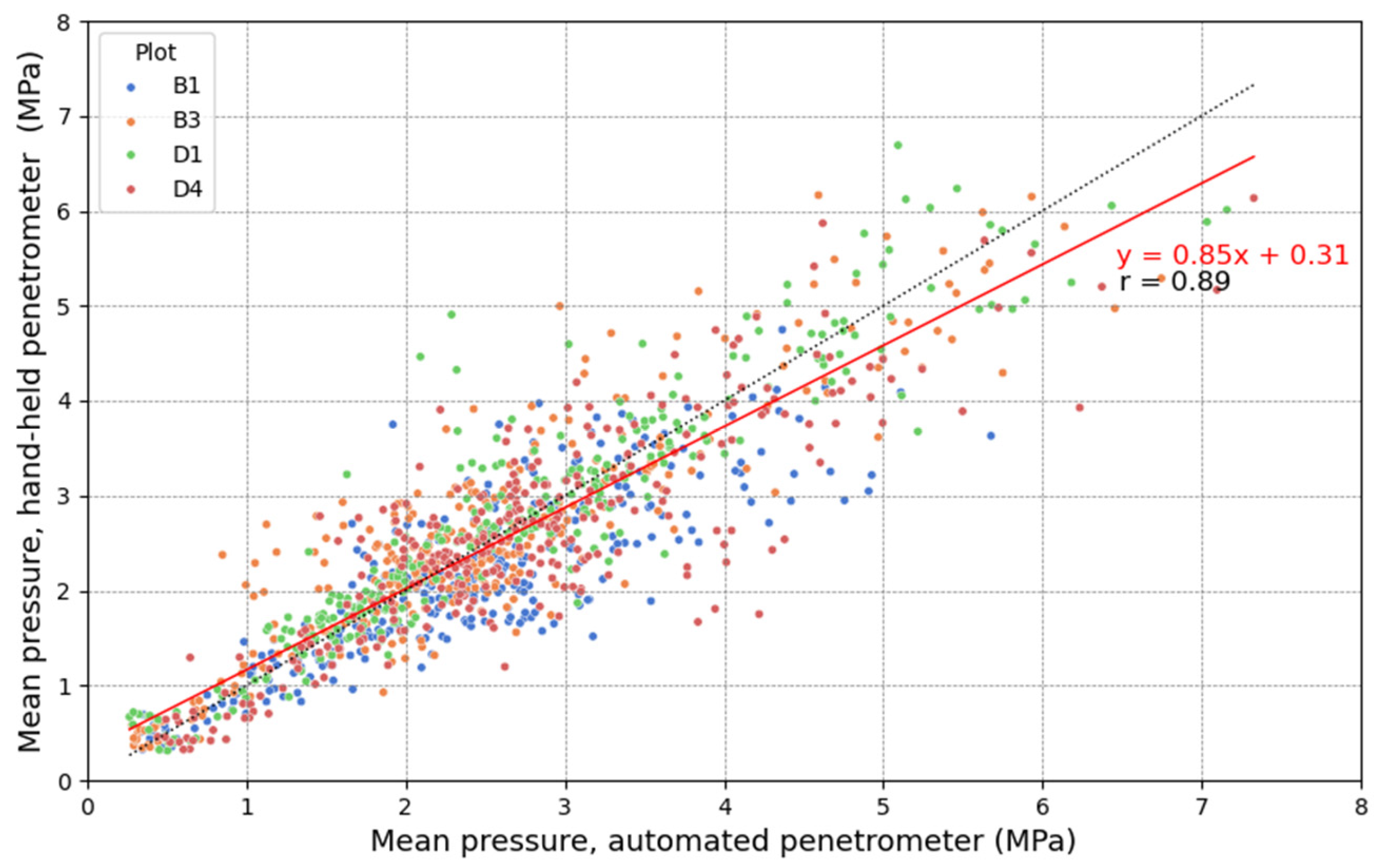
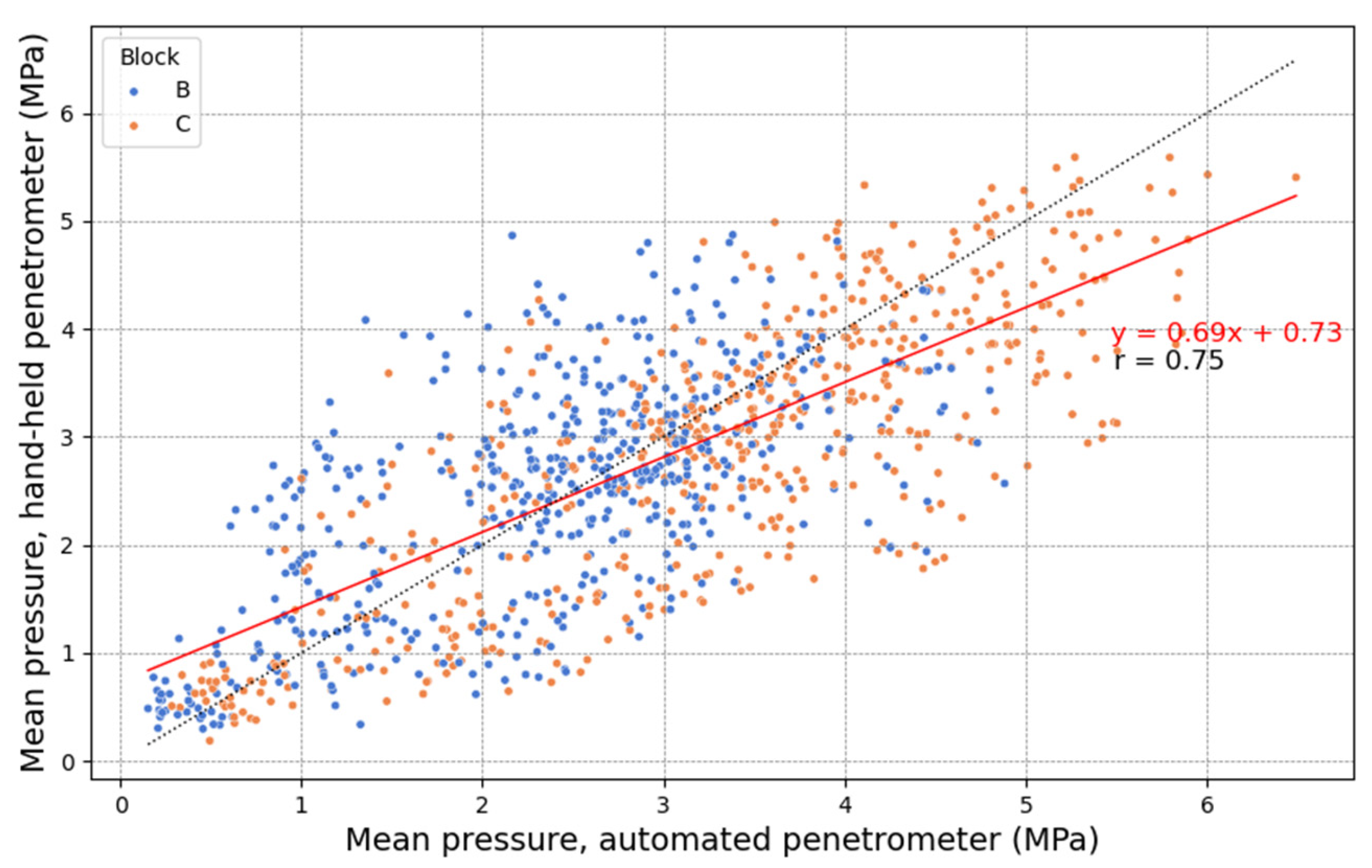
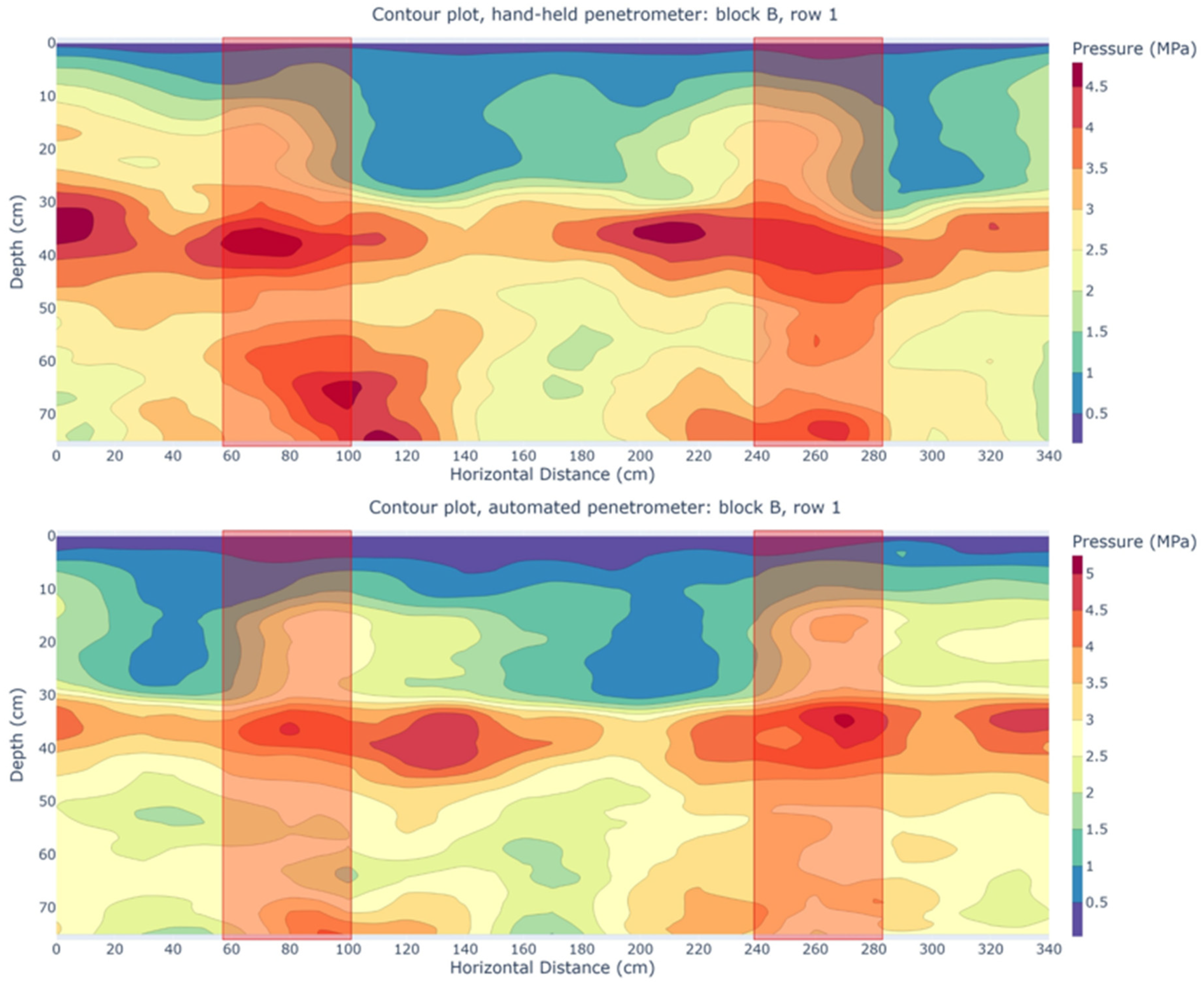
3.2. Field Validation
3.3. Study Limitations and Future Perspectives
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gu, D.; Andreev, K.; Dupre, M.E. Major trends in population growth around the world. China CDC Wkly. 2021, 3, 604. [Google Scholar] [CrossRef] [PubMed]
- Hartemink, A.E. Soil science, population growth and food production: Some historical developments. In Proceedings of the Biannual Meeting on Advances in Integrated Soil Fertility Management in Sub-Saharan Africa—Challenges and Opportunities, Yaounde, Cameroon, 25 September 2004; pp. 85–97. [Google Scholar]
- Van Kernebeek, H.R.; Oosting, S.J.; Van Ittersum, M.K.; Bikker, P.; De Boer, I.J. Saving land to feed a growing population: Consequences for consumption of crop and livestock products. Int. J. Life Cycle Assess. 2016, 21, 677–687. [Google Scholar] [CrossRef]
- Keller, T.; Lamandé, M.; Naderi-Boldaji, M.; de Lima, R.P. Soil Compaction Due to Agricultural Field Traffic: An Overview of Current Knowledge and Techniques for Compaction Quantification and Mapping. In Advances in Understanding Soil Degradation; Saljnikov, E., Mueller, L., Lavrishchev, A., Eulenstein, F., Eds.; Innovations in Landscape Research; Springer: Cham, Switzerland, 2022; pp. 287–312. [Google Scholar]
- Schjønning, P.; van den Akker, J.J.; Keller, T.; Greve, M.H.; Lamandé, M.; Simojoki, A.; Stettler, M.; Arvidsson, J.; Breuning-Madsen, H. Driver-pressure-state-impact-response (DPSIR) analysis and risk assessment for soil compaction—A European perspective. Adv. Agron. 2015, 133, 183–237. [Google Scholar] [CrossRef]
- Keller, T.; Sandin, M.; Colombi, T.; Horn, R.; Or, D. Historical increase in agricultural machinery weights enhanced soil stress levels and adversely affected soil functioning. Soil Tillage Res. 2019, 194, 104293. [Google Scholar] [CrossRef]
- Vermeulen, G.D.; Verwijs, B.R.; Van den Akker, J. Vergelijking van de Bodembelasting bij Agrarisch Veldwerk in 1980 en 2010; Plant Research International, Business Unit Agrosysteemkunde: Wageningen, The Netherlands, 2013; p. 38. [Google Scholar]
- Huber, S.; Prokop, G.; Arrouays, D.; Banko, G.; Bispo, A.; Jones, R.J.A.; Kibblewhite, M.G.; Lexer, W.; Möller, A.; Rickson, R.J.; et al. Environmental Assessment of Soil for Monitoring: Volume I Indicators & Criteria; Office for the Official Publications of the European Communities: Luxembourg, 2015; p. 339. [Google Scholar]
- Smith, D.; Dickson, J. Contributions of vehicle weight and ground pressure to soil compaction. J. Agric. Eng. Res. 1990, 46, 13–29. [Google Scholar] [CrossRef]
- Keller, T.; Or, D. Farm vehicles approaching weights of sauropods exceed safe mechanical limits for soil functioning. Proc. Natl. Acad. Sci. USA 2022, 119, e2117699119. [Google Scholar] [CrossRef]
- Defossez, P.; Richard, G.; Boizard, H.; O’Sullivan, M. Modeling change in soil compaction due to agricultural traffic as function of soil water content. Geoderma 2003, 116, 89–105. [Google Scholar] [CrossRef]
- Arvidsson, J.; Sjöberg, E.; van den Akker, J.J. Subsoil compaction by heavy sugarbeet harvesters in southern Sweden: III. Risk assessment using a soil water model. Soil Tillage Res. 2003, 73, 77–87. [Google Scholar] [CrossRef]
- Batey, T. Soil compaction and soil management–a review. Soil Use Manag. 2009, 25, 335–345. [Google Scholar] [CrossRef]
- Gan-Mor, S.; Clark, R.L. DGPS-based automatic guidance–implementation and economical analysis. In Proceedings of the 2001 ASAE Annual Meeting, Sacramento, CA, USA, 30 July–1 August 2001; p. 13. [Google Scholar]
- Nawaz, M.F.; Bourrié, G.; Trolard, F. Soil compaction impact and modelling. A review. Agron. Sustain. Dev. 2013, 33, 291–309. [Google Scholar] [CrossRef]
- Sadras, V.O.; Villalobos, F.J.; Fereres, E. Crop development and growth. In Principles of Agronomy for Sustainable Agriculture; Villalobos, F.J., Fereres, E., Eds.; Springer: Cham, Switzerland, 2016; Volume 1, pp. 141–158. [Google Scholar]
- Ishaq, M.; Ibrahim, M.; Hassan, A.; Saeed, M.; Lal, R. Subsoil compaction effects on crops in Punjab, Pakistan. Soil Tillage Res. 2001, 60, 153–161. [Google Scholar] [CrossRef]
- Berisso, F.E.; Schjønning, P.; Keller, T.; Lamandé, M.; Etana, A.; de Jonge, L.W.; Iversen, B.V.; Arvidsson, J.; Forkman, J. Persistent effects of subsoil compaction on pore size distribution and gas transport in a loamy soil. Soil Tillage Res. 2012, 122, 42–51. [Google Scholar] [CrossRef]
- Haunz, F.; Maidl, F.; Fischbeck, G. Effect of soil compaction on the dynamics of soil and fertilizer nitrogen under winter wheat. Z. Pflanzenernährung Bodenkd. 1992, 155, 129–134. [Google Scholar] [CrossRef]
- Iversen, B.V.; Børgesen, C.D.; Lægdsmand, M.; Greve, M.H.; Heckrath, G.; Kjærgaard, C. Risk predicting of macropore flow using pedotransfer functions, textural maps, and modeling. Vadose Zone J. 2011, 10, 1185–1195. [Google Scholar] [CrossRef]
- Alakukku, L. Response of annual crops to subsoil compaction in a field experiment on clay soil lasting 17 years. Adv. Geoecology 2000, 32, 205–208. [Google Scholar]
- Alblas, J.; Wanink, F.; Van den Akker, J.; Van der Werf, H.M.G. Impact of traffic-induced compaction of sandy soils on the yield of silage maize in The Netherlands. Soil Tillage Res. 1994, 29, 157–165. [Google Scholar] [CrossRef]
- Shaheb, M.R.; Venkatesh, R.; Shearer, S.A. A review on the effect of soil compaction and its management for sustainable crop production. J. Biosyst. Eng. 2021, 46, 417–439. [Google Scholar] [CrossRef]
- Nevens, F.; Reheul, D. The consequences of wheel-induced soil compaction and subsoiling for silage maize on a sandy loam soil in Belgium. Soil Tillage Res. 2003, 70, 175–184. [Google Scholar] [CrossRef]
- Håkansson, I.; Reeder, R.C. Subsoil compaction by vehicles with high axle load—Extent, persistence and crop response. Soil Tillage Res. 1994, 29, 277–304. [Google Scholar] [CrossRef]
- Voorhees, W. Long-term effect of subsoil compaction on yield of maize. Adv. Geoecology 2003, 32, 331–338. [Google Scholar]
- Chan, K.Y.; Oates, A.; Swan, A.D.; Hayes, R.C.; Dear, B.S.; Peoples, M.B. Agronomic consequences of tractor wheel compaction on a clay soil. Soil Tillage Res. 2006, 89, 13–21. [Google Scholar] [CrossRef]
- Godwin, R.; Misiewicz, P.; White, D.; Smith, E.; Chamen, T.; Galambošová, J.; Stobart, R. Results from recent traffic systems research and the implications for future work. Acta Technol. Agric. 2015, 18, 57–63. [Google Scholar] [CrossRef]
- Larson, W.; Eynard, A.; Hadas, A.; Lipiec, J. Chapter 25-Control and avoidance of soil compaction in practice. In Soil Compaction in Crop Production; Soane, B.D., van Ouwerkerk, C., Eds.; Developments in Agricultural Engineering; Elsevier: Amsterdam, The Netherlands, 1994; Volume 11, pp. 597–625. [Google Scholar]
- Håkansson, I.; Voorhees, W. Soil compaction. In Methods for Assessment of Soil Degradation; CRC Press: Boca Raton, FL, USA, 1997; Volume 1, pp. 167–179. [Google Scholar]
- Hamza, M.; Anderson, W. Combinations of ripping depth and tine spacing for compacted sandy and clayey soils. Soil Tillage Res. 2008, 99, 213–220. [Google Scholar] [CrossRef]
- Kichler, C.; Fulton, J.; Raper, R.; McDonald, T.; Zech, W. Effects of transmission gear selection on tractor performance and fuel costs during deep tillage operations. Soil Tillage Res. 2011, 113, 105–111. [Google Scholar] [CrossRef]
- Horn, R.; Fleige, H. A method for assessing the impact of load on mechanical stability and on physical properties of soils. Soil Tillage Res. 2003, 73, 89–99. [Google Scholar] [CrossRef]
- Or, D.; Keller, T.; Schlesinger, W.H. Natural and managed soil structure: On the fragile scaffolding for soil functioning. Soil Tillage Res. 2021, 208, 104912. [Google Scholar] [CrossRef]
- Busscher, W.; Bauer, P.; Frederick, J. Recompaction of a coastal loamy sand after deep tillage as a function of subsequent cumulative rainfall. Soil Tillage Res. 2002, 68, 49–57. [Google Scholar] [CrossRef]
- Vanderhasselt, A.; Steinwidder, L.; D’Hose, T.; Cornelis, W. Opening up the subsoil: Subsoiling and bio-subsoilers to remediate subsoil compaction in three fodder crop rotations on a sandy loam soil. Soil Tillage Res. 2024, 237, 105956. [Google Scholar] [CrossRef]
- Munkholm, L.J.; Schjønning, P.; Jørgensen, M.H.; Thorup-Kristensen, K. Mitigation of subsoil recompaction by light traffic and on-land ploughing: II. Root and yield response. Soil Tillage Res. 2005, 80, 159–170. [Google Scholar] [CrossRef]
- Spoor, G.; Tijink, F.; Weisskopf, P. Subsoil compaction: Risk, avoidance, identification and alleviation. Soil Tillage Res. 2003, 73, 175–182. [Google Scholar] [CrossRef]
- EEA. Soil Monitoring in Europe-Indicators and Thresholds for Soil Health Assessments; European Environment Agency: Copenhagen, Denmark, 2022; p. 181.
- Van Ouwerkerk, C.; Soane, B.D. Chapter 26-Conclusions and recommendations for further research on soil compaction in crop production. In Soil Compaction in Crop Production; Developments in Agricultural Engineering; Elsevier: Amsterdam, The Netherlands, 1994; Volume 11, pp. 627–642. [Google Scholar]
- Oldeman, L.R.; Hakkeling, R.; Sombroek, W.G. World Map of the Status of Human-Induced Soil Degradation: An Explanatory Note; International Soil Reference and Information Centre: Wageningen, The Netherlands, 1990; p. 27. [Google Scholar]
- Vanderhasselt, A. Prevention and Remediation of Soil Compaction from Field Operations on Arable Land. Ph.D. Thesis, Ghent University, Gent, Belgium, 2023. [Google Scholar]
- Alaoui, A.; Rogger, M.; Peth, S.; Blöschl, G. Does soil compaction increase floods? A review. J. Hydrol. 2018, 557, 631–642. [Google Scholar] [CrossRef]
- Alaoui, A.; Diserens, E. Mapping soil compaction–A review. Curr. Opin. Environ. Sci. Health 2018, 5, 60–66. [Google Scholar] [CrossRef]
- Suzuki, L.; Reichert, J.; Reinert, D. Degree of compactness, soil physical properties and yield of soybean in six soils under no-tillage. Soil Res. 2013, 51, 311–321. [Google Scholar] [CrossRef]
- Usowicz, B.; Lipiec, J. Spatial variability of soil properties and cereal yield in a cultivated field on sandy soil. Soil Tillage Res. 2017, 174, 241–250. [Google Scholar] [CrossRef]
- Yang, P.; Dong, W.; Heinen, M.; Qin, W.; Oenema, O. Soil Compaction Prevention, Amelioration and Alleviation Measures Are Effective in Mechanized and Smallholder Agriculture: A Meta-Analysis. Land 2022, 11, 645. [Google Scholar] [CrossRef]
- Raper, R.L.; Schwab, E.B.; Dabney, S.M. Measurement and variation of site-specific hardpans for silty upland soils in the Southeastern United States. Soil Tillage Res. 2005, 84, 7–17. [Google Scholar] [CrossRef]
- Raper, R.L. Site-specific tillage for site-specific compaction: Is there a need. In Proceedings of the International Conference of Dryland Conservation/Zone Tillage, Beijing, China; 1999; pp. 66–68. [Google Scholar]
- Sirjacobs, D.; Hanquet, B.; Lebeau, F.; Destain, M.-F. On-line soil mechanical resistance mapping and correlation with soil physical properties for precision agriculture. Soil Tillage Res. 2002, 64, 231–242. [Google Scholar] [CrossRef]
- Koolen, A.J.; Kuipers, H. Agricultural Soil Mechanics; Springer: Berlin/Heidelberg, Germany, 1983; Volume 13, p. 244. [Google Scholar]
- Rickson, R.J.; Deeks, L.K.; Corstanje, R.; Newell-Price, P.; Kibblewhite, M.G.; Chambers, B.; Bellamy, P.; Holman, I.P.; James, I.; Jones, R. Indicators of Soil Quality-Physical Properties (SP1611). Final Report to Defra; Department for Environment, Food and Rural Affairs (Defra): London, UK, 2012.
- Jafri, N.J.S.; Ab Rahim, M.A.; Zahid, M.Z.A.M.; Bawadi, N.F.; Ahmad, M.M.; Mansor, A.F.; Omar, W.M.S.W. Assessment of soil compaction properties based on surface wave techniques. In Proceedings of the International Conference on Civil & Environmental Engineering, Penang, Malaysia, 28–29 November 2017. [Google Scholar]
- García-Tomillo, A.; Figueiredo, T.d.; Dafonte, J.D.; Almeida, A.; Paz-González, A. Effects of machinery trafficking in an agricultural soil assessed by Electrical Resistivity Tomography (ERT). Open Agric. 2018, 3, 378–385. [Google Scholar] [CrossRef]
- Kowalczyk, S.; Maślakowski, M.; Tucholka, P. Determination of the correlation between the electrical resistivity of non-cohesive soils and the degree of compaction. J. Appl. Geophys. 2014, 110, 43–50. [Google Scholar] [CrossRef]
- Yoon, H.-K.; Jung, S.-H.; Lee, J.-S. Characterisation of subsurface spatial variability using a cone resistivity penetrometer. Soil Dyn. Earthq. Eng. 2011, 31, 1064–1071. [Google Scholar] [CrossRef]
- Krajco, J. Detection of Soil Compaction Using Soil Electrical Conductivity. Master’s Thesis, Cranfield University, Cranfield, UK, 2007. [Google Scholar]
- Carrera, A.; Peruzzo, L.; Longo, M.; Cassiani, G.; Morari, F. Uncovering soil compaction: Performance of electrical and electromagnetic geophysical methods. Soil 2024, 10, 843–857. [Google Scholar] [CrossRef]
- Mansourian, D.; Vanderhasselt, A.; Cornelis, W.; Hermans, T. Response to soil compaction of the electrical resistivity tomography, induced polarisation, and electromagnetic induction methods: A case study in Belgium. Soil Res. 2023, 62, SR22260. [Google Scholar] [CrossRef]
- Muñiz, E.; Shaw, R.K.; Gimenez, D.; Williams, C.A.; Kenny, L. Use of ground-penetrating radar to determine depth to compacted layer in soils under pasture. In Digital Soil Morphometrics; Hartemink, A., Minasny, B., Eds.; Springer: Cham, Switzerland, 2016; pp. 411–421. [Google Scholar]
- Freeland, R.; Sorochan, J.; Goddard, M.; McElroy, J. Using ground-penetrating radar to evaluate soil compaction of athletic turfgrass fields. Appl. Eng. Agric. 2008, 24, 509–514. [Google Scholar] [CrossRef]
- Raper, R.; Asmussen, L.; Powell, J. Sensing hard pan depth with ground-penetrating radar. Trans. ASAE 1990, 33, 41–46. [Google Scholar] [CrossRef]
- Alihamsyah, T.; Humphries, E.G.; Bowers, C.G. A technique for horizontal measurement of soil mechanical impedance. Trans. ASAE 1990, 33, 73–77. [Google Scholar] [CrossRef]
- Verschoore, R.; Pieters, J.; Seps, T.; Spriet, Y.; Vangeyte, J. Development of a sensor for continuous soil resistance measurement. In Precision Agriculture; Stafford, J., Werner, A., Eds.; Wageningen Academic: Wageningen, The Netherlands, 2003; pp. 689–695. [Google Scholar]
- Topakci, M.; Unal, I.; Canakci, M.; Celik, H.K.; Karayel, D. Design of a horizontal penetrometer for measuring on-the-go soil resistance. Sensors 2010, 10, 9337–9348. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Ramon, H. Development of on-line measurement system of bulk density based on on-line measured draught, depth and soil moisture content. Soil Tillage Res. 2006, 86, 218–229. [Google Scholar] [CrossRef]
- Sharifi, A.; Godwin, R.J.; O’Dogherty, M.J.; Dresser, M.L. Evaluating the performance of a soil compaction sensor. Soil Use Manag. 2007, 23, 171–177. [Google Scholar] [CrossRef]
- Soane, G.; Godwin, R.; Marks, M.; Spoor, G. Crop and soil response to subsoil loosening, deep incorporation of phosphorus and potassium fertilizer and subsequent soil management on a range of soil types.: Part 2: Soil structural conditions. Soil Use Manag. 1987, 3, 123–130. [Google Scholar] [CrossRef]
- Benevenute, P.A.; de Morais, E.G.; Souza, A.A.; Vasques, I.C.; Cardoso, D.P.; Sales, F.R.; Severiano, E.C.; Homem, B.G.; Casagrande, D.R.; Silva, B.M. Penetration resistance: An effective indicator for monitoring soil compaction in pastures. Ecol. Indic. 2020, 117, 106647. [Google Scholar] [CrossRef]
- Molua, O.; Ukpene, A.; Ighrakpata, F.; Emagbetere, J.; Nwachuku, D. Review on nondestructive methods of detecting compacted soils and effects of compacted soil on crop production. Open J. Agric. Sci. 2023, 4, 1–16. [Google Scholar] [CrossRef]
- De Moraes, M.T.; Zwirtes, A.L.; Carlesso, R.; da Silva, V.R. Use of penetrometers in agriculture: A review. Eng. Agrícola 2014, 34, 179–193. [Google Scholar] [CrossRef]
- Vaz, C.M.P.; Manieri, J.M.; de Maria, I.C.; Tuller, M. Modeling and correction of soil penetration resistance for varying soil water content. Geoderma 2011, 166, 92–101. [Google Scholar] [CrossRef]
- Al-Sammarraie, M.A.J.; Kırılmaz, H. Technological advances in soil penetration resistance measurement and prediction algorithms. Rev. Agric. Sci. 2023, 11, 93–105. [Google Scholar] [CrossRef]
- ASABE. Soil Cone Penetrometer. Date: February 1999. American Society of Agricultural and Biological Engineers. St. Joseph, Michigan, USA. Available online: https://elibrary.asabe.org/abstract.asp?aid=44232&t=2 (accessed on 6 March 2025).
- Mahore, V.; Soni, P.; Patidar, P.; Machavaram, R. An IoT-enabled penetrometer with constant-rate penetration for accurate measurement of soil cone index. Cogent Eng. 2024, 11, 2372088. [Google Scholar] [CrossRef]
- Boon, N.; Yahya, A.; Kheiralla, A.; Wee, B.; Gew, S. A tractor-mounted, automated soil penetrometer–shearometer unit for mapping soil mechanical properties. Biosyst. Eng. 2005, 90, 381–396. [Google Scholar] [CrossRef]
- Nisha, K.; Upadhyay, G.; Patel, B.; Choudhary, S.; Rani, V. A tractor hydraulic assisted embedded microprocessor-based penetrometer for soil compaction measurement. J. Terramechanics 2023, 110, 1–12. [Google Scholar] [CrossRef]
- Kumar, M.; Dadhich, H.; Dadhich, S.M. Development of a tractor operated soil compaction measurement device. In Proceedings of the International Conference on Technologies for Sustainable Development (ICTSD), Mumbai, India, 4–6 February 2015; pp. 1–4. [Google Scholar]
- Raper, R.L.; Reeves, D.W.; Schwab, E.B.; Burmester, C.H. Reducing soil compaction of Tennessee Valley soils in conservation tillage systems. J. Cotton Sci. 2000, 4, 84–90. [Google Scholar]
- Fentanes, J.P.; Gould, I.; Duckett, T.; Pearson, S.; Cielniak, G. 3-d soil compaction mapping through kriging-based exploration with a mobile robot. IEEE Robot. Autom. Lett. 2018, 3, 3066–3072. [Google Scholar] [CrossRef]
- Scholz, C.; Moeller, K.; Ruckelshausen, A.; Hinck, S.; Göttinger, M. Automatic soil penetrometer measurements and GIS based documentation with the autonomous field robot platform bonirob. In Proceedings of the 12th International Conference of Precision Agriculture, Sacramento, CA, USA, 20–23 July 2014. [Google Scholar]
- Willekens, A.; Temmerman, S.; Wyffels, F.; Pieters, J.G.; Cool, S.R. The architecture and evaluation of the Agricultural Robot Taskmap Operation Framework. Field Robot. 2023. [Google Scholar]
- Royal Eijkelkamp. Penetrologger User manual. Available online: https://www.royaleijkelkamp.com/media/nrwjyah3/m-0615sae-penetrologger.pdf (accessed on 6 March 2025).
- D’Hose, T.; Ruysschaert, G.; Viaene, N.; Debode, J.; Vanden Nest, T.; Van Vaerenbergh, J.; Cornelis, W.; Willekens, K.; Vandecasteele, B. Farm compost amendment and non-inversion tillage improve soil quality without increasing the risk for N and P leaching. Agric. Ecosyst. Environ. 2016, 225, 126–139. [Google Scholar] [CrossRef]
- Plotly Technologies Inc. Collaborative Data Science; Plotly Technologies Inc.: Montreal, QC, USA, 2015. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Junior, D.D.V.; Biachini, A.; Valadão, F.C.A.; Rosa, R.P. Penetration resistance according to penetration rate, cone base size and different soil conditions. Bragantia 2014, 73, 171–177. [Google Scholar] [CrossRef]
- Spektor, M. Principles of soil-tool interaction. J. Terramechanics 1981, 18, 51–65. [Google Scholar] [CrossRef]
- Hendrick, J.G.; Gill, W.R. Soil reaction to high speed cutting. Trans. ASAE 1973, 16, 401–403. [Google Scholar] [CrossRef]
- Mohawesh, O.; Ishida, T.; Fukumura, K.; Yoshino, K. Assessment of spatial variability of penetration resistance and hardpan characteristics in a cassava field. Soil Res. 2008, 46, 210–218. [Google Scholar] [CrossRef]
- Kirkham, M.B. Penetrometer measurements. In Principles of Soil and Plant Water Relations; Elsevier: Amsterdam, The Netherlands, 2005; pp. 117–128. [Google Scholar]
- Mosaddeghi, M.; Hajabbasi, M.; Hemmat, A.; Afyuni, M. Soil compactibility as affected by soil moisture content and farmyard manure in central Iran. Soil Tillage Res. 2000, 55, 87–97. [Google Scholar] [CrossRef]
- Rücknagel, J.; Christen, O.; Hofmann, B.; Ulrich, S. A simple model to estimate change in precompression stress as a function of water content on the basis of precompression stress at field capacity. Geoderma 2012, 177–178, 1–7. [Google Scholar] [CrossRef]
- Nowatzki, E.; Karafiath, L.L. The effect of cone angle on penetration resistance. Highw. Res. Rec. 1972, 31. Available online: https://www.semanticscholar.org/paper/The-Effect-of-Cone-Angle-on-Penetration-Resistance-Nowatzki-Karafiath/f64e1aa777cc9f74ddcbeef113b394b0aa0f690b (accessed on 6 March 2025).
- Carrara, M.; Castrignanò, A.; Comparetti, A.; Febo, P.; Orlando, S. Mapping of penetrometer resistance in relation to tractor traffic using multivariate geostatistics. Geoderma 2007, 142, 294–307. [Google Scholar] [CrossRef]
- Mome Filho, E.A.; da Silva, A.P.; Figueiredo, G.C.; Gimenes, F.H.S.; Vitti, A.C. Compared performance of penetrometers and effect of soil water content on penetration resistance measurements. Rev. Bras. Ciência Solo 2014, 38, 744–754. [Google Scholar] [CrossRef]
- Herrick, J.E.; Jones, T.L. A dynamic cone penetrometer for measuring soil penetration resistance. Soil Sci. Soc. Am. J. 2002, 66, 1320–1324. [Google Scholar] [CrossRef]
- Schmittmann, O.; Lammers, P.S. Assessing Subsoil Conditions with an ASABE Conform Vertical Penetrometer—Development and Evaluation. Sensors 2023, 23, 1306. [Google Scholar] [CrossRef]
- Obour, P.B.; Ugarte, C.M. A meta-analysis of the impact of traffic-induced compaction on soil physical properties and grain yield. Soil Tillage Res. 2021, 211, 105019. [Google Scholar] [CrossRef]
- Schjønning, P.; Rasmussen, K.J. Danish experiments on subsoil compaction by vehicles with high axle load. Soil Tillage Res. 1994, 29, 215–227. [Google Scholar] [CrossRef]
- Håkansson, I.; Lipiec, J. A review of the usefulness of relative bulk density values in studies of soil structure and compaction. Soil Tillage Res. 2000, 53, 71–85. [Google Scholar] [CrossRef]
- Naderi-Boldaji, M.; Kazemzadeh, A.; Hemmat, A.; Rostami, S.; Keller, T. Changes in soil stress during repeated wheeling: A comparison of measured and simulated values. Soil Res. 2017, 56, 204–214. [Google Scholar] [CrossRef]
- Botta, G.F.; Becerra, A.T.; Tourn, F.B. Effect of the number of tractor passes on soil rut depth and compaction in two tillage regimes. Soil Tillage Res. 2009, 103, 381–386. [Google Scholar] [CrossRef]
- Chamen, T.; Alakukku, L.; Pires, S.; Sommer, C.; Spoor, G.; Tijink, F.; Weisskopf, P. Prevention strategies for field traffic-induced subsoil compaction: A review: Part 2. Equipment and field practices. Soil Tillage Res. 2003, 73, 161–174. [Google Scholar] [CrossRef]









| Plot | B1 | B3 | D1 | D4 | Spraying Track B | Spraying Track C |
|---|---|---|---|---|---|---|
| Depth (cm) | Mean Gravimetric Soil Moisture Content (%) ± Standard Deviation (%) | |||||
| 0–10 | 19.20 ± 0.15 | 20.96 ± 0.31 | 18.43 ± 0.25 | 20.63 ± 0.42 | 19.52 ± 0.09 | 21.94 ± 0.36 |
| 10–30 | 19.03 ± 0.36 | 17.91 ± 0.22 | 18.88 ± 0.58 | 17.83 ± 0.36 | 18.87 ± 0.46 | 17.63 ± 0.14 |
| 30–60 | 18.52 ± 0.41 | 18.02 ± 0.28 | 17.13 ± 0.23 | 17.48 ± 0.22 | 17.88 ± 0.07 | 16.92 ± 0.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Cauwer, V.; Cool, S.; Willekens, A.; Temmerman, S.; Nuyttens, D.; D’ Hose, T.; Pieters, J.; Leroux, S. Development and In-Field Validation of an Autonomous Soil Mechanical Resistance Sensor. Sensors 2025, 25, 1919. https://doi.org/10.3390/s25061919
De Cauwer V, Cool S, Willekens A, Temmerman S, Nuyttens D, D’ Hose T, Pieters J, Leroux S. Development and In-Field Validation of an Autonomous Soil Mechanical Resistance Sensor. Sensors. 2025; 25(6):1919. https://doi.org/10.3390/s25061919
Chicago/Turabian StyleDe Cauwer, Valentijn, Simon Cool, Axel Willekens, Sébastien Temmerman, David Nuyttens, Tommy D’ Hose, Jan Pieters, and Sam Leroux. 2025. "Development and In-Field Validation of an Autonomous Soil Mechanical Resistance Sensor" Sensors 25, no. 6: 1919. https://doi.org/10.3390/s25061919
APA StyleDe Cauwer, V., Cool, S., Willekens, A., Temmerman, S., Nuyttens, D., D’ Hose, T., Pieters, J., & Leroux, S. (2025). Development and In-Field Validation of an Autonomous Soil Mechanical Resistance Sensor. Sensors, 25(6), 1919. https://doi.org/10.3390/s25061919






