Developing Synthetic Parameters Using Frequency Band Ratios for Muscle Fatigue Analysis During Isometric Contractions by Using Shoulder Muscles
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
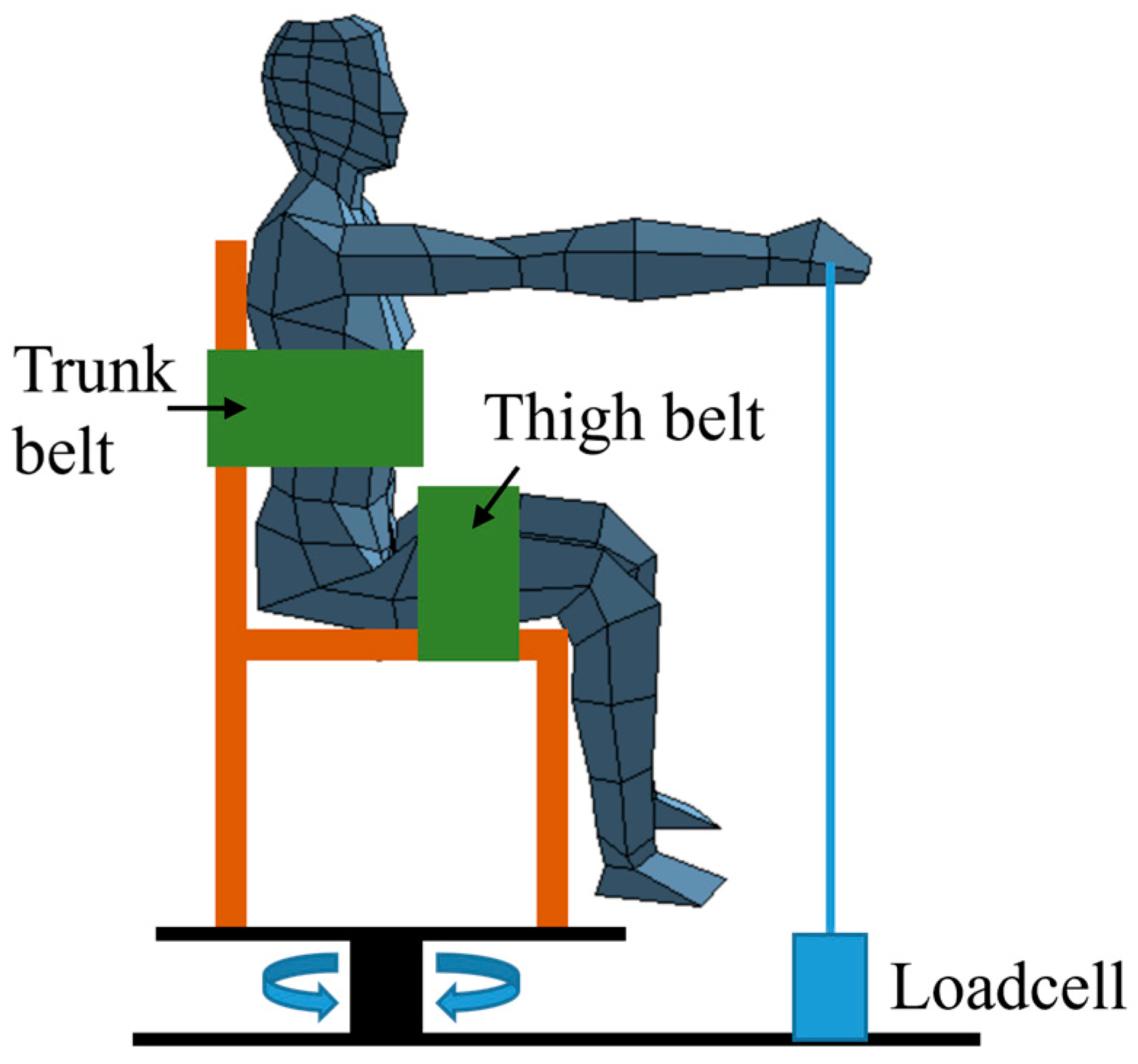
2.2. Apparatus
2.3. Procudure
2.4. Frequency Band Ratio Parameters
2.5. Statistics
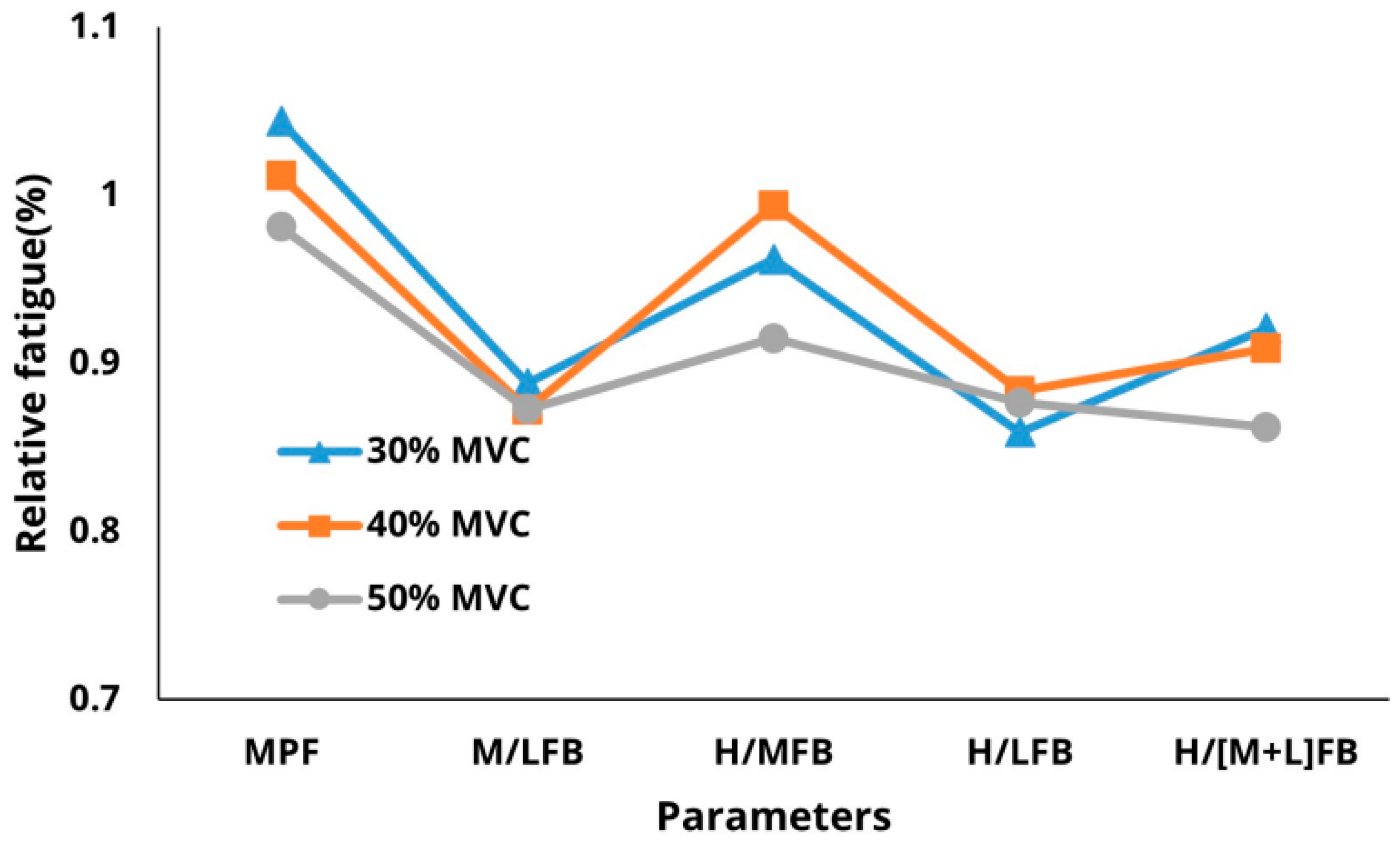
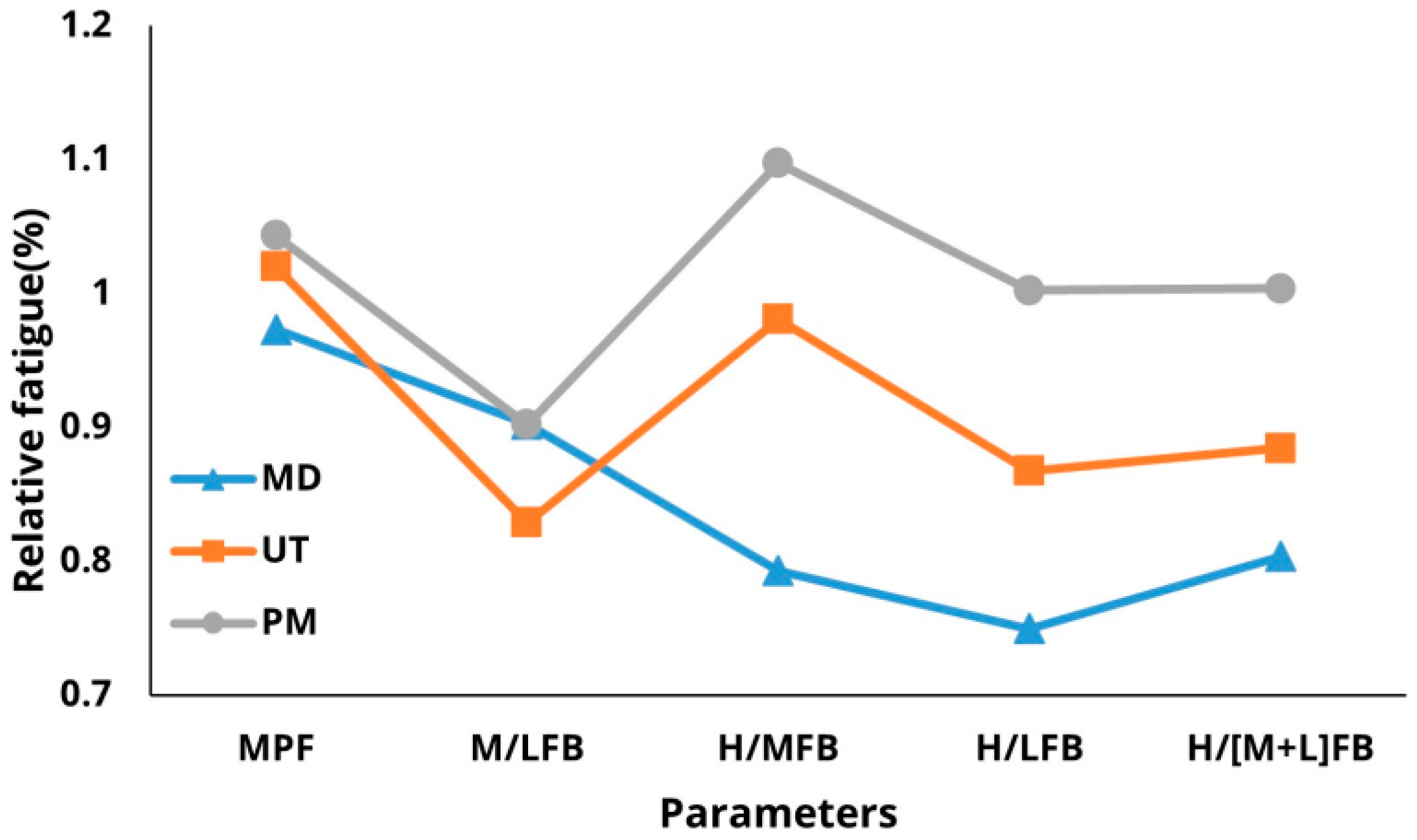
3. Results
3.1. Descriptive Statistics
3.2. MANOVA
3.3. Sensitivity of Parameters
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mesin, L.; Cescon, C.; Gazzoni, M.; Merletti, R.; Rainoldi, A. A bi-dimensional index for the selective assessment of myoelectric manifestations of peripheral and central muscle fatigue. J. Electromyogr. Kinesiol. 2009, 19, 851–863. [Google Scholar] [CrossRef] [PubMed]
- Basmajian, J.V.; De Luca, C.J. Muscle Alive—Their Functions Revealed by Electromyography, 5th ed.; Williams & Wilkins: Baltimore, MD, USA, 1985. [Google Scholar]
- Cifrek, M.; Medved, V.; Tonković, S.; Ostojić, S. Surface EMG based muscle fatigue evaluation in biomechanics. Clin. Biomech. 2009, 24, 327–340. [Google Scholar] [CrossRef]
- Farina, D.; Merletti, R. Comparisons of algorithms for estimation of EMG variables during voluntary isometric contractions. J. Electromyogr. Kinesiol. 2000, 10, 337–349. [Google Scholar] [CrossRef] [PubMed]
- Hagberg, M.; Ericson, B.E. Myoelectric power spectrum dependence on muscular contraction level of elbow flexors. Eur. J. Appl. Physiol. 1982, 48, 147–156. [Google Scholar] [CrossRef]
- Allison, G.T.; Fujiwara, T. The relationship between EMG median frequency and low frequency band amplitude changes at different levels of muscle capacity. Clin. Biomech. 2002, 17, 464–469. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.J.; Kim, J.Y. The Effect of the Signal Stationarity on the EMG Frequency Analysis. J. Ergon. Soc. Korea 2010, 29, 183–188. [Google Scholar] [CrossRef]
- Kadefors, R.; Kaiser, E.; Petersěn, I. Dynamic spectrum analysis of myo-potentials with special reference to muscle fatigue. Electromyography 1968, 8, 39–73. [Google Scholar]
- Bellemare, F.; Grassino, A. Evaluation of human diaphragm fatigue. J. Appl. Physiol. 1982, 53, 1196–1206. [Google Scholar] [CrossRef]
- Bigland-Ritchie, B.; Donovan, E.F.; Roussos, C.S. Conduction velocity and EMG power spectrum changes in fatigue of sustained maximal efforts. J. Appl. Physiol. 1981, 51, 1300–1305. [Google Scholar] [CrossRef]
- Gross, D.; Grassino, A.; Ross, W.R.; Macklem, P.T. Electromyogram pattern of diaphragmatic fatigue. J. Appl. Physiol. 1979, 46, 1–7. [Google Scholar] [CrossRef]
- Schweitzer, T.W.; Fitzgerald, J.W.; Bowden, J.A.; Lynne-Davies, P. Spectral analysis of human inspiratory diaphragmatic electromyograms. J. Appl. Physiol. 1979, 46, 152–165. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.Y.; Shin, K.Y.; Kim, H.S.; Mun, J.H. Estimating muscle fatigue of the biceps brachii using high to low band ratio in EMG during isotonic exercise. Int. J. Precis. Eng. Man. 2009, 10, 147–153. [Google Scholar] [CrossRef]
- Dimitrov, G.V.; Arabadzhiev, T.I.; Hogrel, J.Y.; Dimitrova, N.A. Simulation analysis of interference EMG during fatiguing voluntary contractions. Part II—Changes in amplitude and spectral characteristics. J. Electromyogr. Kinesiol. 2008, 18, 35–43. [Google Scholar] [CrossRef] [PubMed]
- Farina, D.; Fattorini, L.; Felici, F.; Filligoi, G. Nonlinear surface EMG analysis to detect changes of motor unit conduction velocity and synchronization. J. Appl. Physiol. 2002, 93, 1753–1763. [Google Scholar] [CrossRef]
- Au, A.K.; Keir, P.J. Interfering effects of multitasking on muscle activity in the upper extremity. J. Electromyogr. Kinesiol. 2007, 17, 578–586. [Google Scholar] [CrossRef]
- Carvalho, J.L.A.; Rocha, A.F.; Junqueira, L.F.; Neto, J.S.; Nascimento, F.A.O. A tool for time-frequency analysis of heart rate variability. In Proceedings of the 25th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (IEEE Cat. No.03CH37439), Cancun, Mexico, 17–21 September 2003; IEEE: New York, NY, USA, 2004. [Google Scholar] [CrossRef]
- Dolan, P.; Mannion, A.F.; Adams, M.A. Fatigue of the erector spinae muscles. A quantitative assessment using “frequency banding” of the surface electromyography signal. Spine 1995, 20, 149–159. [Google Scholar] [CrossRef]
- Maisetti, O.; Guével, A.; Legros, P.; Hogrel, J.Y. Prediction of endurance capacity of quadriceps muscles in humans using surface electromyogram spectrum analysis during submaximal voluntary isometric contractions. Eur. J. Appl. Physiol. 2002, 87, 509–519. [Google Scholar] [CrossRef]
- Esau, S.A.; Bellemare, F.; Grassino, A.; Permutt, S.; Roussos, C.; Pardy, R.L. Changes in relaxation rate with diaphragmatic fatigue in humans. J. Appl. Physiol. 1983, 54, 1353–1360. [Google Scholar] [CrossRef]
- Karthick, P.A.; Ramakrishnan, S. Muscle fatigue analysis using surface EMG signals and time–frequency based medium-to-low band power ratio. Electron. Lett. 2016, 52, 185–186. [Google Scholar] [CrossRef]
- von Tscharner, V.; Ullrich, M.; Mohr, M.; Comaduran Marquez, D.; Nigg, B.M. Beta, gamma band, and high-frequency coherence of EMGs of vasti muscles caused by clustering of motor units. Exp. Brain Res. 2018, 236, 3065–3075. [Google Scholar] [CrossRef]
- Lowery, M.M.; Vaughan, C.L.; Nolan, P.J.; O’Malley, M.J. Spectral compression of the electromyographic signal due to decreasing muscle fiber conduction velocity. IEEE T. Rehabil. Eng. 2000, 8, 353–361. [Google Scholar] [CrossRef] [PubMed]
- Moxham, J.; Edwards, R.H.T.; Aubier, M.; Troyer, D.; Farkas, G.; Macklem, P.T.; Roussos, C. Changes in EMG power spectrum (high-to-low ratio) with force fatigue in humans. J. Appl. Physiol. 1982, 53, 1094–1099. [Google Scholar] [CrossRef]
- Yassierli, M.A.; Nussbaum, M.A. Utility of traditional and alternative EMG-based measures of fatigue during low-moderate level isometric efforts. J. Electromyogr. Kinesiol. 2008, 18, 44–53. [Google Scholar] [CrossRef] [PubMed]
- Hintze, J. Power Analysis & Sample Size (PASS) 2020. Available online: https://www.ncss.com/software/pass/ (accessed on 4 April 2020).
- Dark, A.; Ginn, K.A.; Halaki, M. Shoulder muscle recruitment patterns during commonly used rotator cuff exercises: An electromyographic study. Phys. Ther. 2007, 87, 1039–1046. [Google Scholar] [CrossRef] [PubMed]
- Seth, A.; Dong, M.; Matias, R.; Delp, S. Muscle Contributions to upper-extremity movement and work from a musculoskeletal model of the human shoulder. Front. Neurorobot. 2019, 13, 90. [Google Scholar] [CrossRef]
- Perotto, A.O. Anatomical Guide for the Electromyographer: The Limbs and Trunk, 5th ed.; Charles, C. Thomas: Springfield, IL, USA, 2016. [Google Scholar]
- Reese, N.B.; Bandy, W.D. Joint Range of Motion and Muscle Length Testing, 3rd ed.; Elsevier: St. Louis, MO, USA, 2017. [Google Scholar]
- Kumar, S. Biomichanics in Ergonomics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Gagey, O.; Hue, E. Mechanics of the deltoid muscle: A new approach. Clin. Orthop. Relat. R. 2000, 375, 250–257. [Google Scholar] [CrossRef]
- Hecker, A.; Aguirre, J.; Eichenberger, U.; Rosner, J.; Schubert, M.; Sutter, R.; Wieser, K.; Bouaicha, S. Deltoid muscle contribution to shoulder flexion and abduction strength—An experimental approach. J. Shoulder Elb. Surg. 2021, 30, e60–e68. [Google Scholar] [CrossRef]
- Escamilla, R.F.; Yamashiro, K.; Paulos, L.; Andrews, J.R. Shoulder muscle activity and function in common shoulder rehabilitation exercises. Sports Med. 2009, 39, 663–685. [Google Scholar] [CrossRef]
- Peterson, S.L.; Rayan, G.M. Shoulder and upper arm muscle architecture. J. Hand Surg. Am. 2011, 36, 881–889. [Google Scholar] [CrossRef]
- Blache, Y.; Dal Maso, F.; Desmoulins, L.; Plamondon, A.; Begon, M. Superficial shoulder muscle co-activations during lifting tasks: Influence of lifting height, weight and phase. J. Electromyogr. Kinesiol. 2015, 25, 355–362. [Google Scholar] [CrossRef]
- Jakobsen, M.D.; Sundstrup, E.; Andersen, C.H.; Zebis, M.K.; Mortensen, P.; Andersen, L.L. Evaluation of muscle activity during a standardized shoulder resistance training bout in novice individuals. J. Strength Cond. Res. 2012, 26, 2515–2522. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hermens, H.J.; Freriks, B.; Disselhorst-Klug, C.; Rau, G. Development of recommendations for SEMG sensors and sensor placement procedures. J. Electromyogr. Kinesiol. 2000, 10, 361–374. [Google Scholar] [CrossRef]
- Åstrand, P.O.; Rodahl, K. Textbook of Work Physiology: Physiological Bases of Exercise, 3rd ed.; McGraw-Hill: New York, NY, USA, 1986. [Google Scholar]
- Nardo, F.D.; Basili, T.; Meletani, S.; Scaradozzi, D. Wavelet-based assessment of the muscle-activation frequency range by EMG analysis. IEEE Access 2022, 10, 9793–9805. [Google Scholar] [CrossRef]
- Li, N.; Zhou, R.; Krishna, B.; Pradhan, A.; Lee, H.; He, J.; Jiang, N. Non-invasive techniques for muscle fatigue monitoring: A comprehensive survey. ACM Comput. Surv. 2024, 56, 1–40. [Google Scholar] [CrossRef]
- Kim, J.Y.; Park, J.S.; Kim, D.J.; Im, S. Evaluation of fatigue patterns in individual shoulder muscles under various external conditions. Appl. Ergon. 2021, 91, 103280. [Google Scholar] [CrossRef]
- Kumar, S.; Amell, T.; Narayan, Y.; Prasad, N. Indices of Muscle Fatigue. In Proceedings of the Human Factors and Ergonomics Society, 4th Annual Meeting 2019, Seattle, WA, USA, 28 October–1 November 2019. [Google Scholar]
- Öberg, T.; Sandsjö, L.; Kadefors, R. EMG mean power frequency: Obtaining a reference value. Clin. Biomech. 1994, 9, 253–257. [Google Scholar] [CrossRef]
- Szucs, K.; Navalgund, A.; Borstad, J.D. Scapular muscle activation and co-activation following a fatigue task. Med. Biol. Eng. 2009, 47, 487–495. [Google Scholar] [CrossRef]
- Minning, S.; Eliot, C.A.; Uhl, T.L.; Malone, T.R. EMG analysis of shoulder muscle fatigue during resisted isometric shoulder elevation. J. Electromyogr. Kinesiol. 2007, 17, 153–159. [Google Scholar] [CrossRef]
- Ebaugh, D.D.; McClure, P.W.; Karduna, A.R. Effects of shoulder muscle fatigue caused by repetitive overhead activities on scapulothoracic and glenohumeral kinematics. J. Electromyogr. Kinesiol. 2006, 16, 224–235. [Google Scholar] [CrossRef]
- Wattanaprakornkul, D.; Cathers, I.; Halaki, M.; Ginn, K.A. The rotator cuff muscles have a direction specific recruitment pattern during shoulder flexion and extension exercises. J. Sci. Med. Sport 2011, 14, 376–382. [Google Scholar] [CrossRef]
- Cardozo, A.C.; Gonçalves, M.; Dolan, P. Back extensor muscle fatigue at submaximal workloads assessed using frequency banding of the electromyographic signal. Clin. Biomech. 2011, 26, 971–976. [Google Scholar] [CrossRef]

 indicates conditions with a <10% decrease in each parameter value;
indicates conditions with a <10% decrease in each parameter value;  indicates conditions with a 10–19% reduction in each parameter value;
indicates conditions with a 10–19% reduction in each parameter value;  indicates conditions with a 20–29% decrease in each parameter value; and
indicates conditions with a 20–29% decrease in each parameter value; and  indicates conditions with a ≥30% decrease in each parameter value).
indicates conditions with a ≥30% decrease in each parameter value).
 indicates conditions with a <10% decrease in each parameter value;
indicates conditions with a <10% decrease in each parameter value;  indicates conditions with a 10–19% reduction in each parameter value;
indicates conditions with a 10–19% reduction in each parameter value;  indicates conditions with a 20–29% decrease in each parameter value; and
indicates conditions with a 20–29% decrease in each parameter value; and  indicates conditions with a ≥30% decrease in each parameter value).
indicates conditions with a ≥30% decrease in each parameter value).| Muscle | %MVC | Parameter | Time (s) | Mean (SD) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | ||||
| Mid-deltoid | 30% | MPF | 0.93 | 0.97 | 1.01 | 0.92 | 0.99 | 0.99 | 0.91 | 0.86 | 0.97 (0.04) |
| M/LFB | 0.87 | 0.85 | 0.88 | 0.82 | 0.73 | 0.77 | 0.77 | 0.61 | 0.80 (0.08) | ||
| H/MFB | 1.08 | 0.93 | 0.88 | 0.90 | 0.87 | 0.80 | 0.75 | 0.79 | 0.89 (0.12) | ||
| H/LFB | 0.94 | 0.80 | 0.78 | 0.74 | 0.64 | 0.62 | 0.57 | 0.48 | 0.72 (0.14) | ||
| H/(M + L)/FB | 1.03 | 0.88 | 0.84 | 0.84 | 0.78 | 0.73 | 0.68 | 0.65 | 0.82 (0.13) | ||
| (H + M)/LFB | 0.89 | 0.84 | 0.86 | 0.80 | 0.71 | 0.74 | 0.72 | 0.58 | 0.78 (0.09) | ||
| 40% | MPF | 1.02 | 1.11 | 1.06 | 1.21 | 1.24 | 1.26 | 1.31 | 1.31 | 0.96 (0.08) | |
| M/LFB | 1.01 | 0.92 | 0.94 | 0.89 | 0.96 | 0.90 | 0.90 | 0.89 | 0.81 (0.07) | ||
| H/MFB | 0.87 | 0.70 | 0.66 | 0.62 | 0.58 | 0.53 | 0.51 | 0.50 | 0.83 (0.13) | ||
| H/LFB | 1.00 | 0.84 | 0.78 | 0.82 | 0.74 | 0.73 | 0.71 | 0.71 | 0.67 (0.14) | ||
| H/(M + L)/FB | 0.92 | 1.11 | 1.06 | 0.97 | 0.93 | 1.06 | 0.98 | 0.85 | 0.76 (0.13) | ||
| (H + M)/LFB | 1.07 | 1.17 | 1.12 | 1.11 | 1.16 | 1.04 | 1.23 | 1.49 | 0.78 (0.08) | ||
| 50% | MPF | 0.96 | 1.05 | 1.08 | 1.14 | 1.14 | 1.12 | 1.10 | 1.19 | 0.97 (0.08) | |
| M/LFB | 0.99 | 0.92 | 0.95 | 0.88 | 0.96 | 0.88 | 0.90 | 1.16 | 0.96 (0.09) | ||
| H/MFB | 0.91 | 0.82 | 0.73 | 0.74 | 0.54 | 0.69 | 0.59 | 0.52 | 0.72 (0.11) | ||
| H/LFB | 1.01 | 0.89 | 0.76 | 0.76 | 0.72 | 0.87 | 0.71 | 0.77 | 0.69 (0.14) | ||
| H/(M + L)/FB | 0.75 | 0.90 | 0.77 | 0.74 | 0.69 | 0.60 | 0.60 | 0.65 | 0.71 (0.12) | ||
| (H + M)/LFB | 0.91 | 0.84 | 0.89 | 0.92 | 0.76 | 0.85 | 0.76 | 1.09 | 0.90 (0.10) | ||
| Pectoralis major | 30% | MPF | 0.89 | 0.98 | 1.10 | 1.16 | 1.18 | 1.21 | 1.36 | 1.38 | 1.13 (0.14) |
| M/LFB | 0.99 | 0.95 | 0.99 | 1.04 | 1.12 | 0.98 | 1.06 | 1.07 | 1.02 (0.06) | ||
| H/MFB | 0.94 | 1.11 | 0.98 | 0.89 | 1.04 | 1.19 | 1.08 | 1.098 | 1.04 (0.11) | ||
| H/LFB | 0.93 | 1.06 | 0.96 | 0.93 | 1.17 | 1.16 | 1.14 | 1.17 | 1.06 (0.12) | ||
| H/(M + L)/FB | 0.93 | 1.08 | 0.97 | 0.91 | 1.11 | 1.17 | 1.12 | 1.13 | 1.05 (0.11) | ||
| (H + M)/LFB | 0.98 | 0.97 | 0.98 | 1.02 | 1.13 | 1.00 | 1.07 | 1.08 | 1.02 (0.06) | ||
| 40% | MPF | 1.01 | 0.92 | 0.94 | 0.89 | 0.96 | 0.90 | 0.90 | 0.89 | 1.09 (0.10) | |
| M/LFB | 0.92 | 1.11 | 1.06 | 0.97 | 0.93 | 1.06 | 0.98 | 0.85 | 1.04 (0.07) | ||
| H/MFB | 1.07 | 1.17 | 1.12 | 1.11 | 1.16 | 1.04 | 1.23 | 1.49 | 1.15 (0.12) | ||
| H/LFB | 0.93 | 0.92 | 0.95 | 1.03 | 0.98 | 0.93 | 1.07 | 0.94 | 1.19 (0.13) | ||
| H/(M + L)/FB | 0.83 | 0.74 | 0.72 | 0.74 | 0.73 | 0.81 | 0.68 | 0.71 | 1.18 (0.12) | ||
| (H + M)/LFB | 1.04 | 0.83 | 0.82 | 0.80 | 0.83 | 0.81 | 0.81 | 0.81 | 1.06 (0.07) | ||
| 50% | MPF | 0.99 | 0.92 | 0.95 | 0.88 | 0.96 | 0.88 | 0.90 | 1.16 | 0.99 (0.10) | |
| M/LFB | 0.75 | 0.90 | 0.77 | 0.74 | 0.69 | 0.60 | 0.60 | 0.65 | 0.91 (0.07) | ||
| H/MFB | 0.91 | 0.84 | 0.89 | 0.92 | 0.76 | 0.85 | 0.76 | 1.09 | 0.90 (0.08) | ||
| H/LFB | 0.85 | 0.90 | 0.85 | 0.87 | 1.06 | 0.97 | 0.96 | 1.27 | 0.82 (0.08) | ||
| H/(M + L)/FB | 1.04 | 0.96 | 0.94 | 0.92 | 0.78 | 0.91 | 0.84 | 0.79 | 0.93 (0.07) | ||
| (H + M)/LFB | 1.02 | 0.93 | 0.87 | 0.87 | 0.83 | 0.82 | 0.73 | 0.83 | 0.90 (0.07) | ||
| Upper trapezius | 30% | MPF | 0.92 | 1.00 | 1.06 | 0.93 | 0.97 | 1.01 | 1.04 | 1.10 | 1.01 (0.05) |
| M/LFB | 1.05 | 0.89 | 0.96 | 0.88 | 0.87 | 0.85 | 0.84 | 0.80 | 0.93 (0.10) | ||
| H/MFB | 1.01 | 1.07 | 0.99 | 0.90 | 0.91 | 0.85 | 0.89 | 0.85 | 0.93 (0.06) | ||
| H/LFB | 1.06 | 0.95 | 0.95 | 0.79 | 0.79 | 0.73 | 0.75 | 0.68 | 0.87 (0.12) | ||
| H/(M + L)/FB | 1.03 | 1.03 | 0.97 | 0.86 | 0.86 | 0.81 | 0.84 | 0.79 | 0.91 (0.08) | ||
| (H + M)/LFB | 1.05 | 0.91 | 0.96 | 0.86 | 0.85 | 0.82 | 0.82 | 0.77 | 0.91 (0.10) | ||
| 40% | MPF | 0.93 | 0.92 | 0.95 | 1.03 | 0.98 | 0.93 | 1.07 | 0.94 | 1.17 (0.11) | |
| M/LFB | 0.96 | 0.82 | 0.73 | 0.70 | 0.70 | 0.71 | 0.69 | 0.65 | 0.87 (0.08) | ||
| H/MFB | 0.97 | 1.00 | 1.02 | 1.07 | 1.04 | 1.03 | 0.91 | 1.06 | 0.94 (0.05) | ||
| H/LFB | 1.09 | 1.00 | 0.98 | 0.86 | 0.99 | 0.97 | 0.84 | 0.94 | 0.81 (0.09) | ||
| H/(M + L)/FB | 0.98 | 0.83 | 0.80 | 0.72 | 0.68 | 0.56 | 0.61 | 0.58 | 0.89 (0.06) | ||
| (H + M)/LFB | 0.96 | 0.96 | 0.88 | 0.95 | 0.82 | 0.82 | 0.80 | 0.79 | 0.85 (0.08) | ||
| 50% | MPF | 0.85 | 0.90 | 0.85 | 0.87 | 1.06 | 0.97 | 0.96 | 1.27 | 1.09 (0.06) | |
| M/LFB | 0.95 | 0.82 | 0.84 | 0.84 | 0.74 | 0.67 | 0.67 | 0.62 | 0.88 (0.11) | ||
| H/MFB | 0.89 | 0.93 | 0.90 | 1.01 | 0.98 | 0.95 | 1.07 | 0.80 | 0.92 (0.07) | ||
| H/LFB | 1.17 | 1.03 | 1.12 | 1.01 | 0.91 | 0.91 | 0.94 | 0.91 | 0.80 (0.10) | ||
| H/(M + L)/FB | 0.87 | 0.82 | 0.73 | 0.75 | 0.59 | 0.70 | 0.62 | 0.57 | 0.88 (0.07) | ||
| (H + M)/LFB | 1.00 | 0.93 | 0.81 | 0.81 | 0.80 | 0.99 | 0.87 | 0.85 | 0.86 (0.10) | ||
| Source | Variables | SS | df | MS | F | p |
|---|---|---|---|---|---|---|
| %MVC | MPF | 0.709 | 2 | 0.354 | 63.206 | 0.001 |
| M/LFB | 0.057 | 2 | 0.028 | 3.239 | 0.040 | |
| H/MFB | 1.141 | 2 | 0.570 | 45.684 | 0.001 | |
| H/LFB | 0.111 | 2 | 0.056 | 3.328 | 0.036 | |
| H/(M + L)FB | 0.698 | 2 | 0.349 | 27.610 | 0.001 | |
| (H + M)/LFB | 0.020 | 2 | 0.010 | 1.124 | 0.326 | |
| Muscle | MPF | 0.920 | 2 | 0.460 | 82.006 | 0.001 |
| M/LFB | 1.300 | 2 | 0.650 | 74.062 | 0.001 | |
| H/MFB | 16.966 | 2 | 8.483 | 679.477 | 0.001 | |
| H/LFB | 11.543 | 2 | 5.772 | 345.082 | 0.001 | |
| H/(M + L)FB | 7.282 | 2 | 3.641 | 287.965 | 0.001 | |
| (H + M)/LFB | 0.712 | 2 | 0.356 | 39.308 | 0.001 | |
| %MVC × Muscle | MPF | 0.728 | 4 | 0.182 | 32.447 | 0.001 |
| M/LFB | 2.395 | 4 | 0.599 | 68.198 | 0.001 | |
| H/MFB | 2.222 | 4 | 0.556 | 44.498 | 0.001 | |
| H/LFB | 0.377 | 4 | 0.094 | 5.639 | 0.001 | |
| H/(M + L)FB | 0.536 | 4 | 0.134 | 10.589 | 0.001 | |
| (H + M)/LFB | 2.302 | 4 | 0.576 | 63.531 | 0.001 |
| %MVC | Muscle | Parameters | Slope | Intercept | Standardized Coefficients | R2 | 95% CI | |
|---|---|---|---|---|---|---|---|---|
| Low | High | |||||||
| 30% MVC | Mid- deltoid | M/LFB | −0.004 | 0.895 | −0.694 | 0.481 | 0.895 | 0.932 |
| H/MFB | −0.009 | 1.079 | −0.915 | 0.837 | 1.047 | 1.111 | ||
| H/LFB | −0.011 | 0.953 | −0.931 | 0.866 | 0.918 | 0.988 | ||
| H/(M + L)FB | −0.010 | 1.034 | −0.943 | 0.890 | 1.006 | 0.062 | ||
| Pectoralis major | M/LFB | 0.002 | 0.985 | 0.302 | 0.091 | 0.948 | 1.022 | |
| H/MFB | 0.006 | 0.927 | 0.626 | 0.392 | 0.872 | 0.982 | ||
| H/LFB | 0.007 | 0.910 | 0.722 | 0.521 | 0.895 | 0.965 | ||
| H/(M + L)FB | 0.007 | 0.916 | 0.710 | 0.504 | 0.865 | 0.968 | ||
| Upper trapezius | M/LFB | −0.006 | 1.059 | −0.775 | 0.601 | 1.019 | 1.099 | |
| H/MFB | −0.003 | 0.999 | −0.586 | 0.343 | 0.965 | 1.033 | ||
| H/LFB | −0.009 | 1.051 | −0.874 | 0.765 | 1.013 | 1.089 | ||
| H/(M + L)FB | −0.005 | 1.015 | −0.797 | 0.635 | 0.985 | 1.045 | ||
| 40% MVC | Mid- deltoid | M/LFB | −0.004 | 1.049 | −0.531 | 0.282 | 1.003 | 1.095 |
| H/MFB | −0.010 | 1.035 | −0.924 | 0.854 | 1.003 | 1.067 | ||
| H/LFB | −0.006 | 0.945 | −0.848 | 0.718 | 0.914 | 0.977 | ||
| H/(M + L)FB | −0.005 | 1.071 | −0.528 | 0.279 | 1.015 | 1.127 | ||
| Pectoralis major | M/LFB | −0.005 | 1.071 | −0.528 | 0.279 | 1.015 | 1.127 | |
| H/MFB | 0.007 | 1.015 | 0.627 | 0.393 | 0.952 | 1.079 | ||
| H/LFB | 0.001 | 0.947 | 0.302 | 0.091 | 0.912 | 0.982 | ||
| H/(M + L)FB | −0.005 | 0.889 | −0.820 | 0.672 | 0.859 | 0.918 | ||
| Upper trapezius | M/LFB | −0.009 | 0.951 | −0.902 | 0.814 | 0.919 | 0.983 | |
| H/MFB | −0.003 | 0.999 | −0.663 | 0.440 | 0.973 | 1.026 | ||
| H/LFB | −0.005 | 1.104 | −0.690 | 0.477 | 1.062 | 1.145 | ||
| H/(M + L)FB | −0.011 | 0.983 | −0.960 | 0.921 | 0.958 | 1.007 | ||
| 50% MVC | Mid- deltoid | M/LFB | −0.002 | 0.994 | −0.217 | 0.047 | 0.941 | 1.047 |
| H/MFB | −0.008 | 0.886 | −0.887 | 0.787 | 0.853 | 0.919 | ||
| H/LFB | −0.006 | 0.936 | −0.717 | 0.514 | 0.888 | 0.985 | ||
| H/(M + L)FB | −0.007 | 0.889 | −0.802 | 0.643 | 0.848 | 0.930 | ||
| Pectoralis major | M/LFB | −0.007 | 0.889 | −0.802 | 0.643 | 0.848 | 0.93 | |
| H/MFB | 0.001 | 0.891 | 0.050 | 0.003 | 0.836 | 0.946 | ||
| H/LFB | 0.004 | 0.863 | 0.552 | 0.305 | 0.814 | 0.913 | ||
| H/(M + L)FB | −0.007 | 1.033 | −0.797 | 0.636 | 0.994 | 1.071 | ||
| Upper trapezius | M/LFB | −0.010 | 0.976 | −0.929 | 0.863 | 0.946 | 1.005 | |
| H/MFB | −0.001 | 0.935 | −0.144 | 0.021 | 0.892 | 0.979 | ||
| H/LFB | −0.006 | 1.142 | −0.727 | 0.528 | 1.098 | 1.186 | ||
| H/(M + L)FB | −0.010 | 0.903 | −0.924 | 0.853 | 0.872 | 0.934 | ||
| Muscle | %MVC | MPF | M/LFB | H/LFB | H/MFB | H/(M + L)FB | (H + M)/LFB |
|---|---|---|---|---|---|---|---|
| Mid- deltoid | 30% | Decreased | Decreased | Decreased | Decreased | Decreased | Decreased |
| 40% | N/A | Decreased | Decreased | Decreased | Slightly decreased | N/A | |
| 50% | N/A | Decreased | Decreased | Decreased | Decreased | N/A | |
| Pectoralis major | 30% | N/A | N/A | N/A | N/A | N/A | N/A |
| 40% | Decreased | Decreased | N/A | N/A | Decreased | Decreased | |
| 50% | N/A | Decreased | N/A | N/A | Decreased | Decreased | |
| Upper trapezius | 30% | N/A | Decreased | Decreased | Decreased | Decreased | Decreased |
| 40% | Slightly decreased | Decreased | N/A | N/A | Decreased | Decreased | |
| 50% | Slightly decreased | Decreased | N/A | N/A | Decreased | Decreased |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.S.; Jung, M.-C.; Kim, J.Y.; Mo, S.-M. Developing Synthetic Parameters Using Frequency Band Ratios for Muscle Fatigue Analysis During Isometric Contractions by Using Shoulder Muscles. Sensors 2025, 25, 2191. https://doi.org/10.3390/s25072191
Park JS, Jung M-C, Kim JY, Mo S-M. Developing Synthetic Parameters Using Frequency Band Ratios for Muscle Fatigue Analysis During Isometric Contractions by Using Shoulder Muscles. Sensors. 2025; 25(7):2191. https://doi.org/10.3390/s25072191
Chicago/Turabian StylePark, Ji Soo, Myung-Chul Jung, Jung Yong Kim, and Seung-Min Mo. 2025. "Developing Synthetic Parameters Using Frequency Band Ratios for Muscle Fatigue Analysis During Isometric Contractions by Using Shoulder Muscles" Sensors 25, no. 7: 2191. https://doi.org/10.3390/s25072191
APA StylePark, J. S., Jung, M.-C., Kim, J. Y., & Mo, S.-M. (2025). Developing Synthetic Parameters Using Frequency Band Ratios for Muscle Fatigue Analysis During Isometric Contractions by Using Shoulder Muscles. Sensors, 25(7), 2191. https://doi.org/10.3390/s25072191






