Federated Subgraph Learning via Global-Knowledge-Guided Node Generation
Abstract
1. Introduction
- We propose a novel method called MN-FGAGN, which employs an innovative global generation strategy. This strategy personalizes the injection of global knowledge to eliminate the local biases present in generated data. By enhancing the local node representations and the quality of local data, our approach improves the node classification capability of FGL.
- Our method utilizes the value of the loss function to transmit global knowledge. Compared to transferring data and model parameters, our approach offers enhanced privacy.
- We conducted experiments on four real-world datasets, and our method achieved superior results compared to existing approaches.
2. Related Works
2.1. Federated Learning
2.2. Federated Graph Learning
3. Problem Formulation and Preliminaries
3.1. Graph Neural Network
3.2. Federated Learning of Graph Neural Network
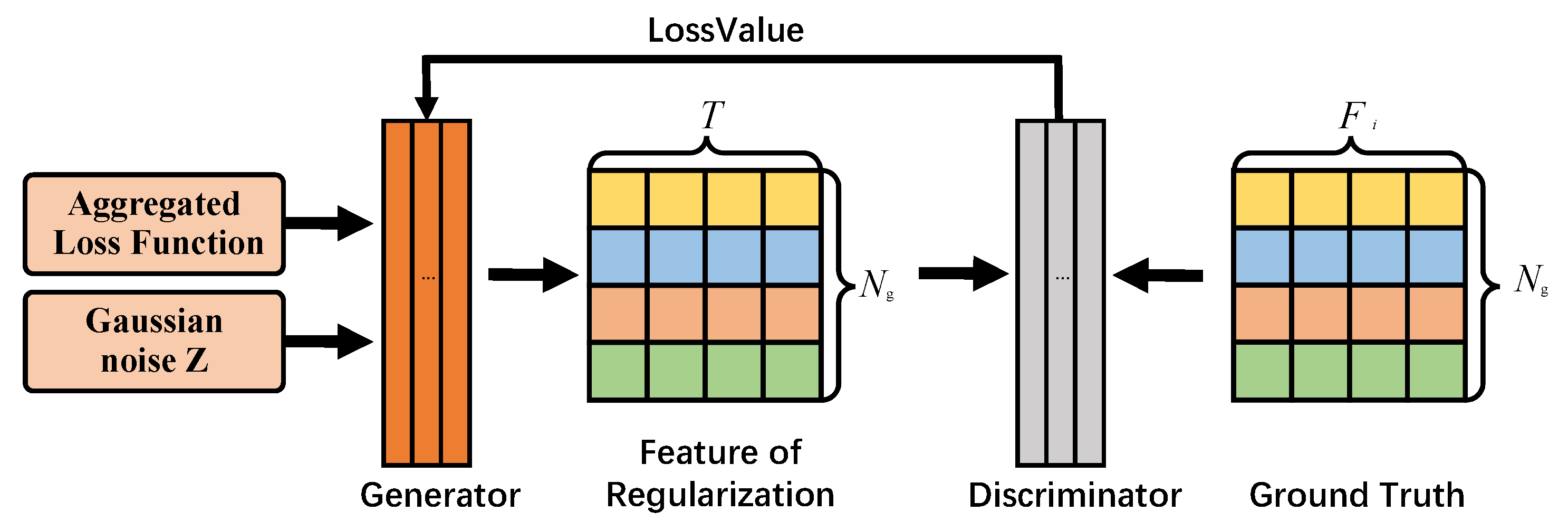
3.3. Generative Adversarial Network
3.4. Problem Setup
- : the union of the node sets of each subgraph is the node set of the global graph.
- : the union of the edge sets of each subgraph and the union of the sets of missing edges between subgraphs form the set of edges of the global graph.
- , if , then : each vertex belongs to only one subset.
- If a and b are nodes at the ends of the missing edge , where edge , node , and node , then nodes a and b are missing nodes for the subgraphs and , respectively.
4. System Model
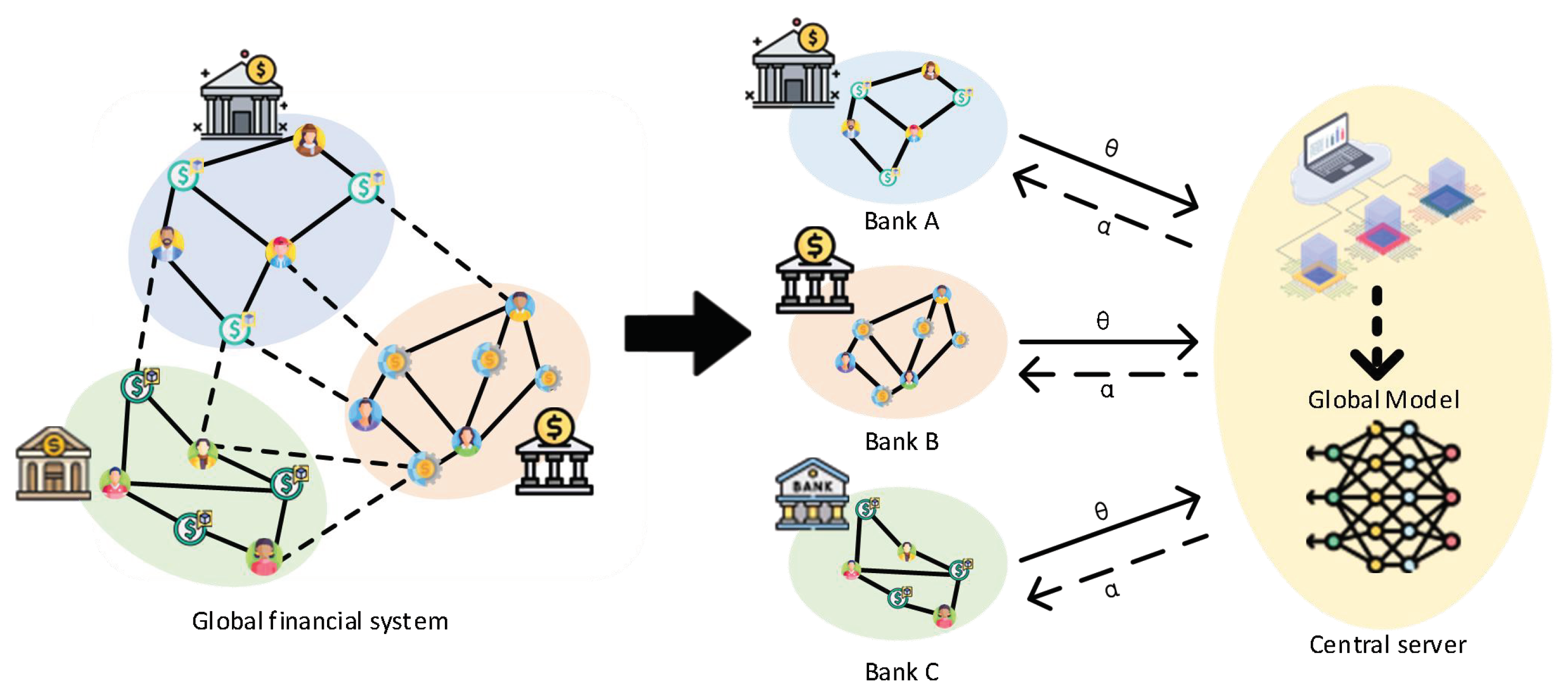
4.1. Overview
4.2. MN-FGAGN
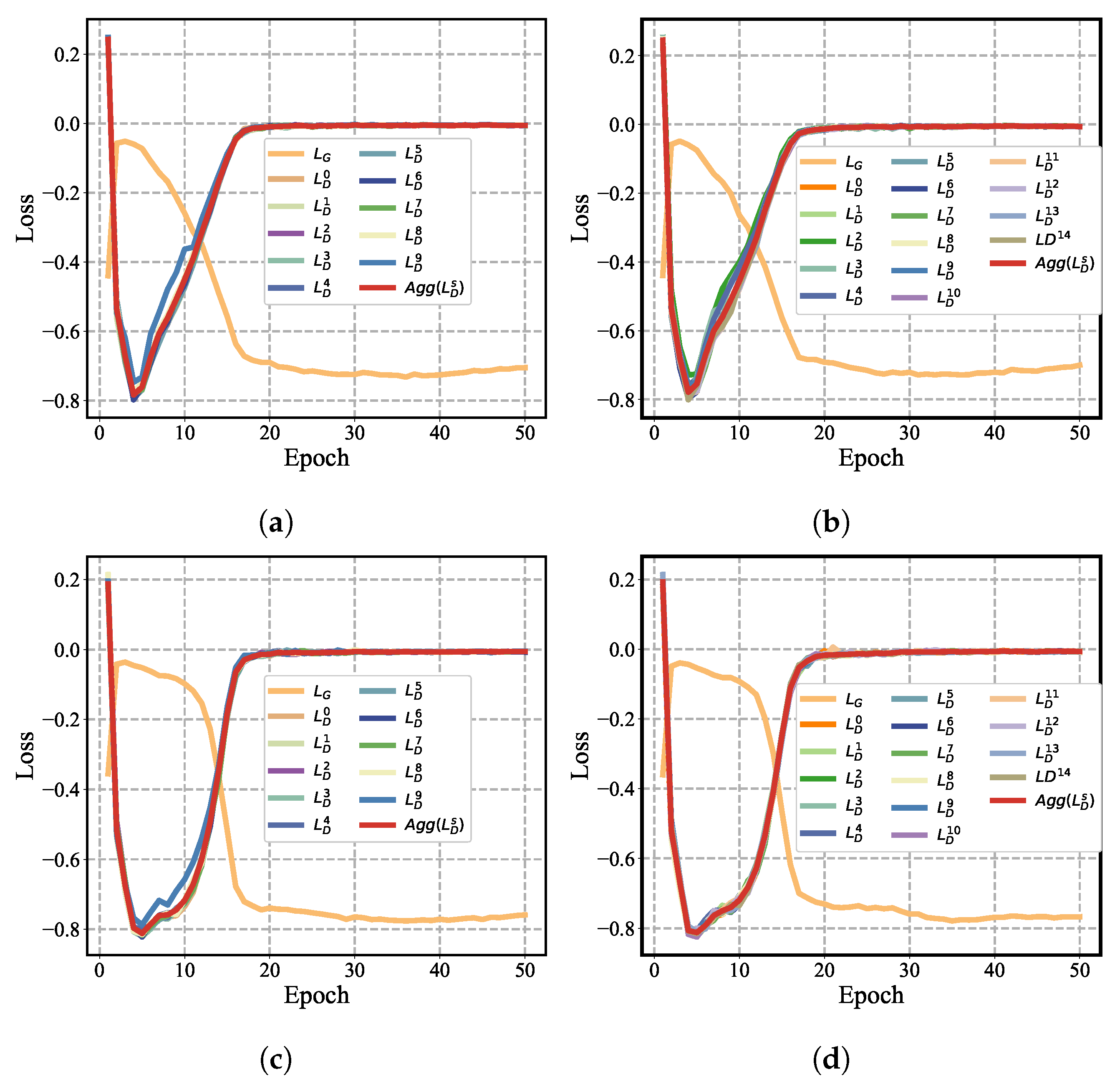
4.3. Regularization
4.4. Classifier Training
4.5. Algorithms
| Algorithm 1: MN-FGAGN algorithm |
 |
4.6. Discussion of MN-FGAGN
4.6.1. Privacy Discussion
4.6.2. Real-World Applications and Impact of MN-FGAGN
4.6.3. Complexity and Scalability Analysis
5. Experiments
5.1. Experimental Setup
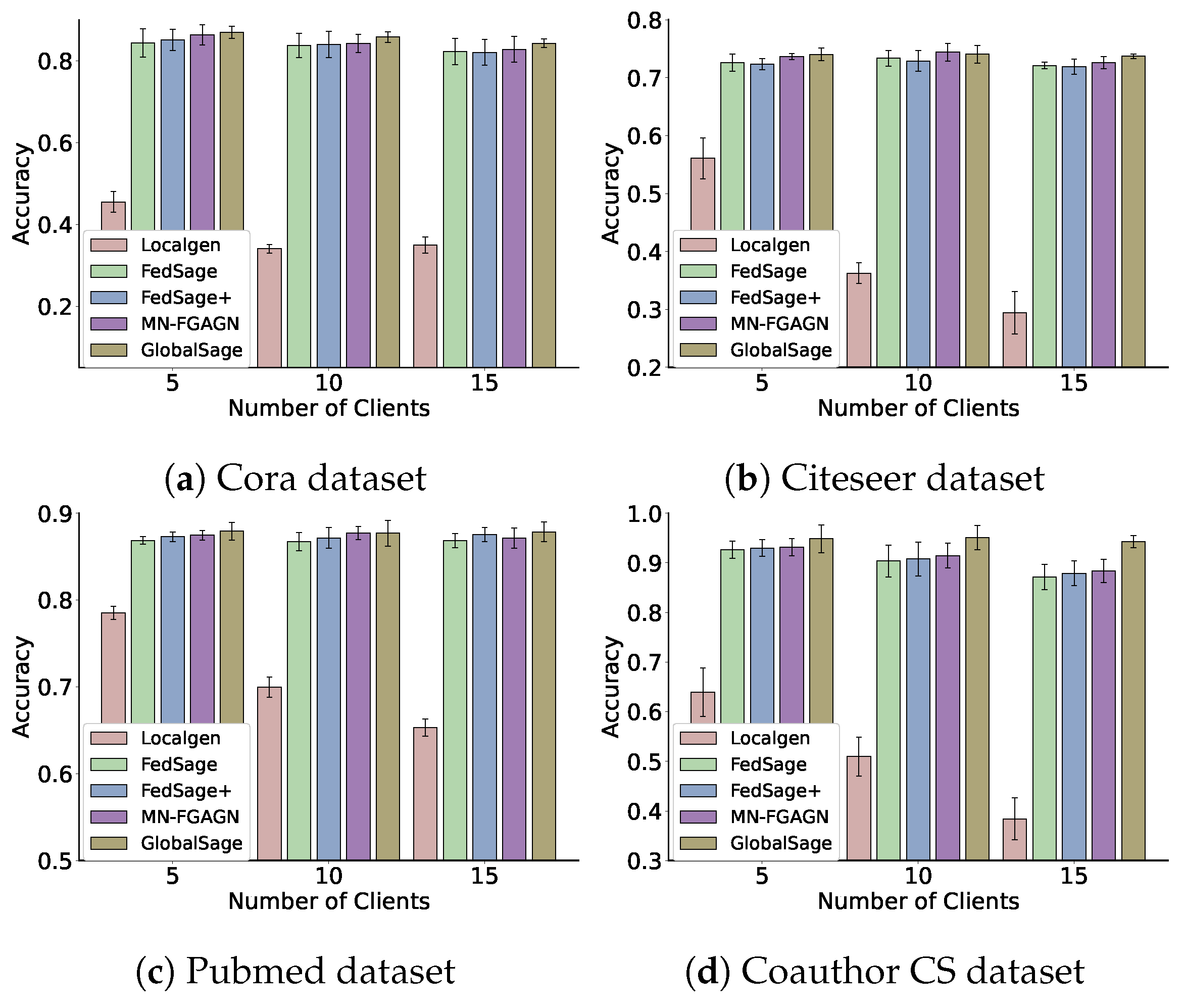
5.2. Comparison with Alternative Methods
- GlobalSage: This method assumes that the data are centralized, and a Global GraphSAGE [43] is trained on the original global graph data, which is constructed similarly to our subgraph construction. The accuracy of this model’s test represents the training accuracy limit of the model.
- Localgen: Localgen first performs local repair on the subgraphs and then evaluates the Local GraphSAGE node classification accuracy using the repaired subgraph data.
- FedSage: This algorithm, based on FedAvg [40], trains a GraphSAGE model to learn node features, edge structures, and task labels for multiple local subgraphs. It employs GraphSAGE as a node classifier. Unlike GCN, which samples all neighboring nodes to obtain node embeddings, GraphSAGE only samples a fixed number of neighbors, significantly reducing memory consumption [50]. FedSage outperforms FedAvg in processing graph data and classifying nodes for graphs.
- FedSage+: As a representative method for subgraph information repair, FedSage+ enhances FedSage by training a generator that creates missing neighbors. It is trained using structurally adjacent devices on the topology to improve the generalization ability of the generator. The generator’s loss function is defined as , where denote the topological adjacency of devices i and j, respectively, and represent the features of the missing nodes for devices i and j, respectively, and denote the degree of missing nodes for devices i and j, respectively, and and represent the labels of the missing information for devices i and j, respectively.
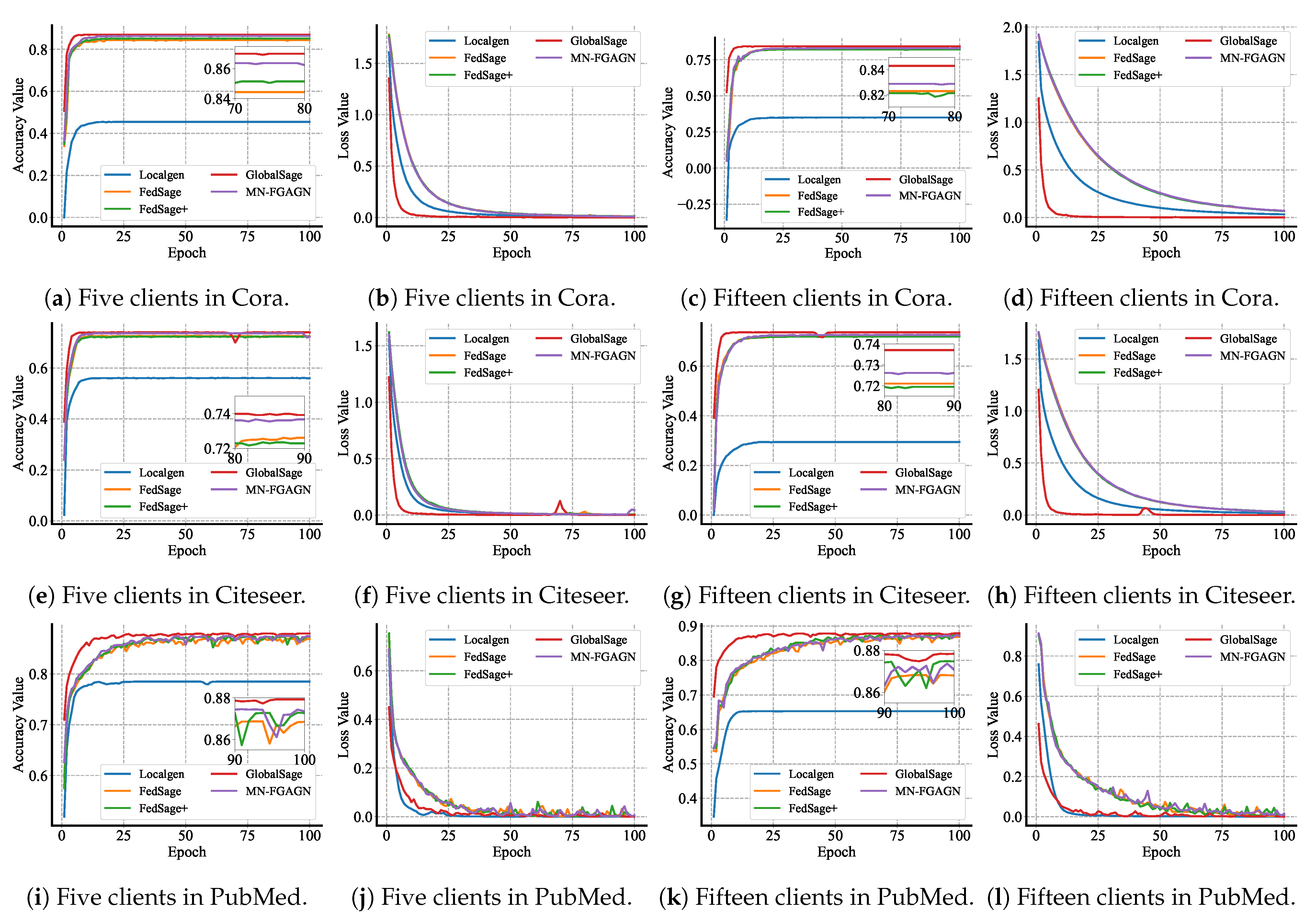
5.3. Performance Evaluation
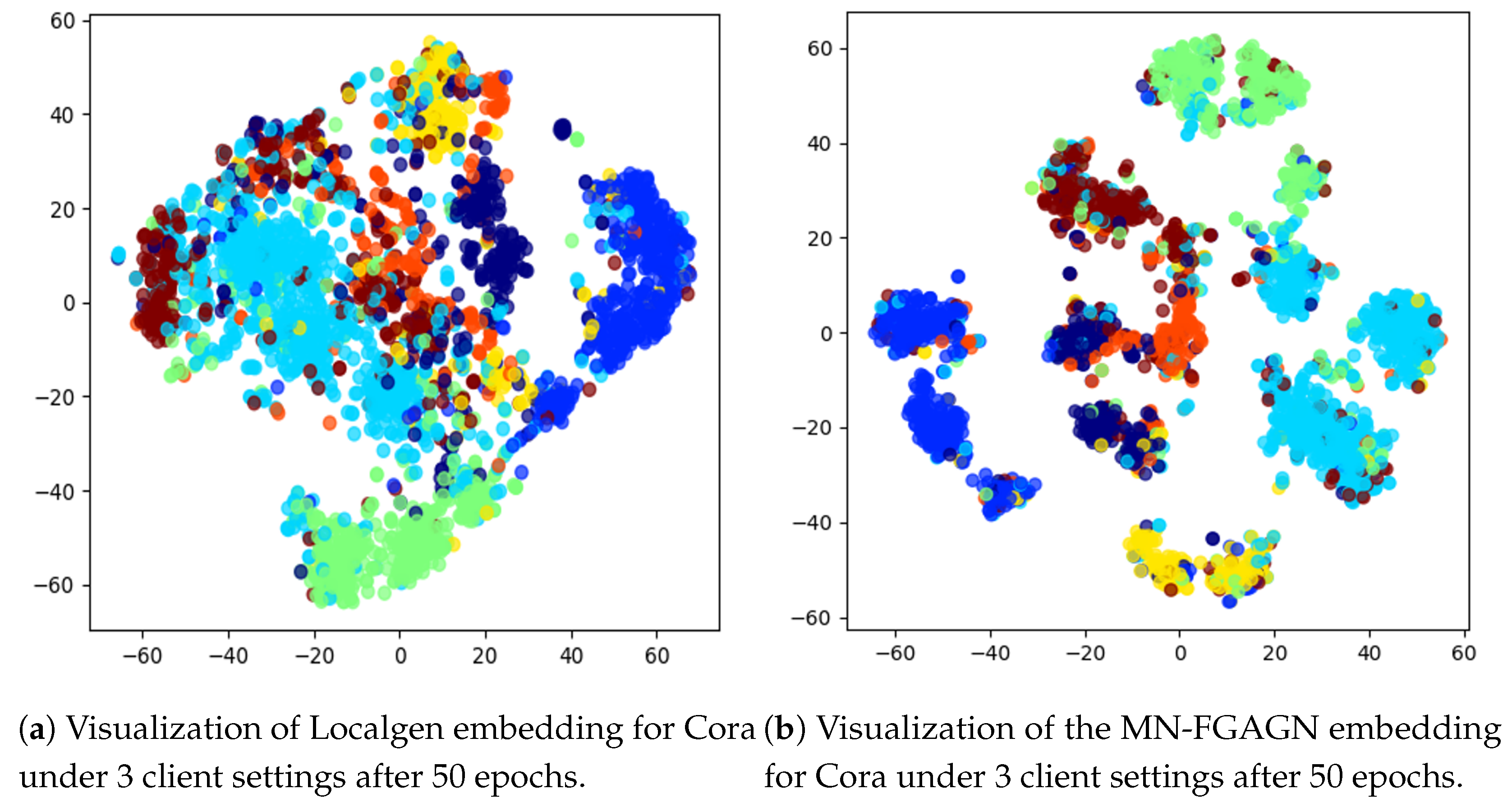
5.4. Ablation Experiment
5.5. Parameters Sensitivity Analysis
- 1.
- Systematic grid search: We tested various values of h (0.1, 0.2, 0.3, …, 1) on multiple datasets and calculated the model’s classification accuracy to determine the optimal range of h.
- 2.
- Stability analysis: To ensure the reliability of the experimental results, we repeated the experiments under different random seeds and data splits to assess whether the effect of h on model performance remained consistent.
- 3.
- Cross-dataset validation: We conducted experiments across multiple datasets to verify the general applicability of the empirical value .
6. Conclusions
7. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Zhou, L.; Zhan, X.; Sun, G.; Liu, Y. 3D mmW sparse imaging via complex-valued composite penalty function within collaborative multitasking framework. Signal Process. 2025, 233, 109939. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Y.; Zhang, C.; Zhan, X.; Sun, G.; Liu, Y.; Mao, Y. Array Three-Dimensional SAR Imaging via Composite Low-Rank and Sparse Prior. Remote Sens. 2025, 17, 321. [Google Scholar] [CrossRef]
- Cruz Castañeda, W.A.; Bertemes Filho, P. Improvement of an Edge-IoT Architecture Driven by Artificial Intelligence for Smart-Health Chronic Disease Management. Sensors 2024, 24, 7965. [Google Scholar] [CrossRef]
- Li, L.; Zhu, L.; Li, W. Cloud–Edge–End Collaborative Federated Learning: Enhancing Model Accuracy and Privacy in Non-IID Environments. Sensors 2024, 24, 8028. [Google Scholar] [CrossRef] [PubMed]
- Sun, R.; Cao, X.; Zhao, Y.; Wan, J.; Zhou, K.; Zhang, F.; Wang, Z.; Zheng, K. Multi-modal knowledge graphs for recommender systems. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, Online, 19–23 October 2020; pp. 1405–1414. [Google Scholar]
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 974–983. [Google Scholar]
- Tang, T.; Han, Z.; Cai, Z.; Yu, S.; Zhou, X.; Oseni, T.; Das, S.K. Personalized Federated Graph Learning on Non-IID Electronic Health Records. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 11843–11856. [Google Scholar] [PubMed]
- Messinis, S.C.; Protonotarios, N.E.; Doulamis, N. Differentially Private Client Selection and Resource Allocation in Federated Learning for Medical Applications Using Graph Neural Networks. Sensors 2024, 24, 5142. [Google Scholar] [CrossRef]
- Cao, M.; Zhang, L.; Cao, B. Toward on-device federated learning: A direct acyclic graph-based blockchain approach. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 2028–2042. [Google Scholar]
- Kong, X.; Zhang, W.; Wang, H.; Hou, M.; Chen, X.; Yan, X.; Das, S.K. Federated graph anomaly detection via contrastive self-supervised learning. IEEE Trans. Neural Netw. Learn. Syst. 2024. [Google Scholar] [CrossRef]
- He, C.; Balasubramanian, K.; Ceyani, E.; Yang, C.; Xie, H.; Sun, L.; He, L.; Yang, L.; Philip, S.Y.; Rong, Y.; et al. Fedgraphnn: A federated learning benchmark system for graph neural networks. arXiv 2021, arXiv:2104.07145. [Google Scholar]
- Wu, Y.; Kang, Y.; Luo, J.; He, Y.; Fan, L.; Pan, R.; Yang, Q. FedCG: Leverage Conditional GAN for Protecting Privacy and Maintaining Competitive Performance in Federated Learning. arXiv 2021, arXiv:2111.08211. [Google Scholar]
- Zhang, K.; Yang, C.; Li, X.; Sun, L.; Yiu, S.M. Subgraph federated learning with missing neighbor generation. Adv. Neural Inf. Process. Syst. 2021, 34, 6671–6682. [Google Scholar]
- Peng, L.; Wang, N.; Dvornek, N.; Zhu, X.; Li, X. Fedni: Federated graph learning with network inpainting for population-based disease prediction. IEEE Trans. Med. Imaging 2022, 42, 2032–2043. [Google Scholar] [CrossRef] [PubMed]
- Ramezani, M.; Cong, W.; Mahdavi, M.; Kandemir, M.T.; Sivasubramaniam, A. Learn locally, correct globally: A distributed algorithm for training graph neural networks. arXiv 2021, arXiv:2111.08202. [Google Scholar]
- Fu, X.; Chen, Z.; Zhang, B.; Chen, C.; Li, J. Federated Graph Learning with Structure Proxy Alignment. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 25–29 August 2024; pp. 827–838. [Google Scholar]
- Tan, Y.; Liu, Y.; Long, G.; Jiang, J.; Lu, Q.; Zhang, C. Federated learning on non-iid graphs via structural knowledge sharing. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 9953–9961. [Google Scholar]
- Wang, H.; Xu, H.; Li, Y.; Xu, Y.; Li, R.; Zhang, T. FedCDA: Federated Learning with Cross-rounds Divergence-aware Aggregation. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Wang, H.; Li, Y.; Xu, W.; Li, R.; Zhan, Y.; Zeng, Z. Dafkd: Domain-aware federated knowledge distillation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 20412–20421. [Google Scholar]
- Liu, Y.; Wang, H.; Wang, S.; He, Z.; Xu, W.; Zhu, J.; Yang, F. Disentangle Estimation of Causal Effects from Cross-Silo Data. In Proceedings of the ICASSP 2024-2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 6290–6294. [Google Scholar]
- Zhukabayeva, T.; Zholshiyeva, L.; Karabayev, N.; Khan, S.; Alnazzawi, N. Cybersecurity Solutions for Industrial Internet of Things–Edge Computing Integration: Challenges, Threats, and Future Directions. Sensors 2025, 25, 213. [Google Scholar] [CrossRef]
- Dong, Y.; Luo, W.; Wang, X.; Zhang, L.; Xu, L.; Zhou, Z.; Wang, L. Multi-Task Federated Split Learning Across Multi-Modal Data with Privacy Preservation. Sensors 2025, 25, 233. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Roosta, F.; Xu, P.; Mahoney, M.W. Giant: Globally improved approximate newton method for distributed optimization. Adv. Neural Inf. Process. Syst. 2018, 31, 1–11. [Google Scholar]
- Smith, V.; Forte, S.; Chenxin, M.; Takáč, M.; Jordan, M.I.; Jaggi, M. CoCoA: A general framework for communication-efficient distributed optimization. J. Mach. Learn. Res. 2018, 18, 230. [Google Scholar]
- Mahajan, D.; Agrawal, N.; Keerthi, S.S.; Sundararajan, S.; Bottou, L. An efficient distributed learning algorithm based on effective local functional approximations. arXiv 2013, arXiv:1310.8418. [Google Scholar]
- Wang, H.; Qu, Z.; Guo, S.; Wang, N.; Li, R.; Zhuang, W. LOSP: Overlap Synchronization Parallel With Local Compensation for Fast Distributed Training. IEEE J. Sel. Areas Commun. 2021, 39, 2541–2557. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, P.; Han, X.; Xu, W.; Li, R.; Zhang, T. FedNLR: Federated Learning with Neuron-wise Learning Rates. In Proceedings of the the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, KDD 2024, Barcelona, Spain, 25–29 August 2024; pp. 3069–3080. [Google Scholar]
- Liu, Z.; Hu, S.; Wu, Z.S.; Smith, V. On privacy and personalization in cross-silo federated learning. arXiv 2022, arXiv:2206.07902. [Google Scholar]
- Bietti, A.; Wei, C.Y.; Dudik, M.; Langford, J.; Wu, S. Personalization improves privacy-accuracy tradeoffs in federated learning. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 1945–1962. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Hospedales, T.; Antoniou, A.; Micaelli, P.; Storkey, A. Meta-learning in neural networks: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 5149–5169. [Google Scholar]
- Zhang, X.; Chen, X.; Hong, M.; Wu, S.; Yi, J. Understanding clipping for federated learning: Convergence and client-level differential privacy. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA , 17–23 July 2022; pp. 26048–26067. [Google Scholar]
- Pan, Q.; Zhu, Y. FedWalk: Communication Efficient Federated Unsupervised Node Embedding with Differential Privacy. arXiv 2022, arXiv:2205.15896. [Google Scholar]
- Marchand, T.; Muzellec, B.; Beguier, C.; du Terrail, J.O.; Andreux, M. SecureFedYJ: A safe feature Gaussianization protocol for Federated Learning. arXiv 2022, arXiv:2210.01639. [Google Scholar]
- Caldarola, D.; Mancini, M.; Galasso, F.; Ciccone, M.; Rodolà, E.; Caputo, B. Cluster-driven graph federated learning over multiple domains. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 2749–2758. [Google Scholar]
- Xie, H.; Ma, J.; Xiong, L.; Yang, C. Federated graph classification over non-iid graphs. Adv. Neural Inf. Process. Syst. 2021, 34, 18839–18852. [Google Scholar]
- Wang, Z.; Kuang, W.; Xie, Y.; Yao, L.; Li, Y.; Ding, B.; Zhou, J. Federatedscope-gnn: Towards a unified, comprehensive and efficient package for federated graph learning. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 4110–4120. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Baek, J.; Jeong, W.; Jin, J.; Yoon, J.; Hwang, S.J. Personalized Subgraph Federated Learning. arXiv 2022, arXiv:2206.10206. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Tan, Y.; Long, G.; Liu, L.; Zhou, T.; Lu, Q.; Jiang, J.; Zhang, C. Fedproto: Federated prototype learning across heterogeneous clients. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 22 February–1 March 2022; Volume 36, pp. 8432–8440. [Google Scholar]
- Sen, P.; Namata, G.; Bilgic, M.; Getoor, L.; Galligher, B.; Eliassi-Rad, T. Collective classification in network data. AI Mag. 2008, 29, 93. [Google Scholar]
- Giles, C.L.; Bollacker, K.D.; Lawrence, S. CiteSeer: An automatic citation indexing system. In Proceedings of the Third ACM Conference on Digital Libraries, New York, NY, USA, 23–26 June 1998; pp. 89–98. [Google Scholar]
- Namata, G.; London, B.; Getoor, L.; Huang, B.; Edu, U. Query-driven active surveying for collective classification. In Proceedings of the 10th International Workshop on Mining and Learning with Graphs, Edinburgh, Scotland, 1 July 2012; Volume 8, p. 1. [Google Scholar]
- Shchur, O.; Mumme, M.; Bojchevski, A.; Günnemann, S. Pitfalls of graph neural network evaluation. arXiv 2018, arXiv:1811.05868. [Google Scholar]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Welling, M.; Kipf, T.N. Semi-supervised classification with graph convolutional networks. In Proceedings of the 5th International Conference on Learning Representations (ICLR 2017), Toulon, France, 24–26 April 2017. [Google Scholar]




| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| Number of clients | Number of missing nodes | ||
| S | Central server of MN-FGAG | generated by the local generator | |
| Server-side global generator | Degree of masked nodes | ||
| Discriminator of client n | Masked nodes | ||
| Global undirected graph | Degree of predicted missing nodes | ||
| V | Set of nodes | ||
| F | Node feature | Predicted missing nodes | |
| E | Set of edges | Total number of missing nodes | |
| Set of selected regularized data | across all clients | ||
| Set of locally generated | h | Masked ratio of local graphs | |
| biased nodes | New feature after regularization | ||
| Feature distance calculation | Weight factor for combining local | ||
| function | and regularized data |
| Datasets | Cora | Citeseer | Pubmed | Coauthor CS |
|---|---|---|---|---|
| Nodes | 2708 | 3312 | 19,717 | 34,493 |
| Edges | 5429 | 4715 | 44,338 | 247,962 |
| Classes | 7 | 6 | 3 | 5 |
| Dimension | 1433 | 3703 | 500 | 8415 |
| Layer | Details (Localgen) | Layer | Details (Generator) | Layer | Details (Discriminator) |
|---|---|---|---|---|---|
| 1 | G-conv (D, 128) + RELU | 1 | Random-noise (D) | 1 | Linear (D, 128) + RELU |
| 2 | G-conv (128, 64) + RELU | 2 | Linear (D, 128) + RELU | 2 | Linear (128, 256) + RELU |
| 3 | FC (64, 1) + Sigmoid | 3 | Linear (128, D) + tanh | 3 | Linear (256, 1) + Sigmoid |
| 4 | Random-noise (64) | ||||
| 5 | FC (64, 256) + RELU | ||||
| 6 | FC (256, D) + tanh |
| Datasets | Cora | Citeseer | ||||
| Methods | = 5 | = 10 | = 15 | =5 | = 10 | = 15 |
| Global Model | 87.01 | 85.87 | 84.32 | 74.04 | 75.75 | 73.71 |
| (±0.0143) | (±0.0129) | (±0.0104) | (±0.0109) | (±0.0085) | (±0.004) | |
| LocalSage | 45.49 | 34.04 | 34.95 | 56.08 | 36.26 | 29.45 |
| (±0.0255) | (±0.0101) | (±0.0200) | (±0.0351) | (±0.0176) | (±0.0367) | |
| FedSage | 84.44 | 83.81 | 82.28 | 72.35 | 72.90 | 71.95 |
| (±0.0349) | (±0.0296) | (±0.0325) | (±0.0093) | (±0.0181) | (±0.0131) | |
| FedSage+ | 85.15 | 84.05 | 82.11 | 72.61 | 73.35 | 72.10 |
| (±0.0256) | (±0.0324) | (±0.0312) | (±0.0151) | (±0.0138) | (±0.0057) | |
| MN-GAGN | 86.37 | 84.30 | 82.86 | 73.67 | 74.40 | 72.61 |
| (±0.0244) | (±0.0219) | (±0.0316) | (±0.0056) | (±0.0156) | (±0.0107) | |
| Datasets | PubMed | Coauthor CS | ||||
| Methods | = 5 | = 10 | = 15 | = 5 | = 10 | = 15 |
| Global Model | 87.93 | 87.70 | 87.84 | 94.84 | 95.10 | 94.22 |
| (±0.0103) | (±0.0149) | (±0.0114) | (±0.0279) | (±0.0242) | (±0.0122) | |
| LocalSage | 78.52 | 69.95 | 65.31 | 63.94 | 50.95 | 38.43 |
| (±0.0074) | (±0.0117) | (±0.0101) | (±0.0487) | (±0.0388) | (±0.0419) | |
| FedSage | 86.87 | 86.74 | 86.85 | 92.69 | 90.36 | 87.15 |
| (±0.0046) | (±0.0106) | (±0.0081) | (±0.0173) | (±0.032) | (±0.0258) | |
| FedSage+ | 87.28 | 87.15 | 87.13 | 92.96 | 90.76 | 87.90 |
| (±0.0055) | (±0.0119) | (±0.0116) | (±0.0167) | (±0.0337) | (±0.0247) | |
| MN-GAGN | 87.46 | 87.72 | 87.52 | 93.12 | 91.46 | 88.37 |
| (±0.0054) | (±0.0076) | (±0.0081) | (±0.0174) | (±0.0252) | (±0.0230) | |
| Datasets | Localgen | FGAGN | Cora | Citeseer | ||||
| Methods | = 5 | = 10 | = 15 | = 5 | = 10 | = 15 | ||
| Variant 1 | ✔ | - | 68.52 | 54.72 | 51.43 | 66.17 | 56.72 | 52.27 |
| Variant 2 | - | ✔ | 83.49 | 84.04 | 79.42 | 76.62 | 76.65 | 73.88 |
| MN-FGAGN | ✔ | ✔ | 83.67 | 82.45 | 79.38 | 76.09 | 76.20 | 73.84 |
| Global Model | ✔ | ✔ | 85.42 | 85.92 | 83.30 | 76.02 | 76.35 | 74.14 |
| Datasets | Localgen | FGAGN | PubMed | Coauthor CS | ||||
| Methods | = 5 | = 10 | = 15 | = 5 | = 10 | = 15 | ||
| Variant 1 | ✔ | - | 83.86 | 77.47 | 74.24 | 87.18 | 86.82 | 86.17 |
| Variant 2 | - | ✔ | 88.15 | 87.20 | 86.76 | 91.67 | 88.34 | 85.33 |
| MN-FGAGN | ✔ | ✔ | 88.00 | 88.40 | 88.72 | 91.89 | 89.67 | 86.74 |
| Global Model | ✔ | ✔ | 89.01 | 89.41 | 89.14 | 92.87 | 93.39 | 93.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; He, Z.; Wang, S.; Wang, Y.; Wang, P.; Huang, Z.; Sun, Q. Federated Subgraph Learning via Global-Knowledge-Guided Node Generation. Sensors 2025, 25, 2240. https://doi.org/10.3390/s25072240
Liu Y, He Z, Wang S, Wang Y, Wang P, Huang Z, Sun Q. Federated Subgraph Learning via Global-Knowledge-Guided Node Generation. Sensors. 2025; 25(7):2240. https://doi.org/10.3390/s25072240
Chicago/Turabian StyleLiu, Yuxuan, Zhiming He, Shuang Wang, Yangyang Wang, Peichao Wang, Zhangshen Huang, and Qi Sun. 2025. "Federated Subgraph Learning via Global-Knowledge-Guided Node Generation" Sensors 25, no. 7: 2240. https://doi.org/10.3390/s25072240
APA StyleLiu, Y., He, Z., Wang, S., Wang, Y., Wang, P., Huang, Z., & Sun, Q. (2025). Federated Subgraph Learning via Global-Knowledge-Guided Node Generation. Sensors, 25(7), 2240. https://doi.org/10.3390/s25072240







