THRU–REFLECT Method for Scattering Parameter Extraction from Back-to-Back Measurements of Waveguide Components
Abstract
:1. Introduction
2. Theory of Scattering Parameter Extraction
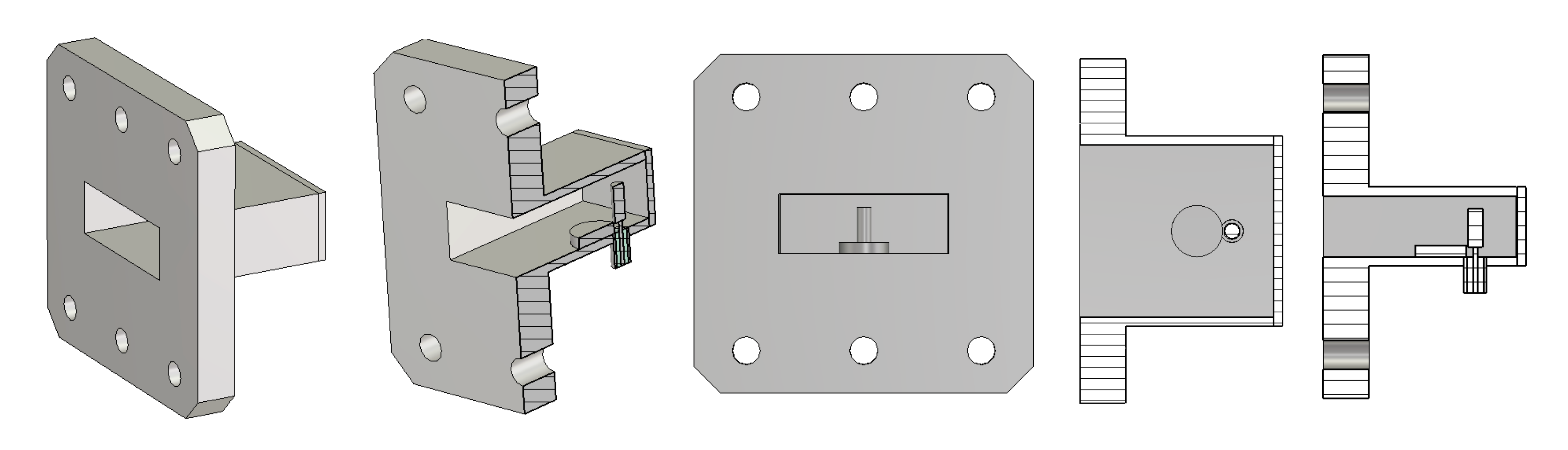
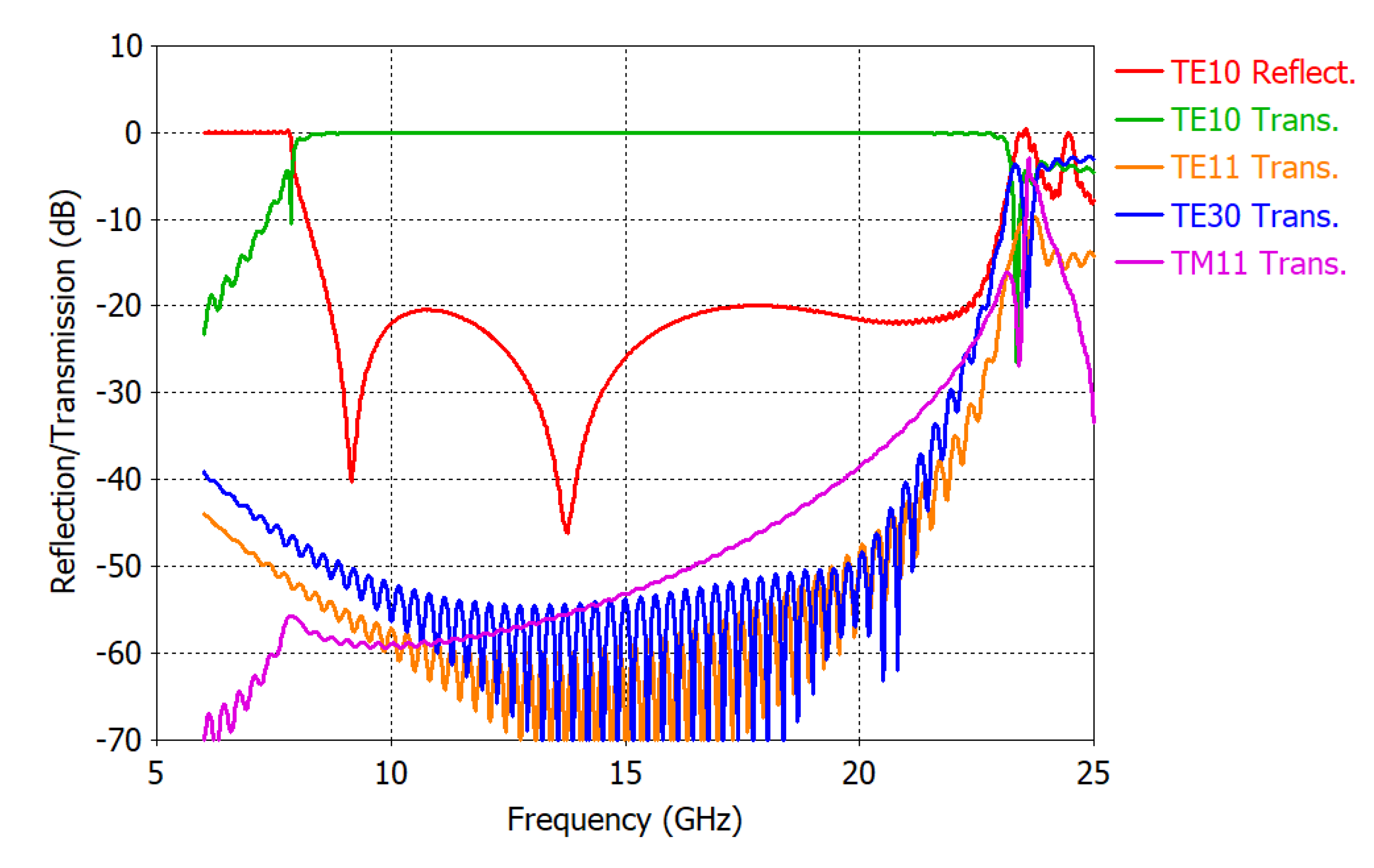
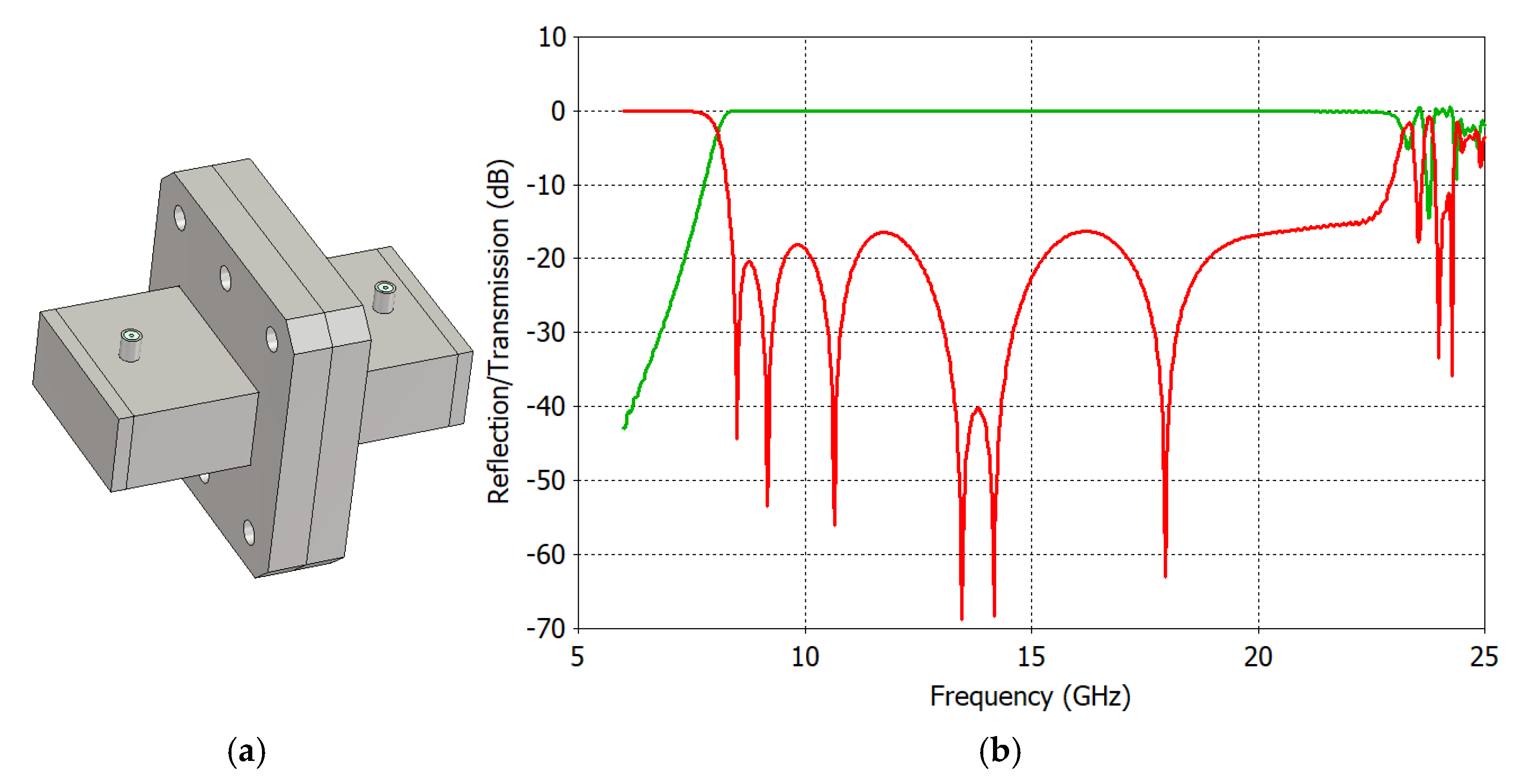
3. Example of Scattering Parameter Extraction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, K.; Li, H.; Li, B.; Zhu, L. Short-open-load (SOL) calibration technique for accurate parameter extraction in micro-coaxial-line circuit. In Proceedings of the 2022 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Harbin, China, 12–15 August 2022. [Google Scholar]
- Nazrin, M.; Hashim, S.J.; Rokhani, F.Z.; Ali, B.M.; Yusoff, Z. Error correction and uncertainty measurement of short-open-load calibration standards on a new concept of software defined instrumentation for microwave network analysis. J. Meas. Eng. 2019, 7, 107–118. [Google Scholar]
- Kim, Y.-G.; Kim, K.W.; Cho, Y.-K. An ultra-wideband microstrip-to-CPW transition. In The analysis of circular waveguide phased arrays. In Proceedings of the 2008 IEEE MTT-S International Microwave Symposium Digest, Atlanta, GA, USA, 15–20 June 2008. [Google Scholar]
- Li, G.M.; Li, Q. The design of Ka band waveguide-to-microstrip transition. In Proceedings of the International Conference on Computational Problem-Solving (ICCP), Chengdu, China, 21–23 October 2011. [Google Scholar]
- Nghia, N.-T.; Kaufmann, T.; Fumeaux, C. Wideband transition from coaxial cable to half-mode substrate integrated waveguide. In Proceedings of the 2013 Asia-Pacific Microwave Conference (APMC), Seoul, Republic of Korea, 5–8 November 2013. [Google Scholar]
- Shams, S.I.; Kish, A.A. Waveguide coaxial to ridge gap waveguide transition. IEEE Trans. Microw. Theory Tech. 2016, 64, 4117–4125. [Google Scholar]
- Cano, J.L.; Mediavilla, A. Octave bandwidth in-line rectangular waveguide-to-coaxial transition using oversized mode convers. Electron. Lett. 2017, 53, 1370–1371. [Google Scholar]
- Dong, Y.; Johansen, T.K.; Zhurbenko, V.; Hanberg, P.J. A rectangular waveguide-to-coplanar waveguide transition at D-band using wideband patch antenna. In Proceedings of the 46th European Microwave Conference (EuMC), Madrid, Spain, 23–27 September 2018. [Google Scholar]
- Herraiz, D.; Esteban, H.; Martínez, J.A.; Belenguer, A.; Cogollos, S.; Nova, V.; Boria, V.E. Transition from microstrip line to ridge empty substrate integrated waveguide based on the equations of the superellipse. Appl. Sci. 2020, 10, 8101. [Google Scholar] [CrossRef]
- Liu, Z.; Cheng, X.; Yao, Y.; Yu, T.; Yu, J.; Chen, X. Broadband transition from rectangular waveguide to groove gap waveguide for mm-wave contactless connections. Electronics 2020, 9, 1820. [Google Scholar] [CrossRef]
- Pérez, J.A.G.; Goussetis, G.; Fan, H.; Ding, Y. A low-loss Ka-band waveguide to substrate integrated waveguide transition based on ridged stepped-impedance transformer. Electron. Lett. 2021, 57, 662–664. [Google Scholar]
- Xu, Q.; Jiang, Z.; Guo, C. A design of waveguide-to-microstrip transition for V-band device testing. In Proceedings of the 2022 International Conference Microwave Millimeter Wave Technology (ICMMT), Harbin, China, 12–15 August 2022. [Google Scholar]
- Pittermann, M.; Zwick, T.; Bhutani, A. A 53–125 GHz chip to double-ridge rectangular waveguide transition. Electron. Lett. 2024, 60, 1–4. [Google Scholar]
- Kim, H.; Kim, G.; Cho, J.; Park, K.; Kim, S. Design of wideband right-angle CPWG-to-waveguide transition for Ku-band application. IEEE Microw. Wireless Comp. Lett. 2024, 34, 149–152. [Google Scholar]
- Lee, Y.-C.; Wang, C.-L. Compact and broadband rectangular waveguide-to-circular waveguide transition. In Proceedings of the 2024 IEEE 4th International Conference Electronic Communications Internet Things & Big Data (ICEIB), Taipei, Taiwan, 19–21 April 2024. [Google Scholar]
- Sorokosz, L.; Zieniutycz, W. Estimation of a single balun parameters on the base of back-to-back measurements. In Proceedings of the 2016 21st International Conference Microwave, Radar and Wireless Communications (MIKON), Krakow, Poland, 9–11 May 2016. [Google Scholar]
- Chang, W.-C.; Wunsch, G.J.; Schaubert, D.H. Back-to-back measurement for characterization of phased-array antennas. IEEE Trans. Antennas Propagat. 2000, 48, 1079–1085. [Google Scholar]
- Pittermann, M.; Zwick, T.; Bhutani, A. A DC to 125 GHz probe pad design. In Proceedings of the 54th European Microwave Conference, Paris, France, 24–26 September 2024. [Google Scholar]
- Silvonen, K.J. Calibration of test fixtures using at least two standards. IEEE Trans. Microw. Theory Tech. 1991, 39, 624–630. [Google Scholar]
- Silvonen, K.J. A general approach to network analyzer calibration. IEEE Trans. Microw. Theory Tech. 1992, 40, 754–759. [Google Scholar]
- Zúňiga-Juárez, J.E.; Reynoso-Hernández, J.A.; Loo-Yau, J.R.; Maya-Sánchez, M.C. An improved two-tier L-L method for characterizing symmetrical microwave test fixtures. Measurements 2011, 44, 1491–1498. [Google Scholar]
- Stephens, D.; Young, P.R.; Robertson, I.D. Millimeter-wave substrate integrated waveguides and filters in photoimageable thick-film technology. IEEE Trans. Microw. Theory Tech. 2005, 53, 3832–3838. [Google Scholar]
- Kang, T.-G.; Park, J.-K.; Kim, B.-H.; Lee, J.J.; Choi, H.H.; Lee, H.-J.; Yook, J.-G. Microwave characterization of conducting polymer PEDOT: PPS film using a microstrip line for humidity sensor application. Measurements 2019, 137, 272–277. [Google Scholar]
- Liu, Z.; Xu, J.; Wang, W. Wideband transition from microstrip line-to-empty substrate-integrated waveguide without sharp dielectric taper. IEEE Microw. Wireless Comp. Lett. 2019, 29, 20–22. [Google Scholar]
- Rho, J.-E.; Li, J.-W.; Ahn, B.-C.; Park, C.-S.; Cha, E.-J. Novel approach to optimizing a broadband right-angle coaxial-to-microstrip transition. Microw. Opt. Technol. Lett. 2007, 49, 451–456. [Google Scholar]
- Moon, S.-J.; Ye, X.; Smith, R. Comparison of TRL calibration vs. 2x thru de-embedding methods. In Proceedings of the 2015 IEEE Symposium on Electromagnetic Compatibility and Signal Integrity, Santa Clara, CA, USA, 15–21 March 2015. [Google Scholar]
- Chen, Y.; Chen, B.; He, J.; Zai, R.; Fan, J.; Drewniak, J. De-embedding comparisons of 1x-reflect SFD, 1-port AFR, and 2x-thru SFD. In Proceedings of the 2018 IEEE International Symposium on Electromagnetic Compatibility and 2018 IEEE Asia-Pacific Symposium on Electromagnetic Compatibility, Suntec City, Singapore, 14–18 May 2018. [Google Scholar]
- Ellison, J.; Smith, S.B.; Agili, S. Using a 2x-thru standard to achieve accurate de-embedding of measurements. Microw. Opt. Technol. Lett. 2020, 62, 675–682. [Google Scholar]
- Simion, S. A new unterminating method for de-embedding the coaxial to waveguide transitions. Prog. Electromagn. Res. C 2022, 121, 255–264. [Google Scholar]
- Torres-Torres, R.; Hernández-Sosa, G.; Romo, G.; Sánchez, A. Characterization of electrical transitions using transmission line measurements. IEEE Trans. Adv. Packag. 2009, 32, 45–52. [Google Scholar]
- Han, X.; Zhu, W.; Yang, Q. An embedded auto-calibration approach used in one-port calibration of VNA. In Proceedings of the 11th IEEE International Conference on Electronic Measurement Instruments, Harbin, China, 16–19 August 2013. [Google Scholar]
- Ou, J.; Caggiano, M.F. Determine two-port S-parameters from one-port measurements using calibration substrate standards. In Proceedings of the 2005 Electronic Components and Technology (ECTC ’05), Lake Buena Vista, FL, USA, 20 June 2005. [Google Scholar]
- Scalzi, G.J.; Slobodnik, A.J., Jr.; Roberts, G.A. Network analyzer calibration using offset shorts. IEEE Trans. Microw. Theory Tech. 1988, 36, 1097–1100. [Google Scholar]
- Horibe, M.; Kishikawa, R. Improvement of offset short calibration technique in waveguide VNA measurement at millimeter and sub-millimeter wave frequency. In Proceedings of the 29th Conference on Precision Electromagnetic Measurements (CPEM 2014), Rio de Janeiro, Brazil, 24–29 August 2014. [Google Scholar]
- Hunton, J.K. Analysis of microwave measurement techniques by means of signal flow graphs. IRE Trans. Microw. Theory Tech. 1960, 8, 206–212. [Google Scholar]
- Buff, P.M.; Nath, J.; Steer, M.B. Origin of the half-wavelength errors in microwave measurements using through−line calibrations. IEEE Trans. Instrum. Meas. 2007, 56, 1610–1615. [Google Scholar]
- Fuh, K.-F. Formulation for propagation factor extractions in thru-reflect-line/line-reflect-line calibrations and related applications. IEEE Trans. Microw. Theory Tech. 2016, 64, 1594–1606. [Google Scholar]
- Marks, R.B. A multiline method of network analyzer calibration. IEEE Trans. Microw. Theory Tech. 1991, 39, 1205–1215. [Google Scholar]
- Zhang, Q.; Xu, X.; Heo, J.; Atlanzaya, E.; Ariunbold, G.-Y.; Otgonbat, D.; Lee, C.-S.; Ahn, B.-C.; Li, S.; Choi, S.-G. Computational design of a broadband in-line coaxial-to-rectangular waveguide transition. Appl. Sci. 2023, 14, 74. [Google Scholar] [CrossRef]
- Lozano-Guerrero, A.J.; Monzó-Cabrera, J.; Pitarch, J.; Clemente-Fernández, F.J.; Fayos-Fernández, J.; Pedreño-Molina, J.L.; Matínez-González, A.; Díaz-Morcillo, A. Multimodal retrieval of the scattering parameters of a coaxial-to-waveguide transition. IEEE Trans. Microw. Theory Tech. 2021, 69, 5241–5249. [Google Scholar]
- Panzner, B.; Jöstingmeier, A.; Omar, A. A novel multimodal waveguide technique for the broadband characterization of dielectric material parameters. In Proceedings of the 42nd European Microwave Conference, Amsterdam, The Netherlands, 29 October–1 November 2012. [Google Scholar]
- Eccleston, K.W. A new interpretation of through-line deembedding. IEEE Trans. Microw. Theory Tech. 2016, 64, 3887–3893. [Google Scholar]
- Ehlers, E.R. Symmetric text fixture calibration. In Proceedings of the 1986 IEEE MTT-S International Microwave Symposium, Baltimore, MD, USA, 2−4 June 1986. [Google Scholar]
- Daniel, E.S.; Harff, N.E.; Sokolov, V.; Schreiber, S.M.; Gilbert, B.K. Network analyzer measurement de-embedding utilizing a distributed transmission matrix bisection of a single THRU structure. In Proceedings of the ARFTG 63rd Conference, Fort Worth, TX, USA, 11 June 2004. [Google Scholar]
- Gronau, G.; Wolff, I. A simple broad-band device de-embedding method using an automatic network analyzer with time-domain option. IEEE Trans. Microw. Theory Tech. 1989, 37, 479–483. [Google Scholar]

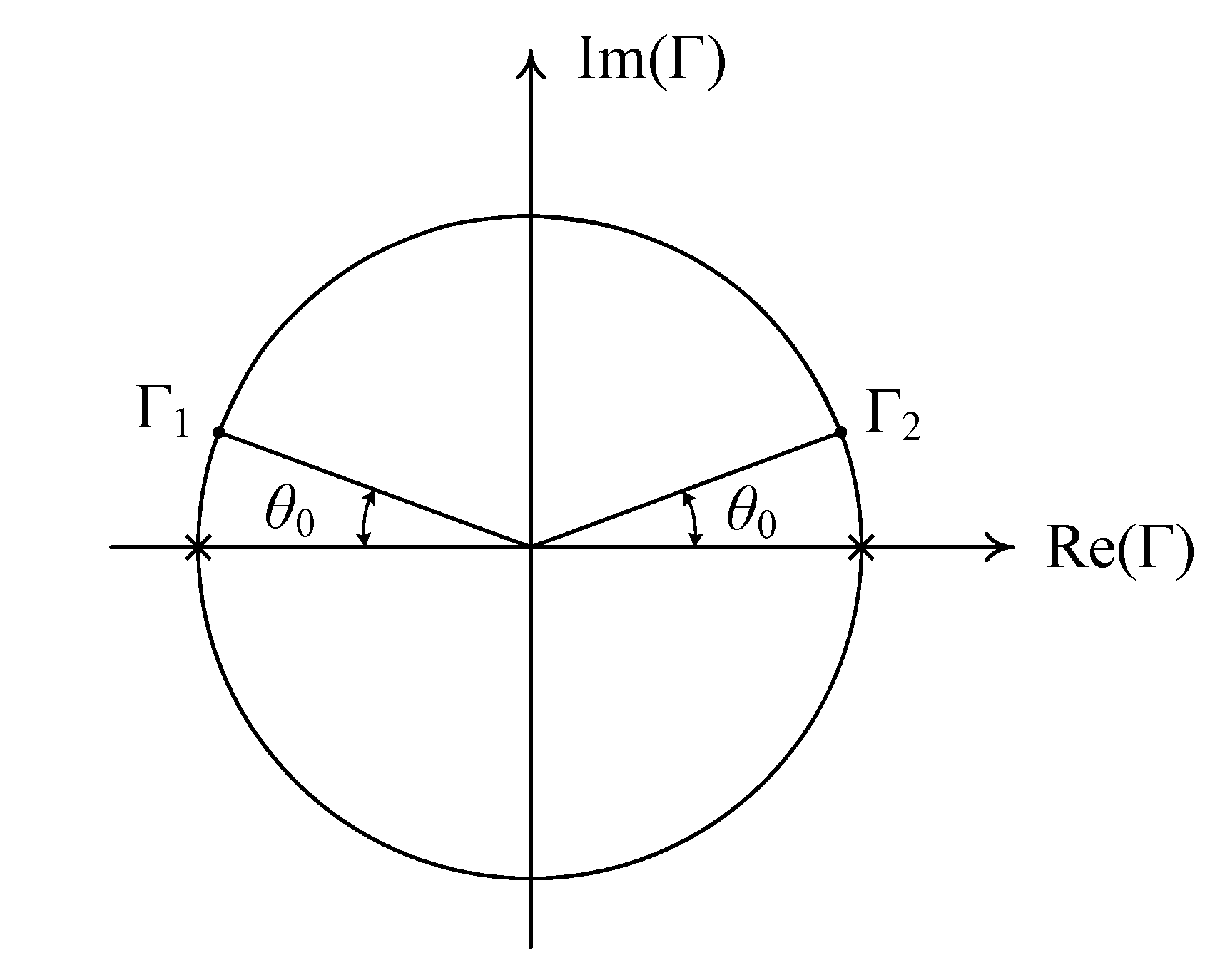

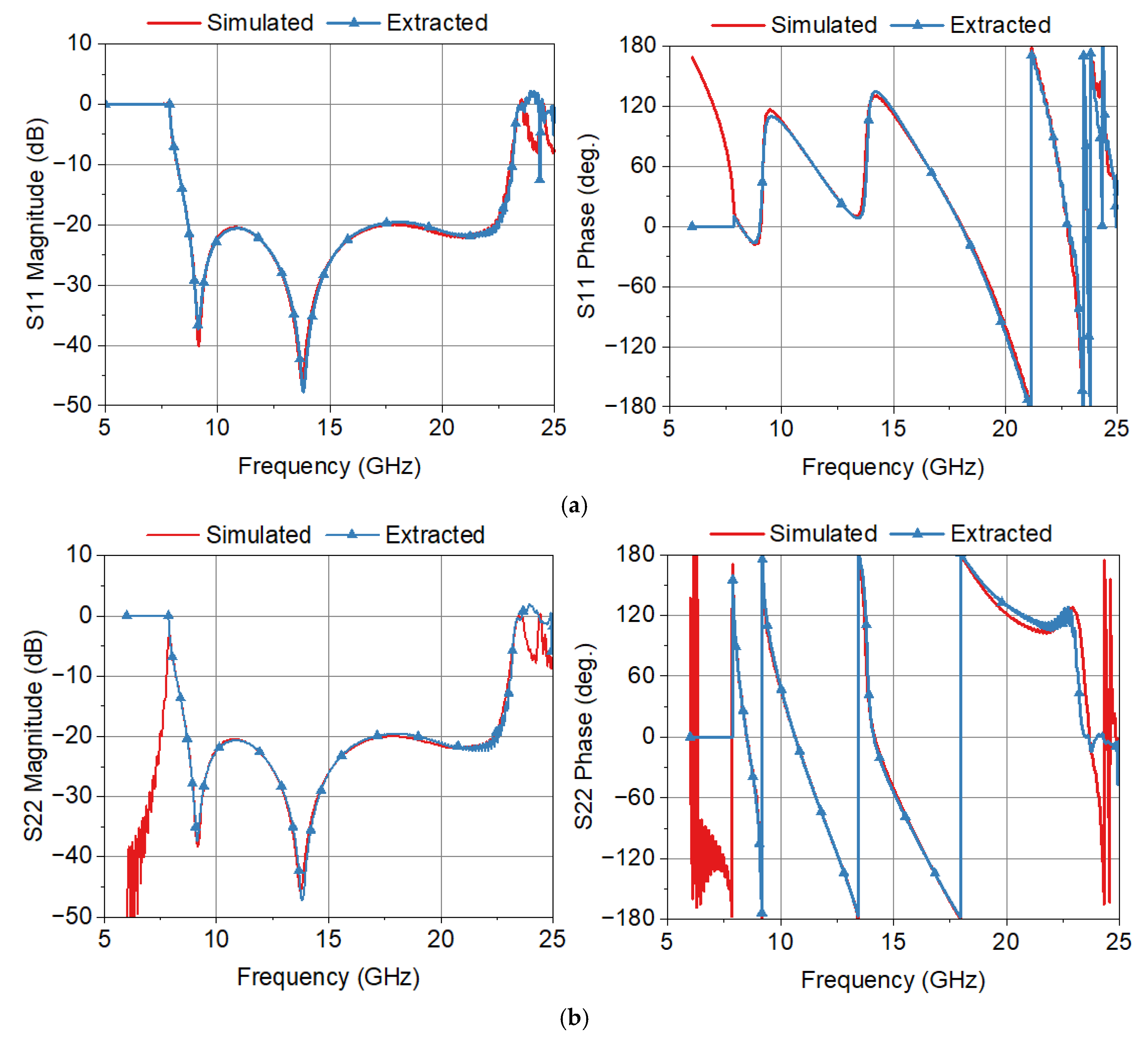
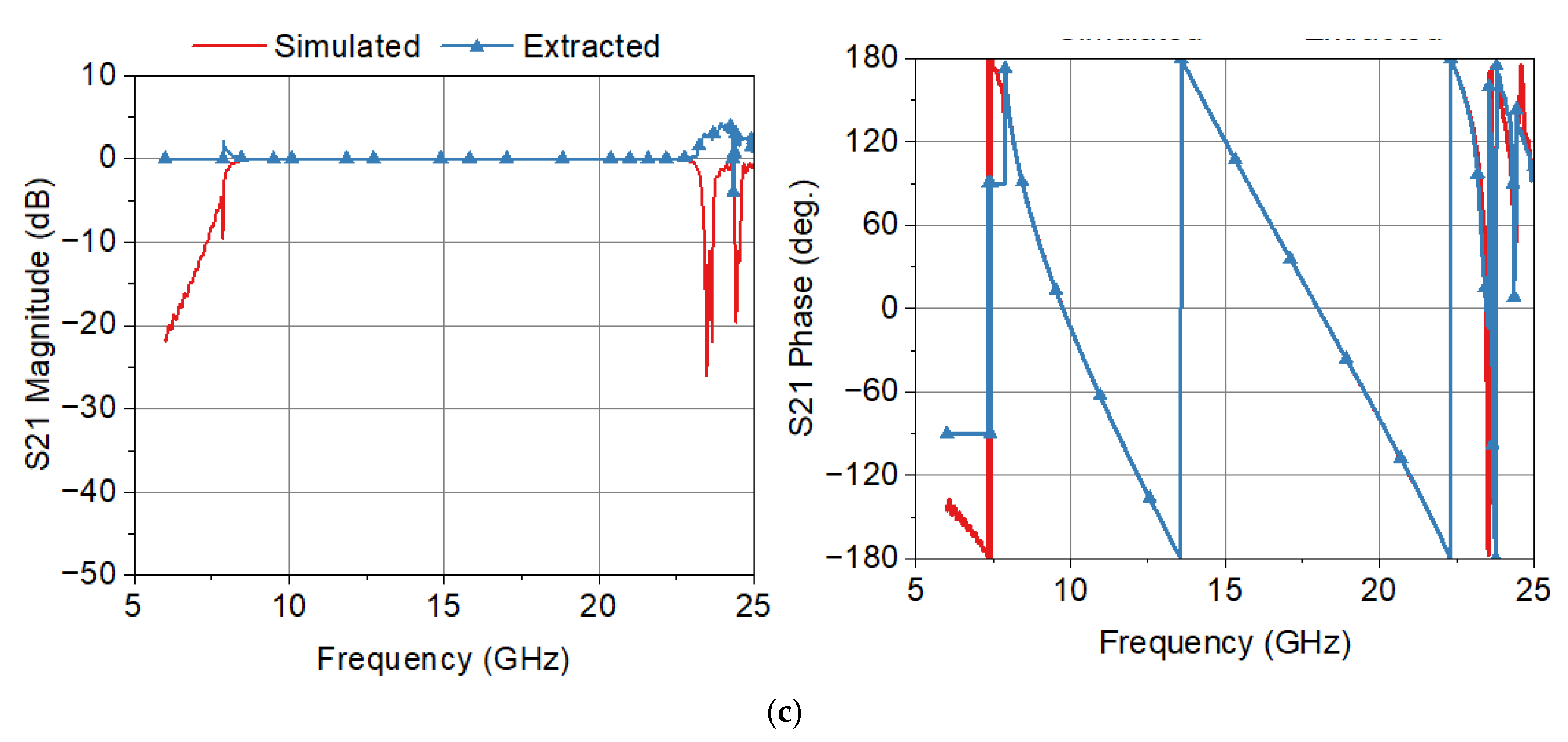
| Quantities (Units: dB, deg.) | Frequency (GHz) | ||
|---|---|---|---|
| 10 | 15 | 20 | |
| Mag./Phase of M11 | −18.86/61.84 | −21.84/150.14 | −17.35/−68.80 |
| Mag./Phase of M21 | −0.0561/−28.08 | −0.0293/−119.67 | −0.0837−159.54 |
| Mag./Phase of Q11 | −0.0002/105.18 | −0.0000/−31.70 | 0.0019/−114.84 |
| Mag./Phase of T | 0/0 | 0/0 | 0/0 |
| Mag./Phase of Γ | 0/133.95 | 0/84.87 | 0/43.08 |
| Mag./Phase of S11, Simulated | −22.05/105.16 | −26.00/118.83 | −21.60/−100.42 |
| Mag./Phase of S11, Extracted | −22.37/102.98 | −26.09/115.10 | −21.02/−107.66 |
| Mag./Phase of S22, Simulated | −22.04/46.00 | −26.02/−51.19 | −21.54/121.47 |
| Mag./Phase of S22, Extracted | −22.36/48.53 | −26.10/−54.91 | −21.15/130.76 |
| Mag./Phase of S21, Simulated | −0.0402/−14.17 | −0.0247/120.23 | −0.0428/−79.69 |
| Mag./Phase of S21, Extracted | 0.0255/−14.21 | 0.0103/120.23 | 0.0308/−79.53 |
| Differences | Average | Standard Deviation | Max./Freq. (GHz) | Min./Freq. (GHz) |
|---|---|---|---|---|
| In Mag. of S11 (dB) | 0.0088 | 0.63 | 3.28/9.17 | −3.50/13.85 |
| In Phase of S11 (deg.) | −1.77 | 4.34 | 12.32/9.14 | −31.16/13.77 |
| In Mag. of S22 (dB) | 0.0098 | 0.69 | 2.38/13.66 | −4.19/13.90 |
| In Phase of S22 (deg.) | 2.18 | 4.34 | 38.03/13.77 | −25.56/9.12 |
| In Mag. of S21 (dB) | 0.0093 | 0.18 | 2.19/8.01 | 0.0011/9.06 |
| In Phase of S21 (deg.) | 0.040 | 0.077 | 0.57/8.09 | −0.61/8.033 |
| Methods | Number of Interface Connections | Number of Calibration Standards | Applicable to Asymmetric Devices? | Features |
|---|---|---|---|---|
| THRU-LINE [42] | 4 | 1 | No |
|
| THRU-MATCH [43] | 3 | 1 | No |
|
| THRU-Only [44] | 2 | 0 | No |
|
| 2x-THRU [45] | 2 | 1 | Yes |
|
| Proposed Method | 3 | 1 | No |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Heo, J.; Lee, C.-S.; Kim, K.-H.; Ahn, B.-C. THRU–REFLECT Method for Scattering Parameter Extraction from Back-to-Back Measurements of Waveguide Components. Sensors 2025, 25, 2277. https://doi.org/10.3390/s25072277
Xu S, Heo J, Lee C-S, Kim K-H, Ahn B-C. THRU–REFLECT Method for Scattering Parameter Extraction from Back-to-Back Measurements of Waveguide Components. Sensors. 2025; 25(7):2277. https://doi.org/10.3390/s25072277
Chicago/Turabian StyleXu, Songyuan, Jiwon Heo, Chan-Soo Lee, Ki-Hong Kim, and Bierng-Chearl Ahn. 2025. "THRU–REFLECT Method for Scattering Parameter Extraction from Back-to-Back Measurements of Waveguide Components" Sensors 25, no. 7: 2277. https://doi.org/10.3390/s25072277
APA StyleXu, S., Heo, J., Lee, C.-S., Kim, K.-H., & Ahn, B.-C. (2025). THRU–REFLECT Method for Scattering Parameter Extraction from Back-to-Back Measurements of Waveguide Components. Sensors, 25(7), 2277. https://doi.org/10.3390/s25072277








