Compressive Wideband Spectrum Sensing Aided Intelligence Transmitter Design
Abstract
1. Introduction
- An NYFR-based self-interference cancellation architecture is proposed to support real-time wideband spectrum sensing in intelligent transmitters, addressing the challenge of co-platform interference suppression under complex electromagnetic environments.
- Closed-form analytical expressions for the residual interference power and cancellation performance are derived, taking into account the impact of time synchronization errors and sampling inaccuracies, which quantitatively reveal the performance limitations of the proposed scheme.
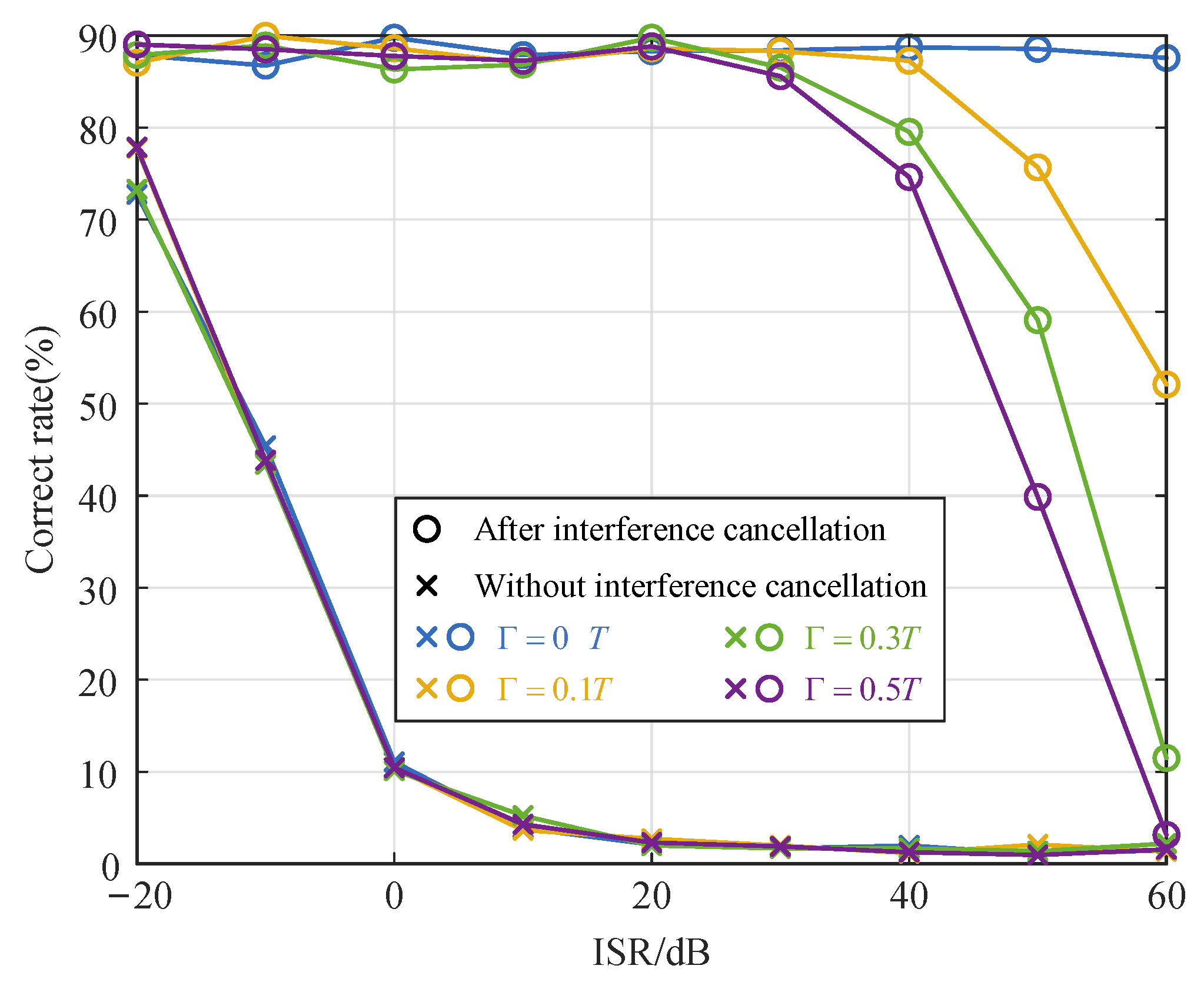
- Theoretical analysis and simulation results demonstrate the effectiveness of the proposed method. Specifically, it is shown that the interference cancellation performance degrades with increasing synchronization errors and folding factors. Moreover, simulation results verify that, at an SI-to-NCS power ratio of 0 dB, the proposed scheme improves the frequency detection probability by approximately 80%.
2. System Model
3. NYFR-Based Self-Interference Cancellation Performance Analysis
3.1. NYFR-Based Signal Folding
3.2. Time Synchronization Errors
3.3. Effects on Self-Interference Cancellation Performance
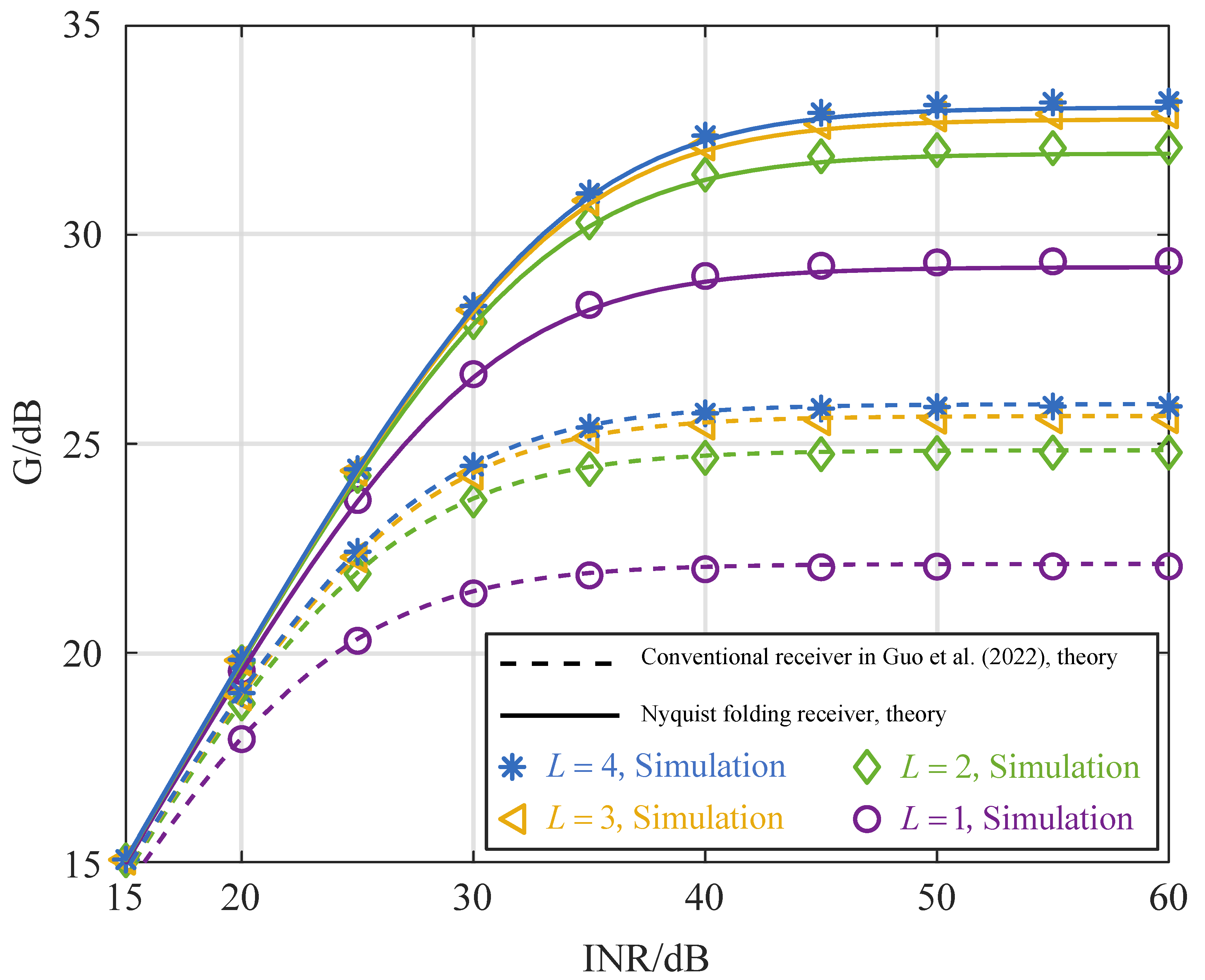
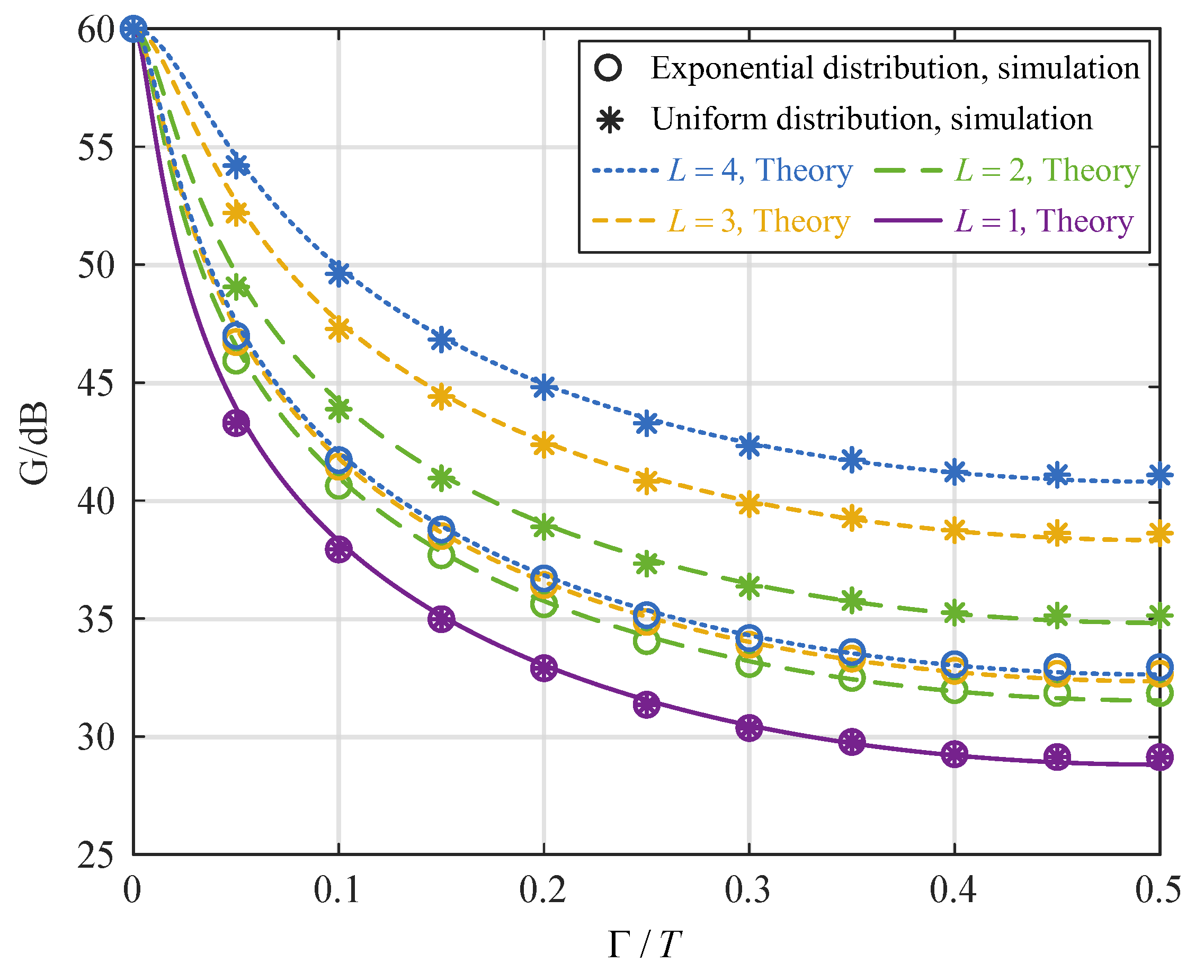
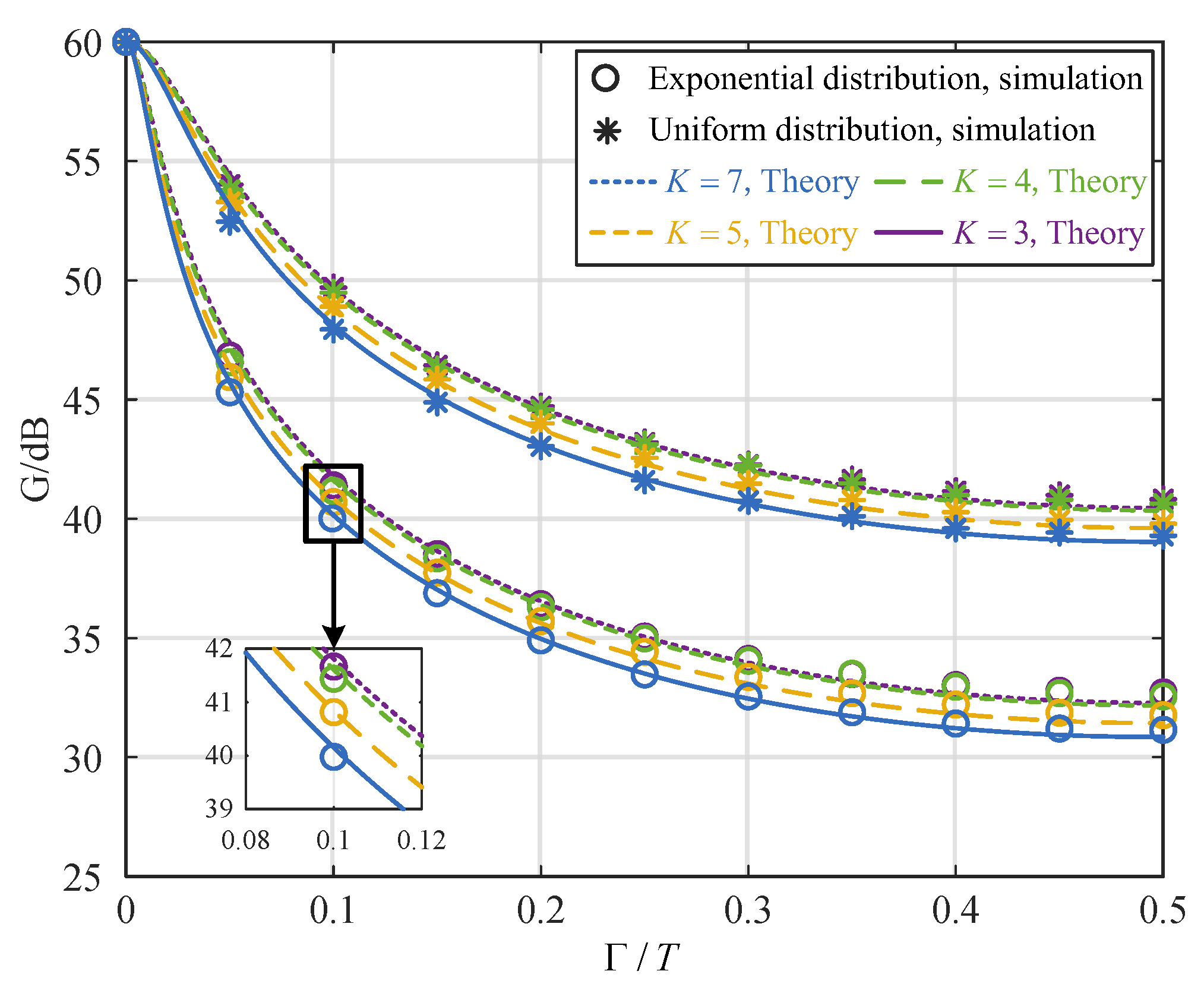
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CS | Compressed sensing |
| NYFR | Nyquist folding receiver |
| 3GPP | Third Generation Partnership Project |
| ADC | Analog-to-digital converter |
| NCS | Non-cooperative signal |
| SI | Self-interference signal |
| DAC | Digital-to-analog converter |
| RF | Radio-frequency |
| ISI | Inter-symbol interference |
| INR | SI to noise power ratio |
| ISR | SI to NCS power ratio |
References
- Zhang, Y.; Xiang, Y.; Zhang, L.Y.; Rong, Y.; Guo, S. Secure Wireless Communications Based on Compressive Sensing: A Survey. IEEE Commun. Surv. Tutor. 2019, 21, 1093–1111. [Google Scholar] [CrossRef]
- Hussain, B.; Du, Q.; Sun, B.; Han, Z. Deep Learning-Based DDoS-Attack Detection for Cyber-Physical System over 5G network. IEEE Trans. Ind. Inform. 2021, 17, 860–870. [Google Scholar] [CrossRef]
- Yang, C.; Li, J.; Ni, Q.; Anpalagan, A.; Guizani, M. Interference-Aware Energy Efficiency Maximization in 5G Ultra-Dense Networks. IEEE Trans. Commun. 2017, 65, 728–739. [Google Scholar] [CrossRef]
- Zhao, Z.; Du, Q.; Karagiannidis, G.K. Improved Grant-Free Access for URLLC via Multi-Tier-Driven Computing: Network-Load Learning, Prediction, and Resource Allocation. IEEE J. Sel. Areas Commun. 2023, 41, 607–622. [Google Scholar] [CrossRef]
- Integrated Sensing and Communication, 3GPP. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=4198 (accessed on 3 July 2023).
- Xiao, Y.; Du, Q.; Cheng, W.; Zhang, W. Adaptive Sampling and Transmission for Minimizing Age of Information in Metaverse. IEEE J. Select. Areas Commun. 2024, 42, 588–602. [Google Scholar] [CrossRef]
- Xiao, Y.; Du, Q. Statistical Age-of-Information Optimization for Status Update over Multi-State Fading Channels. IEEE Trans. Veh. Technol. 2024, 73, 6018–6023. [Google Scholar] [CrossRef]
- Jiang, K.; Zhang, X.; Li, Y.; Wang, M. Distributed UAV Swarm Augmented Wideband Spectrum Sensing Using Nyquist Folding Receiver. IEEE Trans. Wirel. Commun. 2024, 23, 14171–14184. [Google Scholar] [CrossRef]
- Xie, H.; Wang, Y.; Andrieux, G.; Ren, X. Efficient Compressed Sensing-Based Non-Sample Spaced Sparse Channel Estimation in OFDM System. IEEE Access 2019, 7, 133362–133370. [Google Scholar] [CrossRef]
- Odejide, O.O.; Akujuobi, C.M.; Annamalai, A.; Fudge, G. Application of Analytic Wavelet Transform for Signal Detection in Nyquist Folding Analog-to-Information Receiver. In Proceedings of the IEEE International Conference on Communications, Dresden, Germany, 14–18 June 2009; pp. 1–5. [Google Scholar]
- Maleh, R.; Fudge, G.L.; Boyle, F.A.; Pace, P.E. Analog-to-Information and the Nyquist Folding Receiver. IEEE J. Emerg. Sel. Top. Circuits Syst. 2012, 2, 564–578. [Google Scholar] [CrossRef]
- Chen, S.; Jiang, K.; Wu, S.; Zhu, J.; Tang, B. The impact of NYFR’s parameters on reconstruction. In Proceedings of the Wireless Communications, Signal Processing and Networking, Chennai, India, 23–25 March 2016; pp. 1686–1692. [Google Scholar]
- Mohammadi, M.; Mobini, Z.; Galappaththige, D.; Tellambura, C. A comprehensive survey on full-duplex communication: Current solutions, future trends, and open issues. IEEE Commun. Surv. Tutor. 2023, 25, 2190–2244. [Google Scholar] [CrossRef]
- Yunhao, J.; Zhipeng, L.; Lei, Y.; Anfei, X.; Hang, W.; Nan, Z.; Minghu, W. Multitap RF Canceller with Single LMS Loop for Adaptive Co-Site Broadband Interference Cancellation. China Commun. 2024, 21, 179–197. [Google Scholar] [CrossRef]
- Liu, G.; Yu, F.R.; Ji, H.; Leung, V.C.; Li, X. In-Band Full-Duplex Relaying: A Survey, Research Issues and Challenges. IEEE Commun. Surv. Tutor. 2017, 17, 500–524. [Google Scholar] [CrossRef]
- Liang, Y.Z.; Chen, F.C.; Xiang, K.R.; Zeng, W.F. Wideband Co-Polarized Stacked Patch Antenna for In-Band Full-Duplex Applications. IEEE Trans. Antennas Propag. 2023, 17, 9920–9925. [Google Scholar] [CrossRef]
- Cheng, W.; Xiao, Y.; Zhang, S.; Wang, J. Adaptive Finite Blocklength for Ultra-Low Latency in Wireless Communications. IEEE Trans. Wirel. Commun. 2022, 21, 4450–4463. [Google Scholar] [CrossRef]
- Guo, W.; Li, C.; Zhao, H.; Wen, R.; Tang, Y. Comprehensive Effects of Imperfect Synchronization and Channel Estimation on Known Interference Cancellation. IEEE Trans. Veh. Technol. 2020, 69, 457–470. [Google Scholar] [CrossRef]
- Guo, W.; Hu, H.; He, Y.; Yan, M.; Zhao, H.; Shao, S. Impacts of Clock Jitter on Cooperative Jamming Cancellation. In Proceedings of the IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; pp. 4142–4147. [Google Scholar]
- He, Y.; Zhao, H.; Guo, W.; Tang, Y. Robust Nonlinear Interference Cancellation with Time Alignment Error in Full-Duplex Systems. Proceedings of IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Mao, Y.; Zhao, H.; Li, W.; Shao, S. Joint Transceiver Optimization for CJ-Aided Security Communication Systems with Frequency Mismatch. IEEE Wirel. Commun. Lett. 2024, 13, 1631–1635. [Google Scholar] [CrossRef]
- Huo, X.; Guo, W.; Liu, Y.; Zhao, H.; Tang, Y. Analysis and Compensation of Frequency Offset in Co-site Adjacent Channel Interference Suppression. China Commun. 2023, 20, 116–128. [Google Scholar] [CrossRef]
- Olkkonen, J.T.; Olkkonen, H. Fractional delay filter based on the B-spline transform. IEEE Signal Process. Lett. 2007, 14, 97–100. [Google Scholar]
- Chen, P.; Qi, C.; Wu, L.; Wang, X. Estimation of Extended Targets Based on Compressed Sensing in Cognitive Radar System. IEEE Trans. Veh. Technol. 2017, 66, 941–951. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, L.; Chen, Y.; Zhong, L.; Zhao, H. Compressive Wideband Spectrum Sensing Aided Intelligence Transmitter Design. Sensors 2025, 25, 2400. https://doi.org/10.3390/s25082400
Qin L, Chen Y, Zhong L, Zhao H. Compressive Wideband Spectrum Sensing Aided Intelligence Transmitter Design. Sensors. 2025; 25(8):2400. https://doi.org/10.3390/s25082400
Chicago/Turabian StyleQin, Lizhi, Yuming Chen, Leli Zhong, and Hongzhi Zhao. 2025. "Compressive Wideband Spectrum Sensing Aided Intelligence Transmitter Design" Sensors 25, no. 8: 2400. https://doi.org/10.3390/s25082400
APA StyleQin, L., Chen, Y., Zhong, L., & Zhao, H. (2025). Compressive Wideband Spectrum Sensing Aided Intelligence Transmitter Design. Sensors, 25(8), 2400. https://doi.org/10.3390/s25082400




