A Survey of the State of the Art in Monocular 3D Human Pose Estimation: Methods, Benchmarks, and Challenges
Abstract
1. Introduction
- A comprehensive review of contemporary deep learning-based techniques for 3D human pose estimation is provided, including systematic analysis of emerging innovations such as diffusion models and state-space models within the 3D HPE domain.
- 3D HPE methods from monocular RGB data are systematically categorized based on their input modalities and architectural designs, with an emphasis on their distinctive features, advantages, and limitations.
- A critical analysis of the challenges inherent to monocular 3D HPE—such as dataset limitations, depth ambiguity, occlusion, and motion artifacts—is provided, along with a discussion of potential solutions.
- Emerging research avenues are explored, including data-efficient learning, cross-domain generalization, real-time performance, and the integration of novel paradigms such as large language models (LLMs), neural radiance fields (NeRFs), and physics-based constraints, thereby providing valuable guidance for advancing the state of monocular 3D HPE.
2. Human Body Models
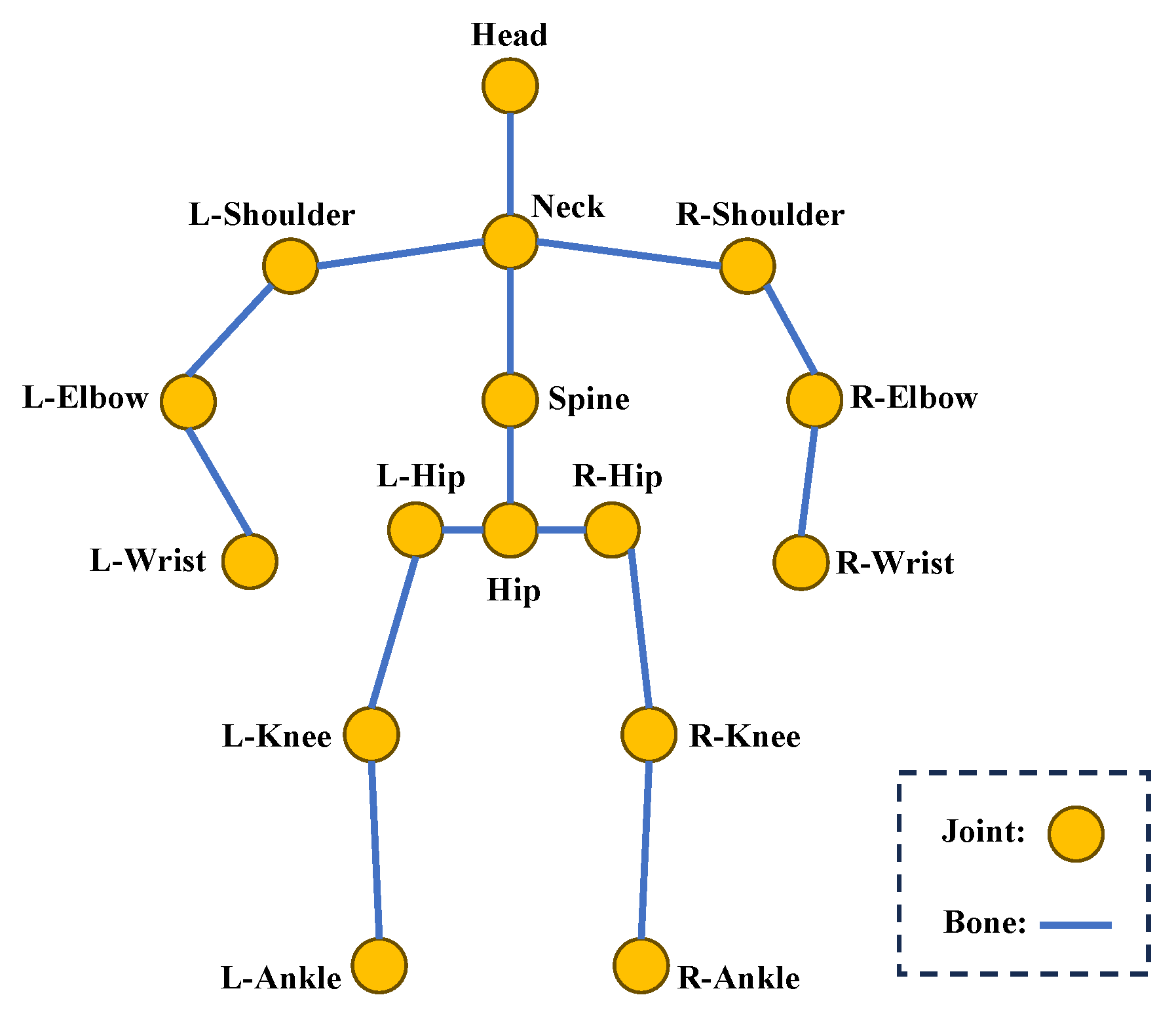
2.1. Kinematic Model
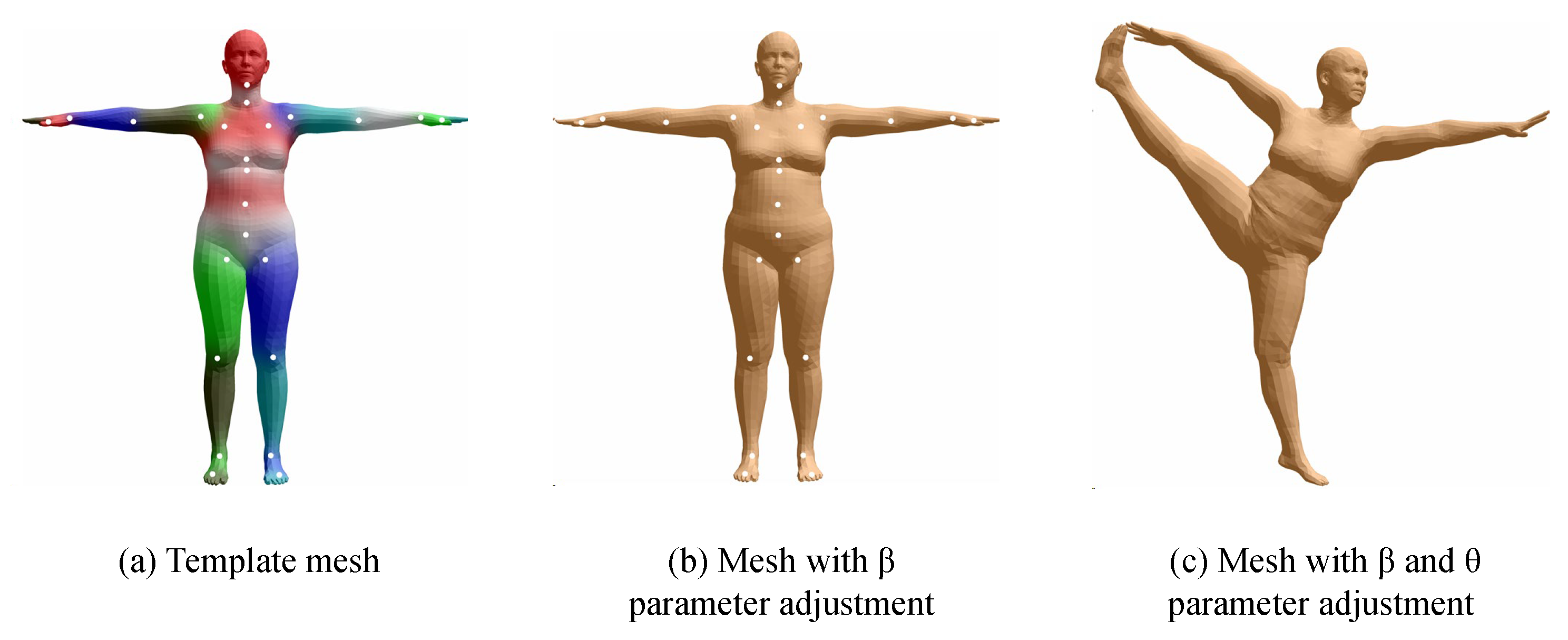
2.2. Volumetric Model
2.3. Comparison
3. Three-Dimensional HPE from RGB Images
3.1. Single-Person 3D HPE
3.1.1. End-to-End Estimation
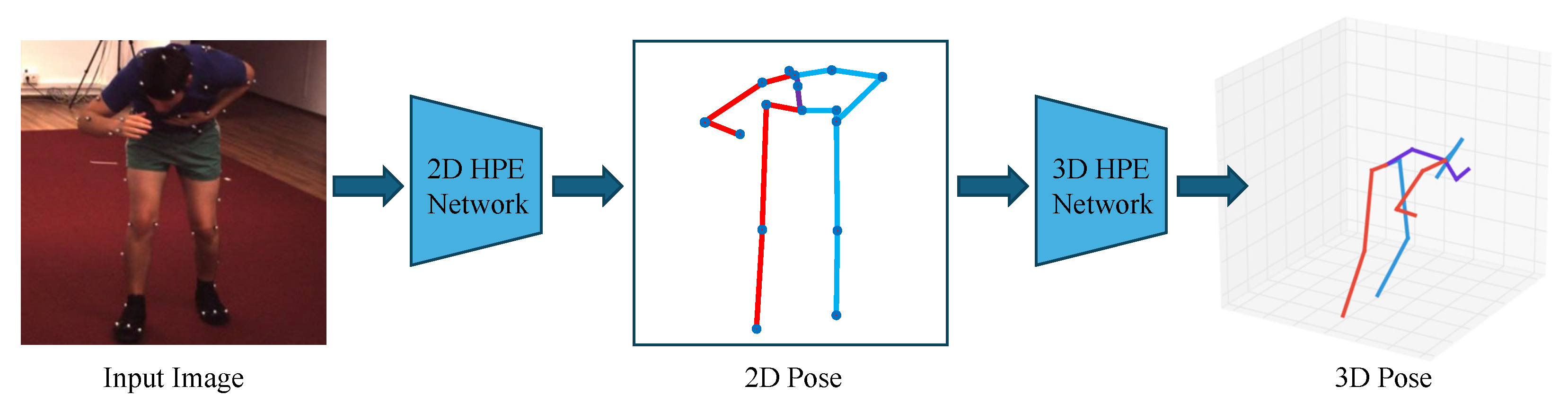
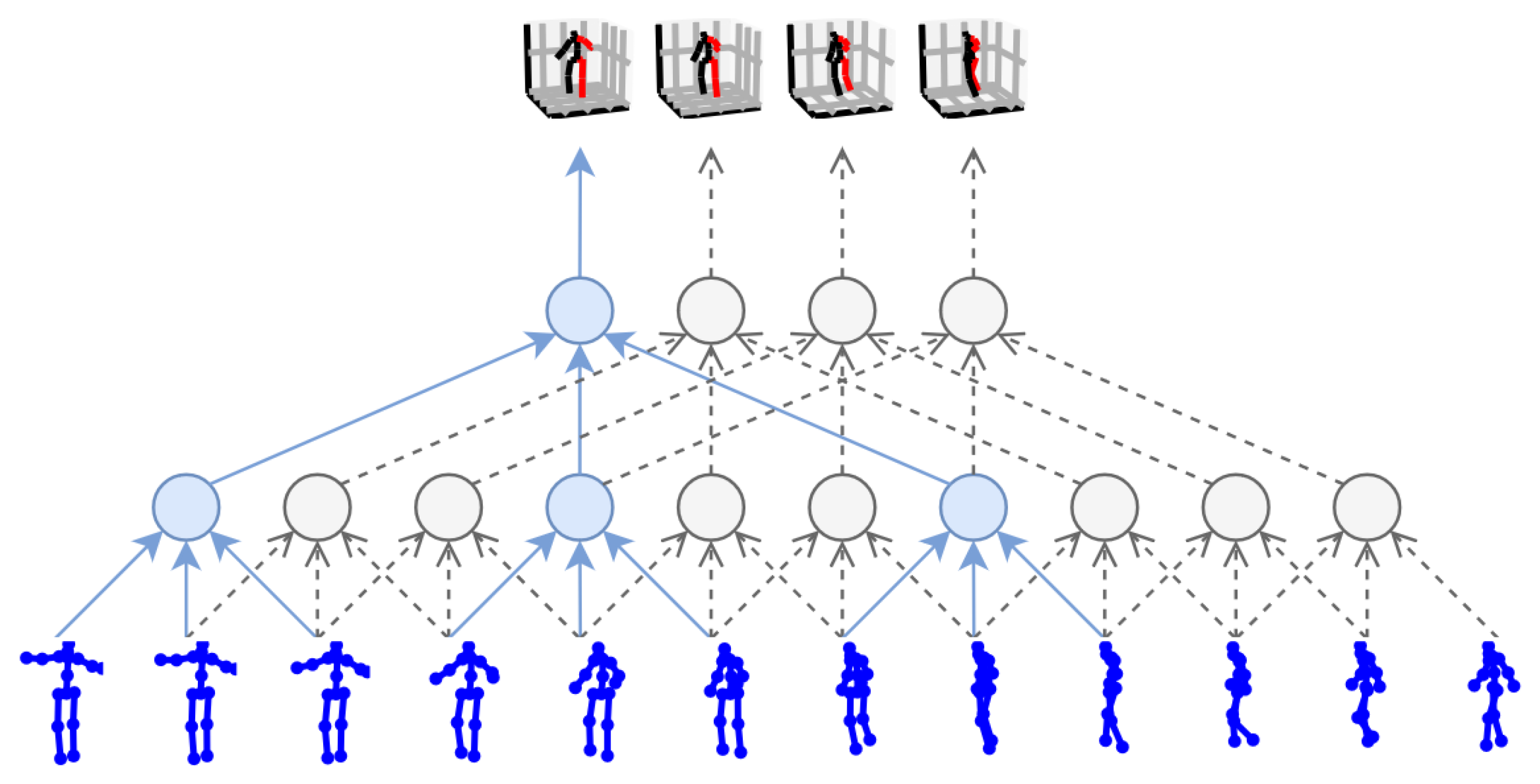
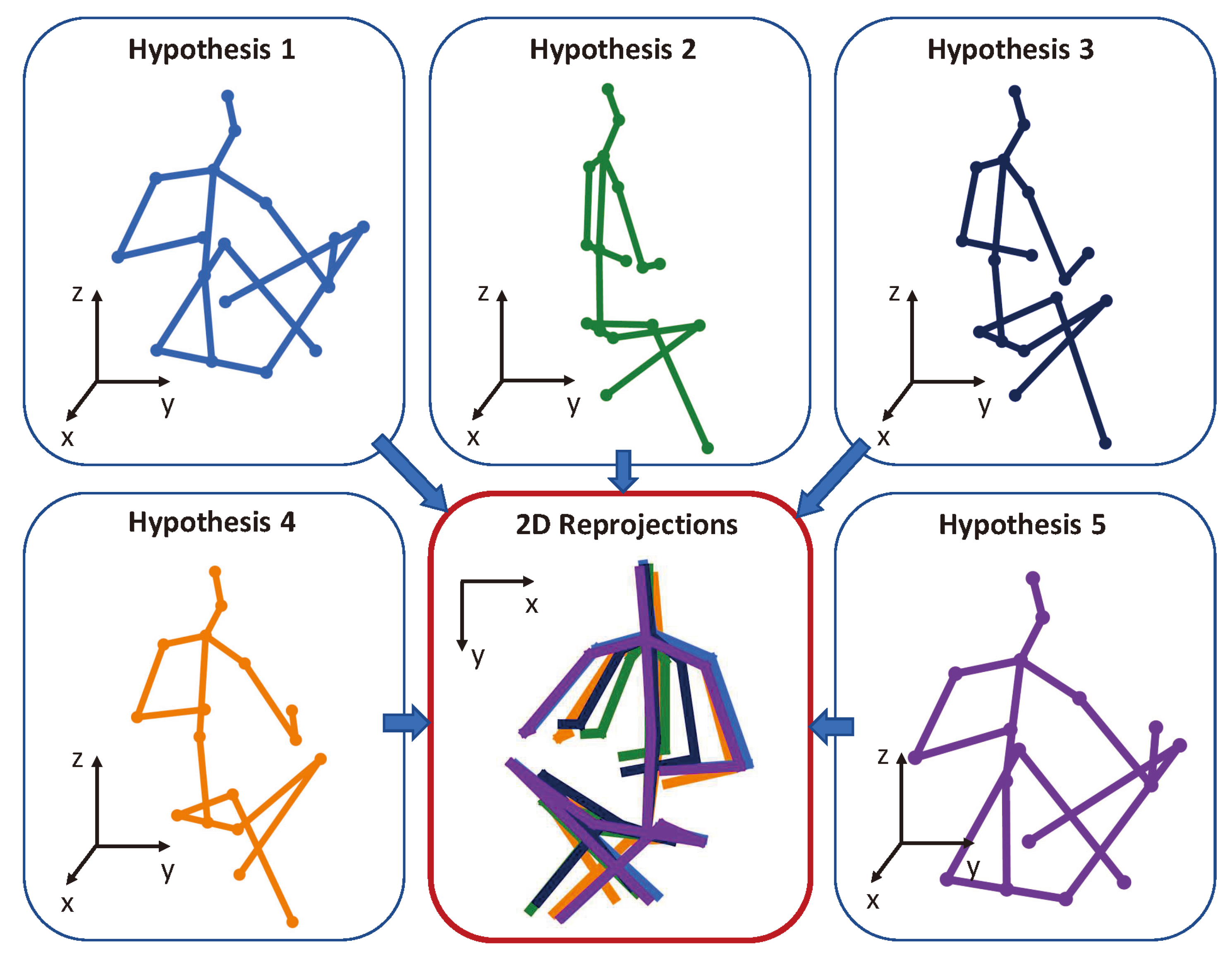
3.1.2. Two-Dimensional-to-Three-Dimensional Lifting
3.1.3. Comparison
3.2. Multi-Person 3D HPE
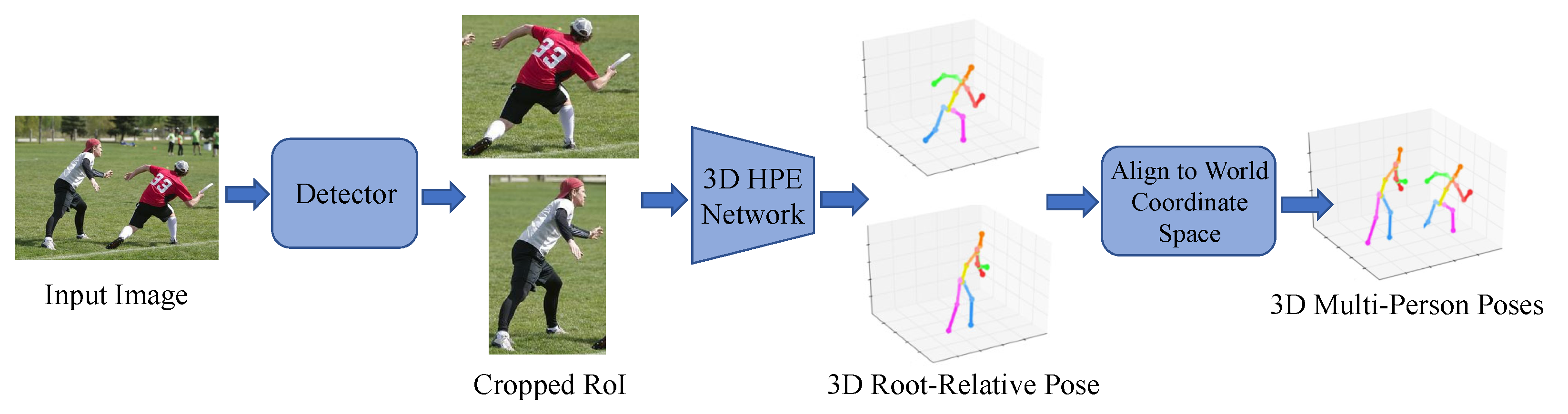
3.2.1. Top-Down Methods
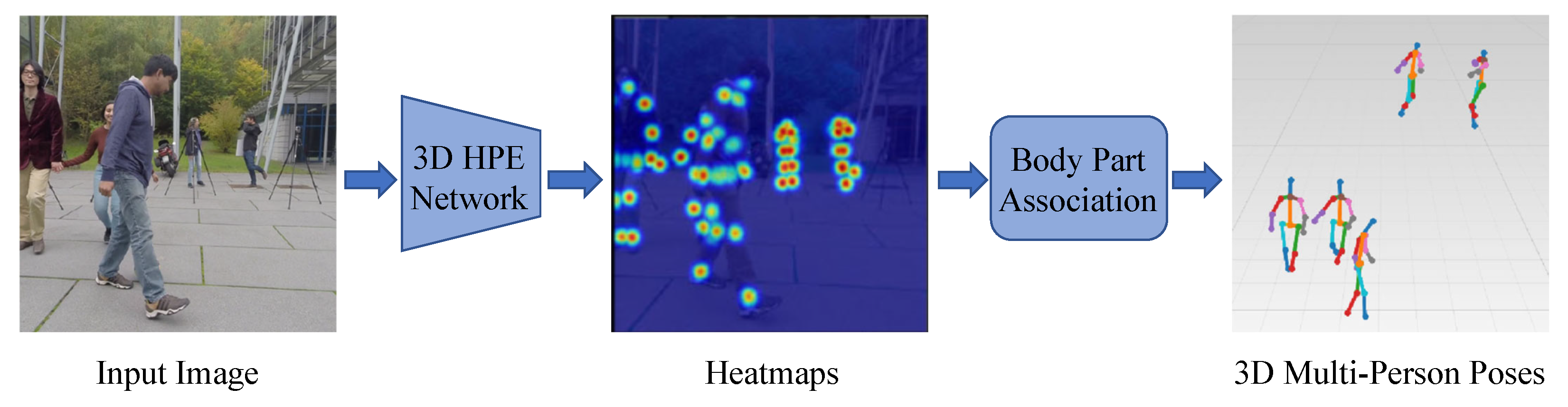
3.2.2. Bottom-Up Methods
3.2.3. Comparison
4. Three-Dimensional HPE from Videos
4.1. Recurrent-Based Methods
4.2. TCN-Based Methods
4.3. Transformer-Based Methods
4.4. Mamba-Based Methods
4.5. Comparison
5. Datasets and Evaluation Metrics
5.1. Datasets
5.2. Evaluation Metrics
6. Challenges
| Challenge | Reference | Input | Frames | Network | Dataset | EP 1 | Score |
|---|---|---|---|---|---|---|---|
| Scarcity of datasets | [80] | Video | 243 | TCN | Human3.6M | MPJPE | 46.8 |
| [115] | Video | 243 | CNN | Human3.6M | MPJPE | 44.8 | |
| [124] | Image | - | CNN | Human3.6M | MPJPE | 50.2 | |
| [118] | Image | - | CNN | Human3.6M | MPJPE | 47.0 | |
| Depth ambiguity | [126] | Image | - | Real-NVP | Human3.6M | MPJPE | 44.3 |
| [48] | Image | - | GCN | Human3.6M | MPJPE | 52.7 | |
| [114] | Video | 7 | GCN | Human3.6M | MPJPE | 48.8 | |
| [61] | Video | 243 | Transformer | Human3.6M | MPJPE | 40.0 | |
| Occlusion | [128] | Video | 64 | TCN | Human3.6M | MPJPE | 41.2 |
| [129] | Video | 243 | Transformer | Human3.6M | MPJPE | 42.1 | |
| [131] | Video | 128 | TCN | Human3.6M | MPJPE | 44.1 | |
| [69] | Image | - | CNN | JTA [138] | 3DPCK | 83.2 | |
| [134] | Video | 243 | GCN+TCN | 3DPW | MPJPE | 64.2 | |
| Motion smoothness | [9] | Video | 81 | Transformer | Human3.6M | MPJPE | 44.3 |
| [89] | Video | 243 | Transformer | Human3.6M | MPJPE | 40.9 | |
| Kinematic distortion | [116] | Video | 243 | CNN | Human3.6M | MPJPE | 44.1 |
| [136] | Video | - | CNN | Human3.6M | MPJPE | 54.59 |
7. Applications
8. Conclusions and Future Direction
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Guo, P.; Li, P.; Lee, G.H.; Chirikjian, G. Multi-person 3D Pose Estimation in Crowded Scenes Based on Multi-view Geometry. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020; pp. 541–557. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, J.; Cai, Y.; Yan, S.; Feng, J. Direct Multi-view Multi-person 3D Pose Estimation. In Proceedings of the Advances in Neural Information Processing Systems, Online, 6–14 December 2021; Ranzato, M., Beygelzimer, A., Dauphin, Y., Liang, P., Vaughan, J.W., Eds.; Curran Associates, Inc.: New York, NY, USA, 2021; Volume 34, pp. 13153–13164. [Google Scholar]
- Karagoz, B.; Suat, O.; Uguz, B.; Akbas, E. Dense depth alignment for human pose and shape estimation. Signal Image Video Process. 2024, 18, 8577–8584. [Google Scholar] [CrossRef]
- Carraro, M.; Munaro, M.; Burke, J.; Menegatti, E. Real-Time Marker-Less Multi-person 3D Pose Estimation in RGB-Depth Camera Networks. In Proceedings of the Intelligent Autonomous Systems 15, Baden-Baden, Germany, 11–15 June 2018; Strand, M., Dillmann, R., Menegatti, E., Ghidoni, S., Eds.; Springer: Cham, Switzerland, 2019; pp. 534–545. [Google Scholar] [CrossRef]
- Pascual-Hernández, D.; De Frutos, N.O.; Mora-Jiménez, I.; Cañas-Plaza, J.M. Efficient 3D human pose estimation from RGBD sensors. Displays 2022, 74, 102225. [Google Scholar] [CrossRef]
- Rim, B.; Sung, N.J.; Ma, J.; Choi, Y.J.; Hong, M. Real-time human pose estimation using RGB-D images and deep learning. J. Internet Comput. Serv. 2020, 21, 113–121. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of Oriented Gradients for Human Detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar] [CrossRef]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 2, pp. 1150–1157. [Google Scholar]
- Zheng, C.; Zhu, S.; Mendieta, M.; Yang, T.; Chen, C.; Ding, Z. 3D Human Pose Estimation with Spatial and Temporal Transformers. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 11636–11645. [Google Scholar] [CrossRef]
- Holte, M.B.; Tran, C.; Trivedi, M.M.; Moeslund, T.B. Human Pose Estimation and Activity Recognition From Multi-View Videos: Comparative Explorations of Recent Developments. IEEE J. Sel. Top. Signal Process. 2012, 6, 538–552. [Google Scholar] [CrossRef]
- Chen, L.; Wei, H.; Ferryman, J. A survey of human motion analysis using depth imagery. Pattern Recognit. Lett. 2013, 34, 1995–2006. [Google Scholar] [CrossRef]
- Perez-Sala, X.; Escalera, S.; Angulo, C.; Gonzàlez, J. A Survey on Model Based Approaches for 2D and 3D Visual Human Pose Recovery. Sensors 2014, 14, 4189–4210. [Google Scholar] [CrossRef]
- Wang, P.; Li, W.; Ogunbona, P.; Wan, J.; Escalera, S. RGB-D-based human motion recognition with deep learning: A survey. Comput. Vis. Image Underst. 2018, 171, 118–139. [Google Scholar] [CrossRef]
- Zheng, C.; Wu, W.; Chen, C.; Yang, T.; Zhu, S.; Shen, J.; Kehtarnavaz, N.; Shah, M. Deep Learning-based Human Pose Estimation: A Survey. ACM Comput. Surv. 2024, 56, 1–37. [Google Scholar] [CrossRef]
- Chen, Y.; Tian, Y.; He, M. Monocular human pose estimation: A survey of deep learning-based methods. Comput. Vis. Image Underst. 2020, 192, 102897. [Google Scholar] [CrossRef]
- Gong, W.; Zhang, X.; Gonzàlez, J.; Sobral, A.; Bouwmans, T.; Tu, C.; Zahzah, E.h. Human Pose Estimation from Monocular Images: A Comprehensive Survey. Sensors 2016, 16, 1966. [Google Scholar] [CrossRef]
- Munea, T.L.; Jembre, Y.Z.; Weldegebriel, H.T.; Chen, L.; Huang, C.; Yang, C. The Progress of Human Pose Estimation: A Survey and Taxonomy of Models Applied in 2D Human Pose Estimation. IEEE Access 2020, 8, 133330–133348. [Google Scholar] [CrossRef]
- Wang, J.; Tan, S.; Zhen, X.; Xu, S.; Zheng, F.; He, Z.; Shao, L. Deep 3D human pose estimation: A review. Comput. Vis. Image Underst. 2021, 210, 103225. [Google Scholar] [CrossRef]
- Liu, W.; Bao, Q.; Sun, Y.; Mei, T. Recent Advances of Monocular 2D and 3D Human Pose Estimation: A Deep Learning Perspective. ACM Comput. Surv. 2023, 55, 1–41. [Google Scholar] [CrossRef]
- Neupane, R.B.; Li, K.; Boka, T.F. A survey on deep 3D human pose estimation. Artif. Intell. Rev. 2024, 58, 24. [Google Scholar] [CrossRef]
- Ionescu, C.; Papava, D.; Olaru, V.; Sminchisescu, C. Human3.6M: Large Scale Datasets and Predictive Methods for 3D Human Sensing in Natural Environments. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1325–1339. [Google Scholar] [CrossRef]
- Sigal, L.; Balan, A.O.; Black, M.J. HumanEva: Synchronized Video and Motion Capture Dataset and Baseline Algorithm for Evaluation of Articulated Human Motion. Int. J. Comput. Vis. 2010, 87, 4–27. [Google Scholar] [CrossRef]
- Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; Black, M.J. SMPL: A skinned multi-person linear model. ACM Trans. Graph. 2015, 34, 1–16. [Google Scholar] [CrossRef]
- Pavlakos, G.; Choutas, V.; Ghorbani, N.; Bolkart, T.; Osman, A.A.; Tzionas, D.; Black, M.J. Expressive Body Capture: 3D Hands, Face, and Body From a Single Image. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 10967–10977. [Google Scholar] [CrossRef]
- Santesteban, I.; Garces, E.; Otaduy, M.A.; Casas, D. SoftSMPL: Data-driven Modeling of Nonlinear Soft-tissue Dynamics for Parametric Humans. Comput. Graph. Forum 2020, 39, 65–75. [Google Scholar] [CrossRef]
- Osman, A.A.A.; Bolkart, T.; Black, M.J. STAR: Sparse Trained Articulated Human Body Regressor. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020; pp. 598–613. [Google Scholar] [CrossRef]
- Wang, H.; Güler, R.A.; Kokkinos, I.; Papandreou, G.; Zafeiriou, S. BLSM: A Bone-Level Skinned Model of the Human Mesh. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020; pp. 1–17. [Google Scholar] [CrossRef]
- Xu, H.; Bazavan, E.G.; Zanfir, A.; Freeman, W.T.; Sukthankar, R.; Sminchisescu, C. GHUM & GHUML: Generative 3D Human Shape and Articulated Pose Models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 6184–6193. [Google Scholar]
- Li, S.; Chan, A.B. 3D Human Pose Estimation from Monocular Images with Deep Convolutional Neural Network. In Proceedings of the Computer Vision—ACCV 2014, Singapore, 1–5 November 2014; Cremers, D., Reid, I., Saito, H., Yang, M.H., Eds.; Springer: Cham, Switzerland, 2015; pp. 332–347. [Google Scholar] [CrossRef]
- Park, S.; Hwang, J.; Kwak, N. 3D Human Pose Estimation Using Convolutional Neural Networks with 2D Pose Information. In Proceedings of the Computer Vision—ECCV 2016 Workshops, Amsterdam, The Netherlands, 8–10, 15–16 October 2016; Hua, G., Jégou, H., Eds.; Springer: Cham, Switzerland, 2016; pp. 156–169. [Google Scholar] [CrossRef]
- Mehta, D.; Rhodin, H.; Casas, D.; Fua, P.; Sotnychenko, O.; Xu, W.; Theobalt, C. Monocular 3D Human Pose Estimation in the Wild Using Improved CNN Supervision. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 506–516, ISSN 2475-7888. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, Q.; Sun, X.; Xue, X.; Wei, Y. Towards 3D Human Pose Estimation in the Wild: A Weakly-Supervised Approach. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 398–407. [Google Scholar] [CrossRef]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic Routing Between Capsules. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30, pp. 3859–3869. [Google Scholar]
- Ramírez, I.; Cuesta-Infante, A.; Schiavi, E.; Pantrigo, J.J. Bayesian capsule networks for 3D human pose estimation from single 2D images. Neurocomputing 2020, 379, 64–73. [Google Scholar] [CrossRef]
- Garau, N.; Conci, N. CapsulePose: A variational CapsNet for real-time end-to-end 3D human pose estimation. Neurocomputing 2023, 523, 81–91. [Google Scholar] [CrossRef]
- Hinton, G.E.; Sabour, S.; Frosst, N. Matrix capsules with EM routing. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018; pp. 2048–2062. [Google Scholar]
- Zhao, Q.; Zheng, C.; Liu, M.; Chen, C. A Single 2D Pose with Context is Worth Hundreds for 3D Human Pose Estimation. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023; Oh, A., Naumann, T., Globerson, A., Saenko, K., Hardt, M., Levine, S., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2023; Volume 36, pp. 27394–27413. [Google Scholar]
- Cao, Z.; Simon, T.; Wei, S.E.; Sheikh, Y. Realtime Multi-person 2D Pose Estimation Using Part Affinity Fields. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1302–1310. [Google Scholar] [CrossRef]
- Newell, A.; Yang, K.; Deng, J. Stacked Hourglass Networks for Human Pose Estimation. In Proceedings of the Computer Vision—ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, Switzerland, 2016; pp. 483–499. [Google Scholar] [CrossRef]
- Chen, C.H.; Ramanan, D. 3D Human Pose Estimation = 2D Pose Estimation + Matching. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5759–5767. [Google Scholar] [CrossRef]
- Martinez, J.; Hossain, R.; Romero, J.; Little, J.J. A Simple Yet Effective Baseline for 3d Human Pose Estimation. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2659–2668. [Google Scholar] [CrossRef]
- Nie, Q.; Liu, Z.; Liu, Y. Unsupervised 3D Human Pose Representation with Viewpoint and Pose Disentanglement. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020; pp. 102–118. [Google Scholar] [CrossRef]
- Kundu, J.N.; Seth, S.; M V, R.; Rakesh, M.; Radhakrishnan, V.B.; Chakraborty, A. Kinematic-Structure-Preserved Representation for Unsupervised 3D Human Pose Estimation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 11312–11319. [Google Scholar] [CrossRef]
- Moreno-Noguer, F. 3D Human Pose Estimation from a Single Image via Distance Matrix Regression. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1561–1570. [Google Scholar] [CrossRef]
- Zhao, L.; Peng, X.; Tian, Y.; Kapadia, M.; Metaxas, D.N. Semantic Graph Convolutional Networks for 3D Human Pose Regression. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3420–3430. [Google Scholar] [CrossRef]
- Liu, K.; Ding, R.; Zou, Z.; Wang, L.; Tang, W. A Comprehensive Study of Weight Sharing in Graph Networks for 3D Human Pose Estimation. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020; pp. 318–334. [Google Scholar] [CrossRef]
- Zou, Z.; Tang, W. Modulated Graph Convolutional Network for 3D Human Pose Estimation. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 11457–11467. [Google Scholar] [CrossRef]
- Ci, H.; Wang, C.; Ma, X.; Wang, Y. Optimizing Network Structure for 3D Human Pose Estimation. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2262–2271. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z.; Yuan, C.; Li, B.; Deng, Y.; Hu, W. Channel-wise Topology Refinement Graph Convolution for Skeleton-Based Action Recognition. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 13339–13348. [Google Scholar] [CrossRef]
- Zou, Z.; Liu, K.; Wang, L.; Tang, W. High-order Graph Convolutional Networks for 3D Human Pose Estimation. In Proceedings of the BMVC, Virtual Event, UK, 7–10 September 2020; p. 550. [Google Scholar]
- Quan, J.; Hamza, A.B. Higher-order implicit fairing networks for 3D human pose estimation. arXiv 2021, arXiv:2111.00950. [Google Scholar]
- Li, W.; Liu, M.; Liu, H.; Guo, T.; Wang, T.; Tang, H.; Sebe, N. GraphMLP: A graph MLP-like architecture for 3D human pose estimation. Pattern Recognit. 2025, 158, 110925. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N., Weinberger, K., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2014; Volume 27, pp. 2672–2680. [Google Scholar]
- Deng, Y.; Sun, Y.; Zhu, J. SVMA: A GAN-based model for Monocular 3D Human Pose Estimation. arXiv 2021, arXiv:2106.05616. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Sharma, S.; Varigonda, P.T.; Bindal, P.; Sharma, A.; Jain, A. Monocular 3D Human Pose Estimation by Generation and Ordinal Ranking. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2325–2334. [Google Scholar] [CrossRef]
- Levy, M.; Shrivastava, A. V-VIPE: Variational View Invariant Pose Embedding. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 16–22 June 2024; pp. 1633–1642. [Google Scholar] [CrossRef]
- Sohl-Dickstein, J.; Weiss, E.; Maheswaranathan, N.; Ganguli, S. Deep Unsupervised Learning using Nonequilibrium Thermodynamics. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 7–9 July 2015; Volume 37, pp. 2256–2265. [Google Scholar]
- Gong, J.; Foo, L.G.; Fan, Z.; Ke, Q.; Rahmani, H.; Liu, J. DiffPose: Toward More Reliable 3D Pose Estimation. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 13041–13051. [Google Scholar] [CrossRef]
- Shan, W.; Liu, Z.; Zhang, X.; Wang, Z.; Han, K.; Wang, S.; Ma, S.; Gao, W. Diffusion-Based 3D Human Pose Estimation with Multi-Hypothesis Aggregation. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 14715–14725. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhou, Z.; Li, L.; Chai, W.; Yang, C.Y.; Hwang, J.N. Back to Optimization: Diffusion-based Zero-Shot 3D Human Pose Estimation. In Proceedings of the 2024 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2024; pp. 6130–6140. [Google Scholar] [CrossRef]
- Cai, Q.; Hu, X.; Hou, S.; Yao, L.; Huang, Y. Disentangled Diffusion-Based 3D Human Pose Estimation with Hierarchical Spatial and Temporal Denoiser. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 26–27 February 2024; Volume 38, pp. 882–890. [Google Scholar] [CrossRef]
- Ji, H.; Deng, H.; Dai, Y.; Li, H. Unsupervised 3D Pose Estimation with Non-Rigid Structure-from-Motion Modeling. In Proceedings of the 2024 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2024; pp. 3302–3311. [Google Scholar] [CrossRef]
- Xu, J.; Guo, Y.; Peng, Y. FinePOSE: Fine-Grained Prompt-Driven 3D Human Pose Estimation via Diffusion Models. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 17–21 June 2024; pp. 561–570. [Google Scholar] [CrossRef]
- Song, J.; Meng, C.; Ermon, S. Denoising diffusion implicit models. arXiv 2020, arXiv:2010.02502. [Google Scholar]
- Song, Y.; Sohl-Dickstein, J.; Kingma, D.P.; Kumar, A.; Ermon, S.; Poole, B. Score-based generative modeling through stochastic differential equations. arXiv 2020, arXiv:2011.13456. [Google Scholar]
- Moon, G.; Chang, J.Y.; Lee, K.M. Camera Distance-Aware Top-Down Approach for 3D Multi-Person Pose Estimation From a Single RGB Image. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 10132–10141. [Google Scholar] [CrossRef]
- Benzine, A.; Chabot, F.; Luvison, B.; Pham, Q.C.; Achard, C. PandaNet: Anchor-Based Single-Shot Multi-Person 3D Pose Estimation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 6855–6864. [Google Scholar] [CrossRef]
- Khirodkar, R.; Chari, V.; Agrawal, A.; Tyagi, A. Multi-Instance Pose Networks: Rethinking Top-Down Pose Estimation. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 3102–3111. [Google Scholar] [CrossRef]
- Wang, C.; Li, J.; Liu, W.; Qian, C.; Lu, C. HMOR: Hierarchical Multi-person Ordinal Relations for Monocular Multi-person 3D Pose Estimation. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020; pp. 242–259. [Google Scholar] [CrossRef]
- Qiu, Z.; Yang, Q.; Wang, J.; Fu, D. Dynamic Graph Reasoning for Multi-person 3D Pose Estimation. In Proceedings of the 30th ACM International Conference on Multimedia, Lisboa, Portugal, 10–14 October 2022; pp. 3521–3529. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, B.; Tan, R.T. Dual Networks Based 3D Multi-Person Pose Estimation From Monocular Video. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 1636–1651. [Google Scholar] [CrossRef]
- Zanfir, A.; Marinoiu, E.; Zanfir, M.; Popa, A.I.; Sminchisescu, C. Deep Network for the Integrated 3D Sensing of Multiple People in Natural Images. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2018; Volume 31, pp. 8410–8419. [Google Scholar]
- Fabbri, M.; Lanzi, F.; Calderara, S.; Alletto, S.; Cucchiara, R. Compressed Volumetric Heatmaps for Multi-Person 3D Pose Estimation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 7202–7211. [Google Scholar] [CrossRef]
- Zhen, J.; Fang, Q.; Sun, J.; Liu, W.; Jiang, W.; Bao, H.; Zhou, X. SMAP: Single-Shot Multi-person Absolute 3D Pose Estimation. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020; pp. 550–566. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, Y.; Bai, S.; Yuille, A. Explicit Occlusion Reasoning for Multi-person 3D Human Pose Estimation. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer: Cham, Switzerland, 2022; pp. 497–517. [Google Scholar] [CrossRef]
- Mehta, D.; Sotnychenko, O.; Mueller, F.; Xu, W.; Sridhar, S.; Pons-Moll, G.; Theobalt, C. Single-Shot Multi-person 3D Pose Estimation from Monocular RGB. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 120–130. [Google Scholar] [CrossRef]
- Li, W.; Liu, H.; Ding, R.; Liu, M.; Wang, P.; Yang, W. Exploiting Temporal Contexts With Strided Transformer for 3D Human Pose Estimation. IEEE Trans. Multimed. 2023, 25, 1282–1293. [Google Scholar] [CrossRef]
- Pavllo, D.; Feichtenhofer, C.; Grangier, D.; Auli, M. 3D Human Pose Estimation in Video With Temporal Convolutions and Semi-Supervised Training. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7745–7754. [Google Scholar] [CrossRef]
- Lin, M.; Lin, L.; Liang, X.; Wang, K.; Cheng, H. Recurrent 3D Pose Sequence Machines. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5543–5552. [Google Scholar] [CrossRef]
- Lee, K.; Lee, I.; Lee, S. Propagating LSTM: 3D Pose Estimation based on Joint Interdependency. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 119–135. [Google Scholar]
- Hossain, M.R.I.; Little, J.J. Exploiting temporal information for 3D human pose estimation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 68–84. [Google Scholar]
- Liu, R.; Shen, J.; Wang, H.; Chen, C.; Cheung, S.c.; Asari, V. Attention Mechanism Exploits Temporal Contexts: Real-Time 3D Human Pose Reconstruction. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 5063–5072. [Google Scholar] [CrossRef]
- Shan, W.; Lu, H.; Wang, S.; Zhang, X.; Gao, W. Improving Robustness and Accuracy via Relative Information Encoding in 3D Human Pose Estimation. In Proceedings of the 29th ACM International Conference on Multimedia, Virtual Event, 20–24 October 2021; pp. 3446–3454. [Google Scholar] [CrossRef]
- Yuan, S.; Zhou, L. GTA-Net: An IoT-integrated 3D human pose estimation system for real-time adolescent sports posture correction. Alex. Eng. J. 2025, 112, 585–597. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.U.; Polosukhin, I. Attention is All you Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2017; Volume 30, pp. 5998–6008. [Google Scholar]
- Zhang, J.; Tu, Z.; Yang, J.; Chen, Y.; Yuan, J. MixSTE: Seq2seq Mixed Spatio-Temporal Encoder for 3D Human Pose Estimation in Video. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 13222–13232. [Google Scholar] [CrossRef]
- Li, W.; Liu, H.; Tang, H.; Wang, P.; Van Gool, L. MHFormer: Multi-Hypothesis Transformer for 3D Human Pose Estimation. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 13137–13146. [Google Scholar] [CrossRef]
- Wang, W.; Chen, W.; Qiu, Q.; Chen, L.; Wu, B.; Lin, B.; He, X.; Liu, W. CrossFormer++: A Versatile Vision Transformer Hinging on Cross-Scale Attention. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 3123–3136. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Wang, W.; Tian, Y. GraFormer: Graph-oriented Transformer for 3D Pose Estimation. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 20406–20415. [Google Scholar] [CrossRef]
- Chen, H.; He, J.Y.; Xiang, W.; Cheng, Z.Q.; Liu, W.; Liu, H.; Luo, B.; Geng, Y.; Xie, X. HDFormer: High-order Directed Transformer for 3D Human Pose Estimation. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, Macau SAR, China, 19–25 August 2023; pp. 581–589. [Google Scholar] [CrossRef]
- Mehraban, S.; Adeli, V.; Taati, B. MotionAGFormer: Enhancing 3D Human Pose Estimation with a Transformer-GCNFormer Network. In Proceedings of the 2024 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2024; pp. 6905–6915. [Google Scholar] [CrossRef]
- Wei, M.; Xie, X.; Zhong, Y.; Shi, G. Learning Pyramid-structured Long-range Dependencies for 3D Human Pose Estimation. IEEE Trans. Multimed. 2025, 1–14. [Google Scholar] [CrossRef]
- Peng, J.; Zhou, Y.; Mok, P.Y. KTPFormer: Kinematics and Trajectory Prior Knowledge-Enhanced Transformer for 3D Human Pose Estimation. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 1123–1132. [Google Scholar] [CrossRef]
- Einfalt, M.; Ludwig, K.; Lienhart, R. Uplift and Upsample: Efficient 3D Human Pose Estimation with Uplifting Transformers. In Proceedings of the 2023 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 2–7 January 2023; pp. 2902–2912. [Google Scholar] [CrossRef]
- Zhao, Q.; Zheng, C.; Liu, M.; Wang, P.; Chen, C. PoseFormerV2: Exploring Frequency Domain for Efficient and Robust 3D Human Pose Estimation. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 8877–8886. [Google Scholar] [CrossRef]
- Li, W.; Liu, M.; Liu, H.; Wang, P.; Cai, J.; Sebe, N. Hourglass Tokenizer for Efficient Transformer-Based 3D Human Pose Estimation. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 604–613. [Google Scholar] [CrossRef]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar]
- Huang, Y.; Liu, J.; Xian, K.; Qiu, R.C. PoseMamba: Monocular 3D Human Pose Estimation with Bidirectional Global-Local Spatio-Temporal State Space Model. arXiv 2024, arXiv:2408.03540. [Google Scholar]
- Zhang, X.; Bao, Q.; Cui, Q.; Yang, W.; Liao, Q. Pose Magic: Efficient and Temporally Consistent Human Pose Estimation with a Hybrid Mamba-GCN Network. arXiv 2024, arXiv:2408.02922. [Google Scholar]
- Li, Y.; Wang, Z.; Niu, W. SMGNFORMER: Fusion Mamba-graph transformer network for human pose estimation. IET Comput. Vis. 2025, 19, e12339. [Google Scholar] [CrossRef]
- Wei, S.E.; Ramakrishna, V.; Kanade, T.; Sheikh, Y. Convolutional Pose Machines. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4724–4732. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Z.; Peng, Y.; Zhang, Z.; Yu, G.; Sun, J. Cascaded Pyramid Network for Multi-person Pose Estimation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7103–7112. [Google Scholar] [CrossRef]
- Joo, H.; Liu, H.; Tan, L.; Gui, L.; Nabbe, B.; Matthews, I.; Kanade, T.; Nobuhara, S.; Sheikh, Y. Panoptic Studio: A Massively Multiview System for Social Motion Capture. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 3334–3342. [Google Scholar] [CrossRef]
- Trumble, M.; Gilbert, A.; Malleson, C.; Hilton, A.; Collomosse, J. Total Capture: 3D Human Pose Estimation Fusing Video and Inertial Sensors. In Proceedings of the Procedings of the British Machine Vision Conference 2017, London, UK, 4–7 September 2017; p. 14. [Google Scholar] [CrossRef]
- Von Marcard, T.; Henschel, R.; Black, M.J.; Rosenhahn, B.; Pons-Moll, G. Recovering Accurate 3D Human Pose in The Wild Using IMUs and a Moving Camera. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 601–617. [Google Scholar]
- Zhu, L.; Rematas, K.; Curless, B.; Seitz, S.M.; Kemelmacher-Shlizerman, I. Reconstructing NBA Players. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020; pp. 177–194. [Google Scholar] [CrossRef]
- Cao, Z.; Gao, H.; Mangalam, K.; Cai, Q.Z.; Vo, M.; Malik, J. Long-Term Human Motion Prediction with Scene Context. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020; pp. 387–404. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Qiu, W.; Qin, W.; Zeng, W. AdaFuse: Adaptive Multiview Fusion for Accurate Human Pose Estimation in the Wild. Int. J. Comput. Vis. 2021, 129, 703–718. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, J.; Cao, Q.; Tao, D. PoseBench: Benchmarking the Robustness of Pose Estimation Models under Corruptions. arXiv 2024, arXiv:2406.14367. [Google Scholar]
- Li, C.; Lee, G.H. Generating Multiple Hypotheses for 3D Human Pose Estimation with Mixture Density Network. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9879–9887. [Google Scholar] [CrossRef]
- Cai, Y.; Ge, L.; Liu, J.; Cai, J.; Cham, T.J.; Yuan, J.; Thalmann, N.M. Exploiting Spatial-Temporal Relationships for 3D Pose Estimation via Graph Convolutional Networks. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2272–2281. [Google Scholar] [CrossRef]
- Zeng, A.; Sun, X.; Huang, F.; Liu, M.; Xu, Q.; Lin, S. SRNet: Improving Generalization in 3D Human Pose Estimation with a Split-and-Recombine Approach. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020; pp. 507–523. [Google Scholar] [CrossRef]
- Chen, T.; Fang, C.; Shen, X.; Zhu, Y.; Chen, Z.; Luo, J. Anatomy-Aware 3D Human Pose Estimation with Bone-Based Pose Decomposition. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 198–209. [Google Scholar] [CrossRef]
- Yang, Y.; Qiao, Y.; Sun, X. Mask asSupervision: Leveraging Unified Mask Information for Unsupervised 3D Pose Estimation. In Proceedings of the Computer Vision—ECCV 2024, Milan, Italy, 29 September–4 October 2024; Leonardis, A., Ricci, E., Roth, S., Russakovsky, O., Sattler, T., Varol, G., Eds.; Springer: Cham, Switzerland, 2025; pp. 38–55. [Google Scholar] [CrossRef]
- Du, S.; Yuan, Z.; Lai, P.; Ikenaga, T. JoyPose: Jointly learning evolutionary data augmentation and anatomy-aware global–local representation for 3D human pose estimation. Pattern Recognit. 2024, 147, 110116. [Google Scholar] [CrossRef]
- Ji, B.; Yang, C.; Shunyu, Y.; Pan, Y. HPOF:3D Human Pose Recovery from Monocular Video with Optical Flow. In Proceedings of the 2021 International Conference on Multimedia Retrieval, Taipei, Taiwan, 21–24 August 2021; pp. 144–154. [Google Scholar] [CrossRef]
- Zhao, C.; Uchitomi, H.; Ogata, T.; Ming, X.; Miyake, Y. Reducing the device complexity for 3D human pose estimation: A deep learning approach using monocular camera and IMUs. Eng. Appl. Artif. Intell. 2023, 124, 106639. [Google Scholar] [CrossRef]
- Rogez, G.; Schmid, C. MoCap-guided Data Augmentation for 3D Pose Estimation in the Wild. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Lee, D., Sugiyama, M., Luxburg, U., Guyon, I., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2016; Volume 29, pp. 3108–3116. [Google Scholar]
- Wang, J.; Yang, F.; Li, B.; Gou, W.; Yan, D.; Zeng, A.; Gao, Y.; Wang, J.; Jing, Y.; Zhang, R. FreeMan: Towards Benchmarking 3D Human Pose Estimation Under Real-World Conditions. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 21978–21988. [Google Scholar] [CrossRef]
- Peng, Q.; Zheng, C.; Chen, C. A Dual-Augmentor Framework for Domain Generalization in 3D Human Pose Estimation. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 2240–2249. [Google Scholar] [CrossRef]
- Gong, K.; Zhang, J.; Feng, J. PoseAug: A Differentiable Pose Augmentation Framework for 3D Human Pose Estimation. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 8571–8580. [Google Scholar] [CrossRef]
- Doersch, C.; Zisserman, A. Sim2real transfer learning for 3D human pose estimation: Motion to the rescue. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2019; Volume 32, pp. 12949–12961. [Google Scholar]
- Wehrbein, T.; Rudolph, M.; Rosenhahn, B.; Wandt, B. Probabilistic Monocular 3D Human Pose Estimation with Normalizing Flows. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 11179–11188. [Google Scholar] [CrossRef]
- Jahangiri, E.; Yuille, A.L. Generating Multiple Diverse Hypotheses for Human 3D Pose Consistent with 2D Joint Detections. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 22–29 October 2017; pp. 805–814. [Google Scholar] [CrossRef]
- Cheng, Y.; Yang, B.; Wang, B.; Tan, R.T. 3D Human Pose Estimation Using Spatio-Temporal Networks with Explicit Occlusion Training. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 10631–10638. [Google Scholar] [CrossRef]
- Shan, W.; Liu, Z.; Zhang, X.; Wang, S.; Ma, S.; Gao, W. P-STMO: Pre-trained Spatial Temporal Many-to-One Model for 3D Human Pose Estimation. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer: Cham, Switzerland, 2022; pp. 461–478. [Google Scholar] [CrossRef]
- Ghafoor, M.; Mahmood, A. Quantification of Occlusion Handling Capability of a 3D Human Pose Estimation Framework. IEEE Trans. Multimed. 2023, 25, 3311–3318. [Google Scholar] [CrossRef]
- Cheng, Y.; Yang, B.; Wang, B.; Wending, Y.; Tan, R. Occlusion-Aware Networks for 3D Human Pose Estimation in Video. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 723–732. [Google Scholar] [CrossRef]
- Kundu, J.N.; Seth, S.; Jampani, V.; Rakesh, M.; Venkatesh Babu, R.; Chakraborty, A. Self-Supervised 3D Human Pose Estimation via Part Guided Novel Image Synthesis. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 6151–6161. [Google Scholar] [CrossRef]
- Kundu, J.N.; Seth, S.; Ym, P.; Jampani, V.; Chakraborty, A.; Babu, R.V. Uncertainty-Aware Adaptation for Self-Supervised 3D Human Pose Estimation. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 20416–20427. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, B.; Yang, B.; Tan, R.T. Graph and Temporal Convolutional Networks for 3D Multi-person Pose Estimation in Monocular Videos. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 1157–1165. [Google Scholar] [CrossRef]
- Xu, J.; Yu, Z.; Ni, B.; Yang, J.; Yang, X.; Zhang, W. Deep Kinematics Analysis for Monocular 3D Human Pose Estimation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 896–905. [Google Scholar] [CrossRef]
- Shi, M.; Aberman, K.; Aristidou, A.; Komura, T.; Lischinski, D.; Cohen-Or, D.; Chen, B. MotioNet: 3D Human Motion Reconstruction from Monocular Video with Skeleton Consistency. ACM Trans. Graph. 2021, 40, 1–15. [Google Scholar] [CrossRef]
- Wang, K.; Lin, L.; Jiang, C.; Qian, C.; Wei, P. 3D Human Pose Machines with Self-supervised Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 1069–1082. [Google Scholar] [CrossRef]
- Fabbri, M.; Lanzi, F.; Calderara, S.; Palazzi, A.; Vezzani, R.; Cucchiara, R. Learning to Detect and Track Visible and Occluded Body Joints in a Virtual World. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 430–446. [Google Scholar]
- Zhou, Y.; Cheng, Z.Q.; Li, C.; Fang, Y.; Geng, Y.; Xie, X.; Keuper, M. Hypergraph transformer for skeleton-based action recognition. arXiv 2022, arXiv:2211.09590. [Google Scholar]
- Du, W.; Li, A.; Zhou, P.; Niu, B.; Wu, D. PrivacyEye: A Privacy-Preserving and Computationally Efficient Deep Learning-Based Mobile Video Analytics System. IEEE Trans. Mob. Comput. 2022, 21, 3263–3279. [Google Scholar] [CrossRef]
- Ahmad, S.; Morerio, P.; Del Bue, A. Event Anonymization: Privacy-Preserving Person Re-Identification and Pose Estimation in Event-Based Vision. IEEE Access 2024, 12, 66964–66980. [Google Scholar] [CrossRef]
- Jain, A.; Akerkar, R.; Srivastava, A. Privacy-Preserving Human Activity Recognition System for Assisted Living Environments. IEEE Trans. Artif. Intell. 2024, 5, 2342–2357. [Google Scholar] [CrossRef]
- Sun, M.; Wang, Q.; Liu, Z. Human Action Image Generation with Differential Privacy. In Proceedings of the 2020 IEEE International Conference on Multimedia and Expo (ICME), London, UK, 6–10 July 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Huo, R.; Chen, J.; Zhang, Y.; Gao, Q. 3D skeleton aware driver behavior recognition framework for autonomous driving system. Neurocomputing 2025, 613, 128743. [Google Scholar] [CrossRef]
- Patel, C.; Liao, Z.; Pons-Moll, G. TailorNet: Predicting Clothing in 3D as a Function of Human Pose, Shape and Garment Style. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 7363–7373. [Google Scholar] [CrossRef]
- Liu, J.; Fu, H.; Tai, C.L. PoseTween: Pose-driven Tween Animation. In Proceedings of the 33rd Annual ACM Symposium on User Interface Software and Technology, Virtual Event, USA, 20–23 October 2020; pp. 791–804. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, Y.; Huang, H.; Zou, H.; Xie, L. MetaFi: Device-Free Pose Estimation via Commodity WiFi for Metaverse Avatar Simulation. In Proceedings of the 2022 IEEE 8th World Forum on Internet of Things (WF-IoT), Yokohama, Japan, 26 October–11 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Jiang, J.; Streli, P.; Qiu, H.; Fender, A.; Laich, L.; Snape, P.; Holz, C. AvatarPoser: Articulated Full-Body Pose Tracking from Sparse Motion Sensing. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer: Cham, Switzerland, 2022; pp. 443–460. [Google Scholar] [CrossRef]
- Zhang, H.; Sciutto, C.; Agrawala, M.; Fatahalian, K. Vid2Player: Controllable Video Sprites That Behave and Appear Like Professional Tennis Players. ACM Trans. Graph. 2021, 40, 1–16. [Google Scholar] [CrossRef]
- Lu, M.; Poston, K.; Pfefferbaum, A.; Sullivan, E.V.; Fei-Fei, L.; Pohl, K.M.; Niebles, J.C.; Adeli, E. Vision-Based Estimation of MDS-UPDRS Gait Scores for Assessing Parkinson’s Disease Motor Severity. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2020, Lima, Peru, 4–8 October 2020; Martel, A.L., Abolmaesumi, P., Stoyanov, D., Mateus, D., Zuluaga, M.A., Zhou, S.K., Racoceanu, D., Joskowicz, L., Eds.; Springer: Cham, Switzerland, 2020; pp. 637–647. [Google Scholar] [CrossRef]
- Amorim, A.; Guimares, D.; Mendona, T.; Neto, P.; Costa, P.; Moreira, A.P. Robust human position estimation in cooperative robotic cells. Robot. Comput.-Integr. Manuf. 2021, 67, 102035. [Google Scholar] [CrossRef]
- Zimmermann, C.; Welschehold, T.; Dornhege, C.; Burgard, W.; Brox, T. 3D Human Pose Estimation in RGBD Images for Robotic Task Learning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 1986–1992. [Google Scholar] [CrossRef]
- Chang, Y.; Wang, X.; Wang, J.; Wu, Y.; Yang, L.; Zhu, K.; Chen, H.; Yi, X.; Wang, C.; Wang, Y.; et al. A Survey on Evaluation of Large Language Models. ACM Trans. Intell. Syst. Technol. 2024, 15, 1–45. [Google Scholar] [CrossRef]








| Survey | Year | Journal | Content |
|---|---|---|---|
| Holte et al. [10] | 2012 | JSTSP | Discussed multi-view HPE and activity recognition. |
| Chen et al. [11] | 2013 | PRL | Reviewed human motion analysis using depth imagery, covering sensor technologies, datasets, and recognition methods. |
| Perez-Sala et al. [12] | 2014 | Sensors | Reviewed model-based approaches for 2D and 3D human pose recovery, focusing on appearance, viewpoint, spatial relations, temporal consistence, and behavior. |
| Gong et al. [16] | 2016 | Sensors | Surveys monocular HPE, covering both traditional and deep learning-based methods. |
| Munea et al. [17] | 2020 | IEEE Access | Classified pose estimation by the number of people (single vs. multi-person), and briefly discussed significant papers for both cases. |
| Chen et al. [15] | 2020 | CVIU | Reviewed deep learning-based monocular HPE, categorizing methods into 2D and 3D approaches, and discussing datasets, evaluation metrics, and future directions. |
| Wang et al. [18] | 2021 | CVIU | Reviewed deep learning-based 3D HPE methods, categorizing them into monocular, multi-view, and sequential approaches, and discussed datasets, evaluation metrics, and future directions. |
| Liu et al. [19] | 2022 | CSUR | Provided a comprehensive 2D-to-3D overview of monocular HPE with deep learning, covering skeleton- and model-based methods and future directions. |
| Zheng et al. [14] | 2023 | CSUR | Reviewed deep learning-based methods for 2D and 3D human pose estimation, summarizing key approaches, benchmark datasets, and evaluation metrics. |
| Neupane et al. [20] | 2024 | AIR | Surveyed deep 3D HPE paradigms, explored alternative learning and data augmentation, categorized challenges, and proposed future directions. |
| Feature | Kinematic Model | Volumetric Model |
|---|---|---|
| Construction method | Keypoints | Mesh |
| Occlusion handling | Less robust | More robust |
| Computational complexity | Low | High |
| Model detail | Low detail | High detail |
| Application scenario | Real time | Detail-oriented |
| Category | Type | References | Advantages | Limitations |
|---|---|---|---|---|
| End-to-end | CNN-based | [29,30] | Global image analysis, simple pipeline | High computational cost, environmental sensitivity |
| Transfer learning | [31,32] | |||
| Capsule network | [34,35] | |||
| 2D to 3D | CNN-based | [40,41,42,43,44] | 2D geometric relationships | Dependence on 2D keypoint accuracy |
| GCN-based | [45,46,47,48,49,50,51] | |||
| Diffusion-based | [59,60,61,62,63,64,65] |
| Category | References | Procedure | Region | Computational Complexity | Scale Sensitivity |
|---|---|---|---|---|---|
| Top-down | [68,69,70,71,72] | (1) Human detection (2) Estimate 3D pose | Cropped RoI | Grows with people | Low |
| Bottom-up | [74,75,76,77,78] | (1) Joint detection; (2) Joint clustering | Whole image | Linear complexity | High |
| Architecture | RNN and LSTM | TCN | Transformer | Mamba |
|---|---|---|---|---|
| Reference | [81,82,83] | [80,84,85] | [9,79,89,91,92,93,94,96,99] | [60,103] |
| Parameter Quantity | Low | Moderate | High | Moderate |
| Parallel Processing | Low | High | High | High |
| Model Flexibility | Fixed | Moderate | Adaptable | Adaptable |
| Long-Term Dependency | Limited | Moderate | Strong | Strong |
| Gradient Stability | Unstable | Stable | Stable | Stable |
| Computation Cost |
| Architecture | Reference | 2D Detector | Frames | Params (M) | FLOPs (M) | FPS | MPJPE |
|---|---|---|---|---|---|---|---|
| RNN | [81] | CNN | - | - | - | - | 80.15 |
| LSTM | [82] | CNN | - | - | - | - | 55.8 |
| [83] | CPM [104] | - | 16.95 | 33.88 | - | 58.3 | |
| TCN | [80] | CPN [105] | 243 | 16.95 | 33.87 | 863 | 46.8 |
| [84] | CPN | 243 | 11.25 | - | - | 45.1 | |
| [85] | CPN | 243 | - | - | - | 44.3 | |
| Transformer | [9] | CPN | 81 | 9.6 | 1358 | 269 | 44.3 |
| [79] | CPN | 243 | 4.23 | 1372 | 108 | 44.0 | |
| [89] | CPN | 243 | 33.7 | 645 | - | 40.9 | |
| [93] | HR-Net [75] | 96 | 3.7 | - | - | 42.6 | |
| [90] | CPN | 243 | 24.72 | 4812 | - | 43.2 | |
| Mamba | [101] | Hourglass [39] | 243 | 6.7 | - | - | 38.1 |
| [102] | Hourglass | 243 | 14.42 | 40.58 | - | 37.5 |
| Datasets | Year | Annotation Type | Joint | Environment | Size | EP a | MP b | MV c | Key Features |
|---|---|---|---|---|---|---|---|---|---|
| Real Dataset | |||||||||
| HumanEva | 2010 | 3D joints | 15 | Indoor | 40k frames | MPJPE | ✕ | ✓ | 6 subjects, 7 actions |
| Human3.6M | 2014 | 3D joints, mesh | 17 | Indoor | 3.6M frames | MPJPE | ✕ | ✓ | 11 subjects, 17 actions, bounding box, depth data |
| CMU Panoptic | 2016 | 3D joints | 15 | Indoor | 1.5M frames | 3DPCK | ✓ | ✓ | 8 subjects, depth data |
| MPI-INF-3DHP | 2017 | 3D joints | 15 | Indoor, outdoor | 1.3M frames | 3DPCK | ✕ | ✓ | 8 subjects, 8 actions, various scenarios |
| TotalCapture | 2017 | 3D joints | 26 | Indoor | 1.9M frames | MPJPE | ✕ | ✓ | 5 subjects, 5 actions |
| 3DPW | 2018 | 3D joints, mesh | 24 | Indoor, outdoor | 51k frames | MPJPE | ✓ | ✕ | 7 subjects, 18 clothing styles |
| Synthetic Dataset | |||||||||
| NBA2K | 2020 | 3D joints, mesh | 35 | Indoor | 27k frames | MPJPE | ✕ | ✕ | 27 subjects, 27k poses, basketball-specific |
| GTA-IM | 2020 | 3D joints, mesh | 98 | Indoor | 1M frames | MPJPE | ✕ | ✕ | 50 subjects, RGB-D images |
| Occlusion-Person | 2020 | 3D joints | 15 | Indoor | 73k frames | MPJPE | ✕ | ✓ | 13 subjects, RGB-D images, occlusion-focused |
| Approach | Reference | 2D Detector | Input | MPJPE | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Direct | Disc. | Eat | Greet | Phone | Photo | Pose | Purch. | Sit | SitD. | Smoke | Wait | WalkD. | Walk | WalkT. | Avg | ||||
| End-to-end | [34] | - | Image | 73.33 | 83.45 | 85.33 | 79.08 | 89.99 | 109.95 | 76.08 | 73.61 | 104.12 | 136.27 | 87.59 | 79.19 | 87.13 | 66.31 | 76.88 | 87.22 |
| [35] | - | Image | 70.16 | 76.67 | 78.41 | 76.87 | 87.99 | 109.49 | 72.23 | 73.12 | 108.84 | 149.53 | 87.29 | 75.14 | 87.7 | 65.38 | 75.76 | 86.17 | |
| 2D to 3D | [80] | CPN | Video | 45.2 | 46.7 | 43.3 | 45.6 | 48.1 | 55.1 | 44.6 | 44.3 | 57.3 | 65.8 | 47.1 | 44 | 49 | 32.8 | 33.9 | 46.8 |
| [113] | Hourglass | Image | 43.8 | 48.6 | 49.1 | 49.8 | 57.6 | 61.5 | 45.9 | 48.3 | 62 | 73.4 | 54.8 | 50.6 | 56 | 43.4 | 45.5 | 52.7 | |
| [114] | CPN | Video | 44.6 | 47.4 | 45.6 | 48.8 | 50.8 | 59 | 47.2 | 43.9 | 57.9 | 61.9 | 49.7 | 46.6 | 51.3 | 37.1 | 39.4 | 48.8 | |
| [115] | CPN | Video | 46.6 | 47.1 | 43.9 | 41.6 | 45.8 | 49.6 | 46.5 | 40 | 53.4 | 61.1 | 46.1 | 42.6 | 43.1 | 31.5 | 32.6 | 44.8 | |
| [116] | CPN | Video | 41.4 | 43.5 | 40.1 | 42.9 | 46.6 | 51.9 | 41.7 | 42.3 | 53.9 | 60.2 | 45.4 | 41.7 | 46 | 31.5 | 32.7 | 44.1 | |
| [47] | CPN | Image | 45.4 | 49.2 | 45.7 | 49.4 | 50.4 | 58.2 | 47.9 | 46 | 57.5 | 63 | 49.7 | 46.6 | 52.2 | 38.9 | 40.8 | 49.4 | |
| [9] | CPN | Video | 41.5 | 44.8 | 39.8 | 42.5 | 46.5 | 51.6 | 42.1 | 42 | 53.3 | 60.7 | 45.5 | 43.3 | 46.1 | 31.8 | 32.2 | 44.3 | |
| [79] | CPN | Video | 40.3 | 43.3 | 40.2 | 42.3 | 45.6 | 52.3 | 41.8 | 40.5 | 55.9 | 60.6 | 44.2 | 43 | 44.2 | 30 | 30.2 | 43.7 | |
| [89] | CPN | Video | 37.6 | 40.9 | 37.3 | 39.7 | 42.3 | 49.9 | 40.1 | 39.8 | 51.7 | 55 | 42.1 | 39.8 | 41 | 27.9 | 27.9 | 40.9 | |
| [93] | HR-Net | Video | 34.7 | 41.7 | 36 | 38.4 | 41.1 | 45.3 | 39.6 | 37.4 | 49 | 63.1 | 39.8 | 38.9 | 40.2 | 29.3 | 29.1 | 40.3 | |
| [62] | Hourglass | Image | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 51.4 | |
| [63] | CPN | Video | 36.4 | 39.5 | 34.9 | 37.6 | 40.1 | 45.9 | 37.8 | 37.8 | 51.5 | 52.2 | 40.8 | 38.3 | 38.3 | 27.0 | 27.0 | 39.0 | |
| [65] | CPN | Video | 31.4 | 31.5 | 28.8 | 29.7 | 34.3 | 36.5 | 29.2 | 30.0 | 42.0 | 42.5 | 33.3 | 31.9 | 31.4 | 22.6 | 22.7 | 31.9 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Gao, T.; Dong, A.; Jiang, X.; Zhu, Z.; Wang, F. A Survey of the State of the Art in Monocular 3D Human Pose Estimation: Methods, Benchmarks, and Challenges. Sensors 2025, 25, 2409. https://doi.org/10.3390/s25082409
Guo Y, Gao T, Dong A, Jiang X, Zhu Z, Wang F. A Survey of the State of the Art in Monocular 3D Human Pose Estimation: Methods, Benchmarks, and Challenges. Sensors. 2025; 25(8):2409. https://doi.org/10.3390/s25082409
Chicago/Turabian StyleGuo, Yan, Tianhan Gao, Aoshuang Dong, Xinbei Jiang, Zichen Zhu, and Fuxin Wang. 2025. "A Survey of the State of the Art in Monocular 3D Human Pose Estimation: Methods, Benchmarks, and Challenges" Sensors 25, no. 8: 2409. https://doi.org/10.3390/s25082409
APA StyleGuo, Y., Gao, T., Dong, A., Jiang, X., Zhu, Z., & Wang, F. (2025). A Survey of the State of the Art in Monocular 3D Human Pose Estimation: Methods, Benchmarks, and Challenges. Sensors, 25(8), 2409. https://doi.org/10.3390/s25082409







