Real-Time Monitoring-Based Stability Analysis of an Extra-Large LNG Tank Roof Under Construction
Abstract
:Highlights
- The stability of the steel roof in the LNG tank is controlled by the construction load.
- The roof rise–span ratio has the greatest influence on stability.
- It is necessary to monitor the roof concrete pouring construction process.
- Increasing the rise–span ratio is an effective method to enhance roof stability.
Abstract
1. Introduction
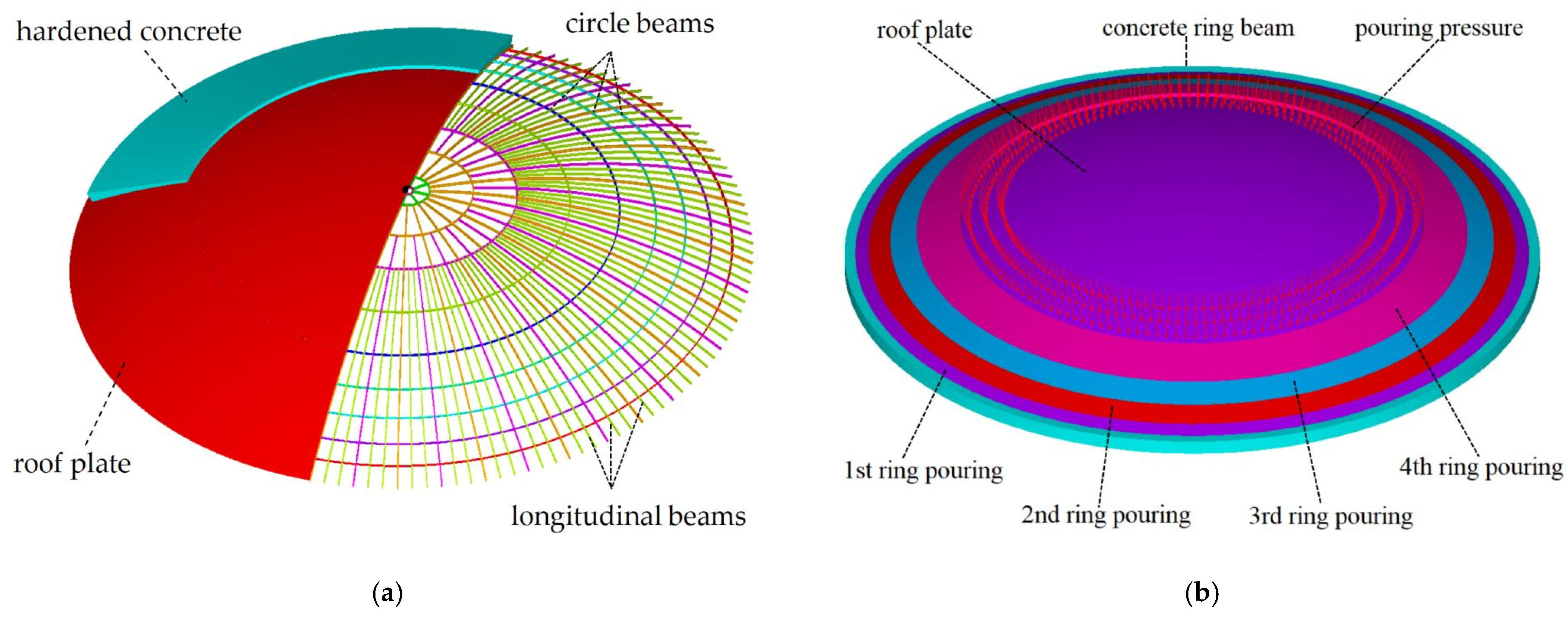
2. FEA Methods for Roofs Under Construction Conditions
2.1. Numerical Simulation Methods
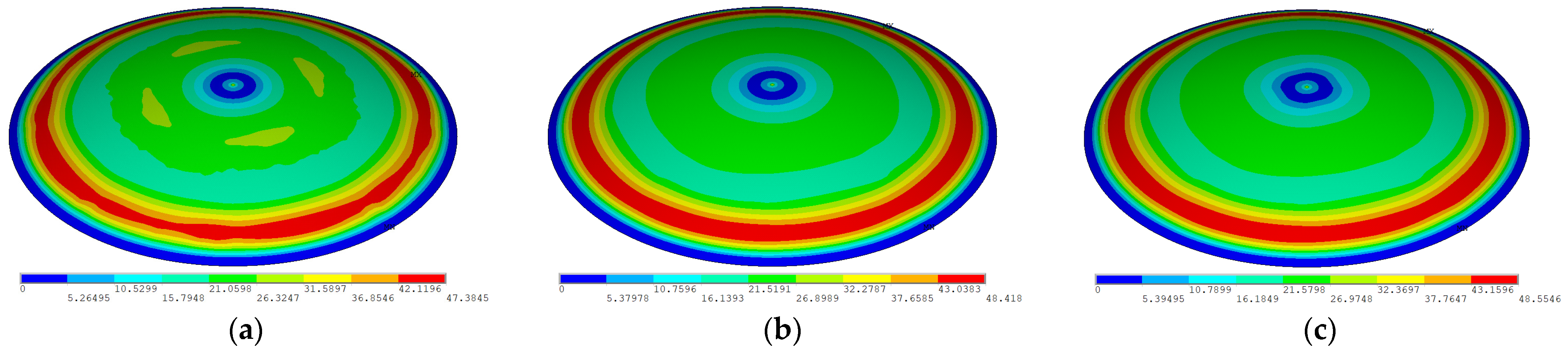
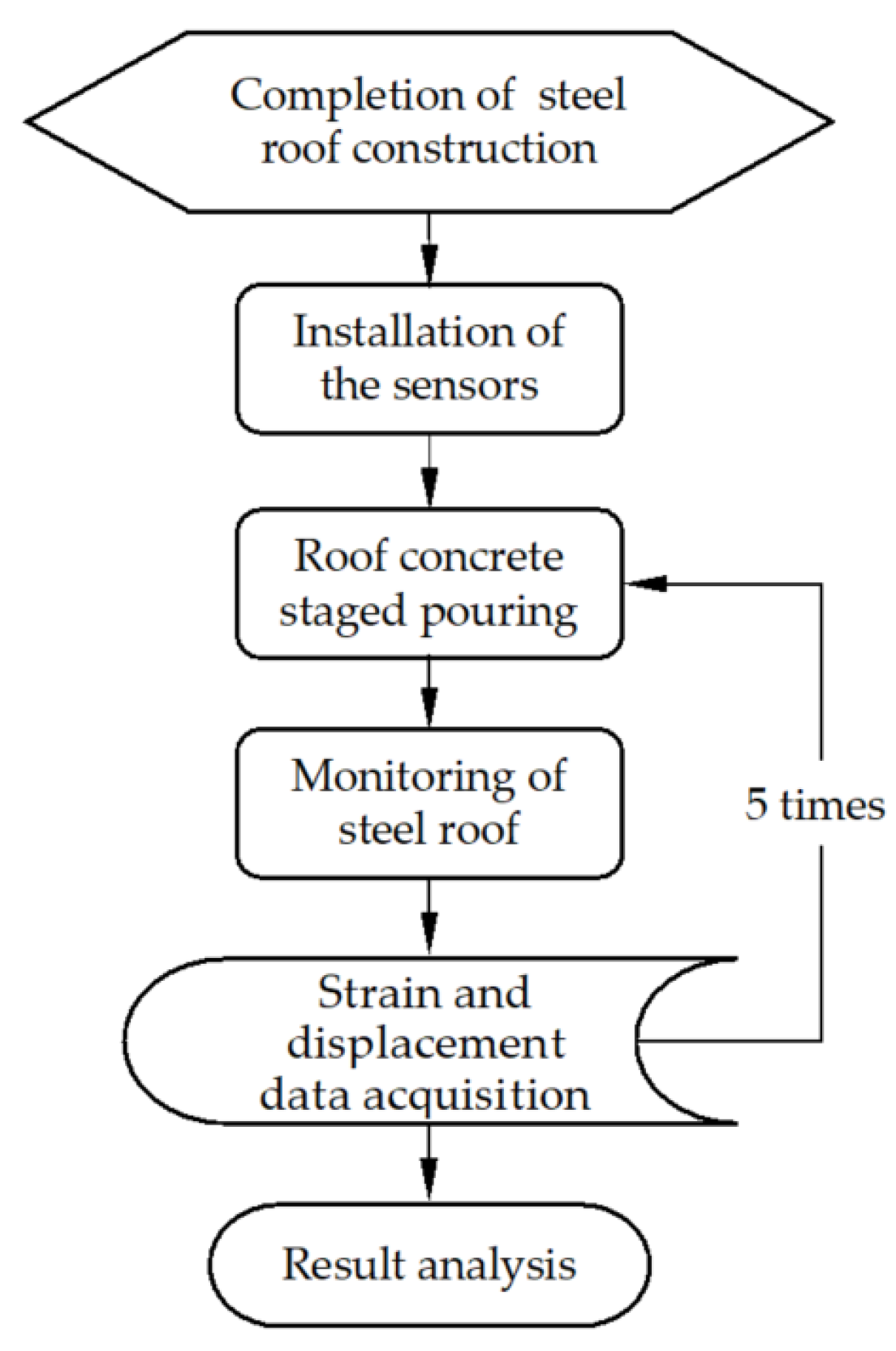
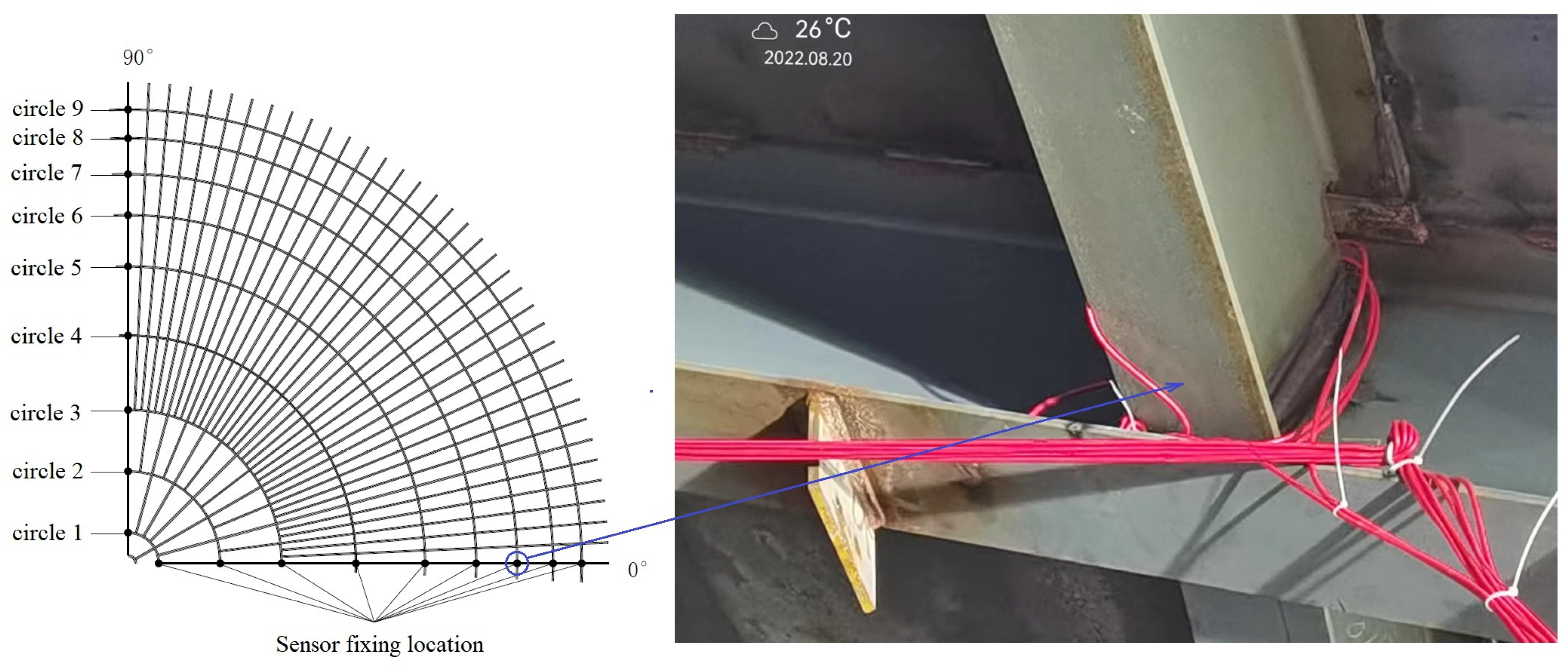
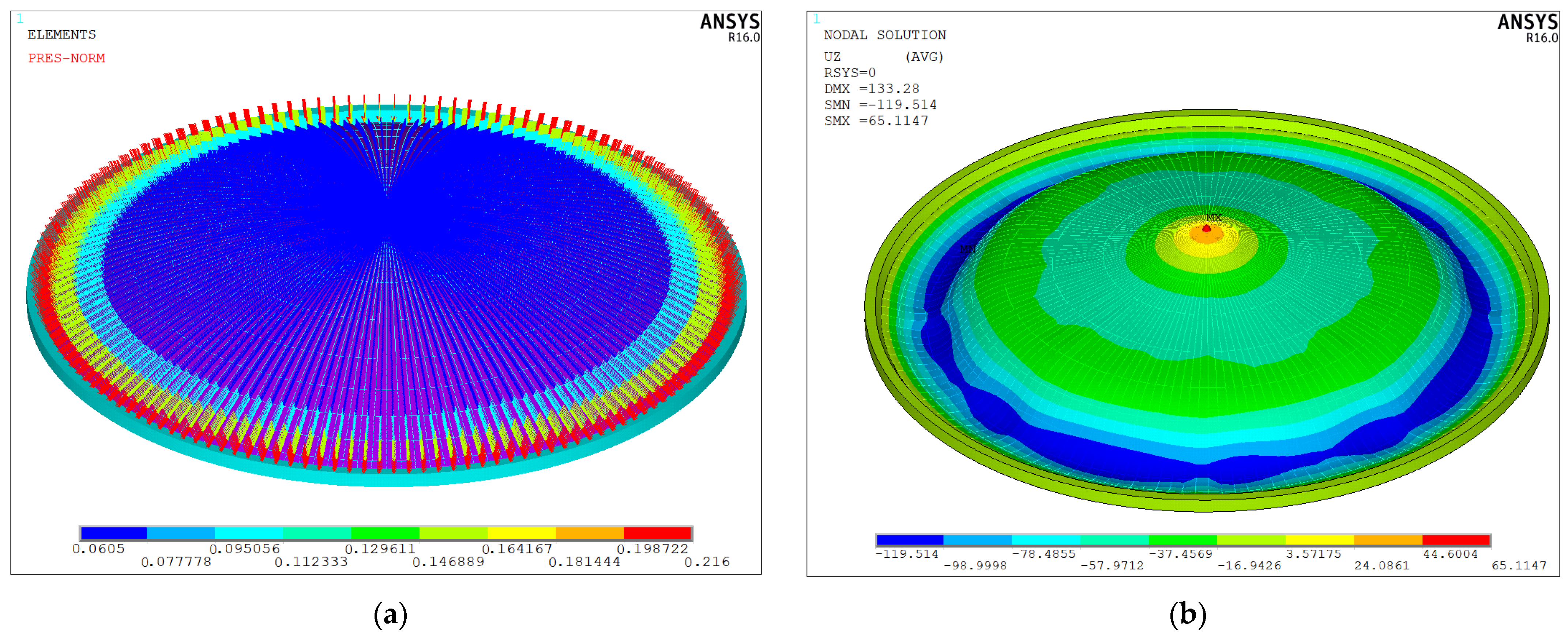
2.2. Validation Based on Real-Time Monitoring Results
3. Buckling Analysis Under Construction Conditions
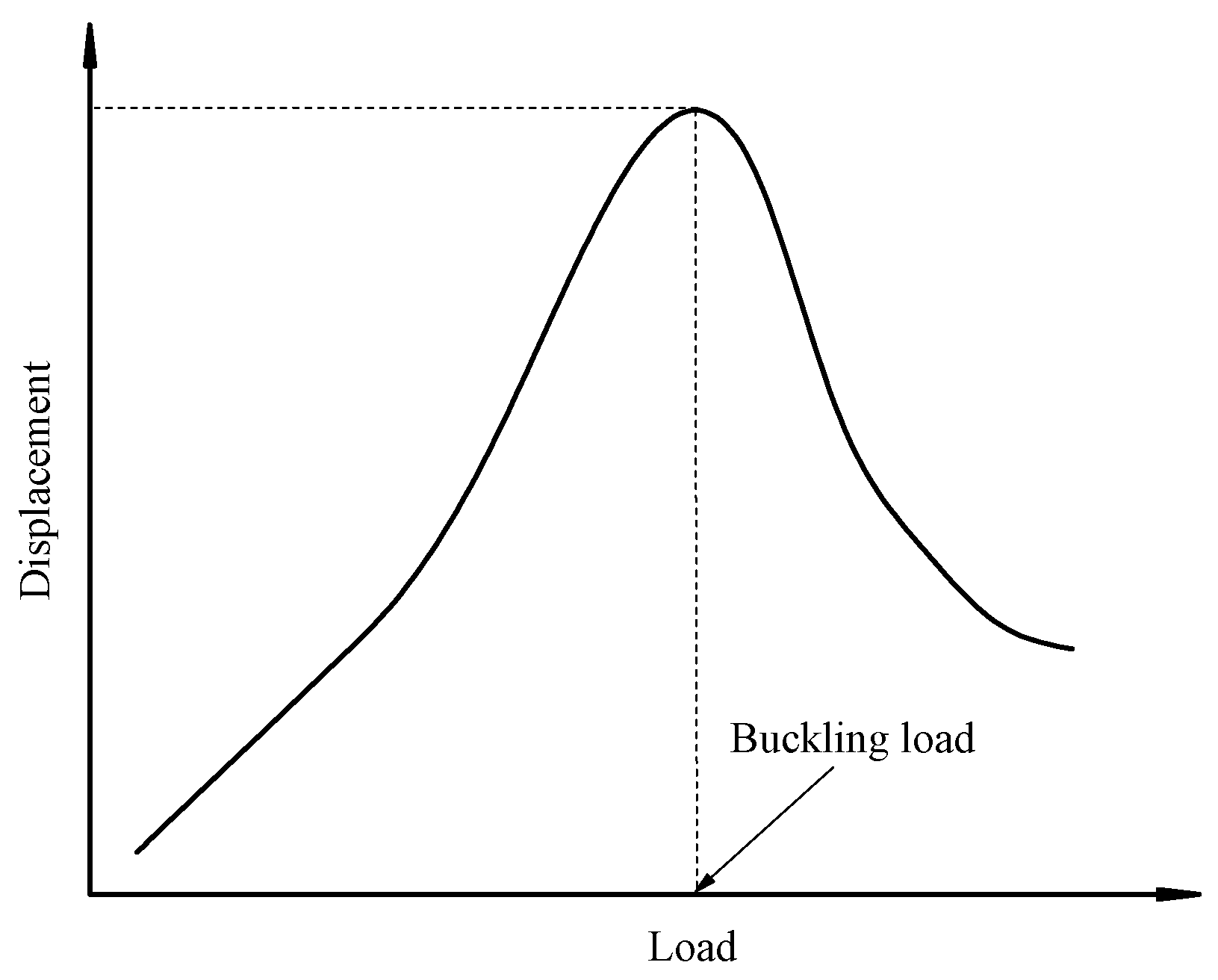
3.1. Buckling Analysis Method
3.2. Non-Stage Pouring Buckling Analysis
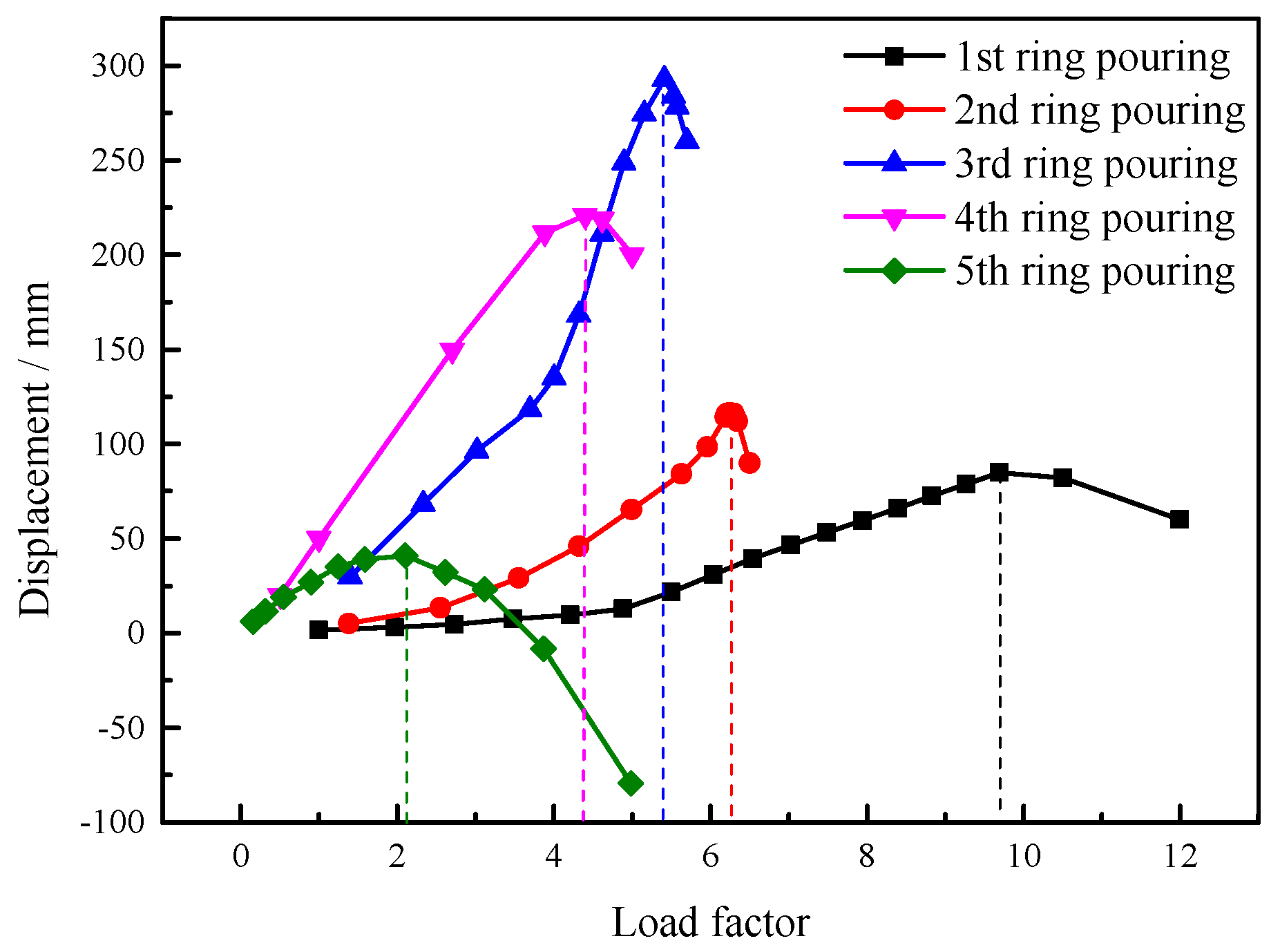
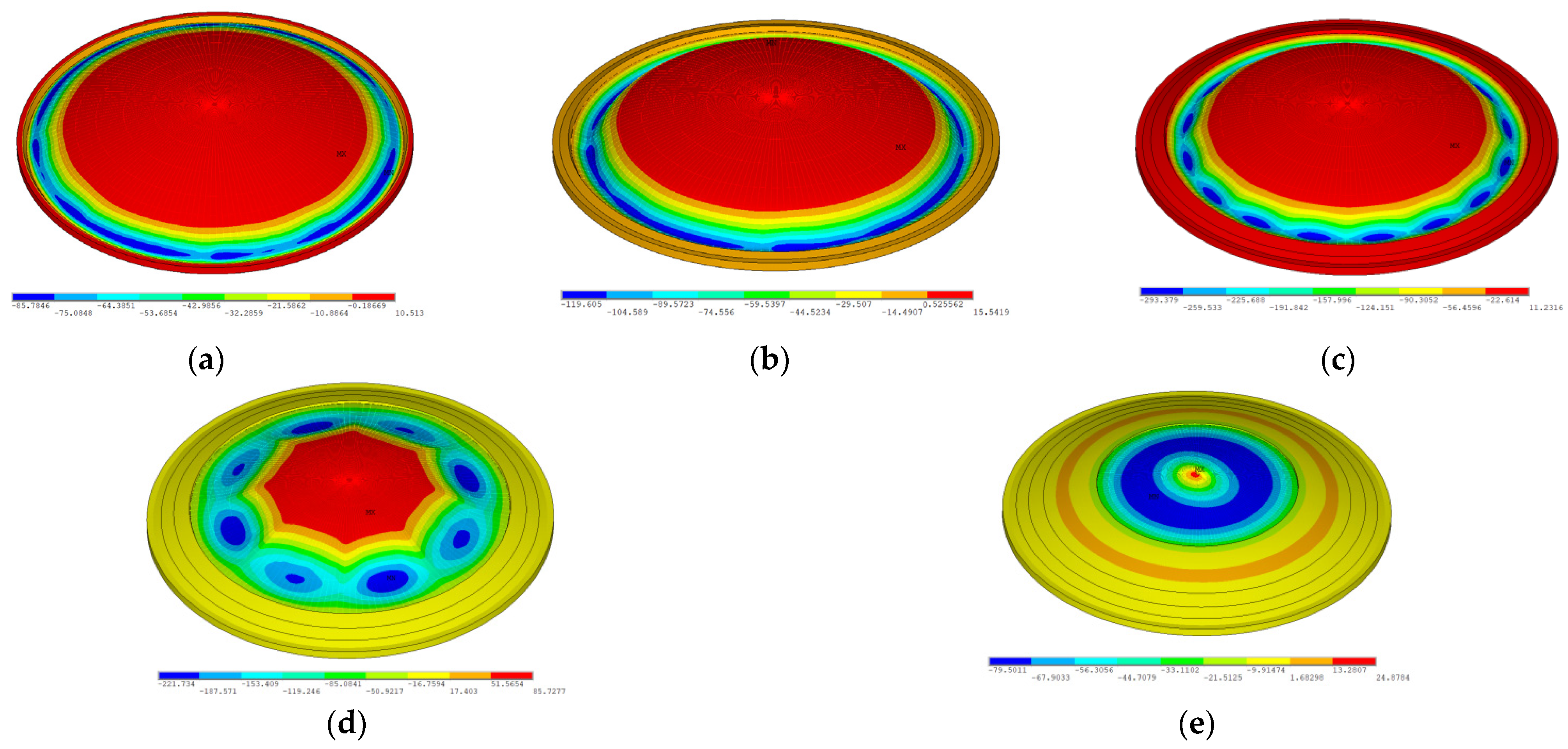
3.3. Staged Pouring Buckling Analysis
4. Parameter Sensitivity Analysis of Tank Roof Stability
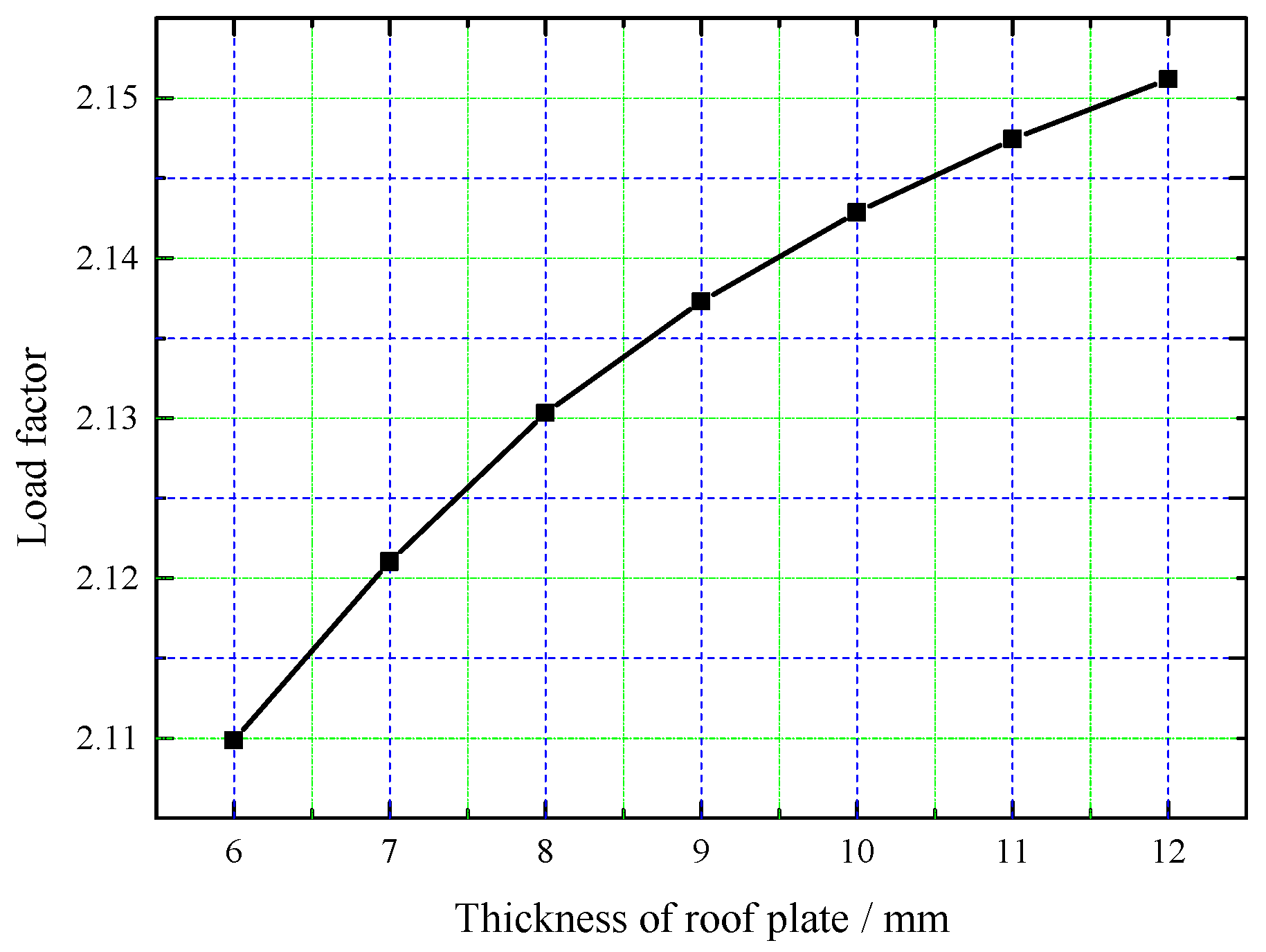
4.1. Influence of Roof Plate Thickness
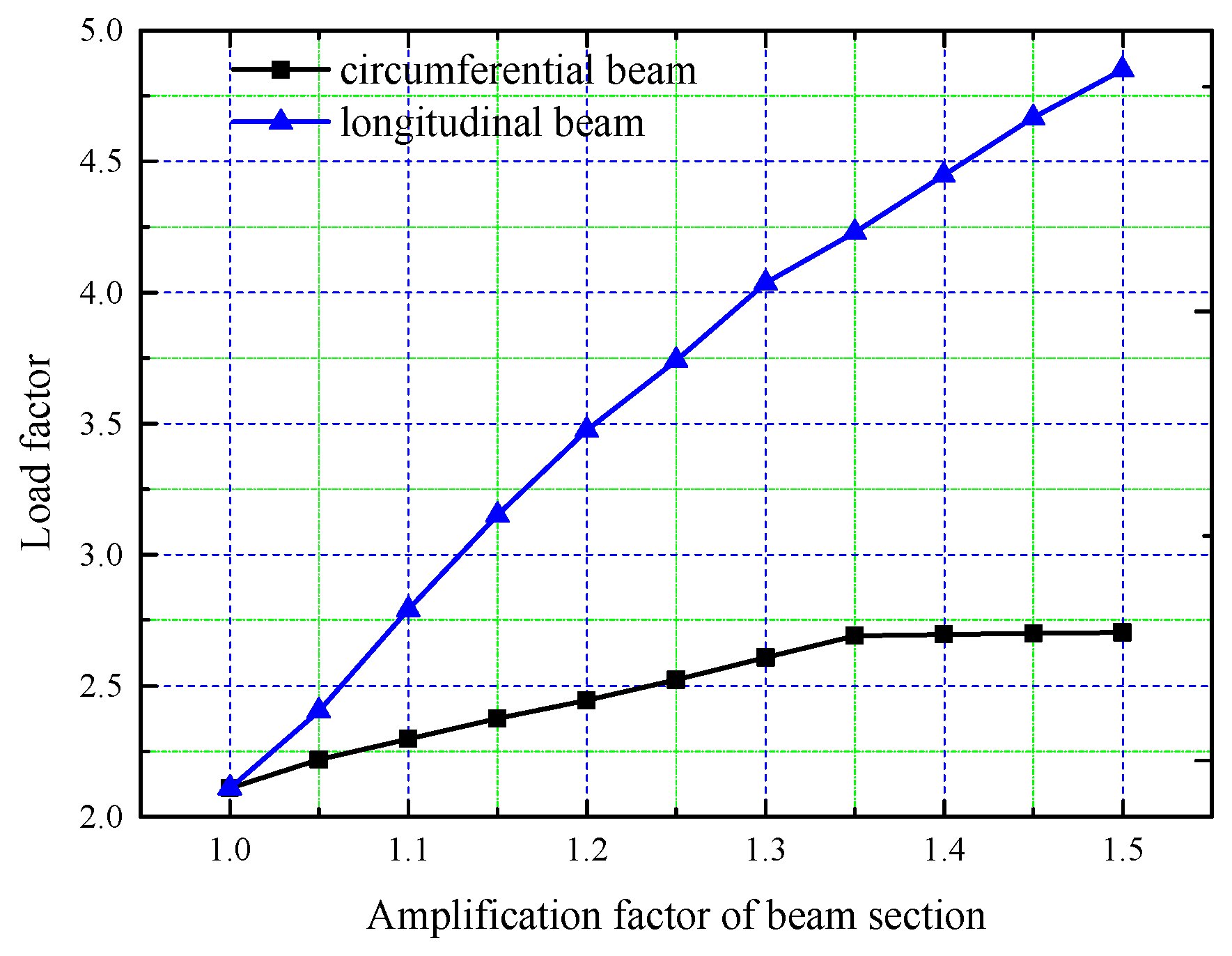
4.2. Influence of Beam Section Size
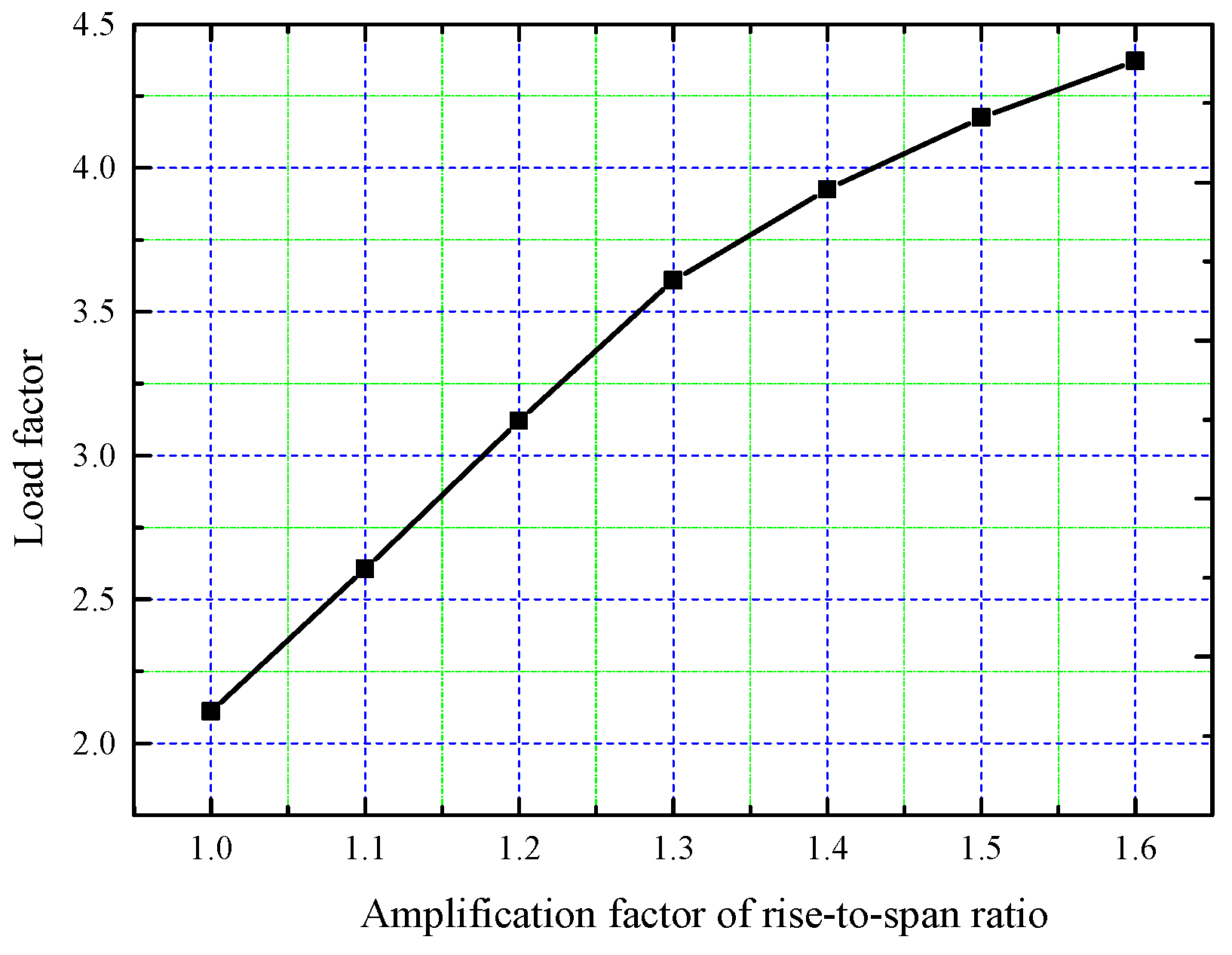
4.3. Influence of Rise–Span Ratio
5. Conclusions
- (1)
- For ultra-large LNG tanks, staged roof pouring is essential in order to meet stability requirements. Real-time monitoring data demonstrate that the FEA method, including the “birth and death” technique, can accurately simulate roof stability under staged pouring conditions.
- (2)
- The roof plate thickness, beam section size, and rise–span ratio all positively affect tank roof stability. Among these, the longitudinal beam section size and the rise–span ratio have the greatest impact on stability, followed by the circle beam section size, which has a limiting value. The roof plate thickness has a minimal effect on stability and can be considered negligible.
- (3)
- Taking into account both material usage and construction factors, appropriately increasing the rise–span ratio within a reasonable range is the optimal method for enhancing LNG tank stability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, T.; Zhang, C.; Xiao, L.; Yang, F.; Liu, Y. Analysis of roof stability in ultra-large LNG storage tanks based on field measurements. Ships Offshore Struct. 2024, 19, 1–8. [Google Scholar] [CrossRef]
- Kameshwar, S.; Padgett, J.E. Stiffening Ring Design for Prevention of Storm-Surge Buckling in Above Ground Storage Tanks. J. Struct. Eng. 2019, 145, 04019002. [Google Scholar] [CrossRef]
- Shokrzadeh, A.R.; Sohrabi, M.R. Strengthening effects of spiral stairway on the buckling behavior of metal tanks under wind and vacuum pressures. Thin-Walled Struct. 2016, 106, 437–447. [Google Scholar] [CrossRef]
- Huang, M.; Chen, G.; Yang, P.; Hu, K.; Zhou, L.; Men, J.; Zhao, J. Multi-hazard coupling vulnerability analysis for buckling failure of vertical tank: Floods and hurricanes. Process Saf. Environ. Prot. 2022, 161, 528–541. [Google Scholar] [CrossRef]
- Pan, J.; Liang, S. A study on the buckling behavior of in-service large open-topped oil-storage tanks. Structures 2021, 29, 211–224. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, Y. Buckling of cylindrical open-topped steel tanks under wind load. Thin-Walled Struct. 2014, 79, 83–94. [Google Scholar] [CrossRef]
- Uematsu, Y.; Yamaguchi, T.; Yasunaga, J. Effects of wind girders on the buckling of open-topped storage tanks under quasi-static wind loading. Thin-Walled Struct. 2018, 124, 1–12. [Google Scholar] [CrossRef]
- Sobhan, M.; Rofooei, F.; Attari, N.K. Buckling behavior of the anchored steel tanks under horizontal and vertical ground motions using static pushover and incremental dynamic analyses. Thin-Walled Struct. 2017, 112, 173–183. [Google Scholar] [CrossRef]
- Maheri, M.R.; Abdollahi, A. The effects of long term uniform corrosion on the buckling of ground based steel tanks under seismic loading. Thin-Walled Struct. 2013, 62, 1–9. [Google Scholar] [CrossRef]
- Uematsu, Y.; Koo, C.; Yasunaga, J. Design wind force coefficients for open-topped oil storage tanks focusing on the wind-induced buckling. J. Wind. Eng. Ind. Aerodyn. 2014, 130, 16–29. [Google Scholar] [CrossRef]
- Yasunaga, J.; Uematsu, Y. Dynamic buckling of cylindrical storage tanks under fluctuating wind loading. Thin-Walled Struct. 2020, 150, 106677. [Google Scholar] [CrossRef]
- Burgos, C.A.; Jaca, R.C.; Lassig, J.L.; Godoy, L.A. Wind buckling of tanks with conical roof considering shielding by another tank. Thin-Walled Struct. 2014, 84, 226–240. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, J.; Yu, Y.; Wang, Z.; Xing, Z.; Zhang, Q. Thermal buckling of oil-filled fixed-roof tanks subjected to heat radiation by a burning tank. Eng. Fail. Anal. 2022, 138, 106393. [Google Scholar] [CrossRef]
- Chen, C.; Chen, H.; Mo, L.; Xiao, S.; Li, C.; Yang, M.; Reniers, G. Buckling failure analysis of storage tanks under the synergistic effects of fire and wind loads. J. Loss Prev. Process. Ind. 2024, 87, 105208. [Google Scholar] [CrossRef]
- Zhao, Y.; Lei, X.; Wang, Z.; Cao, Q.S. Buckling behavior of floating-roof steel tanks under measured differential settlement. Thin-Walled Struct. 2013, 70, 70–80. [Google Scholar] [CrossRef]
- Fan, H.; Chen, Z.; Shen, J.; Cheng, J.; Chen, D.; Jiao, P. Buckling of steel tanks under measured settlement based on Poisson curve prediction model. Thin-Walled Struct. 2016, 106, 284–293. [Google Scholar] [CrossRef]
- Cao, Q.; Zhao, Y. Buckling strength of cylindrical steel tanks under harmonic settlement. Thin-Walled Struct. 2010, 48, 391–400. [Google Scholar] [CrossRef]
- Yan, S.; Lyu, J.; Wu, A. Buckling resistance of steel circular tubes strengthened by welding cover plates. J. Constr. Steel Res. 2022, 199, 107631. [Google Scholar] [CrossRef]
- Zhu, B.; Guo, Y.; Zhang, Y.-H. Stability capacity design of grid cylindrical-lattice shells loaded axially. J. Constr. Steel Res. 2022, 193, 107284. [Google Scholar] [CrossRef]
- Cheng, X.; Wu, Z.; Zhen, C.; Li, W.; Ma, C. A novel stability analysis method of single-layer ribbed reticulated shells with roof plates. Thin-Walled Struct. 2024, 200, 111902. [Google Scholar] [CrossRef]
- Cheng, X.; Zhen, C.; Ai, J.; Gao, S.; Han, M. A new stability analysis method for steel roof of large LNG tank. J. China Univ. Pet. (Ed. Nat. Sci.) 2022, 46, 168–175. (In Chinese) [Google Scholar] [CrossRef]
- Zhai, X.; Wang, H. Complete process analysis of reticulated roof with steel plates of LNG tank in the construction period. J. Harbin Inst. Technol. 2015, 47, 31–36. (In Chinese) [Google Scholar] [CrossRef]
- Zhai, X.; Wang, Y.; Wang, H. Stability of reticulated shell with steel panel as the bracing and time-varying structure for LNG tank during concrete dome casting. Int. J. Steel Struct. 2017, 17, 1145–1156. [Google Scholar] [CrossRef]
- Zhang, C. A design algorithm used for the roof frame and liner system of extra-large LNG storage tanks. Nat. Gas Ind. B 2018, 5, 276–281. [Google Scholar] [CrossRef]
- GB 50496-2009; Standard for Construction of Mass Concrete. Ministry of Housing and Urban Rural Development of the People’s Republic of China, Architecture & Building Press: Beijing, China, 2018. (In Chinese)
- Hooputra, H.; Gese, H.; Dell, H.; Werner, H. A comprehensive failure model for crashworthiness simulation of aluminium extrusions. Int. J. Crashworthiness 2004, 9, 449–464. [Google Scholar] [CrossRef]
- Martucci, D.; Civera, M.; Surace, C. Bridge monitoring: Application of the extreme function theory for damage detection on the I-40 case study. Eng. Struct. 2023, 279, 115573. [Google Scholar] [CrossRef]
- Hornung, U.; Saal, H. Buckling loads of tank shells with imperfections. Int. J. Non-linear Mech. 2002, 37, 605–621. [Google Scholar] [CrossRef]
- Zhang, H.; El Ansary, A.; Zhou, W. Prediction of buckling capacity of liquid-filled steel conical tanks considering field-measured imperfections. Eng. Struct. 2022, 262, 114351. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, J.; Zhang, Y.; Zhao, X.; Shangguan, G. Data-driven strategy for geometric imperfection analysis of assembled large-span ring truss components. J. Constr. Steel Res. 2024, 212, 108280. [Google Scholar] [CrossRef]
- JGJ7-2010; Technical Specification for Space Frame Structures. Ministry of Housing and Urban Rural Development of the People’s Republic of China, Architecture & Building Press: Beijing, China, 2010. (In Chinese)



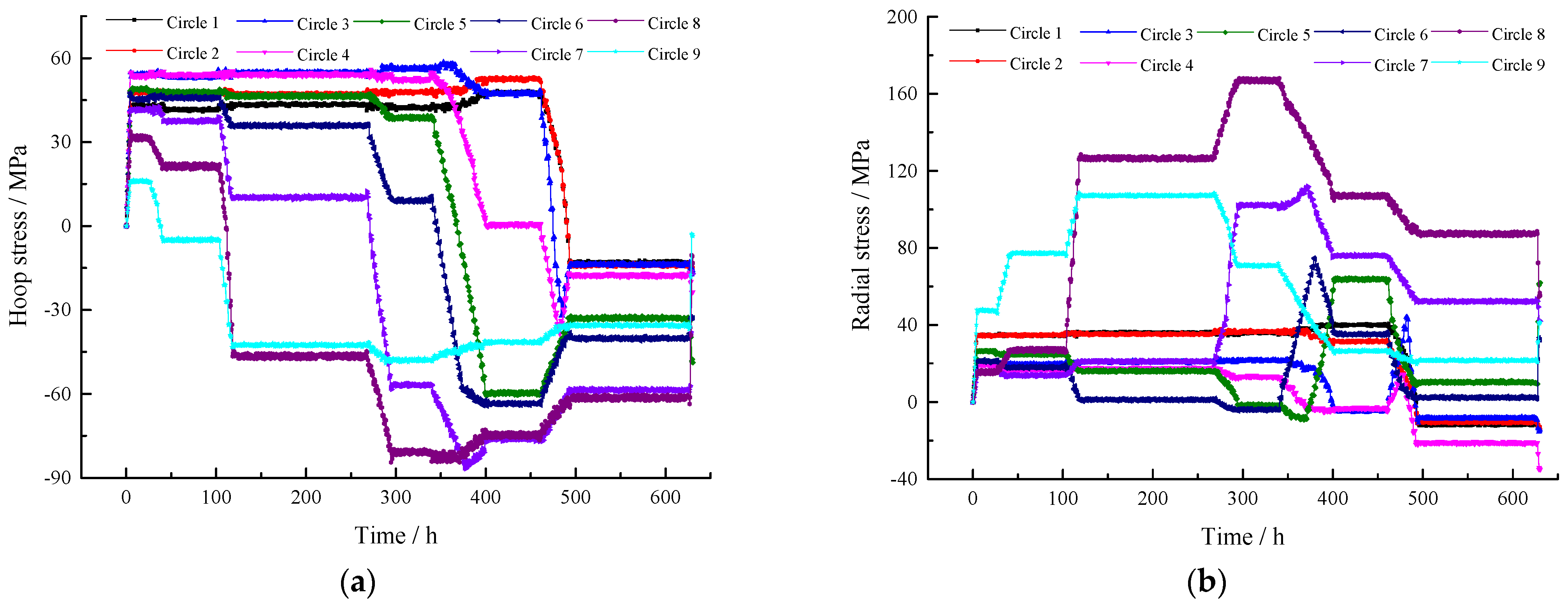
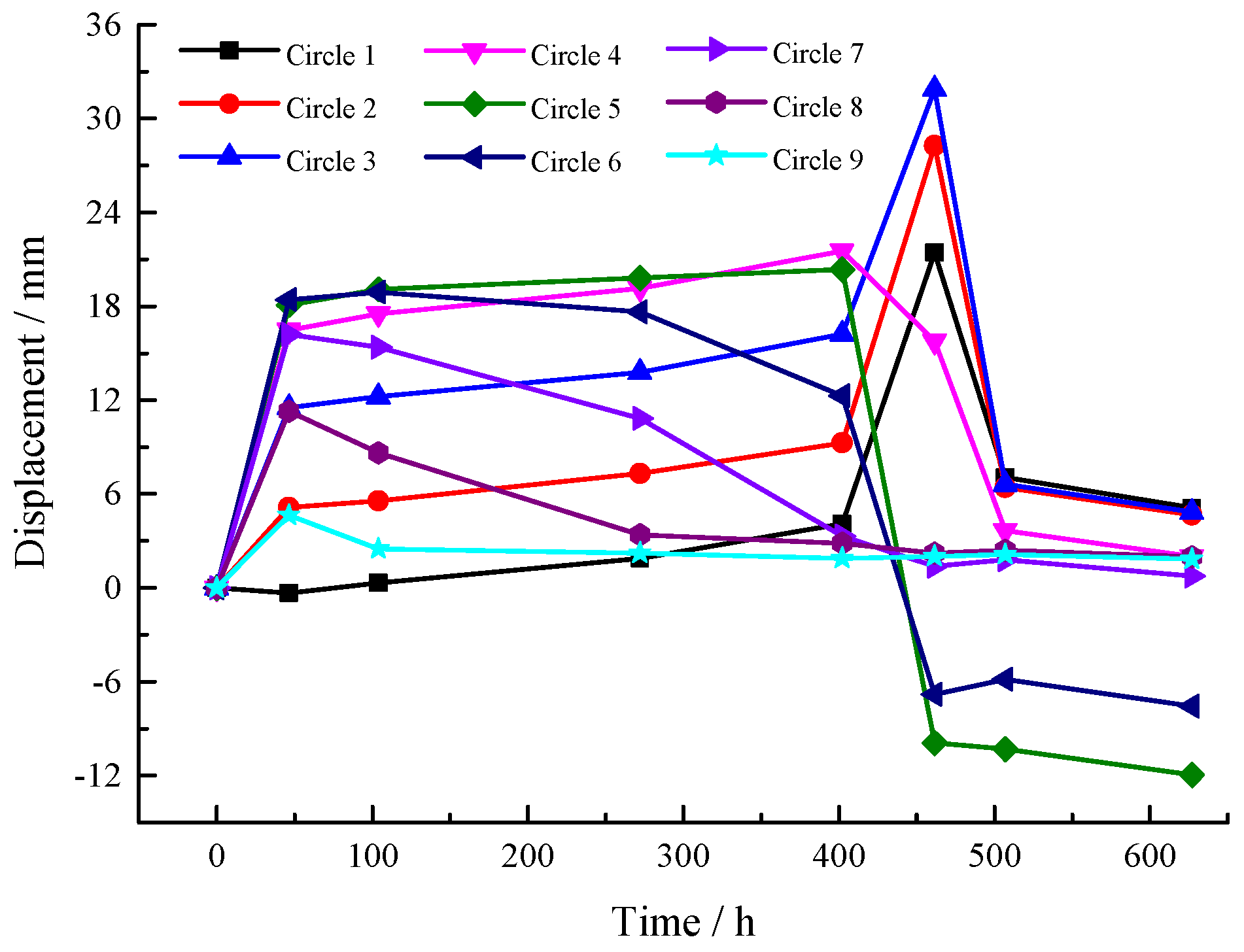
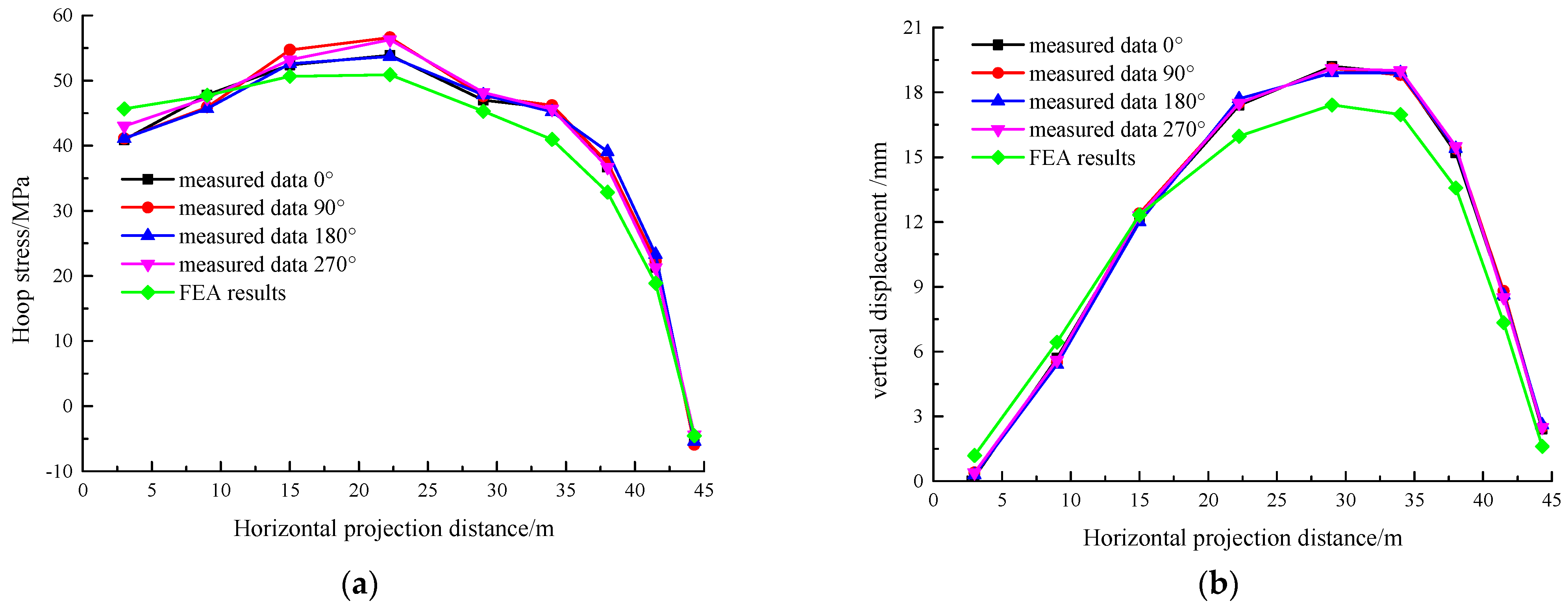
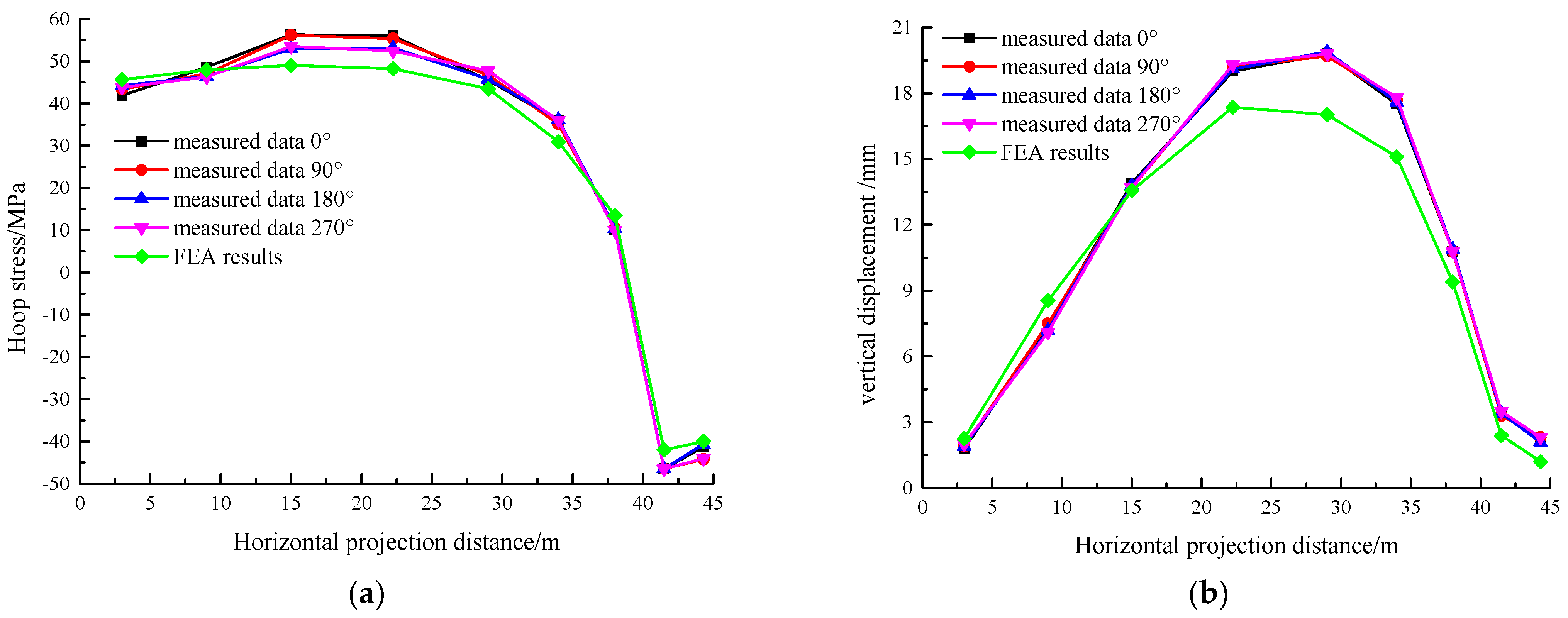


| Component | Material Grade | Elastic Modulus/MPa | Poisson’s Ratio | Compressive Yield Stress/MPa | Tensile Yield Strength/MPa |
|---|---|---|---|---|---|
| Roof beams | S355 J2 | 206,000 | 0.3 | 355 | 355 |
| Roof plate | S275 J2 | 206,000 | 0.3 | 275 | 275 |
| Roof concrete | C50 | 34,500 | 0.2 | 32.4 | 2.64 |
| No. of Rings | Pouring to Radius/m | Pouring Width/m | Concrete Self-Weight Pressure/kPa |
|---|---|---|---|
| 0 | 46 | / | / |
| 1 | 44.3 | 1.7 | 43.2 |
| 2 | 41.5 | 2.8 | 30.2 |
| 3 | 38 | 3.5 | 20.0 |
| 4 | 25 | 13 | 12.4 |
| 5 | 0 | 25 | 12.1 |
| Amplification Factor | 1 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 |
| Increase ratio of buckling load/% | 0 | 32.34 | 64.75 | 91.33 | 110.75 | 129.88 |
| Increase ratio of material consumption/% | 0 | 7.95 | 16.65 | 26.11 | 36.32 | 47.30 |
| Amplification Factor | 1 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 |
| Increase ratio of buckling load/% | 0 | 23.48 | 47.88 | 71.03 | 86.02 | 97.86 | 107.2 |
| Increase ratio of material consumption/% | 0 | 0.87 | 1.83 | 2.85 | 3.94 | 5.10 | 6.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Chen, T.; Zhang, K.; Song, Y. Real-Time Monitoring-Based Stability Analysis of an Extra-Large LNG Tank Roof Under Construction. Sensors 2025, 25, 2498. https://doi.org/10.3390/s25082498
Yang Y, Chen T, Zhang K, Song Y. Real-Time Monitoring-Based Stability Analysis of an Extra-Large LNG Tank Roof Under Construction. Sensors. 2025; 25(8):2498. https://doi.org/10.3390/s25082498
Chicago/Turabian StyleYang, Yong, Tuanhai Chen, Kezheng Zhang, and Yu Song. 2025. "Real-Time Monitoring-Based Stability Analysis of an Extra-Large LNG Tank Roof Under Construction" Sensors 25, no. 8: 2498. https://doi.org/10.3390/s25082498
APA StyleYang, Y., Chen, T., Zhang, K., & Song, Y. (2025). Real-Time Monitoring-Based Stability Analysis of an Extra-Large LNG Tank Roof Under Construction. Sensors, 25(8), 2498. https://doi.org/10.3390/s25082498








