Multi-Sensor Collaborative Positioning in Range-Only Single-Beacon Systems: A Differential Chan–Gauss–Newton Algorithm with Sequential Data Fusion
Abstract
1. Introduction
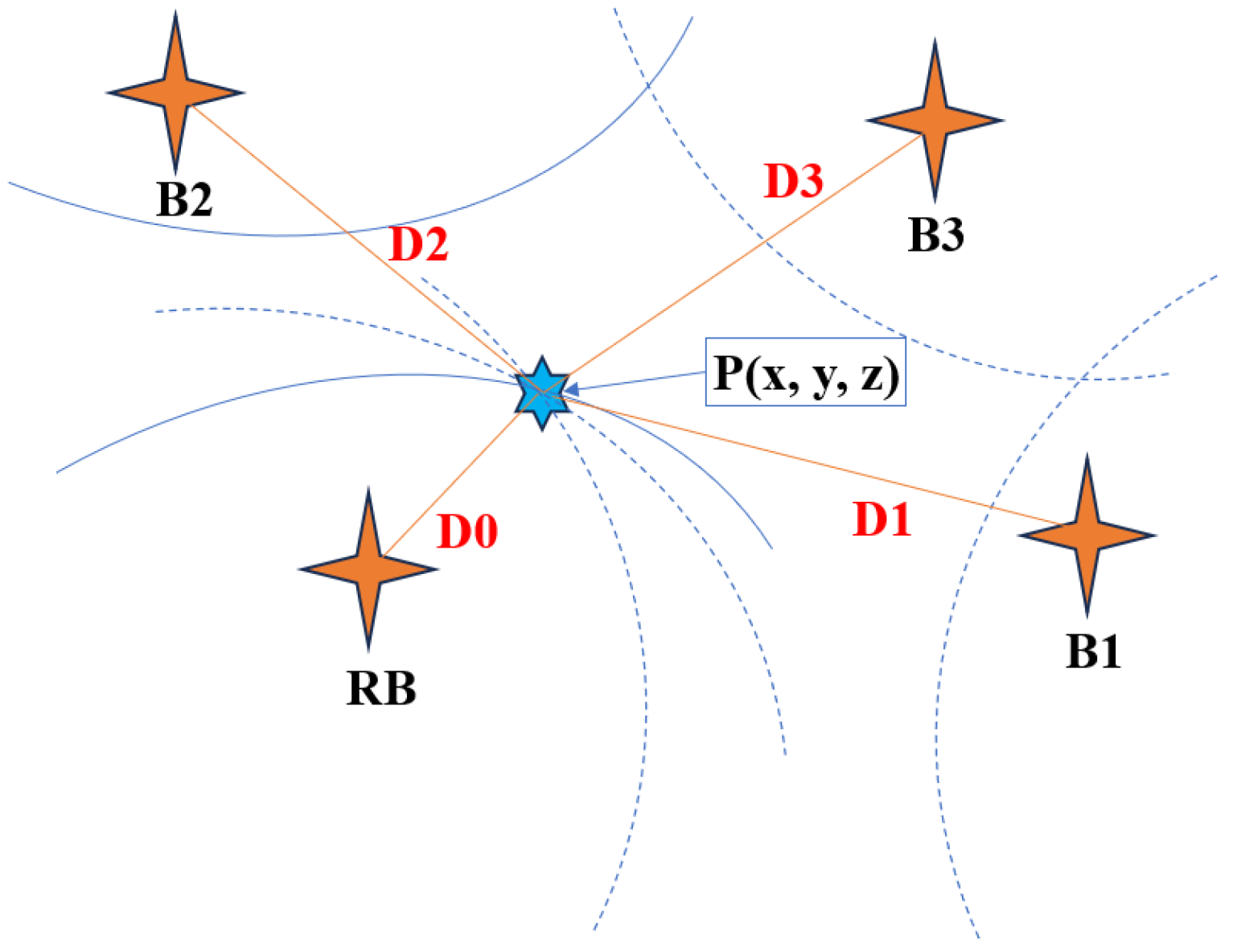
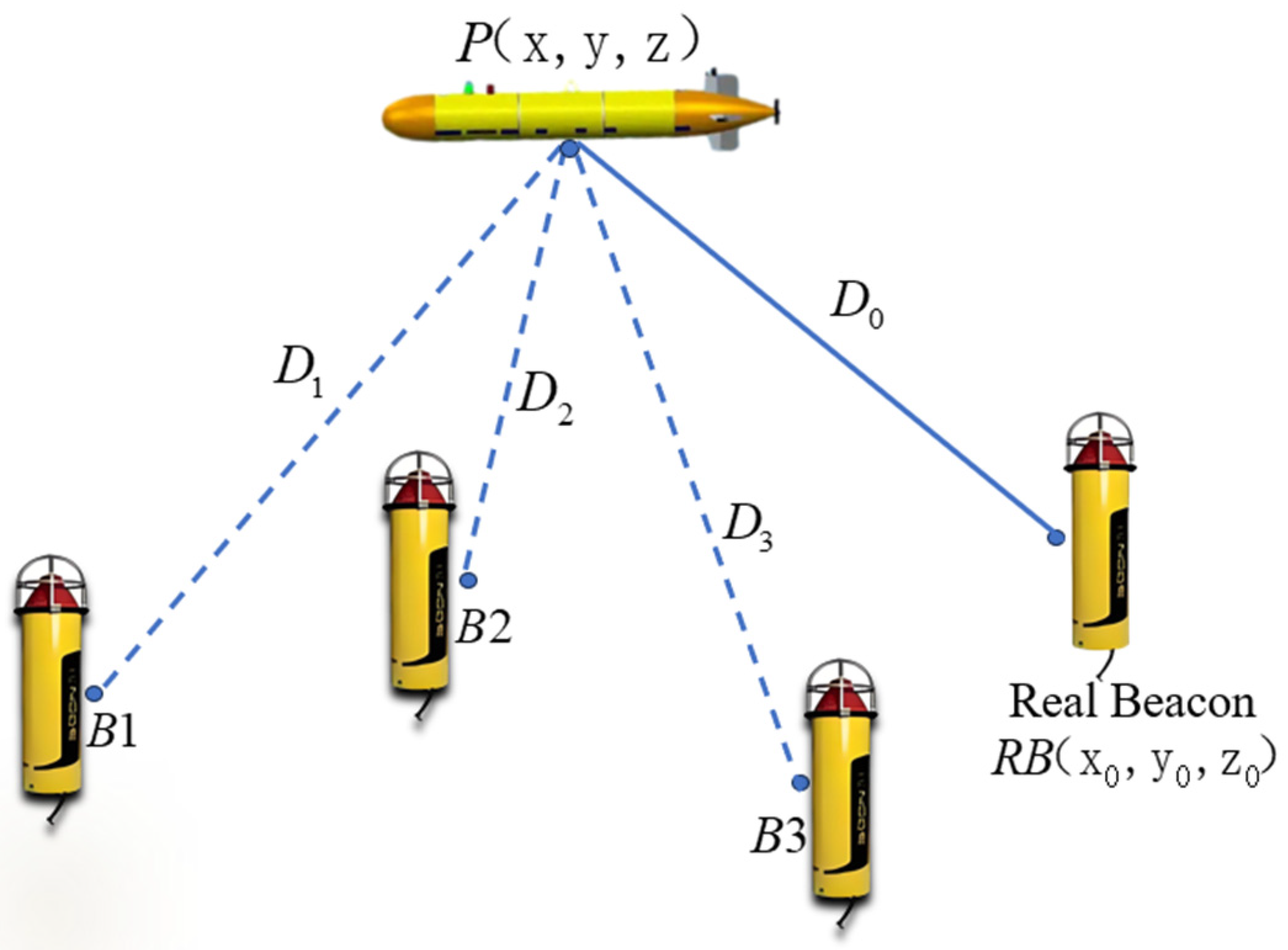
2. Motion Parameter Transfer and Framework of Virtual Beacon
2.1. Motion Parameter Transfer Analysis
2.2. Framework of Virtual Beacon Positioning
3. Basic Principle of Positioning Algorithm
3.1. Chan Algorithm
3.2. Gauss–Newton Algorithm
4. DCGN Positioning Method with Underwater Virtual Beacon
5. Simulation Test and Lake Trial Test Research
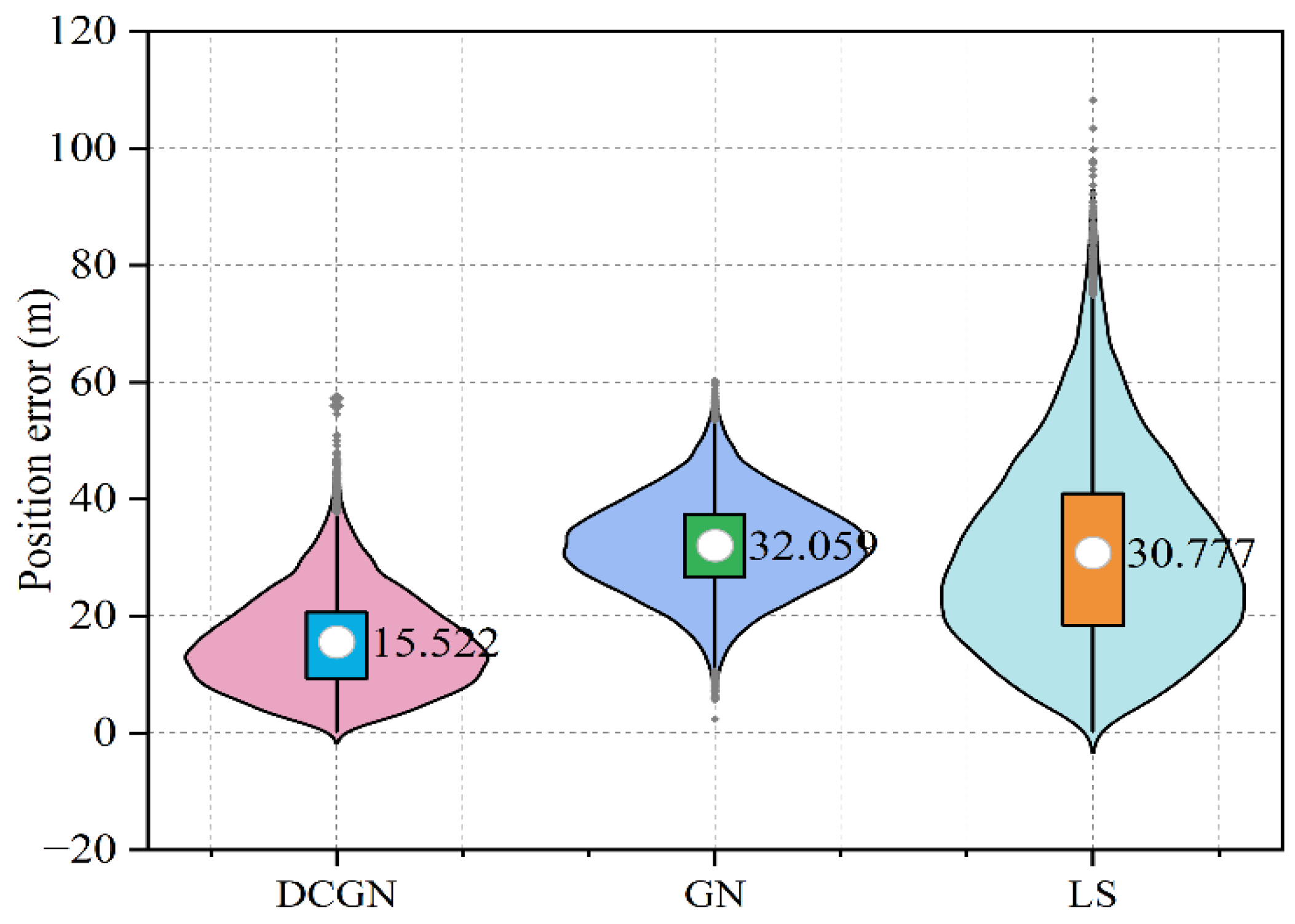
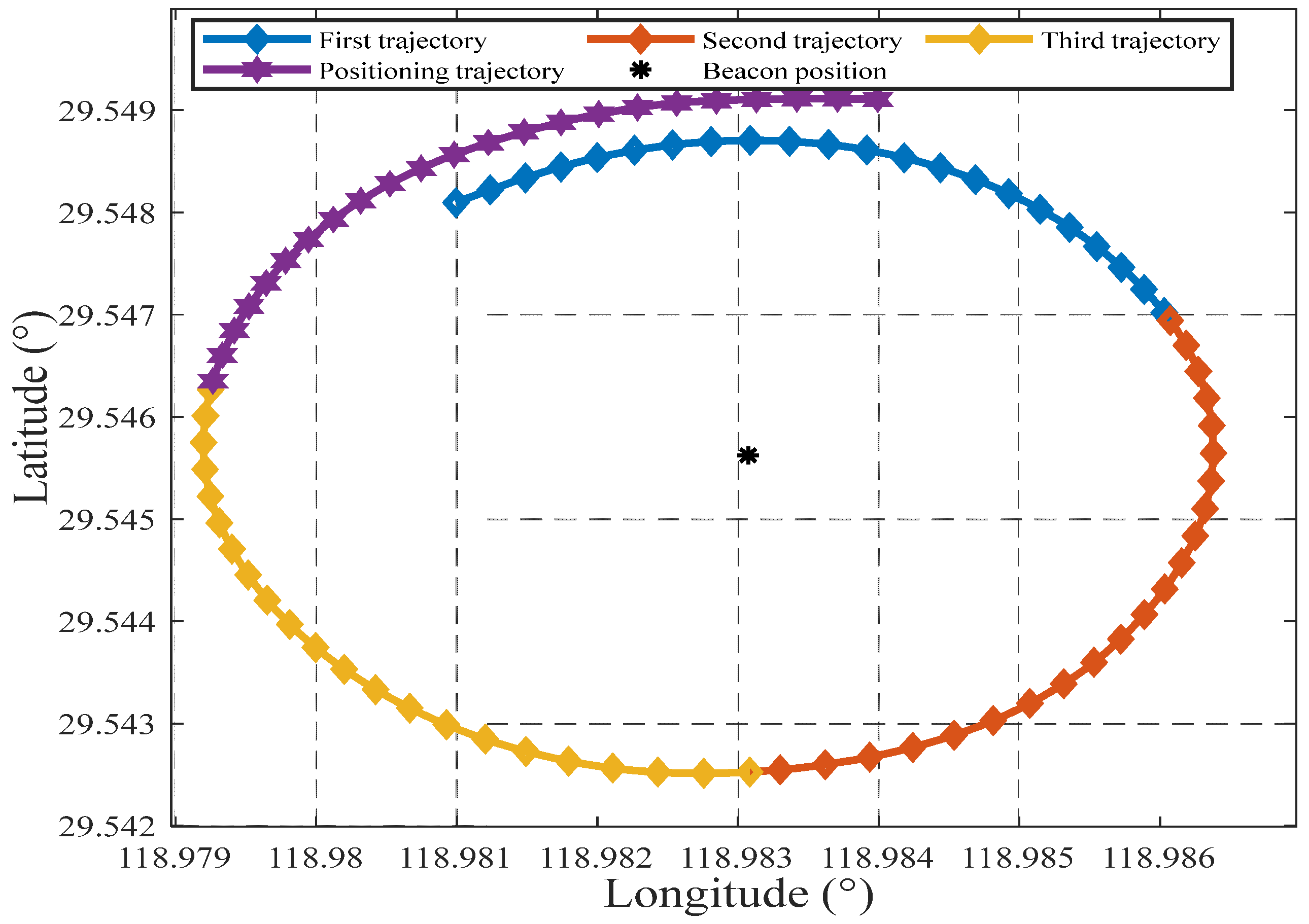
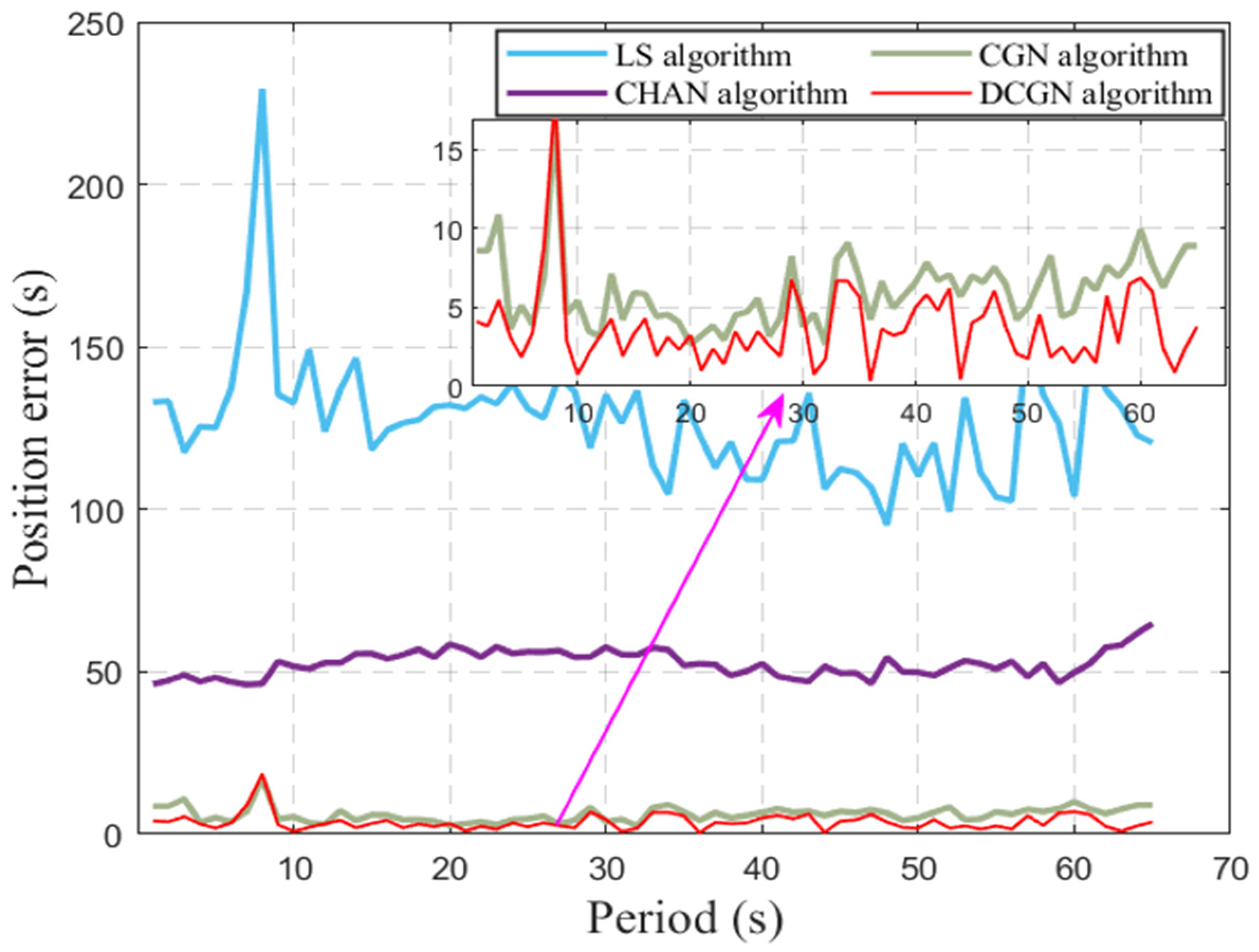
5.1. Simulation Test Analysis
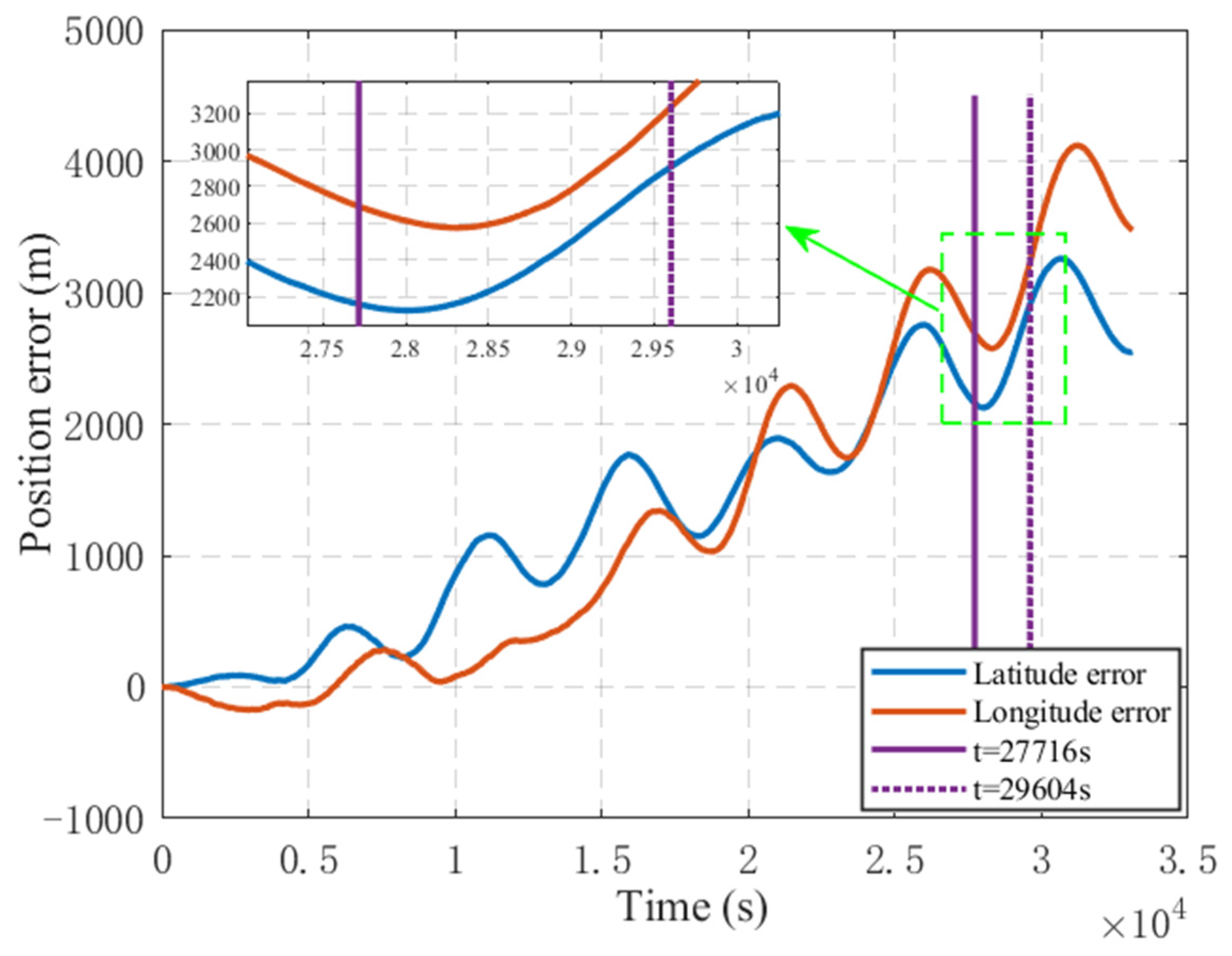
5.2. Lake Trial Test Research
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, C.; Du, P.; Wang, Z.; Wang, Z. An Underwater Acoustic Network Positioning Method Based on Spatial-Temporal Self-Calibration. Sensors 2022, 22, 5571. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Wang, B.; Huang, H.; Xu, X.; Yao, Y. A novel calibration algorithm of SINS/USBL navigation system based on smooth variable structure. IEEE Trans. Instrum. Meas. 2023, 72, 1–14. [Google Scholar] [CrossRef]
- Thomson, D.J.M.; Dosso, S.E.; Barclay, D.R. Modeling AUV localization error in a long baseline acoustic positioning system. IEEE J. Ocean. Eng. 2018, 43, 955–968. [Google Scholar] [CrossRef]
- Cheng, W.H. Research for enhancing the precision of asymmetrical SBL system for any vessels. Ocean Eng. 2006, 33, 1271–1282. [Google Scholar] [CrossRef]
- Su, X.; Ullah, I.; Liu, X.; Choi, D. A Review of Underwater Localization Techniques, Algorithms, and Challenges. J. Sens. 2020, 2020, 6403161. [Google Scholar] [CrossRef]
- Qin, H.; Yu, X.; Zhu, Z.; Deng, Z. A variational Bayesian approximation based adaptive single beacon navigation method with unknown ESV. Ocean Eng. 2020, 209, 107484. [Google Scholar] [CrossRef]
- Cao, J.; Han, Y.; Zhang, D.; Sun, D. Linearized iterative method for determining effects of vessel attitude error on single-beacon localization. Appl. Acoust. 2017, 116, 297–302. [Google Scholar] [CrossRef]
- Webster, S.E.; Walls, J.M.; Whitcomb, L.L.; Eustice, R.M. Decentralized extended information filter for single-beacon cooperative acoustic navigation: Theory and experiments. IEEE Trans. Robot. 2013, 29, 957–974. [Google Scholar] [CrossRef]
- Gadre, A.S. Observability Analysis in Navigation Systems with an Underwater Vehicle Application. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 26 June 2007. [Google Scholar]
- Scherbatyuk, A.P. The AUV positioning using ranges from one transponder LBL. In Proceedings of the ‘Challenges of Our Changing Global Environment′—Conference Proceedings. OCEANS ′95 MTS/IEEE, San Diego, CA, USA, 9–12 October 1995. [Google Scholar]
- Gadre, A.S.; Stilwell, D.J. Toward underwater navigation based on range measurements from a single location. In Proceedings of the IEEE International Conference on Robotics and Automation, 2004. Proceedings—ICRA ‘04. 2004, New Orleans, LA, USA, 26 April–1 May 2004. [Google Scholar]
- Gadre, A.S.; Stilwell, D.J. Underwater navigation in the presence of unknown currents based on range measurements from a single location. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005. [Google Scholar]
- Vaganay, J.; Baccou, P.; Jouvencel, B. Homing by acoustic ranging to a single-beacon. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition, Providence, RI, USA, 11–14 September 2000. [Google Scholar]
- Webster, S.E.; Eustice, R.M.; Singh, H.; Whitcomb, L.L. Advances in single-beacon one-way-travel-time acoustic navigation for underwater vehicles. Int. J. Robot. Res. 2012, 31, 935–950. [Google Scholar] [CrossRef]
- Larsen, M.B. Synthetic long baseline navigation of underwater vehicles. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition. Conference Proceedings (Cat. No.00CH37158), Providence, RI, USA, 11–14 September 2002. [Google Scholar]
- Yu, H.; Zhou, X. Observability Degree-Based AUV Single Beacon Navigation Trajectory Optimization with Range-Only Measurements. Complexity 2018, 2018, 4056870–4056881. [Google Scholar] [CrossRef]
- Zou, Z.; Wang, W.; Wu, B.; Ye, L.; Ochieng, W.Y. Tightly coupled INS/APS passive single beacon navigation. Remote Sens. 2023, 15, 1854. [Google Scholar] [CrossRef]
- Zhao, W.; Zhao, S.; Liu, G.; Meng, W. Range-Only Single Beacon Based Multisensor Fusion Positioning for AUV. IEEE Sens. J. 2023, 23, 23399–23409. [Google Scholar] [CrossRef]
- LaPointe, C.E.G. Virtual Long Baseline (VLBL) Autonomous Underwater Vehicle Navigation Using a Single Transponder. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2006. [Google Scholar]
- Jin, B.; Xu, X.; Zhu, Y.; Zhang, T.; Fei, Q. Single-source aided semi-autonomous passive location for correcting the position of an underwater vehicle. IEEE Sens. J. 2019, 19, 3267–3275. [Google Scholar] [CrossRef]
- Yu, Y.; Xu, J.; Lin, E.; Wu, M. Research status and application prospect of single beacon underwater acoustic positioning technology. J. Navig. Position. 2022, 10, 13–20. [Google Scholar]
- Tang, H.; He, H.; Li, F.; Xu, J. Underwater inertial error rectification with limited acoustic observations. Satell. Navig. 2024, 5, 3. [Google Scholar] [CrossRef]
- Pedro, M.; Moreno, D.S.; Crasta, N.; Pascoal, A. Underwater single-beacon localization: Optimal trajectory planning and minimum-energy estimation. IFAC-PapersOnLine 2015, 48, 155–160. [Google Scholar] [CrossRef]
- Webster, S.E. Decentralized Single-Beacon Acoustic Navigation: Combined Communication and Navigation for Underwater Vehicles. Ph.D. Thesis, Johns Hopkins University, Baltimore, MD, USA, 2010. [Google Scholar]
- Webster, S.E.; Whitcomb, L.L.; Eustice, R.M. Advances in decentralized single-beacon acoustic navigation for underwater vehicles: Theory and simulation. In Proceedings of the 2010 IEEE/OES Autonomous Underwater Vehicles, Monterey, CA, USA, 1–3 September 2010. [Google Scholar]
- Hao, K.; Yu, K.; Gong, Z.; Du, X.; Liu, Y.; Zhao, L. An enhanced AUV-aided TDoA localization algorithm for underwater acoustic sensor network. Mob. Netw. Appl. 2020, 25, 1673–1682. [Google Scholar] [CrossRef]
- Yang, H.; Gao, X.; Huang, H.; Li, B.; Xiao, B. An LBL positioning algorithm based on an EMD–ML hybrid method. EURASIP J. Adv. Signal Process. 2022, 2022, 38–58. [Google Scholar] [CrossRef]
- Yang, H.; Gao, X.; Li, B.; Xiao, B.; Huang, H. Development of Hydroacoustic Localization Algorithms for AUV Based on the Error-Corrected WMChan-Taylor Algorithm. J. Mar. Sci. Eng. 2024, 12, 974. [Google Scholar] [CrossRef]
- Hua, C.; Zhao, K.; Dong, D.; Zheng, Z.Q.; Yu, C.; Zhang, Y.; Zhao, T.T. Multipath map method for TDOA based indoor reverse positioning system with improved Chan-Taylor algorithm. Sensors 2020, 20, 3223. [Google Scholar] [CrossRef]
- Paek, J.; Kim, J.; Govindan, R. Energy-efficient rate-adaptive GPS-based positioning for smartphones. In Proceedings of the 8th International Conference on Mobile Systems, Applications, and Services, San Francisco, CA, USA, 15–18 June 2010. [Google Scholar]
- Liu, Q.; Wang, S.; Wei, Y. A Gauss-Newton method for mixed least squares-total least squares problems. Calcolo 2024, 61, 18–32. [Google Scholar] [CrossRef]
- Zhou, X.; Zhu, W.; Guo, Q. Ultrasonic echo signal parameter estimation based on Genetic algorithm and Gauss Newton method. J. PLA Univ. Sci. Technol. (Nat. Sci. Ed.) 2012, 13, 247–251. [Google Scholar]
- Shin, H.; Ku, B.; Nelson, J.K.; Ko, H. Robust Target Tracking with Multi-Static Sensors under Insufficient TDOA Information. Sensors 2018, 18, 1481. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Oussalah, M. Combination of Taylor and Chan method in mobile positioning. In Proceedings of the 2011 IEEE 10th International Conference on Cybernetic Intelligent Systems (CIS), London, UK, 1–2 September 2011. [Google Scholar]
- Chan, Y.T.; Ho, K.C. A simple and Efficient Estimator for Hyperbolic Location. IEEE Trans. Aerosp. Electron. Syst. 1994, 42, 1905–1915. [Google Scholar] [CrossRef]
- Wang, L. Research on Multi-Source Navigation Information Fusion Method for Deep-Sea AUV. Ph.D. Thesis, Southeast University, Nanjing, China, 2015. [Google Scholar]
- Chen, J.; Li, W. Convergence of Gauss–Newton’s method and uniqueness of the solution. Appl. Math. Comput. 2005, 47, 1057–1067. [Google Scholar] [CrossRef]
- Chen, J. The convergence analysis of inexact Gauss–Newton methods for nonlinear problems. Comput. Optim. Appl. 2008, 40, 97–118. [Google Scholar] [CrossRef]
- Kim, M.; Kim, S.; Tingleff, O. Optimization Methods for Non-linear Least Squares. J. Inst. Control Robot. Syst. 2024, 30, 723–729. [Google Scholar] [CrossRef]
- Bian, S.; Ji, B.; Li, H. Introduction to Satellite Navigation Systems, 2nd ed.; Surveying and Mapping Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Yan, G.; Weng, J. Strapdown Inertial Navigation Algorithm and Integrated Navigation Principles; Northwestern Polytechnical University Press: Xi’an, China, 2019. (In Chinese) [Google Scholar]






| Sensors | Parameters | Values |
|---|---|---|
| Gyroscope | bias stability | |
| angular random walk | ||
| scale factor nonlinearity | <2 ppm | |
| output frequency | 200 Hz | |
| Accelerometer | bias stability | |
| random walk coefficient | ||
| scale factor nonlinearity | <2 ppm | |
| output frequency | 200 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Y.; He, H.; Lin, E.; Tang, H. Multi-Sensor Collaborative Positioning in Range-Only Single-Beacon Systems: A Differential Chan–Gauss–Newton Algorithm with Sequential Data Fusion. Sensors 2025, 25, 2577. https://doi.org/10.3390/s25082577
Ye Y, He H, Lin E, Tang H. Multi-Sensor Collaborative Positioning in Range-Only Single-Beacon Systems: A Differential Chan–Gauss–Newton Algorithm with Sequential Data Fusion. Sensors. 2025; 25(8):2577. https://doi.org/10.3390/s25082577
Chicago/Turabian StyleYe, Yun, Hongyang He, Enfan Lin, and Hongqiong Tang. 2025. "Multi-Sensor Collaborative Positioning in Range-Only Single-Beacon Systems: A Differential Chan–Gauss–Newton Algorithm with Sequential Data Fusion" Sensors 25, no. 8: 2577. https://doi.org/10.3390/s25082577
APA StyleYe, Y., He, H., Lin, E., & Tang, H. (2025). Multi-Sensor Collaborative Positioning in Range-Only Single-Beacon Systems: A Differential Chan–Gauss–Newton Algorithm with Sequential Data Fusion. Sensors, 25(8), 2577. https://doi.org/10.3390/s25082577






