Synthetic Tactile Sensor for Macroscopic Roughness Estimation Based on Spatial-Coding Contact Processing
Abstract
1. Introduction
2. Apparatus
2.1. Workbench Configuration
2.2. Transparent and Compliant Pad with Ridges
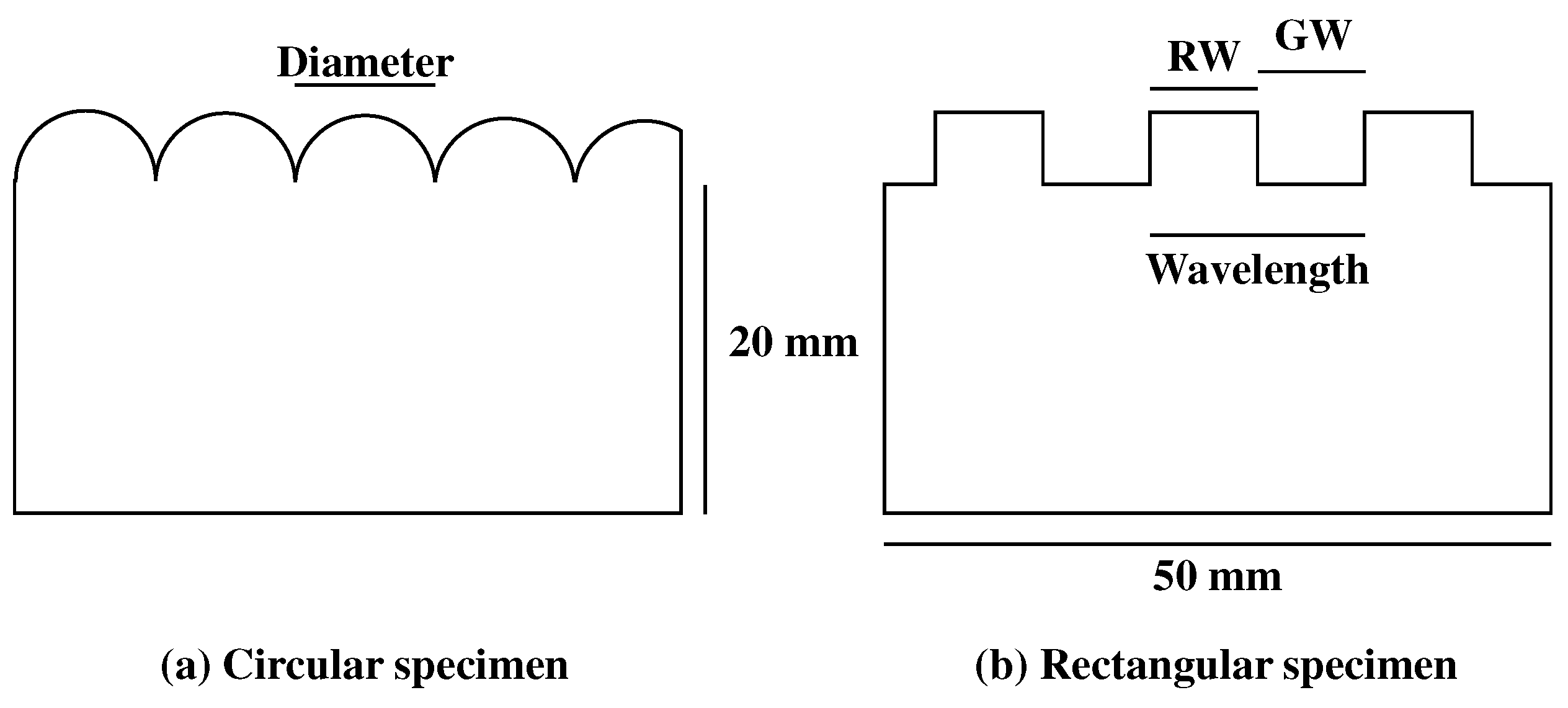
2.3. Roughness Specimens
3. Methods
3.1. Magnitude Estimation Method to Collect Roughness Perceived from Specimens
- A single specimen, labeled R3, was designated as the reference stimulus and assigned a roughness value of 1.0. Participants could freely touch this reference specimen while evaluating other specimens.
- Only pressing motions were permitted; sliding motions were strictly prohibited. This was enforced through clear instructions and continuous monitoring by the experimenters. Any deviation from the instructed motion was promptly addressed with a verbal reminder or, if necessary, by repeating the trial. The level of pressing force was not instructed in order to encourage natural interaction.
- To ensure that roughness estimations were based solely on tactile perception, participants wore glasses with textured stickers to block their vision.
- After touching each test specimen with their index finger, participants rated its subjective roughness relative to the reference specimen.
- This procedure was repeated until all randomly presented test specimens had been evaluated within a single session.
- Each participant completed three separate sessions to ensure data reliability.
3.2. Acquisition of Contact Images
- Each specimen was mounted on the workbench, and a pressing force of 1 N was applied. An image of the contact area was then captured.
- The pressing force was increased to 2 N, and a second image of the contact area was taken.
- The specimen was replaced, and the imaging process was repeated for the next specimen.
- This procedure was performed 10 times for each specimen to capture multiple images, accounting for slight variations across trials.
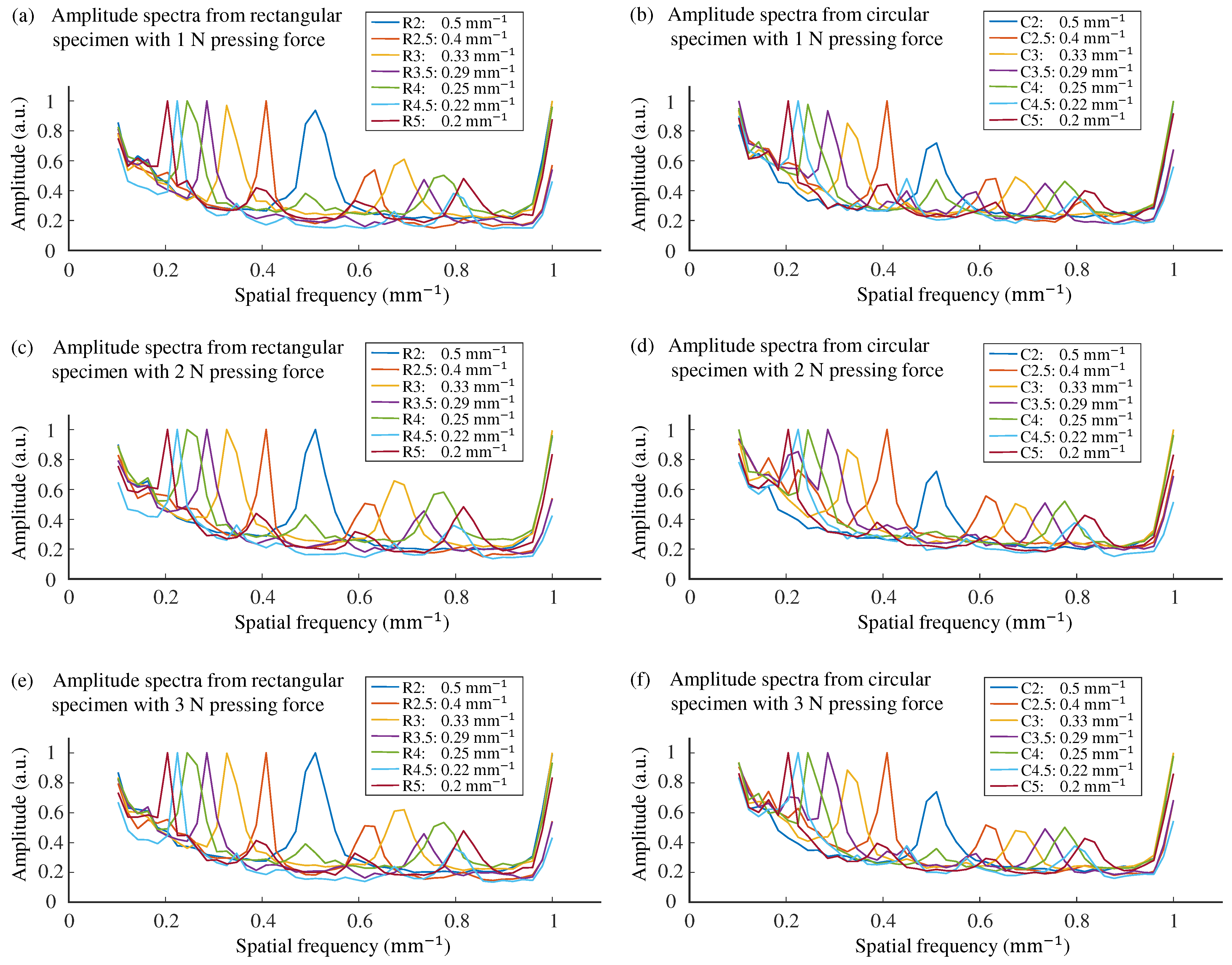
3.3. Prediction of Roughness Perception from Weighted Spatial Spectra of Contact Area
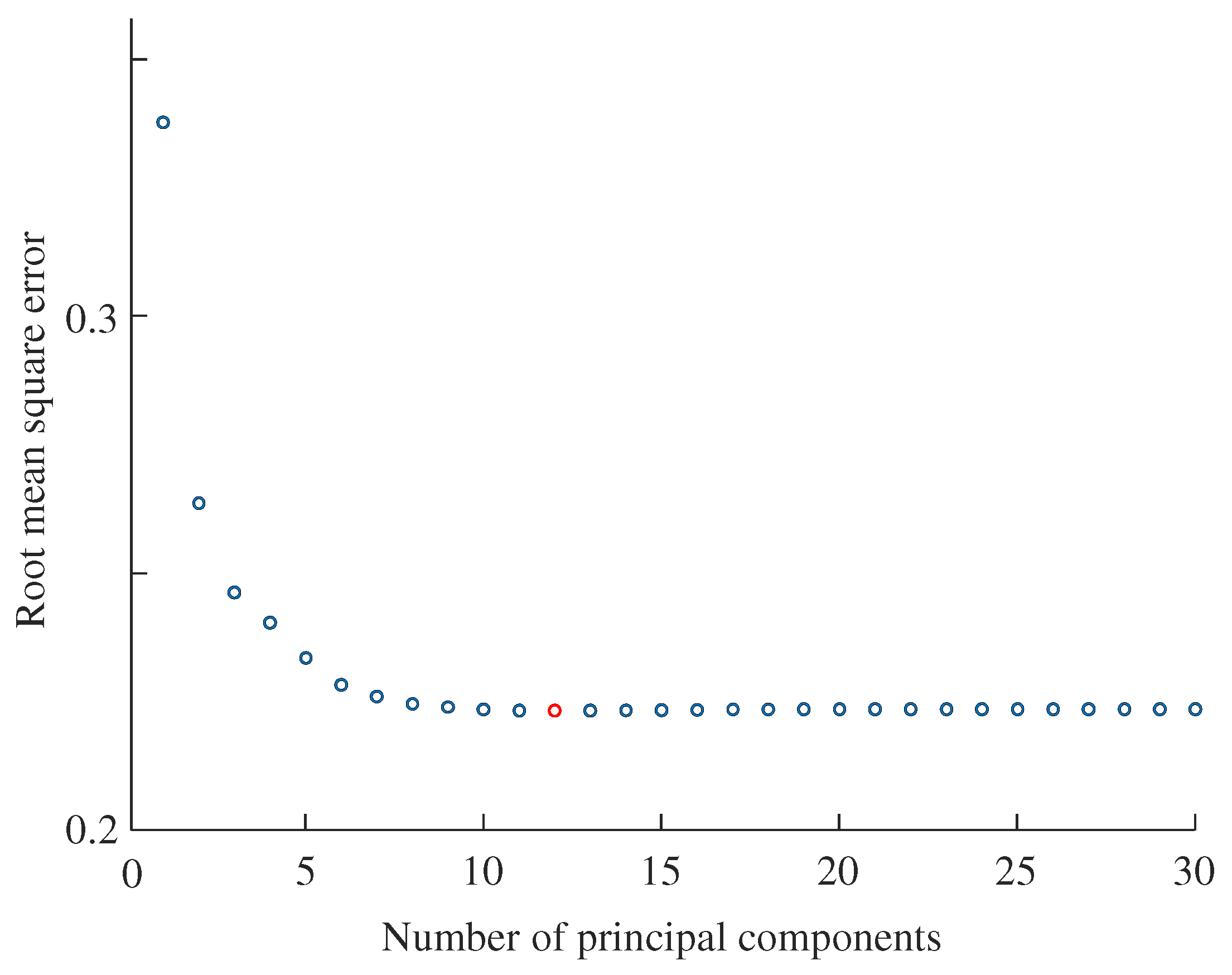
3.4. Performance Indices
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kawabata, S.; Niwa, M. Objective measurement of fabric hand. In Modern Textile Characterization Methods; Raheel, M., Ed.; CRC Press: Boca Raton, FL, USA, 1996; pp. 329–354. [Google Scholar]
- Peck, J.; Childers, T.L. Individual differences in haptic information processing: The “need for touch” scale. J. Consum. Res. 2003, 30, 430–442. [Google Scholar] [CrossRef]
- Chen, X.; Barnes, C.J.; Childs, T.H.C.; Henson, B.; Shao, F. Materials’ tactile testing and characterization for consumer products’ affective packaging design. Mater. Des. 2009, 30, 4299–4310. [Google Scholar] [CrossRef]
- Klöcker, A.; Arnould, C.; Penta, M.; Thonnard, J.L. Rasch-built measure of pleasant touch through active fingertip explorations. Front. Neurorobot. 2012, 6, 5. [Google Scholar] [CrossRef] [PubMed]
- Kadoya, Y.; Khan, M.S.R.; Watanapongvanich, S.; Fukada, M.; Kurita, Y.; Takahashi, M.; Machida, H.; Yarimizu, K.; Kimura, N.; Sakurai, H.; et al. Consumers’ willingness to pay for tactile impressions: A study using smartphone covers. IEEE Access 2022, 10, 85180–85188. [Google Scholar] [CrossRef]
- Richardson, B.A.; Kuchenbecker, K.J. Learning to predict perceptual distributions of haptic adjectives. Front. Neurorobot. 2020, 13, 116. [Google Scholar] [CrossRef] [PubMed]
- Bicchi, A.; Schilingo, E.P.; De Rossi, D. Haptic discrimination of softness in teleoperation: The role of the contact area spread rate. IEEE Trans. Robot. Autom. 2000, 16, 496–504. [Google Scholar] [CrossRef]
- Scilingo, E.P.; Bianchi, M.; Grioli, G.; Bicchi, A. Rendering softness: Integration of kinesthetic and cutaneous information in a haptic device. IEEE Trans. Haptics 2010, 3, 109–118. [Google Scholar] [CrossRef]
- Asaga, E.; Takemura, K.; Maeno, T.; Ban, A.; Toriumi, M. Tactile evaluation based on human tactile perception mechanism. Sens. Actuators A Phys. 2013, 203, 69–75. [Google Scholar] [CrossRef]
- Hashim, I.H.M.; Kumamoto, S.; Takemura, K.; Maeno, T.; Okuda, S.; Mori, Y. Tactile evaluation feedback system for multi-layered structure inspired by human tactile perception mechanism. Sensors 2017, 17, 2601. [Google Scholar] [CrossRef]
- Saito, N.; Matsumori, K.; Kazama, T.; Sakaguchi, S.; Okazaki, R.; Arakawa, N.; Okamoto, S. Skin quality sensor to evaluate vibration and friction generated when sliding over skins. Int. J. Cosmet. Sci. 2023, 45, 851–861. [Google Scholar] [CrossRef]
- Ahirwar, M.; Behera, B.K. Fabric hand research translates senses into numbers—A review. J. Text. Inst. 2021, 113, 2531–2548. [Google Scholar] [CrossRef]
- Bensmaïa, S.J. Texture from touch. Scholarpedia 2009, 4, 7956. [Google Scholar] [CrossRef]
- Okamoto, S.; Nagano, H.; Yamada, Y. Psychophysical dimensions of tactile perception of textures. IEEE Trans. Haptics 2013, 6, 81–93. [Google Scholar] [CrossRef]
- Wettels, N.; Loeb, G.E. Haptic feature extraction from a biomimetic tactile sensor: Force, contact location and curvature. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Karon Beach, Thailand, 7–11 December 2011; pp. 2471–2478. [Google Scholar] [CrossRef]
- Culbertson, H.; Kuchenbecker, K.J. Importance of matching physical friction, hardness, and texture in creating realistic haptic virtual surfaces. IEEE Trans. Haptics 2017, 10, 63–74. [Google Scholar] [CrossRef]
- Ding, S.; Pan, Y.; Tong, M.; Zhao, X. Tactile perception of roughness and hardness to discriminate materials by friction-induced vibration. Sensors 2017, 17, 2748. [Google Scholar] [CrossRef]
- Mukaibo, Y.; Shirado, H.; Konyo, M.; Maeno, T. Development of a texture sensor emulating the tissue structure and perceptual mechanism of human fingers. In Proceedings of the IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2565–2570. [Google Scholar]
- Kim, S.J.; Choi, J.Y.; Moon, H.; Choi, H.R.; Koo, J.C. Biomimetic hybrid tactile sensor with ridged structure that mimics human fingerprints to acquire surface texture information. Sens. Mater. 2020, 32, 3787–3799. [Google Scholar] [CrossRef]
- Kim, K.; Sim, M.; Lim, S.H.; Kim, D.; Lee, D.; Shin, K.; Moon, C.; Choi, J.W.; Jang, J.E. Tactile avatar: Tactile sensing system mimicking human tactile cognition. Adv. Sci. 2021, 8, 2002362. [Google Scholar] [CrossRef] [PubMed]
- Shirakawa, K.; Tanaka, Y.; Hashimoto, M.; Watarai, E.; Igarashi, T. Wearable Artificial Fingers with Skin Vibration and Multi-Axis Force Sensors. IEEE Trans. Haptics 2021, 14, 242–247. [Google Scholar] [CrossRef] [PubMed]
- Ke, A.; Huang, J.; Chen, L.; Gao, Z.; Han, J.; Wang, C.; Zhou, J.; He, J. Fingertip Tactile Sensor with Single Sensing Element Based on FSR and PVDF. IEEE Sens. J. 2019, 19, 11100–11112. [Google Scholar] [CrossRef]
- Liu, W.; Yu, P.; Gu, C.; Cheng, X.; Fu, X. Fingertip Piezoelectric Tactile Sensor Array for Roughness Encoding Under Varying Scanning Velocity. IEEE Sens. J. 2017, 17, 6867–6879. [Google Scholar] [CrossRef]
- Yanwari, M.I.; Okamoto, S. Healing function for abraded fingerprint ridges in tactile texture sensors. Sensors 2024, 24, 4078. [Google Scholar] [CrossRef] [PubMed]
- Hollins, M.; Bensmaïa, S.J. The coding of roughness. Can. J. Exp. Psychol. 2007, 61, 184–195. [Google Scholar] [CrossRef]
- Hollins, M.; Bensmaïa, S.; Roy, E. Vibrotaction and texture perception. Behav. Brain Res. 2002, 135, 51–56. [Google Scholar] [CrossRef]
- Johansson, R.S.; Vallbo, B.Å. Tactile sensory coding in the glabrous skin of the human hand. Trends Neurosci. 1983, 6, 27–32. [Google Scholar] [CrossRef]
- Phillips, J.R.; Johnson, K.O. Tactile spatial resolution. III. A continuum mechanics model of skin predicting mechanoreceptor responses to bars, edges, and gratings. J. Neurophysiol. 1981, 46, 1204–1225. [Google Scholar] [CrossRef]
- Lesniak, D.R.; Gerling, G.J. Predicting SA-I mechanoreceptor spike times with a skin-neuron model. Math. Biosci. 2009, 220, 15–23. [Google Scholar] [CrossRef] [PubMed]
- Corniani, G.; Saal, H.P. Tactile innervation densities across the whole body. J. Neurophysiol. 2020, 124, 1229–1240. [Google Scholar] [CrossRef]
- Johansson, R.S. Tactile sensibility in the human hand: Receptive field characteristics of mechanoreceptive units in the glabrous skin area. J. Physiol. 1978, 281, 101–125. [Google Scholar] [CrossRef]
- Blake, D.T.; Hsiao, S.S.; Johnson, K.O. Neural Coding Mechanisms in Tactile Pattern Recognition: The Relative Contributions of Slowly and Rapidly Adapting Mechanoreceptors to Perceived Roughness. J. Neurosci. 1997, 17, 7480–7489. [Google Scholar] [CrossRef]
- Connor, C.E.; Johnson, K.O. Neural Coding of Tactile Texture: Comparison of Spatial and Temporal Mechanisms for Roughness Perception. J. Neurosci. 1992, 12, 3414–3426. [Google Scholar] [CrossRef]
- Weber, A.I.; Saal, H.P.; Lieber, J.D.; Cheng, J.W.; Manfredi, L.R.; Dammann, J.F.I.; Bensmaïa, S.J. Spatial and temporal codes mediate the tactile perception of natural textures. Proc. Natl. Acad. Sci. USA 2013, 110, 17107–17112. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Okamoto, S.; Akiyama, Y.; Yamada, Y. Multiple Spatial Spectral Components of Static Skin Deformation for Predicting Macroscopic Roughness Perception. IEEE Trans. Haptics 2022, 15, 646–654. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, S.; Oishi, A. Relationship between spatial variations in static skin deformation and perceived roughness of macroscopic surfaces. IEEE Trans. Haptics 2020, 13, 66–72. [Google Scholar] [CrossRef]
- Lamb, G.D. Tactile discrimination of textured surfaces: Psychophysical performance measurements in humans. J. Physiol. 1983, 338, 551–565. [Google Scholar] [CrossRef]
- Meftah, E.M.; Belingard, L.; Chapman, C.E. Relative effects of the spatial and temporal characteristics of scanned surfaces on human perception of tactile roughness using passive touch. Exp. Brain Res. 2000, 132, 351–361. [Google Scholar] [CrossRef]
- Hollins, M.; Rinser, S.R. Evidence for the Duplex Theory of Tactile Texture Perception. Atten. Percept. Psychophys. 2000, 62, 695–705. [Google Scholar] [CrossRef]
- Tymms, C.; Zorin, D.; Gardne, E.P. Tactile perception of the roughness of 3D-printed textures. J. Neurophysiol. 2018, 119, 862–876. [Google Scholar] [CrossRef] [PubMed]
- Arvidsson, M.; Ringstad, L.; Skedung, L.; Duvefelt, K.; Rutland, M.W. Feeling fine—The effect of topography and friction on perceived roughness and slipperiness. Biotribology 2017, 11, 92–101. [Google Scholar] [CrossRef]
- Johnson, M.K.; Adelson, E.H. Retrographic sensing for the measurement of surface texture and shape. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1070–1077. [Google Scholar] [CrossRef]
- Maheshwari, V.; Saraf, R.F. High-Resolution Thin-Film Device to Sense Texture by Touch. Science 2006, 312, 1501–1504. [Google Scholar] [CrossRef]
- Li, R.; Adelson, E.H. Sensing and Recognizing Surface Textures Using a GelSight Sensor. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1241–1247. [Google Scholar]
- Ito, Y.; Kim, Y.; Nagai, C.; Obinata, G. Vision-Based Tactile Sensing and Shape Estimation Using a Fluid-Type Touchpad. IEEE Trans. Autom. Sci. Eng. 2012, 9, 734–744. [Google Scholar] [CrossRef]
- Saga, S.; Kajimoto, H.; Tachi, S. High-resolution tactile sensor using the deformation of a reflection image. Sens. Rev. 2007, 27, 35–42. [Google Scholar] [CrossRef]
- Cummins, H.; Waits, W.J.; McQuitty, J.T. The breadths of epidermal ridges on the finger tips and palms: A study of variation. Am. J. Anat. 1941, 68, 127–150. [Google Scholar] [CrossRef]
- Maeno, T.; Kobayashi, K.; Yamazaki, N. Relationship between structure of finger tissue and location of tactile receptors. Trans. Jpn. Soc. Mech. Eng. C 1997, 63, 881–888. [Google Scholar] [CrossRef][Green Version]
- Dai, K.; Wang, X.; Rojas, A.M.; Harber, E.; Tian, Y.; Paiva, N.; Gnehm, J.; Schindewolf, E.; Choset, H.; Webster-Wood, V.A.; et al. Design of a biomimetic tactile sensor for material classification. In Proceedings of the International Conference on Robotics and Automation, Philadelphia, PA, USA, 23–27 May 2022; pp. 10774–10780. [Google Scholar] [CrossRef]
- Yamada, D.; Maeno, T.; Yamada, Y. Artificial finger skin having ridges and distributed tactile sensors used for grasp force control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001; Volume 2, pp. 686–691. [Google Scholar] [CrossRef]
- Wandersman, E.; Candelier, R.; Debrégeas, G.; Prevost, A. Texture-induced modulations of friction force: The fingerprint effect. Phys. Rev. Lett. 2011, 107, 164301. [Google Scholar] [CrossRef]
- Gerling, G.J.; Thomas, G.W. The effect of fingertip microstructures on tactile edge perception. In Proceedings of the Joint Eurohaptics Conference and Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems, World Haptics Conference, Pisa, Italy, 18–20 March 2005; pp. 63–72. [Google Scholar] [CrossRef]
- Gerling, G.J. SA-I mechanoreceptor position in fingertip skin may impact sensitivity to edge stimuli. Appl. Bionics Biomech. 2010, 7, 19–29. [Google Scholar] [CrossRef]
- Yum, S.M.; Baek, I.K.; Hong, D.; Kim, J.; Jung, K.; Kim, S.; Eom, K.; Jang, J.; Kim, S.; Sattorov, M.; et al. Fingerprint ridges allow primates to regulate grip. Proc. Natl. Acad. Sci. USA 2020, 117, 31665–31673. [Google Scholar] [CrossRef] [PubMed]
- Fagiani, R.; Massi, F.; Chatelet, E.; Berthier, Y.; Akay, A. Tactile perception by friction induced vibrations. Tribol. Int. 2011, 44, 1100–1110. [Google Scholar] [CrossRef]
- Maeno, T.; Kobayashi, K. FE analysis of the dynamic characteristics of the human finger pad in contact with objects with/without surface roughness. In Proceedings of the Dynamic Systems and Control, Anaheim, CA, USA, 15–20 November 1998; pp. 279–286. [Google Scholar] [CrossRef]
- Scheibert, J.; Leurent, S.; Prevost, A.; Debrégeas, G. The role of fingerprints in the coding of tactile information probed with a biomimetic sensor. Science 2009, 323, 1503–1506. [Google Scholar] [CrossRef]
- Adams, M.J.; Johnson, S.A.; Lefèvre, P.; Lévesque, V.; Hayward, V.; André, T.; Thonnard, J.L. Finger pad friction and its role in grip and touch. J. R. Soc. Interface 2013, 10, 20120467. [Google Scholar] [CrossRef]
- Dzidek, B.M.; Adams, M.J.; Andrews, J.W.; Zhang, Z.; Johnson, S.A. Contact mechanics of the human finger pad under compressive loads. J. R. Soc. Interface 2017, 14, 20160935. [Google Scholar] [CrossRef]
- Park, G.S. The function of fingerprints: How can we grip? Open Access Gov. 2023, 38, 280–281. [Google Scholar] [CrossRef]
- Okamoto, S.; Konyo, M.; Tadokoro, S. Discriminability-based evaluation of transmission capability of tactile transmission systems. Virtual Real. 2012, 16, 141–150. [Google Scholar] [CrossRef]
- Hollins, M.; Bensmaïa, S.J.; Washburn, S. Vibrotactile adaptation impairs discrimination of fine, but not coarse, textures. Somatosens. Mot. Res. 2001, 18, 253–262. [Google Scholar] [CrossRef] [PubMed]
- Fox, R.R.; Maikala, R.V.; Bao, S.; Dempsey, P.G.; Brogmus, G.; Cort, J.; Maikala, R.V. The relevance of psychophysical methods research for the practitioner. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2017, 61, 997–999. [Google Scholar] [CrossRef]
- Han, S.H.; Song, M.; Kwahk, J. A systematic method for analyzing magnitude estimation data. Int. J. Ind. Ergon. 1999, 23, 513–524. [Google Scholar] [CrossRef]
- Lawrence, M.A.; Kitada, R.; Klatzky, R.L.; Lederman, S.J. Haptic roughness perception of linear gratings via bare finger or rigid probe. Perception 2007, 36, 547–557. [Google Scholar] [CrossRef]
- Lederman, S.J.; Taylor, M.M. Fingertip force, surface geometry, and the perception of roughness by active touch. Percept. Psychophys. 1972, 12, 401–408. [Google Scholar] [CrossRef]
- Tanaka, Y.; Bergmann Tiest, W.M.; Kappers, A.M.L.; Sano, A. Contact force and scanning velocity during active roughness perception. PLoS ONE 2014, 9, e93363. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Ruhe, A.; Wold, H.; Dunn, W. The Collinearity Problem in Linear Regression. The Partial Least Squares (PLS) Approach to Generalized Inverses. Siam J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef]
- Manne, R. Analysis of two partial-least-squares algorithms for multivariate calibration. Chemom. Intell. Lab. Syst. 1987, 2, 187–197. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Bastien, P.; Vinzi, V.E.; Tenenhaus, M. PLS generalised linear regression. Comput. Stat. Data Anal. 2005, 48, 17–46. [Google Scholar] [CrossRef]
- Stott, A.E.; Kanna, S.; Mandic, D.P. Widely linear complex partial least squares for latent subspace regression. Signal Process. 2018, 152, 350–362. [Google Scholar] [CrossRef]
- de Jong, S. SIMPLS: An alternative approach to partial least squares regression. Chemom. Intell. Lab. Syst. 1993, 18, 251–263. [Google Scholar] [CrossRef]
- MathWorks. Plsregress: Partial Least-Squares (PLS) Regression; MathWorks: Natick, MA, USA, 2024. [Google Scholar]
- Walker, S.G. A New Measure of Overlap: An Alternative to the p–value. arXiv 2021, arXiv:2106.01821. [Google Scholar] [CrossRef]
- Eidous, O.; Daradkeh, S. On inference of weitzman overlapping coefficient Δ(X,Y) in the case of two normal distributions. Int. J. Theor. Appl. Math. 2024, 10, 14–22. [Google Scholar] [CrossRef]
- Yoshioka, T.; Gibb, B.; Dorsch, A.; Hsiao, S.S.; Johnson, K.O. Neural coding mechanisms underlying perceived roughness of finely textured surfaces. J. Neurosci. 2001, 21, 6905–6916. [Google Scholar] [CrossRef] [PubMed]
- Drewing, K. Judged Roughness as a Function of Groove Frequency and Groove Width in 3D-Printed Gratings; Springer: Berlin/Heidelberg, Germany, 2018; pp. 258–269. [Google Scholar] [CrossRef]
- Sathian, K.; Goodwin, A.W.; John, K.T.; Darian-Smith, I. Perceived roughness of a grating: Correlationn with responses of mechanoreceptive afferents innervating the monkey’s fingerpad. J. Neurosci. 1989, 9, 1273–1279. [Google Scholar] [CrossRef]
- Taylor, M.M.; Lederman, S.J. Tactile roughness of grooved surfaces: A model and the effect of friction. Percept. Psychophys. 1975, 17, 23–36. [Google Scholar] [CrossRef]
- Lederman, S.J. Tactile roughness of grooved surfaces: The touching process and effects of macro-and microsurface structure. Percept. Psychophys. 1974, 16, 385–395. [Google Scholar] [CrossRef]
- Kuroki, S.; Sawayama, M.; Nishida, S. The roles of lower- and higher-order surface statistics in tactile texture perception. J. Neurophysiol. 2021, 126, 95–111. [Google Scholar] [CrossRef] [PubMed]






| Specimen | Perceived | Prediction | |||
|---|---|---|---|---|---|
| Roughness | Dataset 1 N | Dataset 2 N | Dataset 3 N | Dataset Combination | |
| R2 | |||||
| R2.5 | |||||
| R3 | |||||
| R3.5 | |||||
| R4 | |||||
| R4.5 | |||||
| R5 | |||||
| C2 | |||||
| C2.5 | |||||
| C3 | |||||
| C3.5 | |||||
| C4 | |||||
| C4.5 | |||||
| C5 | |||||
| Specimen | Overlap Coefficient (OVL) | |||
|---|---|---|---|---|
| Dataset 1 N | Dataset 2 N | Dataset 3 N | Dataset Combination | |
| R2 | ||||
| R2.5 | ||||
| R3 | − | − | − | − |
| R3.5 | ||||
| R4 | ||||
| R4.5 | ||||
| R5 | ||||
| C2 | ||||
| C2.5 | ||||
| C3 | ||||
| C3.5 | ||||
| C4 | ||||
| C4.5 | ||||
| C5 | ||||
| Rectangular: | ||||
| Mean ± S.D. | ||||
| Circular: | ||||
| Mean ± S.D. | ||||
| Overall: | ||||
| Mean ± S.D. | ||||
| Specimen | Root Mean Squared Error (RMSE) | |||
|---|---|---|---|---|
| Dataset 1 N | Dataset 2 N | Dataset 3 N | Dataset Combination | |
| R2 | ||||
| R2.5 | ||||
| R3 | ||||
| R3.5 | ||||
| R4 | ||||
| R4.5 | ||||
| R5 | ||||
| C2 | ||||
| C2.5 | ||||
| C3 | ||||
| C3.5 | ||||
| C4 | ||||
| C4.5 | ||||
| C5 | ||||
| Mean ± S.D. | ||||
| Specimen | Perceived | Prediction | |||
|---|---|---|---|---|---|
| Roughness | Dataset 1 N | Dataset 2 N | Dataset 3 N | Dataset Combination | |
| R2 | |||||
| R2.5 | |||||
| R3 | |||||
| R3.5 | |||||
| R4 | |||||
| R4.5 | |||||
| R5 | |||||
| C2 | |||||
| C2.5 | |||||
| C3 | |||||
| C3.5 | |||||
| C4 | |||||
| C4.5 | |||||
| C5 | |||||
| Specimen | Overlap Coefficient (OVL) | |||
|---|---|---|---|---|
| Dataset 1 N | Dataset 2 N | Dataset 3 N | Dataset Combination | |
| R2 | ||||
| R2.5 | ||||
| R3 | − | − | − | − |
| R3.5 | ||||
| R4 | ||||
| R4.5 | ||||
| R5 | ||||
| C2 | ||||
| C2.5 | ||||
| C3 | ||||
| C3.5 | ||||
| C4 | ||||
| C4.5 | ||||
| C5 | ||||
| Rectangular: | ||||
| Mean ± S.D. | ||||
| Circular: | ||||
| Mean ± S.D. | ||||
| Overall: | ||||
| Mean ± S.D. | ||||
| Specimen | Root Mean Squared Error (RMSE) | |||
|---|---|---|---|---|
| Dataset 1 N | Dataset 2 N | Dataset 3 N | Dataset Combination | |
| R2 | ||||
| R2.5 | ||||
| R3 | ||||
| R3.5 | ||||
| R4 | ||||
| R4.5 | ||||
| R5 | ||||
| C2 | ||||
| C2.5 | ||||
| C3 | ||||
| C3.5 | ||||
| C4 | ||||
| C4.5 | ||||
| C5 | ||||
| Mean ± S.D. | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yanwari, M.I.; Okamoto, S. Synthetic Tactile Sensor for Macroscopic Roughness Estimation Based on Spatial-Coding Contact Processing. Sensors 2025, 25, 2598. https://doi.org/10.3390/s25082598
Yanwari MI, Okamoto S. Synthetic Tactile Sensor for Macroscopic Roughness Estimation Based on Spatial-Coding Contact Processing. Sensors. 2025; 25(8):2598. https://doi.org/10.3390/s25082598
Chicago/Turabian StyleYanwari, Muhammad Irwan, and Shogo Okamoto. 2025. "Synthetic Tactile Sensor for Macroscopic Roughness Estimation Based on Spatial-Coding Contact Processing" Sensors 25, no. 8: 2598. https://doi.org/10.3390/s25082598
APA StyleYanwari, M. I., & Okamoto, S. (2025). Synthetic Tactile Sensor for Macroscopic Roughness Estimation Based on Spatial-Coding Contact Processing. Sensors, 25(8), 2598. https://doi.org/10.3390/s25082598







