Accurate Conversion of Land Surface Reflectance for Drone-Based Multispectral Remote Sensing Images Using a Solar Radiation Component Separation Approach
Abstract
:1. Introduction
- It is recommended that the solar elevation angle is as large as possible (e.g., to capture images at noon), and the flight routes are perpendicular to the solar azimuth angle to minimize the impact of tilting effect; however, the method cannot completely eliminate the tilting effect.
- If a multi-rotor drone is used as the platform, hovering mode is recommended to minimize the impact of tilting effect. However, the light intensity sensor can only remain horizontal when there is no wind at all; otherwise, it cannot guarantee that the sensor is horizontal, and therefore, it still cannot eliminate the impact of tilting effect. Experimental tests have indicated that the tilting angle can exceed 15° in hovering mode when the wind speed is relatively higher. The primary advantage of hovering mode is that it can eliminate motion blurring, yet a significant drawback is that the operation efficiency is extremely low.
2. Theory and Methods
2.1. Solar Radiation Component Separation
- (1)
- Direct solar radiation
- (2)
- Atmospheric scattering radiation
- (3)
- Ground reflection radiation
2.2. Land Surface Reflectance Conversion
- (1)
- Method for calculation of radiance
- (2)
- Method for calculation of
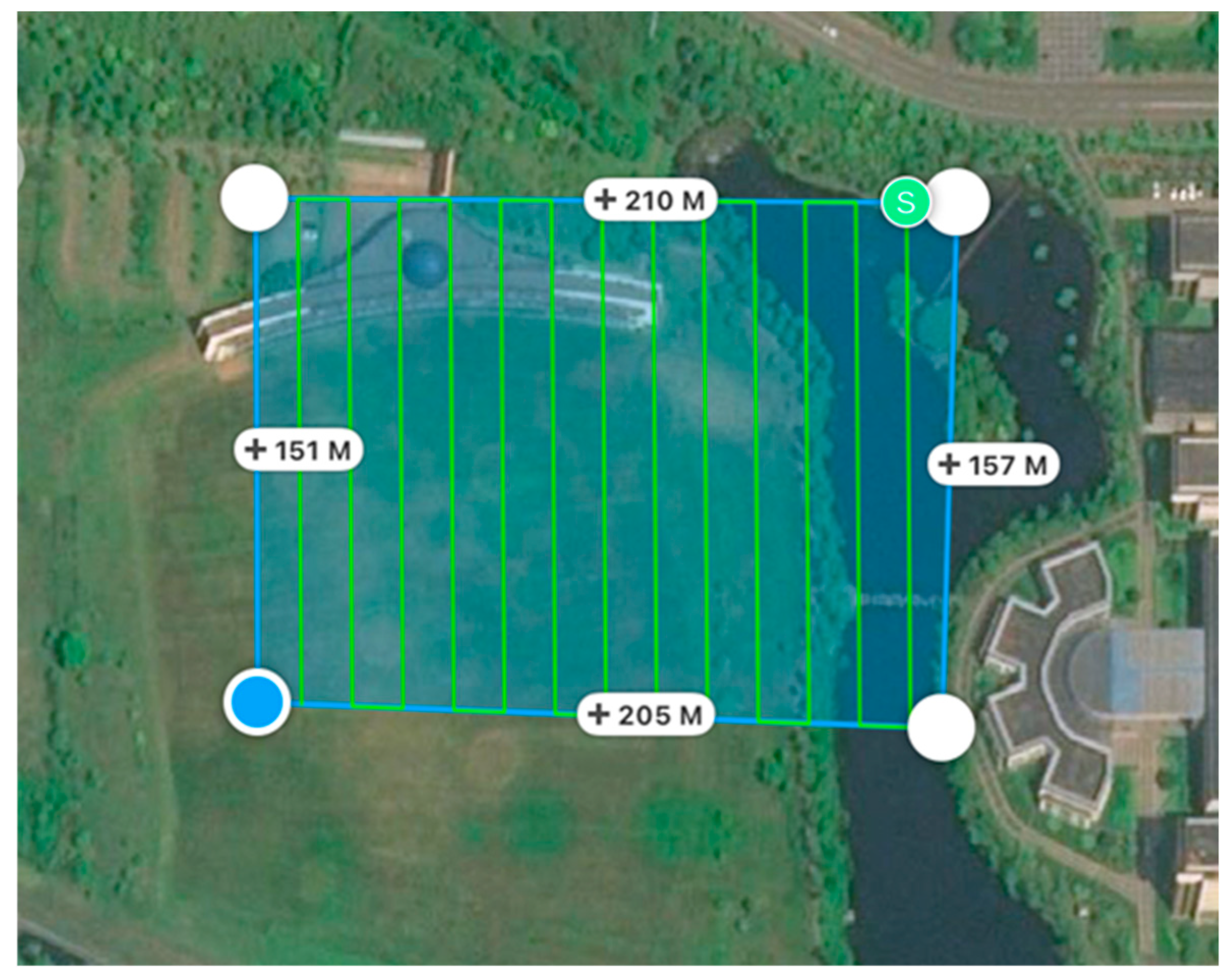
3. Experiments
4. Results and Analysis
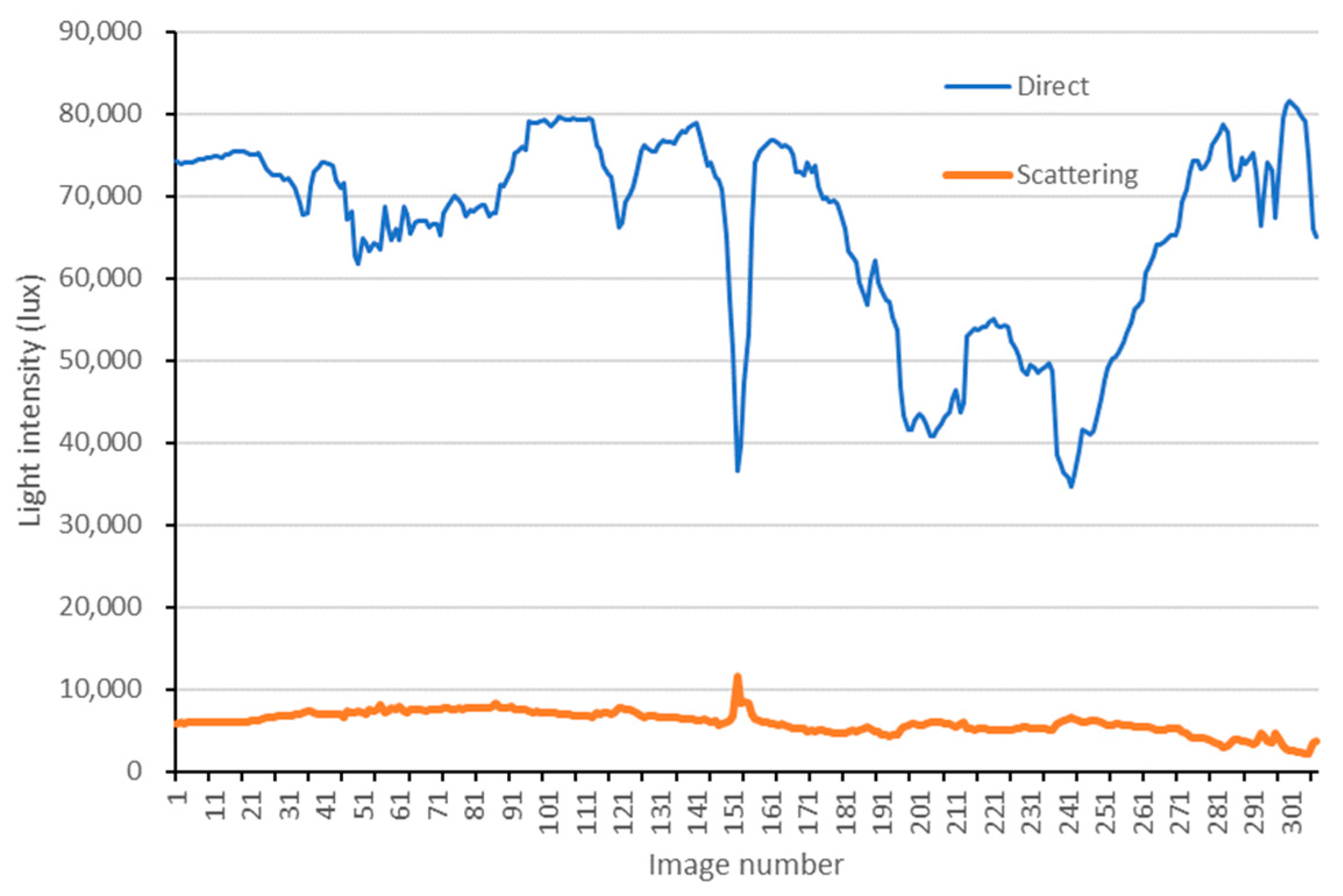
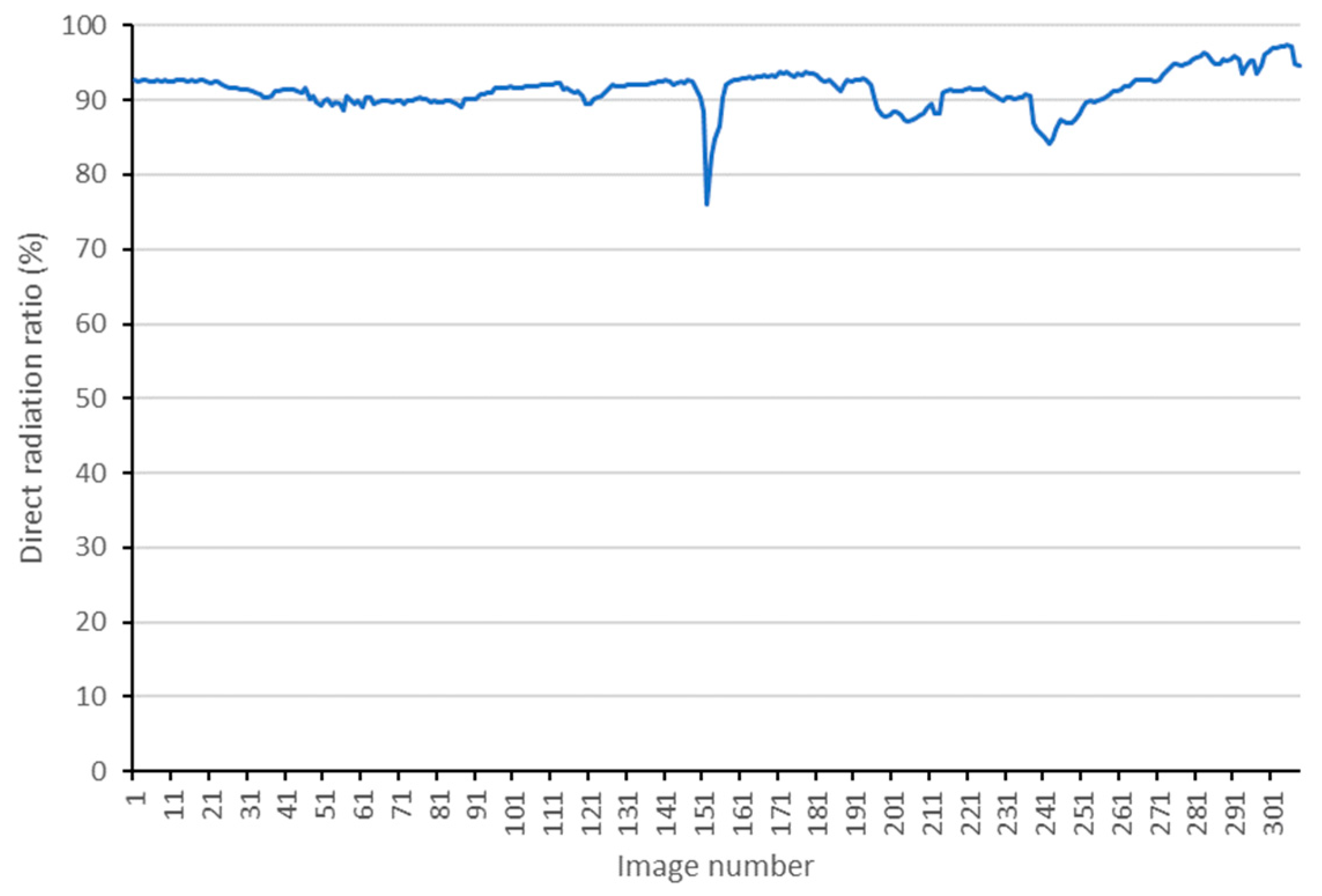
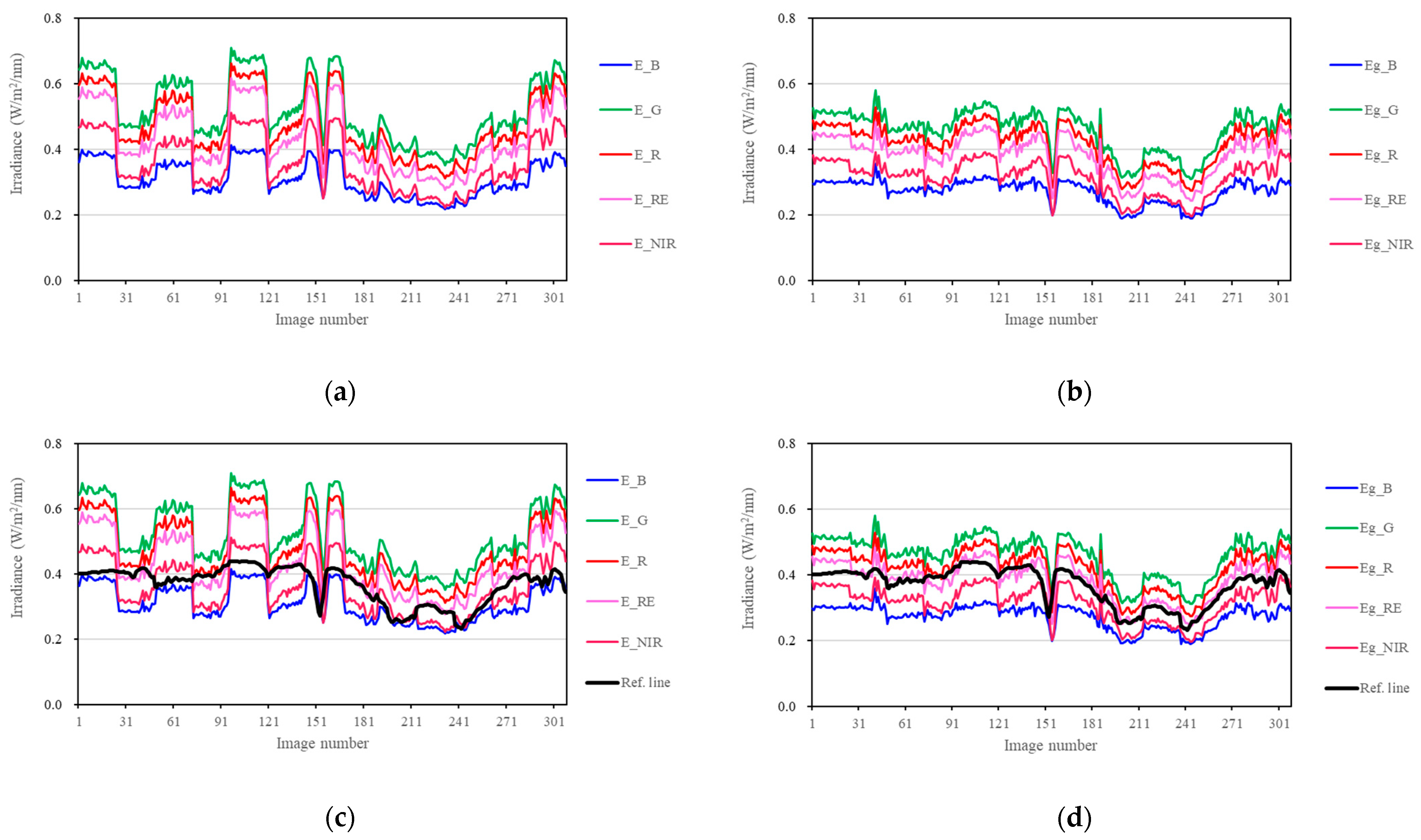
4.1. Radiation Components
4.2. Reflectance Conversion
4.3. Accuracy Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- (1)
- The incidence angle of direct solar radiation on a horizontal ground can be calculated by Equation (A1):
- (2)
- The slope angle of a tilted sensor () can be calculated by Equation (A3):
- (3)
- The incidence angle of direct solar radiation on a tilted sensor () can be calculated by Equation (A4):
References
- Deng, L.; Mao, Z.; Li, X.; Hu, Z.; Duan, F.; Yan, Y. UAV-based multispectral remote sensing for precision agriculture: A comparison between different cameras. ISPRS J. Photogramm. Remote Sens. 2018, 146, 124–136. [Google Scholar] [CrossRef]
- Khose, S.B.; Mailapalli, D.R.; Biswal, S.; Chatterjee, C. UAV-based multispectral image analytics for generating crop coefficient maps for rice. Arab. J. Geosci. 2022, 15, 1681. [Google Scholar] [CrossRef]
- Pan, W.; Wang, X.; Sun, Y.; Wang, J.; Li, Y.; Li, S. Karst vegetation coverage detection using UAV multispectral vegetation indices and machine learning algorithm. Plant Methods 2023, 19, 7. [Google Scholar] [CrossRef]
- Berry, A.; Vivier, M.A.; Poblete-Echeverría, C. Evaluation of canopy fraction-based vegetation indices, derived from multispectral UAV imagery, to map water status variability in a commercial vineyard. Irrig. Sci. 2025, 43, 135–153. [Google Scholar] [CrossRef]
- Nurmukhametov, A.L.; Sidorchuk, D.S.; Skidanov, R.V. Harmonization of Hyperspectral and Multispectral Data for Calculation of Vegetation Index. J. Commun. Technol. Electron. 2024, 69, 38–45. [Google Scholar] [CrossRef]
- Bukowiecki, J.; Rose, T.; Holzhauser, K.; Rothardt, S.; Rose, M.; Komainda, M.; Herrmann, A.; Kage, H. UAV-based canopy monitoring: Calibration of a multispectral sensor for green area index and nitrogen uptake across several crops. Precis. Agric. 2024, 25, 1556–1580. [Google Scholar] [CrossRef]
- Cheng, Q.; Ding, F.; Xu, H.; Guo, S.; Li, Z.; Chen, Z. Quantifying corn LAI using machine learning and UAV multispectral imaging. Precis. Agric. 2024, 25, 1777–1799. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, P.; Wang, Z.; Wang, Y. Potential of multi-seasonal vegetation indices to predict rice yield from UAV multispectral observations. Precis. Agric. 2024, 25, 1235–1261. [Google Scholar] [CrossRef]
- Tatsumi, K.; Usami, T. Plant-level prediction of potato yield using machine learning and unmanned aerial vehicle (UAV) multispectral imagery. Discov. Appl. Sci. 2024, 6, 649. [Google Scholar] [CrossRef]
- Heinemann, P.; Prey, L.; Hanemann, A.; Ramgraber, L.; Seidl-Schulz, J.; Noack, P.O. Enhancing model performance through date fusion in multispectral and RGB image-based field phenotyping of wheat grain yield. Precis. Agric. 2025, 26, 20. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Niu, Y.; Han, W. Mapping Maize Water Stress Based on UAV Multispectral Remote Sensing. Remote Sens. 2019, 11, 605. [Google Scholar] [CrossRef]
- Tang, Z.; Jin, Y.; Alsina, M.M.; McElrone, A.J.; Bambach, N.; Kustas, W.P. Vine water status mapping with multispectral UAV imagery and machine learning. Irrig. Sci. 2022, 40, 715–730. [Google Scholar] [CrossRef]
- Sun, G.; Hu, T.; Chen, S.; Sun, J.; Zhang, J.; Ye, R.; Zhang, S.; Liu, J. Using UAV-based multispectral remote sensing imagery combined with DRIS method to diagnose leaf nitrogen nutrition status in a fertigated apple orchard. Precis. Agric. 2023, 24, 2522–2548. [Google Scholar] [CrossRef]
- Sun, G.; Chen, S.; Hu, T.; Zhang, S.; Li, H.; Li, A.; Zhao, L.; Liu, J. Identifying optimal ground feature classification and assessing leaf nitrogen status based on UAV multispectral images in an apple orchard. Plant Soil 2024, 1–20. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, Z.; Ding, B.; Wang, T.; Zhang, J.; Liu, C.; Zhang, Q.; Zuo, X.; Chen, J.; Cui, N.; et al. Evaluation of winter-wheat water stress with UAV-based multispectral data and ensemble learning method. Plant Soil 2024, 497, 647–668. [Google Scholar] [CrossRef]
- Bagheri, N.; Rahimi Jahangirlou, M.; Jaberi Aghdam, M. Determining Variable Rate Fertilizer Dosage in Forage Maize Farm Using Multispectral UAV Imagery. J. Indian Soc. Remote Sens. 2025, 53, 59–66. [Google Scholar] [CrossRef]
- Narmilan, A.; Gonzalez, F.; Salgadoe, A.S.A.; Powell, K. Detection of White Leaf Disease in Sugarcane Using Machine Learning Techniques over UAV Multispectral Images. Drones 2022, 6, 230. [Google Scholar] [CrossRef]
- de Lima, G.S.A.; Ferreira, M.E.; Sales, J.C.; de Souza Passos, J.; Maggiotto, S.R.; Madari, B.E.; de Melo Carvalho, M.T.; de Almeida Machado, P.L.O. Evapotranspiration measurements in pasture, crops, and native Brazilian Cerrado based on UAV-borne multispectral sensor. Environ. Monit. Assess. 2024, 196, 1105. [Google Scholar] [CrossRef]
- Blanco-Sacristán, J.; Johansen, K.; Elías-Lara, M.; Tu, Y.; Duarte, C.M.; McCabe, M.F. Quantifying mangrove carbon assimilation rates using UAV imagery. Sci. Rep. 2024, 14, 4648. [Google Scholar] [CrossRef]
- Reyes, J.; Wiedemann, W.; Brand, A.; Franke, J.; Lie, M. Predictive monitoring of soil organic carbon using multispectral UAV imagery: A case study on a long-term experimental field. Spat. Inf. Res. 2024, 32, 683–696. [Google Scholar] [CrossRef]
- Rossi, F.S.; Della-Silva, J.L.; Teodoro, L.P.R.; Teodoro, P.E.; Santana, D.C.; Baio, F.H.R.; Morinigo, W.B.; Crusiol, L.G.T.; Scala, N.L., Jr.; da Silva, C.A., Jr. Assessing soil CO2 emission on eucalyptus species using UAV-based reflectance and vegetation indices. Sci. Rep. 2024, 14, 20277. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Niu, B.; Li, X.; Kang, X.; Wan, H.; Shi, X.; Li, Q.; Xue, Y.; Hu, X. Inversion of soil salinity in China’s Yellow River Delta using unmanned aerial vehicle multispectral technique. Environ. Monit. Assess. 2023, 195, 245. [Google Scholar] [CrossRef]
- Gallardo-Salazar, J.L.; Rosas-Chavoya, M.; Pompa-García, M.; López-Serrano, P.M.; García-Montiel, E.; Meléndez-Soto, A.; Jiménez-Jiménez, S.I. Multi-temporal NDVI analysis using UAV images of tree crowns in a northern Mexican pine-oak forest. J. For. Res. 2023, 34, 1855–1867. [Google Scholar] [CrossRef]
- De Petris, S.; Ruffinatto, F.; Cremonini, C.; Negro, F.; Zanuttini, R.; Borgogno-Mondino, E. Exploring the potential of multispectral imaging for wood species discrimination. Eur. J. Wood Wood Prod. 2024, 82, 1541–1550. [Google Scholar] [CrossRef]
- Krause, S.; Sanders, T. European beech spring phenological phase prediction with UAV-derived multispectral indices and machine learning regression. Sci. Rep. 2024, 14, 15862. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.; Guan, H.; Chen, K.; Zang, Y.; Yu, Y. Urban Tree Species Classification Using UAV-Based Multispectral Images and LiDAR Point Clouds. J. Geovis. Spat. Anal. 2024, 8, 5. [Google Scholar] [CrossRef]
- Ngo, T.D. Assessing the characteristics and seasonal changes of mangrove forest in Dong Rui commune, Quang Ninh Province, Vietnam based on multispectral UAV data. Landsc. Ecol. Eng. 2024, 20, 223–235. [Google Scholar] [CrossRef]
- Fu, L.; Lo, Y.; Lu, T.C.; Zhang, C. Water Quality Inversion of UAV Multispectral Data Using Machine Learning. In Towards a Carbon Neutral Future. ICSBS 2023. Lecture Notes in Civil Engineering; Papadikis, K., Zhang, C., Tang, S., Liu, E., Di Sarno, L., Eds.; Springer: Singapore, 2024; Volume 393, pp. 357–365. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, A.; Lv, R.; Zhang, Y.; Ma, J.; Li, T. Machine learning algorithm inversion experiment and pollution analysis of water quality parameters in urban small and medium-sized rivers based on UAV multispectral data. Environ. Sci. Pollut. Res. 2023, 30, 78913–78932. [Google Scholar] [CrossRef]
- von Bueren, S.K.; Burkart, A.; Hueni, A.; Rascher, U.; Tuohy, M.P.; Yule, I.J. Deploying Four Optical UAV-Based Sensors over Grassland: Challenges and Limitations. Biogeosciences 2015, 12, 163–175. [Google Scholar] [CrossRef]
- Hakala, T.; Markelin, L.; Honkavaara, E.; Scott, B.; Theocharous, T.; Nevalainen, O.; Näsi, R.; Suomalainen, J.; Viljanen, N.; Greenwell, C.; et al. Direct Reflectance Measurements from Drones: Sensor Absolute Radiometric Calibration and System Tests for Forest Reflectance Characterization. Sensors 2018, 18, 1417. [Google Scholar] [CrossRef]
- Markelin, L.; Suomalainen, J.; Hakala, T.; Oliveira, R.A.; Viljanen, N.; Näsi, R.; Scott, B.; Theocharous, T.; Greenwell, C.; Fox, N.; et al. Methodology for Direct Reflectance Measurement from A Drone: System Description, Radiometric Calibration and Latest Results; The International Archives of the Photogrammetry Remote Sensing and Spatial Information Sciences: Hannover, Germany, 2018; Volume XLII-1, pp. 283–288. [Google Scholar] [CrossRef]
- Hakala, T.; Honkavaara, E.; Saari, H.; Mäkynen, J.; Pölönen, I. Spectral Imaging from UAVs Under Varying Illumination Conditions; The International Archives of the Photogrammetry Remote Sensing and Spatial Information Sciences: Hannover, Germany, 2013; Volume XL-1/W2, pp. 189–194. [Google Scholar] [CrossRef]
- Honkavaara, E.; Hakala, T.; Markelin, L.; Jaakkola, A.; Saari, H.; Ojanen, H.; Pölönen, I.; Tuominen, S.; Näsi, R.; Rosnell, T.; et al. Autonomous Hyperspectral UAS Photogrammetry for Environmental Monitoring Applications; The International Archives of the Photogrammetry Remote Sensing and Spatial Information Sciences: Hannover, Germany, 2014; Volume XL-1/W2, pp. 155–159. [Google Scholar] [CrossRef]
- Burkart, A.; Hecht, V.L.; Kraska, T.; Rascher, U. Phenological Analysis of Unmanned Aerial Vehicle Based Time Series of Barley Imagery with High Temporal Resolution. Precis. Agric. 2017, 19, 134–146. [Google Scholar] [CrossRef]
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Berni, J.A.; Zarco-Tejada, P.J.; Suárez, L.; Fereres, E. Thermal and narrowband multispectral remote sensing for vegetation monitoring from an unmanned aerial vehicle. IEEE Trans. Geosci. Remote Sens. 2009, 47, 722–738. [Google Scholar] [CrossRef]
- Honkavaara, E.; Saari, H.; Kaivosoja, J.; Pölönen, I.; Hakala, T.; Litkey, P.; Mäkynen, J.; Pesonen, L. Processing and Assessment of Spectrometric, Stereoscopic Imagery Collected Using a Lightweight UAV Spectral Camera for Precision Agriculture. Remote Sens. 2013, 5, 5006–5039. [Google Scholar] [CrossRef]
- Miyoshi, G.T.; Imai, N.N.; Tommaselli, A.M.G.; Honkavaara, E.; Roope, N.; Moriya, É.A.S. Radiometric Block Adjustment of Hyperspectral Image Blocks in the Brazilian Environment. Int. J. Remote Sens. 2018, 39, 4910–4930. [Google Scholar] [CrossRef]
- Honkavaara, E.; Khoramshahi, E. Radiometric Correction of Close-Range Spectral Image Blocks Captured Using an Unmanned Aerial Vehicle with a Radiometric Block Adjustment. Remote Sens. 2018, 10, 256. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Shi, Y.; Zhao, M. A New Method for Direct Measurement of Land Surface Reflectance With UAV-Based Multispectral Cameras. Spectrosc. Spect. Anal. 2022, 42, 1581–1587. [Google Scholar] [CrossRef]



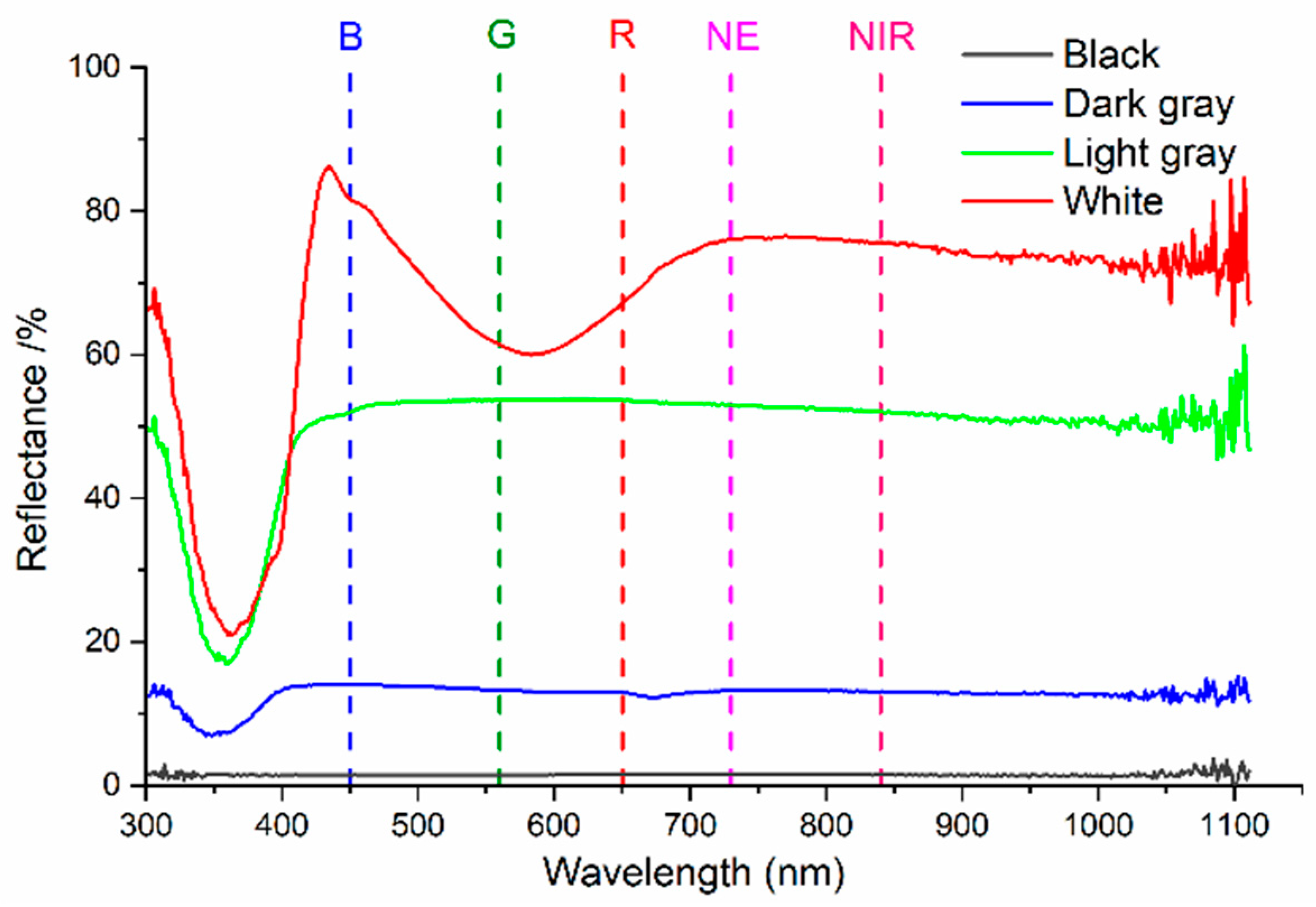


| Bands | B | G | R | RE | NIR |
|---|---|---|---|---|---|
| Wavelength range | 450 nm ± 16 nm | 560 nm ± 16 nm | 650 nm ± 16 nm | 730 nm ± 16 nm | 840 nm ± 26 nm |
| Bands | B | G | R | RE | NIR |
|---|---|---|---|---|---|
| Gain () | 0.8375 | 0.6989 | 0.7742 | 0.9955 | 0.8153 |
| Bias () | −4.3830 | −8.5053 | −7.9623 | −13.4527 | −16.2095 |
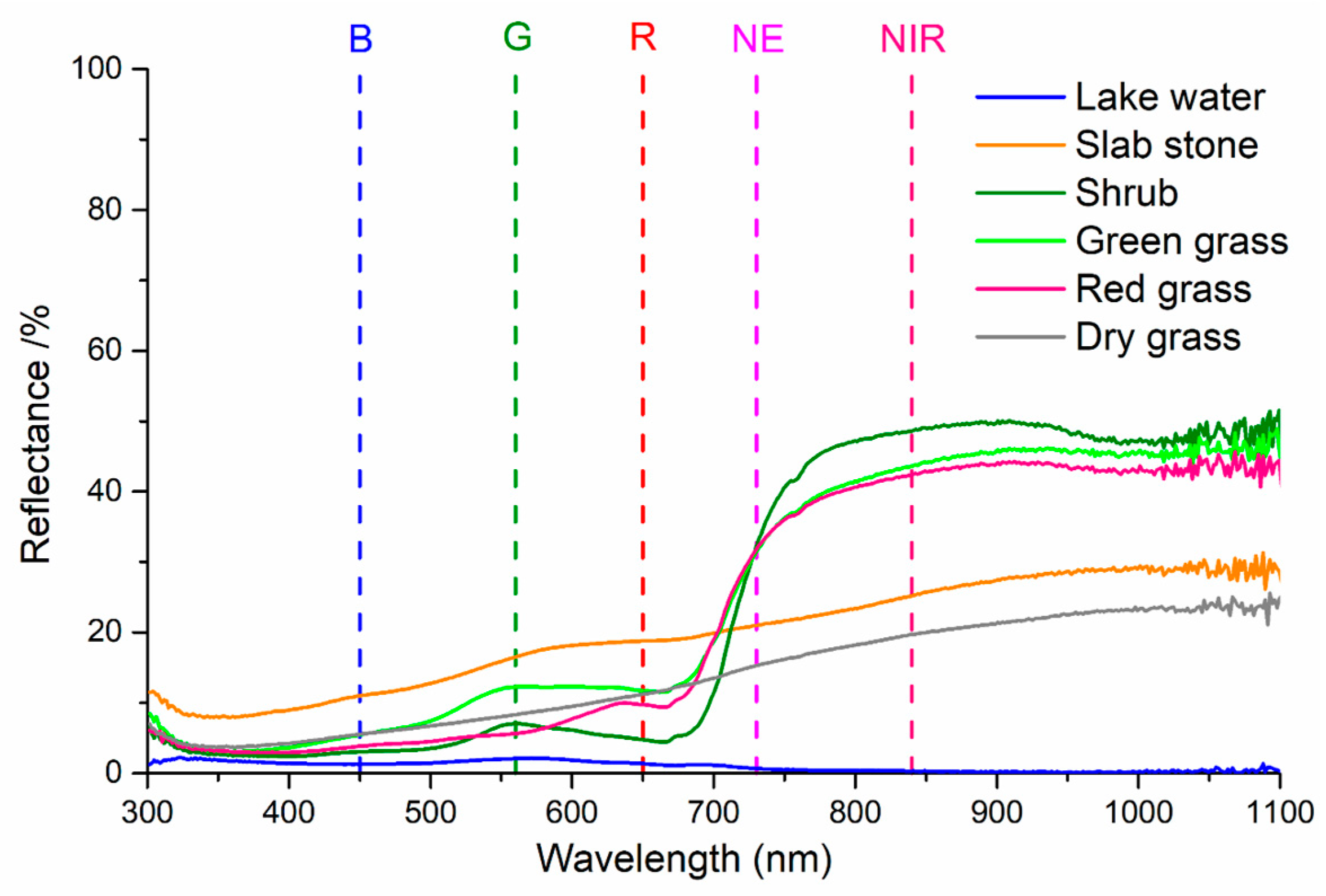
| Land Cover Types | B (%) | G (%) | R (%) | RE (%) | NIR (%) | MAE (%) | |
|---|---|---|---|---|---|---|---|
| Lake water | Calculated | 1.77 | 2.08 | 1.59 | 1.46 | 1.38 | |
| Measured | 1.29 | 2.06 | 1.34 | 0.69 | 0.31 | ||
| Errors | 0.48 | 0.02 | 0.25 | 0.77 | 1.07 | 0.52 | |
| Slab stone | Calculated | 9.71 | 15.76 | 19.17 | 22.60 | 27.28 | |
| Measured | 10.96 | 16.46 | 18.76 | 20.96 | 25.24 | ||
| Errors | −1.24 | −0.71 | 0.41 | 1.63 | 2.03 | 0.82 | |
| Shrub | Calculated | 3.34 | 5.73 | 5.00 | 30.02 | 47.34 | |
| Measured | 3.03 | 6.81 | 4.77 | 31.15 | 48.69 | ||
| Errors | 0.31 | −1.08 | 0.24 | −1.13 | −1.35 | ||
| Green grass | Calculated | 5.08 | 9.92 | 8.08 | 29.64 | 44.22 | |
| Measured | 5.45 | 12.12 | 11.76 | 30.78 | 43.67 | ||
| Errors | −0.36 | −2.20 | −3.68 | −1.14 | 0.55 | 1.59 | |
| Red grass | Calculated | 4.74 | 6.31 | 9.34 | 31.17 | 40.99 | |
| Measured | 3.82 | 5.67 | 9.71 | 31.16 | 42.41 | ||
| Errors | 0.93 | 0.64 | −0.37 | 0.01 | −1.42 | 0.67 | |
| Dry grass | Calculated | 7.41 | 11.56 | 15.97 | 21.81 | 27.44 | |
| Measured | 7.22 | 11.63 | 14.86 | 21.01 | 26.64 | ||
| Errors | 0.19 | −0.07 | 1.11 | 0.80 | 0.81 | 0.60 | |
| MAE (%) | 0.59 | 0.79 | 1.01 | 0.91 | 1.21 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Guo, L.; Zhang, Y. Accurate Conversion of Land Surface Reflectance for Drone-Based Multispectral Remote Sensing Images Using a Solar Radiation Component Separation Approach. Sensors 2025, 25, 2604. https://doi.org/10.3390/s25082604
Sun H, Guo L, Zhang Y. Accurate Conversion of Land Surface Reflectance for Drone-Based Multispectral Remote Sensing Images Using a Solar Radiation Component Separation Approach. Sensors. 2025; 25(8):2604. https://doi.org/10.3390/s25082604
Chicago/Turabian StyleSun, Huasheng, Lei Guo, and Yuan Zhang. 2025. "Accurate Conversion of Land Surface Reflectance for Drone-Based Multispectral Remote Sensing Images Using a Solar Radiation Component Separation Approach" Sensors 25, no. 8: 2604. https://doi.org/10.3390/s25082604
APA StyleSun, H., Guo, L., & Zhang, Y. (2025). Accurate Conversion of Land Surface Reflectance for Drone-Based Multispectral Remote Sensing Images Using a Solar Radiation Component Separation Approach. Sensors, 25(8), 2604. https://doi.org/10.3390/s25082604







