Overview of Research on Digital Image Denoising Methods
Abstract
1. Introduction
2. Image-Denoising Framework
2.1. Traditional Denoising Methods
- (1)
- Noise removal using filter techniques
- (2)
- Denoising using sparse coding
- (3)
- Use of external prior for denoising, also known as model-based denoising
2.2. Deep Learning Denoising Approaches
- (1)
- Denoising approaches for additive Gaussian white noise images
- (2)
- Denoising methods for real noisy images
- (3)
- Denoising methods for blind noise images
- (4)
- Denoising methods for mixed noise images
3. Datasets
4. Evaluation Standards
5. Experimental Result
5.1. Grayscale White Gaussian Noise Image Denoising
5.2. Color Image Denoising
5.3. Real Image Denoising
6. Challenges, Opportunities, and Future Directions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J.; Lu, M.X.; Li, J.K. Noisy image denoising method based on residual dense convolutional self-coding. Comput. Sci. 2024, 51, 555–561. [Google Scholar]
- Katkovnik, V.; Egiazarian, K. Sparse phase imaging based on complex domain nonlocal BM3D techniques. Digit. Signal Process. 2017, 63, 72–85. [Google Scholar] [CrossRef]
- Shevkunov, I.; Katkovnik, V.; Claus, D.; Pedrini, G.; Petrov, N.V.; Egiazarian, K. Hyperspectral phase imaging based on denoising in complex-valued eigensubspace. Opt. Lasers Eng. 2020, 127, 105973. [Google Scholar] [CrossRef]
- Dutta, B.; Root, K.; Ullmann, I.; Wagner, F.; Mayr, M.; Seuret, M.; Huang, Y. Deep learning for terahertz image denoising in nondestructive historical document analysis. Sci. Rep. 2022, 12, 22554. [Google Scholar] [CrossRef]
- Wu, G.Y.; Yuan, Z.Q.; Liang, Y.M. Unsupervised denoising method for retinal OCT images based on deep learning. Acta Opt. Sin. 2023, 43, 2010002. [Google Scholar]
- Bianco, V.; Memmolo, P.; Paturzo, M.; Finizio, A.; Javidi, B.; Ferraro, P. Quasi noise-free digital holography. Light Sci. Appl. 2016, 5, e16142. [Google Scholar] [CrossRef]
- Ogose, S. Optimum Gaussian filter for MSK with 2-bit differential detection. IEICE Trans. 1983, 66, 459–460. [Google Scholar]
- Martins, A.L.; Mascarenhas, N.D.; Suazo, C.A. Spatio-temporal resolution enhancement of vocal tract MRI sequences based on image registration. Integr. Comput. Aided Eng. 2011, 18, 143–155. [Google Scholar] [CrossRef]
- Raman, S.; Chaudhuri, S. Bilateral Filter Based Compositing for Variable Exposure Photography. Eurographics 2009, 1, 1–4. [Google Scholar]
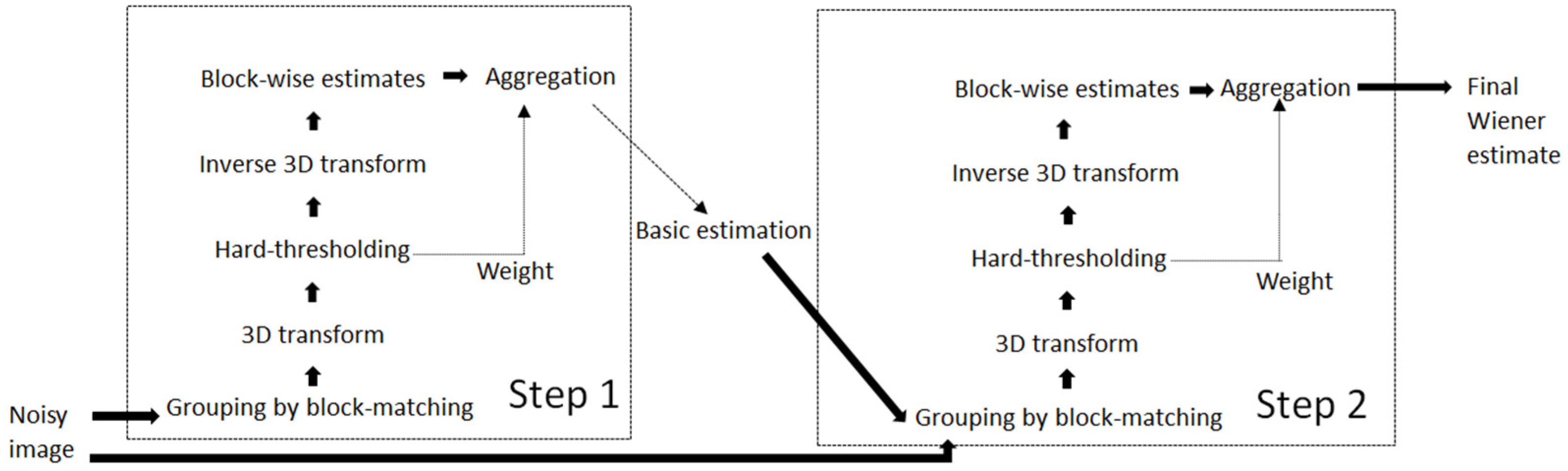
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef]
- Cai, S.; Zheng, X.; Dong, X. CBM3d, a novel subfamily of family 3 carbohydrate-binding modules identified in Cel48A exoglucanase of Cellulosilyticum ruminicola. J. Bacteriol. 2011, 193, 5199–5206. [Google Scholar] [CrossRef] [PubMed]
- Maggioni, M.; Katkovnik, V.; Egiazarian, K.; Foi, A. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans. Image Process. 2012, 22, 119–133. [Google Scholar] [CrossRef] [PubMed]
- Mafi, M.; Martin, H.; Cabrerizo, M.; Andrian, J.; Barreto, A.; Adjouadi, M. A comprehensive survey on impulse and Gaussian denoising filters for digital images. Signal Process. 2019, 157, 236–260. [Google Scholar] [CrossRef]
- Yadava, P.C.; Srivastava, S. Denoising of poisson-corrupted microscopic biopsy images using fourth-order partial differential equation with ant colony optimization. Biomed. Signal Process. Control. 2024, 93, 106207. [Google Scholar] [CrossRef]
- Kulya, M.; Petrov, N.V.; Katkovnik, V.; Egiazarian, K. Terahertz pulse time-domain holography with balance detection: Complex-domain sparse imaging. Appl. Opt. 2019, 58, G61–G70. [Google Scholar] [CrossRef]
- Tang, C.; Xv, J.L.; Zhou, Z.G. Improved curvature filtering strong noise image denoising method. Chin. J. Image Graph. 2019, 24, 346–356. [Google Scholar]
- Cheng, L.B.; Li, X.Y.; Li, C. Remote sensing image denoising method based on curvilinear wave transform and goodness-of-fit test. J. Jilin Univ. 2023, 53, 3207–3213. [Google Scholar]
- Zhang, H.J.; Zhang, D.M.; Yan, W. Wavelet transform image denoising algorithm based on improved threshold function. Comput. Appl. Res. 2020, 37, 1545–1548. [Google Scholar]
- Elan, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar]
- Li, G.H.; Li, J.J.; Fan, H. Adaptive matching tracking image denoising algorithm. Comput. Sci. 2020, 47, 176–185. [Google Scholar]
- Li, K.; Wang, C.; Ming, X.F. A denoising method for chip ultrasound signals based on improved multipath matched tracking. J. Instrum. 2023, 44, 93–100. [Google Scholar]
- Yuan, X.J.; Zhou, T.; Li, C. Research on image denoising algorithm based on non-local clustering with sparse prior. Comput. Eng. Appl. 2020, 56, 177–185. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 60–65. [Google Scholar]
- Bai, T.L.; Zhang, C.F. Image Denoising based on External Non-local self-similarity priors. Telecommun. Eng. 2021, 61, 211–217. [Google Scholar]
- Ziad, L.; Oubbih, O.; Karami, F.; Sniba, F. A nonlocal model for image restoration corrupted by multiplicative noise. Signal Image Video Process. 2024, 18, 5701–5718. [Google Scholar] [CrossRef]
- Lecouat, B.; Ponce, J.; Mairal, J. Fully trainable and interpretable non-local sparse models for image restoration. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; pp. 238–254. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Osher, S.; Burger, M.; Goldfarb, D. An iterative regularization method for total variation-based image restoration. Multiscale Model. Simul. 2005, 4, 460–489. [Google Scholar] [CrossRef]
- Zuo, W.; Zhang, L.; Song, C. Gradient histogram estimation and preservation for texture enhanced image denoising. IEEE Trans. Image Process. 2014, 23, 2459–2472. [Google Scholar]
- Roth, S.; Black, M.J. Fields of experts: A framework for learning image priors. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 860–867. [Google Scholar]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Weighted nuclear norm minimization with application to image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 2862–2869. [Google Scholar]
- Liu, C.S.; Zhao, Z.G.; Li, Q. Enhanced denoising algorithm for low-rank representation images. Comput. Eng. Appl. 2020, 56, 216–225. [Google Scholar]
- Lv, J.R.; Luo, X.G.; Qi, S.F. Weighted kernel-paradigm minimization image denoising with preserving local structure. Adv. Lasers Optoelectron. 2019, 56, 57–64. [Google Scholar]
- Chen, J. Application of full-variance curvilinear waveform transform in medical image denoising. J. Yanbian Univ. 2021, 47, 361–364. [Google Scholar]
- Chen, Y.; Xu, H.L.; Xing, Q.; Zhuang, J. SICM image noise reduction algorithm combining wavelet transform and bilateral filtering. Electron. Meas. Technol. 2022, 45, 114–119. [Google Scholar]
- Wu, X.L.; Wang, Z.Z.; Xi, B.Q.; Zhen, R. Ground-penetrating radar denoising based on wavelet adaptive thresholding method. Sci. Technol. Eng. 2023, 23, 4686–4692. [Google Scholar]
- Romano, Y.; Elad, M. Boosting of Image Denoising Algorithms. Siam J. Imaging Sci. 2015, 8, 1187–1219. [Google Scholar] [CrossRef]
- Dong, W.; Zhang, L.; Shi, G. Nonlocally centralized sparse representation for image restoration. IEEE Trans. Image Process. 2012, 22, 1620–1630. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, L.; Zhang, D. A trilateral weighted sparse coding scheme for real-world image denoising. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 20–36. [Google Scholar]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G.; Zisserman, A. Non-local sparse models for image restoration. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2272–2279. [Google Scholar]
- Wei, Y.; Han, L.L.; Li, L. Joint group dictionary-based structural sparse representation for image restoration. Digit. Signal Process. 2023, 137, 104029. [Google Scholar]
- Qian, C.; Chang, D.X. Graph Laplace regularised sparse transform learning image denoising algorithm. Comput. Eng. Appl. 2022, 58, 232–239. [Google Scholar]
- Zoran, D.; Weiss, Y. From learning models of natural image patches to whole image restoration. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 479–486. [Google Scholar]
- Hou, Y.K.; Xu, J.; Liu, M.X. NLH: A blind pixel-level non-local method for real-world image denoising. IEEE Trans. Image Process. 2020, 29, 5121–5135. [Google Scholar] [CrossRef]
- Chen, Y.; Cao, X.; Zhao, Q.; Meng, D.; Xu, Z. Denoising hyperspectral image with non-iid noise structure. IEEE Trans. Syst. Man Cybern. 2018, 48, 1054–1066. [Google Scholar]
- Zuo, W.; Zhang, L.; Song, C.; Zhang, D. Texture enhanced image denoising via gradient histogram preservation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 25–27 June 2013; pp. 1203–1210. [Google Scholar]
- Wang, Y.; Peng, J.; Zhao, Q.; Leung, Y.; Zhao, X.L.; Meng, D. Hyperspectral image restoration via total variation regularized low-rank tensor decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 1227–1243. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, L.; Zhang, D.; Feng, X. Multi-channel weighted nuclear norm minimization for real color image denoising. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1096–1104. [Google Scholar]
- Hu, H.; Froment, J.; Liu, Q. A note on patch-based low-rank minimization for fast image denoising. J. Vis. Commun. Image Represent. 2018, 50, 100–110. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, L.; Zuo, W.; Zhang, D.; Feng, X. Patch group-based nonlocal self-similarity prior learning for image denoising. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 13–16 December 2015; pp. 244–252. [Google Scholar]
- Zhuang, L.N.; Bioucas-dias, J.M. Fast hyperspectral image denoising and inpainting based on low-rank and sparse representations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 730–742. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, L.; Zhang, D. External prior guided internal prior learning for real-world noisy image denoising. IEEE Trans. Image Process. 2018, 27, 2996–3010. [Google Scholar] [CrossRef] [PubMed]
- Mao, X.; Shen, C.; Yang, Y.B. Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections. Adv. Neural Inf. Process. Syst. 2016, 29, 2802–2810. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. Memnet: A persistent memory network for image restoration. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4539–4547. [Google Scholar]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 2016, 26, 3142–3155. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Zhang, L. Ffdnet: Toward a fast and flexible solution for CNN-based image denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, C.; Zhang, Y.; Liu, S.; Wang, X. Multi-scale feature learning convolutional neural network for image denoising. Sensors 2023, 23, 7713. [Google Scholar] [CrossRef]
- Valsesia, D.; Fracastoro, G.; Magli, E. Deep graph-convolutional image denoising. IEEE Trans. Image Process. 2020, 29, 8226–8237. [Google Scholar] [CrossRef]
- Burger, H.C.; Schuler, C.J.; Harmeling, S. Image denoising: Can plain neural networks compete with BM3D? In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2392–2399. [Google Scholar]
- Chen, Y.; Pock, T. Trainable nonlinear reaction-diffusion: A flexible framework for fast and effective image restoration. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1256–1272. [Google Scholar] [CrossRef]
- Tian, C.; Xu, Y.; Fei, L.; Wang, J.; Wen, J.; Luo, N. Enhanced CNN for image denoising. CAAI Trans. Intell. Technol. 2019, 4, 17–23. [Google Scholar] [CrossRef]
- Schmidt, U.; Roth, S. Shrinkage fields for effective image restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 2774–2781. [Google Scholar]
- Chen, M.Y.; Li, R.X.; Liu, H. Pre-filtering-based group sparse residual constraint image denoising model. Transducer Microsyst. Technol. 2020, 39, 48–51. [Google Scholar]
- Tian, C.; Xu, Y.; Li, Z.; Zuo, W.; Fei, L.; Liu, H. Attention-guided CNN for image denoising. Neural Netw. 2020, 124, 117–129. [Google Scholar] [CrossRef] [PubMed]
- Tian, C.; Xu, Y.; Zuo, W. Image denoising using deep CNN with batch renormalization. Neural Netw. 2020, 121, 461–473. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Wen, B.H.; Fan, Y.C. Non-local recurrent network for image restoration. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 1680–1689. [Google Scholar]
- Mou, C.; Zhang, J.; Wu, Z. Dynamic attentive graph learning for image restoration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Nashville, TN, USA, 11–17 October 2021; pp. 4328–4337. [Google Scholar]
- Miranda-González, A.A.; Rosales-Silva, A.J.; Mújica-Vargas, D.; Escamilla-Ambrosio, P.J.; Gallegos-Funes, F.J.; Vianney-Kinani, J.M.; Velázquez-Lozada, E.; Pérez-Hernández, L.M.; Lozano-Vázquez, L.V. Denoising Vanilla Autoencoder for RGB and GS Images with Gaussian Noise. Entropy 2023, 25, 1467. [Google Scholar] [CrossRef] [PubMed]
- Tang, Z.; Jian, X. Thermal fault diagnosis of complex electrical equipment based on infrared image recognition. Sci. Rep. 2024, 14, 5547. [Google Scholar] [CrossRef]
- Huang, J.J.; Dragotti, P.L. WINNet: Wavelet-Inspired Invertible Network for Image Denoising. IEEE Trans. Image Process. 2022, 31, 4377–4392. [Google Scholar] [CrossRef]
- Ren, C.; He, X.; Wang, C.; Zhao, Z. Adaptive consistency prior based deep network for image denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 8596–8606. [Google Scholar]
- Hu, Y.; Xu, S.; Cheng, X.; Zhou, C.; Hu, Y. A Triple Deep Image Prior Model for Image Denoising Based on Mixed Priors and Noise Learning. Appl. Sci. 2023, 13, 5265. [Google Scholar] [CrossRef]
- Li, X.; Han, J.; Yuan, Q.; Zhang, Y.; Fu, Z.; Zou, M.; Huang, Z. FEUSNet: Fourier Embedded U-Shaped Network for Image Denoising. Entropy 2023, 25, 1418. [Google Scholar] [CrossRef]
- Lai, Z.; Wei, K.; Fu, Y. Deep plug-and-play prior for hyperspectral image restoration. Neurocomputing 2022, 481, 281–293. [Google Scholar] [CrossRef]
- Zhang, J.; Cao, L.; Wang, T.; Fu, W.; Shen, W. NHNet: A non-local hierarchical network for image denoising. IET Image Process. 2022, 16, 2446–2456. [Google Scholar] [CrossRef]
- Yan, H.; Chen, X.; Tan, V.Y.; Yang, W.; Wu, J.; Feng, J. Unsupervised image noise modeling with self-consistent GAN. arXiv 2019, arXiv:1906.05762. [Google Scholar]
- Zhao, D.; Ma, L.; Li, S.; Yu, D. End-to-end denoising of dark burst images using recurrent fully convolutional networks. arXiv 2019, arXiv:1904.07483. [Google Scholar]
- Abuya, T.K.; Rimiru, R.M.; Okeyo, G.O. An Image Denoising Technique Using Wavelet-Anisotropic Gaussian Filter-Based Denoising Convolutional Neural Network for CT Images. Appl. Sci. 2023, 13, 12069. [Google Scholar] [CrossRef]
- Gou, Y.; Hu, P.; Lv, J.; Zhou, J.T.; Peng, X. Multi-scale adaptive network for single image denoising. Adv. Neural Inf. Process. Syst. 2022, 35, 14099–14112. [Google Scholar]
- Bao, L.; Yang, Z.; Wang, S.; Bai, D.; Lee, J. Real image denoising based on multi-scale residual dense block and cascaded U-Net with block-connection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 448–449. [Google Scholar]
- Zhang, K.; Zuo, W.; Gu, S.; Zhang, L. Learning deep CNN denoiser prior for image restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 22–25 July 2017; pp. 3929–3938. [Google Scholar]
- Yue, Z.; Zhao, Q.; Zhang, L.; Meng, D. Dual adversarial network: Toward real-world noise removal and noise generation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; pp. 41–58. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H.; Shao, L. Learning enriched features for real image restoration and enhancement. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; pp. 492–511. [Google Scholar]
- Yuan, N.; Wang, L.; Ye, C.; Deng, Z.; Zhang, J.; Zhu, Y. Self-supervised structural similarity-based convolutional neural network for cardiac diffusion tensor image denoising. Med. Phys. 2023, 50, 6137–6150. [Google Scholar] [CrossRef]
- Du, H.; Yuan, N.; Wang, L. Node2Node: Self-Supervised Cardiac Diffusion Tensor Image Denoising Method. Appl. Sci. 2023, 13, 10829. [Google Scholar] [CrossRef]
- Huang, R.; Li, X.; Fang, Y.; Cao, Z.; Xia, C. Robust Hyperspectral Unmixing with Practical Learning-Based Hyperspectral Image Denoising. Remote Sens. 2023, 15, 1058. [Google Scholar] [CrossRef]
- Fan, C.M.; Liu, T.J.; Liu, K.H. SUNet: Swin Transformer UNet for Image Denoising. In Proceedings of the 2022 IEEE International Symposium on Circuits and Systems (ISCAS), Austin, TX, USA, 27 May–1 June 2022; pp. 2333–2337. [Google Scholar]
- Zhang, J.; Zhu, Y.; Yu, W.; Ma, J. Considering Image Information and Self-Similarity: A Compositional Denoising Network. Sensors 2023, 23, 5915. [Google Scholar] [CrossRef]
- Anwar, S.; Barnes, N. Real Image Denoising With Feature Attention. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3155–3164. [Google Scholar]
- Zhang, J.; Qu, M.; Wang, Y.; Cao, L. A multi-head convolutional neural network with multi-path attention improves image denoising. In Proceedings of the Pacific Rim International Conference on Artificial Intelligence, Shanghai, China, 10–13 November 2022; pp. 338–351. [Google Scholar]
- Yang, J.; Liu, X.; Song, X.; Li, K. Estimation of signal-dependent noise level function using multi-column convolutional neural network. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 2418–2422. [Google Scholar]
- Guo, S.; Yan, Z.; Zhang, K.; Zuo, W.; Zhang, L. Toward convolutional blind denoising of real photographs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 1712–1722. [Google Scholar]
- Tao, H.; Guo, W.; Han, R.; Yang, Q.; Zhao, J. Rdasnet: Image denoising via a residual dense attention similarity network. Sensors 2023, 23, 1486. [Google Scholar] [CrossRef]
- Wei, X.; Xiao, J.; Gong, Y. Blind Hyperspectral Image Denoising with Degradation Information Learning. Remote Sens. 2023, 15, 490. [Google Scholar] [CrossRef]
- Tian, C.; Xu, Y.; Zuo, W.; Du, B.; Lin, C.W.; Zhang, D. Designing and training of a dual CNN for image denoising. Knowl. Based Syst. 2021, 226, 106949. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Chao, H.; Yang, M. Image blind denoising with generative adversarial network-based noise modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3155–3164. [Google Scholar]
- Isogawa, K.; Ida, T.; Shiodera, T.; Takeguchi, T. Deep shrinkage convolutional neural network for adaptive noise reduction. IEEE Signal Process. Lett. 2017, 25, 224–228. [Google Scholar] [CrossRef]
- Jaszewski, M.; Parameswaran, S. Exploring efficient and tunable convolutional blind image denoising networks. In Proceedings of the 2019 IEEE Applied Imagery Pattern Recognition Workshop (AIPR), Washington, DC, USA, 15–17 October 2019; pp. 1–9. [Google Scholar]
- Chen, K.; Pu, X.; Ren, Y.; Qiu, H.; Li, H.; Sun, J. Low-dose ct image blind denoising with graph convolutional networks. In Proceedings of the International Conference on Neural Information Processing, Bangkok, Thailand, 23–27 November 2020; pp. 423–435. [Google Scholar]
- Zhang, K.; Zuo, W.; Zhang, L. Learning a single convolutional super-resolution network for multiple degradations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 19–21 June 2018; pp. 3262–3271. [Google Scholar]
- Li, B.Z.; Liu, X.; Zhao, Z.X.; Li, L.; Jin, W.Q. Self-supervised two-stage denoising algorithm for EBAPS images based on blind spot network. Acta Opt. Sin. 2024, 44, 2210001. [Google Scholar]
- Siddique, N.; Paheding, S.; Elkin, C.P.; Devabhaktuni, V. U-net and its variants for medical image segmentation: A review of theory and applications. IEEE Access 2021, 9, 82031–82057. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, D.; Law, K.L.; Wang, X.; Qin, H.; Li, H. IDR: Self-supervised image denoising via iterative data refinement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 21–24 June 2022; pp. 2098–2107. [Google Scholar]
- Yeh, R.A.; Lim, T.Y.; Chen, C.; Schwing, A.G.; Hasegawa-Johnson, M.; Do, M.N. Image restoration with deep generative models. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 6772–6776. [Google Scholar]
- Islam, M.T.; Rahman, S.M.; Ahmad, M.O.; Swamy, M.N.S. Mixed Gaussian-impulse noise reduction from images using convolutional neural network. Signal Process. Image Commun. 2018, 68, 26–41. [Google Scholar] [CrossRef]
- Kim, Y.; Soh, J.W.; Park, G.Y.; Cho, N.I. Transfer learning from synthetic to real-noise denoising with adaptive instance normalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 3482–3492. [Google Scholar]
- Wang, H.; Yang, X.; Wang, Z.; Yang, H.; Wang, J.; Zhou, X. Improved CycleGAN for Mixed Noise Removal in Infrared Images. Appl. Sci. 2024, 14, 6122. [Google Scholar] [CrossRef]
- Chiang, Y.W.; Sullivan, B.J. Multi-frame image restoration using a neural network. In Proceedings of the 32nd Midwest Symposium on Circuits and Systems, Champaign, IL, USA, 14–16 August 1989; pp. 744–747. [Google Scholar]
- Zhou, Y.T.; Chellappa, R.; Vaid, A.; Jenkins, B.K. Image restoration using a neural network. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1141–1151. [Google Scholar] [CrossRef]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human-segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the eighth IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001; pp. 416–423. [Google Scholar]
- Ma, K.; Duanmu, Z.; Wu, Q.; Wang, Z.; Zhang, L. Waterloo exploration database: New challenges for image quality assessment models. IEEE Trans. Image Process. 2017, 26, 1004–1016. [Google Scholar] [CrossRef]
- Agustsson, E.; Timofte, R. Ntire 2017 challenge on single image super-resolution: Dataset and study. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 22–25 July 2017; pp. 1122–1131. [Google Scholar]
- Reeves, G. Conditional central limit theorems for Gaussian projections. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 3045–3049. [Google Scholar]
- Nam, S.; Hwang, Y.; Matsushita, Y.; Kim, S.J. A holistic approach to cross-channel image noise modeling and its application to image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26–30 June 2016; pp. 1683–1691. [Google Scholar]
- Plotz, T.; Roth, S. Benchmarking denoising algorithms with real photographs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 22–25 July 2017; pp. 1586–1595. [Google Scholar]
- Abdelhamed, A.; Lin, S.; Brown, M.S. A High-Quality Denoising Dataset for Smartphone Cameras. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1692–1700. [Google Scholar]
- Xu, J.; Li, H.; Liang, Z.; Zhang, D.; Zhang, L. Real-world noisy image denoising: A new benchmark. arXiv 2018, arXiv:1804.02603. [Google Scholar]
- Chang, Y.; Yan, L.; Fang, H.; Zhong, S.; Liao, W. HSI-DeNet: Hyperspectral image restoration via convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 57, 667–682. [Google Scholar] [CrossRef]
- Zhao, T.; McNitt-Gray, M.; Ruan, D. A convolutional neural network for ultra-low-dose CT denoising and emphysema screening. Med. Phys. 2019, 46, 3941–3950. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, L.; Liu, S.; Wu, X.; Zhang, Y.; Wang, X. Dilated residual networks with symmetric skip connection for image denoising. Neurocomputing 2019, 345, 67–76. [Google Scholar] [CrossRef]
- Xi, Z.; Chakrabarti, A. Identifying recurring patterns with deep neural networks for natural image denoising. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Long Beach, CA, USA, 14–19 June 2020; pp. 2426–2434. [Google Scholar]
- Yue, Z.; Yong, H.; Zhao, Q.; Meng, D.; Zhang, L. Variational denoising network: Toward blind noise modeling and removal. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, CA, USA, 8–14 December 2019; pp. 1688–1699. [Google Scholar]
- Song, Y.; Zhu, Y.; Du, X. Grouped multi-scale network for real-world image denoising. IEEE Signal Process. Lett. 2020, 27, 2124–2128. [Google Scholar] [CrossRef]
- Rajaei, B.; Rajaei, S.; Damavandi, H. An analysis of multi-stage progressive image restoration network (MPRNet). Image Process. Line 2023, 13, 140–152. [Google Scholar] [CrossRef]
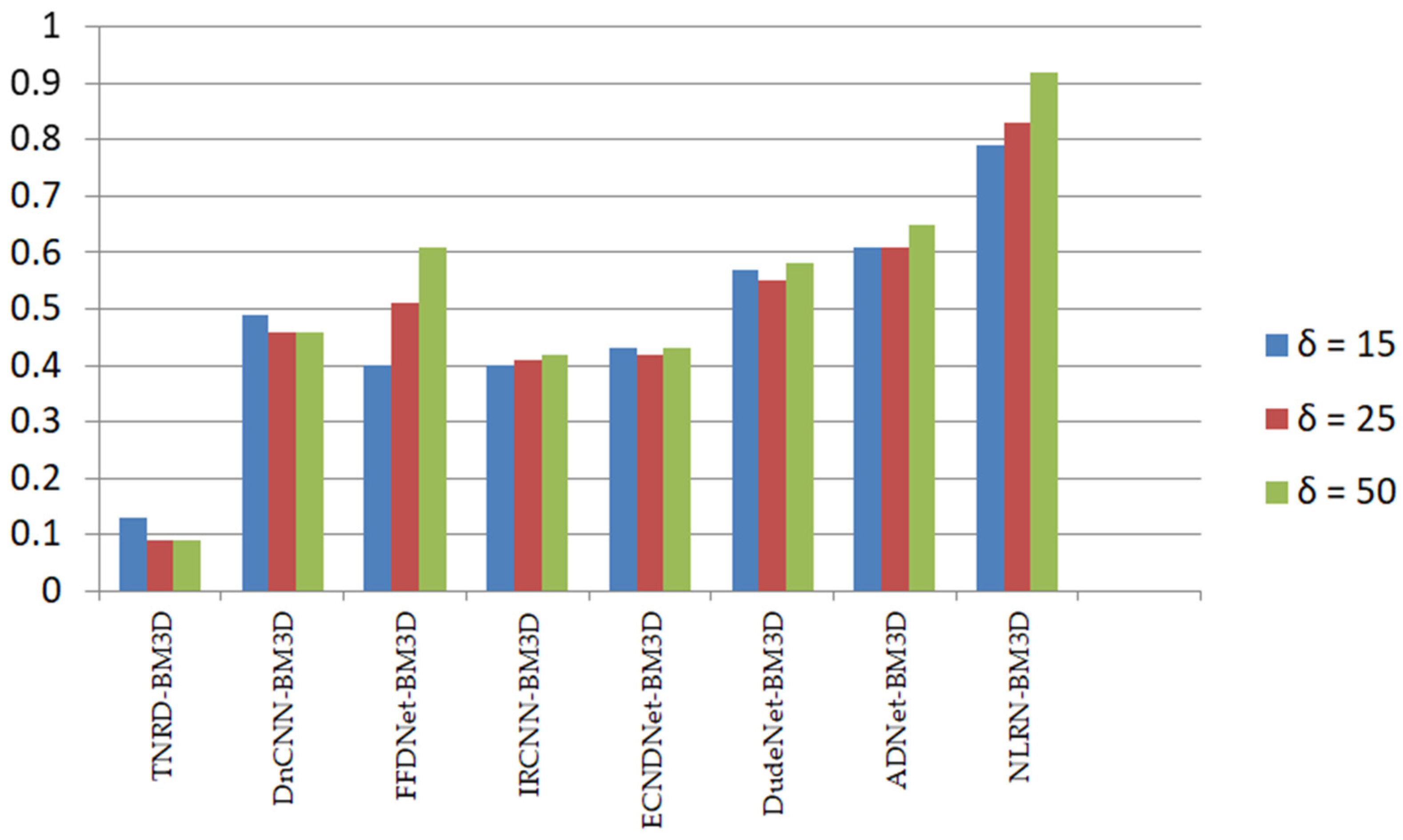







| Type of Method | Method Name | Type of Noise | Descriptions |
|---|---|---|---|
| Filter | TVCT [34] | AWGN | Fully variable difference curve wave transform algorithm |
| BFWIT [35] | Mixed noise | Bilateral filtering for hierarchical thresholding of wavelets | |
| AWT [36] | AWGN | Adaptive thresholding wavelet denoising | |
| BIDA [37] | AWGN | Enhanced image-denoising algorithm | |
| NLM [23] | AWGN | Nonlocal mean filtering | |
| BM3D [10] | AWGN | Sparse 3D transform-domain co-filtering | |
| CBM3D [11] | AWGN | BM3D YUV color mode conversion | |
| Sparse coding | K-SVD [19] | AWGN | Sparse and redundant representation denoising methods |
| NCSR [38] | AWGN | Nonlocalized concentration | |
| TWSC [39] | real noise | Three-sided weighted sparse coding | |
| LSSC [40] | Real, mixed noise | Nonlocal sparse model | |
| GDSR [41] | AWGN | Sparse representation denoising based on joint group dictionary | |
| GLRSTL [42] | AWGN | Graph Laplace regularized sparse transform learning | |
| Model-based | EPLL [43] | AWGN | Model learning from natural image blocks |
| NLH [44] | AWGN | Pixel-level nonlocal self-similarity | |
| NMOG [45] | AWGN | Low-rank matrix recovery methods | |
| WNNM [31] | AWGN | Weighted nuclear norm minimization | |
| GHP [46] | AWGN | Gradient histogram and texture enhancement | |
| LRTDTV [47] | AWGN | Low-rank tensor approach | |
| WCNNM [48] | AWGN | Multi-channel weighted nuclear specification minimization | |
| PLR [49] | AWGN | Fast image denoising based on patch with low-rank minimization | |
| PGPD [50] | AWGN | Nonlocal self-similarity based on patch groups | |
| FastHyde [51] | AWGN | Low-rank and sparse representation denoising methods | |
| GID [52] | AWGN | External data guidance and internal a priori learning |
| Method | Technical Characteristics |
|---|---|
| MLP [59] | Multilayer perceptron. |
| TNRD [60] | An unfolded network structure based on nonlinear reaction–diffusion models; Combining traditional optimization methods with deep learning. |
| ECNDNet [61] | Residual learning and batch normalization techniques to address network training difficulties; Expanding the capture of contextual information using null convolution. |
| IDDRL [62] | A cascaded Gaussian conditional random field was used to optimize the model parameters through iterative learning; Deep residual learning network. |
| PSN-K [63] | A sparse representation and residual constraints were used to remove the noise. |
| DnCNN [55] | Residual learning and batch normalization. |
| ADNet [64] | Introducing an attention mechanism to dynamically assign feature weights. |
| BRDNet [65] | Combine two networks to increase network width; Combine two-way loop structure to capture image local and global dependencies. |
| NLRN [66] | Fusion of nonlocal similarity modeling with recurrent network stepwise refinement of denoising results. |
| DAGL [67] | Combination of graph convolutional networks and dynamic attention for effective modeling of nonlocal information in images. |
| DVA [68] | Unsupervised neural network and self-encoder architecture. |
| WAGFNet [69] | Wavelet anisotropic convolutional neural networks. |
| WINNet [70] | A two-branch architecture integrating wavelet transform and deep learning; Using reversible neural network (INN) architecture to avoid information loss during image sampling. |
| DeamNet [71] | Multiscale feature fusion and edge-aware design. |
| TripleDIP [72] | Deep Image Prior (DIP) framework; Three constraints (noise distribution, structural similarity, and sparsity) were introduced to optimize the generation process. |
| FEUSNet [73] | Fourier-embedded U-Net. |
| DPHSIR [74] | Combining pre-trained deep neural networks as a priori knowledge with classical optimization algorithms. |
| NHNet [75] | Using two sub-paths to process noisy images with different resolutions; Combining nonlocal operations to obtain effective features. |
| Method | Technical Characteristics |
|---|---|
| IRCNN [81] | Training a set of fast and efficient CNNs and integrating them into a model-based optimization approach; Accelerating training using batch normalization and residual learning. |
| DANet [82] | Removing real noise by the confrontation between the denoising network and noise-generating network. |
| MIRNet [83] | Parallel convolutional and multiscale fusion networks. |
| DNCNN [55] | Residual learning and batch normalization. |
| SSECNN [84] | Self-supervised structural similarity-based convolutional network. |
| Node2Node [85] | Self-supervised cardiac diffusion tensor. |
| RHUPL [86] | Robust hyperspectral unmixing with practical learning. |
| SUNet [87] | Transformer combined with U-Net improved ability to capture contextual information; Dual upsampling module prevented artifacts. |
| FEUSNet [73] | Fusion of Fourier features, based on their amplitude spectrum and phase spectrum properties; Embedding the learned features as a priori modules in a U-Net. |
| CDN [88] | Image information path (IIP) and noise estimation path (NEP) combined; Compositing information and self-similarity. |
| RIDNet [89] | Integrating multiscale feature extraction and attention mechanism. |
| MHCNN [90] | Multiple head convolutional neural network; A new multipath attention mechanism (MPA). |
| Method | Technical Characteristics |
|---|---|
| CBDNet [92] | The model was composed of a noise estimation subnetwork and a non-blind denoising subnetwork. |
| DIBD [94] | De-noising network based on degraded information learning. |
| DudeNet [95] | Using the dual-path network to increase the width of the network, to obtain more features; Using sparse mechanisms to extract global and local features |
| GCBD [96] | GAN-based blind denoiser. |
| SCNN [97] | The alternate direction multiplier (ADMM) method and the semi-quadratic segmentation method were used; Integrate the trained CNN noise-canceller into the model-based optimization method. |
| DNW [98] | Tunable convolutional neural network. |
| RDASNet [93] | Residual learning and dense connection and attention mechanism. |
| FFDNet [56] | Input noise level adjustable convolutional neural network. |
| GCDN [99] | Graph convolutional denoising network. |
| Method | Technical Characteristics |
|---|---|
| SRMDNF [100] | Single convolutional super-resolution network for multiple degradations. |
| DnGAN [104] | Learning prior deep generative model. |
| TLCNN [105] | A new mapping from noisy to noise-free images using a four-stage CNN architecture; Adoption of transfer learning. |
| AINDNet + TF [106] | Adopting an adaptive instance normalization to build a denoiser |
| ICycleGAN [107] | Adding the EMA attention mechanism to the traditional residual module structure; Proposing a Resnet-E feature extraction module. |
| Category | Name | Color | Number | Size |
|---|---|---|---|---|
| Training dataset | BSD432 | gray | 432 | 481 × 321, 321 × 481 |
| CBSD432 | gray | 432 | 481 × 321, 321 × 481 | |
| DIV2K | Gray, RGB | 800 | Sizes vary, about 1 k, 2 k | |
| Test dataset | Set5 | gray | 5 | 280 × 280 |
| Set12 | gray | 12 | 256 × 256 | |
| BSD68 | gray | 68 | 481 × 321, 321 × 481 | |
| CBSD68 | RGB | 68 | 481 × 321, 321 × 481 | |
| Kodak24 | RGB | 24 | 500 × 500 | |
| McMaster | RGB | 18 | 500 × 500 |
| Category | Name | Acquisition Mode | Camera | ISO |
|---|---|---|---|---|
| Test dataset | CC [114] | The third method | Canon 5D Mark | 3.2 k |
| Nikon D600 | 1.6 k | |||
| Nikon D800 | 1.6 k, 3.2 k, 6.4 k | |||
| Test dataset | DND [115] | The second method | Sony A7R | 100~25.6 k |
| Olympus E-M10 | 200~25.6 k | |||
| Sony RX100 IV | 125~8 k | |||
| Huawei Nexus 6P | 100~6.4 k | |||
| Test dataset | SIDD [116] | The third method | Google Pixel | 50~10 k |
| iPhone 7 | 100~2 k | |||
| Samsung Galaxy S6 Edge | 100~3.2 k | |||
| Motorola Nexus 6 | 100~3.2 k | |||
| LG G4 | 100~800 | |||
| Training dataset | Poly [117] | The third method | Canon 5D | 3.2 k, 6.4 k |
| Canon 80D | 800~12.8 k | |||
| Canon 600D | 1.6 k, 3.2 k | |||
| Nikon D800 | 1.6 k~6.4 k | |||
| Sony A7 | 1.6 k, 3.2 k, 6.4 k |
| Method | |||
|---|---|---|---|
| NLM | 30.89 | 28.56 | 22.55 |
| BM3D | 32.37 | 29.97 | 26.72 |
| WNNM | 32.70 | 30.26 | 27.05 |
| EPLL | 32.14 | 29.69 | 26.47 |
| MLP | — | 30.03 | 26.78 |
| TNRD | 32.50 | 30.06 | 26.81 |
| DnCNN | 32.86 | 30.43 | 27.18 |
| FFDNet | 32.77 | 30.48 | 27.33 |
| IRCNN | 32.77 | 30.38 | 27.14 |
| ECNDNet | 32.80 | 30.39 | 27.15 |
| DudeNet | 32.94 | 30.52 | 27.30 |
| ADNet | 32.98 | 30.58 | 27.37 |
| NLRN | 33.16 | 30.80 | 27.64 |
| RNAN | - | - | 27.62 |
| Method | NLM | BM3D | WNNM | EPLL | TNRD | DnCNN | DudeNet | FFDNet | IRCNN | NLRN |
|---|---|---|---|---|---|---|---|---|---|---|
| Time(s) | 230 | 2.26 | 740 | 42 | 1.96 | 3.12 | 7.19 | 1.16 | 6.31 | 4.17 |
| Dataset | σ | CBM3D | DNCNN | FFDNET | DSNet | BRDNet | RPCNN | IRCNN |
|---|---|---|---|---|---|---|---|---|
| CBSD68 | 15 | 33.52 | 33.98 | 33.871 | 33.91 | 34.10 | - | 33.86 |
| 25 | 30.71 | 31.31 | 31.21 | 31.28 | 31.43 | 31.24 | 31.16 | |
| 50 | 27.38 | 28.01 | 27.96 | 28.04 | 28.16 | 28 06 | 27.86 | |
| Kodak24 | 15 | 34.28 | 34.73 | 34.55 | 34.63 | 34.88 | - | 34.56 |
| 25 | 31.68 | 32.23 | 32.11 | 32.l6 | 32.41 | 32 34 | 32.03 | |
| 50 | 28.46 | 29.02 | 28.99 | 29.05 | 29.22 | 29.25 | 28.81 | |
| Set5 | 15 | 34.04 | 34.29 | 34.31 | 34.17 | 34.57 | - | 34.26 |
| 25 | 31.65 | 31.91 | 32.11 | 32.29 | 32.51 | 32.14 | 31.98 | |
| 50 | 28.69 | 28.96 | 29.22 | 29.06 | 29.31 | 29.04 | 29.00 | |
| McMaster | 15 | 34.06 | 33.45 | 34.66 | 33.92 | 35.08 | 34.96 | 34.58 |
| 25 | 31.66 | 31.52 | 32.35 | 32.14 | 32.75 | 32.34 | 32.18 | |
| 50 | 28.51 | 28.62 | 29.18 | 28.93 | 29.52 | 29.31 | 28.91 |
| Method | CBM3D | DNCNN | FFDNET | BRDNet | IRCNN |
|---|---|---|---|---|---|
| Time (s) | 1.46 | 1.37 | 0.63 | 3.23 | 4.82 |
| Method | SIDD | DND | ||
|---|---|---|---|---|
| PSNR (dB) | SSIM | PSNR (dB) | SSIM | |
| CBM3D | 25.65 | 0.685 | 34.51 | 0.851 |
| EPLL | 27.11 | 0.870 | 33.51 | 0.824 |
| K-SVD | 26.88 | 0.842 | 36.49 | 0.899 |
| DnCNN | 32.59 | 0.861 | 37.90 | 0.943 |
| FFDNet | 38.27 | 0.948 | 37.61 | 0.942 |
| CBDNet | 33.28 | 0.868 | 38.06 | 0.942 |
| RIDNet | 38.71 | 0.951 | 39.26 | 0.953 |
| VDNet [122] | 39.26 | 0.955 | 39.38 | 0.952 |
| GMSNet-A [123] | 39.51 | 0.958 | 40.15 | 0.961 |
| GMSNet-B [123] | 39.69 | 0.958 | 40.24 | 0.962 |
| MPRNet [124] | 39.71 | 0.958 | 39.80 | 0.954 |
| Dataset | CBM3D | NLH | DNCNN | FFDNet | MIRNet |
|---|---|---|---|---|---|
| CC15 | 37.95 | 38.49 | 37.47 | 37.68 | 36.06 |
| PolyU | 38.81 | 38.36 | 38.51 | 38.56 | 37.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, J.; Sun, L.; Chen, J.; Yu, S. Overview of Research on Digital Image Denoising Methods. Sensors 2025, 25, 2615. https://doi.org/10.3390/s25082615
Mao J, Sun L, Chen J, Yu S. Overview of Research on Digital Image Denoising Methods. Sensors. 2025; 25(8):2615. https://doi.org/10.3390/s25082615
Chicago/Turabian StyleMao, Jing, Lianming Sun, Jie Chen, and Shunyuan Yu. 2025. "Overview of Research on Digital Image Denoising Methods" Sensors 25, no. 8: 2615. https://doi.org/10.3390/s25082615
APA StyleMao, J., Sun, L., Chen, J., & Yu, S. (2025). Overview of Research on Digital Image Denoising Methods. Sensors, 25(8), 2615. https://doi.org/10.3390/s25082615








