Elevation Data Statistical Analysis and Maximum Likelihood Estimation-Based Vehicle Type Classification for 4D Millimeter-Wave Radar
Abstract
1. Introduction
2. Related Work
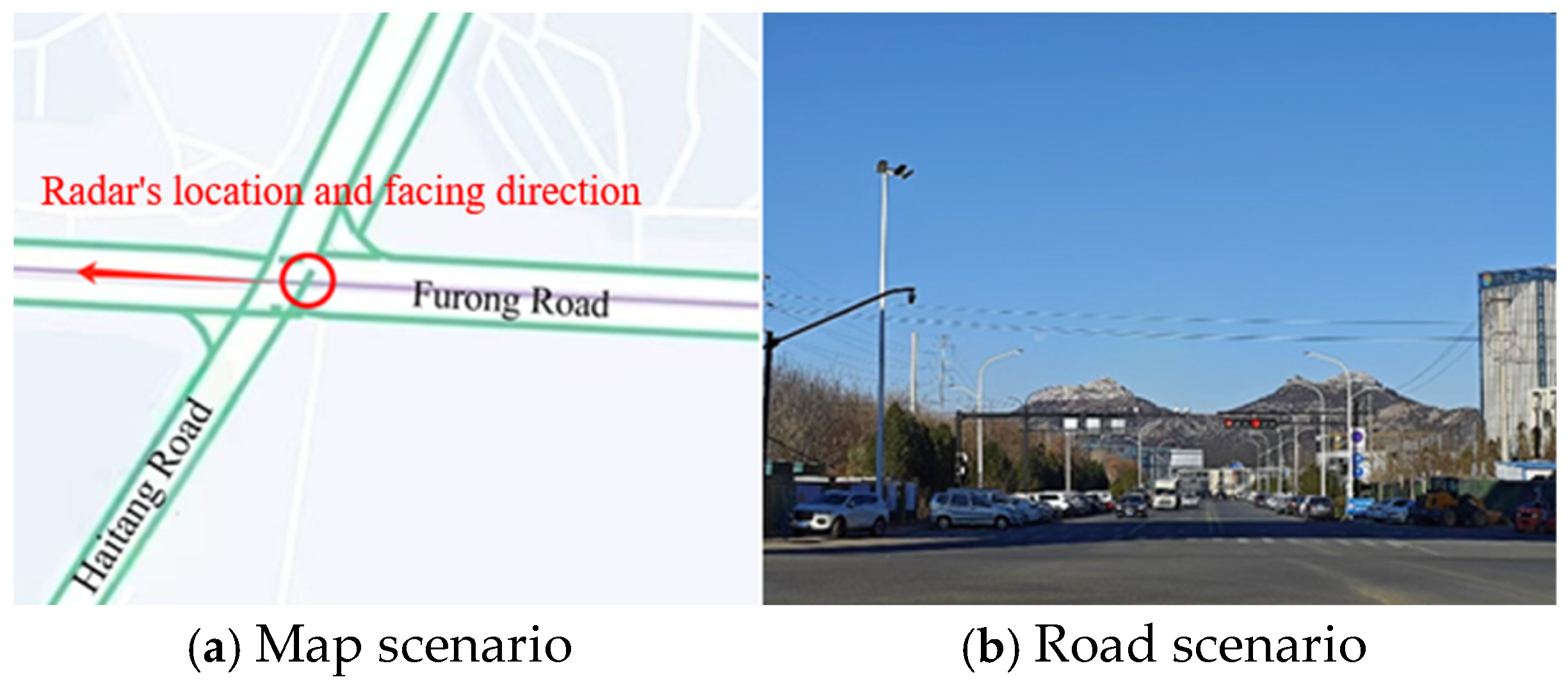
3. Experimental Scenario
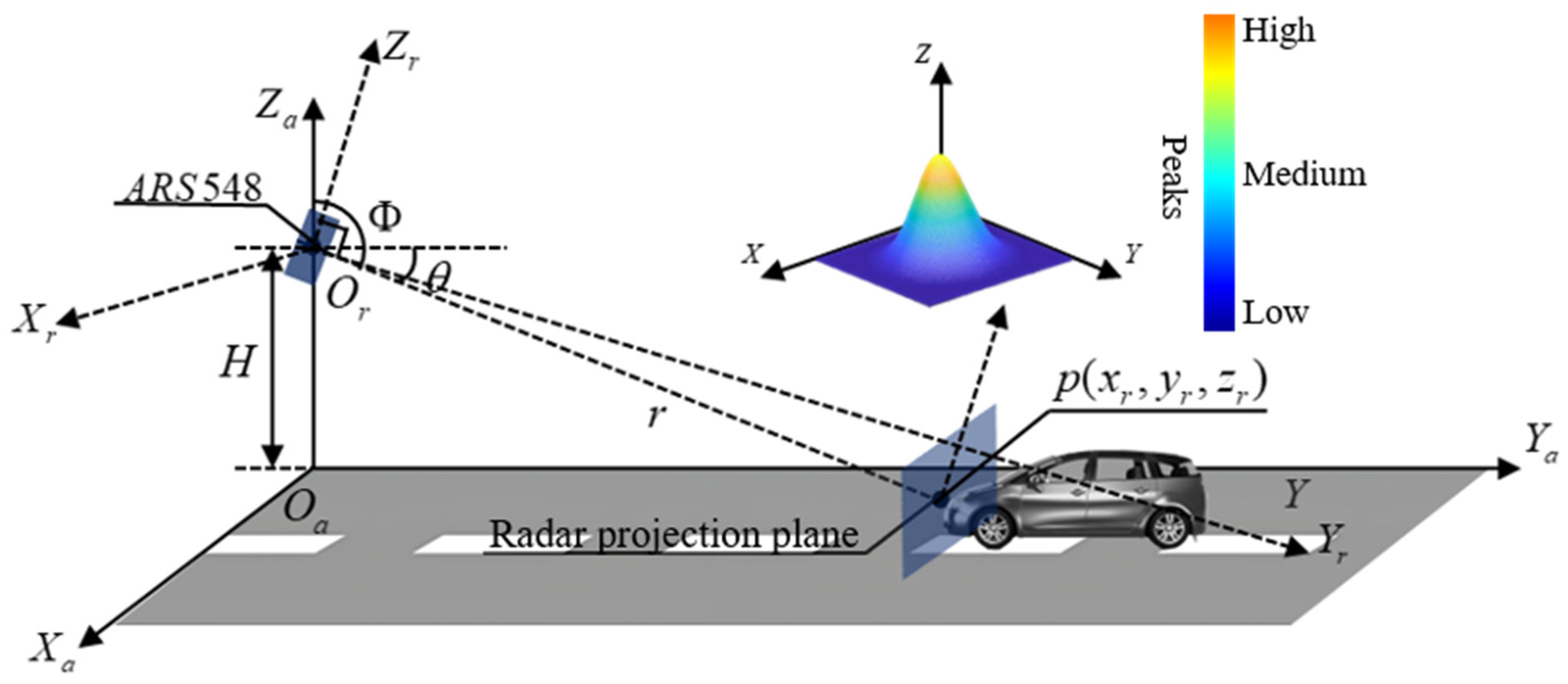
4. Statistical Modeling of Elevation Data and Maximum Likelihood Classification Method
4.1. Statistical Modeling of Elevation Data
4.2. Maximum Likelihood Estimation Classification Model Based on Gaussian Distribution
5. Experimental Results and Analysis
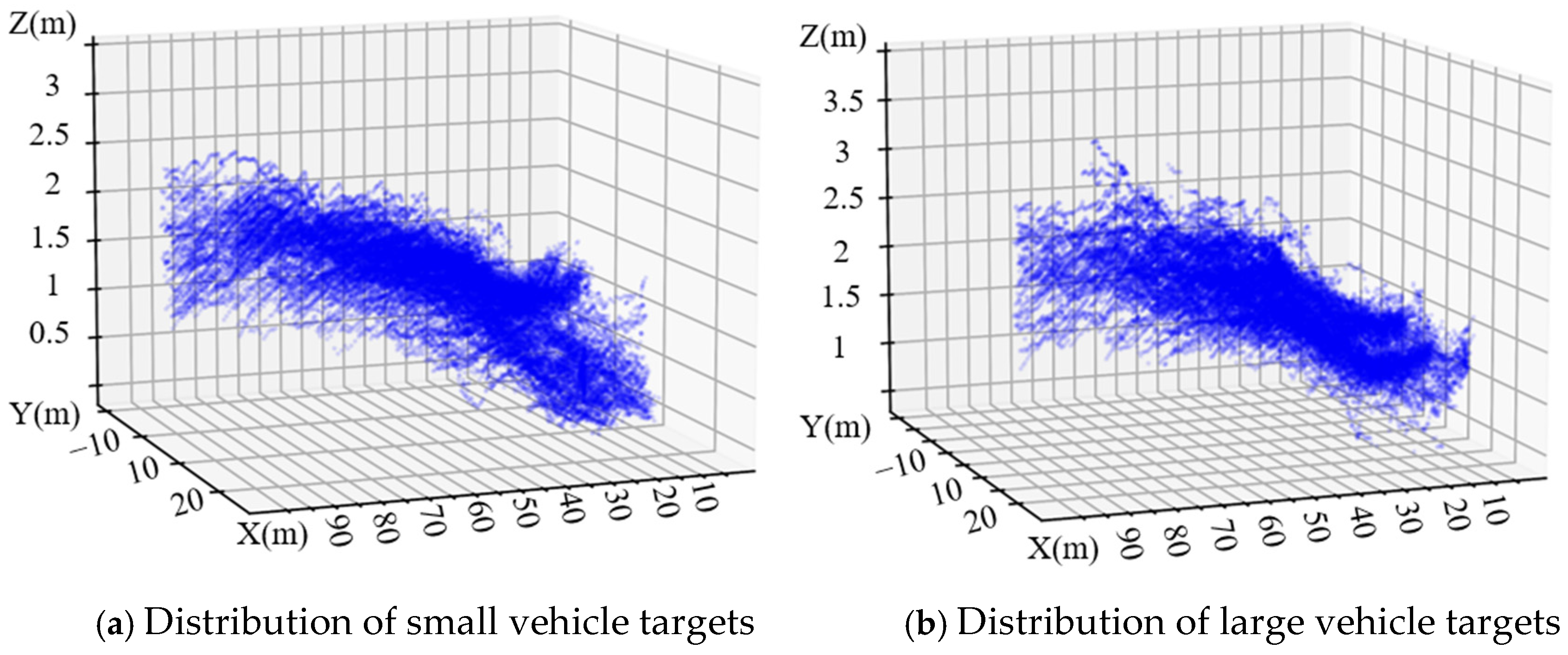
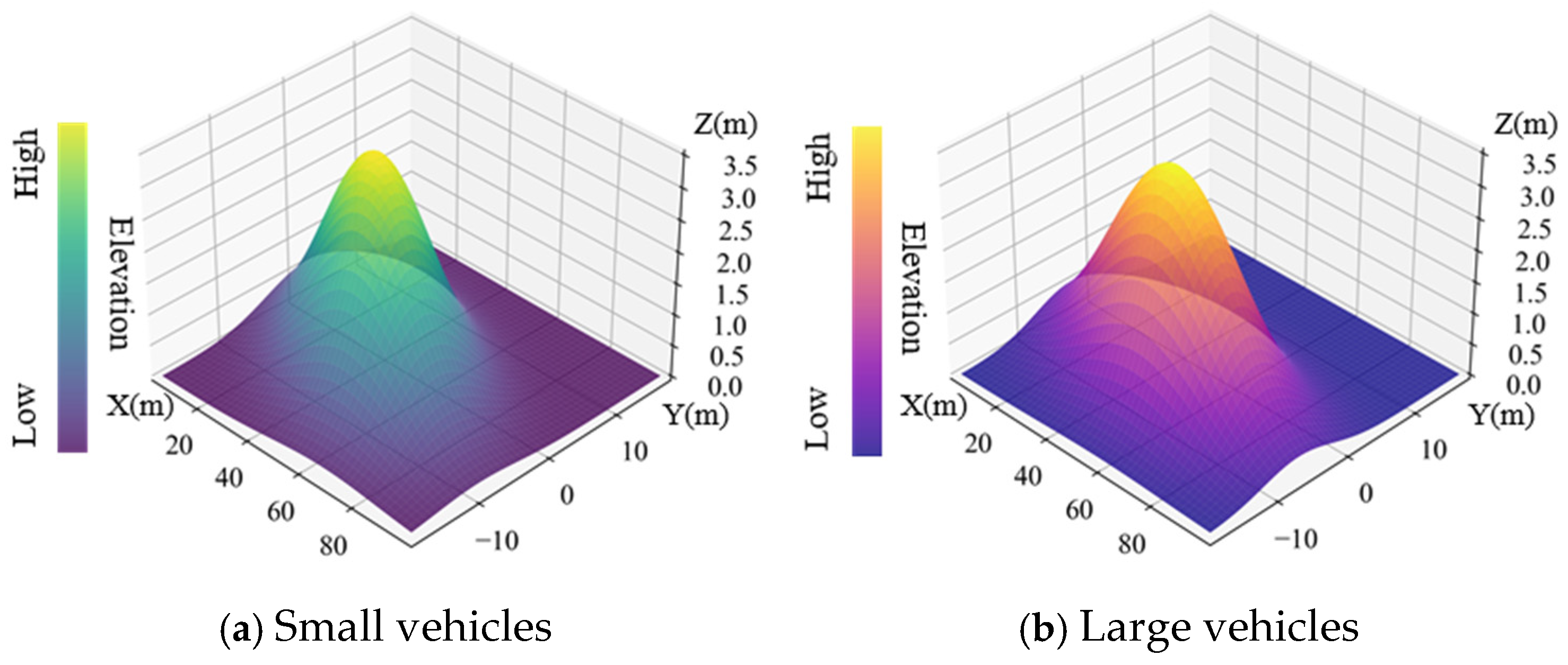
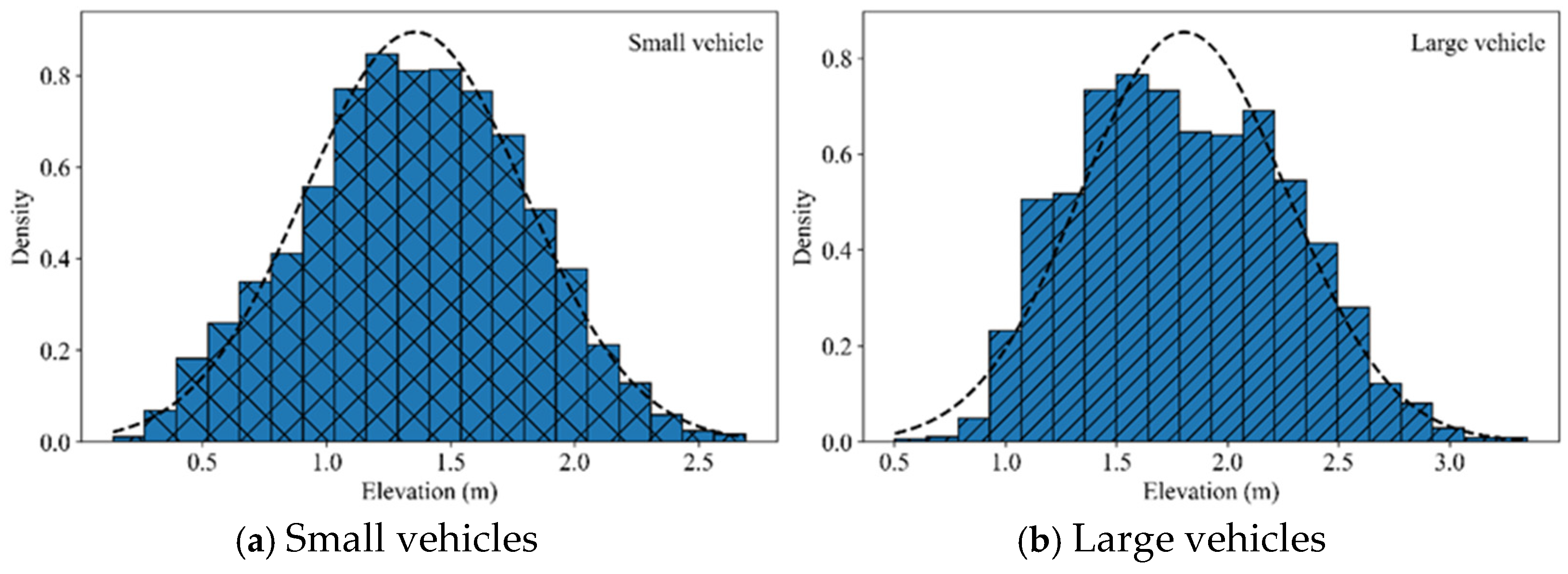
5.1. Elevation Data Feature Analysis
5.1.1. Statistical Features of Overall Elevation Data
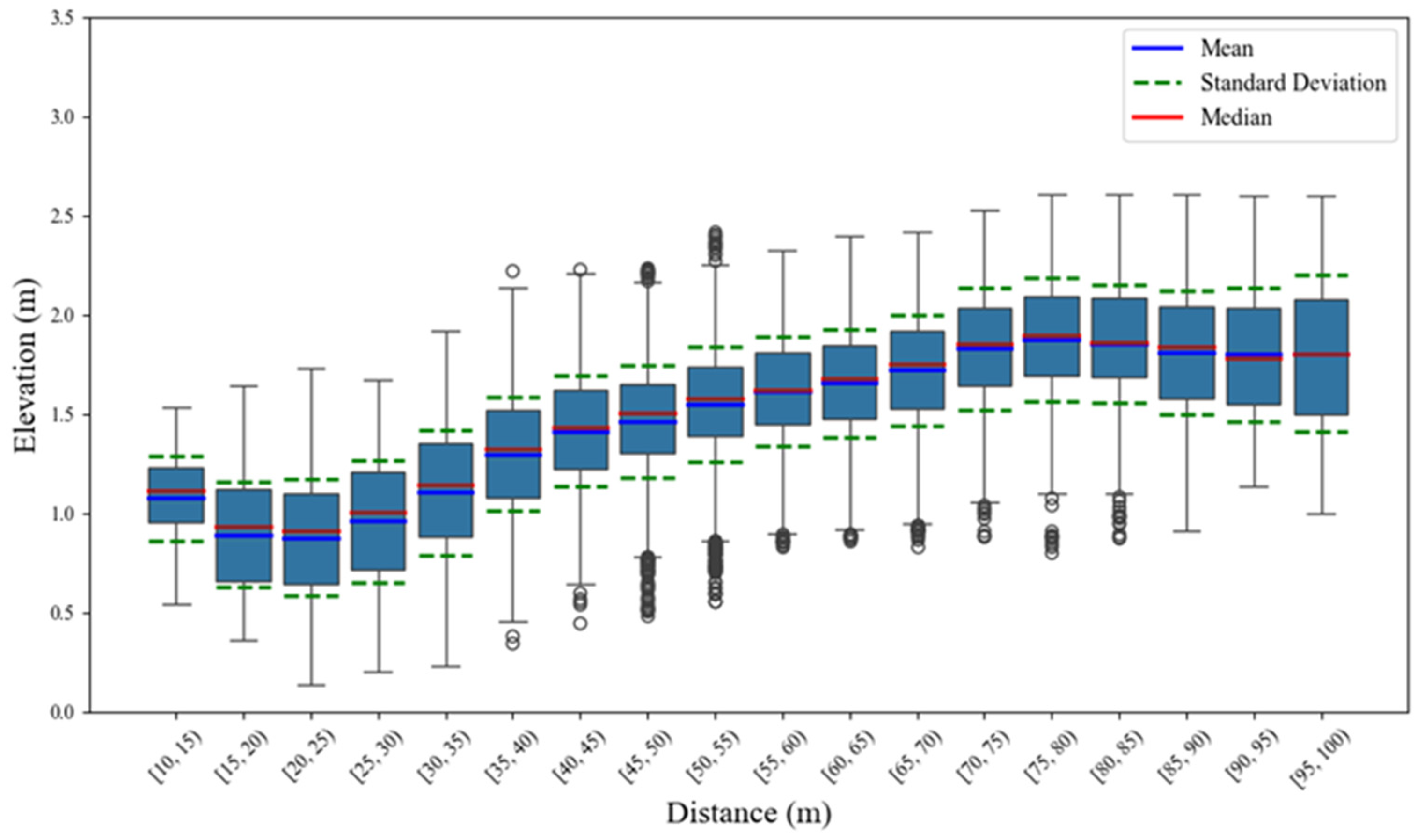
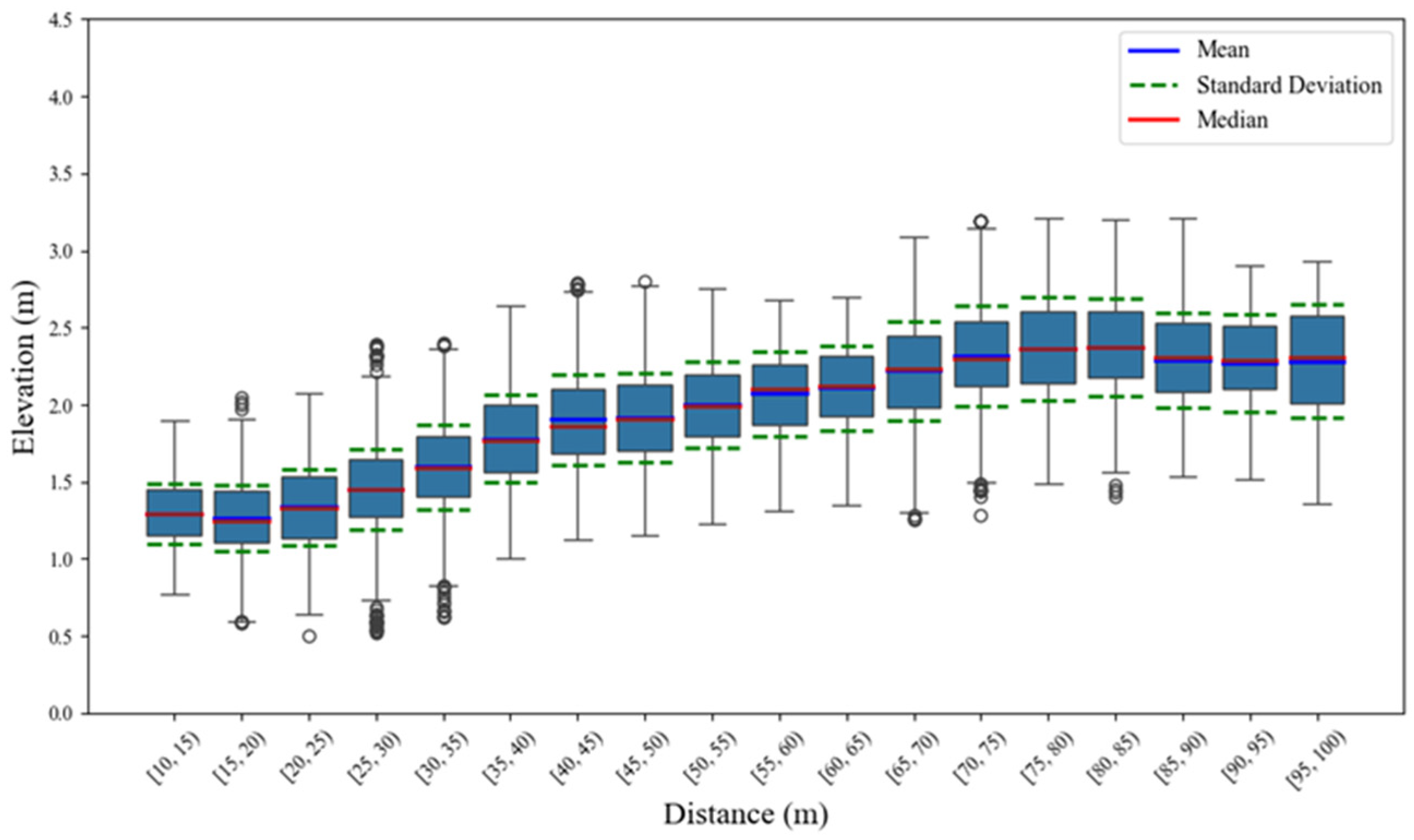
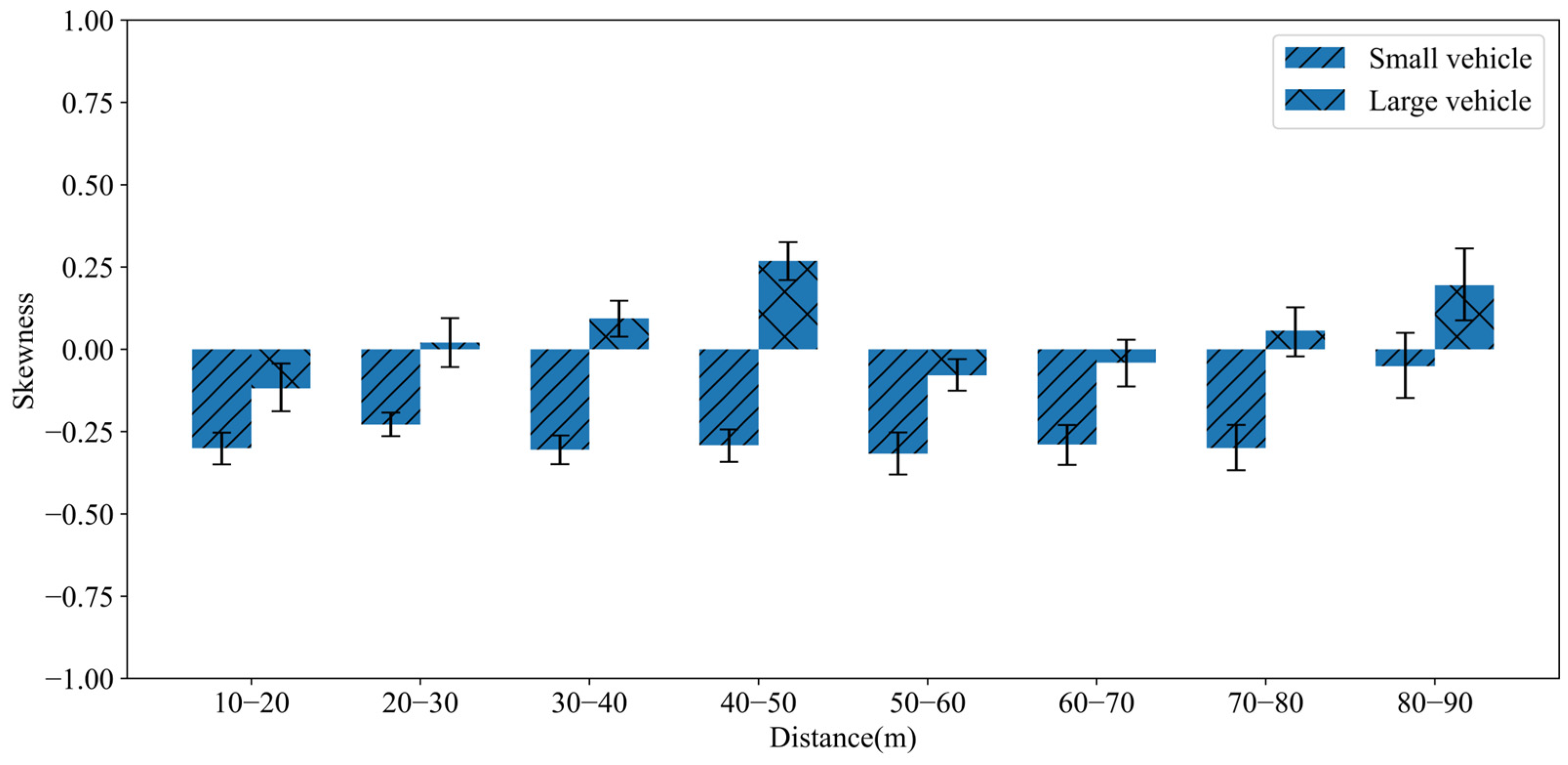
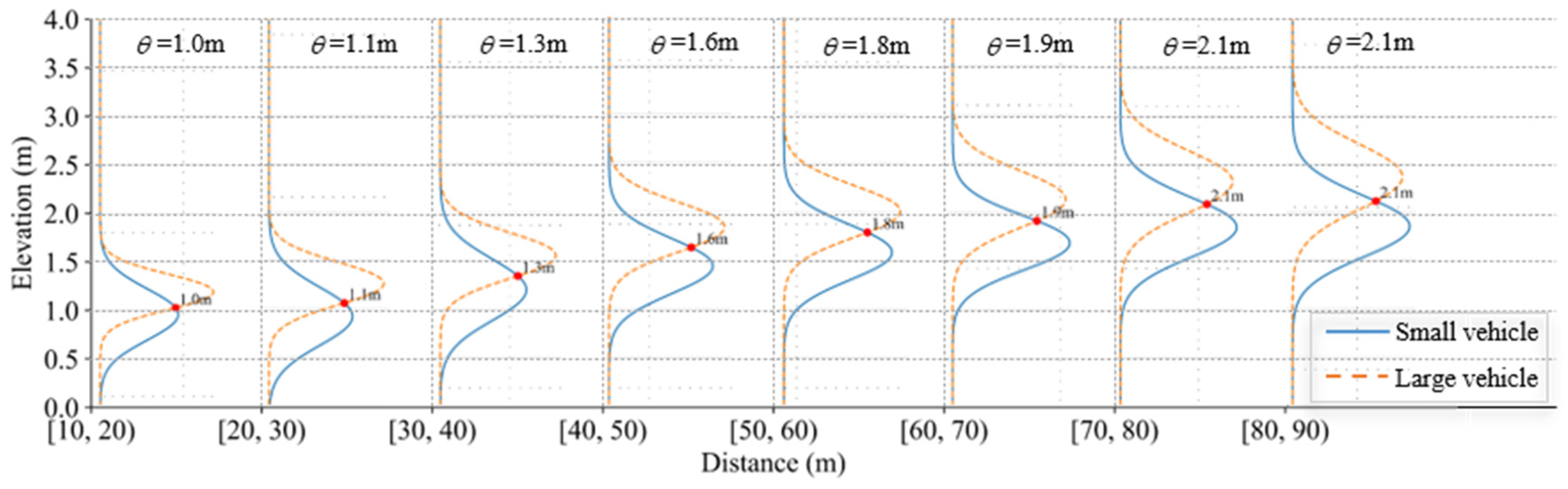
5.1.2. Statistical Features of Cross-Section Elevation Data
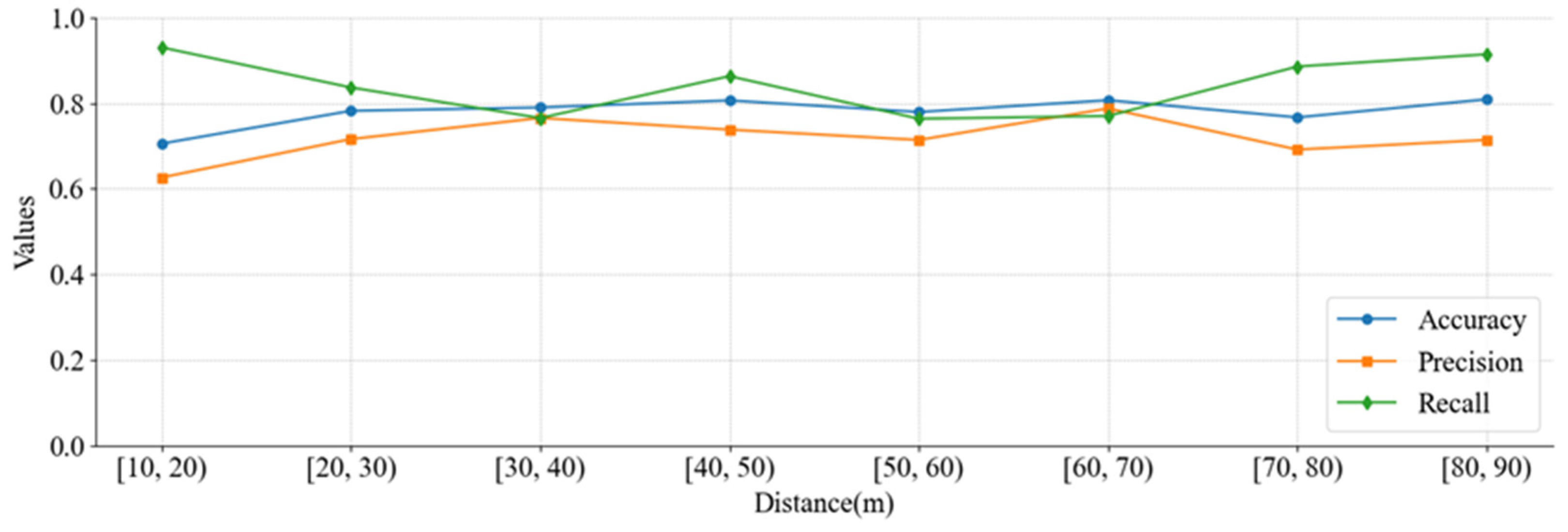
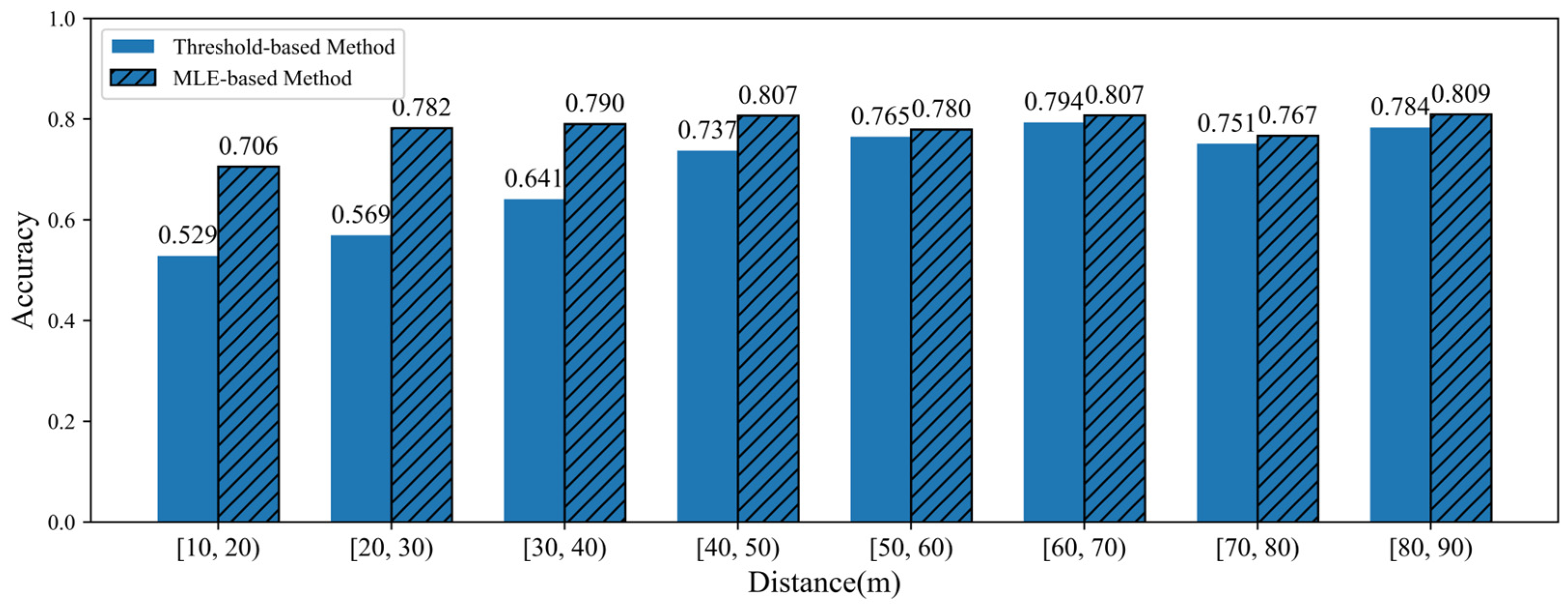
5.2. Vehicle Type Classification Results Based on Maximum Likelihood Estimation
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Karimian-Sichani, N.; Alaee-Kerahroodi, M.; Rao, B.S.M.R.; Mehrshahi, E.; Ghorashi, S.A. Antenna array and waveform design for 4-D-Imaging mm wave MIMO radar sensors. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 1848–1864. [Google Scholar] [CrossRef]
- Kamel, A.; Sayed, T. Transferability of real-time EVT safety models: An investigation using autonomous vehicles data. Transp. A. Transp. Sci. 2024, 20, 1–26. [Google Scholar] [CrossRef]
- Yacoub, M.; Antkiewicz, M.; Czarnecki, K.; McPhee, J. Gain-scheduled model predictive controller for vehicle-following trajectory generation for autonomous vehicles. Veh. Syst. Dyn. 2024, 62, 1–26. [Google Scholar] [CrossRef]
- Baumann, M.V.; Weyland, C.M.; Ellmers, J.; Fuchs, L.; Grau, J.; Vortisch, P. Determining desired speeds from vehicle trajectory data. Transp. Res. Rec. 2024, 2678, 1341–1352. [Google Scholar] [CrossRef]
- Akhtar, M.M.; Li, Y.; Cheng, W.; Dong, L.; Tan, Y. OHDL: Radar target detection using optimized hybrid deep learning for automotive FMCW. Digit. Signal Process. 2025, 158, 104962. [Google Scholar] [CrossRef]
- Singh, J.; Gupta, A.; Jagannatham, A.K.; Hanzo, L. Multi-beam object-localization for millimeter-wave ISAC-aided connected autonomous vehicles. IEEE Trans. Veh. Technol. 2025, 74, 1725–1729. [Google Scholar] [CrossRef]
- Hwangbo, S.; Cho, S.; Kim, J.; Lee, S. Efficient target classification based on vehicle volume estimation in high-resolution radar systems. Remote Sens. 2024, 16, 1522. [Google Scholar] [CrossRef]
- Loc, H.D.; Son, L.A.; Nang, H.X. Accurate 3D multi-object detection and tracking on Vietnamese street scenes based on sparse point cloud data. IEEE Trans. Intell. Transp. Syst. 2025, 26, 92–101. [Google Scholar] [CrossRef]
- Tegowski, B.; Koelpin, A. Accuracy limitations of interferometric radar owing to the radar cross section of its antenna. IEEE Trans. Microw. Theory Tech. 2024, 72, 4317–4324. [Google Scholar] [CrossRef]
- Tegowski, B.; Koelpin, A. Calibration of the self-radar-cross-section of continuous-wave radars. IEEE Trans. Microw. Theory Tech. 2025, 1–8. [Google Scholar] [CrossRef]
- Al-Jameel, H.A.; Al-Jumaili, M.A. Analysis of traffic stream characteristics using loop detector data. Jordan J. Civ. Eng. 2016, 10, 403–416. [Google Scholar]
- Kwon, Y.J.; Kim, D.H.; Choi, K.H. A single node vehicle detection system using an adaptive signal adjustment technique. In Proceedings of the 2017 20th International Symposium on Wireless Personal Multimedia Communications (WPMC), Bali, Indonesia, 17–20 December 2017; pp. 349–353. [Google Scholar] [CrossRef]
- Sharma, S.; LuBmann, J.; So, J. Controller independent software-in-the-loop approach to evaluate rule-based traffic signal retiming strategy by utilizing floating car data. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3585–3594. [Google Scholar] [CrossRef]
- Rodríguez-Esparza, E.; Ramos-Soto, O.; Masegosa, A.D.; Onieva, E.; Oliva, D.; Arriandiaga, A.; Ghosh, A. Optimizing road traffic surveillance: A robust hyper-heuristic approach for vehicle segmentation. IEEE Access 2024, 12, 29503–29524. [Google Scholar] [CrossRef]
- Shokri, D.; Larouche, C.; Homayouni, S. Proposing an efficient deep learning algorithm based on segment anything model for detection and tracking of vehicles through uncalibrated urban traffic surveillance cameras. Electronics 2024, 13, 2883. [Google Scholar] [CrossRef]
- Muja, R.; Anghel, A.; Cacoveanu, R.; Ciochina, S. Real-time interference mitigation in automotive radars using the short-time fourier transform and L-statistics. IEEE Trans. Veh. Technol. 2024, 73, 14617–14632. [Google Scholar] [CrossRef]
- Rangasamy, S.; Goh, W.L.; Zhigang, Z. A Study on 77 GHz Automotive Radar for Radar-Camera Fusion Module. In Proceedings of the 2021 3rd International Conference on Electrical Engineering and Control Technologies (CEECT), Macao, China, 16–18 December 2021; pp. 198–202. [Google Scholar] [CrossRef]
- Zhang, C.; Cao, M.; Gong, Y.; Li, Y.; Huang, Y.; Wang, H. Calibration of motional frequency spread for wide-band FMCW automotive millimeter-wave radar. IEEE Access 2020, 8, 14355–14366. [Google Scholar] [CrossRef]
- Zhao, C.; Ding, D.; Du, Z.; Shi, Y.; Su, G.; Yu, S. Analysis and verification of the perception accuracy of millimeter-wave radars on smart roads. China J. Highw. Transp. 2023, 37, 205–214. [Google Scholar] [CrossRef]
- Lin, Y.J.; Chen, N.; Lu, K. Vehicle trajectory tracking at intersections based on millimeter-wave radar point cloud. J. South China Univ. Technol. 2023, 51, 110–125. [Google Scholar] [CrossRef]
- Xing, Z.R.; Zhu, D.C.; Jin, X. An efficient range and velocity measurement method for multi-target FMCW radar. Acta Electron. Sin. 2016, 44, 2148–2157. [Google Scholar] [CrossRef]
- Coşkun, A.; Bilicz, S. Target classification using radar cross-section statistics of millimeter-wave scattering. COMPEL 2023, 42, 1119–1211. [Google Scholar] [CrossRef]
- Coşkun, A.; Bilicz, S. Analysis of data-driven approaches for radar target classification. COMPEL 2024, 43, 507–518. [Google Scholar] [CrossRef]
- Liu, H.; Li, N.; Guan, D.; Rai, L. Data feature analysis of non-scanning multi target millimeter-wave radar in traffic flow detection applications. Sensor 2018, 18, 2756. [Google Scholar] [CrossRef]
- Feng, D.; Cui, Y.H.; Zhang, X.Y. Vehicle obstacle classification recognition based on RCS. J. Zhengzhou Univ. 2011, 43, 114–117. [Google Scholar]
- Liu, H.; Wan, J.; Zhou, P.; Ding, S.; Huang, W. Augmented millimeter wave radar and vision fusion simulator for roadside perception. Electronics 2024, 13, 2729. [Google Scholar] [CrossRef]
- Yang, S.; Choi, M.; Han, S.; Choi, K.-H.; Kim, K.-S. 4D radar-camera sensor fusion for robust vehicle pose estimation in foggy environments. IEEE Access 2024, 12, 16178–16188. [Google Scholar] [CrossRef]
- Lu, S.; Zhuo, G.; Xiong, L.; Zhu, X.; Zheng, L.; He, Z.; Zhou, M.; Lu, X.; Bai, J. Efficient deep-learning 4D automotive radar odometry method. IEEE Trans. Intell. Veh. 2024, 9, 879–892. [Google Scholar] [CrossRef]
- Jin, C.; Zhu, B.; Deng, J.; Hu, Z.; Wen, X. Automatic calibration and association for roadside radar and camera based on fluctuating traffic volume. Meas. Sci. Technol. 2024, 35, 055118. [Google Scholar] [CrossRef]
- Zheng, L.; Ma, Z.; Zhu, X.; Tan, B.; Li, S.; Long, K.; Bai, J. TJ4DRadSet: A 4D radar dataset for autonomous driving. In Proceedings of the 2022 IEEE International Intelligent Transportation Systems Conference (ITSC 2022), Macau, China, 8–12 October 2022. [Google Scholar]
- Paek, D.; Kong, S.; Wijaya, K. K-Radar: 4D radar object detection for autonomous driving in various weather conditions. In Proceedings of the Neural Information Processing Systems Track on Datasets and Benchmarks 2022, New Orleans, LA, USA, 2–10 December 2022. [Google Scholar]
- Fernández-Calatayud, F.; Coto, L.; Alejo, D.; Carpio, J.J.; Caballero, F.; Merino, L. Ars548_ros: An ARS548 RDI radar driver for ROS. SoftwareX 2025, 30, 102111. [Google Scholar] [CrossRef]
- Li, K.; Hu, Y.; Cao, R. Gaussian mixture model-based RCS distribution fitting for stratosphere aerostats. Electron. Meas. Technol. 2021, 44, 110–115. [Google Scholar] [CrossRef]


| Category | Unit |
|---|---|
| Distance with reference to vehicle rear axle (X, Y, Z) | m |
| Relative and absolute velocity (X, Y) | m/s |
| Relative and absolute acceleration (X, Y) | m2/s |
| Width, length, leading | m |
| Radar cross-section | dB |
| RCS existence probability | - |
| Dynamic property (moving, stationary) | - |
| Category | Range |
|---|---|
| Resolution distance measuring | 0~0.22 m |
| Azimuth/Elevation resolution | −0.1~0.1° |
| Detection azimuth angle | −90~90° |
| Detection elevation angle | −90~90° |
| Detection radial distance | −100~1600 m |
| Detection radial velocity | −120~120 m/s |
| Detection RCS | −128~127 dBm2 |
| Object X coordinate | −100~1600 m |
| Object Y coordinate | −1600~1600 m |
| Object Z coordinate | −1600~1600 m |
| Horizontal Distance | Mean Value | Standard Deviation | Median Value | Interquartile Range |
|---|---|---|---|---|
| [10, 20) | 0.97 | 0.07 | 0.20 | 1.0 |
| [20, 30) | 0.92 | 0.09 | 0.30 | 0.95 |
| [30, 40) | 1.20 | 0.10 | 0.32 | 1.23 |
| [40, 50) | 1.44 | 0.08 | 0.28 | 1.46 |
| [50, 60) | 1.58 | 0.08 | 0.29 | 1.59 |
| [60, 70) | 1.68 | 0.08 | 0.28 | 1.71 |
| [70, 80) | 1.85 | 0.10 | 0.31 | 1.87 |
| [80, 90) | 1.85 | 0.10 | 0.32 | 1.86 |
| Horizontal Distance | Mean Value | Standard Deviation | Median Value | Interquartile Range |
|---|---|---|---|---|
| [10, 20) | 1.28 | 0.04 | 0.20 | 1.27 |
| [20, 30) | 1.39 | 0.06 | 0.26 | 1.40 |
| [30, 40) | 1.69 | 0.08 | 0.30 | 1.67 |
| [40, 50) | 1.91 | 0.08 | 0.29 | 1.88 |
| [50, 60) | 2.04 | 0.08 | 0.28 | 2.06 |
| [60, 70) | 2.16 | 0.09 | 0.30 | 2.17 |
| [70, 80) | 2.35 | 0.11 | 0.33 | 2.34 |
| [80, 90) | 2.38 | 0.11 | 0.33 | 2.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, M.; Liu, H.; Guo, F.; Gong, X. Elevation Data Statistical Analysis and Maximum Likelihood Estimation-Based Vehicle Type Classification for 4D Millimeter-Wave Radar. Sensors 2025, 25, 2766. https://doi.org/10.3390/s25092766
Jing M, Liu H, Guo F, Gong X. Elevation Data Statistical Analysis and Maximum Likelihood Estimation-Based Vehicle Type Classification for 4D Millimeter-Wave Radar. Sensors. 2025; 25(9):2766. https://doi.org/10.3390/s25092766
Chicago/Turabian StyleJing, Mengyuan, Haiqing Liu, Fuyang Guo, and Xiaolong Gong. 2025. "Elevation Data Statistical Analysis and Maximum Likelihood Estimation-Based Vehicle Type Classification for 4D Millimeter-Wave Radar" Sensors 25, no. 9: 2766. https://doi.org/10.3390/s25092766
APA StyleJing, M., Liu, H., Guo, F., & Gong, X. (2025). Elevation Data Statistical Analysis and Maximum Likelihood Estimation-Based Vehicle Type Classification for 4D Millimeter-Wave Radar. Sensors, 25(9), 2766. https://doi.org/10.3390/s25092766





