Digital Twin-Based Technical Research on Comprehensive Gear Fault Diagnosis and Structural Performance Evaluation
Abstract
:1. Introduction
2. Integrated Form-Performance Gearbox Monitoring System Framework
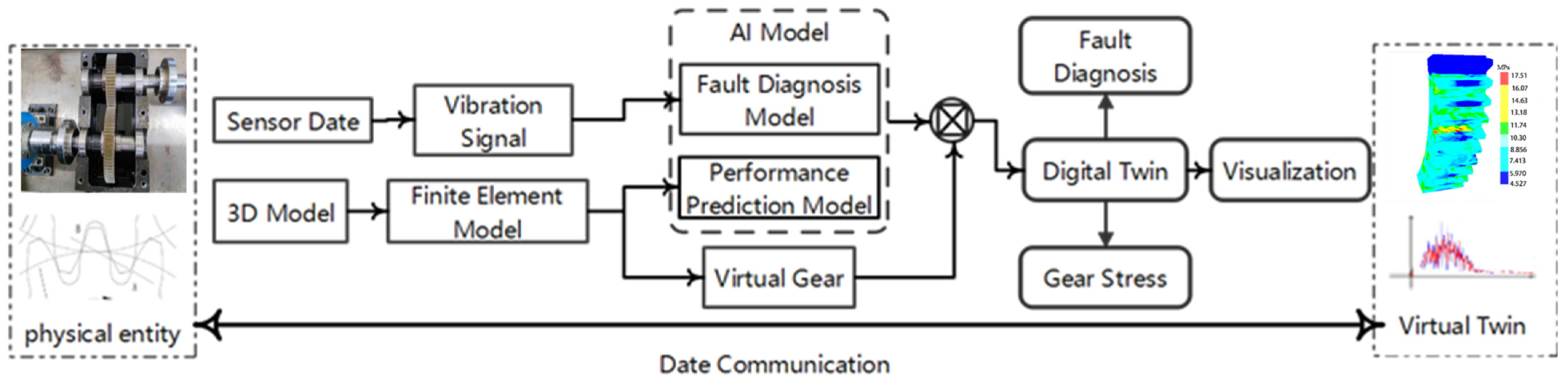
2.1. Integrated Form-Performance Digital Twin Framework
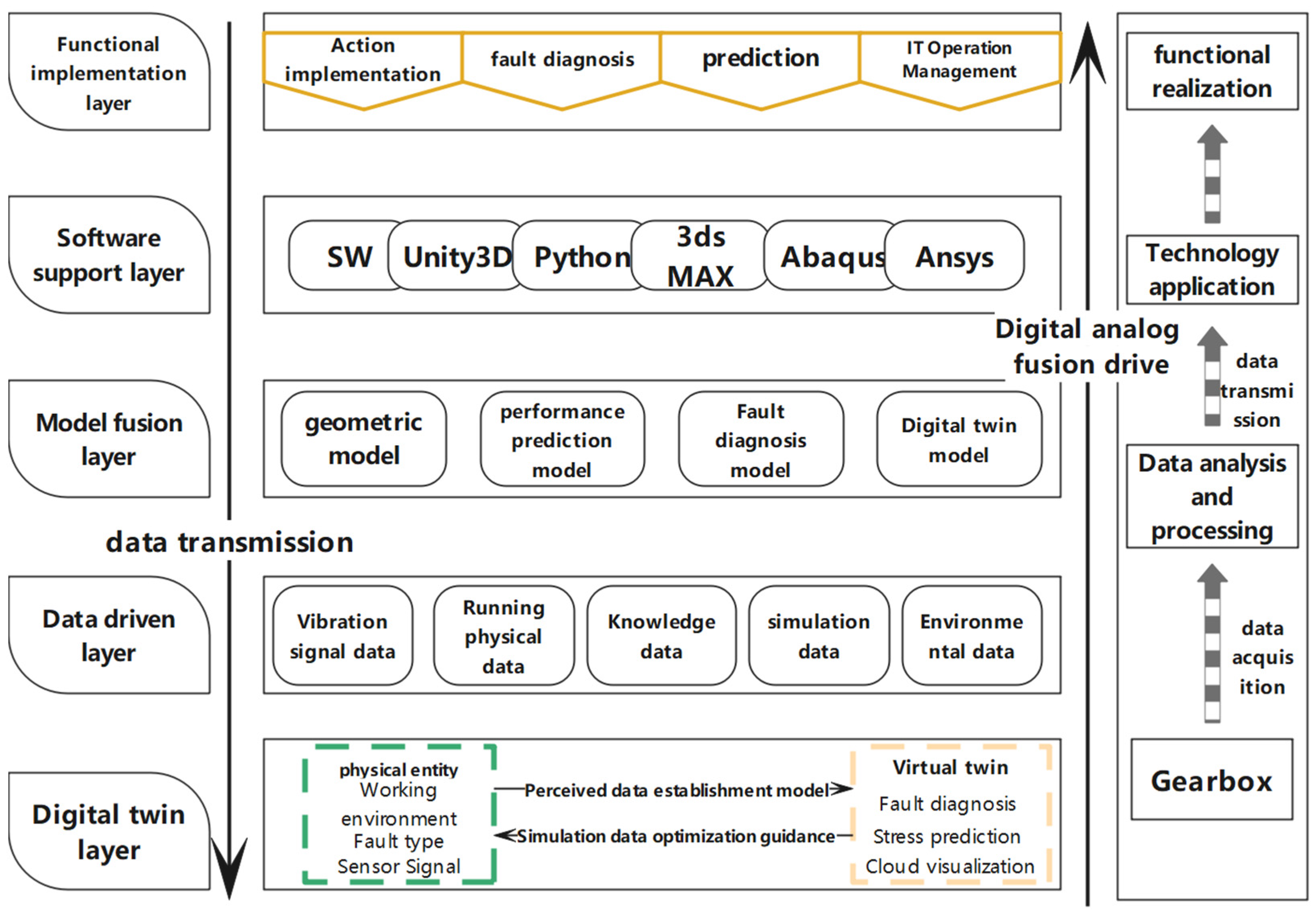
2.2. Integrated Shape and Performance Gearbox Monitoring System Architecture
- (1)
- Functional Service Layer
- (2)
- Software Support Layer
- (3)
- Model Fusion Layer
- (4)
- Data-Driven Layer
- (5)
- Digital Twin Layer
3. Construction Method for the Integrated Shape and Performance Gearbox Control System
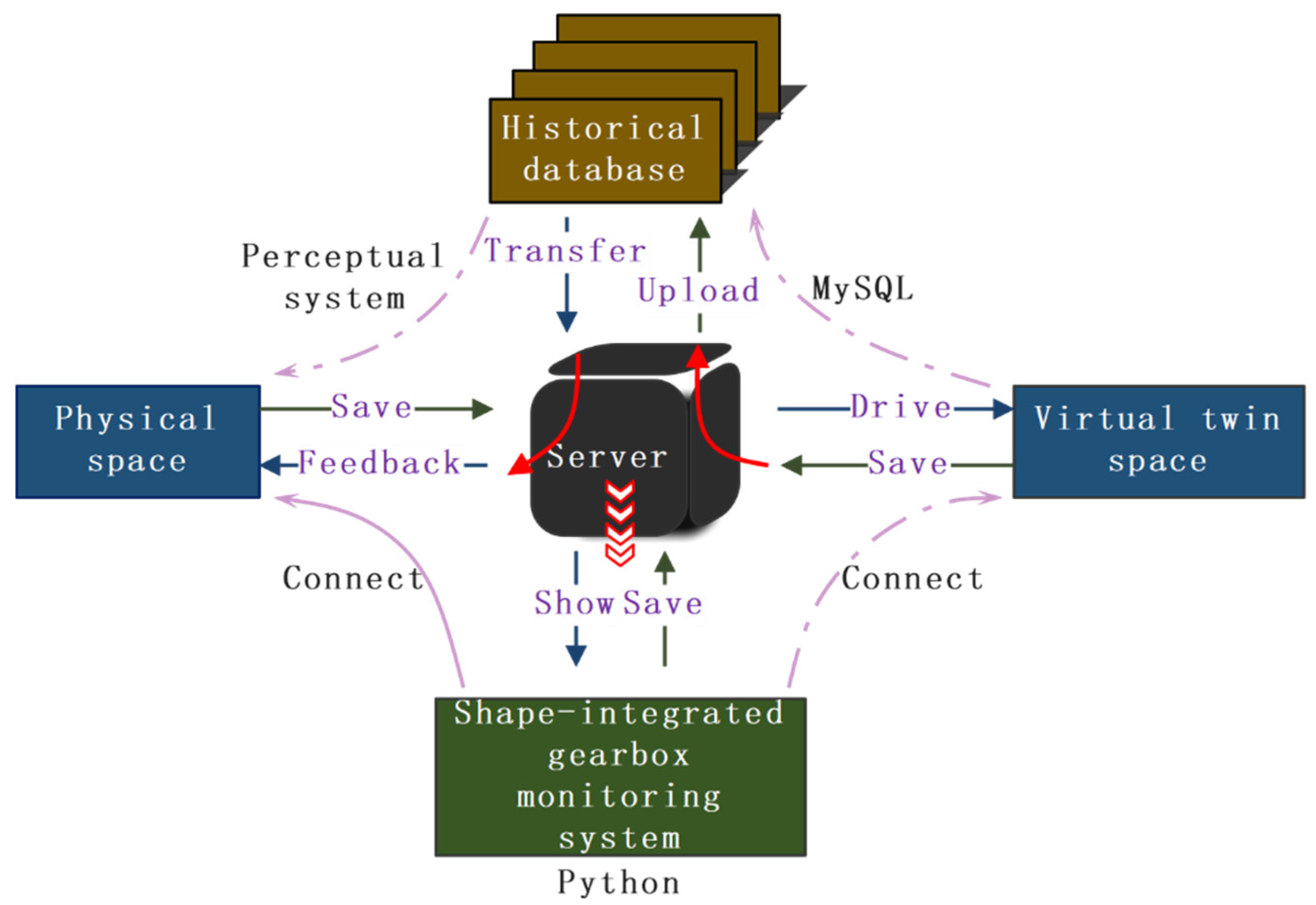
3.1. Virtual-Physical Mapping
- (1)
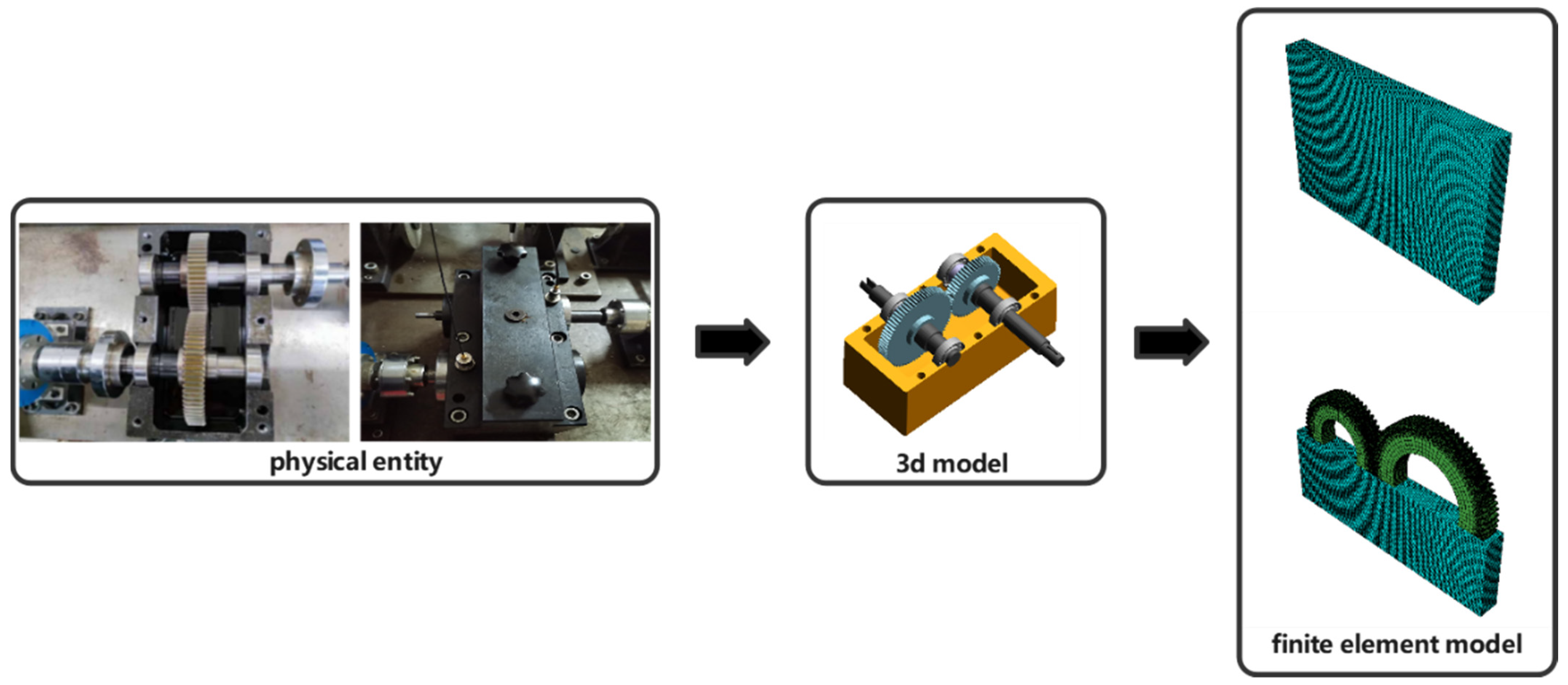
- Physical Space
- (2)
- Virtual Twin Space
| Algorithm 1. Proxy Model Partial Pseudo Code |
| Input: Angle command θ_input from Unity (format: ‘feaXXX’) Output: Predicted stress sequence y_pred (JSON encoded) Load surrogate model array Func [1:26510] using joblib Initialize TCP socket server and bind to port 8000 Start listening and accept client connection from Unity While system is running: Receive message data_unity from Unity If ‘fea’ in data_unity: Strip ‘fea’ and parse θ_input ← float(data_unity) Initialize empty list y_pred ← [] For j = 1 to 26,510 do: y_j ← Func[j].predict([[θ_input]]) Append round(y_j, 5) to y_pred Encode y_pred to JSON format Send y_pred to Unity through socket |
- (3)
- Virtual-Physical Mapping Process
- (1)
- Condition Determination: Based on historical operational data of the gearbox, determine the load magnitude within the gear rotation cycle. Obtain 10 sets of different load conditions within the historical load range. Simulate these 10 conditions in Abaqus and collect simulation data, with each condition providing 500 frames of stress data covering one full 365° rotation of the gear. In addition to the 10 different condition simulation models, an 11th condition model is added.
- (2)
- Mesh Generation and Refinement: After preprocessing the first 10 conditions by assigning material properties and setting boundary conditions, refine the mesh to provide more accurate simulation results. For the 11th condition model, perform a coarse mesh generation. Export the model in .STL format and use a Python script to remove duplicate vertex information from the triangular facets of the model. Export the unique vertex coordinates and vertex indices as two text files to achieve mesh dimensionality reduction.
- (3)
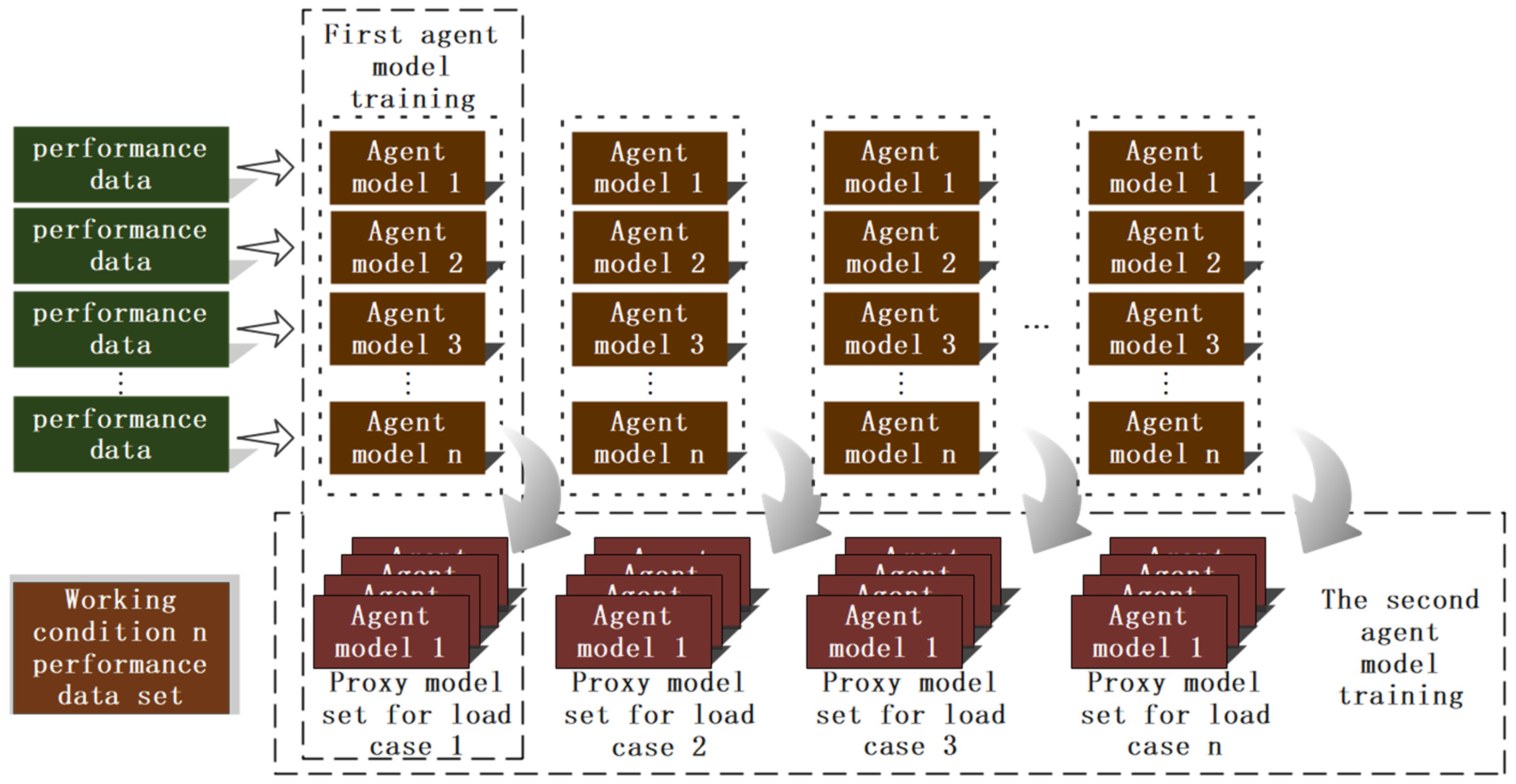
- Construction of Fault Diagnosis and Performance Prediction Algorithms: For fault diagnosis, use experimental data to train the fault diagnosis model. For performance prediction, first apply the KNN algorithm to average the stress of neighboring mesh nodes, and then use the GPR algorithm to construct a GPR surrogate model. Figure 8 illustrates the surrogate model workflow with load condition predictions and the associated surrogate model sets as outputs. The GPR surrogate model will train two prediction models: the first model predicts node stress based on 500 frames of stress data with angle as input, and the second model predicts load conditions and includes the surrogate model sets based on the sensor data. During the offline phase, the models are validated, and during the online phase, the fault diagnosis model and GPR surrogate model can be used for rapid diagnosis and prediction. The fault diagnosis model can be exported as a .PTH format file, while the two surrogate models for each condition and node will be packaged into .PKL format files.
- (4)
- Loading PTH and PKL Files and Running the Main Program: Integrate the two model files into the integrated gear monitoring system. Diagnose fault types based on real-time sensor data and obtain the current load condition’s gear stress prediction set using the GPR proxy model based on fine mesh simulation data.
- (5)
- Fault Model and Stress Cloud Map Visualization: Use a Python main program combined with Socket communication to interact with Unity3D using C# scripts. Finally, display the three-dimensional fault model of the gear and the corresponding stress cloud map visualization in Unity3D.
| Algorithm 2. Process Pseudo Code: pseudo code of virtual real mapping part |
| Input: Angular command θ_input from Unity, Fault type Fault_Type Output: Predicted stress sequence y_pred, Maximum stress σ_max Initialize GUI and start Socket server (e.g., port 8000/8001) Load the corresponding GPR surrogate model array Func [1:N] based on Fault_Type While system is running: Wait for incoming angle command from Unity marked as “feaXXX” Parse θ_input into a float θ Initialize empty list y_pred ← [] For i = 1 to N do: y_i ← Func[i].predict(θ) Append round(y_i, 5) to y_pred σ_max ← max(y_pred) Encode y_pred as JSON and send it to Unity via Socket Append σ_max to GUI time-series plot Update the GUI with current stress curve and value display |
3.2. Data Interaction
4. Artificial Intelligence Models
4.1. Gaussian Process Regression
4.2. Fault Diagnosis Algorithm Based on Wavelet Transform and Deep Residual Networks
4.2.1. Wavelet Transform
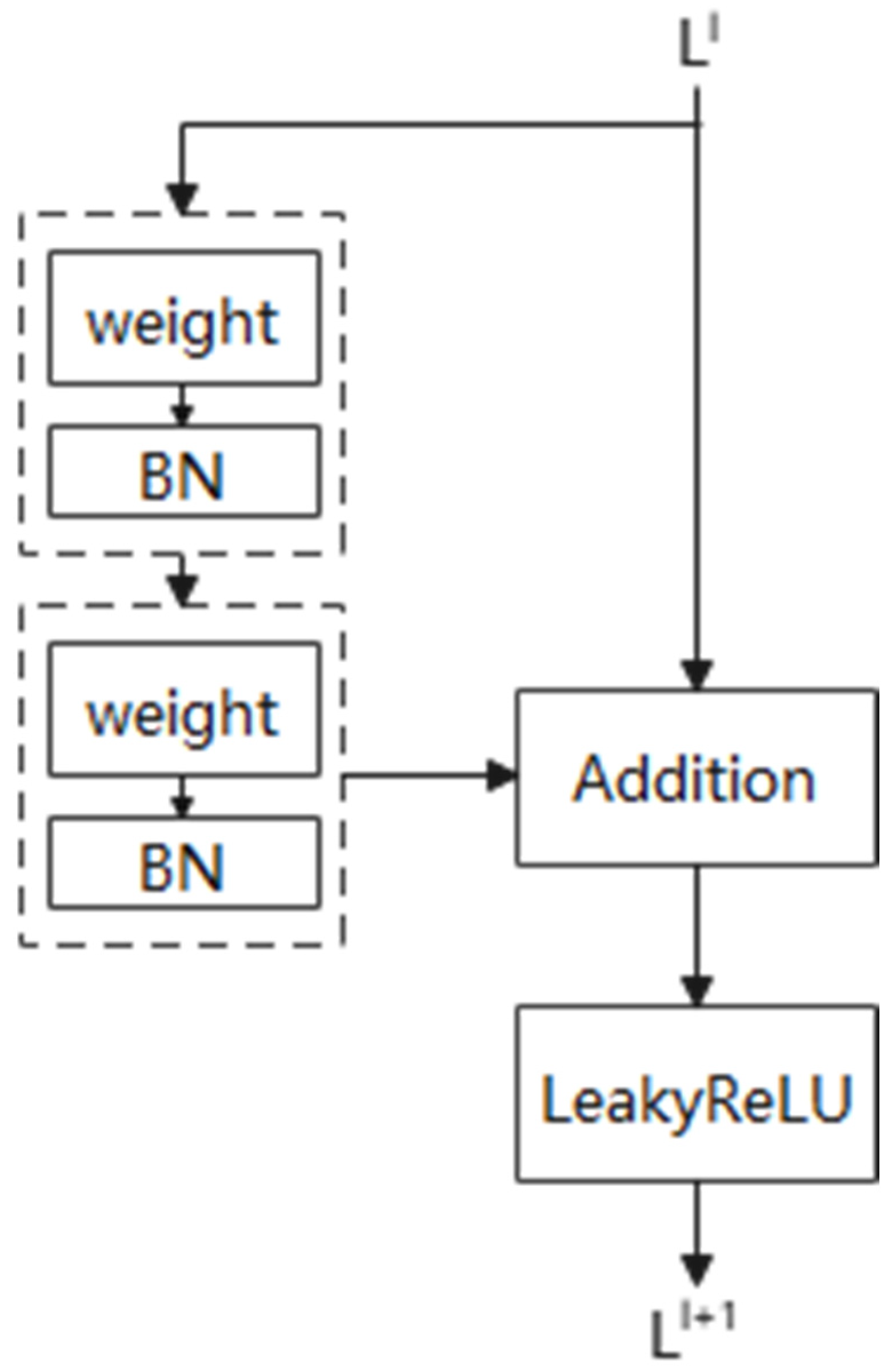
4.2.2. Deep Residual Networks
- (1)
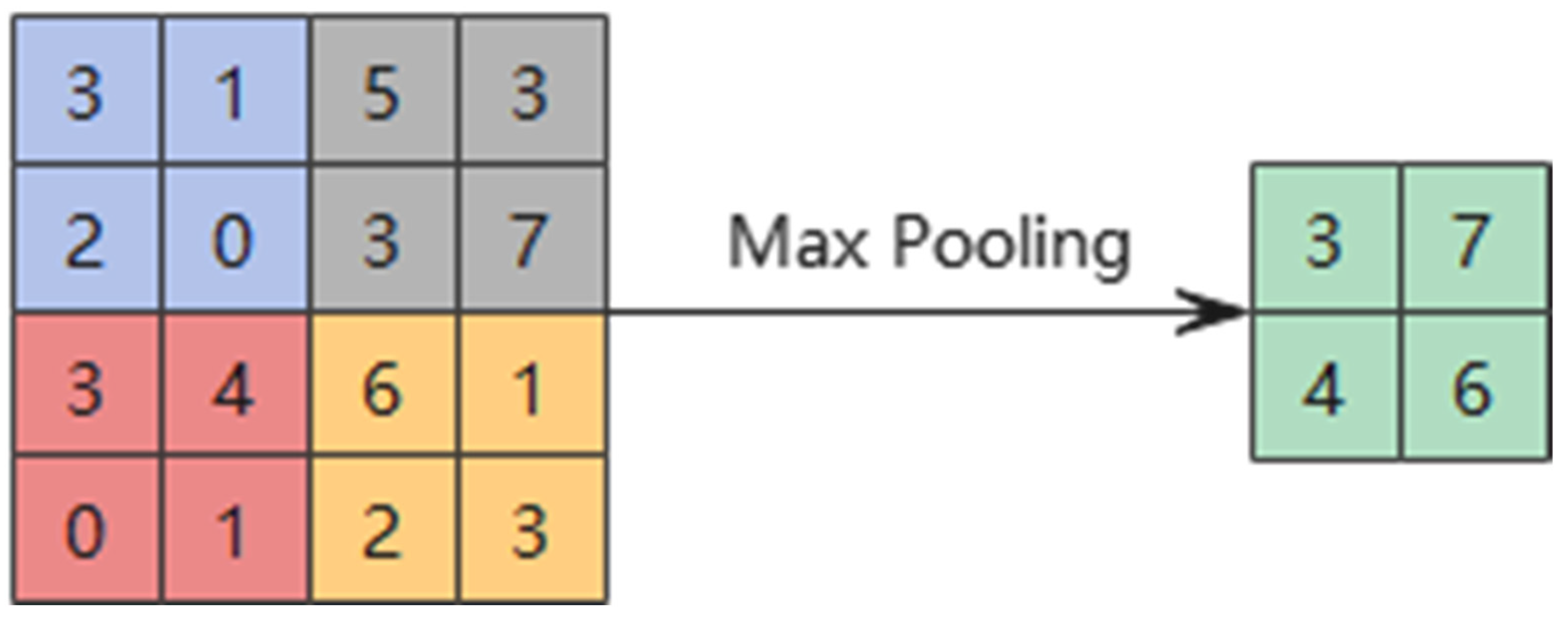
- Convolutional Neural Networks
- (2)
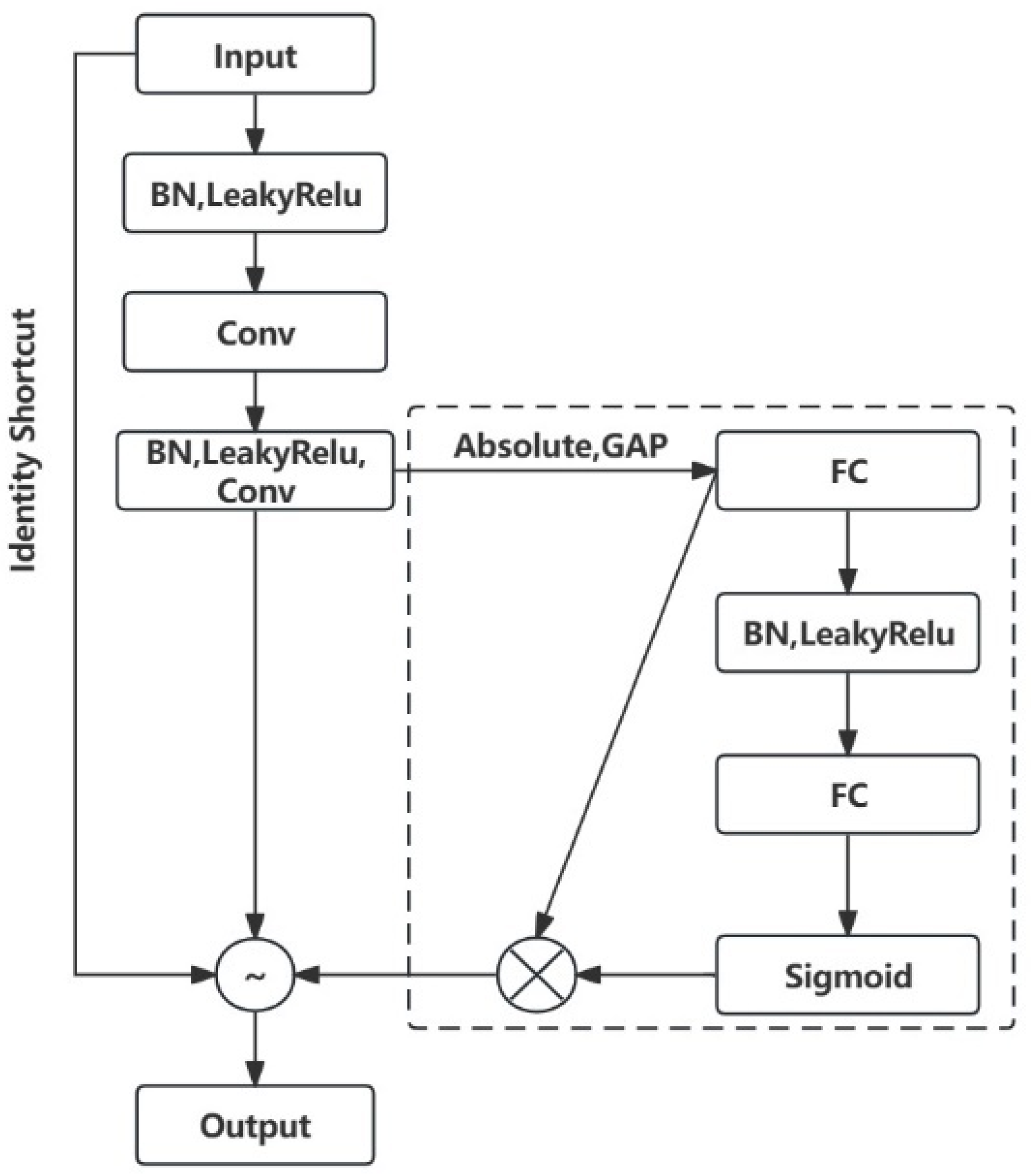
- Deep Residual Shrinkage Network
- (3)
- The fault diagnosis method based on wavelet transform and deep residual shrinkage network.
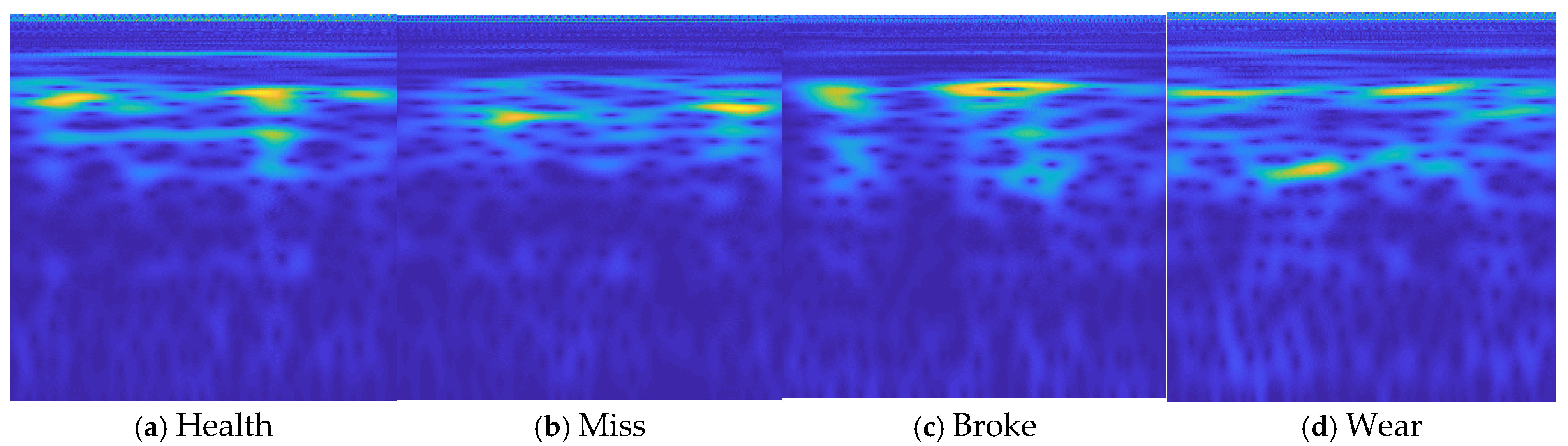
- Input the obtained raw signals into the continuous wavelet transform algorithm to generate wavelet time-frequency maps.
- Remove the axes, labels, and legends from the time-frequency maps to facilitate processing by the neural network.
- Perform grid-based normalization and compression of the images, setting the pixel dimensions to 224 × 224.
5. Development of an Integrated Form-Performance Gearbox Control System Platform
5.1. Platform Development
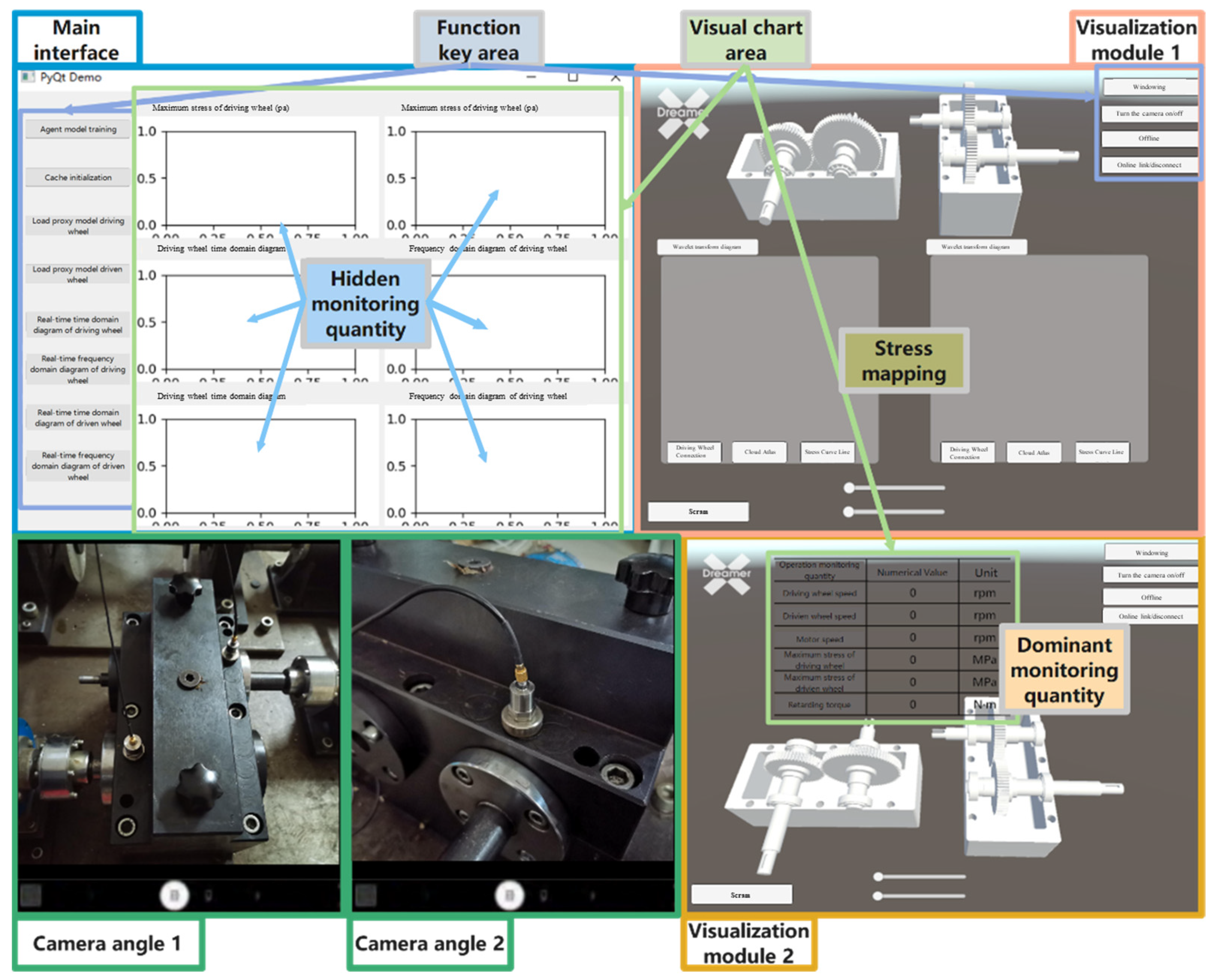
5.2. Data Fusion and Visualization
6. Experimental Case
6.1. Gearbox Data Collection and Data Communication
- (1)
- Sensor Distribution
- (2)
- Data Communication between Physical Entities and Twin Models
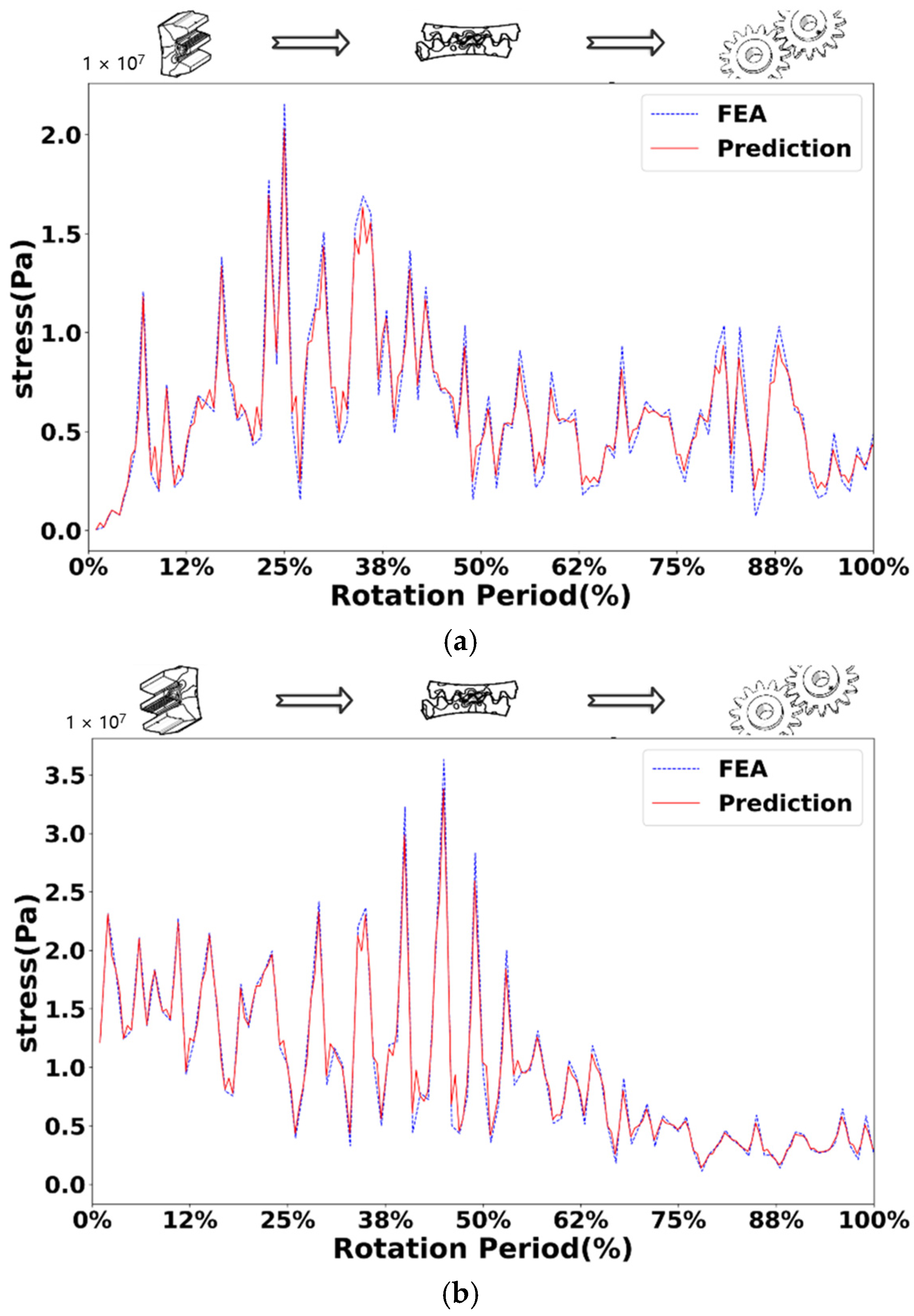
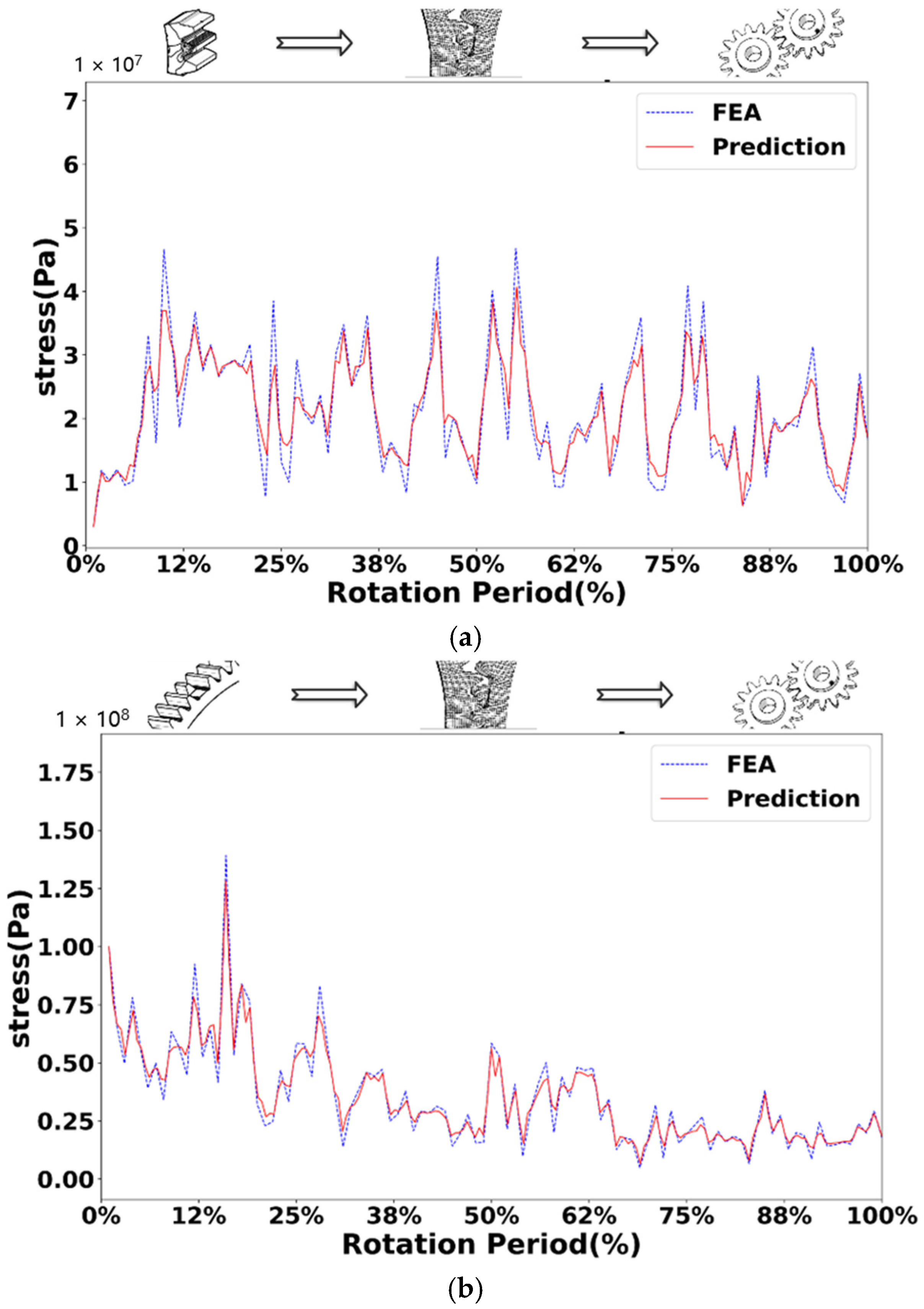
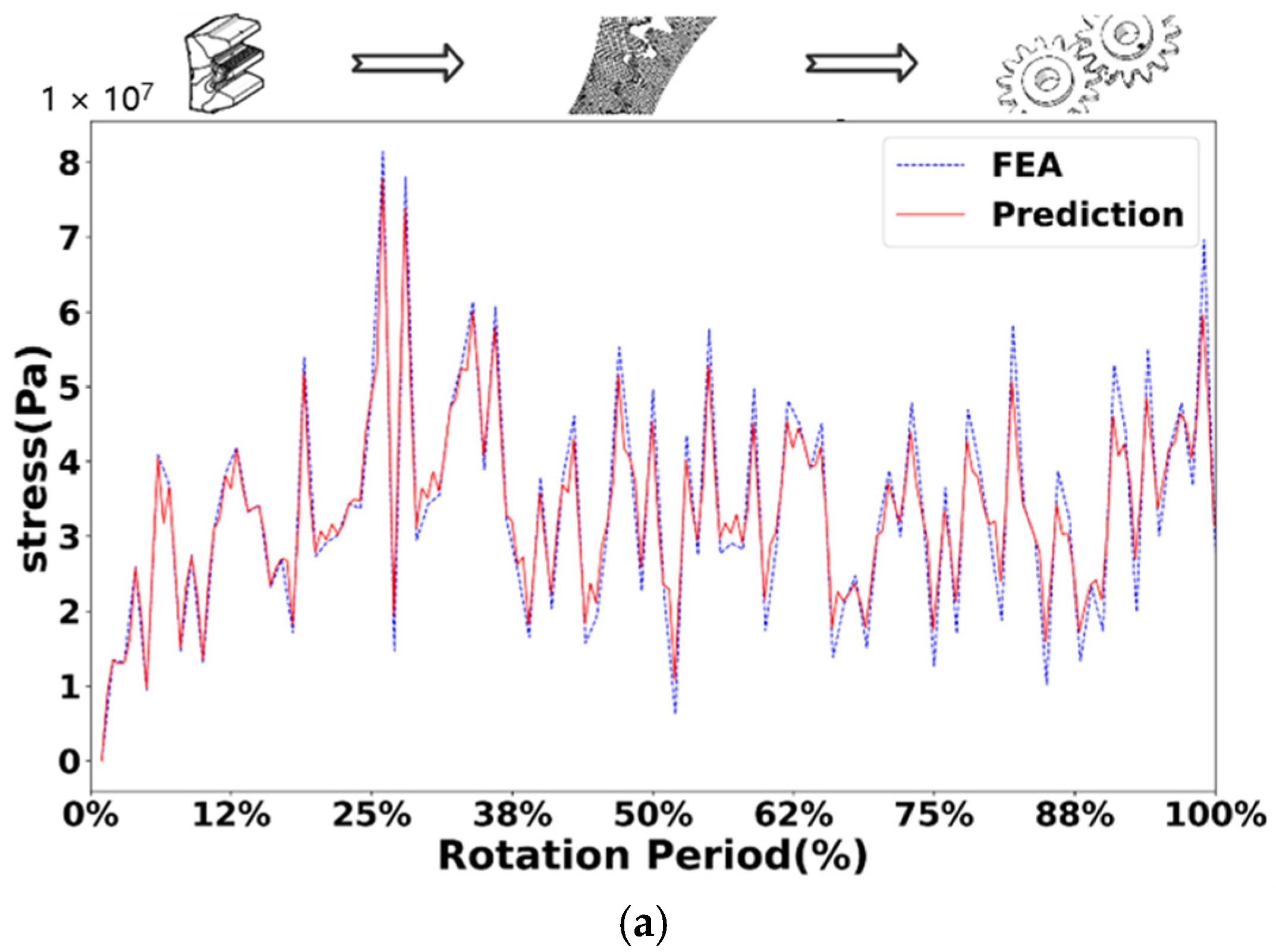
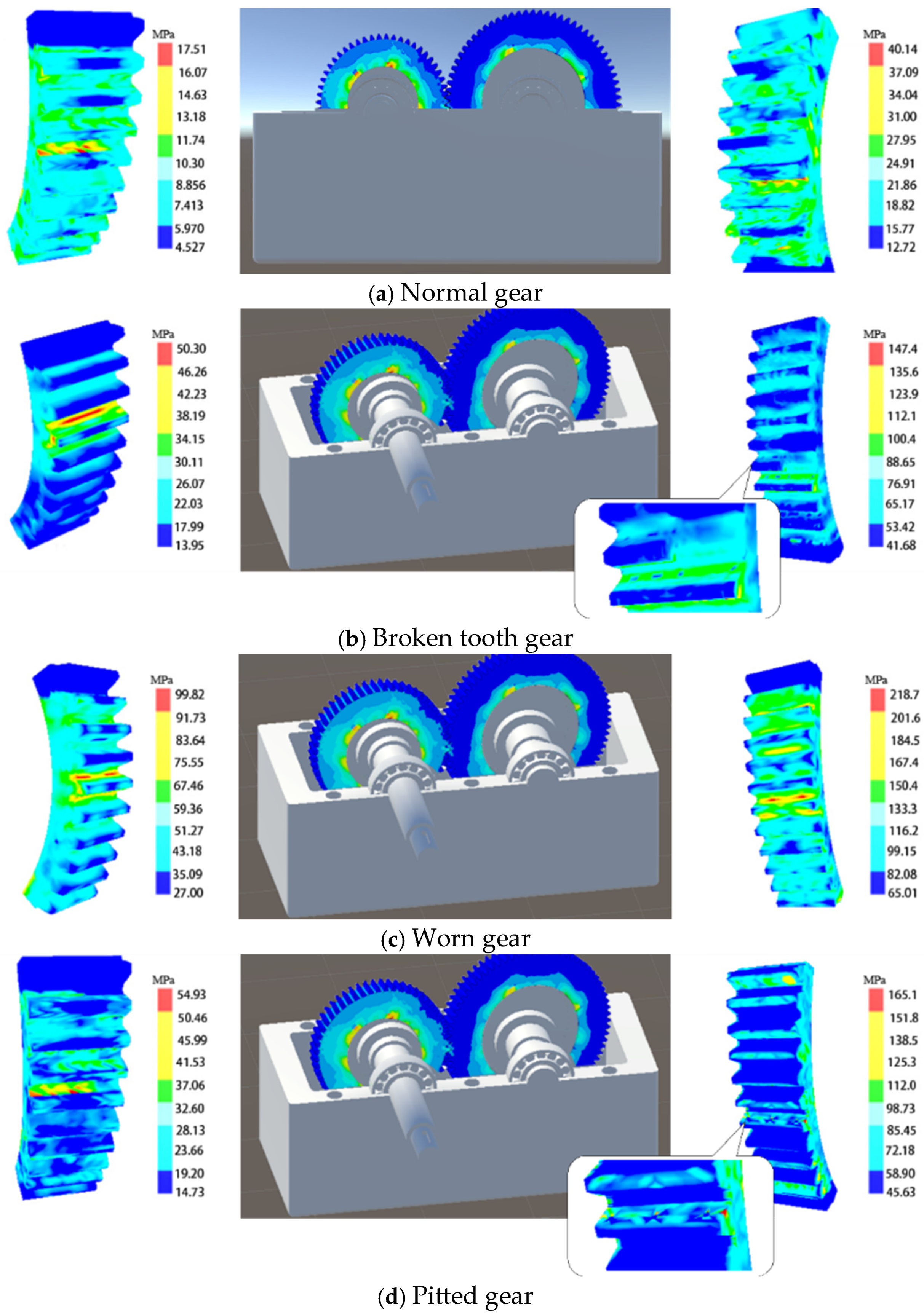
6.2. Experimental Verification
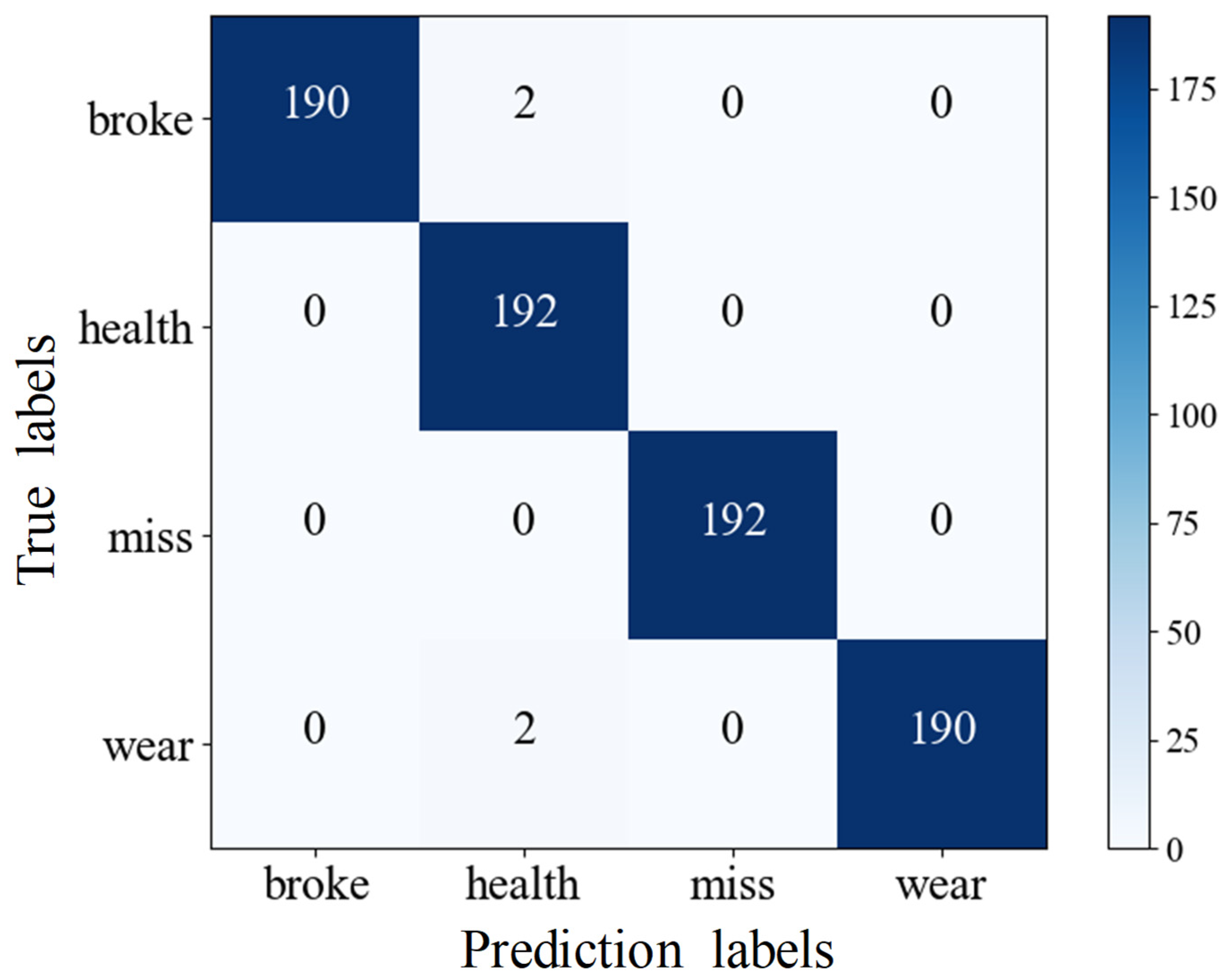
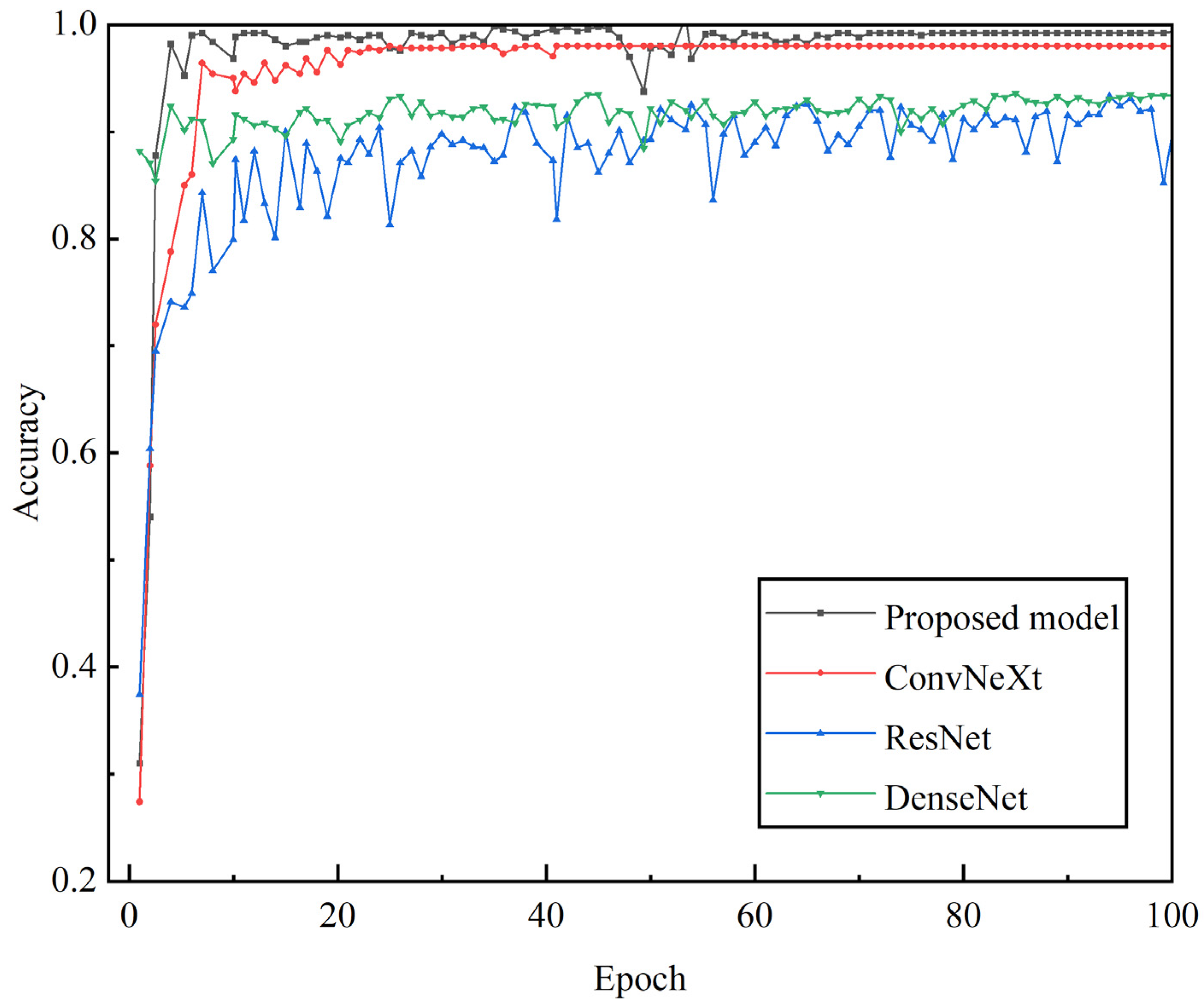
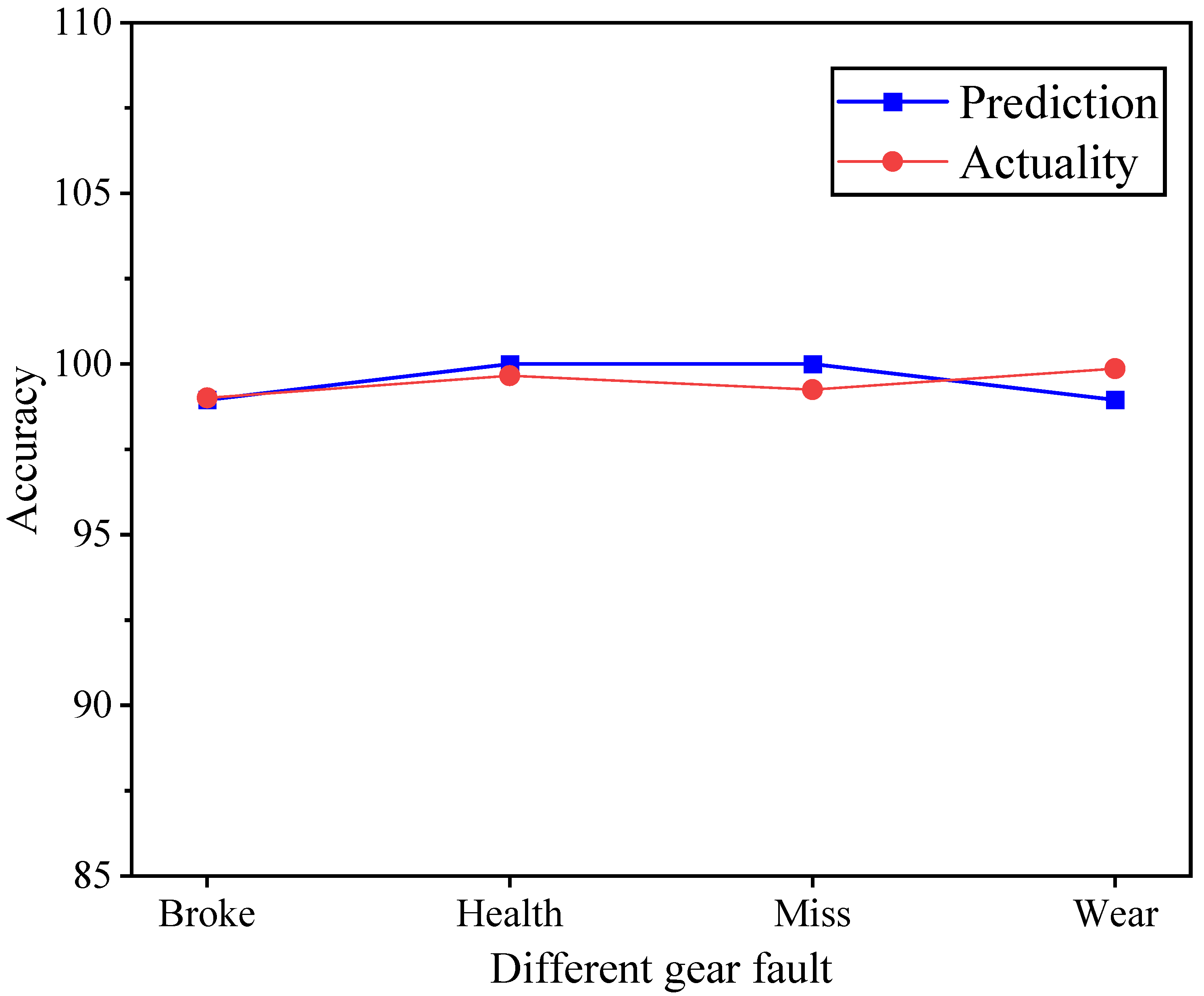
6.2.1. Fault Prediction Accuracy Experiment
6.2.2. Performance Correlation Prediction Experiment
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vijay, A.; Paulson, N.; Sadeghi, F. A 3D finite element modelling of crystalline anisotropy in rolling contact fatigue. Int. J. Fatigue 2018, 106, 92–102. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, J.; Jiang, J.; Pang, X.; Ge, Z. Application of Improved Fault Detection and Robust Adaptive Algorithm in GNSS/INS Integrated Navigation. Remote Sens. 2025, 17, 804. [Google Scholar] [CrossRef]
- Khorram, A.; Khalooei, M.; Rezghi, M. End-to-End CNN+ LSTM Deep Learning Approach for Bearing Fault Diagnosis. Appl. Intell. 2021, 51, 736–751. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Lei, Y.; Jia, F.; Zhou, X.; Lin, J. Health Monitoring Method of Mechanical Equipment Based on Deep Learning Theory. J. Mech. Eng. 2015, 51, 49–56. [Google Scholar] [CrossRef]
- Grieves, M.; Vickers, J. Digital twin: Mitigating unpredictable, undesirable emergent behavior in complex systems. In Transdisciplinary Perspectives on Complex Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 85–113. [Google Scholar]
- Glaessgen, E.; Stargel, D. The digital twin paradigm for future NASA and US Air Force vehicles. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 20th AIAA/ASME/AHS Adaptive Structures Conference 14th AIAA, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar] [CrossRef]
- Uhlemann, T.H.J.; Lehmann, C.; Steinhilper, R. The digital twin: Realizing the cyber-physical production system for industry 4.0. Procedia CIRP 2017, 61, 335–340. [Google Scholar] [CrossRef]
- Seshadri, B.R.; Krishnamurthy, T. Structural health management of damaged aircraft structures using digital twin concept. In Proceedings of the 25th AIAA/AHS Adaptive Structures Conference 2017, Grapevine, TX, USA, 9–13 January 2017; p. 1675. [Google Scholar]
- Qiu, Y. Digital Twin Health Monitoring System for Human Lumbar Vertebra and Key Technologies. Master’s Thesis, Dalian University of Technology, Dalian, China, 2022. [Google Scholar]
- Moi, T.; Cibicik, A.; Rølvåg, T. Digital twin based condition monitoring of a knuckle boom crane: An experimental study. Eng. Fail. Anal. 2020, 112, 104517. [Google Scholar] [CrossRef]
- Feng, C.; Li, L.; Chen, N.; Wu, Y.; Xue, Z. Design and Development of Numerical Control Machine Tool Operation Monitoring System based on Digital Twin. Tool Technol. 2024, 58, 105–109. [Google Scholar]
- Zhang, W.; Wu, J.; Ruan, K. Based on the number of twin mine hoist pulley structure performance monitoring. Ind. Autom. 2024, 1–8. [Google Scholar] [CrossRef]
- Zou, Y.; Lai, X.; Wang, X.; Guo, Y.; Qiao, J.; Li, G.; Song, X. Integrated Digital Twin Method for Mining Electric Shovels and Its Validation. Mech. Electr. Prod. Dev. Innov. 2021, 34, 20–22. [Google Scholar]
- Conforti, I.; Mileti, I.; Del Prete, Z.; Palermo, E. Measuring Biomechanical Risk in Lifting Load Tasks Through Wearable System and Machine-Learning Approach. Sensors 2020, 20, 1557. [Google Scholar] [CrossRef]
- Chakraborty, S.; Adhikari, S.; Ganguli, R. The role of surrogate models in the development of digital twins of dynamic systems. Appl. Math. Model. 2021, 90, 662–681. [Google Scholar] [CrossRef]
- Liu, W.; Wu, M.; Wan, G.; Xu, M. Digital Twin of Space Environment: Development, Challenges, Applications, and Future Outlook. Remote Sens. 2024, 16, 3023. [Google Scholar] [CrossRef]
- Karve, P.M.; Guo, Y.; Kapusuzoglu, B.; Mahadevan, S.; Haile, M.A. Digital twin approach for damage-tolerant mission planning under uncertainty. Eng. Fract. Mech. 2020, 225, 106–766. [Google Scholar] [CrossRef]
- Lai, X.; Wang, S.; Guo, Z.; Zhang, C.; Sun, W.; Song, X. Designing a Shape–Performance Integrated Digital Twin Based on Multiple Models and Dynamic Data: A Boom Crane Example. J. Mech. Des. 2021, 143, 071–703. [Google Scholar] [CrossRef]
- Yang, C.; Wu, Z.; Peng, T.; Zhu, H.; Yang, C. A Fractional Steepest Ascent Morlet Wavelet Transform-based Transient Fault Diagnosis Method for Traction Drive Control System. IEEE Trans. Transp. Electrif. 2020, 7, 147–160. [Google Scholar] [CrossRef]
- Huang, J.; Qu, H.; Li, X. Classification of Power Quality Mixed Disturbances Based on Short-Time Fourier Transform and Spectral Kurtosis. Power Syst. Technol. 2016, 40, 3184–3191. [Google Scholar]
- Zhao, M.; Zhong, S.; Fu, X.; Tang, B.; Pecht, M. Deep residual shrinkage networks for fault diagnosis. IEEE Trans. Ind. Inform. 2019, 16, 4681–4690. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef] [PubMed]













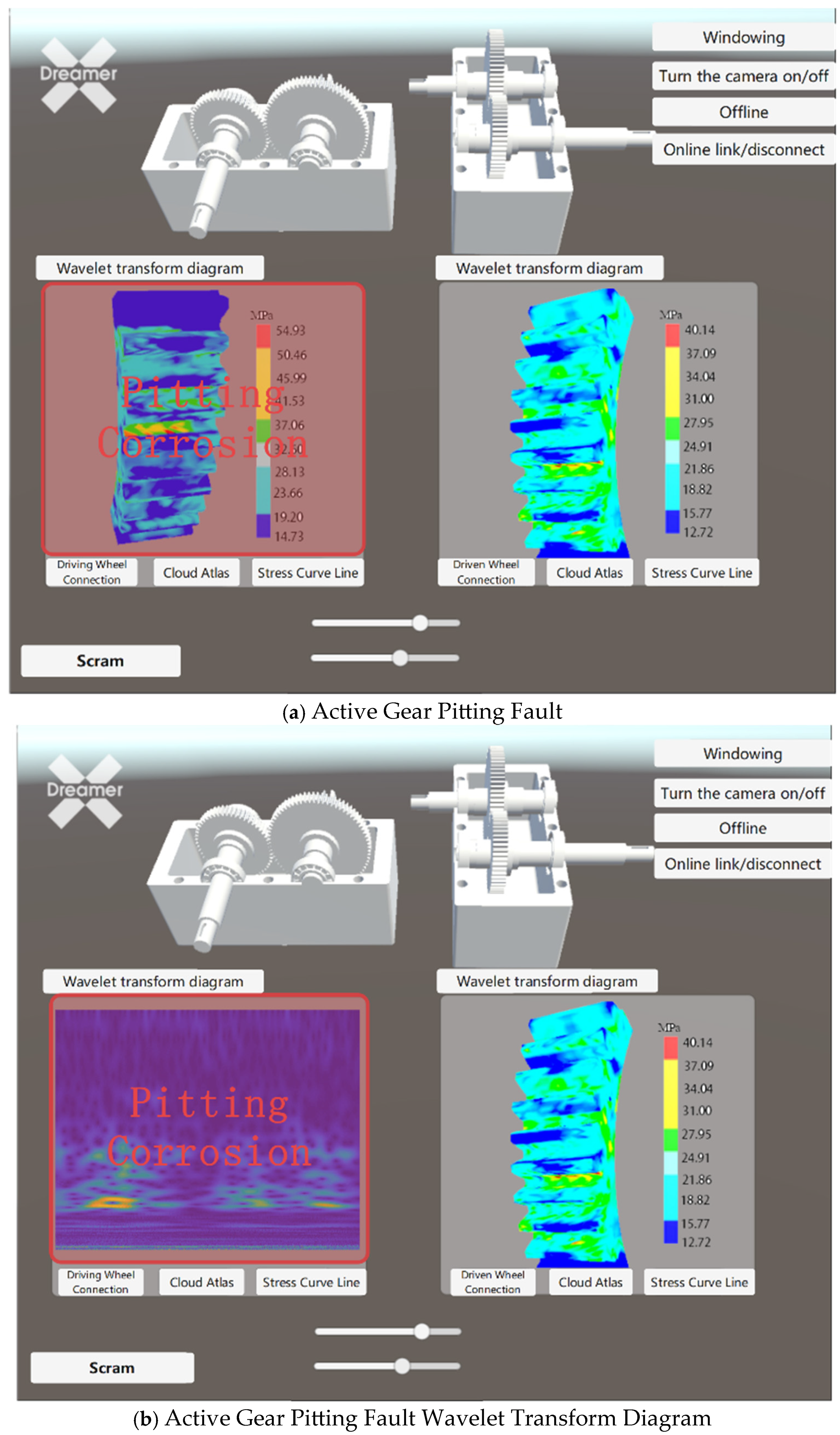

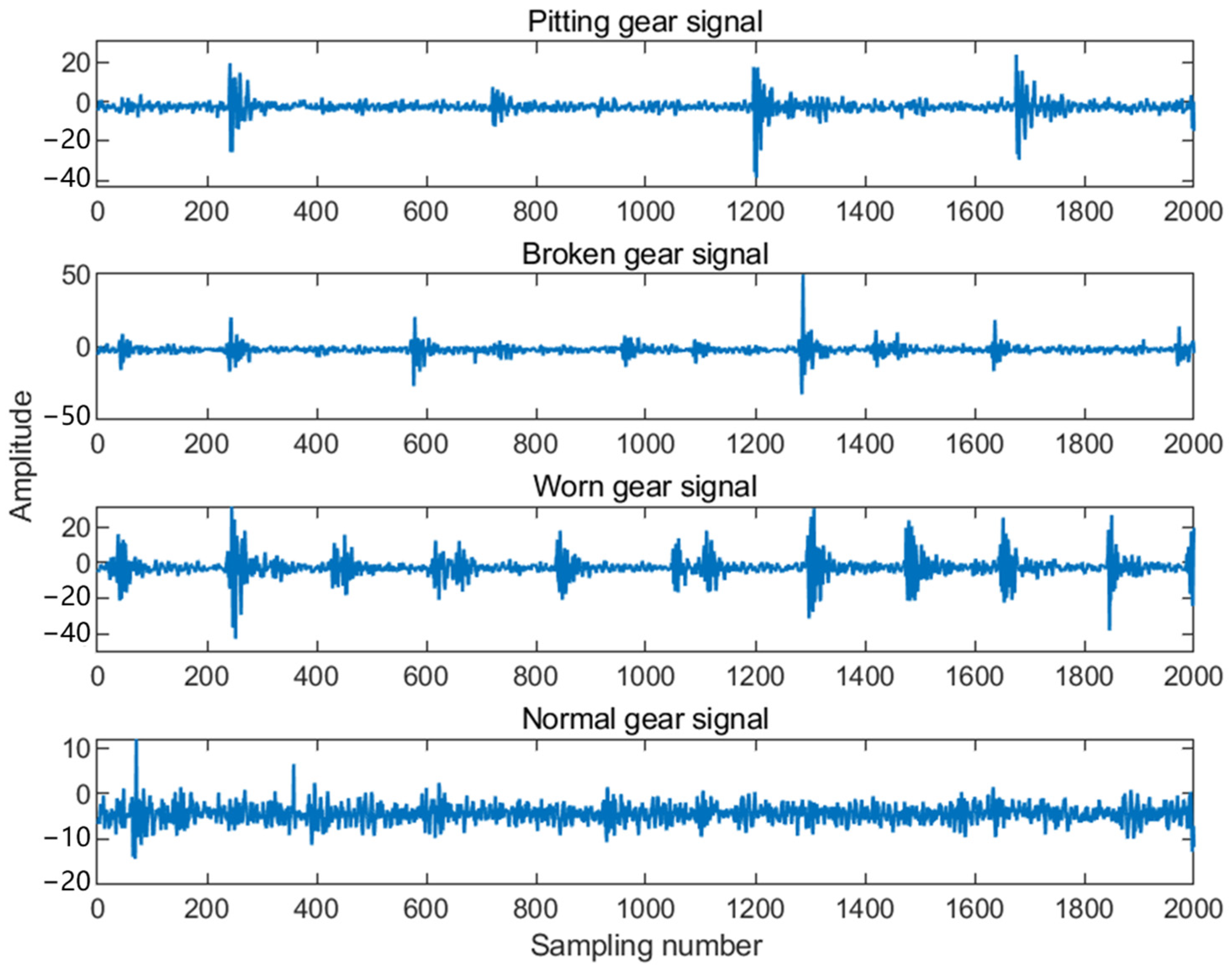


| Component | Number of Meshes |
|---|---|
| Lubricating Oil | 185,900 |
| Driving Gear | 67,100 |
| Driven Gear | 97,500 |
| Hardware | Specifications | Parameters |
|---|---|---|
| Three-Phase AC Frequency Converter Motor | Voltage: 220 V, Frequency: 50/60 Hz | Power: 0.55 kW, Maximum Speed: 1450 rpm |
| Magnetic Powder Clutch and Brake | — | Maximum Torque: 5 N·m |
| Gearbox | Oil-Immersed, Two N205 Rolling Bearings, Two S45C Gears | Large Gear: Module 2, Number of Teeth 75 Small Gear: Module 2, Number of Teeth 55 |
| Full-Steel Anti-Vibration Base | Adjustable Pivot Position with ±2° Angular Adjustment Range | — |
| Normal Gear | Broken Tooth Gear | Worn Gear | Pitting Gear | Average Value | |
|---|---|---|---|---|---|
| Driving wheel stress R2 | 0.9341 | 0.9217 | 0.9434 | 0.9273 | 0.9355 |
| Driven wheel stress R2 | 0.9469 | 0.9521 | 0.9634 | 0.9546 | 0.9479 |
| Structural Layers | Layer Parameters | |||
|---|---|---|---|---|
| Convolution Kernels | Number | Stride | Output | |
| Conv1 | 3 × 3 × 3 | 64 | 1 | (64,H,W) |
| Conv2 | 64 × 3 × 3 | 64 | 1 | (64,H,W) |
| Conv3 | 64 × 3 × 3 | 128 | 2 | (128,H/2,W/2) |
| Conv4 | 128 × 3 × 3 | 256 | 2 | (256,H/4,W/4) |
| Conv5 | 256 × 3 × 3 | 512 | 2 | (512,H/8,W/8) |
| GAP | — | — | — | (512,1,1) |
| Flatten | — | — | — | 512 |
| FC | — | — | — | 512 |
| Type | Description |
|---|---|
| Health | Normal gear |
| Miss | Gear broken teeth missing teeth |
| Wear | Gear wear |
| Broke | Gear pitting |
| Different Models | Recognition Accuracy/% | Accuracy Rate/% | Recall Rate/% | F1 Value/% | Loss Rate |
|---|---|---|---|---|---|
| ResNet | 92.06 | 93.27 | 92.06 | 92.18 | 1 × 10−4 |
| DenseNet | 96.22 | 96.60 | 96.27 | 96.21 | 1 × 10−4 |
| ConvNeXt | 97.53 | 97.40 | 97.22 | 97.23 | 1 × 10−5 |
| Proposed model | 99.45 | 99.49 | 99.48 | 99.48 | 1 × 10−5 |
| Normal Gear | Tooth Breakage Gear | Worn Gear | Pitting Gear | Average Value | |
|---|---|---|---|---|---|
| R2 of the driving wheel stress | 0.9452 | 0.9167 | 0.9413 | 0.9323 | 0.9339 |
| R2 of the driven wheel stress | 0.9557 | 0.9645 | 0.9373 | 0.9412 | 0.9497 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Wu, Z.; An, B.; Sun, R.; Cui, Y. Digital Twin-Based Technical Research on Comprehensive Gear Fault Diagnosis and Structural Performance Evaluation. Sensors 2025, 25, 2775. https://doi.org/10.3390/s25092775
Zhang Q, Wu Z, An B, Sun R, Cui Y. Digital Twin-Based Technical Research on Comprehensive Gear Fault Diagnosis and Structural Performance Evaluation. Sensors. 2025; 25(9):2775. https://doi.org/10.3390/s25092775
Chicago/Turabian StyleZhang, Qiang, Zhe Wu, Boshuo An, Ruitian Sun, and Yanping Cui. 2025. "Digital Twin-Based Technical Research on Comprehensive Gear Fault Diagnosis and Structural Performance Evaluation" Sensors 25, no. 9: 2775. https://doi.org/10.3390/s25092775
APA StyleZhang, Q., Wu, Z., An, B., Sun, R., & Cui, Y. (2025). Digital Twin-Based Technical Research on Comprehensive Gear Fault Diagnosis and Structural Performance Evaluation. Sensors, 25(9), 2775. https://doi.org/10.3390/s25092775





