A Pharmacodynamic Study of Aminoglycosides against Pathogenic E. coli through Monte Carlo Simulation
Abstract
:1. Introduction
2. Results
2.1. MIC and MBC
2.2. Time–Kill Curves against E. coli
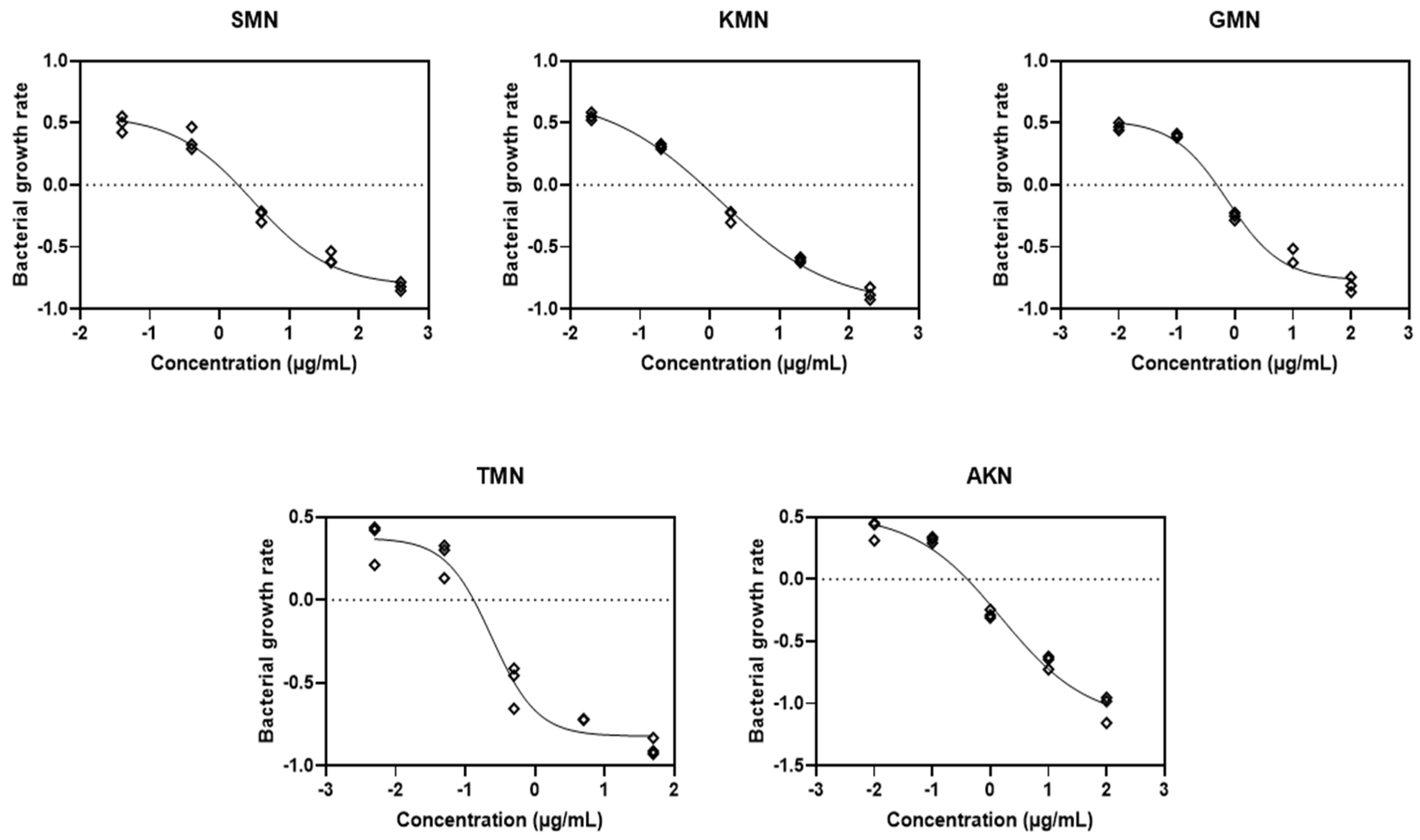
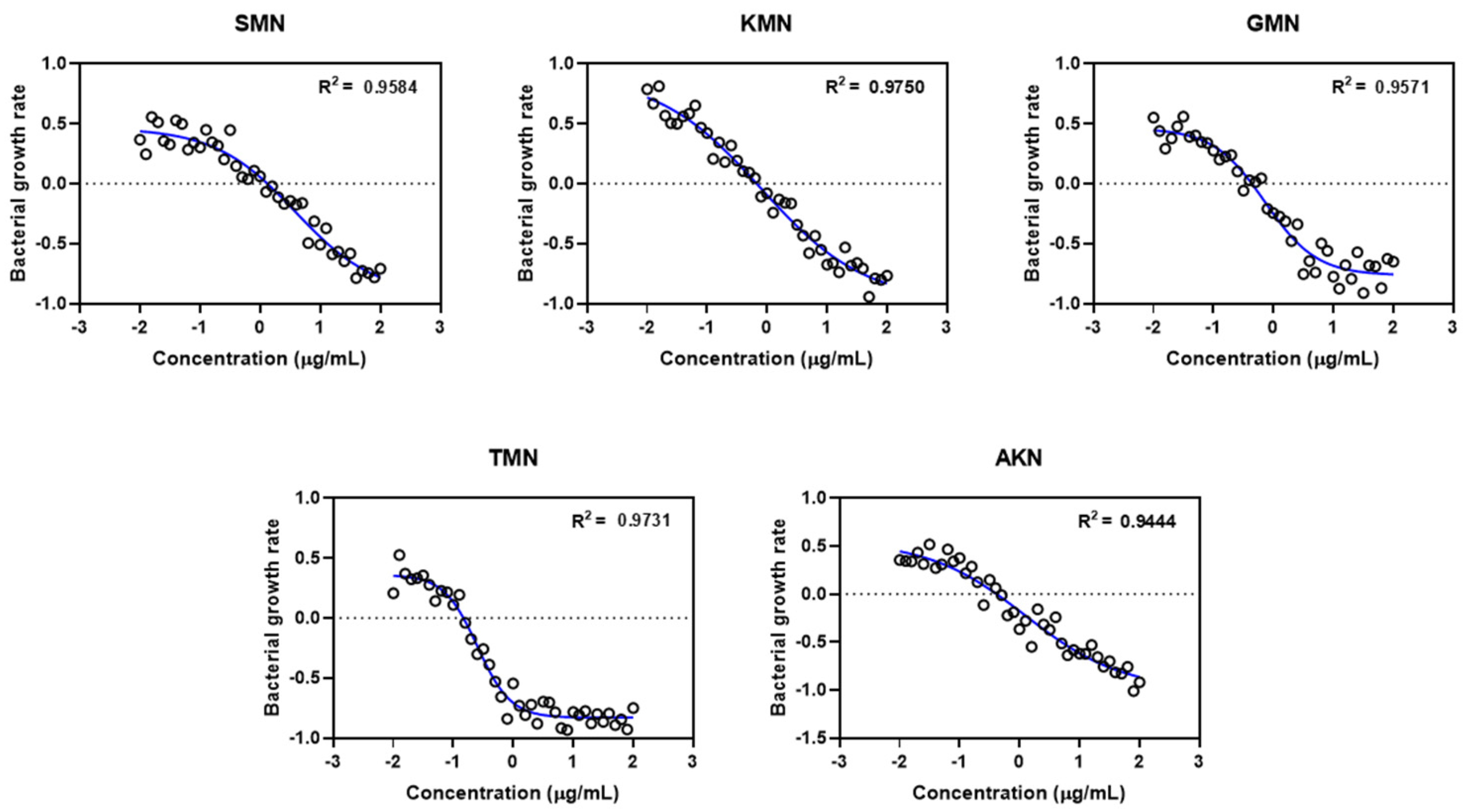
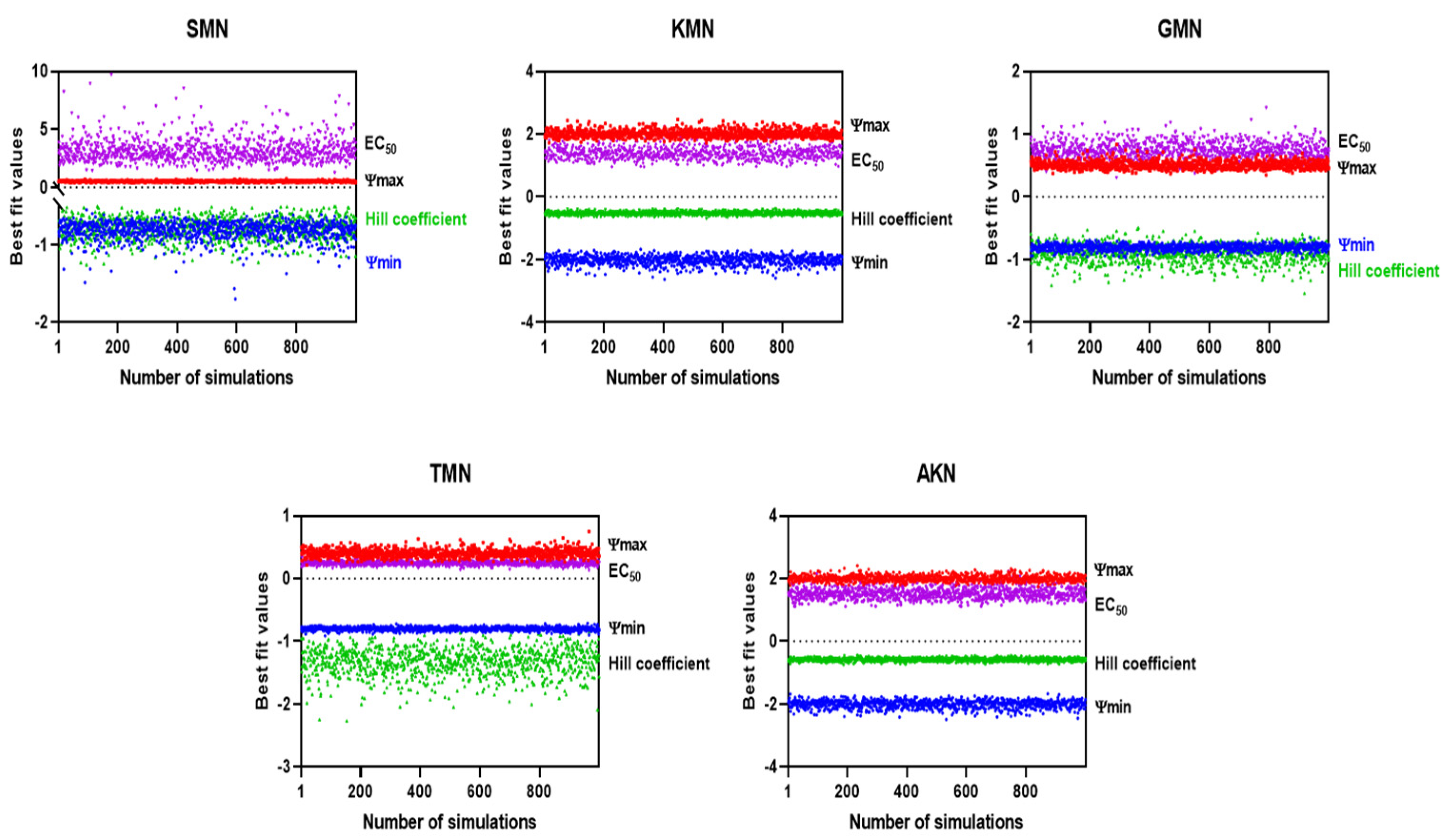
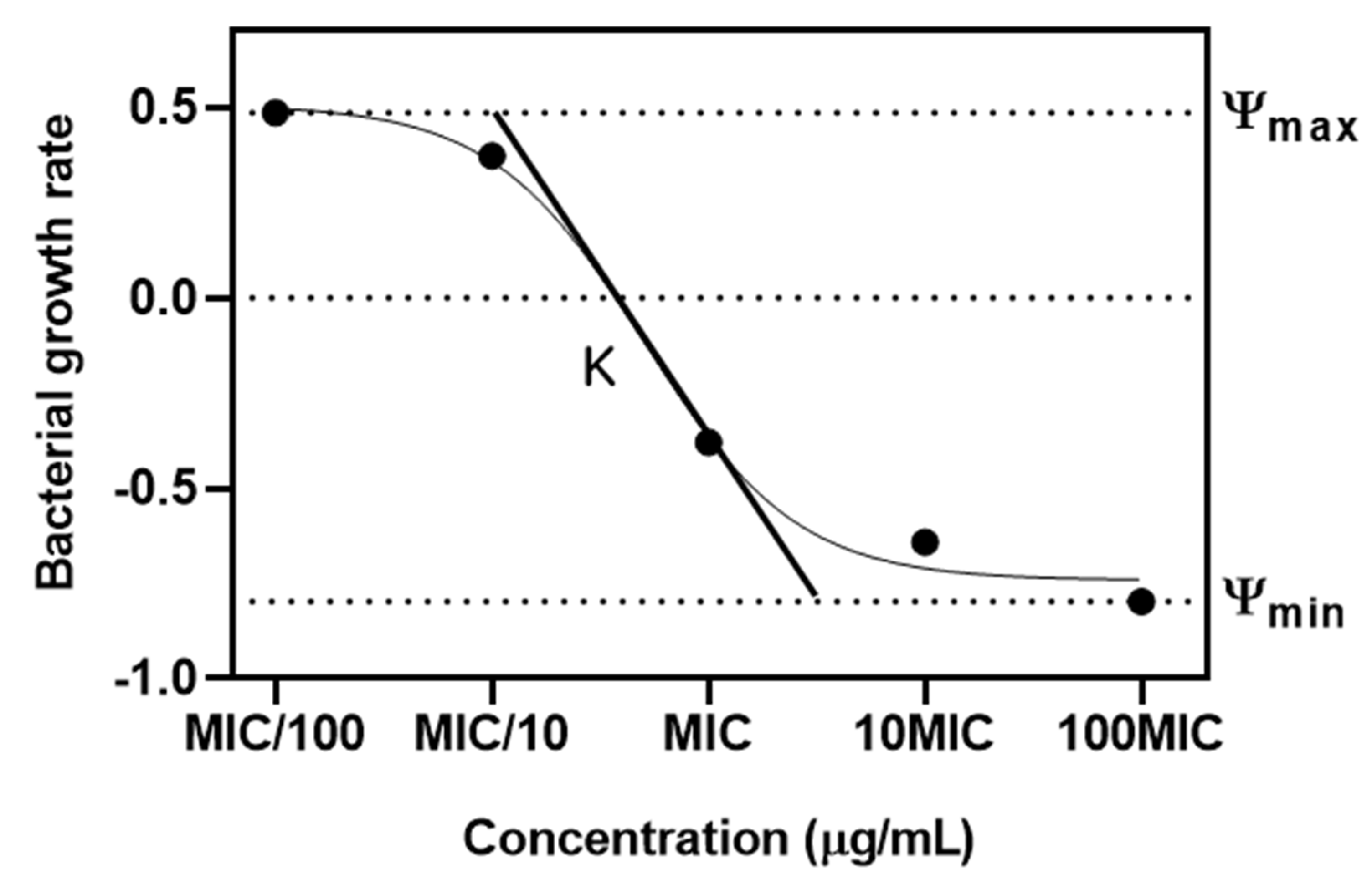
2.3. PD Modeling through Simulation
3. Discussion
4. Materials and Methods
4.1. Chemicals and Reagents
4.2. Bacteria Culture
4.3. Minimum Inhibitory Concentration (MIC) and Minimum Bactericidal Concentration (MBC) of Antibiotics against E. coli
4.4. Time–Kill Curves of Antibiotics against E. coli
4.5. PD Modeling
4.6. Monte Carlo Simulation
4.7. Statistical Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- French, G. The continuing crisis in antibiotic resistance. Int. J. Antimicrob. Agents 2010, 36, S3–S7. [Google Scholar] [CrossRef] [PubMed]
- Poirel, L.; Madec, J.-Y.; Lupo, A.; Schink, A.-K.; Kieffer, N.; Nordmann, P.; Schwarz, S. Antimicrobial Resistance in Escherichia coli. Microbiol. Spectr. 2018, 6. [Google Scholar] [CrossRef] [PubMed]
- Goverment of Canada. Responsible Use of Medically Important Antimicrobials in Animals; Goverment of Canada: Ottawa, ON, Canada, 2018.
- Thibaut, A.; Schiff, N.; Giacino, J.; Laureys, S.; Gosseries, O. Therapeutic interventions in patients with prolonged disorders of consciousness. Lancet Neurol. 2019, 18, 600–614. [Google Scholar] [CrossRef] [PubMed]
- Krause, K.M.; Serio, A.W.; Kane, T.R.; Connolly, L.E. Aminoglycosides: An overview. Cold Spring Harb. Perspect. Med. 2016, 6, a027029. [Google Scholar] [CrossRef]
- Davis, B.D. Mechanism of bactericidal action of aminoglycosides. Microbiol. Rev. 1987, 51, 341–350. [Google Scholar] [CrossRef] [PubMed]
- Serio, A.W.; Magalhães, M.L.; Blanchard, J.S.; Connolly, L.E. Aminoglycosides: Mechanisms of action and resistance. In Antimicrobial Drug Resistance; Springer: Cham, Switzerland, 2017; Volume 1, pp. 213–229. [Google Scholar]
- Kirst, H.A.; Sides, G.D. New directions for macrolide antibiotics: Pharmacokinetics and clinical efficacy. Antimicrob. Agents Chemother. 1989, 33, 1419–1422. [Google Scholar] [CrossRef]
- Marino, M.; Jamal, Z.; Zito, P.M. Pharmacodynamics; StatPearls Publishing: Treasure Island, FL, USA, 2018. [Google Scholar]
- Rizk, M.L.; Bhavnani, S.M.; Drusano, G.; Dane, A.; Eakin, A.E.; Guina, T.; Jang, S.H.; Tomayko, J.F.; Wang, J.; Zhuang, L.; et al. Considerations for Dose Selection and Clinical Pharmacokinetics/Pharmacodynamics for the Development of Antibacterial Agents. Antimicrob. Agents Chemother. 2019, 63, e02309-18. [Google Scholar] [CrossRef]
- Sun, D.; Mi, K.; Hao, H.; Xie, S.; Chen, D.; Huang, L. Optimal regimens based on PK/PD cutoff evaluation of ceftiofur against Actinobacillus pleuropneumoniae in swine. BMC Vet. Res. 2020, 16, 366. [Google Scholar] [CrossRef]
- Hansson, E.; Ma, G.; Amantea, M.; French, J.; Milligan, P.; Friberg, L.; Karlsson, M. PKPD Modeling of Predictors for Adverse Effects and Overall Survival in Sunitinib-Treated Patients with GIST. CPT Pharmacomet. Syst. Pharmacol. 2013, 2, e85. [Google Scholar] [CrossRef]
- Mathews, A.; Bailie, G.R. Clinical pharmacokinetics, toxicity and cost effectiveness analysis of aminoglycosides and aminoglycoside dosing services. J. Clin. Pharm. Ther. 1987, 12, 273–291. [Google Scholar] [CrossRef]
- Demczar, D.J.; Nafziger, A.N.; Bertino, J.S., Jr. Pharmacokinetics of gentamicin at traditional versus high doses: Implications for once-daily aminoglycoside dosing. Antimicrob. Agents Chemother. 1997, 41, 1115–1119. [Google Scholar] [CrossRef] [PubMed]
- Llor, C.; Bjerrum, L. Antimicrobial resistance: Risk associated with antibiotic overuse and initiatives to reduce the problem. Ther. Adv. Drug Saf. 2014, 5, 229–241. [Google Scholar] [CrossRef] [PubMed]
- Macdougall, J. Analysis of dose–response studies—Emax model. In Dose Finding in Drug Development; Springer: Berlin/Heidelberg, Germany, 2006; pp. 127–145. [Google Scholar]
- Dutta, S.; Matsumoto, Y.; Ebling, W.F. Is it possible to estimate the parameters of the sigmoid Emax model with truncated data typical of clinical studies? J. Pharm. Sci. 1996, 85, 232–239. [Google Scholar] [CrossRef] [PubMed]
- Regoes, R.R.; Wiuff, C.; Zappala, R.M.; Garner, K.N.; Baquero, F.; Levin, B.R. Pharmacodynamic Functions: A Multiparameter Approach to the Design of Antibiotic Treatment Regimens. Antimicrob. Agents Chemother. 2004, 48, 3670–3676. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Melcón, C.; Alonso-Calleja, C.; García-Fernández, C.; Carballo, J.; Capita, R. Minimum Inhibitory Concentration (MIC) and Minimum Bactericidal Concentration (MBC) for Twelve Antimicrobials (Biocides and Antibiotics) in Eight Strains of Listeria monocytogenes. Biology 2021, 11, 46. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, N.; Sevillano, D.; Alou, L.; Cafini, F.; Gimenez, M.-J.; Gomez-Lus, M.-L.; Prieto, J.; Aguilar, L. Influence of the MBC/MIC ratio on the antibacterial activity of vancomycin versus linezolid against methicillin-resistant Staphylococcus aureus isolates in a pharmacodynamic model simulating serum and soft tissue interstitial fluid concentrations reported in diabetic patients. J. Antimicrob. Chemother. 2013, 68, 2291–2295. [Google Scholar] [CrossRef]
- Levison, M.E.; Levison, J.H. Pharmacokinetics and Pharmacodynamics of Antibacterial Agents. Infect. Dis. Clin. N. Am. 2009, 23, 791–815. [Google Scholar] [CrossRef]
- Bouvier D’yvoire, M.J.; Maire, P.H. Dosage Regimens of Antibacterials. Clin. Drug Investig. 1996, 11, 229–239. [Google Scholar] [CrossRef]
- Nyhoegen, C.; Uecker, H. Sequential antibiotic therapy in the laboratory and in the patient. J. R. Soc. Interface 2023, 20, 20220793. [Google Scholar] [CrossRef]
- Greenfield, B.K.; Shaked, S.; Marrs, C.F.; Nelson, P.; Raxter, I.; Xi, C.; McKone, T.E.; Jolliet, O. Modeling the Emergence of Antibiotic Resistance in the Environment: An Analytical Solution for the Minimum Selection Concentration. Antimicrob. Agents Chemother. 2018, 62, e01686-17. [Google Scholar] [CrossRef]
- Turnidge, J. Pharmacodynamics and dosing of aminoglycosides. Infect. Dis. Clin. N. Am. 2003, 17, 503–528. [Google Scholar] [CrossRef] [PubMed]
- Fujimura, A.; Sudoh, T.; Ebihara, A. Time-dependent change in the toxic effects of amikacin on renal functions. Life Sci. 1994, 55, 367–372. [Google Scholar] [CrossRef]
- Bonny, C.; Montandon, P.-E.; Marc-Martin, S.; Stutz, E. Analysis of streptomycin-resistance of Escherichia coli mutants. Biochim. Biophys. Acta (BBA) Gene Struct. Expr. 1991, 1089, 213–219. [Google Scholar] [CrossRef]
- VanCleave, T.T.; Pulsifer, A.R.; Connor, M.G.; Warawa, J.M.; Lawrenz, M.B. Impact of Gentamicin Concentration and Exposure Time on Intracellular Yersinia pestis. Front. Cell. Infect. Microbiol. 2017, 7, 505. [Google Scholar] [CrossRef] [PubMed]
- Foerster, S.; Unemo, M.; Hathaway, L.J.; Low, N.; Althaus, C.L. Time-kill curve analysis and pharmacodynamic modelling for in vitro evaluation of antimicrobials against Neisseria gonorrhoeae. BMC Microbiol. 2016, 16, 216. [Google Scholar] [CrossRef]
- El Shazely, B.; Yu, G.; Johnston, P.R.; Rolff, J. Resistance Evolution Against Antimicrobial Peptides in Staphylococcus aureus Alters Pharmacodynamics Beyond the MIC. Front. Microbiol. 2020, 11, 103. [Google Scholar] [CrossRef]
- Gubenšek, U.; de Laat, M.; Foerster, S.; Boyd, A.; van Dam, A.P. Pharmacodynamics of Ceftriaxone, Ertapenem, Fosfomycin and Gentamicin in Neisseria gonorrhoeae. Antibiotics 2022, 11, 299. [Google Scholar] [CrossRef]
- Foster, A.W.; Clough, S.E.; Aki, Z.; Young, T.R.; Clarke, A.R.; Robinson, N.J. Metalation calculators for E. coli strain JM109 (DE3): Aerobic, anaerobic, and hydrogen peroxide exposed cells cultured in LB media. Metallomics 2022, 14, mfac058. [Google Scholar] [CrossRef]
- CLSI M100; Performance Standards for Antimicrobial Susceptibility Testing, 27th ed. Clinical and Laboratory Standards Institute: Wayne, PA, USA, 2023.
- White, R.L.; Burgess, D.S.; Manduru, M.; A Bosso, J.A. Comparison of three different in vitro methods of detecting synergy: Time-kill, checkerboard, and E test. Antimicrob. Agents Chemother. 1996, 40, 1914–1918. [Google Scholar] [CrossRef]
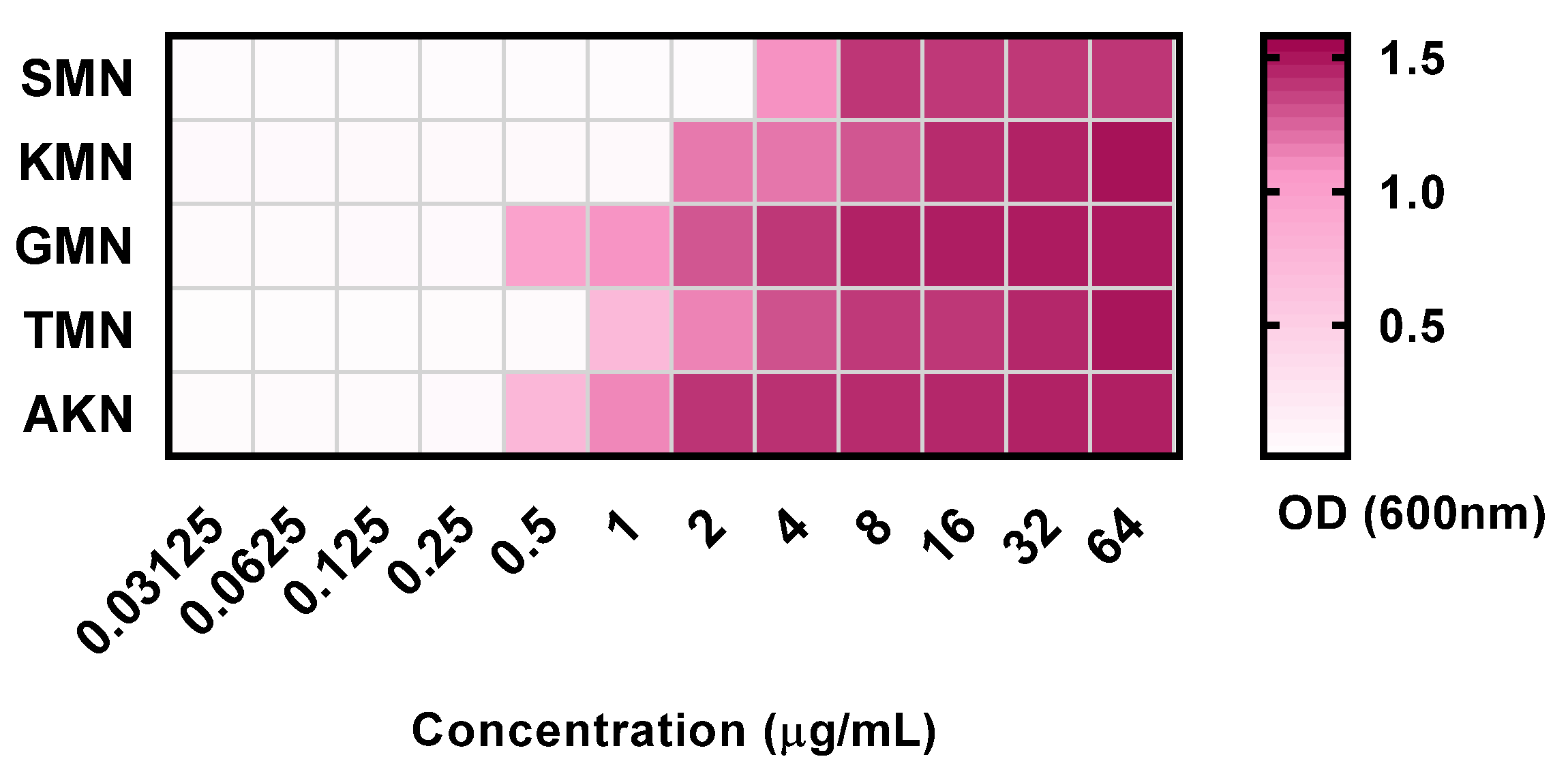
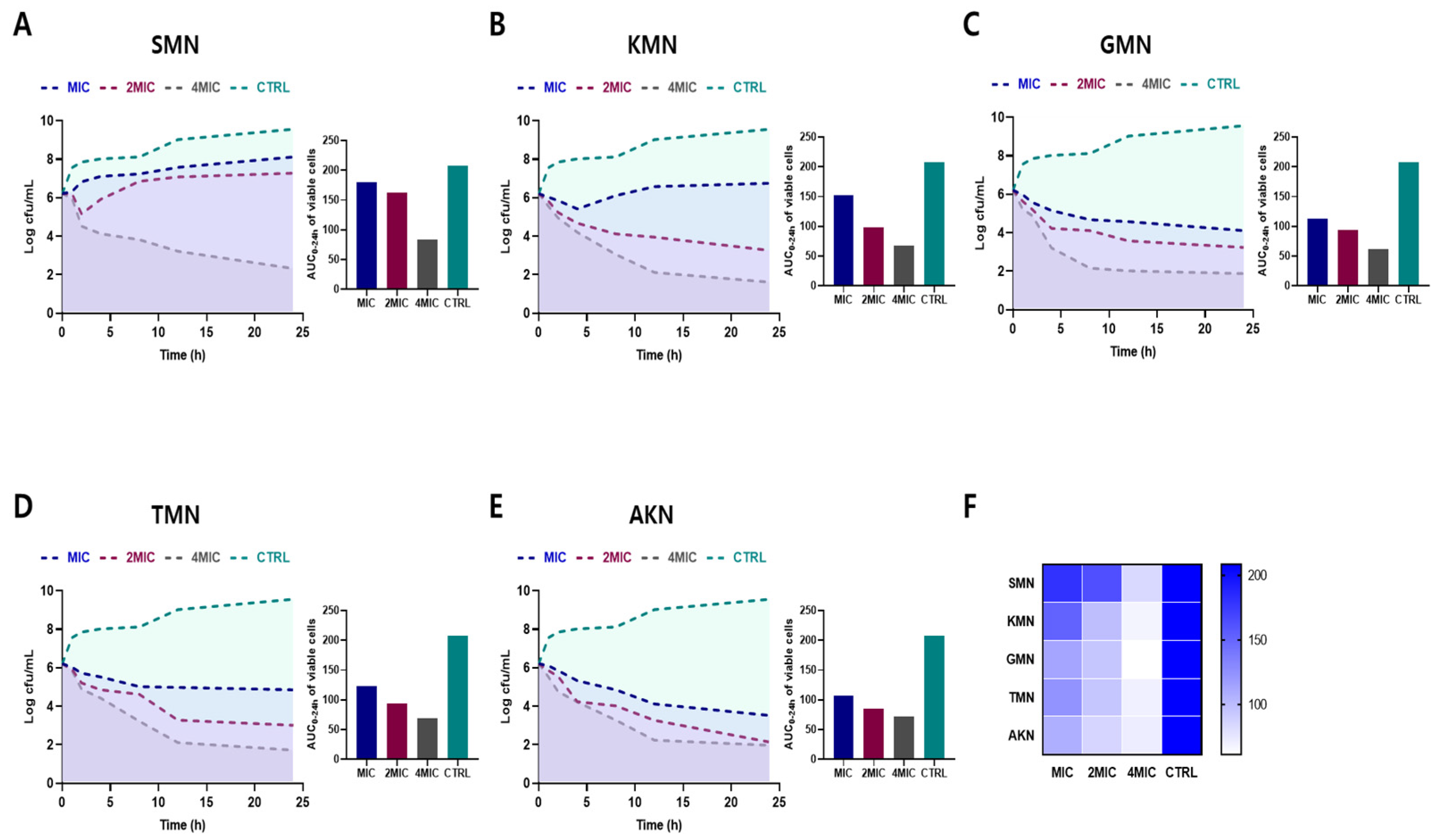
| Antibiotics | MIC | MBC | MBC/MIC |
|---|---|---|---|
| SMN | 2 | 4 | 2 |
| KMN | 1 | 2 | 2 |
| GMN | 0.25 | 1 | 4 |
| TMN | 0.5 | 1 | 2 |
| AKN | 0.25 | 1 | 4 |
| Antibiotics | ψmax (95% CI) | ψmin (95% CI) | Hill Coefficient (95% CI) | EC50 (95% CI) | R2 (95% CI) |
|---|---|---|---|---|---|
| SMN | 0.5651 (0.4419 to 0.7845) | −0.8166 (−1.028 to −0.6976) | −0.7631 (−1.244 to −0.4600) | 2.996 (1.781 to 5.250) | 0.9842 |
| KMN | 0.7290 (0.5889 to 1.022) | −0.9728 (−1.213 to −0.8488) | −0.5324 (−0.7153 to −0.3553) | 1.374 (0.8118 to 2.202) | 0.9938 |
| GMN | 0.5240 (0.4212 to 0.6701) | −0.7685 (−0.9204 to −0.6699) | −0.9266 (−1.694 to −0.5834) | 0.7419 (0.4936 to 1.174) | 0.9854 |
| TMN | 0.3745 (0.2323 to 0.5583) | −0.8218 (−0.9516 to −0.7168) | −1.323 (−2.068 to −0.7063) | 0.2389 (0.1355 to 0.3037) | 0.9682 |
| AKN | 0.5249 (0.3646 to 1.001) | −1.141 (−2.027 to −0.9152) | −0.5799 (−0.9459 to −0.2582) | 1.5290 (0.7134 to 7.856) | 0.9794 |
| ψmax | ψmin | ψmax − ψmin | ψmin/ψmax | Hill Coefficient | zMIC | |
|---|---|---|---|---|---|---|
| SMN | 0.46 ± 0.05 | –0.92 ± 0.13 | 1.38 ± 0.08 | –1.50 ± 0.61 | –0.65 ± 0.12 | 1.22 ± 0.19 |
| KMN | 0.90 ± 0.13 | –0.99 ± 0.12 | 1.89 ± 0.01 | –1.90 ± 0.08 | –0.50 ± 0.09 | 0.89 ± 0.52 |
| GMN | 0.46 ± 0.05 | –0.76 ± 0.04 | 1.22 ± 0.01 | –1.60 ± 0.25 | –1.00 ± 0.16 | 0.21 ± 0.02 |
| TMN | 0.36 ± 0.04 | –0.83 ± 0.02 | 1.19 ± 0.02 | –1.43 ± 1.00 | –1.56 ± 0.20 | 0.32 ± 0.15 |
| AKN | 0.55 ± 0.13 | –0.99 ± 0.15 | 1.54 ± 0.01 | –1.55 ± 0.08 | –0.53 ± 0.14 | 0.13 ± 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, E.-B.; Lee, K. A Pharmacodynamic Study of Aminoglycosides against Pathogenic E. coli through Monte Carlo Simulation. Pharmaceuticals 2024, 17, 27. https://doi.org/10.3390/ph17010027
Lee E-B, Lee K. A Pharmacodynamic Study of Aminoglycosides against Pathogenic E. coli through Monte Carlo Simulation. Pharmaceuticals. 2024; 17(1):27. https://doi.org/10.3390/ph17010027
Chicago/Turabian StyleLee, Eon-Bee, and Kyubae Lee. 2024. "A Pharmacodynamic Study of Aminoglycosides against Pathogenic E. coli through Monte Carlo Simulation" Pharmaceuticals 17, no. 1: 27. https://doi.org/10.3390/ph17010027








